Next Article in Journal / Special Issue
Monoanionic Tin Oligomers Featuring Sn–Sn or Sn–Pb Bonds: Synthesis and Characterization of a Tris(Triheteroarylstannyl)Stannate and -Plumbate
Previous Article in Journal
Olivine-Based Blended Compounds as Positive Electrodes for Lithium Batteries
Previous Article in Special Issue
β,β-Isomer of Open-Wells–Dawson Polyoxometalate Containing a Tetra-Iron(III) Hydroxide Cluster: [{Fe4(H2O)(OH)5}(β,β-Si2W18O66)]9−
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 4
Issue 2
10.3390/inorganics4020018
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

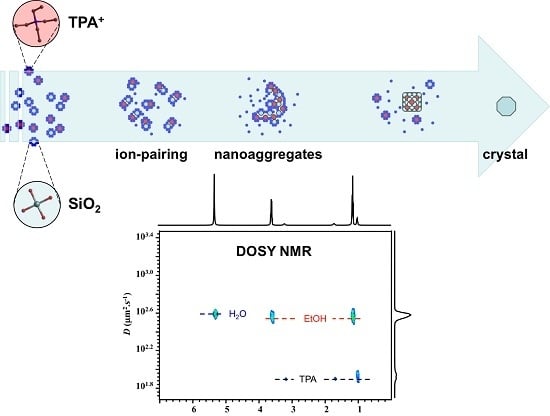
Tetrapropylammonium Occlusion in Nanoaggregates of Precursor of Silicalite-1 Zeolite Studied by 1H and 13C NMR

by
Mohamed Haouas
1,*,
David P. Petry
1,2,
Michael W. Anderson
2 and
Francis Taulelle
1
1
Institut Lavoisier de Versailles, Tectospin, UMR CNRS 8180, Université de Versailles Saint-Quentin-en-Yvelines, 78035 Versailles cedex, France
2
Centre for Nanoporous Materials, School of Chemistry, The University of Manchester, Oxford Road, Manchester M13 9PL, UK
*
Author to whom correspondence should be addressed.
Inorganics 2016, 4(2), 18; https://doi.org/10.3390/inorganics4020018
Submission received: 23 April 2016 / Revised: 18 May 2016 / Accepted: 24 May 2016 / Published: 1 June 2016
(This article belongs to the Special Issue Traversing the Boundaries of Inorganic Chemistry)
Browse Figures
Versions Notes

Abstract

:
The dynamic behavior of tetrapropylammonium (TPA) cations in the clear precursor sols for silicalite synthesis has been investigated by 1H diffusion ordered spectroscopy (DOSY), T1, T2, and T1ρ 1H relaxation, as well as 1H→13C cross polarization (CP) nuclear magnetic resonance. The DOSY NMR experiments showed the presence of strong solute–solvent interactions in concentrated sols, which are decreasing upon dilution. Similarities in dependence of diffusion coefficients with fractional power of the viscosity constant observed for nanoparticles, TPA cations and water led to the conclusion that they aggregate as anisotropic silicate-TPA particles. Relaxation studies as well as 1H→13C CP experiments provide information on dynamic properties of ethanol, water and TPA cations, which are function of silicate aggregates. The general tendency showed that the presence of silicate as oligomers and particles decreases the relaxation times, in particular T2 and T1ρH, as a consequence of involvement of these latter in ion-pairing interactions with water-solvated TPA molecules slowing down their mobility. Furthermore, from the 1H→13C CP dynamics curve profiles a change in the CP transfer regime was observed from fast (TCH << T1ρH) for solutions without silicates to moderate (TCH~T1ρH) when silicates are interacting with the TPA cations that may reflect the occlusion of TPA into flexible silicate hydrate aggregates.

Graphical Abstract

1. Introduction

Silicalite clear precursor sols are generally prepared from tetraethylorthosilicate (TEOS) hydrolysis and consist of a colloidal suspension of nanoparticles in water-ethanol mixture with many coexisting silicate oligomers [1,2,3,4,5,6,7,8]. The nature of the nanoparticles during zeolite formation by heating has been claimed as being an amorphous-like structure [9,10,11]. However, the very early stages of zeolite formation lies in the pre-heating stage, at precursor formation. Since their discovery in the mid 1990s many controversial studies have attempted to derive the exact status of the very early nanoparticles of small size in the range a few nanometers [2,3,12,13,14,15,16,17,18,19,20,21]. The question of whether these nanoparticles contain occluded organic templates or are simply organic-free silica entities has been disputed [9] and a core–shell structure with a negatively charged surface silica core surrounded by a shell of organocations, might seem to be the most accepted description [1,2,10,15,22,23,24,25,26,27,28,29,30]. Alternatively, at precursor formation before any heating, light diffusing nanoparticles have been demonstrated as aggregated oligomeric silicates, and not as dense silica particles [4]. Since oligomeric silicates are present as anionic entities in typical high pH sols, organocations must be ion-paired within nanoaggregates as they are in hydrate silicate crystals [31,32,33]. The knowledge of the location and the role of organocations is key to understanding their structure directing effects. NMR methods have been shown to be a powerful tool for studying structure and dynamics not only for the silicate speciation but also of the organocations. In contrast to many other alternative analysis methods, NMR spectroscopy allows the observation of dispersed particles in their native state without alteration or interference of their surrounding environment. For instance, pulsed-field gradient (PFG) NMR enables self-diffusion measurements [34]. Careful PFG NMR enabling in the pulse sequence to measure accurately diffusion, known under the acronym DOSY NMR, has been proven to be a valuable tool to study diffusion of a variety of molecules, especially chemical objects with different dimensionality [35,36]. Application of 29Si DOSY NMR has been performed successfully on some aqueous silicate solutions for studying silicate speciation and spectral assignment [37,38,39]. Recently, few 1H PFG NMR studies have been conducted in typical precursor sols providing useful insights on dynamic behavior of organocations with respect to silicated nanoparticles [4,27,28,40,41,42]. Although particles are supposed to exhibit solid-state characteristics at a microscopic scale with some softness and flexibility, liquid-state NMR instrumentation enables their measurement in reasonable conditions. In general, theoretical and experimental approaches usually applied for either liquids or solids may be extended to dispersed nanoparticles as well [43,44,45,46,47,48,49]. While a liquid or dissolved component in solution will preserve its full diffusive mobility depending on the overall viscosity, any constituent of the solid structure of the particle will be more or less immobilized within the solid network. Under such circumstances solid-state magnetic resonance methodology can be employed. For example, under magic angle spinning (MAS) conditions, the 1H→29Si CPMAS NMR spectroscopy pioneering works of Burkett and Davis [22,50,51] probed closely the evolution of inorganic-organic interactions during the course of the synthesis. Also, intramolecular cross-polarization experiments between the 1H and 13C nuclei of the template molecule demonstrated that much of the increased efficiency was a result of reduced rotational mobility of the TPA molecule [50,52]. All these studies have been conducted on gel phase precursors and its application on dynamic and inhomogeneous colloidal suspension system would not be necessarily straightforward and must be undertaken to conclude to similar or different behavior.
In the current work we report 1H DOSY NMR studies of water, ethanol and tetrapropylammonium cations present in typical TEOS–TPAOH–H2O system used for silicalite-1 synthesis (Figure 1). The effect of dilution was investigated revealing strong cooperative interactions between solvents, solutes, and nanoparticles. The diffusion coefficients were directly correlated to the viscosity change. Furthermore, 1H T1, T2 and T1ρH relaxation measurements, as well as 1H→13C spin dynamic cross polarization experiments, were carried out in order to shed light on the dynamic behavior and the interactions of the solvated organocations species with the nanoparticles present in the synthesis mixture. Significant effects particularly on T2, measuring rotational diffusion, and T1ρH measuring H–C dipolar fluctuations (rotational, vibrational or distance fluctuations) were monitored with systems containing silicates undergoing restricted dynamic of tetrapropylammonium interacting with nanoparticles. Mobility of species is directly correlated to such parameters [53,54,55,56,57,58]. Temperature changes induce significant modulation of NMR relaxation, and allow following occlusion of tetrapropylammonium cations into nanoparticles. These results are discussed in the general context of zeolite nucleation and crystal growth.

2. Results and Discussion

2.1. 1H NMR DOSY

Diffusion (or self-diffusion) is the motion of particles in solution, known as Brownian molecular motion: translational and rotational. It is directly related to different physical parameters such as the size and shape of the diffusing particle, the temperature, and the viscosity of the solution. It can be characterized by a diffusion tensor D, the trace of it being the diffusion coefficient D. It is a parameter characteristic of the nature and properties of liquids, solutions, and gels [63,64]. Thus it allows access to properties, such as molecular volume and/or weight, mobility and dynamic behavior, and chemical interactions with their environment.
2D DOSY NMR provides spectral edition of different observed species according to their self-diffusion coefficient D. A series of spectra are recorded at different spin echoes with increasing pulsed field gradient strengths, as displayed in the pulse sequence (Figure 2). The gradient pulses are used in order to dephase, during the first evolution period, the magnetization of spins which have diffused to a new location during the period Δ. The pulsed field gradients, during the first half period, label the position of spins with their voxel Larmor frequency, while the second gradient pulses re-phase all nuclear spins except those which have diffused during the time period Δ. Analysis of the resulting resonance decays by inverse Laplace transformation (ILT) allows extraction of each diffusion coefficient. Thus, a DOSY NMR spectrum consists of a correlation between NMR resonances and the diffusion coefficient D of the corresponding NMR detected species. The conventional NMR spectrum is displayed in the direct dimension (f2), while the “diffusion spectrum” with peaks corresponding to the value of the diffusion constant D is displayed in the indirect dimension (f1).
Extraction of diffusion coefficients from DOSY experiments results from the computation of the most probable sum of Gaussian decaying functions taking place between a coding gradient and a decoding one. This is the principle of a stable ILT although this later is an unstable transformation. Such instability can be overcome by performing a Tikhonov regularization and further maximization of entropy (MaxEnt) [65,66]. The diffusion dispersion obtained is a probability histogram of diffusion coefficients. Spectral decomposition has been performed for each spectrum. For each component a vector of areas for each field gradient has been used for ILT transform. A final reconstruction of a 2D spectrum is generated with the spectral component in the direct dimension and its diffusion probability distribution in the indirect dimension.
The 1H NMR spectra of the system 25 TEOS:9 TPAOH:x H2O, where x ranges from 152 to 15,000, exhibit six resonances as expected due to water, ethanol and TPA. For x = 152, the resonances appeared at 5.30 ppm for water, 1.14 and 3.58 ppm for ethanol, and 1.00, 1.70, and 3.19 ppm for TPA molecule. A progressive high field shift was observed for all the resonances with increasing water amount, and the final observed chemical shifts at x = 15,000 were 4.74, 1.07, 3.55, 0.84, 1.59, and 3.05 ppm respectively. As it can be seen clearly, the strength of the effect is different from one species to another. The most affected resonance was the one corresponding to water and the least that of ethanol since on average the observed shifts upon dilution within the studied range of water amount were −0.56 for water, −0.15 ppm for TPA and −0.05 ppm for ethanol. The appreciable dependence of water chemical shift with the molar composition of the system should be directly related to the pH change with dilution. The pH of the studied sols varies from ca. 13.5 to 10.0 when x changes from 152 to 9500 [62]. The moderate changes in TPA chemical shifts could reflect the changes in chemical interaction, in particular with the nanoparticles, with increasing dilution. These interactions have an electrostatic character and decrease with dilution and decreasing pH. However, within the measurement accuracy estimated to be less than 0.02 ppm, no significant change of ethanol chemical shift was observed indicating very small environmental change around this molecule with dilution and so little interaction with the sol components. In order to gain further insight on dynamics and interactions of these three molecules present in the different systems, DOSY experiments were conducted on all these sols. As representative results, the DOSY NMR spectra for x = 152 and 15,000 are depicted in Figure 3. In all cases, one main diffusion behavior for each species was measured as a result of an average diffusion process.
Figure 4 shows the evolution of the diffusion coefficients for H2O, EtOH and TPA upon increase of the water content in the clear precursor sols for silicalite-1 synthesis. Starting with low values for each entity, the diffusion coefficients increase with dilution of the solution. Values for D of water, ethanol and TPA were respectively found to be equal to ca. 390, 370, and 90 μm2·s−1 with the system with the lowest value of x (=152) and reached asymptotic values of ca. 2400, 1300 and 750 μm2·s−1, respectively, at extreme dilution. The limiting values extrapolated to pure water are 2300, 1230, and 820 μm2·s−1 respectively for water [67,68], ethanol [69] and TPA [70]. DLS measurements on the same system exhibited for nanoparticles diffusion coefficients D varying between 16 and 96 μm2·s−1 when x was varied from 152 to 8000 [62].
The observed diffusion coefficients of each chemical entity do correspond to average values for different diffusing species in fast exchange regime on the NMR time scale [27]. The trend of the curves of D as a function of water amount in Figure 4 strengthens this assumption since with increasing dilution the number of interacting species is expected to progressively and continuously diminish, eventually vanishing.
The dependence of observed diffusion coefficients with water content is driven by the change in viscosity of the medium, and gives indications about the different solute–solvent interactions present [71]. For highly concentrated samples with very low values of x, diffusion coefficients of all existing species in solution appeared to be particularly low and those of the solvents, water and ethanol which also can serve as internal reference molecules, were comparable despite the significant difference of their molecular size. Such low values of D for diffusing units, should correspond on average to aggregates of more than one molecule in highly viscous systems, favoring intermolecular interactions. Indeed, viscosity has been found to drop rapidly from ca. 13 to 1 mPa.s when increasing water amount in these sols [62]. In highly viscous systems, translational motion of all observed species would involve cooperative movement of one or more neighboring solvent molecules. Unusually low values of D for water, ethanol and TPA, reflect a slowing down of diffusive motions by strong specific interactions with neighboring solvent molecules. Progressive and similar increase of D for the three molecules, with lowering their concentration and consequently viscosity support this argument. Variation of the diffusion coefficients has therefore to be examined with respect to viscosity.
Figure 5 shows that the logarithm of diffusion coefficients of water, ethanol and TPA decreases linearly with the logarithm of the viscosity of the corresponding clear sol. This means that the diffusion coefficients are dependent on the viscosity of the medium following a relationship of the form [72]:
D ∝ η−α
where 0 ≤ α ≤ 1. This characteristic parameter would be directly related to the strength of interaction of diffusing species with its environment; the higher the value of α the lesser the interaction. Indeed, it has been found that α tends to 1 when the solute/solvent size ratio is greater than 5, and to 0 in extremely highly viscosity media [73]. Furthermore, α has been found to equal to 1 for water in hydrophobic media [71].
Values of α for water, ethanol and TPA obtained from linear least-square fits of the curves in Figure 5 were respectively 0.70 ± 0.03, 0.50 ± 0.03, and 0.77 ± 0.05. The curve lnD = f(lnη) for nanoparticles is also displayed in Figure 5 and it has been found to be parallel to TPA curve and to a lesser extent to water curve with a slope α of 0.75 ± 0.03.
Similarities between α values of nanoaggregates and those of TPA and water indicate roughly the same types of interactions experienced by those species in the different sols studied within the large range of concentration with respect to water. Indeed, water as a strong polar solvent, as well as TPA cation as charge compensating species, both interact strongly with the silicates oligomeric anions in solution, but also within the nanoaggregates. However, ethanol interferes to a much lesser extent with silicates [27].
Each species exhibits a single set of resonances, and is not split in the indirect diffusion dimension. This indicates a fast exchange of species in their different possible locations outside or inside nanoaggregates. Additionally, water, TPA and nanoaggregates exhibit the same viscosity dependency pointing to a single exchanging system. Ethanol has a somehow different behavior with a progressive change from strong association to water at low concentration of water, exhibiting a common diffusion coefficient, to weak association at high dilution with their normal size separation.

2.2. Longitudinal and Transverse 1H NMR Relaxations

Characteristics of samples studied here are presented in Table 1. Such samples are representative of (i) typical sol precursors for silicalite, either in concentrated (S) or dilute system (SD); (ii) systems without silica (S0) and (SD0); and (iii) thermal treated system (SH).
1H NMR spectra of these sols/solutions exhibited, as expected, the six resonances of species present: water (singlet at ~4.6 ppm), ethanol (narrow triplet at ~0.8 ppm and narrow quadruplet at ~3.3 ppm), and TPA species (broad triplet at ~0.6 ppm and unresolved multiplets at ~1.3, and 2.8 ppm). T1 and T2 values were obtained by fitting with an exponential evolution of magnetization as a function of the relaxation delay (see Figures S1 and S2 in Supplementary Materials). All results are summarized in Table 2. As a general trend, diluted samples showed longer T1 relaxation times than other samples. Resonance measured for H2O in the samples without silicates cannot be fitted adequately with a single exponential function.
Under the experimental conditions of our samples, the most effective relaxation mechanism for TPA and ethanol protons would be dominated by intramolecular homonuclear dipole–dipole interaction. Under such circumstances, relaxation rates can be given by the following equations:
R1 = 1/T1 ∝ r−6(3/2)[J1(ω0) + J2(2ω0)]
R2 = 1/T2 ∝ r−6[(3/8)J0(0) + (15/4)J1(ω0) + (3/8)J2(2ω0)]
where r corresponds to dipole-dipole distance, and spectral densities for random isotropic rotation are: Jq(ω0) = Cq [τc/(1 + ω0τc)] for q = 0, 1, and 2, (C0 = 24/15, C0 = 4/15, C0 = 16/15). ω0 is the Larmor frequency and τc the rotational correlation time. Information on mobility and dynamic behavior can be readily obtained from an analysis of relaxation rates.
Unlike T1 relaxation times, T2 were found to be much more sensitive to chemical changes of sample (S) by removing silicates, diluting, or heating. Values for T1 of a given resonance remained substantially within the same order of magnitude whatever the sample. However, T2 values were 2–3 times larger upon dilution, and from 2 to 8 times shorter upon heating for all resonances. Additionally, values of T2 were 2 to 4 times larger in samples containing silicates compared to similar samples without silicates for TPA and water resonances. From such observations, it appears clearly that water molecules and TPA cations are involved in mutual interactions with silicates species, and little or no interaction with ethanol. Fluctuation strength of such interactions would directly affect relaxation rates of NMR observables. This is true in both concentrated and diluted systems (see comparison between S and S0, and on the other hand between SD and SD0). Furthermore, dilution reduces both intermolecular solute–solute and solute–solvent interactions, especially the strong ions pairing and thus the electrostatic interaction. The most affected T2 were those of TPA and water resonances and the least affected those of ethanol resonances when comparing samples S and SD. The situation was reversed comparing samples without silicates, i.e., S0 and SD0 are those where the most affected T2 are ethanol resonances and the least affected those of TPA and water resonances indicating a dominating interaction of the latter taking place with silicates. These results strengthen the idea of involvement of clathrate hydrate interaction-type in presence of silicate species [74].
Because T2 measures rotational diffusion with a period of rotation τc (see Equation (3)), insights about molecular motions and dynamic behaviors of probed species can be deduced. For instance, a decrease of T2 values in system containing silica indicates restricted mobility caused by ion-pairing formation and/or occlusion into aggregates. Consistently, dilution leads to increased values of T2 by diminishing ion-pairing effect and aggregation phenomena. Furthermore, the presence of dispersed nanocrystals in heated sample (SH) would lead to slower diffusion of species and in turn explain a drop of T2 for all resonances.

2.3. Proton Spin-Lattice Relaxation in the Rotating Frame

S, S0, SD, SD0, and SH samples were subjected to proton relaxation in the rotating frame T1ρH study. Results are displayed in Figure 6 and presented in Table 3. The heated sample (SH) has the shortest T1ρH, and samples containing no silicates (S0 and SD0) have larger values than the corresponding samples with silicates (S and SD, respectively). The expression of T1ρH is given in Equation (4) to compare to T2 (Equation (3)) for the same relaxation process:
R1ρH = 1/T1ρH ∝ r−6[(3/8)J0(ω1) + (15/4)J1(ω1) + (3/8)J2(2ω1)],
where ω1 stands for effective radiofrequency field. As T1ρH and T2 are closely comparable the spectral density components seem to be comparable for largely different values between the Larmor and the radio-frequency. This implies that motional behaviors of all observed species have liquid-state-like characteristics (ω1τc << 1 and ω0τc << 1).
At first sight, trends observed with T2 (Table 2) are almost identical to those obtained with T1ρH (Table 3). However, some effects are more accentuated on the T1ρH values by comparison to those on T2. For instance, the effect of presence of silicates on the relaxation rates of TPA resonances is more important since their T1ρH in samples containing silicates was measured to be 4–5 times lower than in samples without silicates. On the other hand, heating which led to increasing the relaxation rates for all resonances, was found to impact less T1ρH values than T2. In particular, almost no change was noticed on T1ρH for water resonance before and after heating.
Relatively low values of T1ρH for TPA resonances are observed in S and SH samples, suggesting restricted motion in sols. Progressive decrease of T1ρH values for proton resonances when changing position from the end-(CH3), to middle-(CH2), and then to beginning of the chain (CH2N) groups confirms that molecular motion predominates the mechanism of T1ρH for this species. Mobility increased progressively when going through the arms of the molecule from the ammonium center to the methyl position. When comparing with diluted sample SD, T1ρH increased significantly (twice) indicating higher mobility of organocations resulting from lowering viscosity. Nevertheless, since dilution did not alter significantly the T1ρH in samples without silicates (S0 and SD0) changes observed in Si containing samples (S and SD) should then mostly be due to interaction with silica.
The situation is different for ethanol. As already observed previously with T2, no significant change in T1ρH values of resonances for this species upon either dilution or addition/removal of silicates species was noticed and the values ranged from 2 to 4 s approximately. This indicates that ethanol, in contrast to TPA, is less affected by intermolecular interaction and so interferes less with the system chemically. It does not seem to play a significant role in these sols apart from as a co-solvent. The decrease of T1ρH in heated samples is therefore related to the presence of nanocrystals. The latter leads to a reduction of molecular diffusion in solution lowering mobility of solutes, as well as solvents.
The relaxation behavior of water appeared closely similar to TPA. Samples containing dissolved silicates always showed lowest values of T1ρH and dilution led to an increase of T1ρH. As for TPA species, the low values of T1ρH could be interpreted as a consequence of a reduction of the mobility of water and higher values of T1ρH as due to increased water mobility. Since only a fraction of water molecules are involved in interaction with the solutes/nanoparticles, the observed phenomena are an average process. Involvement of water molecules in strong hydrogen bond networks interacting directly with silicates [31,32,33,74] induces a reduced mobility of water in silicate sols.
Such results combined to T2 relaxation, point to direct interaction of organocations with silicate species, as ion-pairs, reducing considerably their mobility. Water is also affected by restricted mobility, as being involved in strong hydrogen network surrounding the ion-pairs. In contrast, ethanol appears mostly as spectator component.

2.4. Proton to Carbon Cross-Polarization

1H→13C cross polarization spectra were successfully recorded for all samples providing the five expected resonances at 17.1 and 56.9 ppm due to EtOH and at 10.0, 14.8, and 59.8 ppm corresponding to TPA cation. Even in the absence of silica, ethanol and TPA resonances were obtained with this method. Magnetization transfer occurs through dipolar interaction between 13C and 1H of C–H bonds [75]. The successive NMR spectra of the 1H→13C cross polarization experiment as a function of contact time, for the reference sample (S), are displayed in Figure 7. The contact time dependencies of the resonance intensity in the 1H→13C CP experiments for all samples are depicted in Figure 8. The TPA resonance in the heated sample has faster intensity decay than the reference and diluted samples, whereas for ethanol no major differences appear. This is consistent with shorter T1ρH values of TPA resonances in the heated sample compared to the other samples and no variation in T1ρH values for ethanol resonances, as already noticed previously.
The CP transfer of magnetization between the abundant 1H and rare 13C spins can be described by the simplified thermodynamic model when the average residual 1H–1H homonuclear dipolar interaction is larger than the 1H–13C heteronuclear dipolar interaction. Assuming that relaxation can be neglected for 13C spins, the NMR resonance of these spins as a function of contact time t, can verify the relationship [76]:
I(t) = (I0C/(1 − (TCH/T1ρH)))·(exp(−t/T1ρH) − exp(−t/TCH)),
where I0C is the maximum magnetization of C; 1/TCH is the CP rate. This later is characteristic to a heteronuclear dipole–dipole interaction being inversely proportional to the internuclear distance. Since CP efficiency can be assigned to direct C–H bonds of the corresponding C site, Equation (5) was fitted using T1ρH values measured independently (Table 3). The results of fitting curves of ethanol and TPA 13C resonances in the CP experiments on different samples are presented in Figure 8 and Table 4.
In all cases, we observed smaller TCH for ethanol than for TPA meaning that CP efficiency was better for ethanol than TPA. No significant effect on TCH was observed for either ethanol or TPA upon dilution in non-silicate containing samples. However, samples containing silicate species showed larger TCH for TPA resonances and also for ethanol resonances but to a lesser extent. Characteristic times TCH and T1ρH are shown in Table 4 and Table 3, respectively. The usual condition of CP regime, TCH << T1ρH is met in any case here. If for ethanol resonances TCH was always two magnitude orders smaller than T1ρH, in the case of TPA resonances TCH was only one order of magnitude smaller than T1ρH in absence of silicates, and becomes in the same order of magnitude when silicates were present in solution. In fact, the presence of silicates made the relaxation times for TPA T1ρH decreased and TCH increased reducing therefore their relative difference. The increase of TCH reflects the decrease of the residual dipolar coupling, while the decrease of T1ρH indicates the increase of homonuclear dipolar interaction compared to radiofrequency strength ω1. The change in the CP regime in presence of silicate particles from fast transfer, characteristic of isolated pair of spins C–H, to moderate transfer is consistent with strong ion-pairing formation between TPA and silicates within aggregated particles. Occlusion of TPA into hydrated silicate particles leads, not only to restricted mobility, but also to close contact with immobilized hydrogen network with clathrate like structure that could act as spin bath.
In summary, the present NMR data demonstrate that TPA cations, water and silicate anions are all involved in a mutual attractive interactions in the early stages of the colloidal silicalite precursor formation. Solvated ion-pairing complexes constitute the first components of the primary flexible and dynamic particles produced through aggregation processes. Common viscosity dependency of diffusion rates for water and TPA, as measured by DOSY, as well as silica nanoaggregates from previous DLS data [62], strongly suggests a single interacting system. The significant decrease of T1ρH of TPA end-group methyl protons under the effect of heating (Table 3) is consistent with restricted mobility that increases the homonuclear dipolar interaction. A schematic representation of the progressive occlusion of the organocations into the silicalite particles is depicted in Figure 9. The crystallization course upon heating would imply progressive desolvatation, continuous condensation, and internal structuration inside the primary particles that should affect the mobility and dynamics of all species in the overall system along the different processes.

3. Materials and Methods

3.1. Materials

Tetraethyl orthosilicate (TEOS, 98%) was purchased from Acros Organic. Tetrapropylammonium hydroxide (TPAOH, 40% w/w) was obtained from Alfa Aesar. Deuterium oxide (D2O, 99.9% D) was supplied by Cortecnet. Ethanol (EtOH, >99.5%) was received from Carlo Erba. All these compounds were used as received. Water was distilled twice before use.

3.2. 1H DOSY NMR

For the 1H DOSY experiments, a series of samples with the molar composition 25 TEOS:9 TPAOH:x H2O (x = 152, 400, 900, 1400, 1900, 4000, 6000, 8000, 9500 and 15,000) have been prepared mixing TEOS with aqueous TPAOH solution and the corresponding amount of water. First TEOS was hydrolyzed in 40 wt % TPAOH aqueous solution at ambient conditions under vigorous magnetic stirring for approximately 1 h. Appropriate amounts of water were then added subsequently when it was necessary. The compositions were chosen to be in the range of those used in silica precursor particle studies [14,25,61] and silicalite-1 growth experiments [59]. All samples were allowed to equilibrate for a minimum of three days before NMR measurement.
The diffusion 1H NMR experiments were carried out at on a Bruker AMX 400 spectrometer (Bruker, Karlsruhe, Germany) operating at 9.4 T and resonating frequency of 400.13 MHz. A BBI Bruker 5-mm probe equipped with a z gradient coil up to 53 G/cm was used for these experiments. The measurement temperature was 25 °C for all experiments. Chemical shifts are reported relative to external standard TMS at 0 ppm. To enable field-frequency locking, external D2O solvent was employed using a coaxial insert tube. Spectra were recorded in static conditions with a pulsed-field gradient stimulated echo (PFGSTE) sequence [77], using bipolar gradients and a 90° pulse duration of 10 µs. The corresponding pulse sequence is presented in Figure 2. In a typical experiment, the gradient strength (g) was exponentially varied from 1 to 48 G/cm, the bipolar pulse gradient duration (δ) was 3 ms (half-sine shape, 1.5 ms duration of individual pulses), the gradient recovery delay (τ) was 1 ms, the LED recovery delay (Te) was 20 ms, and the diffusion period (∆) was ca. 160 ms. Under these conditions the resonance intensity attenuation of the slowest diffusive species (TPA) at 48 G/cm was approximately 10% of the value obtained at 1 G/cm. For each data set, 8192 complex points were collected for each increment step with a relaxation delay of 5 s. A total of 50 increments varying gradient were used. The number of scans was adapted to the state of dilution of the sample (n times 16 scans). The total experiment time ranged from 1 to 89 h per sample. DOSY spectra were generated by using the GIFA program [78] implemented in the DOSY Module of NMRNotebook software and consist of chemical shifts on direct f2 dimension (1H NMR spectrum) and Gaussian distribution of self-diffusivity on indirect f1 dimension (plot of peaks corresponding to diffusion coefficient values). Inverse Laplace Transform [65] driven by maximum entropy was used to build the diffusion dimension. In the 1H dimension, the free induction decays (FIDs) were zero filled to 16,384 data points and processed without decaying exponential apodization function. A spline baseline correction was then applied. Correction from chemical shift variations observed along the 2D experiment, due to imperfections of temperature regulation, was used according to the procedure published previously [79]. The DOSY reconstruction was realized with 192 points in the diffusion dimension and 500 MaxEnt iterations.

3.3. Relaxation and Cross Polarization Experiments

The 1H T1, T2, T1ρ and 1H→13C CP experiments were realized on 5 different samples (Table 1) with the following molar composition, 25 TEOS:9 TPAOH:400 H2O/D2O, which will be the reference sol (S); the corresponding solution without silica 9 TPAOH:400 H2O/D2O:100 EtOH (S0); the diluted system 25 TEOS:9 TPAOH:1600 H2O/D2O (SD); its corresponding solution without silica 9 TPAOH:1600 H2O/D2O:100 EtOH (SD0); and the reference sol (S) which has been heated at 95 °C for 24 h (SH) to obtain dispersed silicalite-1 nanocrystals. All samples appeared to the naked eye as a transparent fluid except the last one (SH), having a milky aspect as a result of suspension of bigger particles. First, TEOS was hydrolyzed in aqueous 40 wt % TPAOH. D2O was then added to the mixture to reach the required molar composition. Solutions without silica were prepared mixing aqueous 40 wt % TPAOH, EtOH and D2O in appropriate amounts. All samples were allowed to equilibrate for ten days before NMR measurements.
The spectra were measured at room temperature on a Bruker Avance 500 spectrometer operating at 11.7 T and resonating frequency of 500.13 MHz. A BBO Bruker 10-mm probe was used for these experiments. Longitudinal relaxation times were measured by the saturation-recovery method using variable recycle delay in the range 0.2–15 s. The transverse relaxation times (T2) were determined using the Carr–Purcell–Meiboom–Gill pulse sequence preceded by 32 presaturation pulses, [(ds_90°x)32_dr_90°x_(τ_180°y_τ)n_Acq], which utilizes a 180° pulse train to attenuate resonances from relaxing species [80]. The saturation delay (ds), recovery delay (dr) and the T2 delay (τ) are set to 0.1 s, 10 s, and 0.5 ms respectively and a half-echo was recorded for each T2 relaxation delay 2nτ varied exponentially from 1 ms up to 10 s. The number of scans per sample was 8. The spin-lattice relaxation times in the rotating frame were measured under direct proton detection mode varying the duration of the spin lock pulse from 0.1 to 500 ms. The 90° pulse on protons was 40 μs, the recycle delay 35 s.
Cross-Polarization (CP) through heteronuclear dipolar interaction as obtained by applying the Hartmann–Hahn condition during the contact time of double irradiation. Polarization transfer in liquids has been shown to work as well through hetronuclear spin-lock [75]. Spectra of the 13C NMR were taken under CP conditions with a proton decoupling rf strength of ca. 2.5 kHz. The 90° pulse length on proton nuclei was 31 μs, the recycle delay 61 s, and the number of scans 80. A standard solid-state spin-lock polarization sequence was utilized with variable contact times from 0.1 to 200 ms. Optimization of Hartmann–Hahn condition, with rf(1H) = rf(13C) = 8 kHz, was performed directly on the samples themselves. TMS was used as external shift reference for both 1H and 13C spectra.

4. Conclusions

The interactions involving the organocation TPA and the solvents water and ethanol present in clear precursor sols for silicalite synthesis have been investigated by a variety of methods based on 1H NMR spectroscopy, namely DOSY, relaxation and cross-polarization experiments. The 1H DOSY NMR indicated the strong solute–solvent interactions in concentrated sols which are decreasing with the increase of the water content to finally reach a plateau in the values for the diffusion coefficients from the system 25 TEOS:9 TPAOH:6000 H2O. The dependence of diffusion coefficients with the viscosity was found to obey a power law for which the fractional power coefficient for nanoparticles was similar to the one for TPA and deviated slightly from those of water, and much more from those of ethanol.
The 1H relaxation and CP experiments provided information on dynamic behaviors of observed species in TPAOH/silicate media. They showed that the presence of silicate particles led to a decrease in the relaxation times, especially T2 and T1ρH, as a result of restricted motions. In particular, the most affected species are TPA molecules, water to a lower extent, while ethanol experienced very little effect confirming the involvement of water-solvated TPA in intimate interaction with silicate species. Efficient CP between proton and carbon spins was observed for both ethanol and TPA resonances as a consequence of the existence of residual dipolar interactions in the C–H bonds due to translational motions. In presence of silicates, excess of TPA cations should give rise to a core–shell organization as described in the literature. The overall present results are consistent with fluctuations of density being much shorter than the NMR time scale, and thus support the idea for which the very early stages of zeolite formation would exhibit objects with high plasticity. Different methods of characterization can mark off limits for their lifetime. One can expect, very early stage would have much shorter lifetime than at later stages, after temperature treatment with development of highly reticulated structures.

Supplementary Materials

The following are available online at www.mdpi.com/2304-6740/4/2/18/s1, Figure S1: Relaxation delay dependence of 1H magnetization in T1 saturation-recovery experiment for the different resonances obtained for TPA, ethanol and water in samples S, S0, SH, SD, and SD0; Figure S2: Relaxation delay dependence of 1H magnetization in T2 measurement experiment for the different resonances obtained for TPA, ethanol and water in samples S, S0, SH, SD, and SD0.

Acknowledgments

The authors acknowledge the Engineering and Physical Sciences Research Council (EPSRC) and Exxon-Mobil Research and Engineering for funding within the framework of the international “Nanogrowth” project.

Author Contributions

The preparation of the manuscript was made by all authors. Mohamed Haouas: General idea and design of the experimental plan. David P. Petry: Samples preparation and experiments realization. Francis Taulelle: Careful follow-up and improvement of the manuscript. Michael W. Anderson: Careful follow-up and improvement of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
NMRNuclear Magnetic Resonance
TPAtetrapropylammonium
DOSYdiffusion ordered spectroscopy
CPcross polarization
TEOStetraethyl orthosilicate
PFGpulsed-field gradient
MASmagic angle spinning
PGSEPulsed Gradient Spin Echo
BPBiPolar
STESTimulated Echo
LEDLongitudinal Eddy current Delay
MaxEntMaximum Entropy
DLSdiffusion light scattering
FIDfree induction decay

References

  1. Aerts, A.; Haouas, M.; Caremans, T.P.; Follens, L.R.A.; van Erp, T.S.; Taulelle, F.; Vermant, J.; Martens, J.A.; Kirschhock, C.E.A. Investigation of the Mechanism of Colloidal Silicalite-1 Crystallization by Using DLS, SAXS, and 29Si NMR Spectroscopy. Chem. Eur. J. 2010, 16, 2764–2774. [Google Scholar] [CrossRef] [PubMed]
  2. Caremans, T.P.; Loppinet, B.; Follens, L.R.A.; van Erp, T.S.; Vermant, J.; Goderis, B.; Kirschhock, C.E.A.; Martens, J.A.; Aerts, A. Investigation of Nanoparticles Occurring in the Colloidal Silicalite-1 Zeolite Crystallization Process Using Dissolution Experiments. Chem. Mater. 2010, 22, 3619–3629. [Google Scholar] [CrossRef]
  3. Davis, T.M.; Drews, T.O.; Ramanan, H.; He, C.; Dong, J.S.; Schnablegger, H.; Katsoulakis, M.A.; Kokkoli, E.; McCormick, A.V.; Penn, R.L.; et al. Mechanistic principles of nanoparticle evolution to zeolite crystals. Nat. Mater. 2006, 5, 400–408. [Google Scholar] [CrossRef] [PubMed]
  4. Petry, D.P.; Haouas, M.; Wong, S.C.C.; Aerts, A.; Kirschhock, C.E.A.; Martens, J.A.; Gaskell, S.J.; Anderson, M.W.; Taulelle, F. Connectivity Analysis of the Clear Sol Precursor of Silicalite: Are Nanoparticles Aggregated Oligomers or Silica Particles? J. Phys. Chem. C 2009, 113, 20827–20836. [Google Scholar] [CrossRef]
  5. Eilertsen, E.A.; Haouas, M.; Pinar, A.B.; Hould, N.D.; Lobo, R.F.; Lillerud, K.P.; Taulelle, F. NMR and SAXS Analysis of Connectivity of Aluminum and Silicon Atoms in the Clear Sol Precursor of SSZ-13 Zeolite. Chem. Mater. 2012, 24, 571–578. [Google Scholar] [CrossRef]
  6. Hould, N.; Haouas, M.; Nikolakis, V.; Taulelle, F.; Lobo, R. Mechanisms of Quick Zeolite Beta Crystallization. Chem. Mater. 2012, 24, 3621–3632. [Google Scholar] [CrossRef]
  7. Hrabanek, P.; Zikanova, A.; Drahokoupil, J.; Prokopova, O.; Brabec, L.; Jirka, I.; Matejkova, M.; Fila, V.; de la Iglesia, O.; Kocirik, M. Combined silica sources to prepare preferentially oriented silicalite-1 layers on various supports. Microporous Mesoporous Mater. 2013, 174, 154–162. [Google Scholar] [CrossRef]
  8. Castro, M.; Haouas, M.; Taulelle, F.; Lim, I.; Breynaert, E.; Brabants, G.; Kirschhock, C.E.A.; Schmidt, W. Multidiagnostic analysis of silicate speciation in clear solutions/sols for zeolite synthesis. Microporous Mesoporous Mater. 2014, 189, 158–162. [Google Scholar] [CrossRef]
  9. Fyfe, C.A.; Darton, R.J.; Schneider, C.; Scheffler, F. Solid-state NMR investigation of the possible existence of “Nanoblocks” in the clear solution synthesis of MFI materials. J. Phys. Chem. C 2008, 112, 80–88. [Google Scholar] [CrossRef]
  10. Kragten, D.D.; Fedeyko, J.M.; Sawant, K.R.; Rimer, J.D.; Vlachos, D.G.; Lobo, R.F.; Tsapatsis, M. Structure of the silica phase extracted from silica/(TPA)OH solutions containing nanoparticles. J. Phys. Chem. B 2003, 107, 10006–10016. [Google Scholar] [CrossRef]
  11. Majano, G.; Mintova, S.; Ovsitser, O.; Mihailova, B.; Bein, T. Zeolite beta nanosized assemblies. Microporous Mesoporous Mater. 2005, 80, 227–235. [Google Scholar] [CrossRef]
  12. Corkery, R.W.; Ninham, B.W. Low-temperature synthesis and characterization of a stable colloidal TPA-silicalite-1 suspension. Zeolites 1997, 18, 379–386. [Google Scholar] [CrossRef]
  13. De Moor, P.; Beelen, T.P.M.; van Santen, R.A. In situ observation of nucleation and crystal growth in zeolite synthesis. A small-angle X-ray scattering investigation on Si-TPA-MFI. J. Phys. Chem. B 1999, 103, 1639–1650. [Google Scholar] [CrossRef]
  14. Fedeyko, J.M.; Rimer, J.D.; Lobo, R.F.; Vlachos, D.G. Spontaneous formation of silica nanoparticles in basic solutions of small tetraalkylammonium cations. J. Phys. Chem. B 2004, 108, 12271–12275. [Google Scholar] [CrossRef]
  15. Jin, L.; Auerbach, S.M.; Monson, P.A. Modeling Nanoparticle Formation during Early Stages of Zeolite Growth: A Low-Coordination Lattice Model of Template Penetration. J. Phys. Chem. C 2010, 114, 14393–14401. [Google Scholar] [CrossRef]
  16. Jorge, M.; Auerbach, S.M.; Monson, P.A. Modeling spontaneous formation of precursor nanoparticles in clear-solution zeolite synthesis. J. Am. Chem. Soc. 2005, 127, 14388–14400. [Google Scholar] [CrossRef] [Green Version]
  17. Liang, D.; Follens, L.R.A.; Aerts, A.; Martens, J.A.; Van Tendeloo, G.; Kirschhock, C.E.A. TEM observation of aggregation steps in room-temperature silicalite-1 zeolite formation. J. Phys. Chem. C 2007, 111, 14283–14285. [Google Scholar] [CrossRef]
  18. Liu, S.P.; Chen, L.; Wang, Y.M. The synthesis of mesoporous zeolite beta aggregates without the use of second template and additive. Solid State Sci. 2010, 12, 1070–1075. [Google Scholar] [CrossRef]
  19. Mortola, V.B.; Ferreira, A.P.; Fedeyko, J.M.; Downing, C.; Bueno, J.M.C.; Kung, M.C.; Kung, H.H. Formation of Al-rich nanocrystalline ZSM-5 via chloride-mediated, abrupt, atypical amorphous-to-crystalline transformation. J. Mater. Chem. 2010, 20, 7517–7525. [Google Scholar] [CrossRef]
  20. Patis, A.; Dracopoulos, V.; Nikolakis, V. Investigation of silicalite-1 crystallization using attenuated total Reflection/Fourier transform infrared Spectroscopy. J. Phys. Chem. C 2007, 111, 17478–17484. [Google Scholar] [CrossRef]
  21. Van Tendeloo, L.; Haouas, M.; Martens, J.A.; Kirschhock, C.E.A.; Breynaert, E.; Taulelle, F. Zeolite synthesis in hydrated silicate ionic liquids. Faraday Discuss. 2015, 179, 437–449. [Google Scholar] [CrossRef] [PubMed]
  22. Burkett, S.L.; Davis, M.E. Mechanisms of structure direction in the synthesis of pure-silica zeolites. 1. Synthesis of TPA/Si-ZSM-5. Chem. Mater. 1995, 7, 920–928. [Google Scholar] [CrossRef]
  23. Cundy, C.S.; Cox, P.A. The hydrothermal synthesis of zeolites: History and development from the earliest days to the present time. Chem. Rev. 2003, 103, 663–701. [Google Scholar] [CrossRef] [PubMed]
  24. De Moor, P.; Beelen, T.P.M.; van Santen, R.A.; Tsuji, K.; Davis, M.E. SAXS and USAXS investigation on nanometer-scaled precursors in organic-mediated zeolite crystallization from gelating systems. Chem. Mater. 1999, 11, 36–43. [Google Scholar] [CrossRef]
  25. Fedeyko, J.M.; Vlachos, D.G.; Lobo, R.F. Formation and structure of self-assembled silica nanoparticles in basic solutions of organic and inorganic cations. Langmuir 2005, 21, 5197–5206. [Google Scholar] [CrossRef] [PubMed]
  26. Houssin, C.J.Y.; Kirschhock, C.E.A.; Magusin, P.; Mojet, B.L.; Grobet, P.J.; Jacobs, P.A.; Martens, J.A.; van Santen, R.A. Combined in situ Si-29 NMR and small-angle X-ray scattering study of precursors in MFI zeolite formation from silicic acid in TPAOH solutions. Phys. Chem. Chem. Phys. 2003, 5, 3518–3524. [Google Scholar] [CrossRef]
  27. Li, X.; Shantz, D.F. PFG NMR Investigations of Tetraalkylammonium-Silica Mixtures. J. Phys. Chem. C 2010, 114, 8449–8458. [Google Scholar] [CrossRef]
  28. Li, X.; Shantz, D.F. PFG NMR Investigations of Heated Tetrapropylammonium-Silica Mixtures. J. Phys. Chem. C 2010, 114, 14561–14570. [Google Scholar] [CrossRef]
  29. Lutsko, J.F.; Basios, V.; Nicolis, G.; Caremans, T.P.; Aerts, A.; Martens, J.A.; Kirschhock, C.E.A.; van Erp, T.S. Kinetics of intermediate-mediated self-assembly in nanosized materials: A generic model. J. Chem. Phys. 2010, 132, 11. [Google Scholar] [CrossRef] [PubMed]
  30. Tokay, B.; Karvan, O.; Erdem-Senatalar, A. Nanoparticle silicalite-1 crystallization as monitored by nitrogen adsorption. Microporous Mesoporous Mater. 2010, 131, 230–237. [Google Scholar] [CrossRef]
  31. Bissert, G.; Liebau, F. Crystal-structure of [N(n-C4H9)4]H7[Si8O20]·5.33H2O—A zeolite A-like double-ring silicate with protonated water clusters [H41O16]9+. Z. Kristallogr. 1987, 179, 357–371. [Google Scholar] [CrossRef]
  32. Wiebcke, M.; Hoebbel, D. Structural links between zeolite-type and clathrate hydrate-type materials—Synthesis and crystal-structure of [NMe4]16[Si8O20][OH]8·116H2O. Dalton Trans. 1992, 1, 2451–2455. [Google Scholar] [CrossRef]
  33. Wiebcke, M.; Koller, H. Single-crystal X-ray-diffraction and variable-temperature MAS NMR-study on the heterogeneous network clathrate Na[N(CH3)4]7[Si8O20]·54H2O. Acta Crystallogr. Sect. B Struct. Commun. 1992, 48, 449–458. [Google Scholar] [CrossRef]
  34. Altieri, A.S.; Hinton, D.P.; Byrd, R.A. Association of biomolecular systems via pulsed-field gradient NMR self-diffusion measurements. J. Am. Chem. Soc. 1995, 117, 7566–7567. [Google Scholar] [CrossRef]
  35. Auge, S.; Schmit, P.O.; Crutchfield, C.A.; Islam, M.T.; Harris, D.J.; Durand, E.; Clemancey, M.; Quoineaud, A.A.; Lancelin, J.M.; Prigent, Y.; et al. NMR Measure of Translational Diffusion and Fractal Dimension. Application to Molecular Mass Measurement. J. Phys. Chem. B 2009, 113, 1914–1918. [Google Scholar] [CrossRef] [PubMed]
  36. Floquet, S.; Brun, S.; Lemonnier, J.F.; Henry, M.; Delsuc, M.A.; Prigent, Y.; Cadot, E.; Taulelle, F. Molecular Weights of Cyclic and Hollow Clusters Measured by DOSY NMR Spectroscopy. J. Am. Chem. Soc. 2009, 131, 17254–17259. [Google Scholar] [CrossRef] [PubMed]
  37. Bahlmann, E.K.F.; Harris, R.K.; Metcalfe, K.; Rockliffe, J.W.; Smith, E.G. Silicon-29 NMR self-diffusion and chemical-exchange studies of concentrated sodium silicate solutions. J. Chem. Soc. Faraday Trans. 1997, 93, 93–98. [Google Scholar] [CrossRef]
  38. Harris, R.K.; Kinnear, K.A.; Morris, G.A.; Stchedroff, M.J.; Samadi-Maybodi, A.; Azizi, N. Silicon-29 diffusion-ordered NMR spectroscopy (DOSY) as a tool for studying aqueous silicates. Chem. Commun. 2001, 2422–2423. [Google Scholar] [CrossRef]
  39. Stchedroff, M.J.; Kenwright, A.M.; Morris, G.A.; Nilsson, M.; Harris, R.K. 2D and 3D DOSY methods for studying mixtures of oligomeric dimethylsiloxanes. Phys. Chem. Chem. Phys. 2004, 6, 3221–3227. [Google Scholar] [CrossRef]
  40. Li, X.; Shantz, D.F. PFG NMR studies of lysine-silica solutions. J. Colloid Interface Sci. 2012, 383, 19–27. [Google Scholar] [CrossRef] [PubMed]
  41. Li, X.A.; Shantz, D.F. PFG NMR Investigations of TPA-TMA-Silica Mixtures. Langmuir 2011, 27, 3849–3858. [Google Scholar] [CrossRef] [PubMed]
  42. Rivas-Cardona, A.; Shantz, D.F. In situ PFG NMR of Silicalite-1 Synthesis Mixtures. J. Phys. Chem. C 2011, 115, 13016–13026. [Google Scholar] [CrossRef]
  43. Balinov, B.; Jonsson, B.; Linse, P.; Soderman, O. The NMR self-diffusion method applied to restricted diffusion—Simulation of echo attenuation from molecules in spheres and between planes. J. Magn. Reson. Ser. A 1993, 104, 17–25. [Google Scholar] [CrossRef]
  44. Guinebretiere, S.; Briancon, S.; Lieto, J.; Mayer, C.; Fessi, H. Study of the emulsion-diffusion of solvent: Preparation and characterization of nanocapsules. Drug Dev. Res. 2002, 57, 18–33. [Google Scholar] [CrossRef]
  45. Heald, C.R.; Stolnik, S.; Kujawinski, K.S.; de Matteis, C.; Garnett, M.C.; Illum, L.; Davis, S.S.; Purkiss, S.C.; Barlow, R.J.; Gellert, P.R. Poly(lactic acid)–poly(ethylene oxide) (PLA–PEG) nanoparticles: NMR studies of the central solidlike PLA core and the liquid PEG corona. Langmuir 2002, 18, 3669–3675. [Google Scholar] [CrossRef]
  46. Hoffmann, D.; Mayer, C. Cross polarization induced by temporary adsorption: NMR investigations on nanocapsule dispersions. J. Chem. Phys. 2000, 112, 4242–4250. [Google Scholar] [CrossRef]
  47. Huang, H.Y.; Wooley, K.L.; Schaefer, J. REDOR determination of the composition of shell cross-linked amphiphilic core–shell nanoparticles and the partitioning of sequestered fluorinated guests. Macromolecules 2001, 34, 547–551. [Google Scholar] [CrossRef]
  48. Jenning, V.; Mader, K.; Gohla, S.H. Solid lipid nanoparticles (SLN (TM)) based on binary mixtures of liquid and solid lipids: A 1H-NMR study. Int. J. Pharm. 2000, 205, 15–21. [Google Scholar] [CrossRef]
  49. Sharma, R.; Holland, G.P.; Solomon, V.C.; Zimmermann, H.; Schiffenhaus, S.; Amin, S.A.; Buttry, D.A.; Yarger, J.L. NMR Characterization of Ligand Binding and Exchange Dynamics in Triphenylphosphine-Capped Gold Nanoparticles. J. Phys. Chem. C 2009, 113, 16387–16393. [Google Scholar] [CrossRef]
  50. Burkett, S.L.; Davis, M.E. Mechanism of structure direction in the synthesis of Si-ZSM-5—An investigation by intermolecular 1H–29Si CP MAS NMR. J. Phys. Chem. 1994, 98, 4647–4653. [Google Scholar] [CrossRef]
  51. Burkett, S.L.; Davis, M.E. Mechanism of structure direction in the synthesis of pure-silica zeolites. 2. Hydrophobic hydration and structural specificity. Chem. Mater. 1995, 7, 1453–1463. [Google Scholar] [CrossRef]
  52. Click, C.A.; Assink, R.A.; Brinker, C.J.; Naik, S.J. An investigation of molecular templating in amorphous silicas by cross-polarization NMR spectroscopy. J. Phys. Chem. B 2000, 104, 233–236. [Google Scholar] [CrossRef]
  53. Castelijns, H.J.; Huinink, H.P.; Pel, L.; Zitha, P.L.J. The effect of pH on coupled mass transfer and sol-gel reaction in a two-phase system. J. Phys. Chem. B 2007, 111, 12383–12388. [Google Scholar] [CrossRef] [PubMed]
  54. Mayer, C. Nuclear magnetic resonance on dispersed nanoparticles. Prog. Nucl. Magn. Reson. Spectrosc. 2002, 40, 307–366. [Google Scholar] [CrossRef]
  55. Storas, T.H.; Gjesdal, K.I.; Gadmar, O.B.; Geitung, J.T.; Klow, N.E. Prostate Magnetic Resonance Imaging: Multiexponential T2 Decay in Prostate Tissue. J. Magn. Reson. Imaging 2008, 28, 1166–1172. [Google Scholar] [CrossRef] [PubMed]
  56. Storas, T.H.; Gjesdal, K.I.; Gadmar, O.B.; Geitung, J.T.; Klow, N.E. Three-Dimensional Balanced Steady State Free Precession Imaging of the Prostate: Flip Angle Dependency of the Signal Based on a Two Component T2-decay Model. J. Magn. Reson. Imaging 2010, 31, 1124–1131. [Google Scholar] [CrossRef] [PubMed]
  57. Wissing, S.A.; Muller, R.H.; Manthei, L.; Mayer, C. Structural characterization of Q10-loaded solid lipid nanoparticles by NMR spectroscopy. Pharm. Res. 2004, 21, 400–405. [Google Scholar] [CrossRef] [PubMed]
  58. Zimmerman, J.R.; Brittin, W.E. Nuclear magnetic resonance studies in multiple-phase system—Lifetime of a water molecules in an adsorbing phase on silica gel. J. Phys. Chem. 1957, 61, 1328–1333. [Google Scholar] [CrossRef]
  59. Cundy, C.S.; Forrest, J.O.; Plaisted, R.J. Some observations on the preparation and properties of colloidal silicalites. Part 1: Synthesis of colloidal silicalite-1 and titanosilicalite-1 (TS-1). Microporous Mesoporous Mater. 2003, 66, 143–156. [Google Scholar] [CrossRef]
  60. Kumar, S.; Wang, Z.P.; Penn, R.L.; Tsapatsis, M. A Structural Resolution Cryo-TEM Study of the Early Stages of MFI Growth. J. Am. Chem. Soc. 2008, 130, 17284–17286. [Google Scholar] [CrossRef] [PubMed]
  61. Nikolakis, V.; Kokkoli, E.; Tirrell, M.; Tsapatsis, M.; Vlachos, D.G. Zeolite growth by addition of subcolloidal particles: Modeling and experimental validation. Chem. Mater. 2000, 12, 845–853. [Google Scholar] [CrossRef]
  62. Follens, L.R.A.; Aerts, A.; Haouas, M.; Caremans, T.P.; Loppinet, B.; Goderis, B.; Vermant, J.; Taulelle, F.; Martens, J.A.; Kirschhock, C.E.A. Characterization of nanoparticles in diluted clear solutions for Silicalite-1 zeolite synthesis using liquid 29Si NMR, SAXS and DLS. Phys. Chem. Chem. Phys. 2008, 10, 5574–5583. [Google Scholar] [CrossRef] [PubMed]
  63. Holz, M.; Weingartner, H. Calibration in accurate spin-echo self-diffusion measurements using 1H and less-common nuclei. J. Magn. Reson. 1991, 92, 115–125. [Google Scholar] [CrossRef]
  64. Romoscanu, A.I.; Fenollosa, A.; Acquistapace, S.; Gunes, D.; Martins-Deuchande, T.; Clausen, P.; Mezzenga, R.; Nyden, M.; Zick, K.; Hughes, E. Structure, Diffusion, and Permeability of Protein-Stabilized Monodispersed Oil in Water Emulsions and Their Gels: A Self-Diffusion NMR Study. Langmuir 2010, 26, 6184–6192. [Google Scholar] [CrossRef] [PubMed]
  65. Delsuc, M.A.; Malliavin, T.E. Maximum entropy processing of DOSY NMR spectra. Anal. Chem. 1998, 70, 2146–2148. [Google Scholar] [CrossRef]
  66. Lorenz-Fonfria, V.A.; Kandori, H. Bayesian maximum entropy (two-dimensional) lifetime distribution reconstruction from time-resolved spectroscopic data. Appl. Spectrosc. 2007, 61, 428–443. [Google Scholar] [CrossRef] [PubMed]
  67. Mills, R. Self-diffusion in normal and heavy-water in range 1–45 degrees. J. Phys. Chem. 1973, 77, 685–688. [Google Scholar] [CrossRef]
  68. Yoshida, K.; Matubayasi, N.; Uosaki, Y.; Nakahara, M. Scaled Polynomial Expression for Self-Diffusion Coefficients for Water, Benzene, and Cyclohexane over a Wide Range of Temperatures and Densities. J. Chem. Eng. Data 2010, 55, 2815–2823. [Google Scholar] [CrossRef]
  69. Pratt, K.C.; Wakeham, W.A. Mutual diffusion-coefficient of ethanol–water mixtures—Destribution by a rapid new method. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1974, 336, 393–406. [Google Scholar] [CrossRef]
  70. Rahman, M.A.; Doe, H. Ion transfer of tetraalkylammonium cations at an interface between frozen aqueous solution and 1,2-dichloroethane. J. Electroanal. Chem. 1997, 424, 159–164. [Google Scholar] [CrossRef]
  71. Easteal, A.J. Tracer diffusion of water in organic liquids. J. Chem. Eng. Data 1996, 41, 741–744. [Google Scholar] [CrossRef]
  72. Easteal, A.J. Tracer diffusion in aqueous sucrose and urea solutions. Can. J. Chem. Rev. Can. Chim. 1990, 68, 1611–1615. [Google Scholar] [CrossRef]
  73. Hiss, T.G.; Cussler, E.L. Dffusion in high-viscosity liquids. AIChE J. 1973, 19, 698–703. [Google Scholar] [CrossRef]
  74. Wiebcke, M. Structural links between zeolite-type and clathrate hydrate-type materials. Chem. Commun. 1991, 1507–1508. [Google Scholar] [CrossRef]
  75. Ernst, M.; Griesinger, C.; Ernst, R.R.; Bermel, W. Optimized heteronuclear cross polarization in liquids. Mol. Phys. 1991, 74, 219–252. [Google Scholar] [CrossRef]
  76. Mehring, M. Principles of High Resolution NMR in Solids, 2nd ed.; Springer-Verlag: Berlin, Germany, 1983. [Google Scholar]
  77. Johnson, C.S. Diffusion ordered nuclear magnetic resonance spectroscopy: Principles and applications. Prog. Nucl. Magn. Reson. Spectrosc. 1999, 34, 203–256. [Google Scholar] [CrossRef]
  78. Pons, J.L.; Malliavin, T.E.; Delsuc, M.A. Gifa V 4: A complete package for NMR data set processing. J. Biomol. NMR 1996, 8, 445–452. [Google Scholar] [CrossRef] [PubMed]
  79. Assemat, O.; Coutouly, M.A.; Hajjar, R.; Delsuc, M.A. Validation of molecular mass measurements by means of diffusion-ordered NMR spectroscopy: Application to oligosaccharides. C. R. Chim. 2010, 13, 412–415. [Google Scholar] [CrossRef]
  80. Meiboom, S.; Gill, D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 1958, 29, 688–691. [Google Scholar] [CrossRef]
Inorganics 04 00018 g001 1024
Figure 1. Typical molar composition space for silicalite-1 in the system SiO2-TPAOH-H2O occurring either in concentrated media (yellow area) as investigated by Corkery, van Santen, and Cundy et al. [12,13,24,59], or dilute systems (blue area) as studied by Davis, Tsapatsis, and Shantz et al. [3,22,27,28,41,42,50,51,60,61]. Both domains have also been extensively explored by Nikolakis, Lobo, and Martens et al. [1,2,4,10,14,17,20,25,26,62].
Figure 1. Typical molar composition space for silicalite-1 in the system SiO2-TPAOH-H2O occurring either in concentrated media (yellow area) as investigated by Corkery, van Santen, and Cundy et al. [12,13,24,59], or dilute systems (blue area) as studied by Davis, Tsapatsis, and Shantz et al. [3,22,27,28,41,42,50,51,60,61]. Both domains have also been extensively explored by Nikolakis, Lobo, and Martens et al. [1,2,4,10,14,17,20,25,26,62].
Inorganics 04 00018 g001
Inorganics 04 00018 g002 1024
Figure 2. The pulse sequence BiPolar-Pulse Field Gradient-STimulated Echo-Longitudinal Eddy current Delay (BP-PFG-STE-LED) used for DOSY experiments: δ/2 = length of the diffusion gradient, τ = gradient recovery delay, g = gradient strength, Te = length of the eddy current delay, Δ = the Stejskal–Tanner diffusion delay.
Figure 2. The pulse sequence BiPolar-Pulse Field Gradient-STimulated Echo-Longitudinal Eddy current Delay (BP-PFG-STE-LED) used for DOSY experiments: δ/2 = length of the diffusion gradient, τ = gradient recovery delay, g = gradient strength, Te = length of the eddy current delay, Δ = the Stejskal–Tanner diffusion delay.
Inorganics 04 00018 g002
Inorganics 04 00018 g003 1024
Figure 3. 1H DOSY NMR spectra obtained for the systems 25 TEOS:9 TPAOH:152 H2O (left); and 25 TEOS:9 TPAOH:15,000 H2O (right).
Figure 3. 1H DOSY NMR spectra obtained for the systems 25 TEOS:9 TPAOH:152 H2O (left); and 25 TEOS:9 TPAOH:15,000 H2O (right).
Inorganics 04 00018 g003
Inorganics 04 00018 g004 1024
Figure 4. Diffusion coefficients of water, EtOH and TPA species according to 1H DOSY NMR as a function of water amount in the 25 TEOS:9 TPAOH:x H2O system. When absent error bars are smaller than the symbol size and correspond to standard deviation from measurement of individual resonances for a given species.
Figure 4. Diffusion coefficients of water, EtOH and TPA species according to 1H DOSY NMR as a function of water amount in the 25 TEOS:9 TPAOH:x H2O system. When absent error bars are smaller than the symbol size and correspond to standard deviation from measurement of individual resonances for a given species.
Inorganics 04 00018 g004
Inorganics 04 00018 g005 1024
Figure 5. Dependence of diffusion coefficients on the viscosity in the 25 TEOS:9 TPAOH:x H2O system (x = 152–15,000): closed circles correspond to water, ethanol, and TPA species according to 1H DOSY NMR, and open circles to nanoparticles according to diffusion light scattering (DLS). The viscosities and DLS data are taken from Follens et al. [62].
Figure 5. Dependence of diffusion coefficients on the viscosity in the 25 TEOS:9 TPAOH:x H2O system (x = 152–15,000): closed circles correspond to water, ethanol, and TPA species according to 1H DOSY NMR, and open circles to nanoparticles according to diffusion light scattering (DLS). The viscosities and DLS data are taken from Follens et al. [62].
Inorganics 04 00018 g005
Inorganics 04 00018 g006 1024
Figure 6. Proton spin-lattice relaxation in the rotating frame (T1ρH) curves for the different resonances of TPA, ethanol and water in samples without Si content (a) S0; and (b) SD0; and with Si content (c) S; (d) SD; and (e) SH. The solid lines represent least-square fits of the experimental data using monoexponential decay function (I = I∞exp(−t/T1ρH)).
Figure 6. Proton spin-lattice relaxation in the rotating frame (T1ρH) curves for the different resonances of TPA, ethanol and water in samples without Si content (a) S0; and (b) SD0; and with Si content (c) S; (d) SD; and (e) SH. The solid lines represent least-square fits of the experimental data using monoexponential decay function (I = I∞exp(−t/T1ρH)).
Inorganics 04 00018 g006
Inorganics 04 00018 g007 1024
Figure 7. Staggered view of the successive NMR spectra in the 1H→13C CP experiment as a function of contact time (tct) of the precursor sol (S) with the molar composition 25 TEOS:9 TPAOH:400 H2O/D2O. The two intense resonances at ca. 17 and 57 ppm correspond to EtOH and the three weak resonances at 10, 15, and 60 ppm to TPA cation.
Figure 7. Staggered view of the successive NMR spectra in the 1H→13C CP experiment as a function of contact time (tct) of the precursor sol (S) with the molar composition 25 TEOS:9 TPAOH:400 H2O/D2O. The two intense resonances at ca. 17 and 57 ppm correspond to EtOH and the three weak resonances at 10, 15, and 60 ppm to TPA cation.
Inorganics 04 00018 g007
Inorganics 04 00018 g008 1024
Figure 8. Contact time dependency of the resonance intensity of ethanol and TPA in the 1H→13C CP experiments for samples without Si content (a) S0; and (b) SD0; and with Si content (c) S; (d) SD; and (e) SH. The solid lines represent least-square fits of the experimental data using Equation (5) (I = (I0C/(1 − (TCH/T1ρH)))·(exp(−t/T1ρH) − exp(−t/TCH))).
Figure 8. Contact time dependency of the resonance intensity of ethanol and TPA in the 1H→13C CP experiments for samples without Si content (a) S0; and (b) SD0; and with Si content (c) S; (d) SD; and (e) SH. The solid lines represent least-square fits of the experimental data using Equation (5) (I = (I0C/(1 − (TCH/T1ρH)))·(exp(−t/T1ρH) − exp(−t/TCH))).
Inorganics 04 00018 g008
Inorganics 04 00018 g009 1024
Figure 9. Progressive aggregation steps between hydrated silicate and TPA cations taking place upon increasing concentration, aging, and heating in a typical silicalite precursor.
Figure 9. Progressive aggregation steps between hydrated silicate and TPA cations taking place upon increasing concentration, aging, and heating in a typical silicalite precursor.
Inorganics 04 00018 g009
Table
Table 1. Characteristics and mixture composition of samples investigated.
Table 1. Characteristics and mixture composition of samples investigated.
SampleMolar CompositionPost Synthesis TreatmentGeneral Aspect
S25 SiO2:9 TPAOH:400 H2O/D2O: 100 EtOHNoTransparent and uncolored
S09 TPAOH:400 H2O/D2O: 100 EtOHNoTransparent and uncolored
SD25 SiO2:9 TPAOH:1600 H2O/D2O: 100 EtOHNoTransparent and uncolored
SD09 TPAOH:1600 H2O/D2O: 100 EtOHNoTransparent and uncolored
SH25 SiO2:9 TPAOH:400 H2O/D2O: 100 EtOH95 °C/24 hMilky slurry
Table
Table 2. Longitudinal (T1) and transverse (T2) relaxation times (in s) of the 1H resonances obtained for TPA, ethanol and water in the different samples.
Table 2. Longitudinal (T1) and transverse (T2) relaxation times (in s) of the 1H resonances obtained for TPA, ethanol and water in the different samples.
SampleT1 (s) 1T2 (s) 1
TPAEtOHH2OTPAEtOHH2O
CH3CH2NCH2CH3CH2H2OCH3CH2NCH2CH3CH2
S0.680.390.332.22.41.50.170.0820.0571.61.50.33
S00.620.300.232.52.3- 20.360.220.131.91.51.5
SD0.790.450.373.03.11.60.260.130.102.42.01.0
SD00.800.510.413.13.2- 20.490.260.173.22.41.8
SH0.530.400.362.12.21.40.0640.0420.0330.260.190.19
1 Average standard deviation from calculated fits was within the range of 2%–9%. 2 Multi-exponential behavior.
Table
Table 3. Proton spin-lattice relaxation times (in s) 1 in the rotating frame (T1ρH) of the resonances obtained for TPA, ethanol and water in the different samples.
Table 3. Proton spin-lattice relaxation times (in s) 1 in the rotating frame (T1ρH) of the resonances obtained for TPA, ethanol and water in the different samples.
SampleTPAEtOHH2O
CH3CH2NCH2CH3CH2H2O
S0.180.0620.0432.12.10.39
S00.750.300.192.61.81.4
SD0.350.120.101.92.61.3
SD00.650.340.373.92.52.0
SH0.0790.0540.0441.30.810.29
1 Average standard deviation from calculated fits was within the range of 3%–6%.
Table
Table 4. TCH cross-polarization times (in s) 1 of the resonances obtained for TPA and ethanol in the different samples.
Table 4. TCH cross-polarization times (in s) 1 of the resonances obtained for TPA and ethanol in the different samples.
SampleTPAEtOH
CH3CH2NCH2CH3CH2
S0.0170.0410.0430.0170.015
S00.0090.0130.0120.0100.008
SD0.0200.0360.0630.0200.020
SD00.0100.0150.0120.0120.009
SH0.0290.0310.0270.0190.020
1 Average standard deviation from calculated fits was within the range of 7%–18%.

Share and Cite

MDPI and ACS Style

Haouas, M.; Petry, D.P.; Anderson, M.W.; Taulelle, F. Tetrapropylammonium Occlusion in Nanoaggregates of Precursor of Silicalite-1 Zeolite Studied by 1H and 13C NMR. Inorganics 2016, 4, 18. https://doi.org/10.3390/inorganics4020018

AMA Style

Haouas M, Petry DP, Anderson MW, Taulelle F. Tetrapropylammonium Occlusion in Nanoaggregates of Precursor of Silicalite-1 Zeolite Studied by 1H and 13C NMR. Inorganics. 2016; 4(2):18. https://doi.org/10.3390/inorganics4020018

Chicago/Turabian Style

Haouas, Mohamed, David P. Petry, Michael W. Anderson, and Francis Taulelle. 2016. "Tetrapropylammonium Occlusion in Nanoaggregates of Precursor of Silicalite-1 Zeolite Studied by 1H and 13C NMR" Inorganics 4, no. 2: 18. https://doi.org/10.3390/inorganics4020018

APA Style

Haouas, M., Petry, D. P., Anderson, M. W., & Taulelle, F. (2016). Tetrapropylammonium Occlusion in Nanoaggregates of Precursor of Silicalite-1 Zeolite Studied by 1H and 13C NMR. Inorganics, 4(2), 18. https://doi.org/10.3390/inorganics4020018

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop