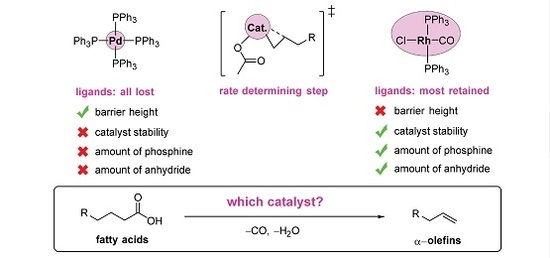
The Mechanism of Rh-Catalyzed Transformation of Fatty Acids to Linear Alpha olefins

Abstract

Linear alpha olefins (LAOs) are key commodity chemicals and petrochemical intermediates that are currently produced from fossil resources. Fatty acids are the obvious renewable starting material for LAOs, which can be obtained via transition-metal-catalyzed decarbonylative dehydration. However, even the best catalysts that have been obtained to date, which are based on palladium, are not active and stable enough for industrial use. To provide insight for design of better catalysts, we here present the first computationally derived mechanism for another attractive transition-metal for this reaction, rhodium. By comparing the calculated mechanisms and free energy profiles for the two metals, Pd and Rh, we single out important factors for a facile, low-barrier reaction and for a stable catalyst. While the olefin formation is rate limiting for both of the metals, the rate-determining intermediate for Rh is, in contrast to Pd, the starting complex, (PPh₃)₂Rh(CO)Cl. This complex largely draws its stability from the strength of the Rh(I)–CO bond. CO is a much less suitable ligand for the high-oxidation state Rh(III). However, for steric reasons, rhodium dissociates a bulkier triphenylphosphine and keeps the carbonyl during the oxidative addition, which is less favorable than for Pd. When compared to Pd, which dissociates two phosphine ligands at the start of the reaction, the catalytic activity of Rh also appears to be hampered by its preference for high coordination numbers. The remaining ancillary ligands leave less space for the metal to mediate the reaction.

1. Introduction

Linear alpha olefins (LAOs) are key commodity chemicals and petrochemical intermediates that are used in applications, such as polyethylene production (where the LAOs are used as co-monomers), synthesis of oxo alcohols to give detergents and plasticizers, and the manufacturing of poly-α-olefins that are used in drilling fluids and synthetic lubricants, to mention but a few [1,2,3]. LAOs are currently produced via oligomerization of ethylene derived from fossil resources [4,5]. Because of the limited supply of fossil resources and the fact that their use releases carbon dioxide to the atmosphere, research on the utilization of renewable feedstocks has gained extraordinary importance [6,7,8]. α-Olefins are produced on a scale of tens of millions of tons per year [3]. The development of a viable route from renewable feedstocks to α-olefins would be a major breakthrough, with a potentially transformative impact on sustainable chemical production.

Fatty acids are attractive as renewable starting materials, and deoxygenation (oxidative decarboxylation or decarbonylative dehydration) of fatty acids and their derivatives is currently being explored as an alternative and more sustainable route to uncommon, odd-numbered LAOs [2,9,10,11].

LAOs may be obtained from fatty acids using homogenous- [12,13,14,15,16,17], heterogeneous- [18], and bio-catalysts [19,20,21]. The highest activities and selectivities have so far been obtained with homogenous catalysts [2,14,22]. Homogeneously catalyzed decarbonylative dehydration has proven to be a promising reaction in the production of LAOs [12,13,14,15,22,23,24,25,26,27,28,29,30], as well as in the toolbox of the synthetic organic chemist [31].

With this promising outlook, transition-metal catalysts based on palladium [12,13,14,15,22,25,29,30,32], rhodium [14,23], iridium [27,33], nickel, [24,34], and iron [28] have been developed. Palladium-based catalysts have so far reached the highest activities [14]. However, even the best catalysts that have been developed to date are insufficiently active for practical purposes. They require high temperatures, normally well above 200 °C, that lead to rapid catalyst decomposition and turnover numbers (TONs) far below the levels (one to ten million) typical of industrial processes [35].

To accelerate development of improved catalysts, researchers have, after decades of trial-and-error, turned to fundamentals for mechanistic and molecular-structural information that should facilitate the rational design of catalysts for decarbonylative dehydration.

Firstly, whereas previous catalysts for decarbonylative dehydration have been formed in situ, we recently reported the first well-defined palladium catalyst precursor for this reaction [12]. The availability of a molecular structure facilitates improvement via structure-activity relationships. The well-defined catalyst also requires less phosphine than the in-situ recipes. They can also be used at relatively low temperatures (110 °C), give high selectivity (>95% for most substrates), and handle a wide range of substrates.

Secondly, molecular-level computational investigations have finally started to appear, offering valuable insight for rational catalyst redesign. The first molecular-level computational study of the mechanism of the Pd-catalyzed reaction was recently reported [32]. This study, which derived its model system (based on the triphenylphosphine (PPh₃) ligand) from an earlier experimental investigation [29] using palladium and PPh₃, found the alkene-forming β-hydrogen transfer step to be rate determining. Prior to this step, the two remaining phosphine ligands dissociate from the complex. This study was followed by a recent report on the Ni-catalyzed mechanism [24] and a study of Pd-based catalysts using combinations of different ligands [30].

To accelerate the development of improved catalysts for the decarbonylative dehydration reaction, we need all of the options on the table, including variation of the central metal atom. Considering whether there could be alternatives to Pd, we note that the second best activity was reported, in 1993, with Rh [14]. More importantly, Rh, in contrast to Pd, does not need the wasteful stoichiometric additions of acidic anhydride to convert the fatty acids [14,23]. The atom-economy outlook for Rh is further boosted by the fact that this metal also does not need the excess phosphine ligand typical of Pd-based catalysts [14]. In other words, in the search for a greener and more atom-economic conversion of fatty acids to LAOs, Rh seems very promising. Surprisingly, since the 1993 report [14], no-one has further explored this metal for decarbonylative dehydration of fatty acids. In light of the above-mentioned recent mechanistic investigations of the Pd-catalyzed reaction, a corresponding and comparable investigation of Rh could now indicate its potential for this reaction and the extent to which future catalyst development should focus on this metal.

To this end, we have investigated the Rh-catalyzed decarbonylative dehydration of a model carboxylic acid (butanoic acid) using density functional theory (DFT), and have established a possible reaction pathway. Comparison of the thus calculated free energy profile with that of Pd affords insight into the catalytic potential of the two metals.

2. Results and Discussion

All of the reported relative free energies (ΔG_BA, [kcal/mol]) correspond to Gibbs energies in butanoic acid (BA) solvent at 523.15 K. Schemes and energies for all of the investigated pathways are given in the Supplementary Materials.

The four-coordinate rhodium(I) complex (PPh₃)₂Rh(CO)Cl is known to be the active compound [14,23], and we thus used this complex as the starting point and reference (zero-point) for the calculation of relative free energies. Before the catalytic cycle, the acetic anhydride and the butanoic acid form a mixed anhydride MA (Scheme 1).

This reaction is calculated to be weakly endergonic (3.0 kcal/mol) and the more reactive mixed anhydride substrate MA will be produced by the excess of butanoic acid and acetic anhydride in the reaction mixture. The mixed anhydride MA first binds and adds oxidatively to the metal before the cycle continues with decarbonylation; alkene formation; and, catalyst regeneration; see Scheme 2.

2.1. Oxidative Addition

The first step of the catalytic cycle leads to the rupture of the C–O bond in the mixed anhydride. In principle, two different C–O bonds may be broken, C(O)–OC(O)CH₃ and C(O)O–C(O)CH₃. Cleavage of the C–O bond in the anhydride part, C(O)O–C(O)CH₃ (blue in the mixed anhydride in Scheme 2), will not lead to the desired α-olefin. Cleavage of this C–O bond can be prevented by using symmetric [15] or more sterically demanding anhydrides [13]. In practice, however, such preventive measures are unnecessary. The DFT-calculated barrier to oxidative addition to Pd is in fact lower when cleaving the intended C–O bond [32]. Moreover, experiments have also shown that the unwanted side reaction may be avoided even without strategies, such as the use of sterically demanding anhydride groups [25]. Hence, we will only consider the C–O bond rupture leading to the intended product (Scheme 3). In experiments at a temperature (70 °C), lower than that of typical decarbonylative dehydration reactions, the anhydride did not add oxidatively to the tetracoordinate Rh(I) catalyst [36]. Instead, the reaction could be observed for a less coordinated rhodium and for smaller and more basic phosphine ligands (PPhMe₂). In agreement with these observations, our calculations show that oxidative addition to the tetracoordinate Rh complex is difficult at higher temperatures as well (ΔG_BA = 41.3 kcal/mol, Scheme S1). From the starting point 1 it is more likely that a phosphine ligand dissociates to form the tricoordinate complex 2 before the reaction continues. Together, the calculations and experimental results suggest that the entropy gain and the steric hindrance from PPh₃ outweigh the benefit of an electron-rich complex that otherwise could be expected to favor oxidative addition followed by dissociation of a neutral donor ligand; see Scheme S1. In general, it is believed that Rh(I) forms a tricoordinate complex before undergoing oxidative addition, the calculated barrier of which is $\Delta G_{BA}^{‡}$ = 24.3 kcal/mol (via TS3-4). This is considerably lower than the corresponding aldehyde reaction [37], illustrating the activating effect of anhydride. A similarity with the aldehyde decarbonylation, however, is that, as here, with Cl as the spectator anionic ligand, CO is preferred over phosphine as the remaining neutral ligand [37]. Finally, following the oxidative addition, the complex rearranges to an essentially octahedral geometry, with the acetate binding in a bidentate (κ²) fashion. As we shall see, acetate facilitates the catalytic cycle throughout by switching between κ¹ and κ² coordination to maintain hexacoordination and the octahedral geometry preferred by rhodium(III).

2.2. Decarbonylation

After the oxidative addition, carbonyl is eliminated from the acyl chain. At this stage of the reaction, a CO molecule will also dissociate from the catalyst. This dissociation may either occur right before or after the decarbonylation, the preference of which depends on the CO pressure that is applied in the calculations, as described in Section 3. As shown in Scheme 4, the decarbonylation at normal pressure involves a barrier of $\Delta G_{BA}^{‡}$ = 39.7 kcal/mol (via TS4′-5, relative to the reference starting point; see above). The alternative route in which CO dissociates before the decarbonylation has a slightly higher decarbonylation barrier ($\Delta G_{BA}^{‡}$ = 42.5 kcal/mol). In contrast, at low CO pressure (10⁻⁵ atm, arbitrarily chosen to model the open system, allowing for CO to escape from the reaction medium) CO dissociation prior to decarbonylation is clearly favorable, with a barrier of only $\Delta G_{BA}^{‡}$ = 30.6 kcal/mol. With CO having left the complex, acetate once again binds in a bidentate fashion and saturates the rhodium alkyl complex, both electronically and coordinatively.

2.3. Alkene Formation

To form the α-olefin, the β-hydrogen atom is transferred from the alkyl chain to the acetate. Our computational exploration shows that the direct, through-space transfer from the alkyl to the acetate is a highly unlikely high-energy process. Rather, the transfer is stabilized by an agostic bond to the metal. To make space for the agostic bond, the acetate may switch to monodentate coordination and/or another ligand must dissociate. A switch to monodentate acetate was found to be energetically favorable, and to give sufficient steric and electronic degrees of freedom to support the formation of the agostic interaction in 7 (Scheme 5 and Scheme S3) prior to the transfer. Complete dissociation of the acetate does not appear to be favorable under the conditions that are modeled here. A highly polar reaction medium (ΔG_4-Heptanone = 41.8 kcal/mol) might change the situation though, which was found to be a competitive alternative for palladium [30].

The hydrogen may either be transferred directly or sequentially by first being eliminated to form a metal hydride, and next being transferred to the acetate in a second elementary step. We found the direct transfer to be preferred, although with a minimal difference in barrier between the direct and sequential transfer (Scheme 5). In fact, the rate determining step is the formation of the agostic bond in 7, with a barrier (relative to the reference starting point) of $\Delta G_{BA}^{‡}$ = 45.4 kcal/mol (Scheme 5). As for the above-mentioned decarbonylation, the alkene-formation barriers are lowered drastically when taking into account the reduced CO pressure to model an open system, to $\Delta G_{BA}^{‡}$ = 33.4 kcal/mol (TS6-7), and $\Delta G_{BA}^{‡}$ = 28.7 kcal/mol (TS7-8).

2.4. Catalyst Regeneration

Next, the olefin that was formed by the above-described β-hydrogen transfer dissociates, creating space for reformation of the catalyst by coordination of a phosphine (Scheme 6). The alternative, binding the phosphine first, is disfavored (Scheme 6). The overall reaction is calculated to be slightly endergonic (ΔG_BA = 3.5 kcal/mol) when modeling all of the species in their standard states. However, using a lower pressure (see Section 3) to model that CO is allowed to escape from the reaction mixture drives the equilibrium toward the product side [30] to reflect an exergonic (ΔG_BA = −8.5 kcal/mol) and catalytic process.

The starting complex 1 is clearly the most stable species of the reaction. A new cycle could start from the tricoordinate 9 (2), but rebinding a phosphine to form 10 (1) is energetically favorable. This may explain the experimentally observed inactivation of the Rh catalyst in phosphine excess. Still, a low, constant concentration of phosphine is required, even for Rh. Presumably phosphine is needed to prevent loss of both phosphine ligands, which would drive the reaction into the less favorable d and e pathways (see the Supplementary Materials), and lead to loss of catalytic activity.

2.5. The Overall Reaction Mechanism and Comparison to the Pd-Catalyzed Reaction

The dominating barriers of the pathways presented above are very high when calculated assuming all of the species in their respective standard states, in particular when compared to the much lower barriers that are calculated for Pd [32]. However, as we have seen above, applying reduced CO pressure to model an open system, from which CO can escape, reduces the barriers subsequent to CO dissociation drastically. For example, the rate-determining barrier is lowered from $\Delta G_{BA}^{‡}$ = 45.4 kcal/mol to $\Delta G_{BA}^{‡}$(10⁻⁵ atm) = 33.4 kcal/mol. This lowering is consistent with experimental observations, as a CO purge is necessary for achieving appreciable reactivity [14]. A corresponding lowering of barriers is not achieved for Pd, because, for this metal, CO dissociates only at the end of the catalytic cycle [32].

Having established the importance of modeling the reduced CO pressure for Rh, we focus on the thus-derived pathways and free energies in the following. The corresponding complete Rh-catalyzed reaction cycle is given in Scheme 7, with less favorable pathways being available in the Supplementary Materials. For example, it is also possible to start from Wilkinson’s catalyst (PPh₃)₃RhCl (12.1 kcal/mol less stable than our reference point (PPh₃)₂Rh(CO)Cl). With this catalyst, route b (see the Supplementary Materials) may be followed. However, after the first decarbonylation and formation of CO, the reaction starting from Wilkinson’s catalyst converges with the most favorable mechanism found in this work, termed pathway a in the Supplementary Materials. This is also the mechanism shown in Scheme 7 (and other schemes) in the main part of the paper.

As explained in the Introduction, the most active catalysts so far have been obtained for palladium. PdCl₂, in combination with an excess of phosphine ligand, is typically used as the catalyst. Pd is then reduced to phosphine-bound Pd(0) before the catalytic cycle. To help to understand the observed differences in the catalytic properties of Rh and Pd, we also calculated the palladium-catalyzed catalytic cycle. Molecular structures corresponding to the lowest-energy profile calculated for decarbonylative dehydration of hydrocinnamic acid and pivalic anhydride [32] were modified to involve our model substrates (butanoic acid and acetic anhydride) before reoptimization and SP calculations using our computational models (defined in Section 3). The thus obtained Pd-catalyzed reaction cycle is shown in Scheme 8.

While the coordination number and other properties of the Pd and Rh complexes of the two catalytic cycles (Scheme 7 and Scheme 8) differ, the different stages of the reaction can still be recognized and compared between the two catalysts. A comparison of the two free energy profiles is given in Figure 1. In the Pd cycle, the lowest free energy was calculated for Pd_9 (−12.9 kcal/mol), and the highest for Pd_TS6-8 (14.6 kcal/mol). Taking the reaction free energy (ΔG_react = −8.5 kcal/mol, due to the above-mentioned reduced pressure of 10⁻⁵ atm) into account for subsequent cycles, the overall barrier relative to Pd_9 is $\Delta G^{RDB}=\left(\Delta G^{\mathit{P}\mathit{d}\_\mathit{T}\mathit{S}\mathbf{6}-\mathbf{8}}-\Delta G_{\mathbf{P}\mathbf{d}\_\mathbf{9}}\right)+\Delta G_{react}$ = 18.1 kcal/mol. The overall barrier from Pd_4″ (−10.7 kcal/mol) is higher, $\Delta G^{RDB}=\left(\Delta G^{\mathit{P}\mathit{d}\_\mathit{T}\mathit{S}\mathbf{6}-\mathbf{8}}-\Delta G_{\mathbf{P}\mathbf{d}\_{\mathbf{4}}^{″}}\right)$ = 25.3 kcal/mol. Thus, Pd_4″ is the rate-determining intermediate (RDI) and also the reference intermediate for the decarbonylation and the alkene formation steps. However, for palladium Pd_9 is the reference intermediate against which to calculate the barrier for oxidative addition of a subsequent cycle. For Pd_TS3-4 (8.4 kcal/mol), we get that $\Delta G^{OA‡}=\left(\Delta G^{\mathit{P}\mathit{d}\_\mathit{T}\mathit{S}\mathbf{3}-\mathbf{4}}-\Delta G_{\mathbf{P}\mathbf{d}\_\mathbf{9}}\right)+\Delta G_{react}$ = 12.8 kcal/mol for the barrier relative to Pd_9. The alternative intermediate Pd_3, (−2.2 kcal/mol) gives a lower barrier, $\Delta G^{OA‡}=\left(\Delta G^{\mathit{P}\mathit{d}\_\mathit{T}\mathit{S}\mathbf{3}-\mathbf{4}}-\Delta G_{\mathbf{P}\mathbf{d}\_\mathbf{3}}\right)$ = 10.6 kcal/mol.

Summarizing, for the Rh-catalyzed cycle, the starting point and zero-level for the free energy, i.e., (PPh₃)₂Rh(CO)Cl and the substrates, is also the RDI. For palladium, our RDI (Pd_4″) is 1.8 kcal/mol lower in energy than Pd_4′, the corresponding RDI found in Ref. [32] for decarbonylative dehydration of hydrocinnamic acid and pivalic anhydride. This difference as well as the somewhat lower barriers obtained here in general when compared to those of Ref. [32] can probably be attributed to the difference between the substrate models, the more extended basis sets used here (VQZ as compared to VTZ in Ref. [32]) for the single-point (SP) energy calculations, and the fact that a different functional was used for geometry optimization.

Turning now to the oxidative addition the barrier (via TS3-4) for Rh(I) is Δ$G_{BA}^{‡}$ = 24.3 kcal/mol (relative to the zero-level starting point), and thus higher than for Pd(0) (Δ$G_{BA}^{‡}$ = 12.9 kcal/mol, relative to Pd_9). The oxidative addition is also thermodynamically disfavored for Rh(I) when compared to Pd(0), with the two energy profiles diverging markedly already at this early stage of the catalytic cycle. Part of the explanation for this difference is presumably that the Pd(0) complex is more electron rich compared to Rh(I). Next, rhodium, as opposed to palladium, carries a ligand (CO) that is known to stabilize low oxidation states. CO is much less able to stabilize higher oxidation states than phosphine. Hence, oxidation of Rh(I) in the presence of CO should be less favorable than that of Pd(0) in the presence of phosphine. In addition, palladium increases its coordination number from only two to the preferred square-planar configuration, with little steric hindrance. In comparison, rhodium increases its coordination number from three to six, in a process that could perhaps be hindered by steric repulsion when compared to the low-coordinate palladium case.

Leading up to the decarbonylation, the Pd complex is slightly stabilized by the loss of a phosphine (Pd_4′ → Pd_4″). In contrast, the Rh complex is slightly destabilized by the loss of a CO molecule, probably due to a temporary reduction in coordination number. The decarbonylation barrier is much higher for Rh (Δ$G_{BA}^{‡}$ = 30.6 kcal/mol, relative to the starting point) than for the Pd counterpart ($\Delta G_{BA}^{‡}$ = 19.3 kcal/mol, relative to Pd_4″). High barriers for decarbonylation have also been calculated for Rh-catalyzed decarbonylation of aldehydes [37], where this step is rate determining. Moreover, as for the oxidative addition, the difference in activation barriers between Rh and Pd is paralleled by a marked difference in the thermodynamical stability of the products. This is consistent with the fact that the metal–CO bond formed in the decarbonylation is expected to be stronger for Pd(II) than for Rh(III), since CO prefers low oxidation states (II is better than III). Indeed, in the subsequent step rhodium does not dissociate a ligand, while Pd dissociates a phosphine and keeps the CO. Because CO stabilizes low oxidation states (Rh(I) and Pd(0)), both of the metals need this ligand during the reductive alkene formation.

Broadly speaking, the alkene-formation step is rate determining for both metals. The marked difference in overall barrier between Rh ($\Delta G_{BA}^{‡}$ = 33.4 kcal/mol) and Pd ($\Delta G_{BA}^{‡}$ = 25.3 kcal/mol, relative to Pd_4″) is in agreement with the fact that palladium has proved to give the most active catalysts. A major difference between the palladium and rhodium mechanisms at this stage is that Pd dissociates both of the phosphine ligands before the β-hydrogen transfer. As mentioned above, this is not favorable for the higher-oxidation state Rh complex, which dissociates a CO molecule instead. Alternative dissociation reactions to make room for the agostic bond to rhodium are presented in Scheme S3. The overall more crowded metal center for Rh most likely also causes steric hindrance for the space-requiring transfer reaction and for binding the resulting alkene. Reducing the steric hindrance is probably part of the reason why, for Pd, the β-hydrogen is transferred in a Pd complex with no (bulky) phosphines. Indeed, the mono-phosphine-coordinated Pd complex has a much higher barrier for the β-hydrogen transfer. A second reason for keeping a CO at this stage, as do both Rh and Pd, is that this ligand stabilizes the reduced metal oxidation state that is resulting from the transfer.

The above-described complete phosphine dissociation comes at cost for Pd. For this metal, as opposed to Rh, an excess of phosphine is needed to ensure catalytic activity, which is consistent with the fact that two phosphines must bind again before a new catalytic cycle can start. A lack of phosphine will lead to olefin isomerization at the phosphine-free and coordinatively available Pd sites [30], and probably also to catalyst decomposition via formation of Pd(0) clusters.

The rate-determining intermediates for Rh ((PPh₃)₂Rh(CO)Cl) and Pd (Pd(CO)PPh₃, Pd_9) are similar, with CO still bonded. However for Pd, while Pd_9 is able to mediate the oxidative addition [32], this intermediate dissociates the carbonyl to give the subsequent, preferred pathway. In contrast, (PPh₃)₂Rh(CO)Cl is a very stable intermediate of the catalytic cycle for Rh. This stability is due to the strong Rh(I)–CO bond, which thus stands out as one of the most important contrasts to the Pd-based catalyst. CO is much less favorable for the Rh(III) oxidation state.

3. Computational Method

All of the calculations have been performed at the DFT level using the Gaussian 09 program [38].

3.1. Geometry Optimization

All of the geometry optimizations were done assuming gas phase using the hybrid range-separated functional ωB97XD [39,40,41], which includes empirical atom-atom dispersion terms. The ωB97XD functional has been shown to reproduce X-ray geometries of transition-metal-based homogeneous catalysts with high accuracy when compared to other density functionals [42]. Input geometries for the Rh complexes were constructed using the Spartan 08 software [43] by modifying available X-ray structures [44] or previously DFT optimized geometries. Conformational searches were performed using the MMFF force-field [45]. The input geometries for the Pd complexes were all taken from Ref. [32]. The substrate (hydrocinnamic acid) used in Ref. [32] was changed to butanoic acid before reoptimization of the geometry. Tight convergence criteria (keyword opt=tight), corresponding to a maximum force of 1.5 × 10⁻⁵ a.u., were used for the geometry optimizations. Numerical integrations were performed with the ultrafine grid of Gaussian (Int=Ultrafine). The SCF density-based convergence criterion was tightened to 10⁻¹⁰ (SCF=(Conver=10)). The located stationary points were characterized by the eigenvalues of the analytically calculated Hessian matrices. The most important transition states of the Rh-catalyzed reaction were connected to the corresponding reactants and products by using the intrinsic reaction coordinate (IRC) [46] method that was implemented in Gaussian. For Rh and Pd, the Stuttgart 28-eletron relativistic effective core potential (ECP28MDF) was used in conjunction with the accompanying correlation-consistent valence double-ζ plus polarization (cc-pVDZ-PP) basis sets [47]. All of the other atoms were described by standard correlation-consistent valence double-ζ plus polarization (cc-pVDZ) basis sets [48,49].

3.2. Thermochemistry

Translational, rotational, and vibrational partition functions for thermal corrections to give total Gibbs free energies were computed within the ideal gas, rigid-rotor, and harmonic oscillator approximations. To reduce the problems that are caused by soft, harmonic modes, all of the frequencies below 100 cm⁻¹ were shifted to 100 cm⁻¹ when calculating entropies [50]. The temperature used in the calculation of thermochemical corrections was set to 523.15 K, which is the temperature that is used in experiments [14].

3.3. Single-Point Calculations (SP)

The reported energies were obtained in SP calculations on optimized geometries using the M06L local density functional [51,52,53], which has been applied to decarbonylative dehydration and has proved to correlate well in benchmark studies of this reaction [32]. To monitor the degree to which the results are dependent on the functional, several other functionals were tested: (i) the gradient-corrected Perdew–Burke–Ernzerhof (PBE) functional [54,55] in combination with Grimme’s empirical dispersion term D3 and the original Becke-Johnson damping [56] (together termed D3-BJ) and the recently modified damping parameters [57] (to give D3-M(BJ)), and, (ii) the hybrid B3LYP functional [58] combined with the modified dispersion correction (to give B3LYP-D3M(BJ)). These additional SP results are available in the Supplementary Materials. Numerical integrations were performed using the ultrafine grid and the SP SCF convergence criterion was set to 10⁻⁵. The Stuttgart 28-electon relativistic effective core potential (ECP28MDF) in conjugation with the accompanying correlation consistent valence quadruple-ζ (cc-pVQZ-PP) basis set was used for the Rh and Pd atom. The C and H atoms were treated with the correlation consistent valence quadruple-ζ plus polarization (cc-pVQZ) basis sets obtained from the ESML basis set exchange website [59]. All of the other atoms were treated with an extended cc-pVQZ basis set with diffuse functions added from the “aug-cc-pVQZ Diffuse” set [60]. The model reaction is solvent free, but in experiments reflecting the present modeling, butanoic acid (the model substrate) and acetic anhydride would be present in excess to drive the equilibrium toward the product. No continuum solvent model parameters are available in Gaussian 09 for the corresponding mixed anhydride (butyric anhydride, ε = 12.00). In addition, two molecules of acetic acid (AA, ε = 6.25) would be produced by the reaction. To mimic this environment, we used butanoic acid (BA, ε = 2.85) and 4-Heptanone (4-Hep, ε = 12.26), respectively, in our calculations. The electrostatic and non-electrostatic solvent effects were taken into account, with default settings, using the SMD [61] solvation model, as implemented in Gaussian 09. All the relative energies (ΔG_BA, [kcal/mol]) reported for the most favorable and alternative reaction pathways in the main part of the paper and in Schemes S1–S3 (Supplementary Materials) are Gibbs free energies in butanoic acid (BA) solvent at 523.15 K. Scheme S4 illustrates the relatively minor effect of modifying the continuum solvent in the SMD calculations.

3.4. Free Energies

Free energies were obtained using a standard state corresponding to a 1 M infinitely diluted solution and a temperature of 523.15 K. Accordingly, for all species but CO (gas), 3.9 kcal·mol⁻¹ $\left(RT\ln 42.9\right)$ was added to account for the change from 1 atm to 1 M [62]. Experimentally, CO is purged from the reaction mixture. We model this by using reduced pressure (10⁻⁵ atm, arbitrarily chosen [32]) when calculating the thermal corrections of CO.

With the above-described energies and corrections, the total free energy becomes $G_{Tot}=G_{Gas}+\Delta G_{Solv}+\Delta G^{1atm\to 1M}$, where $G_{Gas}$ is the gas phase Gibbs free energy resulting from the SCF SP energy and the added thermal correction (G_corr), $\Delta G_{Solv}$ is the solvation free energy obtained as the difference between the SMD and the gas phase SCF energies, and $\Delta G^{1atm\to 1M}$ is the standard-state correction. All of the energies reported are in kcal/mol, unless otherwise stated. Where relevant, we report both of the the energies obtained using normal (1 atm) and reduced (10⁻⁵ atm) CO pressure.

4. Conclusions

Based on molecular-level calculations, we have presented the first reaction mechanism of Rh-catalyzed decarbonylative dehydration of anhydride-activated carboxylic acid. The results for rhodium are compared to those of the corresponding Pd-catalyzed reaction. Firstly, we conclude that the calculated activation barriers are consistent with the observation that Pd gives the most active catalyst. Still, for both of the metals, alkene formation is rate determining. Specifically, for Rh, the rate-limiting elementary step is the formation of the initial agostic interaction leading up to the β-hydrogen transfer from the alkyl, while for Pd, the transfer itself is the bottleneck. The rate-determining intermediate for rhodium is the starting complex (PPh₃)₂Rh(CO)Cl with two phosphines, while the overall cycle only requires a single bonded phosphine. This is consistent with the experimental observation that phosphine excess inhibits the activity of the Rh-based catalyst. Furthermore, this also underlines the contrast to palladium. For the latter metal, all of the phosphine ligands dissociate from the complex during the reaction, but excess phosphine is still required to ensure catalyst regeneration and to prevent olefin isomerization via double-bond migration. A second important difference between the two metals, partly explaining the higher overall barrier for Rh, originates from their difference in oxidation states and differential binding to CO. The Rh(I)–CO bond is much stronger than Rh(III)–CO. Still rhodium keeps the carbonyl ligand during the oxidative addition. Rhodium prefers higher coordination numbers than palladium and dissociates only a single ligand at the start of the reaction, the bulkier triphenylphosphine. This phosphine could otherwise have stabilized the Rh(III) state more than CO does.