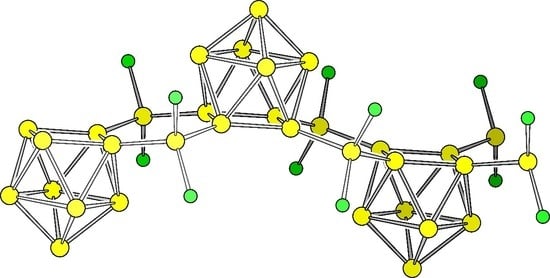
Predicted Siliconoids by Bridging Si₉ Clusters through sp³-Si Linkers

Abstract

Charged and neutral silicon clusters comprising Si atoms that are exclusively connected to atoms of the same type serve as models for bulk silicon surfaces. The experimentally known nido-[Si₉]⁴⁻ Zintl cluster is investigated as a building block and allows for a theoretical prediction of novel silicon-rich oligomers and polymers by interconnection of such building units to larger aggregates. The stability and electronic properties of the polymers $\{{}_{\infty }{}^1([{\mathrm{Si}}_9]–{\left({\mathrm{SiCl}}_2\right)}_2){}_n\}$ and $\{{}_{\infty }{}^1([{\mathrm{Si}}_9]–{\left({\mathrm{SiH}}_2\right)}_2){}_n\}$, as well as of related oligomers are presented.

1. Introduction

Silicon is the element of choice for fulfilling the desire for novel materials with promising properties. Even though, silicon is an indirect band gap semiconductor resulting in poor efficiency of light emission, the observation of visible photoluminescence from porous silicon or silicon nanoparticles at room temperature reported in the early 90s [1,2] triggered the investigations of low-dimensional silicon quantum structures and had been a subject of extensive investigations due to the potential usage of nano-sized silicon in photonic and optoelectronic devices [3,4].

In recent years, some experimental molecular approaches successfully showed that molecules with low-valent Si atoms can be synthesized. So-called siliconoids [5] are stable unsaturated neutral silicon clusters that show the characteristic structural features of silicon nanoparticles and surfaces in the molecular regime generally realized through the occurrence of one or more unsubstituted Si atoms [5,6,7,8].

Computationally, many novel well-ordered Si allotropes of various dimensionality have been proposed [9,10], but only a few of those were experimentally verified, such as the low-density Si allotropes [11] with clathrate-type structures [12,13,14,15,16,17,18,19]. The focus of the research lies on the description, understanding, and discovery of well-performing photovoltaic materials as well as models for bulk silicon surfaces [20,21]. A few such predicted materials are realizable in laboratory to date also applying physical methods such as ultrafast laser-induced confined microexplosion [22].

Currently, one of the most investigated two-dimensional materials is silicene [23], the higher homologue of graphene [24]. It is reported as a buckled sheet of sp³/sp²-hybridized Si atoms connected to wrinkled six membered rings, which is stabilized through intrinsic van-der-Waals interactions [25]. Silicene is experimentally accessible only on metal surfaces [26,27,28]. Theoretical investigations on this material are reviewed in several articles [29,30,31]. Another two-dimensional Si modification results from adding ad-atoms to silicene. Si in this MoS₂-structure type shows a lower relative energy compared to silicene [32]. In our recent work, we introduced two-dimensional materials, which may overcome surface reconstruction problems by using {Si₉} Zintl cages (Figure 1a) that are stable in solution [33].

Our aim is the computational investigation using substructures or molecular building units that are experimentally known, which we call the chemi-inspired attempt [9,10]. We found that Zintl clusters of Group 14 elements, as they occur in neat binary intermetallic solids (Zintl phases) [34], represent ideal candidates for constructing tailor-made materials. They have well-defined structures, which are retained upon solvation, and can thus be functionalized, oligomerized, or even polymerized [35,36]. Best suited for such chemistry is the nine-atomic [E₉]^(2–4)− cluster (E = Si, Ge, Sn, and Pb). For silicon, only a few examples of following-up reactions of Si₉ clusters are known whereas the pure clusters are structurally characterized in solids [37] and in salts obtained from solution [38,39,40,41,42]. In all examples, reactions occur via atoms of the open square of the mono-capped square antiprism of the nido-[Si₉]^4– cluster (Figure 1a); either capped in a η⁴-coordination with phenylzinc (Figure 1b) [39] as well as Cu-NHC (NHC = N-heterocyclic carbene) [43] or two clusters are bridged by Ni(CO)₂ fragments via two neighboring atoms of the open square, each involved in a η¹-coordination (Figure 1c) [40,44].

Further, it was shown that such clusters can serve as seed crystals for the synthesis of Si nanoparticles and nanoscale materials [45,46]. In analogy to Ge₉ clusters for which covalently bonded Ge₉ oligomers and polymers are experimentally known, Si-based materials that contain Si₉ units linked via the atoms of the open square are feasible [39,41,44]. The direct linkage has already been discussed and also the stability and properties of two-dimensional Si materials containing sp³-hybrized Si atoms as linkers between Si₉ clusters were computationally investigated [33]. In this work, we explore the possibilities of introducing tetrahedrally connecting sp³-Si atoms, which might occur from a formal reaction of the anions with SiCl₄ and SiH₂Cl₂ and nido-[Si₉]⁴⁻ clusters. Thus, we investigate the complexes [Si(Si₉)Cl₃]³⁻ and [Si(Si₉)Me₃]³⁻ (Me = –CH₃), [Si(Si₉)₂Cl₂]⁶⁻, [Si(Si₉)₃Cl]⁹⁻, and [Si(Si₉)₄]¹²⁻. Further, we analyze the hypothetical insertion of nido-[Si₉]⁴⁻ clusters into polysilanes resulting in the neutral polymers $\{{}_{\infty }{}^1([{\mathrm{Si}}_9]–{\left({\mathrm{SiCl}}_2\right)}_2){}_n\}$ and $\{{}_{\infty }{}^1([{\mathrm{Si}}_9]–{\left({\mathrm{SiH}}_2\right)}_2){}_n\}$.

2. Computational Details

Neutral polymers containing silane fragments and Si₉ clusters as well as the polysilanes themselves were optimized starting from manually drawn structures pre-optimized using UFF [47,48]. The lattice and atomic positions were allowed to relax during optimization within the constraints given by rod group symmetry [49]. All quantum chemical calculations for the polymers were carried out using the CRYSTAL09 program package [50] with a hybrid DFT functional after Perdew, Burke, and Ernzerhof (DFT-PBE0) [51,52]. For silicon, a modified split-valence + polarization (SVP) basis set [53] was applied. The shrinking factor (SHRINK) for generating the Monkhorst-Pack-type grid of k points in the reciprocal space was set to 4, resulting in three k-points in the irreducible Brillouin zone. For the evaluation of the Coulomb and exchange integrals tight tolerance factors (TOLINTEG) of 8, 8, 8, 8, and 16 were chosen. Default optimization convergence thresholds and an extra-large integration grid (XLGRID) for the density-functional part were applied in all calculations. Harmonic vibrational frequencies were calculated numerically to confirm the stationary point on the potential-energy surface as a true minimum.

The investigations on charged complexes containing nido-[Si₉]^4– as a building block are done with the DFT-PBE0 [51,52] hybrid DFT functional and def2-TVZPP level basis sets for the elements Si, Cl, H, and C using the Gaussian09 program package [54]. For modelling a solvation effect, a solvation model (polarizable continuum model, PCM) with standard settings was applied [55]. For structure optimizations, extremely tight optimization convergence criteria were combined with a large and ultrafine DFT integration grid. The systems were allowed to relax without symmetry restrictions. Harmonic vibrational frequencies were calculated analytically to confirm the stationary point on the potential-energy surface as a true minimum (except for M6).

The position parameters for all optimized compounds are listed in the Supplementary Materials.

3. Results and Discussion

3.1. Neutral Polymers with SiCl₂ or SiH₂ Linkers between the Clusters

Inspired by the [(Ni(CO)₂)₂(μ-Si₉)₂]⁸⁻ complex [40,44] (Figure 1c) and in continuation of our work on 2D structures containing Si₉ clusters [33], we derived two polymers $\{{}_{\infty }{}^1([{\mathrm{Si}}_9]–{\left({\mathrm{SiCl}}_2\right)}_2){}_n\}$ (P1) and $\{{}_{\infty }{}^1([{\mathrm{Si}}_9]–{\left({\mathrm{SiH}}_2\right)}_2){}_n\}$ (P2) by a formal replacement of Ni(CO)₂ with isolobal SiCl₂ or SiH₂. The polymers can also be regarded as silanes with inserting Si₉ units. Pauling electronegativity of Ni and Si are almost identical with a value of χ_Ni = 1.91 and χ_Si = 1.90, respectively, and the electron withdrawing effect of the CO ligands is considered by choosing ligands whose electronegativity is higher if compared to Si (χ_Cl = 3.16 and χ_H = 2.20).

The energetically optimized polymers P1 and P2 possess nearly ideal C_4v symmetric Si₉ units in the rod group pmm2 (relevant bond lengths are listed in Table S1, Supplementary Materials). The two bridging Si atoms and two adjacent atoms of each of the two open squares form a planar hexagon which is compressed along the propagation direction of the polymer. The bond angles at the bridging Si atom consequently lie in the range of tetrahedral angles 103.4°–111.0° for both compounds. The torsional angles between these hexagons and the open square of the nido-clusters are 165.8° and 160.3° for P1 and P2, respectively. In order to compare the total energy with respect to α-Si and since the compounds contain also X = H and Cl atoms we include polysilanes with comparable bond situations according to Equation (1):

$$\Delta {\mathrm{E}}_{\mathrm{rel}}({}_{\infty }{}^1[{\mathrm{Si}}_9–{\left({\mathrm{SiX}}_2\right)}_2])=\Delta {\mathrm{E}}_{\mathrm{tot}}({}_{\infty }{}^1[{\mathrm{Si}}_9–{({\mathrm{SiX}}_2)}_2])-[9·{\mathrm{E}}_{\mathrm{tot}}(\alpha \text{-}\mathrm{Si})+2·{\mathrm{E}}_{\mathrm{tot}}({}_{\infty }{}^1[{\mathrm{SiX}}_2])$$

(1)

The resulting values of 7.28 eV and 7.23 eV for X = Cl and H, respectively refer to one formula unit (Si₉)(SiX₂)₂ (X = Cl, H) for P1 and for P2, respectively (Figure 2). Scaled to one Si atom per formula unit these values result in 0.56 eV for both compounds. On a first glance, the values seem high if compared to α-Si, however the polymers must rather be compared to Si nanoparticles than to bulk materials. In this context the values are rather close to the relative energy of the carbon fullerenes of which for example C₆₀ which is 0.48 eV per atom higher in total energy than diamond [56]. The Si bridged clusters are also much lower in energy than the directly connected clusters (0.96 eV) [33]. Energetically, the differences between Si–Cl and Si–H bonds a negligible.

3.2. Charged Molecules—The Stepwise Ligand Exchange in SiCl₄ to [Si₁₇]¹²⁻

Siliconoid molecules are formed by a stepwise substitution of heteroatomic bonds between ligands bound to a central Si atom with Si terminated groups. We computationally substituted ligands in SiX₄ by [Si₉]^4– for X = Cl, H, and CH₃. The resulting molecular ions [Si(Si₉)Cl₃]³⁻ (M1), [Si(Si₉)H₃]^3– (M2) and [Si(Si₉)Me₃]^3– (M3) differ in the ligands at the sp³-Si atom (

Table 1. Structural analysis of molecular anions (Figure 3). All values are averaged, if more bonds or angles of the same type exist.

Molecular Anions	Distances/Å	Distances/Å	Angles/°	Angles/°	Angles/°
	X3Si–Si(Si9)	Si–Cl	X–Si–X	(Si9)–Si–X	(Si9)–Si–(Si9)
M1	2.58 (η3)	2.20	94.6	-	-
M2	2.33	-	105.3	113.3	-
M3	2.35	-	107.8	111.1	-
M4	2.34	2.14	101.2	107.9	121.7
M5	2.37	2.18	-	100.6	116.7
M6	2.39	-	-	-	109.4

). We started the optimizations for all compounds from a η¹-connected isomer with an ideal C_4v symmetric nido-[Si₉]^4– cluster.

As the energetically most favorite structure of M1 we found an arrangement with an almost perfect D_3h symmetric trigonal prismatic Si₉ cluster with the SiCl₃ group symmetrically capping a triangular face of the Si₉ cluster. The three distances between the Si atoms of the SiCl₃ group and the Si atoms of the clusters are with a value of 2.58 Å identical to the lengths of the triangular face of Si₉, consequently forming an almost undistorted tetrahedron. The three Si–Cl distances are 2.20 Å. The shape of Si₉ cluster distorts to a tricapped trigonal prism with prism heights of 2.69 Å that are elongated with respect to the triangular faces. The opposing trigonal face, which is not capped, has considerable shorter lengths edges of 2.46 Å and 2.49 Å. Thus the coordination of the SiCl₃ group leads to an elongation of edges of the capped triangle.

Interestingly, no local minimum structure with η¹-coordination of the SiCl₃ groups were found. In contrast, for [Si(Si₉)H₃]^3– (M2) and [Si(Si₉)Me₃]^3– (M3) the energetically most favored structures remain with η¹-coordinated Si₉ clusters. For both anions, the Si₉ clusters distort to (pseudo-)C_2v symmetric cages as an intermediate of the mono-capped square anti prism and the tricapped trigonal prism. With the ratio of diagonal lengths of the open square of d₁/d₂ = 1.22 is M2 more distorted than M3 (d₁/d₂ = 1.16). The bond length between the clusters and their ligands are 2.33 Å and 2.35 Å, respectively. The prism heights are 2.63 Å, 2.64 Å, and 3.08 Å for M2 and 2.62 Å, 2.63 Å, and 3.18 Å for M3.

Bridging two clusters by a single SiCl₂ fragment, e.g. attaching two clusters to one central Si atom leads to the anion of composition [SiCl₂(Si₉)₂]^6– (M4). Both Si₉ clusters in M4 form a η¹-coordination with distances between the cluster and the bridge atoms of 2.34 Å. The Si–Cl bonds of 2.13 Å and 2.14 Å are shorter than for M1. Both clusters within M4 deform after optimization to (pseudo-)C_2v symmetric compounds with d₁/d₂ = 1.21 and 1.22. (The distortion of C_4v symmetric monocapped square anti prism can be characterized by the ratio of the diagonal lengths d₁ and d₂ of the open square. For an undistorted cage the ratio is equal to 1. Deviation from this ratio leads to cages with C_2v symmetry.) The bond angle between the central Si atom and the two bonded Si atoms of the clusters is 121.7° and thus larger than the tetrahedral angel, which is most probably due to the steric demands of the Si₉ ligands.

Substitution of another Cl ligand by a third [Si₉]⁴⁻ results in the highly charged cluster [SiCl(Si₉)₃]^9– (M5). In M5 the three (pseudo-)C_2v symmetric clusters have diagonal length ratio in the narrow range of d₁/d₂ = 1.15–1.17 and bond lengths of 2.37 Å between cluster atoms and the central sp³-Si atom for each bond. The distance Si–Cl is 1.18 Å.

A replacement of all Cl ligands by Si₉ units results in [Si(Si₉)₄]^12– (M6). Such highly charged clusters are not unrealistic, since a salt containing a [Ge₄₅]¹²⁻ cluster unit, which is attached to three Au⁺ ions ([Au₃Ge₄₅]^9–) had been isolated and structurally characterized [57]. The distances for all four Si–Si bonds at the central Si atom are 2.39 Å. The angles range between 105.1° and 117.3°. The clusters are again distorted towards C_2v symmetric cages, but stay close to the C_4v symmetric input with ratios of the diagonal lengths of the open square between d₁/d₂ = 1.11–1.15. A table listening all bond distances and relevant cluster parameters is located in the Supplementary Materials.

The building unit M6 can be extended by continuation the building scheme with more SiCl₄. Successive linking [Si₉]⁴⁻ clusters with SiCl₄. under Cl substitution results in a neutral two-dimensional ${}_{\infty }{}^2\{[({\mathrm{Si}}_9)–\mathrm{Si}{]}_n\}$ sheet [33].

4. Conclusion

The modelling of polymeric Si₉ chains gave interesting insights to the chemistry of this up to now hard to functionalize Si₉ cluster. It showed that a replacement of Ni(CO)₂ as a ligand by others bridging sp³-Si units with comparable electron withdrawing effects, namely SiH₂ and SiCl₂, leads to polymers that are energetically in a range for realizable materials. The formation of charged oligomers by the formal substitution of X ligands in SiX₄ by [Si₉]⁴⁻ clusters leads to stable anions [SiCl_4−x(Si₉)_x]^3x–. For all derivatives, stable anions with covalent Si–Si bonds to the central Si atom form, except for x = 1 and X = Cl. Here, a η³-coordination of the cluster to the Si atom of the SiCl₃ group is observed. Whereas the monomeric unit [Si(Si₉)₄]^12– (M6) possesses a relative high charge, further combination with bridging Si atoms leads to a relatively stable two-dimensional neutral Si allotrope.