Ferromagnetic Cluster Spin Wave Theory: Concepts and Applications to Magnetic Molecules

Abstract

Ferromagnetic cluster spin wave theory (FCSWT) provides an exact and concise description of the low-energy excitations from the ferromagnetic ground state in finite magnetic systems, such as bounded magnetic molecules. In particular, this theory is applicable to the description of experimental inelastic neutron scattering (INS) spectra at low temperatures. We provide a detailed conceptual overview of the FCSWT. Additionally, we introduce a pictorial representation of calculated wavefunctions, similar to the usual depiction of vibrational normal modes in molecules. We argue that this representation leads to a better intuitive understanding of the excitations, their symmetry properties, and has links to the energy and wavevector dependence of intensity in the neutron scattering experiments. We apply FCSWT and illustrate the results on a series of examples with available low-temperature INS data, ranging from the Mn₁₀ supertetrahedron, the Mn₇ disk to the Mn₆ single molecule magnet.

1. Introduction

Understanding the ground state and excitations is key to all branches of magnetism, including the magnetism in molecules [1,2,3]. The low-temperature, low-energy magnetism in molecules is typically characterized by relatively few quantities such as the ground state spin, $S$, or the magnetic anisotropy, $D$, in the ground state [3,4,5]. This often is sufficient to describe the basic features observed in experiments. However, obviously, often a much deeper understanding is required, and when put under the magnifying glass the magnetism in molecules in fact can reveal a fascinatingly rich and unique set of phenomena. Recent examples would include spin Möbius strip state in odd antiferromagnetic wheels, quantum phase interference and Néel vector tunneling, proximity to quantum critical point in the Fe₁₀Gd₁₀ molecular wheel, precise detection of entanglement between molecular qubits by neutron scattering, and many more [6,7,8,9,10]. In all these cases, the most pertinent features are not sufficiently well covered by a set of numbers such as $S$ and $D$, but require a detailed inspection of the structure of the magnetic ground state and the elementary excitations. These are most cleanly observed at low temperatures (where “low” depends on the excitation spectrum and thus on the detailed system at hand), and in this work we accordingly will be concerned with low temperatures, or in fact zero temperature.

One of the most successful theories in magnetism for describing magnetic ground states and elementary excitations is spin wave theory (SWT) [1,2,11]. In fact, the term “spin wave theory” does not refer to one single theory, but to a family of theories which use a number of different theoretical tools and approaches. However, all these theories share a common ground in that they start from the assumption of an ordered ground state, which in fact could be regarded as the hallmark feature of the spin wave theories.

SWT is widely applied to extended magnets, in one, two, and three dimensions [12,13,14,15]. The elementary excitations correspond to waves, where the spins precess around the polarized orientation in the ground state, with phase differences between the spins described by a wave vector. Applications of SWT to magnetic clusters as small as magnetic molecules, which typically contain a dozen or so magnetic centers or less, is in contrast very scarce. This is so for a number of reasons, one is that the starting assumption of an ordered ground state is strictly never realized, and the validity of the SWT procedure is thus questionable. A notable exception is the class of magnetic molecules in which predominant ferromagnetic exchange interactions between the spins in the molecule stabilize the ferromagnetic or fully polarized ground state. Here, the theoretical methods of SWT become exact at zero temperature, for molecules of any size or composition. Luckily, this comprises quite a number of experimentally relevant magnetic molecules, such as high-spin molecules, Lanthanide containing clusters, or single molecule magnets.

Few molecules with antiferromagnetic couplings were analyzed using SWT techniques [16,17,18,19,20,21,22]. The focus in this work is however on the ferromagnetically coupled clusters, for which SWT is guaranteed to work exactly for the ground state and the zero-temperature excitations. When applied to small, bounded ferromagnetic clusters, the SWT techniques and their results are similar in many respects to those in extended systems, but also notable differences exist. Therefore, in order to make the distinction apparent, and to avoid potential confusion, we use the term Ferromagnetic Cluster Spin Wave Theory (FCSWT) for the set of techniques relevant in bounded clusters.

It should be mentioned that the use of the word “spin wave” in the context of bounded spin systems is not totally appropriate. This is because the excitations are not waves in the strict sense. The situation is in fact very analogous to that in elastic media, where in the extended systems the normal modes form e.g., acoustic waves, while in the bounded systems such as molecules the normal modes are recognized as vibrations. So it is with the magnetic normal modes discussed in this work: in the extended magnetic systems they form spin waves, while in the bounded spin clusters they form excitations in analogy to the vibrations in molecules. However, in the absence of better language, we simply call them “spin waves” too.

The purpose of this article is threefold. First, the concepts of FCSWT are introduced in both a review and tutorial-like manner. That is, the few descriptions of FCSWT available in the literature are presented in more detail and with greater accuracy, and the discussion is extended by some simple examples for better illustration of the concepts. Second, a graphical representation of the elementary magnetic excitations or spin waves, respectively, is introduced. This should provide great help for better understanding the physics of these excitations, and provide guidance to experimentalists. Graphical representations of e.g., molecular orbitals obtained from density functional theory (DFT) or of molecular vibrations using vibrational coordinates have proven highly useful in research. The representation presented in this work will hopefully establish a similarly useful tool for studying ferromagnetic molecules. Finally, FCSWT is applied to three different molecules, the Mn₁₀ supertetrahedron [23], a Mn₇ disk-like molecule [24], and a Mn₆ single molecule magnet [25]. These three molecules were studied previously using inelastic neutron scattering (INS), which permits direct observation of spin wave excitations and which is thus a primary tool for their experimental investigation [3,26]. The availability of these data facilitates a comparison to the results of FCSWT. Furthermore, these molecules are well suited for FCSWT, but each of them emphasizes a different characteristic aspect. FCSWT analyses were reported before for Mn₁₀ and Mn₇ [23,24], which are reviewed here and significantly extended. Single molecule magnets were, to the best of our knowledge, not yet analyzed with FCSWT, and indeed some additional new aspects need to be considered.

SWT is very well known to physicists, but less so to chemists. The presentation in this work is accordingly geared towards chemists, and where possible analogies to methods familiar to chemists are mentioned. In fact, the basic methods required for applying FCSWT in practice are all part of standard chemistry textbooks. The main new aspect is that they are applied in a different context here. Experimental methods and the calculation of experimental observables such as INS intensities are not discussed, not to overload the presentation. It is mentioned in passing that FCSWT can be a useful tool for a variety of experiments, such as INS [3], four-dimensional polarized neutron spectroscopy [27], paramagnetic nuclear resonance [28], and others.

2. Concepts

2.1. Basics

As indicated in the introduction, several techniques exist for pursuing spin wave calculations. For the ferromagnetic case, which is the topic of this work, they all produce identical, and in fact exact results for the zero-temperature excitations. That is, the calculated energies and wavefunctions are the exact eigenvalues and eigenstates of the Hamiltonian.

The Hamiltonian considered in this work consists of Heisenberg exchange and ligand-field terms, and is written as:

$$\widehat{H}=-{\displaystyle \sum _{i,j}{J}_{ij}{\widehat{S}}_i·{\widehat{S}}_j}+{\displaystyle \sum _i{D}_i\left({\widehat{S}}_{i,z}^2-\frac{1}{3}\right)}$$

(1)

with the standard meaning of the symbols. The length of the $i$-th spin is denoted as $s_i$, and the number of spin centers in the cluster is $N$. As alluded to in the introduction, the single requirement for the presented methods to be valid is that the ground state contains the fully polarized ferromagnetic state:

$$|M=M_{max}\rangle =|M_1=s_1,M_2=s_2,\dots ,M_N=s_N\rangle$$

(2)

or its opposite $|M=-M_{max}\rangle$. Here, $M$ denotes the magnetic quantum number or eigenvalue of the $z$-component of the total spin operator ${\widehat{S}}_z$ and $M_i$ the magnetic quantum number of the $i$-th spin center. The total spin quantum number will be denoted as $S$. The quantum numbers $S$ and $M$ are restricted by the maximum values $M_{max}=S_{max}={{\displaystyle \sum }}_{i=1}^N{s}_i$, which are achieved in the fully polarized state.

Any spin system for which the states $|M=\pm M_{max}\rangle$ are ground state will in the context of this work be called ferromagnetic. Accordingly, the coupling constants, $J_{ij}$, need not to be all ferromagnetic ($J_{ij}>0$), some can be antiferromagnetic ($J_{ij}<0$), but their overall effect must be such that the states Equation (2) are ground state. This happens in a relatively large class of molecules, which could be characterized as “ferromagnetically coupled with Ising anisotropy”.

The Hamiltonian Equation (1) is not the most general Hamiltonian which permits a fully polarized ground state. Examples would be systems with additional higher-order ligand-field terms (see also Section 3.3), Ising exchange interactions, applied magnetic fields, and others. However, it is general enough to present the FCSWT procedures comprehensively, and includes systems of interest, such as several single molecule magnets and lanthanide containing clusters. It should not be difficult to extend the results to other systems.

In this work, two SWT techniques are presented. The first is, so to say, the simplest possible, and relies on basic quantum mechanical concepts. We will find it most convenient for practical calculations. The second method uses the formalism of boson raising and lowering operators, and is the standard approach in physics. It will provide us with deeper insight into the excitations calculated with the first method. The methods will be introduced in two steps: first, the case of a dimer will be treated, and then the results will be generalized to arbitrary clusters.

2.2. Dimers

The Hamiltonian of a dimer with isotropic exchange coupling reads:

$$\widehat{H}=-J{\widehat{S}}_1·{\widehat{S}}_2$$

(3)

and its eigenvalues and states are well known, $E\left(S\right)=-\frac{1}{2}JS\left(S+1\right)$ and $|S,M\rangle$. Let’s first consider a spin-1/2 dimer, for which $s_1=s_2=1/2$ and $S_{max}=M_{max}=1$. Its singlet and triplet eigenstates are:

$$|S=0,M=0\rangle =\frac{1}{\sqrt{2}}\left(|\frac{1}{2},-\frac{1}{2}\rangle -|-\frac{1}{2},\frac{1}{2}\rangle \right)$$

(4)

$$|S=1,M=1\rangle =|\frac{1}{2},\frac{1}{2}\rangle$$

(5a)

$$|S=1,M=0\rangle =\frac{1}{\sqrt{2}}\left(|\frac{1}{2},-\frac{1}{2}\rangle +|-\frac{1}{2},\frac{1}{2}\rangle \right)$$

(5b)

$$|S=1,M=-1\rangle =|-\frac{1}{2},-\frac{1}{2}\rangle$$

(5c)

with a standard notation of the states. Obviously, for a ferromagnetic interaction ($J>0$), the fully polarized states $|M=\pm M_{max}\rangle$ or $|S=1,M=\pm 1\rangle$, respectively, are ground states. Let’s pick the state $|M=M_{max}\rangle$. We can then further observe that the subspace for $M=M_{max}-1=0$ consists of two states. Moreover, we can construct a basis for this subspace by applying the lowering spin operator of each spin site, ${\widehat{S}}_i^{-}$, to the fully polarized state:

$$|i=1\rangle \equiv \frac{1}{\sqrt{2s_1}}{\widehat{S}}_1^{-}|M=M_{max}\rangle =|-\frac{1}{2},\frac{1}{2}\rangle$$

(6a)

$$|i=2\rangle \equiv \frac{1}{\sqrt{2s_2}}{\widehat{S}}_2^{-}|M=M_{max}\rangle =|\frac{1}{2},-\frac{1}{2}\rangle .$$

(6b)

This method for constructing a basis $|i\rangle$ for the subspace $M=M_{max}-1$ works always, for arbitrary number $N$ of spin centers and arbitrary spin lengths $s_i$, because: (i) there are as many spin centers and thus operators ${\widehat{S}}_i^{-}$ as there are states in the subspace; (ii) the states generated by applying ${\widehat{S}}_i^{-}$ to $|M=M_{max}\rangle$ are mutually orthogonal; and (iii) the states generated by applying ${\widehat{S}}_i^{-}$ to $|M=M_{max}\rangle$ all belong to the magnetic quantum number $M=M_{max}-1$. We thus have created a complete basis, and the eigenenergies and wave functions belonging to $M=M_{max}-1$ are obtained by diagonalizing the Hamiltonian matrix in this basis, $H_{ij}=\langle i\left|\widehat{H}\right|j\rangle$. Note that by construction the dimension of the matrix $H_{ij}$ is equal to the number $N$ of spin centers in the system, or two in the present case. The calculation of the matrix elements is straightforward; a general formula will be given in the next chapter. In the present case, the eigenstates and energies can be obtained by inspection, yielding:

$$|k=0\rangle =\frac{1}{\sqrt{2}}\left(|i=1\rangle +|i=2\rangle \right)$$

(7a)

$$|k=1\rangle =\frac{1}{\sqrt{2}}\left(|i=1\rangle -|i=2\rangle \right)$$

(7b)

where $k$ is introduced as an arbitrary label to index the states. It is easily confirmed that the states $|k=0\rangle$ and $|k=1\rangle$ are exactly the states $|S=1,M=0\rangle$ and $|S=0,M=0\rangle$, respectively. Thus, the procedure of constructing a basis for $M=M_{max}-1$ by applying the lowering spin operators ${\widehat{S}}_i^{-}$ to the fully polarized state $|M=M_{max}\rangle$, and diagonalizing the Hamiltonian matrix in this basis, has provided us with the exact eigenstates and energies in that subspace. The resulting set of eigenstates are called “spin waves” (the justification is given later).

Some notational comments. The state created by applying the lowering spin operators ${\widehat{S}}_i^{-}$ to the fully polarized state describes a spin deviation at the site $i$. These states will be called “local spin deviations” and the associated wave functions will be written as $|i\rangle$ or $|j\rangle$. The spin wave states will be written as $|k\rangle$ or $|q\rangle$, where the values of $k$ ($q$) may be chosen as appropriate (if not specified otherwise the states are indexed by integers running from $0$ to $N-1$).

For the spin-1/2 dimer, one arrives at the picture shown in Figure 1. The spin-1/2 dimer exhibits four eigenstates, one of them is the fully polarized ground state, and two of them are calculated by using FCSWT. For the spin-1/2 dimer this is sufficient to completely construct the energy spectrum, since the “missing” fourth state belongs to the $S=1$ multiplet, and thus must be degenerate to the fully polarized state and can be constructed by repeated application of the total spin lowering operator ${\widehat{S}}^{-}={{\displaystyle \sum }}_i{\widehat{S}}_i^{-}$. In the general case, the information obtained from FCSWT will not be sufficient to arrive at a complete energy spectrum (not even close to that), as upcoming examples will demonstrate. However, FCSWT provides a complete description of the excitations relevant at zero temperature. For instance, the neutron scattering intensity is subject to the selection rules $\Delta S=0,\pm 1$ and $\Delta M=0,\pm 1$ [3]. These imply that, at zero temperature, only transitions with energies matching the excitation energies of the spin waves are allowed. The argument applies analogously to other experimental techniques. This is an important finding, and the foundation for the usefulness of FCSWT in practical work.

Before proceeding to the case of a general spin cluster, it is interesting to discuss some extensions. It might be tempting to apply the approach also to the antiferromagnetic dimer ($J<0$). The antiparallel alignment of the spins in the ground state, as it is obtained in the classical model, might be translated into the quantum state $|\uparrow \downarrow \rangle =|+1/2,-1/2\rangle$ (or its opposite), which is known as the Néel state [2]. However, here, application of the lowering spin operators ${\widehat{S}}_i^{-}$ does not produce a viable basis, nor does the diagonalization of the associated Hamiltonian matrix yield reasonable states. This is obviously due to the fact that the Néel state is not an eigenstate of the Heisenberg Hamiltonian Equation (3). Only for systems which undergo an antiferromagnetic phase transition is the ground state correctly described by the Néel state [1,2], and this can happen only in extended systems [2]. Bounded spin systems such as magnetic molecules do not exhibit magnetic phase transitions. Therefore, applying SWT to antiferromagnetic molecules is not justified in general, and needs a careful case-to-case analysis [18,21]. An analogous deficiency occurs in ferromagnetic clusters with easy-axis anisotropy, where a state similar to $|S=1,M=0\rangle$ would be ground state. These findings explain the limitation in this work to “ferromagnetic systems with Ising anisotropy”, as defined before.

Also dimers with spins larger than 1/2 are illustrative examples (we continue with discussing ferromagnetic systems). The application of the lowering spin operators ${\widehat{S}}_i^{-}$ to the fully polarized ground state yields two spin waves, which shall again be denoted as $|k=0\rangle$ and $|k=1\rangle$ (their expansion in terms of $|M_1,M_2\rangle$ functions is of course different from Equation (6)). For the case $s_1=s_2=1$, $S_{max}=M_{max}=2$, which is discussed exemplarily, the energy spectrum is shown in Figure 2, where also the situation of a dimer with additional Ising type anisotropy is presented.

In both the isotropic and the Ising dimers, the fully polarized states are ground states. As before, FCSWT provides the complete zero-temperature excitation spectrum, as observable in e.g., INS. For an isotropic spin cluster the spin wave with the lowest energy, or the state $|k=0\rangle$, respectively, must correspond to the $M=M_{max}-1$ component of the ferromagnetic ground-state spin multiplet. That is, the state $|k=0\rangle$ must be identical to the state $|S=S_{max},M=M_{max}-1\rangle$, and its excitation energy must be zero (this was also observed before for the spin-1/2 dimer). In the presence of an Ising anisotropy, the state $|k=0\rangle$ is raised in energy with respect to the ground state, giving rise to what is known as zero-field splitting (ZFS) [5,29]. One thus arrives at the conclusion that, at zero temperature, the excitation spectrum consists of $N-1$ excitations due to exchange splitting, plus one ZFS excitation due to anisotropy splitting. One can also infer that the energy of the lowest spin wave must be equal to or higher than the energy of the fully polarized states, since otherwise the fully polarized states would not be ground state, and the starting assumption for the validity of the method be violated. These rules are often useful in practice.

At this point, a further comment is appropriate. The physics which underlies the state $|k=0\rangle$ appears to be different from that of the other states $|k>0\rangle$, in as much as the former corresponds to a ZFS, and is a component of the ground-state spin multiplet in the isotropic cluster. In fact, the $|k=0\rangle$ state plays a distinctive role, which in bounded spin clusters is associated with a number of subtleties which need careful attention [18,21]. It would thus be appropriate to exclude the $|k=0\rangle$ state from the spin wave spectrum [18,21]. However, in the present work, such details are irrelevant and the $|k=0\rangle$ state will also be called a spin wave.

2.3. General Concept

The observations for the dimer are generic, and valid for general clusters, consisting of arbitrary number $N$ of spin centers with arbitrary spin lengths $s_i$ (the exchange and anisotropy parameters are not arbitrary, they must result in a fully polarized ground state). The method presented previously is straightforward to extend.

The fully polarized state $|M=M_{max}\rangle$ is picked again. The local spin deviations are then defined as:

$$|i\rangle =\frac{1}{\sqrt{2s_i}}{\widehat{S}}_i^{-}|M=M_{max}\rangle$$

(8)

where the index runs from $i=1,\dots ,N$. In this basis, the matrix elements $H_{ij}=\langle i\left|\widehat{H}\right|j\rangle$ of the Hamiltonian Equation (1) are calculated to:

$$H_{ij}=E_F{\delta }_{ij}-D_i\left(2s_i-1\right){\delta }_{ij}+\left({\displaystyle \sum _n{s}_n\left(J_{in}+J_{ni}\right)}\right){\delta }_{ij}-\sqrt{s_i{s}_j}\left(J_{ij}+J_{ji}\right)$$

(9)

where $E_F=-{{\displaystyle \sum }}_{i,j}{J}_{ij}{s}_i{s}_j+{{\displaystyle \sum }}_i{D}_i\left(s_i^2-1/3\right)$ is the energy of the fully polarized state. This constant is irrelevant in the analysis of experiments, and often will be dropped (set to zero). The formula has an intuitive structure: the first three terms come from the ${\widehat{S}}_{i,z}{\widehat{S}}_{j,z}$ and ${\widehat{S}}_{i,z}^2$ operators in the Heisenberg exchange and magnetic anisotropy terms, and thus contribute to the diagonal elements in the Hamiltonian matrix. The last term however comes from the ${\widehat{S}}_{i,x}{\widehat{S}}_{j,x}+{\widehat{S}}_{i,y}{\widehat{S}}_{j,y}=\left({\widehat{S}}_i^{+}{\widehat{S}}_j^{-}+{\widehat{S}}_i^{-}{\widehat{S}}_j^{+}\right)/2$ operators in the Heisenberg exchange term and thus produce non-diagonal elements. It is due to the latter that the local spin deviations $|i\rangle$ are mixed to form new states, the spin waves $|k\rangle$. Diagonalization of the Hamiltonian matrix yields the eigenvalues and eigenstates, or spin wave energies and spin wave states, ${\epsilon }_k$ and $|k\rangle$, respectively,

$$\overleftrightarrow{H}{\overrightarrow{v}}_k=\left({\epsilon }_k+E_F\right){\overrightarrow{v}}_k$$

(10a)

$$|k\rangle ={\displaystyle \sum _i{v}_{i,k}|i\rangle }$$

(10b)

where $\overleftrightarrow{H}$ represents the Hamiltonian matrix $H_{ij}$, and ${\overrightarrow{v}}_k={\left(v_{1,k},v_{2,k},\dots ,v_{N,k}\right)}^T$ the eigenvector corresponding to the eigenvalue ${\epsilon }_k+E_F$ (the eigenvectors can always be chosen to be real). With knowing the spin wave energies and states, experimental observables such as the neutron scattering intensity can be calculated and compared to experiment. It should be noted that this is achieved by diagonalizing a matrix of dimension $N$, which is generally massively smaller than the dimension of the Hilbert space of the spin system (even when symmetries are exploited). FCSWT can thus be handled easily with e.g., computer algebra systems, which makes it a useful and simple tool in practice.

As an example, for an isotropic, symmetric dimer with $s_1=s_2=s$, one obtains from Equation (9): $E_F=-J{s}^2$, $H_{11}=H_{22}=E_F+Js$, and $H_{12}=H_{21}=-Js$. Diagonalizing this 2 × 2 matrix is a standard text book example, yielding the eigenvalues ${\epsilon }_0=0$, ${\epsilon }_1=2Js$, and the (un-normalized) eigenstates ${\overrightarrow{v}}_0={\left(1,1\right)}^T$ and ${\overrightarrow{v}}_1={\left(1,-1\right)}^T$. The two spin wave states are thus $|k=0\rangle =\left(|i=1\rangle +|i=2\rangle \right)/\sqrt{2}$ and $|k=1\rangle =\left(|i=1\rangle -|i=2\rangle \right)/\sqrt{2}$, which correspond exactly to the states given in Equation (7). Note that these results apply to any value of $s$.

The above procedure, with the key result Equation (9), establishes a straightforward recipe for calculating the observable zero-temperature excitations. It is, however, somewhat of a deus ex machina. It, for example, does not suggest an approach for calculating the remaining energies and states in the energy spectrum, nor higher temperature results. It also does not reveal further insight into the nature of the excitations. Physicists have thus developed more powerful techniques, which at first may appear abstract but are actually well suited for intuition.

One widely used technique is to associate the spins with bosons, or the spin lowering and raising operators ${\widehat{S}}_i^{-}$, ${\widehat{S}}_i^{+}$ with boson creation and annihilation operators ${\widehat{a}}_i^{†}$, ${\widehat{a}}_i$, respectively [2,11]. This renders the spin problem into one of boson particles, which have some favorable properties. It comes at the cost of some approximations (and some subtleties). Nevertheless, the advantages are so numerous that it has become the standard approach in SWT. Gladly, for the topic of this work, this technique is again exact [11,30].

The boson-operator technique essentially replaces each spin center with a harmonic quantum oscillator, and the Heisenberg exchange describes a coupling of these oscillators. The spin Hamiltonian Equation (1) thus becomes a Hamiltonian of N coupled quantum oscillators, which is familiar in many branches of science, such as in the treatment of the elastic modes in molecules (vibrations) and solids (phonons).

The idea is to start, for a single spin, from its fully polarized alignment, $M_i=s_i$, and to treat the deflection of the spin by one step, $M_i\to M_i-1$, as if it was due to the creation of one boson particle. In operator language (up to second order, which is sufficient for the purposes of this work), this leads to:

$${\widehat{S}}_i^{-}=\sqrt{2s_i}{\widehat{a}}_i^{†}$$

(11a)

$${\widehat{S}}_i^{+}=\sqrt{2s_i}{\widehat{a}}_i$$

(11b)

$${\widehat{S}}_{i,z}=s_i-{\widehat{a}}_i^{†}{\widehat{a}}_i$$

(11c)

where ${\widehat{a}}_i^{†}$ creates and ${\widehat{a}}_i$ annihilates a boson at site $i$, and are defined as usually by the matrix elements ${\widehat{a}}_i^{†}|n_i\rangle =\sqrt{n_i+1}|n_i+1\rangle$ and ${\widehat{a}}_i|n_i\rangle =\sqrt{n_i}|n_i-1\rangle$. Here, $|n_i\rangle$ denotes an eigenstate of the number operator ${\widehat{a}}_i^{†}{\widehat{a}}_i$, and the boson number $n_i$ can assume the values $0,1,\cdots ,\infty$. By applying these operators one, so to say, climbs up and down the ladder of states $M_i=s_i$, $s_i-1$, $s_i-2,\cdots$, as sketched in Figure 3.

Obviously, the creation of one boson at site $i$ exactly produces a spin deflection at this site, or the state $|i\rangle$, which implies:

$$|i\rangle =|n_i=1\rangle ={\widehat{a}}_i^{†}|0\rangle .$$

(12)

In this picture, the fully polarized state $|M=M_{max}\rangle$ corresponds to a state with zero bosons, or the boson vacuum written as $|0\rangle$, since in this state all spins are maximally aligned and spin deflections strictly absent. Exploiting Equation (11), the spin Hamiltonian Equation (1) can be reformulated in terms of the boson operators, which yields the boson Hamiltonian:

$${\widehat{H}}_B=E_F-{\displaystyle \sum _i{D}_i\left(2s_i{\widehat{a}}_i^{†}{\widehat{a}}_i-1\right){\widehat{a}}_i^{†}{\widehat{a}}_i}+{\displaystyle \sum _{i,j}{s}_j\left(J_{ij}+J_{ji}\right){\widehat{a}}_i^{†}{\widehat{a}}_i}-{\displaystyle \sum _{i,j}\sqrt{s_i{s}_j}\left(J_{ij}+J_{ji}\right){\widehat{a}}_i^{†}{\widehat{a}}_j}.$$

(13)

The matrix of the boson Hamiltonian ${\widehat{H}}_B$ in the space of the states $|i\rangle ={\widehat{a}}_i^{†}|0\rangle$ or the one-boson sector, respectively, is easily calculated, and exactly reproduces the matrix $H_{ij}$ given in Equation (9). The two techniques are thus indeed equivalent (with respect to the zero-temperature excitations).

The diagonalization of the boson Hamiltonian ${\widehat{H}}_B$ can be accomplished by using the eigenvectors of the Hamiltonian matrix $H_{ij}$ for introducing new boson operators ${\widehat{c}}_k^{†}$, ${\widehat{c}}_k$, which shall be called magnon operators, and the associated particles as magnons:

$${\widehat{c}}_k^{†}={\displaystyle \sum _i{v}_{i,k}{\widehat{a}}_i^{†}},{\widehat{c}}_k={\displaystyle \sum _i{v}_{i,k}^{*}{\widehat{a}}_i}.$$

(14)

The magnon Hamiltonian then assumes the simple form:

$${\widehat{H}}_M=E_F+{\displaystyle \sum _k{\epsilon }_k{\widehat{c}}_k^{†}{\widehat{c}}_k}$$

(15)

where the energies ${\epsilon }_k$ are the eigenvalues obtained before in Equation (10). The eigenstates in the one-magnon sector, which are the zero-temperature spin wave excitations, are generated by:

$$|k\rangle ={\widehat{c}}_k^{†}|0\rangle .$$

(16)

So far, the previous results, obtained with using the spin lowering operator technique, have just been rediscovered. However, the physical picture has changed considerably, namely to a picture in which the Heisenberg interactions dress bare particles, leading to new particles, the magnons. There are $N$ different magnons, distinguished by the index $k$, and each is associated with an excitation energy ${\epsilon }_k$ for its creation. More importantly, the Hamiltonian describing the magnons is exactly that of $N$ independent harmonic quantum oscillators, where each oscillator vibrates with frequency ${\epsilon }_k/h$. This suggests to identify the zero-temperature excitations with the normal modes of the “magnetic harmonic oscillators”, or spin waves, and the magnons with their quanta. This also establishes a connection to the normal modes in elastic media, which is exploited in the next chapter.

2.4. Analogy to Vibrations and Pictorial Representation

In this chapter, we will present a graphical representation of the spin wave excitations, in order to reach a deeper insight into their nature, structure and properties. We will repeatedly stress the analogy with the elastic motion in molecules or vibrations, respectively. The analogy originates from the fact, that both systems are described by a set of coupled harmonic oscillators, and that thus mathematical and pictorial tools widely familiar for the elastic case can largely be carried over to the spin case.

The pictorial representation is based on the solutions of the classical version of the spin Hamiltonian Equation (1), which are essentially identical to the solutions of the quantum version discussed before [2]. This is a well-known fact [2,31] (also well known for the elastic case), and roots in the equivalence of the classical and quantum equations of motion. The treatment is briefly reviewed here, for establishing the required results in a proper context. Only the isotropic case, $D_i=0$, is considered in the following for simplicity; the final results hold equally for the general case.

The equations of motions corresponding to the Hamiltonian Equation (1) read:

$$\frac{d}{dt}{\overrightarrow{S}}_i={\displaystyle \sum _j\left(J_{ij}+J_{ji}\right)\left({\overrightarrow{S}}_i\times {\overrightarrow{S}}_j\right)=}g\frac{{\mu }_B}{\hslash }{\overrightarrow{S}}_i\times {\overrightarrow{B}}_{eff}$$

(17)

where ${\overrightarrow{S}}_i$ is the spin vector of the $i$-th spin, ${\overrightarrow{B}}_{eff}$ an effective magnetic field, and the remaining symbols have the standard meaning. The right-hand side of the equation emphasizes the physical interpretation: The motion of ${\overrightarrow{S}}_i$ is determined by the torque on this spin due to an effective magnetic field generated by the exchange interaction with the other spins in the cluster. The FCSWT results are obtained by linearizing the equations of motions i.e., by assuming:

$${\overrightarrow{S}}_i=s_i{\overrightarrow{e}}_z+S_{i,y}{\overrightarrow{e}}_y+S_{i,x}{\overrightarrow{e}}_x$$

(18)

with constant projections on the $z$ axis, $S_{i.z}\approx s_i$ (the $z$ axis is chosen for the direction of the spins in the fully polarized state). The equations of motions then lead to the eigenvalue equation:

$$\overleftrightarrow{A}{\overrightarrow{c}}_k=\hslash {\omega }_k{\overrightarrow{c}}_k$$

(19)

with the matrix:

$$A_{ij}=\left({\displaystyle \sum _n\left(J_{in}+J_{ni}\right)s_n}\right){\delta }_{ij}-\left(J_{ij}+J_{ji}\right)s_i.$$

(20)

For the $k$-th normal mode, with eigenvalue ${\omega }_k$ and eigenvector ${\overrightarrow{c}}_k={\left(c_{1,k},c_{2,k},\dots ,c_{N,k}\right)}^T$ (which can always be chosen real), the solution for the motion of an individual spin becomes:

$${\overrightarrow{S}}_i(t)=\left(\begin{array}{c}{c}_{i,k}{u}_k\cos ({\phi }_k-{\omega }_{k}t)\\ c_{i,k}{u}_k\sin ({\phi }_k-{\omega }_{k}t)\\ s_i\end{array}\right)$$

(21)

where $u_k$ and ${\phi }_k$ are an arbitrary overall amplitude and phase, which in the following are set to $u_k=1$ and ${\phi }_k=0$, without loss of generality.

The classical motion is described by a precession of each spin around the $z$ axis, with a spin deflection given by the coefficient $c_{i,k}$ in the eigenvector. Importantly, all spins ${\overrightarrow{S}}_i$ precess in phase (note that for negative $c_{i,k}$ the spin appears to be out of phase by π). The collective precession of the spins in a normal mode is thus characterized by different deflection angles for each spin, but equal phases for all spins. This is in difference to waves, or the solutions for extended systems, where the collective precession is characterized by equal deflection angles but different phases for the spin centers. It is, however, in close analogy to the elastic case, and we indeed recover the analogy of a celebrated result for molecular vibrations [32,33]:

All spins precess with identical frequency and all spins involved in the precession pass through, e.g., the x axis simultaneously.

This is a key finding of this chapter. The Hamilton matrix $H_{ij}$ in Equation (9) and the matrix $A_{ij}$ in Equation (20) are not identical, but are similar (in the mathematical sense). They thus exhibit identical eigenvalues, and the classical and quantum eigenvectors are related through:

$$c_{i,k}=\frac{\sqrt{2s_i}}{C_k}{v}_{i,k}$$

(22)

where a factor $\sqrt{2}$ has been included for convenience, and $C_k$ is an obvious normalization constant. The suggested procedure for obtaining the classical eigenvectors is to diagonalize the quantum Hamiltonian matrix Equation (9), and then to apply Equation (22).

Based on the classical solution we suggest two pictorial representations. The first consists of drawing the magnetic core of the molecule, and attaching a deflected arrow and a cone to each spin center, there the length of the cone corresponds to the spin length $s_i$ and its radius to $\left|c_{i,k}\right|$. For larger molecules, this representation can become confusing. The second representation consists of drawing a planar schematic of the magnetic core, and attaching a circle or disk to each spin center, with a radius given by $\left|c_{i,k}\right|$, and an arrow to indicate the location of the tip of the precessing spin vector. In both representations attention is given to the phases of the spin precession by plotting the arrows accordingly, i.e., all spins with positive value of $c_{i,k}$ are plotted in one direction, and those with negative $c_{i,k}$ are plotted with opposite deflection. For the example of a dimer, the two spin wave states are shown for both representations in Figure 4. It is noted that the latter representation could also be drawn without the circles or disks, i.e., with only the arrows representing the amplitudes of the spin deflections $c_{i,k}$, which would produce pictures in close analogy to those commonly used for representing molecular vibrations [32,33]. In the following, arrow heads are omitted for clarity.

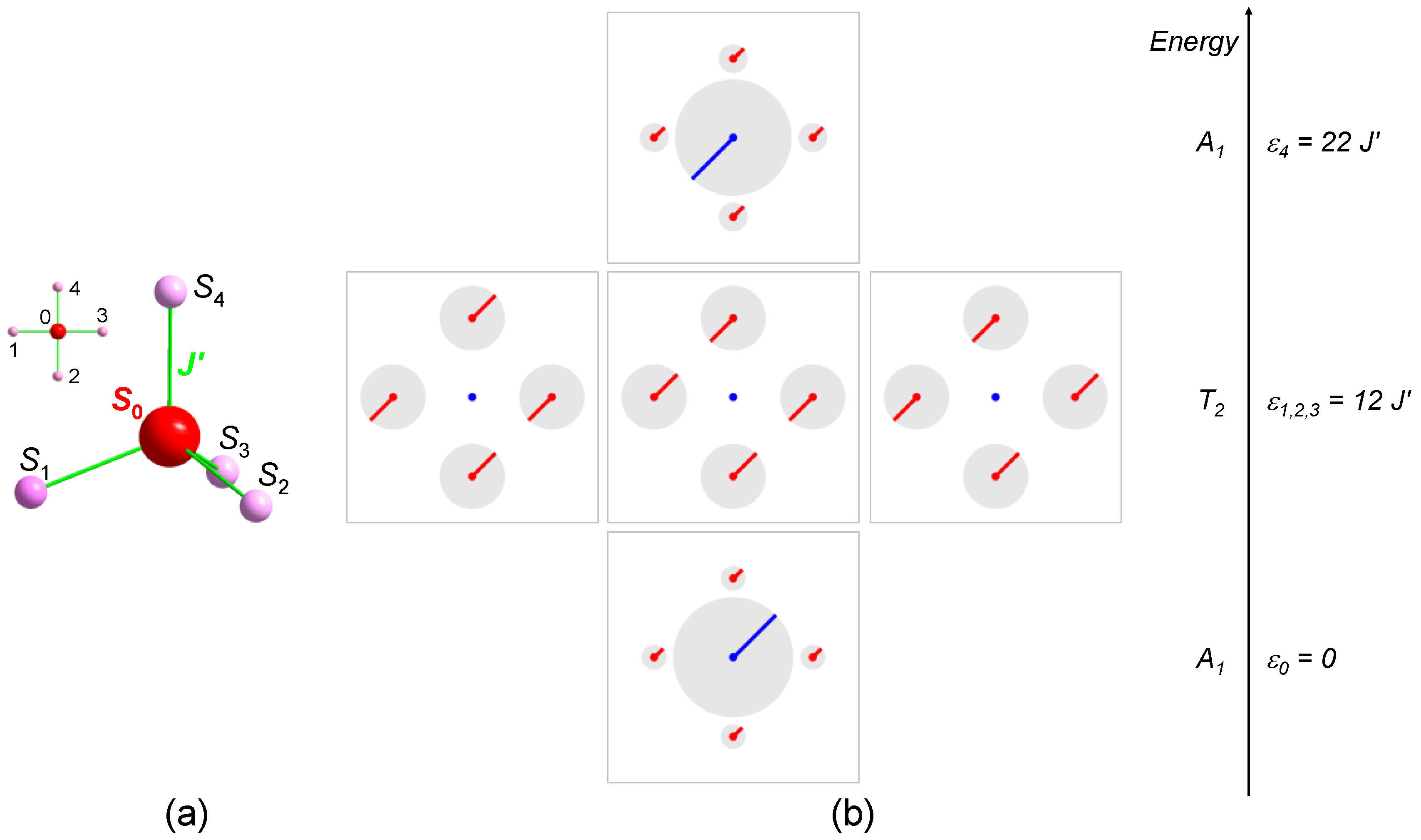
The chapter is concluded with emphasizing that also the mathematical tools familiar for calculating and analyzing molecular vibrations can be carried over, essentially one-to-one, to the case of the spin wave excitations. This is especially true for the symmetry concepts, which is outlined exemplarily for a hypothetical spin cluster of four spin-5/2 spins centered around a spin-12 spin, see Figure 5a. The presentation follows Reference [23]. This five-spin model will also be of use in the discussion of the Mn₁₀ cluster in the next chapter. The spin Hamiltonian is given by:

$$\widehat{H}=-J^{\prime }\left({\widehat{S}}_1+{\widehat{S}}_2+{\widehat{S}}_3+{\widehat{S}}_4\right)·{\widehat{S}}_0.$$

(23)

The energies and eigenstates can be trivially calculated using Kambe’s approach [29,34], the emphasis here is however on the methods discussed in this paper.

The FCSWT procedure starts from the fully polarized state $|M=M_{max}\rangle$ with $M_{max}=22$. The basis states for the subspace with $M=M_{max}-1=21$ are generated by applying Equation (8). This yields five states $|i\rangle$, where $i=0,\dots ,4$. The Hamiltonian matrix $H_{ij}$ is calculated with Equation (9) as:

$$\overleftrightarrow{H}=J^{\prime }\left(\begin{array}{ccccc}10& -\sqrt{30}& -\sqrt{30}& -\sqrt{30}& -\sqrt{30}\\ -\sqrt{30}& 12& 0& 0& 0\\ -\sqrt{30}& 0& 12& 0& 0\\ -\sqrt{30}& 0& 0& 12& 0\\ -\sqrt{30}& 0& 0& 0& 12\end{array}\right)+E_F$$

(24)

where $E_F=-120J^{\prime }$.

This matrix can be analytically diagonalized by using its spatial symmetry properties [33]. The point group of the model is $T_d$ and the five-dimensional Hilbert space decomposes into the irreps $2\times A_1+1\times T_2$. Instead of using the symmetry group $T_d$, it is easier to view the spin cluster as a planar four-pointed star (Figure 5a) and exploit its $D_4$ symmetry (the technique is similar to the descent-in-symmetry technique in ligand-field theory [33]). The $C_4$ symmetry element implies a quantum number κ with values $0,\pm \raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.$, $\pi$, and symmetry adapted linear combinations (SALCs) $|\kappa \rangle \propto {{\displaystyle \sum }}_{n=1}^4\exp \left[i\left(n-1\right)\kappa \right]|n\rangle$. From the five basis states two symmetry adapted states with $\kappa =0$ are obtained, namely $|A_1,0\rangle =|i=0\rangle$ and $|A_1,1\rangle \propto {{\displaystyle \sum }}_{i=1}^4|i\rangle$. Since the symmetry group is $D_4$, the two symmetry adapted states generated for $\kappa =\pm \raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ are energetically degenerate and can be linearly combined. We select $|T_2,0\rangle \propto \left(1+i\right)|\kappa =+\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\rangle +\left(1-i\right)|\kappa =-\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\rangle$ and $|T_2,1\rangle \propto \left(1-i\right)|\kappa =+\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\rangle +\left(1+i\right)|\kappa =-\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\rangle$. Finally, $|T_2,2\rangle \propto \kappa |=\pi \rangle$. The following SALCs result:

$$\begin{array}{c}|A_1,0\rangle =|0\rangle \\ |A_1,1\rangle =\frac{1}{2}\left(|1\rangle +|2\rangle +|3\rangle +|4\rangle \right)\\ |T_2,0\rangle =\frac{1}{2}\left(|1\rangle -|2\rangle -|3\rangle +|4\rangle \right)\\ |T_2,1\rangle =\frac{1}{2}\left(|1\rangle +|2\rangle -|3\rangle -|4\rangle \right)\\ |T_2,2\rangle =\frac{1}{2}\left(|1\rangle -|2\rangle +|3\rangle -|4\rangle \right)\end{array}$$

(25)

which also transform according to the irreps of the $T_d$ group. In this new basis the Hamiltonian matrix factorizes to:

$${\overleftrightarrow{H}}_{SALC}=J^{\prime }\left(\begin{array}{ccccc}10& -2\sqrt{30}& & & \\ -2\sqrt{30}& 12& & & \\ & & 12& & \\ & & & 12& \\ & & & & 12\end{array}\right)+E_F.$$

(26)

It thus remains to diagonalize a $2\times 2$ block, which yields eigenstates with energy $0$ and $22J^{\prime }$, and eigenfunctions $|{\epsilon }_0\rangle =0.739|A_1,0\rangle +0.674|A_1,1\rangle$ and $|{\epsilon }_4\rangle =0.674|A_1,0\rangle -0.739|A_1,1\rangle$, which belong to the irrep $A_1$ of the $T_d$ group. In addition, the energy spectrum exhibits a three-fold degenerate level at an excitation energy of $12J^{\prime }$, with eigenfunctions $|{\epsilon }_{k=1,2,3}\rangle =|T_2,k-1\rangle$, which belong to the irrep $T_2$.

In passing, it is noted that the $2\times 2$ block could also have been block-diagonalized by exploiting properties deduced in Section 2.1. The Hamiltonian Equation (23) is isotropic, and thus one of its eigenstates has to correspond to the $M=M_{max}-1$ component of the fully polarized state $|M=M_{max}\rangle$. Therefore, this eigenstate has the same energy as the ground state, i.e., ${\epsilon }_0=0$, and the corresponding wave function can be obtained by applying the total spin lowering operator ${\widehat{S}}^{-}$ to $|M=M_{max}\rangle$, which yields ${\widehat{S}}^{-}|M=M_{max}\rangle ={{\displaystyle \sum }}_i\sqrt{2s_i}|i\rangle$. Thus, one of the five eigenstates is already known, and can be used to block-diagonalize the sector transforming as the irrep $A_1$.

The resulting spin wave states are sketched in Figure 5b. From the pictorial representation it is immediately obvious that the spin waves at energies of $0$ and $22J^{\prime }$ indeed belong to the trivial irrep $A_1$. Also, they form a symmetric and anti-symmetric pair of states with respect to the spin precession of the central spin and the outer spins. In these two states, the collective spin precession is concentrated on the central spin, with weaker precession of the outer spins. In contrast, in the three $T_2$ states the central spin does not contribute to the precession at all, i.e., here the excitation is completely localized on the outer spin centers. These features are related to non-trivial, observable effects in e.g., the neutron scattering intensity, as will be discussed further below.

3. Applications

In the following, the zero-temperature excitations of three magnetic molecules, denoted here as Mn₁₀, Mn₇, and Mn₆, will be discussed in terms of FCSWT. All three molecules exhibit a fully polarized ground state, and were studied in detail by INS at low temperatures [23,24,25]. For Mn₁₀ and Mn₇ the discussion follows Refs. [23,24], for the single molecule magnet Mn₆ a FCSWT analysis was not attempted before. For all three molecules the spin wave matrix Equation (9) can be analytically diagonalized using symmetry concepts. This is especially true for the Mn₁₀ molecule, for which the matrix is of dimension $10\times 10$ and yet can be fully diagonalized thanks to the molecular $T_d$ point group symmetry. Mn₁₀ thus establishes a showcase example for the application of symmetry concepts. The Mn₇ disk-like molecule is distinguished by its cyclic structure, which results in spin wave excitations which are similar to “real” waves. Finally, the single molecule magnet Mn₆ brings in the additional aspect of a comparatively large Ising anisotropy. In fact, in contrast to most single molecule magnets, which are in the so-called strong exchange limit, Mn₆ is distinguished by a strong spin-mixing, which is favorable for experimentally observing the spin wave excitations by INS in such systems.

3.1. The Mn₁₀ Supetretrahedron

The mixed-valent supertetrahedral aggregate [Mn^III₆Mn^II₄(μ₄-O)₄(μ₃-N₃)₃(μ₃-Br)(Hmpt)₆(Br)] Br_0.7(N₃)_0.3∙2MeOH∙3MeCN (H₃mpt = 3-methylpentan-1,3,5-triol), or Mn₁₀ in short, has received significant interest due to its high-spin $S=22$ ferromagnetic ground state, and the chemical link to other compounds such as the Mn₁₉ cluster with even larger spin-ground states [35]. The magnetic core of the cluster consists of six spin-2 Mn^III ions halfway along the edges of a tetrahedron of four spin-5/2 Mn^II ions to form the supertetrahedron shown in Figure 6.

Due to the high molecular symmetry, magnetic anisotropy is negligible, and the Heisenberg exchange can be characterized by only two different coupling constants, $J_a$ and $J_b$, describing the coupling strengths between the Mn^III ions and between the Mn^II and Mn^III ions, respectively, see Figure 6b. The magnetism of the Mn₁₀ cluster can then be described by a Heisenberg Hamiltonian:

$$\widehat{H}=-J_a{\displaystyle \sum _{i,j\in M{n}^{III}}{\widehat{S}}_i·{\widehat{S}}_j}-J_b{\displaystyle \sum _{i\in M{n}^{II},j\in M{n}^{III}}{\widehat{S}}_i·{\widehat{S}}_j}$$

(27)

where in the second term the index $j$ refers to the Mn^III ions neighboring the $i$-th Mn^II ion. Both couplings are ferromagnetic supporting the experimentally observed $S=22$ ground state, and were determined to $J_a=18.4$ K, $J_b=7.4$ K. In the INS spectra, two cold peaks at 3.5 meV (peak I) and 7.0 meV (peak II) were observed, and associated to spin wave excitations [23].

Following the FCSWT procedure, the basis states in the subspace $M=M_{max}-1$ are generated from the component of the ferromagnetic ground state $|M=M_{max}\rangle$ with $M_{max}=22$, as described before in Equation (8), yielding ten states $|i\rangle$, where $i=0,\dots ,10$. The Hamiltonian matrix $H_{ij}=\langle i|\widehat{H}|j\rangle$ in this space of basis states can be calculated from Equation (9) to be:

$$\overleftrightarrow{H}=\left(\begin{array}{cccccccccc}a& & & & & \beta & \beta & & & \beta \\ & a& & & \beta & & \beta & \beta & & \\ & & a& & \beta & \beta & & & \beta & \\ & & & a& & & & \beta & \beta & \beta \\ & \beta & \beta & & b& \alpha & \alpha & \alpha & \alpha & \\ \beta & & \beta & & \alpha & b& \alpha & & \alpha & \alpha \\ \beta & \beta & & & \alpha & \alpha & b& \alpha & & \alpha \\ & \beta & & \beta & \alpha & & \alpha & b& \alpha & \alpha \\ & & \beta & \beta & \alpha & \alpha & & \alpha & b& \alpha \\ \beta & & & \beta & & \alpha & \alpha & \alpha & \alpha & b\end{array}\right)+E_F.$$

(28)

with the diagonal elements $a=6J_b$, $b=8J_a+5J_b$, the off-diagonal elements $\alpha =-2J_a$, $\beta =-\sqrt{5}{J}_b$, and the ground state energy $E_F=-48J_a-60J_b$. Applying group theory methods, the $M=M_{max}-1$ subspace decomposes into the irreps $2\times A_1+E+2\times T_2$ in $T_d$ and the Hamiltonian matrix is, after a straight forward but lengthy calculation, diagonalized to yield the eigenvalues and eigenstates:

$$\begin{array}{c}{\epsilon }_0=0\\ {\epsilon }_{1,2,3}=\frac{1}{2}\left(8J_a+11J_b-R\right)\\ {\epsilon }_4=11J_b\\ {\epsilon }_{5,6,7}=\frac{1}{2}\left(8J_a+11J_b+R\right)\\ {\epsilon }_{8,9}=12J_a+5J_b\end{array}$$

(29a)

$$\left(\begin{array}{c}{\overrightarrow{v}}_0^T\\ {\overrightarrow{v}}_1^T\\ {\overrightarrow{v}}_2^T\\ {\overrightarrow{v}}_3^T\\ {\overrightarrow{v}}_4^T\\ {\overrightarrow{v}}_5^T\\ {\overrightarrow{v}}_6^T\\ {\overrightarrow{v}}_7^T\\ {\overrightarrow{v}}_8^T\\ {\overrightarrow{v}}_9^T\end{array}\right)=\left(\begin{array}{cccccccccc}\frac{\sqrt{5}}{2}& \frac{\sqrt{5}}{2}& \frac{\sqrt{5}}{2}& \frac{\sqrt{5}}{2}& 1& 1& 1& 1& 1& 1\\ \alpha & -\alpha & -\alpha & \alpha & -1& 0& 0& 0& 0& 1\\ -\alpha & -\alpha & \alpha & \alpha & 0& 0& -1& 0& 1& 0\\ -\alpha & \alpha & -\alpha & \alpha & 0& -1& 0& 1& 0& 0\\ -\frac{3}{\sqrt{5}}& -\frac{3}{\sqrt{5}}& -\frac{3}{\sqrt{5}}& -\frac{3}{\sqrt{5}}& 1& 1& 1& 1& 1& 1\\ -\beta & \beta & \beta & -\beta & -1& 0& 0& 0& 0& 1\\ \beta & \beta & -\beta & -\beta & 0& 0& -1& 0& 1& 0\\ \beta & -\beta & \beta & -\beta & 0& -1& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& -1& 0& -1& 0& 1\\ 0& 0& 0& 0& 0& -1& 1& -1& 1& 0\end{array}\right)$$

(29b)

where $R=\sqrt{64J_a^2-16J_a{J}_b+41J_b^2}$, $\alpha =\left(8J_a+R-J_b\right)/\left(4\sqrt{5}{J}_b\right)$, and $\beta =\left(8J_a-R+J_b\right)/\left(4\sqrt{5}{J}_b\right)$.

Figure 7 shows concisely the spin waves of Mn₁₀ for $J_a/J_b=2.54$, the ratio observed experimentally. A threefold degenerate first excited state $T_2$ is obtained. In these spin wave modes only the outer Mn^II spins show a spin deviation, while the Mn^III spins are not involved at all in the precession. In the next higher lying $A_1$ mode, all Mn^II ions precess with identical amplitudes, and so do the Mn^III spins, but with spin deflections opposite to the Mn^II spins. The lowest and highest $A_1$ modes thus appear to be the symmetric and anti-symmetric pairs with respect to the Mn^II and Mn^III precessions. The $T_2$ and $E$ modes at higher energies show precession of only the core Mn^III spins: in the threefold degenerate $T_2$ mode, the precessing spins are further apart than in the twofold degenerate $E$ mode, where neighboring spins precess in counterphase, resulting in the highest-energy magnon of the system.

In Figure 8a, the low-temperature experimental and simulated INS spectrum for Mn₁₀ is shown. The ferromagnetic ground state is determined by the spin quantum numbers $S=22,M=22$, and two transitions I and II into states with spin quantum numbers $S=21,M=21$ are observed. The spin wave energy spectrum and the observed transitions are indicated in the inset to Figure 8a, showing that the first $T_2$ and second $A_1$ spin wave modes were detected in this experiment. The intense peak I corresponds to the threefold degenerate $T_2$ mode, and the weaker peak II to the $A_1$ magnon.

It is instructive to compare the spin waves in Mn₁₀ with those obtained for the five-spin model previously discussed in Section 2.3, see Figure 5. The five-spin model was introduced in Reference [23] as a low-energy approximation to the full magnetic model of Mn₁₀, by assuming dominant exchange interactions between the six Mn^III spins ($J_a\gg J_b$), in which case these behave like a giant spin $s_0={{\displaystyle \sum }}_{i=5}^{10}{s}_i=12$. The five-spin model thus reduces the full problem by ignoring the individual magnetic degrees of freedom within the strongly connected core of $s=2$ spins. However, it preserves a complete description of the weakly bound outer spins, which are responsible for the low-energy spectrum of the system. Comparison of Figure 5b and Figure 7 shows that the low energy spin wave modes $T_2$ and $A_1$ in the two models are the same in terms of both energies and wavefunctions. The pictorial representation of the spin waves provides us with an immediate justification for the success of the five-spin model for analyzing the low-energy excitations in Mn₁₀.

Based on Figure 7, it is also possible to infer the main INS interference term relevant for each transition [36]. The INS interference terms lead to a characteristic dependence of the INS intensity as function of momentum transfer Q. The Q-dependence is thus sensitive to the internal structure of the wavefunctions involved in the transition, and provides us with an experimentally accessible fingerprint of the wavefunctions. The three wavefunctions of the lowest $T_2$ magnons have non-zero components only at the exterior spins at the vertices of the Mn₁₀ supertetrahedron. Based on the dimensions of the supertetrahedron, the interference term of this transition is expected at low $Q$ of about 1 Å⁻¹. On the other hand, the wavefunction corresponding to the second $A_1$ mode has non-zero components on all spins, so that interference is expected to also occur at larger reciprocal space distances. Figure 8b shows the calculated $Q$-dependence for the $T_2$ and $A_1$ modes, which are indeed markedly different for the two cases. The blue and red arrows indicate the reciprocal space distances obtained by the above simple considerations, clearly showing that the dominant interference terms of the scattering modes can be anticipated from the pictorial representation of the wavefunctions.

3.2. The Mn₇ Disk Molecule

The high ground-state spin ($S=16$) mixed-valence manganese disk (NHEt₃)[Mn₇(N₃)₆(teaH)₆], or Mn₇ in short, was synthesized from a lower-spin ($S=11$) Mn₇ compound by a replacement of a peripheral ligand [24]. The fact that a large change of magnetic properties results from a peripheral chemical modification prompted a detailed investigation of the system [24,37]. The molecular structure is shown in Figure 9. Three spin-2 Mn^III ions and three spin-5/2 Mn^II ions are positioned alternately on the outer hexagon with the remaining spin-5/2 Mn^II ion in the center of the disk.

The Hamiltonian describing the isotropic Heisenberg interactions and single-ion magnetic anisotropy in the molecule is written as:

$$\widehat{H}=-J_a{\displaystyle \sum _{i=1}^3{\widehat{S}}_i·{\widehat{S}}_{i+3}}-J_b\left({\displaystyle \sum _{i=4}^5{\widehat{S}}_i·{\widehat{S}}_{i-2}}+{\widehat{S}}_6·{\widehat{S}}_1\right)-J_1{\displaystyle \sum _{i=1}^3{\widehat{S}}_i·{\widehat{S}}_7}-J_2{\displaystyle \sum _{i=4}^6{\widehat{S}}_i·{\widehat{S}}_7}+D{\displaystyle \sum _{i=1}^3{S}_{i,z}^2}.$$

(30)

The single-ion magnetic anisotropy was found to be zero within experimental error ($D=0$), and the exchange couplings were determined to $J_a=J_b=5.8$ K, $J_1=-2.0$ K and $J_2=2.45$ K, for one of the species [24]. Two cold INS excitations, associated to spin waves, were observed at 0.3 meV and 1.17 meV [24]. Despite the antiferromagnetic coupling $J_1$, the fully polarized state $|M=M_{max}\rangle$ with $M_{max}=16$ is ground state, and FCSWT is applicable. The spin wave sector is spanned by seven basis states obtained by applying the spin-lowering operators to the ground state, Equation (8). The Hamiltonian matrix $H_{ij}$ in this basis can be calculated using Equation (9) to be a $7\times 7$ matrix of the following form:

$$\overleftrightarrow{H}=\left(\begin{array}{ccccccc}a& & & \alpha & & \beta & \gamma \\ & a& & \beta & \alpha & & \gamma \\ & & a& & \beta & \alpha & \gamma \\ \alpha & \beta & & b& & & \delta \\ & \alpha & \beta & & b& & \delta \\ \beta & & \alpha & & & b& \delta \\ \gamma & \gamma & \gamma & \delta & \delta & \delta & c\end{array}\right)+E_F$$

(31)

with the diagonal elements $a=-3D+\frac{5}{2}\left(J_1+J_a+J_b\right)$, $b=\frac{5}{2}{J}_2+2J_a+2J_b$, $c=6J_1+\frac{15}{3}{J}_2$, the off-diagonal elements $\alpha =-\sqrt{5}{J}_a$, $\beta =-\sqrt{5}{J}_b$, $\gamma =-\sqrt{5}{J}_1$, $\delta =-\frac{5}{2}{J}_1$, and the ground state energy $E_F=11D-15\left(J_a+J_b+J_1+\frac{5}{4}{J}_2\right)$.

The symmetry of the Hamiltonian can again be used to block-diagonalize this matrix. Instead of the $D_3$ symmetry of the model, it is simpler to use the $C_3$ point group. The $M=M_{max}-1$ subspace decomposes into the irreducible representations $3\times A+2\times E$ in $C_3$ (and $1\times A_1+2\times A_2+2\times E$ in $D_3$). The following SALCs are constructed:

$$\begin{array}{c}|A,0\rangle =\frac{1}{\sqrt{3}}\left(|1\rangle +|2\rangle +|3\rangle \right)\\ |A,1\rangle =\frac{1}{\sqrt{3}}\left(|4\rangle +|5\rangle +|6\rangle \right)\\ |A,2\rangle =|7\rangle \\ |E,0,\pm \rangle =\frac{1}{\sqrt{3}}\left(|1\rangle +e^{\pm i\phi }|2\rangle +e^{\mp i\phi }|3\rangle \right)\\ |E,1,\pm \rangle =\frac{1}{\sqrt{3}}\left(|4\rangle +e^{\pm i\phi }|5\rangle +e^{\mp i\phi }|6\rangle \right)\end{array}$$

(32)

where $\phi =\frac{2}{3}\pi$. In this basis, the $7\times 7$ Hamilton matrix in Equation (31) reduces to $3\times 3$ and $2\times 2$ block matrices in the $A$ and $E$ subspaces, respectively. The $A$ matrix can be further reduced into $1\times 1$ and $2\times 2$ matrices by exploiting the $D_3$ symmetry, since $A=1\times A_1+2\times A_2$. Alternatively, for the isotropic case $D=0$, one can make use of principles found before, namely that the $M=M_{max}-1$ component of the $S=S_{max}$ ground state multiplet, or the state ${\widehat{S}}^{-}|M=M_{max}\rangle ={{\displaystyle \sum }}_i\sqrt{2s_i}|i\rangle$, is a known eigenstate of the Hamiltonian matrix Equation (31), which belongs to the trivial irrep $A_1$ and has excitation energy ${\epsilon }_0=0$. Expressing this state in terms of the SALCs in Equation (32) yields:

$$|A_1\rangle =\frac{1}{4\sqrt{2}}\left(2\sqrt{3}|A,0\rangle +\sqrt{15}|A,1\rangle +\sqrt{5}|A,2\rangle \right)$$

(33)

which is easily confirmed to belong to $A_1$ and has energy zero. The two basis functions in the $A_2$ subspace are then straightforwardly constructed:

$$|A_2,0\rangle =\frac{1}{2}\left(-|A,1\rangle +\sqrt{3}|A,2\rangle \right)$$

(34a)

$$|A_2,1\rangle =\frac{1}{4\sqrt{2}}\left(2\sqrt{5}|A,0\rangle -3|A,1\rangle -\sqrt{3}|A,2\rangle \right).$$

(34b)

With the above basis functions the two $2\times 2$ block matrices in the $A_2$ and $E$ subspaces, respectively, are finally obtained as:

$${\overleftrightarrow{H}}_{A_2}=\left(\begin{array}{cc}4\left(\kappa +J_1\right)& \sqrt{2}\left(\kappa -3J_1\right)\\ \sqrt{2}\left(\kappa -3J_1\right)& \frac{1}{2}\left(\kappa +9J_1+20J_2\right)\end{array}\right)+E_F$$

(35)

$${\overleftrightarrow{H}}_E=\left(\begin{array}{cc}\frac{5}{2}\left(\kappa +J_1\right)& -\sqrt{5}\left(J_a-e^{-i\phi }{J}_b\right)\\ -\sqrt{5}\left(J_a-e^{+i\phi }{J}_b\right)& 2\kappa +\frac{5}{2}{J}_2\end{array}\right)+E_F$$

(36)

where $\kappa =J_a+J_b$. They both are trivially diagonalized.

The spin waves resulting from Hamiltonian Equation (31) with the parameters of Mn₇ are depicted in Figure 10a. As always, for the $A_1$ spin wave the spin precession is completely in phase. The lowest $A_2$ spin wave is characterized by a dominating spin precession of the central spin, while the spins on the outer ring are essentially not involved. In the remaining five higher-lying spin wave states, it is vice versa, i.e., here the central spin is essentially not involved (for the two $E$ doublets its deflection is strictly zero), and the excitation is concentrated on the ring.

In fact, these spin wave states nearly exactly correspond to the spin waves in a hexanuclear ferromagnetic ring with alternating spins ($s_1=2$ and $s_2=5/2$) and homogenous couplings ($J_a=J_b=J$), which are plotted for comparison in Figure 10b. The first excited $A_2$ spin wave of the Mn₇ molecule is missing in the ring system, since its contribution is dominantly located on the central spin which is not present in the ring system. For the other states, the similarity is however obvious, i.e., all details are reproduced. In both systems, a cosine- or sine-type modulation of the spin deflections on the Mn^II and Mn^III sublattices along the ring can be observed. That is, for the highest $A_2$ spin wave the wave function (for the spins along the ring) is of the form $a|A,0\rangle -b|A,1\rangle \propto a\left(|1\rangle +|2\rangle +|3\rangle \right)-b\left(|5\rangle +|6\rangle +|4\rangle \right)$, with positive real values $a,b$. For the ‘+’ components of the two $E$ doublets the wave functions are of the form $\alpha |E,0,+\rangle +\beta e^{-i\phi }|E,1,+\rangle$ and $-\beta |E,0,+\rangle +\alpha e^{-i\phi }|E,1,+\rangle$, respectively, and similarly for the ‘−’ components, with positive real values $\alpha ,\beta$. The energetically degenerate ‘+’ and ‘−’ components of an $E$ doublet can be linearly combined to yield the real-valued, cosine- and sine-type wave functions $\alpha \left(|1\rangle +\cos \phi |2\rangle +\cos \phi |3\rangle \right)+\beta \left(|5\rangle +\cos \phi |6\rangle +\cos \phi |4\rangle \right)$ and $\alpha \left(\sin \phi |2\rangle -\sin \phi |3\rangle \right)+\beta \left(\sin \phi |6\rangle -\sin \phi |4\rangle \right)$, which give rise to the $\left(1,-\frac{1}{2},-\frac{1}{2}\right)$ and $\left(0,-\frac{1}{2}\sqrt{3},\frac{1}{2}\sqrt{3}\right)$ patterns of the spin deflections on the sublattices visible in the plots in Figure 10 for the cosine- and sine-type wave functions. The values for $a,b$ and $\alpha ,\beta$ are of course not exactly identical for Mn₇ and the ferromagnetic ring, because of the additional coupling to the central spin in the Mn₇ molecule, but they are very close.

Instead of choosing the cosine- and sine-type linear combinations of the two states of an $E$ doublet, one also could express them directly as $\alpha \left(|1\rangle +e^{\pm i\phi }|2\rangle +e^{\mp i\phi }|3\rangle \right)+\beta \left(|5\rangle +e^{\pm i\phi }|6\rangle +e^{\mp i\phi }|4\rangle \right)$ and −$\beta \left(|1\rangle +e^{\pm i\phi }|2\rangle +e^{\mp i\phi }|3\rangle \right)+\alpha \left(|5\rangle +e^{\pm i\phi }|6\rangle +e^{\mp i\phi }|4\rangle \right)$, respectively. These wave functions are nothing else than “real” spin waves, with amplitudes of the form $u\left(x,t\right)\propto u_0{e}^{i\left(kx-\omega t\right)}$, where the pseudo wavevector $k$ assumes the values $k=0,\pm \frac{2}{3}\frac{\pi }{a}$ (and with $u_0$, $x$, and the size of the unit cell $a$, chosen properly). The association of the five highest spin waves in Mn₇ to “real” spin waves on a ferromagnetic chain manifests itself also by comparing energies. A ring consisting of six spins allows for six spin wave modes with only a few distinct $k$ values. Increasing the number of spins would allow for more modes, and more $k$ values. When the number of spins goes to infinity, the $\epsilon \left(k\right)$ dependence becomes continuous and the full dispersion relation $\epsilon \left(k\right)$ of the infinite spin chain is recovered. One can then describe the spectrum in terms of usual running waves for translationally invariant models, rather than the standing waves seen in the finite systems. Figure 11 plots both the spin wave spectrum of Mn₇ and the dispersion relation of a $s_1=2$, $s_2=5/2$ ferromagnetic chain, which is given as [38]:

$${\epsilon }_{\pm }(k)=J\left(s_1+s_2\pm \sqrt{s_1^2+s_2^2+2s_1{s}_2\cos ka}\right).$$

(37)

As expected for the two-spin magnetic unit cell, there are two modes in the infinite chain, the low-energy acoustic magnon branch, and a high-energy optical magnon branch. Comparison between the spin waves in the Mn₇ molecule and the theoretical dispersion of the infinite chain gives a surprisingly good agreement. In Mn₇ the highest $A_2$ spin wave is somewhat raised in energy due to the lower $A_2$ spin wave present in Mn₇. It is finally noted that, as shown before for the case of the Mn₁₀ cluster in Section 3.1, the specific structure of the wave functions is also revealed by a characteristic Q-dependence of the INS intensity, which is discussed in Reference [24].

3.3. The Mn₆ Single Molecule Magnet

The single molecule magnet (SMM) Mn₆O₂(Et-sao)₆(O₂CPh)₂(EtOH)₄(H₂O₂)₂, or Mn₆ in short, consists of six spin-2 Mn^III ions forming two triangles bridged by oxygen atoms, as shown in Figure 12. In contrast to most SMMs, Mn₆ exhibits relatively weak exchange couplings in comparison to the single-ion anisotropies, which leads to a breakdown of the giant-spin model usually employed for describing SMMs, with corresponding interesting effects [25]. It also results in relatively low-lying spin wave excitations, which is useful for experimental observation by INS. The ferromagnetic interactions between the Mn^III spins in Mn₆ result in a $S=12$ ferromagnetic ground state, with a large Ising-type ZFS due to the Mn^III single-ion anisotropies, as it is characteristic for SMMs [4,5].

The magnetic properties of the compound, as relevant for this work, can be described by the Hamiltonian:

$$\begin{array}{cc}\hfill \widehat{H}=& -J_1{\widehat{S}}_1·{\widehat{S}}_{1^{\prime }}-J_2\left({\widehat{S}}_1·{\widehat{S}}_2+{\widehat{S}}_2·{\widehat{S}}_3+{\widehat{S}}_1·{\widehat{S}}_3+{\widehat{S}}_{1^{\prime }}·{\widehat{S}}_{2^{\prime }}+{\widehat{S}}_{2^{\prime }}·{\widehat{S}}_{3^{\prime }}+{\widehat{S}}_{1^{\prime }}·{\widehat{S}}_{3^{\prime }}\right)\hfill \\ & -J_3\left({\widehat{S}}_1·{\widehat{S}}_{3^{\prime }}+{\widehat{S}}_{1^{\prime }}·{\widehat{S}}_3\right)+{\displaystyle \sum _{i=1}^{}{D}_i{S}_{i,z}^2}\hfill \end{array}$$

(38)

which includes the Heisenberg exchange terms and second-order single-ion anisotropies. Smaller anisotropic contributions ($~S_x{}^2-S_y{}^2$, $~O_{40}$) are ignored. The single-ion anisotropy terms for the sites $1$ and $3$ are assumed to be equal ($D_1=D_3$) because of similar ligand environment of the ions. For further details see Reference [25]. In the INS spectrum, six cold transitions were observed in the range of 1 meV to 5 meV, which could be reproduced with $J_1=7.08$ K, $J_2=3.60$ K, $J_3=0.81$ K, $D_1=-2.67$ K, and $D_2=-11.3$ K.

The application of FCSWT to SMMs needs some discussion. The slow magnetic relaxation in SMMs such as Mn₆ is associated with tunneling terms in the full spin Hamiltonian, which are not included in Equation (38). These terms lead to a mixing of the $|M=M_{max}\rangle$ and $|M=-M_{max}\rangle$ states, with a corresponding non-zero tunneling splitting [5]. Therefore, the fully polarized state $|M=M_{max}\rangle$ and its counter part $|M=-M_{max}\rangle$ are not ground states, and the condition for the applicability of FCSWT is strictly violated. However, the tunneling splitting of the states in the $M=\pm M_{max}$ and $M=\pm (M_{max}-1)$ sectors is tiny in comparison to the energies of these states, and therefore can be safely neglected in the calculation of these energies. This has justified using the Hamiltonian Equation (38) in the analysis of the INS data, and within the same realm the application of FCSWT to SMMs is justified.

Within these limits, and according to Equation (38), the ground state of Mn₆ is ferromagnetic $|M=M_{max}\rangle$ with $M_{max}=12$. The spin wave sector is spanned by six basis states obtained again from Equation (8). The Hamiltonian matrix $H_{ij}$ in this basis is calculated as usual from Equation (9), yielding a $6\times 6$ matrix of the form:

$$\overleftrightarrow{H}=\left(\begin{array}{cccccc}a& \beta & \beta & \alpha & & \gamma \\ \beta & b& \beta & & & \\ \beta & \beta & c& \gamma & & \\ \alpha & & \gamma & a& \beta & \beta \\ & & & \beta & b& \beta \\ \gamma & & & \beta & \beta & c\end{array}\right)+E_F$$

(39)

with the diagonal terms $a=-3D_1+2J_1+4J_2+2J_3$, $b=-3D_2+4J_2$, $c=-3D_1+4J_2+2J_3$, the off-diagonal terms $=-2J_1$, $\beta =-2J_2$, $\gamma =-2J_3$, and the ground state energy $E_F=\frac{44}{3}{D}_1+\frac{22}{3}{D}_2-4J_1-24J_2-8J_3$.

As before, one can use the symmetry of the Hamiltonian to reduce the matrix. Within the $C_i$ symmetry group of the molecule, the reducible representation of the spin wave subspace decomposes into $3\times A_g+3\times A_u$. Assuming the $D_2$ symmetry group of the magnetic model, the decomposition yields $3\times A+3\times B_3$, which gives no possibility of further reducing the matrix using point group symmetries. The $3\times 3$ matrices can be solved analytically, but the procedure is tedious and the results lengthy, and not given here.

The final result, for the experimental values of the parameters, is depicted in Figure 13a. All six spin wave modes in Mn₆ are nondegenerate and reflect the inversion symmetry of the spin model. The energy of the lowest excited $A_g$ state corresponds to the ZFS due to the non-zero single-ion anisotropy of the Mn^III ions. The precession in the higher-energy modes shifts from being dominant at the exterior 2 and 3 spins towards the strongly coupled spin 1 in the higher-energy modes.

The INS data recorded on Mn₆ at low temperatures are shown in Figure 13b. In the INS spectrum, six cold magnetic transitions can be identified (I at 1.14 meV, II at 1.38 meV, III at 2.28 meV, IV at 4.19 meV, V at 4.44 meV, and VI at 4.97 meV). The peaks can be well reproduced with the Hamiltonian Equation (38) using the parameters given before [25]. The six experimentally observed INS transitions are immediately associated to the six spin wave modes in Mn₆, as shown in Figure 13c. Therefore, in the case of the SMM Mn₆, all spin waves modes expected from and predicted by FCSWT have been detected in the experiment.

It is finally mentioned that in Reference [25] the INS on an analogous compound Mn₆O₂(Et-sao)₆(O₂CPh(Me)₂)₂(EtOH)₆ was also reported. In this compound, five peaks were observed at low temperatures, which could be understood using the same spin wave approach discussed here, and be associated to the five lowest spin wave modes.

4. Conclusions

In conclusion, we have discussed the concepts and applications of the ferromagnetic cluster spin wave theory (FCSWT) to excitations in finite, bounded, magnetic systems from the ferromagnetic ground state. The focus of the discussion was on high-spin molecular nanomagnets and single molecule magnets, as these two classes of materials have received huge interest from the scientific community over the last two decades. Additionally, we introduced a novel approach for visualizing the calculated spin wave excitations.

In the second part of the paper, a detailed discussion of FCSWT and the spin wave visualization has been presented for three real-world examples: (i) FCSWT applied to a large-spin ground state supertetrahedron Mn₁₀ molecule yields exact results for the energies and wavefunctions, and the visualized spin wave modes of this high-symmetry molecule provide insight into symmetries, energies and interference terms of the spin wave peaks observed in the neutron scattering data; (ii) FCSWT applied to the disk molecule Mn₇ results in wave-like spin wave states for the spins along the disk and provides an understanding of how the spin wave character progresses towards the extended systems; and (iii) FCSWT can be applied to single molecule magnets because of small tunneling splittings between the ground-state and the magnon sectors, as shown exemplarily for the Mn₆ molecule.

As an outlook, it is emphasized that the FCSWT is not restricted to this type of systems, but should be highly useful also, e.g., in connection with magnetocaloric nanomagnetic materials and the advent of new Lanthanide-based molecular nanomagnets. While in the discussion of the specific examples we have focused on analytical and physical insights into the studied molecules, it shall be stressed again that the FCSWT approach in its simple “recipe” form is very well suited for the practical experimentalist looking to describe their data.