Pyridine-2,6-Dicarboxylic Acid Esters (pydicR2) as O,N,O-Pincer Ligands in CuII Complexes
Abstract
1. Introduction
2. Results and Discussion
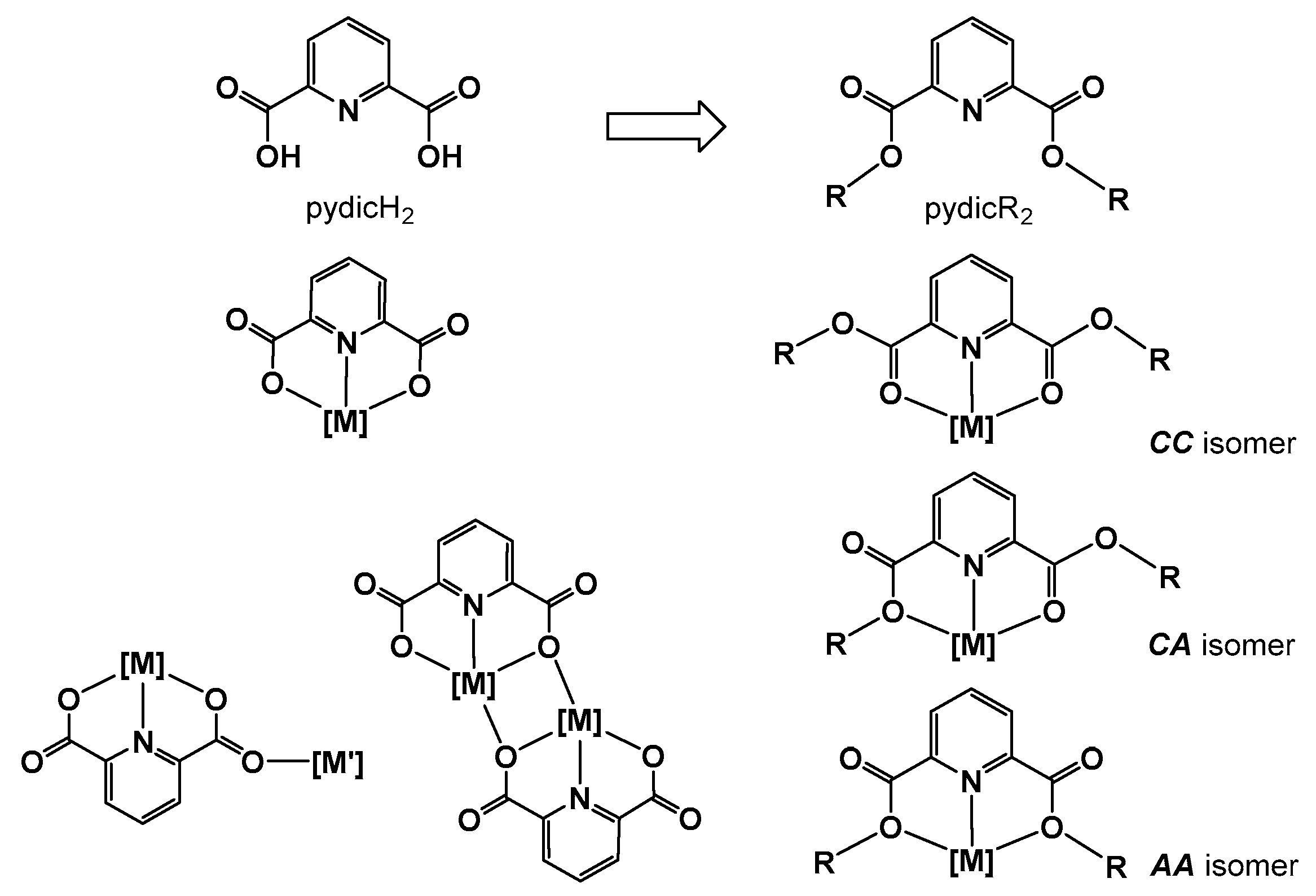
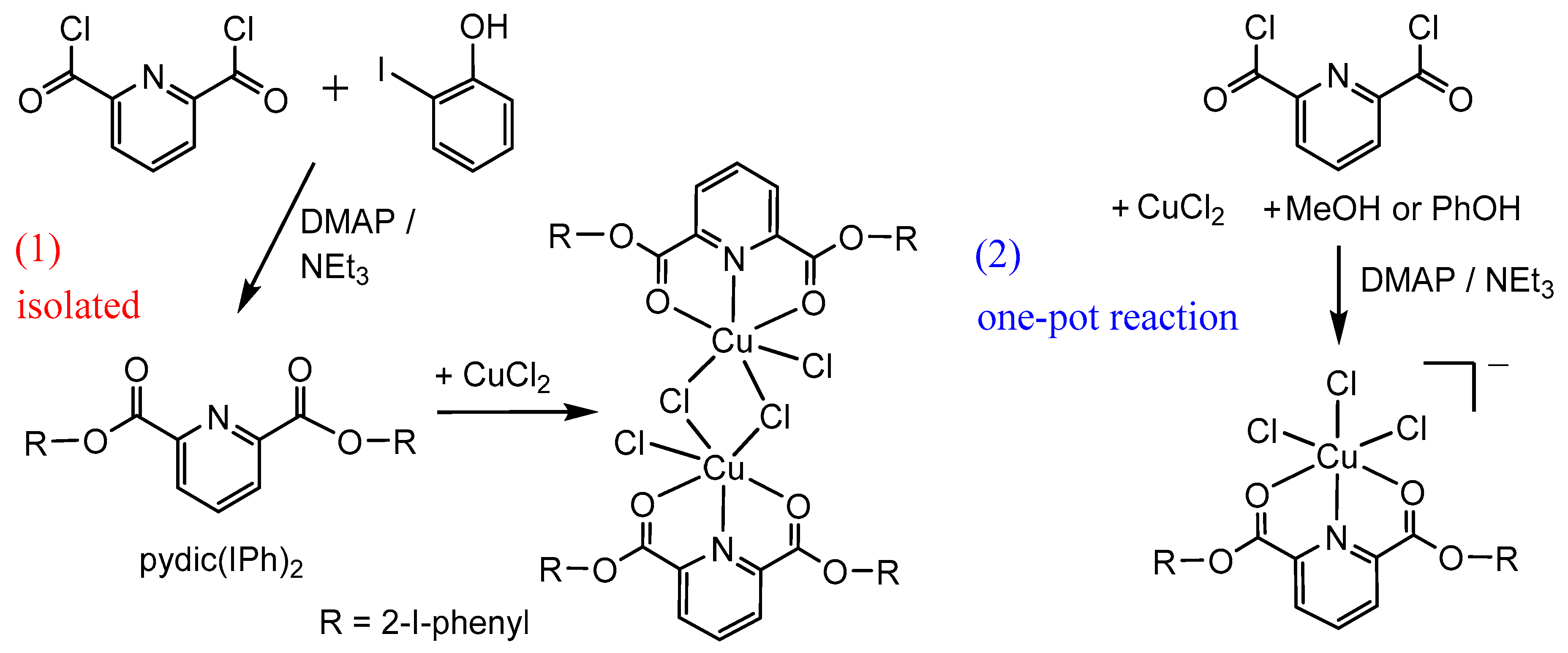
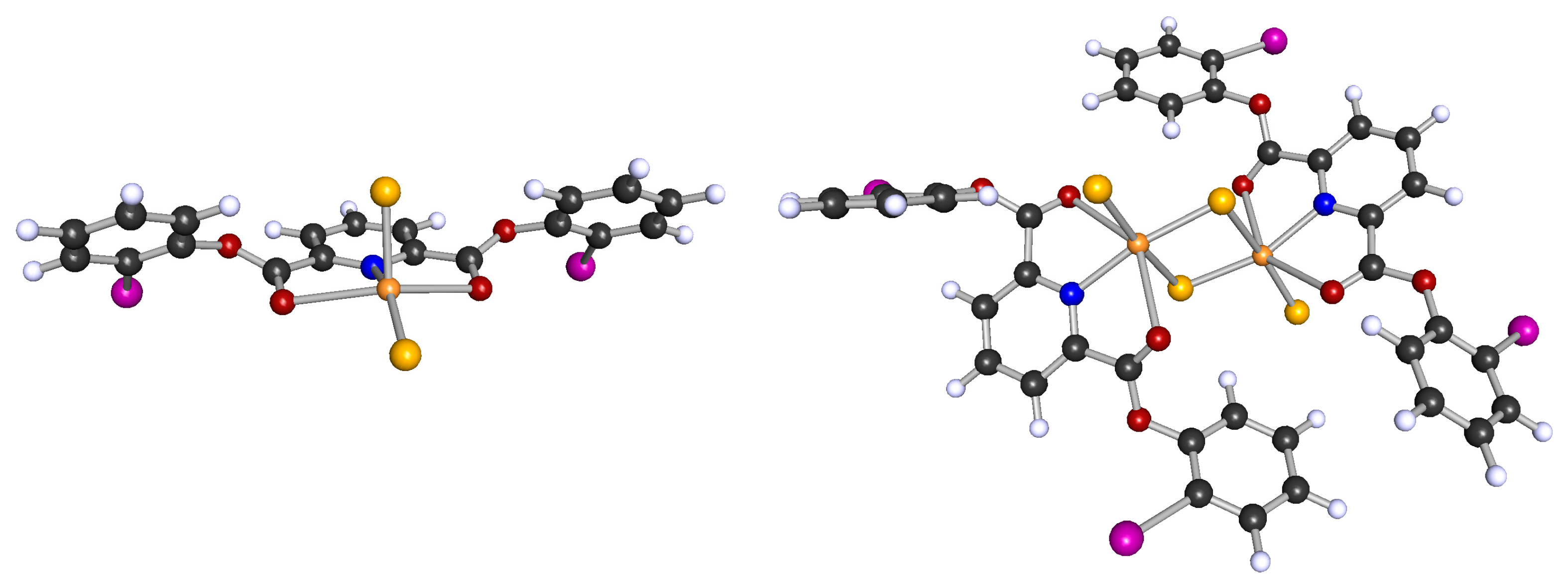
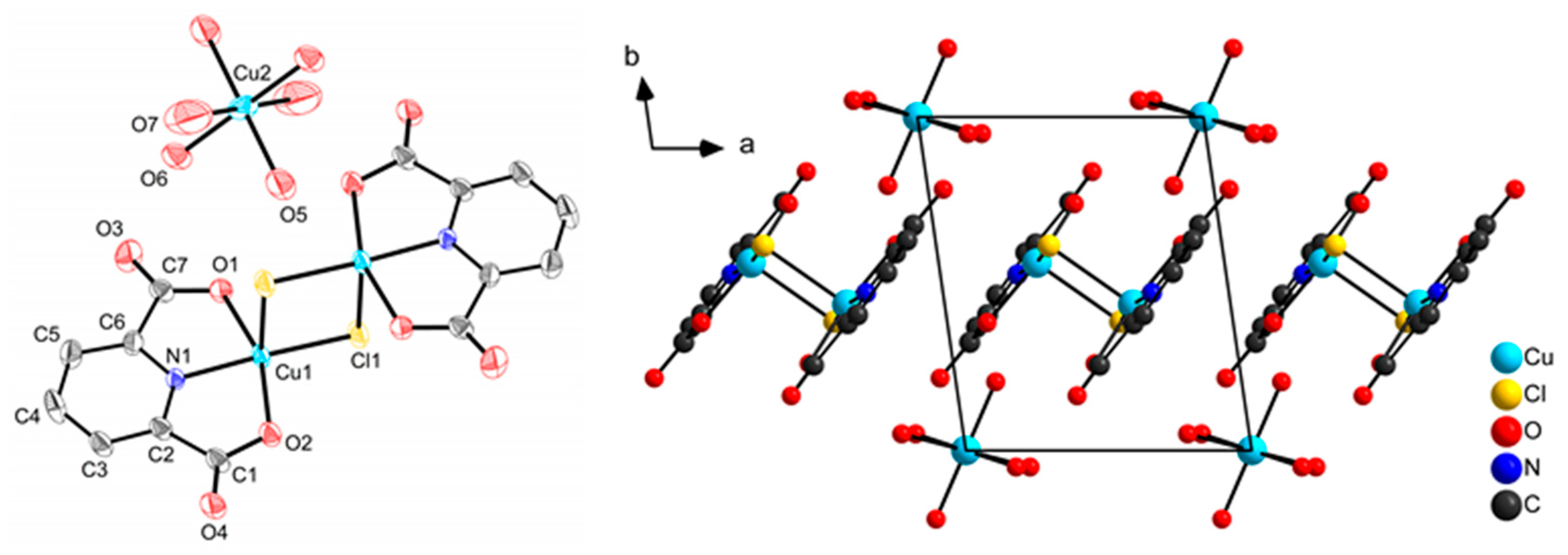
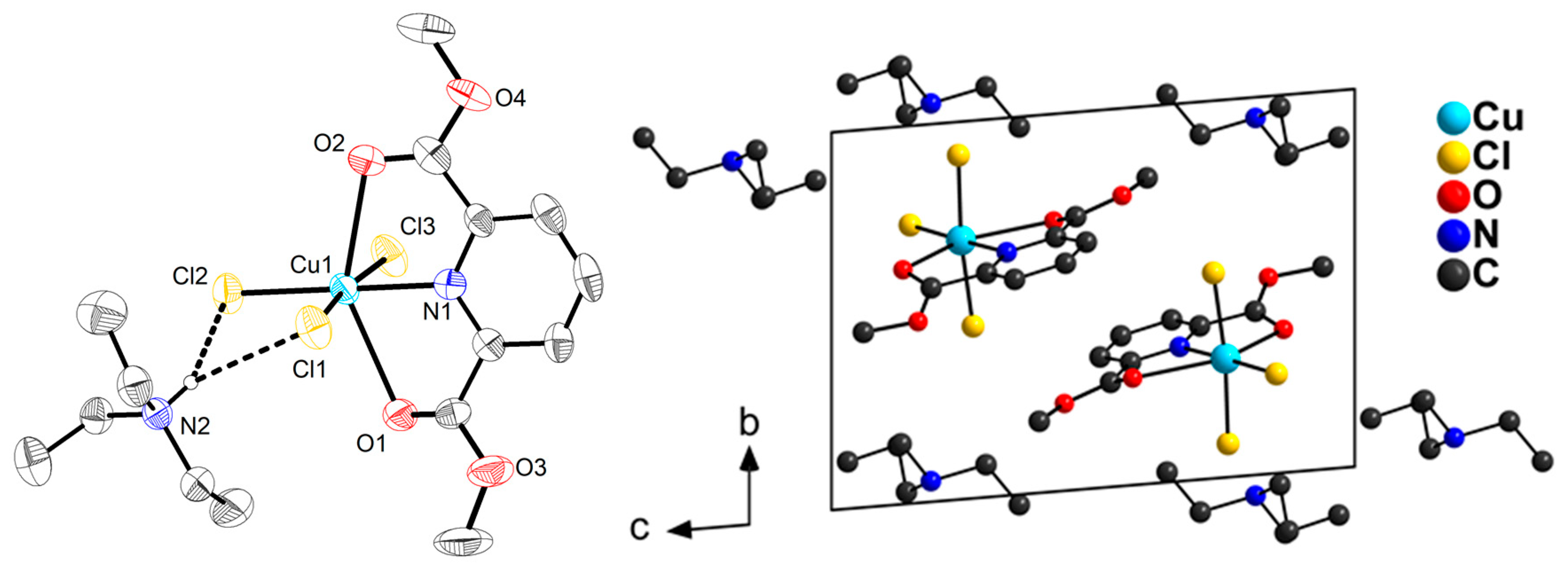
2.1. Synthesis and Molecular Structures of pydicR2 Ligands and their CuII Complexes
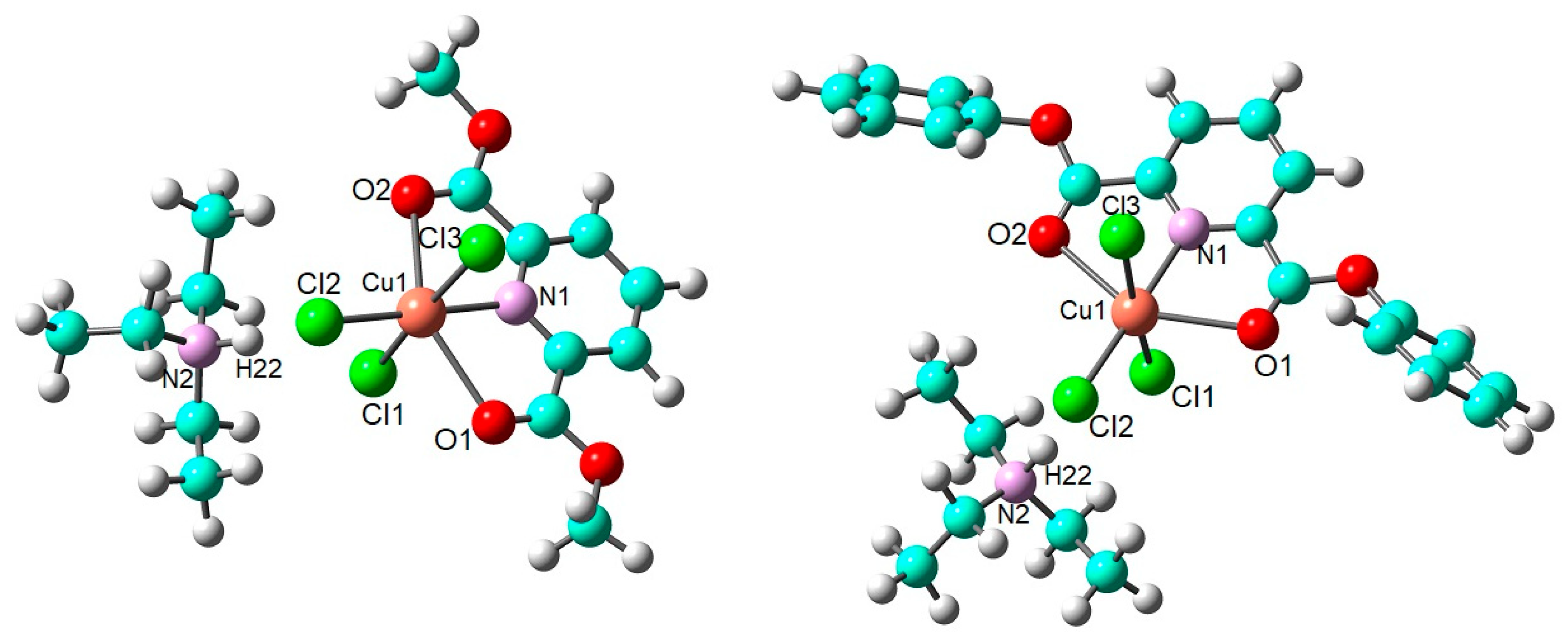
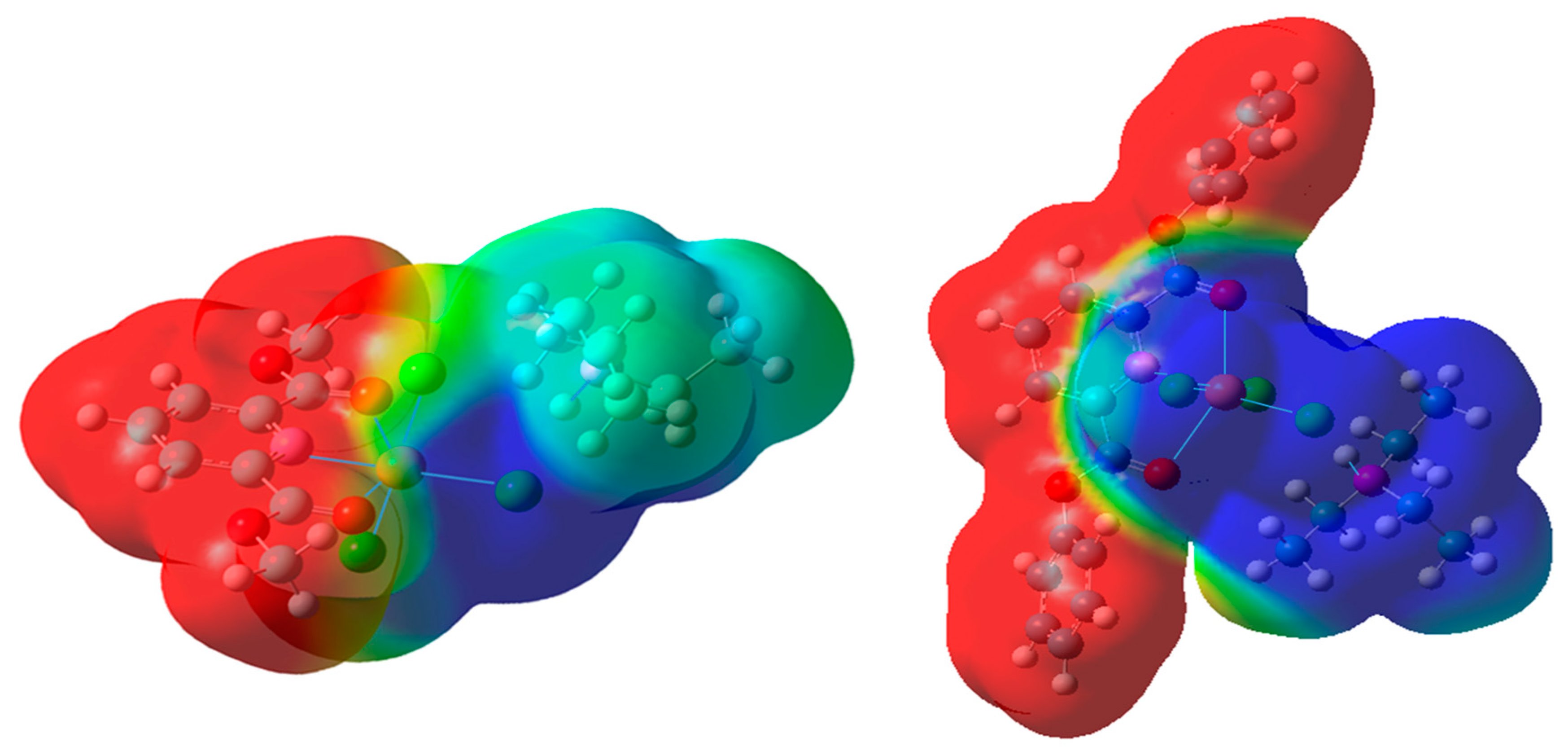
2.2. DFT Calculations on the Solvation of (HNEt3)[Cu(pydicR2)Cl3] (R = Me or Ph)
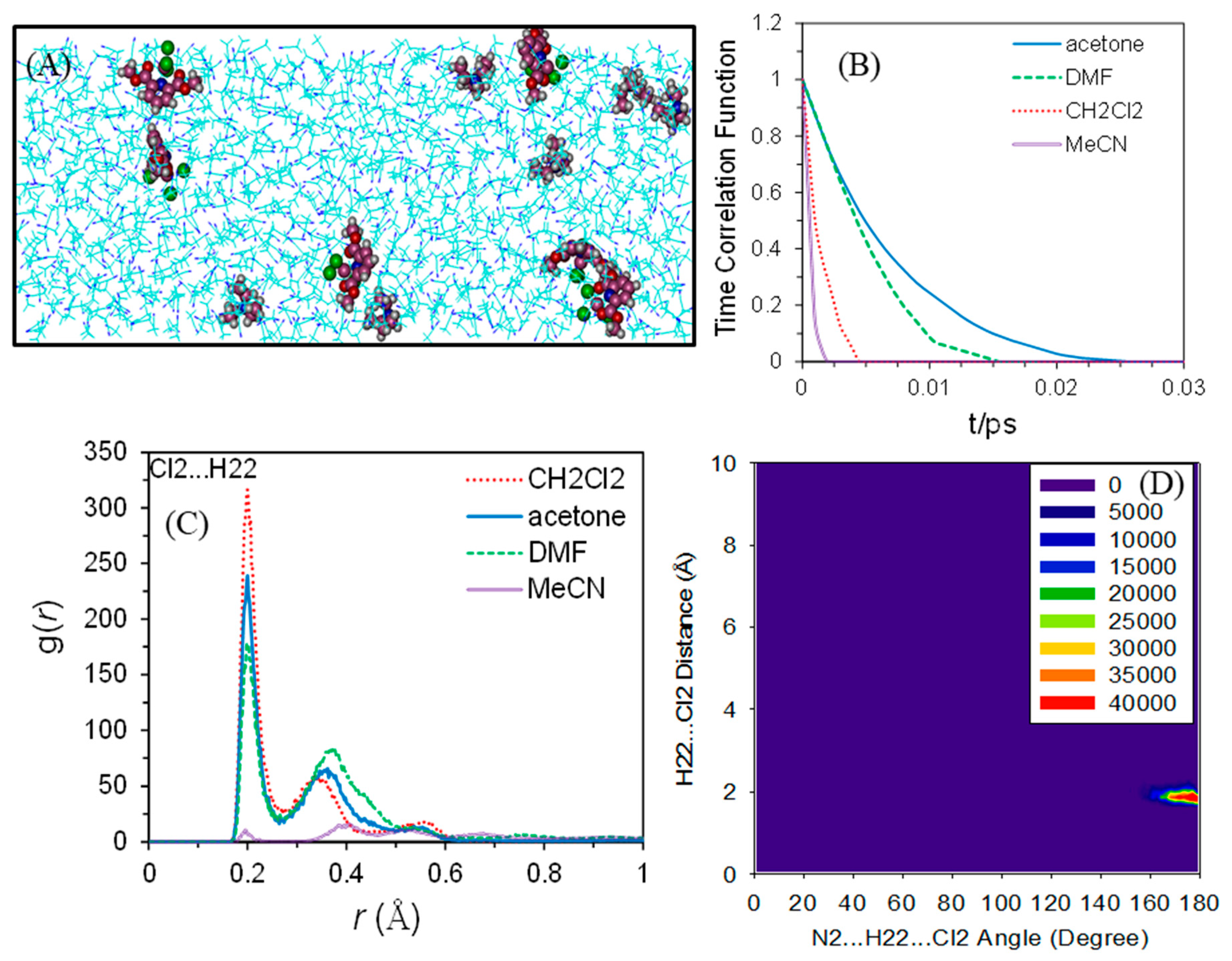
2.3. Molecular Dynamics (MD) Simulations of Bulk Solutions
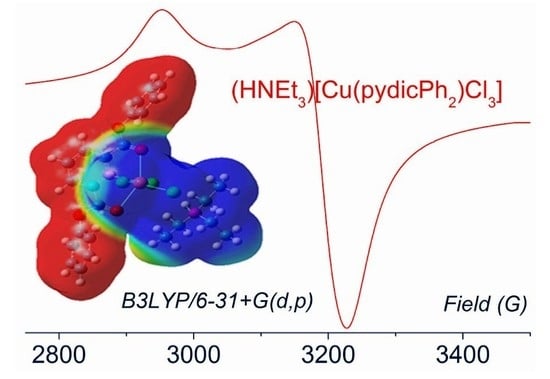
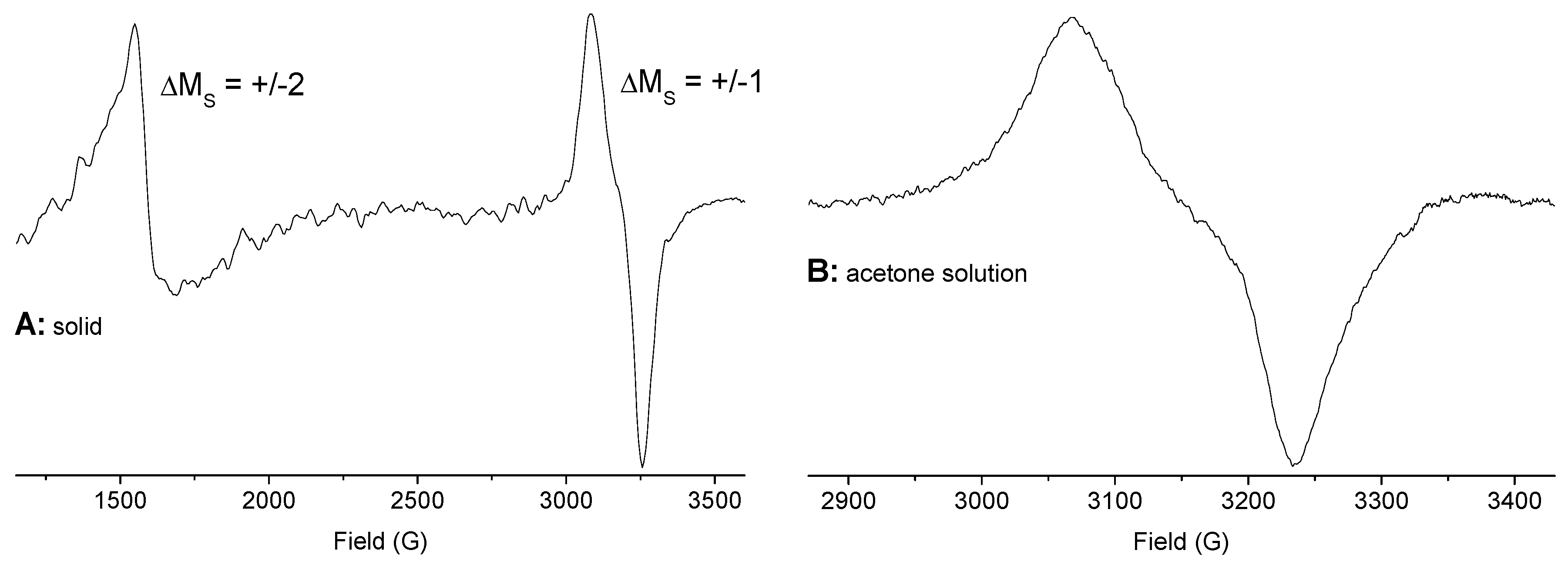
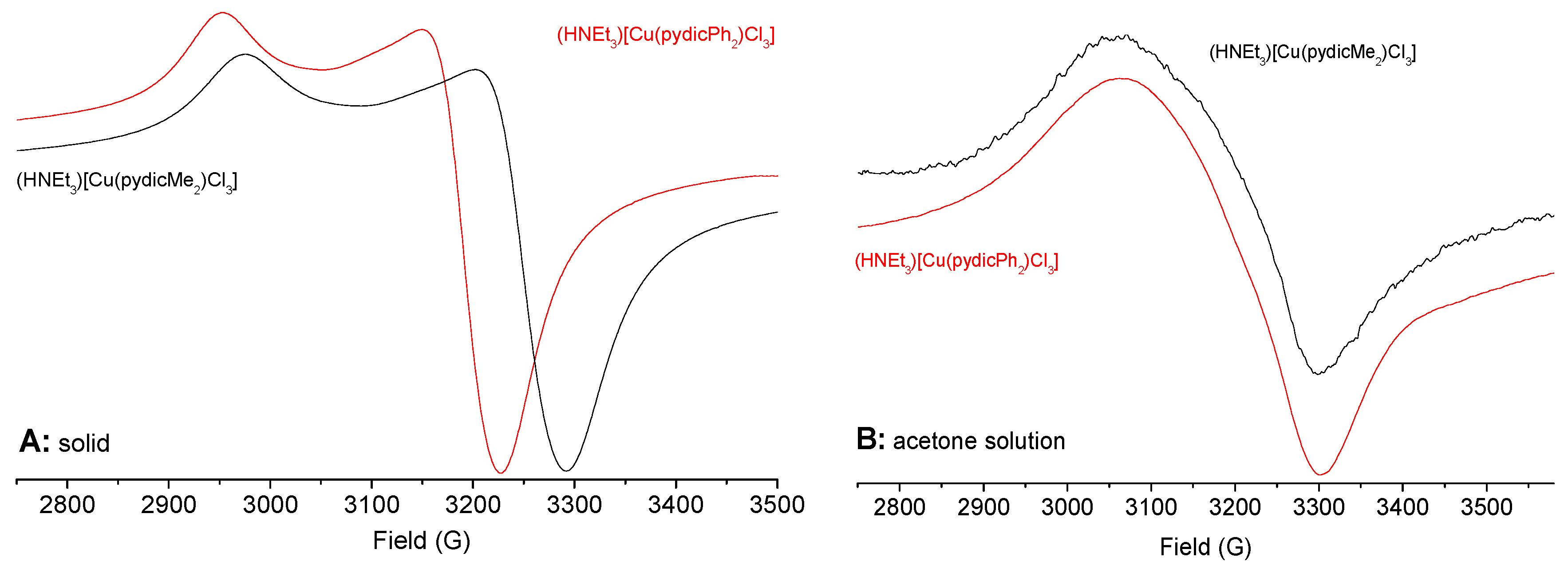
2.4. EPR Spectroscopy of Solids and Solutions
2.5. UV–Vis Absorption Spectroscopy
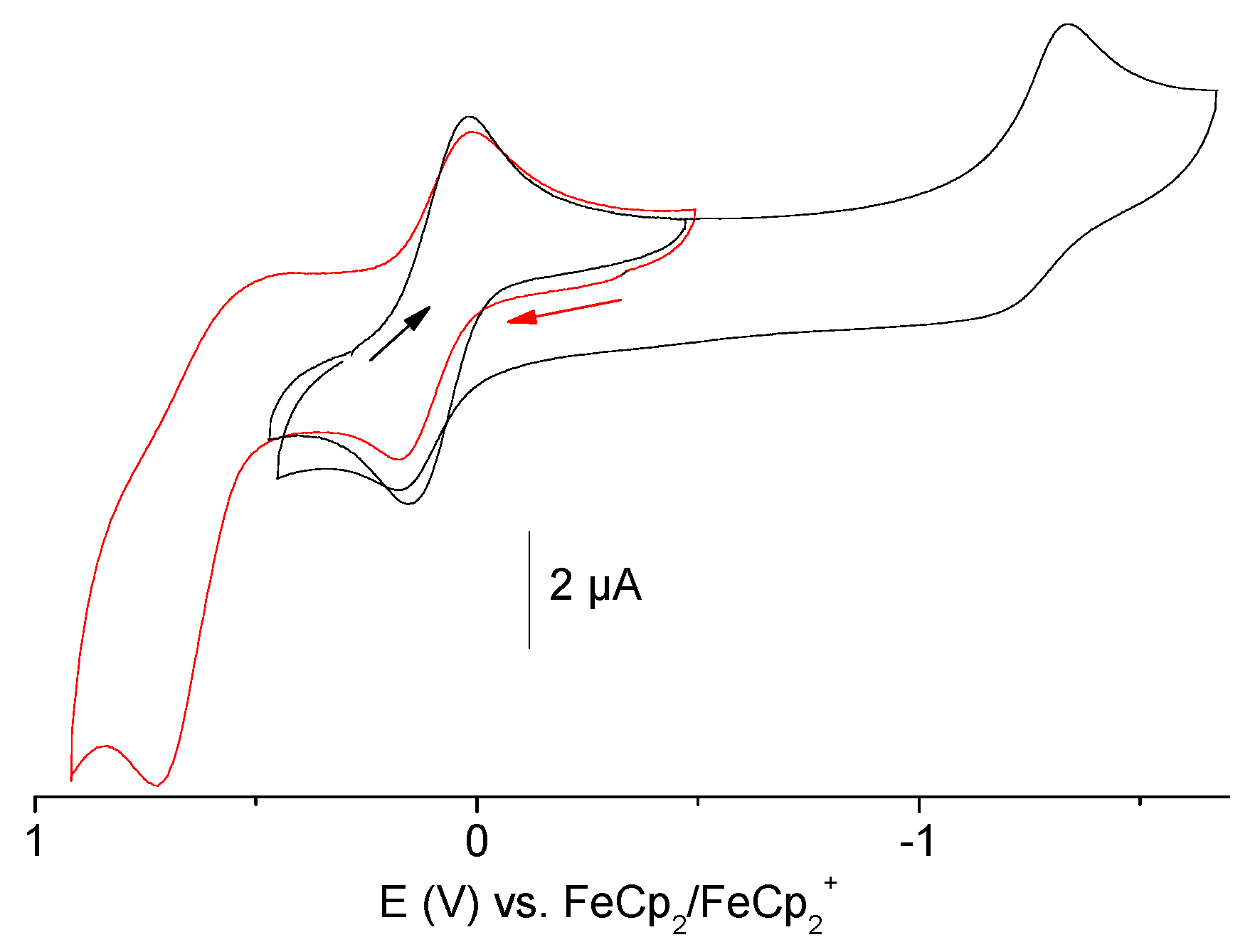
2.6. Electrochemical Measurements
3. Experimental Section
3.1. Methods and Instrumentation
3.2. Crystal Structure Determination
3.3. Quantumchemical and Molecular Dynamics Calculations
3.4. Syntheses
3.4.1. General
3.4.2. Synthesis of bis(2-iodophenyl)pyridine-2,6-dicarboxylic ester pydic(IPh)2 and [{Cu(pydic(IPh)2)Cl}2(µ-Cl)2]
3.4.3. One Pot Reactions
3.4.4. Complexes from pydicCl2 Hydrolysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiang, S.; Bao, D.-X.; Wang, J.; Li, Y.-C.; Zhao, X.-Q. Luminescent lanthanide coordination compounds with pyridine-2,6-dicarboxylic acid. J. Lumin. 2017, 186, 273–282. [Google Scholar] [CrossRef]
- Celestine, M.J.; Bullock, J.L.; Boodram, S.; Rambaran, V.H.; Holder, A.A. Interesting properties of p-, d-, and f-block elements when coordinated with dipicolinic acid and its derivatives as ligands: Their use as inorganic pharmaceuticals. Rev. Inorg. Chem. 2015, 35, 57–67. [Google Scholar] [CrossRef]
- Kirillov, A.M.; Shul’Pin, G.B. Pyrazinecarboxylic acid and analogs: Highly efficient co-catalysts in the metal-complex-catalyzed oxidation of organic compounds. Coord. Chem. Rev. 2013, 257, 732–754. [Google Scholar] [CrossRef]
- Teo, P.; Hor, T.A. Spacer directed metallo-supramolecular assemblies of pyridine carboxylates. Coord. Chem. Rev. 2011, 255, 273–289. [Google Scholar] [CrossRef]
- Abdelhameed, R.M.; Ananias, D.; Silva, A.M.S.; Rocha, J. Building Light-Emitting Metal–Organic Frameworks by Post-Synthetic Modification. ChemistrySelect 2017, 2, 136–139. [Google Scholar] [CrossRef]
- Yang, R.; Li, H.H.; Van Hecke, K.; Cui, G.H. Cobalt(II) and Copper(II) Complexes Constructed from Bis(benzimidazole) and 2,6-Pyridinedicarboxylate Co-ligands: Synthesis, Crystal Structures, and Catalytic Properties. Z. Anorg. Allgem. Chem. 2015, 641, 642–649. [Google Scholar] [CrossRef]
- Derikvand, Z.; Dorosti, N.; Hassanzadeh, F.; Shokrollahi, A.; Mohammadpour, Z.; Azadbakht, A. Three new supramolecular compounds of copper(II), cobalt(II) and zirconium(IV) with pyridine-2,6-dicarboxylate and 3,4-diaminopyridine: Solid and solution states studies. Polyhedron 2012, 43, 140–152. [Google Scholar] [CrossRef]
- Kim, M.K.; Bae, K.-L.; Ok, K.M. From Pincers to Steps: Synthesis, Structure, Characterization, and Transformation of a New Helical Calcium–Organic Framework, Ca[NC5H3(CO2)2](H2O)1.5. Cryst. Growth Des. 2011, 11, 930–932. [Google Scholar] [CrossRef]
- Stavila, V.; Bulimestru, I.; Gulea, A.; Colson, A.C.; Whitmire, K.H. Hexaaquacobalt(II) and hexaaquanickel(II) bis(μ-pyridine-2,6-dicarboxylato)bis[(pyridine-2,6-dicarboxylato)bismuthate(III)] dihydrate. Acta Crystallogr. Sect. C Cryst. Struct. Commun. 2011, 67, m65–m68. [Google Scholar] [CrossRef]
- Zhang, G.-C.; Chen, S.-P.; Yang, Q.; Gao, S.-L. Thermochemistry on K2[M(DPA)2]·7H2O(s) (M = Cu and Ni, H2DPA = pyridine-2,6-dicarboxylic acid). Thermochim. Acta 2011, 518, 66–71. [Google Scholar] [CrossRef]
- Das, B.; Baruah, J.B. Coordinated cations in dipicolinato complexes of divalent metal ions. Inorg. Chim. Acta 2010, 363, 1479–1487. [Google Scholar] [CrossRef]
- Felloni, M.; Blake, A.J.; Hubberstey, P.; Wilson, C.; Schröder, M. Solvent Control of Supramolecular Architectures Derived from 4,4′-Bipyridyl-Bridged Copper(II) Dipicolinate Complexes. Cryst. Growth Des. 2009, 9, 4685–4699. [Google Scholar] [CrossRef]
- Furet, E.; Costuas, K.; Rabiller, P.; Maury, O. On the Sensitivity of f Electrons to Their Chemical Environment. J. Am. Chem. Soc. 2008, 130, 2180–2183. [Google Scholar] [CrossRef]
- Katada, H.; Seino, H.; Mizobe, Y.; Sumaoka, J.; Komiyama, M. Crystal structure of Ce(IV)/dipicolinate complex as catalyst for DNA hydrolysis. J. Biol. Inorg. Chem. 2008, 13, 249–255. [Google Scholar] [CrossRef] [PubMed]
- Hakimi, M.; Mardani, Z.; Moeini, K.; Mohr, F. Coordination behavior of dimethyl pyridine-2,6-dicarboxylate towards mercury(II), cadmium(II) and chromium(III) in the solid- and gaseous state supported by CSD studies. Polyhedron 2015, 102, 569–577. [Google Scholar] [CrossRef]
- Hakimi, M.; Moeini, K.; Mardani, Z.; Schuh, E.; Mohr, F. Silver(I) coordination polymer and nine-coordinated cadmium(II) complex with dimethyl pyridine-2,6-dicarboxylate supported by solid state and electrochemical studies. J. Coord. Chem. 2013, 66, 1129–1141. [Google Scholar] [CrossRef]
- Kapoor, P.; Pathak, A.; Kaur, P.; Venugopalan, P.; Kapoor, R. Steric control of coordination: Unusual coordination mode of dimethylpyridine-2,6-dicarboxylate in a new dinuclear copper(II) complex [(dmpc)(Cl)(µ-Cl)Cu2(µ-Cl)(Cl)(dmpc)] and reversal of the coordination mode in [Cu(dmpc)(H2O)3](ClO4)2. Trans. Met. Chem. 2004, 29, 251–258. [Google Scholar] [CrossRef]
- Steinkamp, T.; Karst, U. Detection scheme for bioassays based on 2,6-pyridinedicarboxylic acid derivatives and enzyme-amplified lanthanide luminescence. Anal. Chim. Acta 2004, 526, 27–34. [Google Scholar] [CrossRef]
- Pointillart, F.; Bourdolle, A.; Cauchy, T.; Maury, O.; le Gal, Y.; Golhen, S.; Cador, O.; Ouahab, L. In Solution Sensitization of Er(III) Luminescence by the 4-Tetrathiafulvalene-2,6-pyridinedicarboxylic Acid Dimethyl Antenna Ligand. Inorg. Chem. 2012, 51, 978–984. [Google Scholar] [CrossRef]
- Creber, M.L.; Orrell, K.G.; Osborne, A.G.; Šik, V.; Hursthouse, M.B.; Light, M.E. Solution fluxionality of some pyridine-2,6-dialdehydes, -diketones and -diesters when acting as bidentate ligands in rhenium(I) and platinum(IV) complexes. Crystal structure of [ReBr(CO)3L] (L = methylethyldipicolinate). Polyhedron 2001, 20, 1973–1982. [Google Scholar] [CrossRef]
- Goher, M.A.; Mautner, F.; Hafez, A.K.; Youssef, A. Synthesis and characterization of copper(I) complexes of dimethyldipicolinate (dmdp) and X-ray structure of the mononuclear six-coordinate complex [Cu(dmdp)2]ClO4. Polyhedron 2003, 22, 515–520. [Google Scholar] [CrossRef]
- Kapoor, P.; Pathak, A.; Kapoor, R.; Venugopalan, P.; Corbella, M.; Rodríguez, M.; Robles, J.; Llobet, A. Structural, Electronic, and Magnetic Consequences of O-Carbonyl vs O-Alkoxy Ester Coordination in New Dicopper Complexes Containing the Cu2(μ-Cl)2 Core. Inorg. Chem. 2002, 41, 6153–6160. [Google Scholar] [CrossRef]
- Platas-Iglesias, C.; Piguet, C.; André, N.; Bünzli, J.-C.G. Lanthanide triple-stranded helical complexes with a substituted 2,6-pyridinedicarboxylate. J. Chem. Soc. Dalton Trans. 2001, 3084–3091. [Google Scholar] [CrossRef]
- Muller, G.; Schmidt, B.; Jiricek, J.; Hopfgartner, G.; Riehl, J.P.; Bünzli, J.-C.G.; Piguet, C. Lanthanide triple helical complexes with a chiral ligand derived from 2,6-pyridinedicarboxylic acid. J. Chem. Soc. Dalton Trans. 2001, 2655–2662. [Google Scholar] [CrossRef][Green Version]
- Renaud, F.; Piguet, C.; Bernardinelli, G.; Bünzli, J.-C.G.; Hopfgartner, G. In Search for Mononuclear Helical Lanthanide Building Blocks with Predetermined Properties: Lanthanide Complexes with Diethyl Pyridine-2, 6-Dicarboxylate. Chem. Eur. J. 1997, 3, 1660–1667. [Google Scholar] [CrossRef]
- Espinet, P.; García-Orodea, E.; Miguel, J.A. Mesogenic Palladium Complexes with Pincer Ligands Derived from Dipicolinic Acid. Inorg. Chem. 2000, 39, 3645–3651. [Google Scholar] [CrossRef] [PubMed]
- Rasshoffer, W.; Müller, V.M.; Vögtle, F. Noncyclic Crown Ether Type Esters and Their Complexes. Chem. Ber. 1979, 112, 2095–2119. [Google Scholar]
- Kirillov, A.M.; Haukka, M.; Da Silva, M.F.C.G.; Pombeiro, A.J.L. Synthesis, Characterization and Redox Behaviour of Mono- and Dicarbonyl Phosphane Rhenium(I) Complexes Bearing N-, N,N- and N,O-Type Ligands. Eur. J. Inorg. Chem. 2007, 2007, 1556–1565. [Google Scholar] [CrossRef]
- Senegas, J.-M.; Bernardinelli, G.; Imbert, D.; Bünzli, J.-C.G.; Morgantini, P.-Y.; Weber, J.; Piguet, C. Connecting Terminal Carboxylate Groups in Nine-Coordinate Lanthanide Podates: Consequences on the Thermodynamic, Structural, Electronic, and Photophysical Properties. Inorg. Chem. 2003, 42, 4680–4695. [Google Scholar] [CrossRef]
- Bogdan, N.; Grosu, I.; Benoît, G.; Toupet, L.; Ramondenc, Y.; Condamine, E.; Silaghi-Dumitrescu, I.; Plé, G. Molecular Rotors: Design, Synthesis, Structural Analysis, and Silver Complex of New [7.7]Cyclophanes. Org. Lett. 2006, 12, 2619–2622. [Google Scholar] [CrossRef]
- Weng, Z.; Teo, S.; Hor, T.S.A. Metal Unsaturation and Ligand Hemilability in Suzuki Coupling. Acc. Chem. Res. 2007, 40, 676–684. [Google Scholar] [CrossRef] [PubMed]
- Demerseman, B.; Toupet, L. Enolate-Phosphane Ligands Providing a Tool for the Selective Substitution of Triphenylphosphane by Carbon Monoxide or Trimethylphosphane in Complex {Ru(Cp)[η2-P,O-Ph2PCH2C(tBu)=O](PPh3)}[PF6], and Subsequent Reactivity Towards Terminal Alkynes. Eur. J. Inorg. Chem. 2006, 2006, 1573–1581. [Google Scholar] [CrossRef]
- Saes, B.W.H.; Verhoeven, D.G.A.; Lutz, M.; Gebbink, R.J.M.K.; Moret, M.-E. Coordination of a Diphosphine−Ketone Ligand to Ni(0), Ni(I), and Ni(II): Reduction-Induced Coordination. Organometallics 2015, 34, 2710–2713. [Google Scholar] [CrossRef]
- Weber, B.; Werner, H. Osmium(II) and Osmium(IV) Complexes with Phosphane–Ethers, –Esters, and –Amines as Mono- and Bidentate Ligands. Eur. J. Inorg. Chem. 2007, 2007, 2072–2082. [Google Scholar] [CrossRef]
- Mecking, S.; Keim, W. Cationic Palladium η3-Allyl Complexes with Hemilabile P,O-Ligands: Synthesis and Reactivity. Insertion of Ethylene into the Pd−Allyl Function. Organometallics 1996, 15, 2650–2656. [Google Scholar] [CrossRef][Green Version]
- Sileo, E.E.; Quinteros-Rivero, M.F.; Rivero, B.E.; Rigotti, G.; Blesa, M.A. Structure and reactivity of copper(II) carboxylates I. Copper(II) dipicolinates. Solid State Ionics 1994, 73, 153–159. [Google Scholar] [CrossRef]
- Cingi, M.B.; Villa, A.C.; Gastini, C.; Nardelli, M. Crystal and molecular structures of divalent metal-complexes with pyridinecarboxylic acids. II. (Pyridine-2,6-dicarboxylato)diaquocopper(II), [Cu(C7H3NO4)(OH2)2]. Gazz. Chim. Ital. 1971, 101, 825–832. [Google Scholar]
- Glowiak, T.; Podgórska, I. X-ray, Spectroscopic and Magnetic Studies of Hexaaquacopper(II) Di(diphenylphosphate) Diglycine. Inorg. Chim. Acta 1986, 125, 83–88. [Google Scholar] [CrossRef]
- Kirillova, M.V.; da Silva, M.F.C.G.; Kirillov, A.M.; da Silva, J.J.R.F.; Pombeiro, A.J.L. 3D hydrogen bonded heteronuclear CoII, NiII, CuII and ZnII aqua complexes derived from dipicolinic acid. Inorg. Chim. Acta 2007, 360, 506–512. [Google Scholar] [CrossRef]
- Yue, C.; Lin, Z.; Chen, L.; Jiang, F.; Hong, M. The 2D–3D networks with infinite channels or difform chains of copper(II) complexes via weak non-covalent interactions. J. Mol. Struct. 2005, 779, 16–22. [Google Scholar] [CrossRef]
- Wang, W.-Z.; Liu, X.; Liao, D.-Z.; Jiang, Z.-H.; Yan, S.-P.; Wang, G.-L. A novel one-dimensional, ferromagnetic copper(II) complex with chloro-bridges and hydrogen bonds: [(PDA)2Cu2(µ-Cl)2][CuPz2(H2O)4] (H2PDA = pyridine-2,6-dicarboxylic acid, Pz = pyrazole). Inorg. Chem. Commun. 2001, 4, 327–331. [Google Scholar] [CrossRef]
- Steiner, T. The Hydrogen Bond in the Solid State. Angew. Chem. Int. Ed. 2002, 41, 48–76. [Google Scholar] [CrossRef]
- Powell, B.J.; Baruah, T.; Bernstein, N.; Brake, K.; McKenzie, R.H.; Meredith, P.; Pederson, M.R. A first-principles density-functional calculation of the electronic and vibrational structure of the key melanin monomers. J. Chem. Phys. 2004, 120, 8608–8615. [Google Scholar] [CrossRef]
- Gussoni, M.; Castiglioni, C. Infrared intensities. Use of the CH-stretching band intensity as a tool for evaluating the acidity of hydrogen atoms in hydrocarbons. J. Mol. Struct. 2000, 521, 1–18. [Google Scholar] [CrossRef]
- Brehm, M.; Kirchner, B. TRAVIS—A Free Analyzer and Visualizer for Monte Carlo and Molecular Dynamics Trajectories. J. Chem. Inf. Model. 2011, 51, 2007–2023. [Google Scholar] [CrossRef] [PubMed]
- Klein, A.; Butsch, K.; Elmas, S.; Biewer, C.; Heift, D.; Nitsche, S.; Schlipf, I.; Bertagnolli, H. Oxido-pincer complexes of copper(II)—An EXAFS and EPR study of mono- and binuclear [(pydotH2)CuCl2]n (n = 1 or 2). Polyhedron 2012, 31, 649–656. [Google Scholar] [CrossRef]
- Halcrow, M.A. Jahn-Teller Distortions in Transition Metal Compounds, and Their Importance in Functional Molecular and Inorganic Materials. Chem. Soc. Rev. 2013, 42, 1784–1795. [Google Scholar] [CrossRef]
- Hathaway, B.; Billing, D. The electronic properties and stereochemistry of mono-nuclear complexes of the copper(II) ion. Coord. Chem. Rev. 1970, 5, 143–207. [Google Scholar] [CrossRef]
- Koval, I.A.; Sgobba, M.; Huisman, M.; Lüken, M.; Saint-Aman, E.; Gamez, P.; Krebs, B.; Reedijk, J. A remarkable anion effect on the crystal packing of two analogous copper complexes from a thiophene-containing phenol-based ligand. Inorg. Chim. Acta 2006, 359, 4071–4078. [Google Scholar] [CrossRef]
- Thakurta, S.; Roy, P.; Rosair, G.; Gómez-García, C.J.; Garribba, E.; Mitra, S. Ferromagnetic exchange coupling in a new bis(µ-chloro)-bridged copper(II) Schiff base complex: Synthesis, structure, magnetic properties and catalytic oxidation of cycloalkanes. Polyhedron 2009, 28, 695–702. [Google Scholar] [CrossRef]
- Yraola, F.; Albericio, F.; Corbella, M.; Royo, M. [{Cu(pzPh)(Opo)}2(μ-Cl)2]: A new dinuclear copper(II) complex with a chloride bridge and mixed blocking ligands. Inorg. Chim. Acta 2008, 361, 2455–2461. [Google Scholar] [CrossRef]
- Pérez, A.L.; Neuman, N.I.; Baggio, R.; Ramos, C.A.; Dalosto, S.D.; Rizzi, A.C.; Brondino, C.D. Exchange interaction between S = 1/2 centers bridged by multiple noncovalent interactions: Contribution of the individual chemical pathways to the magnetic coupling. Polyhedron 2017, 123, 404–410. [Google Scholar] [CrossRef]
- Rieger, P.H. Electron Spin Resonance—Analysis and Interpretation; RCS Publishing: Cambridge, UK, 2007. [Google Scholar]
- Klein, A.; Elmas, S.; Butsch, K. Oxido Pincer Ligands—Exploring the Coordination Chemistry of Bis(hydroxymethyl)pyridine Ligands for the Late Transition Metals. Eur. J. Inorg. Chem. 2009, 2009, 2271–2281. [Google Scholar] [CrossRef]
- Kaim, W.; Fiedler, J. Spectroelectrochemistry: The best of two worlds. Chem. Soc. Rev. 2009, 38, 3373. [Google Scholar] [CrossRef]
- Kaim, W.; Klein, A. Spectroelectrochemistry; RSC Publishing: Cambridge, UK, 2008. [Google Scholar]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A Found. Crystallogr. 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. SHELX-97, Programs for Crystal Structure Analysis; University of Göttingen: Göttingen, Germany, 1997. [Google Scholar]
- Farrugia, L.J. WinGX and ORTEP for Windows: An update. J. Appl. Crystallogr. 2012, 45, 849–854. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXL-2017/1, Program for the Solution of Crystal Structures; University of Göttingen: Göttingen, Germany, 2017. [Google Scholar]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, 71, 3–8. [Google Scholar] [CrossRef]
- STOE X-RED. Data Reduction Program, Version 1.22/Windows; STOE & Cie: Darmstadt, Germany, 2001. [Google Scholar]
- STOE X-SHAPE. Crystal Optimisation for Numerical Absorption Correction, Version 1.06/Windows; STOE & Cie: Darmstadt, Germany, 1999. [Google Scholar]
- Horn, H.; Schäfer, A.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- TURBOMOLE 7.0; TURBOMOLE GmbH: Karlsruhe, Germany, 2015.
- Steffen, C.; Thomas, K.; Huniar, U.; Hellweg, A.; Rubner, O.; Schroer, A. TmoleX-A graphical user interface for TURBOMOLE. J. Comput. Chem. 2010, 31, 2967–2970. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Hess, B.; Kutzner, C.; Van Der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Lemkul, J.A.; Allen, W.J.; Bevan, D.R. Practical Considerations for Building GROMOS-Compatible Small-Molecule Topologies. J. Chem. Inf. Model. 2010, 50, 2221–2235. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.J.; Postma, J.V.; van Gunsteren, W.F.; DiNola, A.R.H.J.; Haak, J.R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
| Compound | Gas Phase | CH2Cl2 | Acetone | MeCN | DMF | |
|---|---|---|---|---|---|---|
| (HNEt3)[Cu(pydicMe2)Cl3] | dipole moment (Debye) | 8.27 | 12.49 | 13.22 | 13.49 | 13.51 |
| solvation energy (kJ/mol) | −110.88 | −128.30 | −134.74 | −135.12 | ||
| ELUMO−EHOMO (kJ/mol) | 323.15 | 382.64 | 390.20 | 392.91 | 393.06 | |
| charge [Cu(pydicMe2)Cl3]− | −0.84006 | −0.90691 | −0.91645 | −0.91969 | −0.92005 | |
| (HNEt3)[Cu(pydicPh2)Cl3] | dipole moment (Debye) | 7.97 | 12.29 | 13.13 | 13.44 | 13.46 |
| solvation energy (kJ/mol) | −124.86 | −139.25 | −146.15 | −146.55 | ||
| ELUMO−EHOMO (kJ/mol) | 314.22 | 369.83 | 376.68 | 379.41 | 379.57 | |
| charge [Cu(pydicPh2)Cl3]− | −0.84929 | −0.90889 | −0.92116 | −0.92426 | −0.92447 |
| Donor | Acceptor | Gas Phase | CH2Cl2 | Acetone | MeCN | DMF |
|---|---|---|---|---|---|---|
| LP*(8) Cu1 | BD*(1) N2–H22 | 18.91 | 8.24 | 7.28 | 6.95 | 6.90 |
| LP(1) Cl1 | LP*(7) Cu1 | 48.53 | 50.54 | 51.21 | 51.42 | 51.46 |
| LP(4) Cl1 | LP*(6) Cu1 | 99.62 | 98.78 | 99.29 | 99.54 | 99.54 |
| LP(4) Cl1 | LP*(7) Cu1 | 167.40 | 179.53 | 181.21 | 181.84 | 181.88 |
| LP(1) Cl2 | LP*(8) Cu1 | 61.30 | 57.91 | 57.74 | 57.61 | 57.70 |
| LP(4) Cl2 | LP*(6) Cu1 | 107.15 | 126.40 | 128.37 | 128.99 | 129.04 |
| LP(4) Cl2 | LP*(8) Cu1 | 153.55 | 157.32 | 156.65 | 156.23 | 156.27 |
| LP(3) Cl2 | BD*(1) N2–H22 | 66.19 | 47.49 | 42.30 | 40.54 | 40.30 |
| LP(1) Cl3 | LP*(7) Cu1 | 72.72 | 64.10 | 63.26 | 63.01 | 63.01 |
| LP(4) Cl3 | LP*(6) Cu1 | 123.85 | 105.31 | 102.84 | 102.00 | 101.96 |
| LP(4) Cl3 | LP*(7) Cu1 | 206.65 | 192.67 | 191.04 | 190.50 | 190.50 |
| LP(1) O1 | LP*(9) Cu1 | 31.59 | 34.64 | 35.15 | 35.40 | 35.40 |
| LP(1) O2 | LP*(9) Cu1 | 36.36 | 37.24 | 37.24 | 37.20 | 37.20 |
| LP(1) N1 | LP*(6) Cu1 | 63.39 | 69.83 | 70.63 | 70.88 | 70.88 |
| LP(1) N1 | LP*(8) Cu1 | 64.52 | 71.55 | 72.72 | 73.18 | 73.22 |
| Compounds | gav | g|| or g1 | g⊥ or g2 | g3 | Δg | State |
|---|---|---|---|---|---|---|
| reported compounds | ||||||
| [{Cu(pydic(IPh)2)Cl}2(µ-Cl)2] | 2.157 | 2.260 | 2.115 | 2.095 | 0.165 | solid |
| [{Cu(pydic(IPh)2)Cl}2(µ-Cl)2] | 2.130 | 2.197 | 2.102 | 2.091 | 0.106 | acetone |
| (HNEt3)[Cu(pydicMe2)Cl3] | 2.182 | 2.351 | 2.098 | 0.253 | solid | |
| (HNEt3)[Cu(pydicMe2)Cl3] | 2.131 | 2.211 | 2.091 | 0.120 | acetone | |
| (HNEt3)[Cu(pydicPh2)Cl3] | 2.196 | 2.362 | 2.113 | 0.249 | solid | |
| (HNEt3)[Cu(pydicPh2)Cl3] | 2.126 | 2.201 | 2.089 | 0.112 | acetone | |
| related mononuclear complexes | ||||||
| [Cu(pydic)(H2O)2] (sqp) b | 2.156 | 2.324 | 2.102 | 2.043 | 0.281 | solid |
| [Cu(pydimH2)Cl2] (sqp) c | 2.158 | 2.311 | 2.094 | 2.068 | 0.243 | solid |
| [Cu(pydipH2)Cl2] (tbp) c | 2.138 | 2.220 | 2.220 | 1.973 e | 0.223 | solid |
| [Cu(pydotH2)(DMF)Cl2] (aeo) c | 2.194 | 2.353 | 2.120 | 2.108 | 0.245 | solid |
| related binuclear complexes | ||||||
| [{Cu(pydicEt2)Cl}2(µ-Cl)2] d | 2.147 | 2.21 | 2.12 | 2.11 | 0.100 | solid |
| [{Cu(pydiciPr2)Cl}2(µ-Cl)2] d | 2.130 | 2.17 | 2.16 | 2.06 | 0.110 | solid |
| [{Cu(pydotH2)Cl}2(µ-Cl)2] c | 2.148 | 2.418 | 2.081 | 1.946 | 0.472 | solid |
| Compounds | λ/nm (ε/L·mol–1·cm–1) c |
|---|---|
| (HNEt3)[Cu(pydicMe2)Cl3] | 261 (48400), 462 (3290), 822 (160) |
| (HNEt3)[Cu(pydicPh2)Cl3] | 261 (44400), 307 (14400) b, 462 (4580), 890 (310) |
| [{Cu(pydic(IPh)2)Cl}2(µ-Cl)2] | 289 (27100), 464 (3740), 830 (200) |
| K2[CuCl4] | 312, 346sh, 462, 1074 |
| Compounds | Epa ox | E½ CuI/CuII | Epc red |
|---|---|---|---|
| pydic(IPh)2 | 0.72 | - | −1.52 |
| pydicPh2 | 0.91 | - | −1.63 |
| pydicMe2 | 0.86 | - | −1.60 |
| [{Cu(pydic(IPh)2)Cl}2(µ-Cl)2] | 0.73 | 0.08 | −1.33 |
| (HNEt3)[Cu(pydicPh2)Cl3] | 1.11 | 0.09 | −1.32 |
| (HNEt3)[Cu(pydicMe2)Cl3] | 0.84 | 0.14 | −1.33 |
| K2[CuCl4] | 1.12 | 0.08 | −1.48 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butsch, K.; Sandleben, A.; Dokoohaki, M.H.; Zolghadr, A.R.; Klein, A. Pyridine-2,6-Dicarboxylic Acid Esters (pydicR2) as O,N,O-Pincer Ligands in CuII Complexes. Inorganics 2019, 7, 53. https://doi.org/10.3390/inorganics7040053
Butsch K, Sandleben A, Dokoohaki MH, Zolghadr AR, Klein A. Pyridine-2,6-Dicarboxylic Acid Esters (pydicR2) as O,N,O-Pincer Ligands in CuII Complexes. Inorganics. 2019; 7(4):53. https://doi.org/10.3390/inorganics7040053
Chicago/Turabian StyleButsch, Katharina, Aaron Sandleben, Maryam Heydari Dokoohaki, Amin Reza Zolghadr, and Axel Klein. 2019. "Pyridine-2,6-Dicarboxylic Acid Esters (pydicR2) as O,N,O-Pincer Ligands in CuII Complexes" Inorganics 7, no. 4: 53. https://doi.org/10.3390/inorganics7040053
APA StyleButsch, K., Sandleben, A., Dokoohaki, M. H., Zolghadr, A. R., & Klein, A. (2019). Pyridine-2,6-Dicarboxylic Acid Esters (pydicR2) as O,N,O-Pincer Ligands in CuII Complexes. Inorganics, 7(4), 53. https://doi.org/10.3390/inorganics7040053