Application of a Tensile Test Method to Identify the Ductile-Brittle Transition of Caramel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Caramel Preparation
2.2. Moisture Analysis
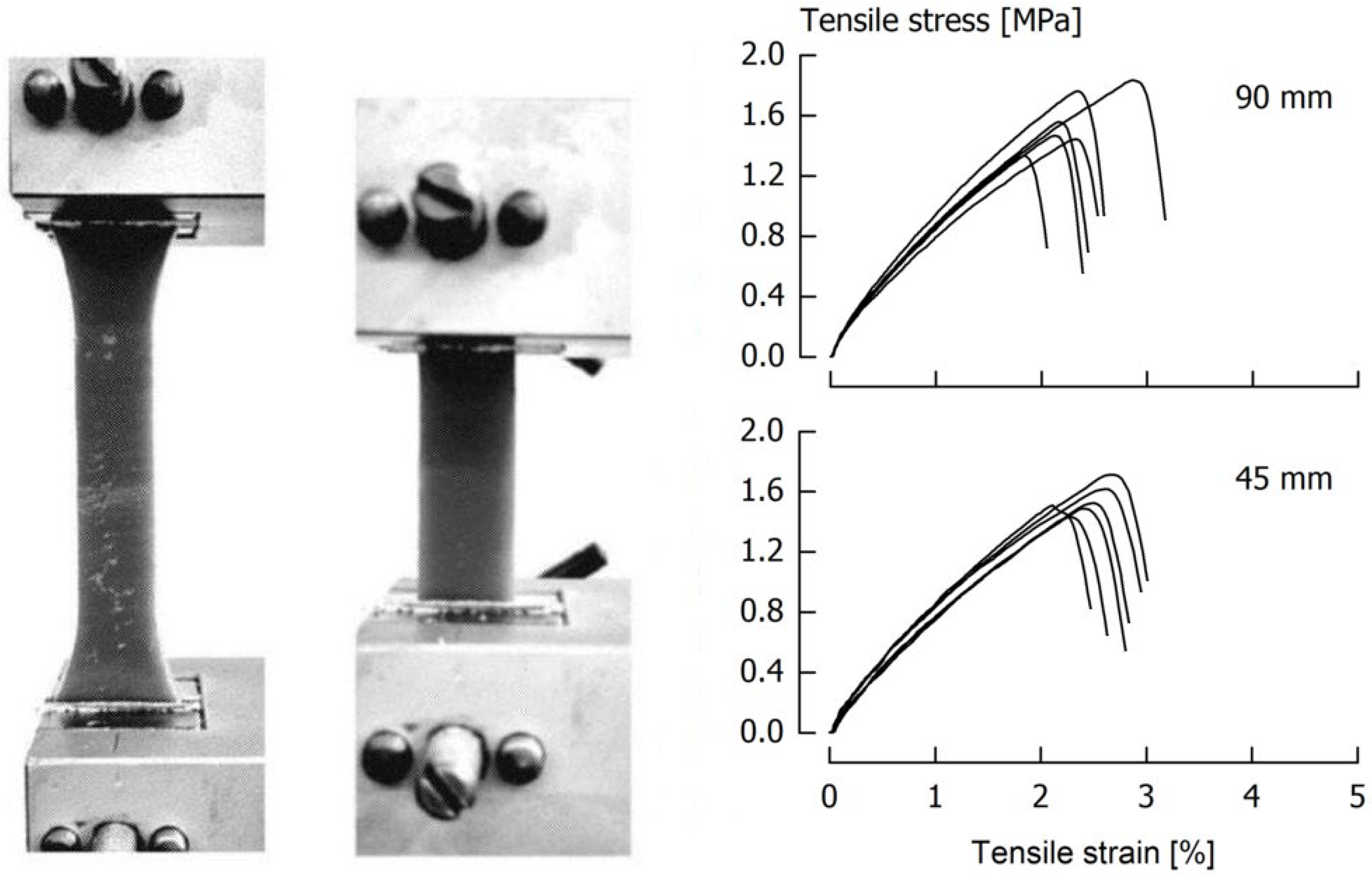
2.3. Execution of Tensile Tests
2.4. Data Calculatiuon
2.5. Data Treatment
3. Results and Discussion
3.1. Preliminary Screening Trials
3.2. Velocity Dependency
3.3. Temperature Dependency
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Steffe, J.F. Rheological Methods in Food Process Engineering; Freeman Press: East Lansing, MI, USA, 1996. [Google Scholar]
- Schuldt, S. Analysis of Rate-Dependent Deformation and Fracture Phenomena during Cutting of Viscoelastic Materials. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2017. Available online: https://nbn-resolving.org/urn:nbn:de:bsz:14-qucosa-235618 (accessed on 16 April 2022).
- Van Vliet, T. Rheology and Fracture Mechanics of Foods; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Van Vliet, T.; Luyten, H.; Walstra, P. Time dependent fracture behavior of food. In Food Colloids and Polymers: Stability and Mechanical Properties; Dickinson, E., Walstra, P., Eds.; Royal Society of Chemistry: London, UK, 1993; pp. 175–190. [Google Scholar]
- van Vliet, T. Large deformation and fracture behavior of gels. Curr. Opin. Colloid Interface Sci. 1996, 1, 740–745. [Google Scholar] [CrossRef]
- Vincent, J.F.V. Application of fracture mechanics to the texture of food. Eng. Fail. Anal. 2004, 11, 695–704. [Google Scholar] [CrossRef]
- Tang, S.; Guo, T.F.; Cheng, L. Rate effects on toughness in elastic nonlinear viscous solids. J. Mech. Phys. Solids 2008, 56, 974–992. [Google Scholar] [CrossRef]
- Swackhamer, C.; Bornhorst, G.M. Fracture properties of foods: Experimental considerations and applications to mastication. J. Food Eng. 2019, 263, 213–226. [Google Scholar] [CrossRef]
- Sala, G.; van de Velde, F.; Cohen Stuart, M.A.; van Aken, G.A. Oil droplet release from emulsion-filled gels in relation to sensory perception. Food Hydrocoll. 2007, 21, 977–985. [Google Scholar] [CrossRef]
- Wang, C.H. Introduction to Fracture Mechanics; DSTO Aeronautical and Maritime Research Laboratory: Melbourne, VIC, Australia, 1996. [Google Scholar]
- Alvarez, M.D.; Saunders, D.E.J.; Vincent, J.F.V.; Jeronimidis, G. An engineering method to evaluate the crisp texture of fruit and vegetables. J. Texture Stud. 2000, 31, 457–473. [Google Scholar] [CrossRef]
- Boisly, M.; Schuldt, S.; Kästner, M.; Schneider, Y.; Rohm, H. Experimental characterisation and numerical modelling of cutting processes in viscoelastic solids. J. Food Eng. 2016, 191, 1–9. [Google Scholar] [CrossRef]
- McCarthy, C.T.; Ní Annaidh, A.; Gilchrist, M.D. On the sharpness of straight edge blades in cutting soft solids: Part II—Analysis of blade geometry. Eng. Fract. Mech. 2010, 77, 437–451. [Google Scholar] [CrossRef]
- Dowgiallo, A. Cutting force of fibrous materials. J. Food Eng. 2005, 66, 57–61. [Google Scholar] [CrossRef]
- Schneider, Y.; Zahn, S.; Schindler, C.; Rohm, H. Ultrasonic excitation affects friction interactions between food materials and cutting tools. Ultrasonics 2009, 49, 588–593. [Google Scholar] [CrossRef]
- Luyten, H.; van Vliet, T. Fracture properties of starch gels and their rate dependency. J. Texture Stud. 1995, 26, 281–298. [Google Scholar] [CrossRef]
- Teratsubo, M.; Tanaka, Y.; Saeki, S. Measurement of stress and strain during tensile testing of gellan gum gels: Effect of deformation speed. Carbohydrate Polym. 2002, 47, 1–5. [Google Scholar] [CrossRef]
- Fife, R.L.; McMahon, D.J.; Oberg, C.J. Test for measuring the stretchability of melted cheese. J. Dairy Sci. 2002, 85, 3539–3545. [Google Scholar] [CrossRef] [Green Version]
- Sharma, P.; Munro, P.A.; Dessev, T.T.; Wiles, P.G.; Foegeding, E.A. Strain hardening and anisotropy in tensile fracture properties of sheared model Mozzarella cheeses. J. Dairy Sci. 2018, 101, 123–134. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, C.; Bornmann, R.; Schneider, Y.; Schuldt, S.; Rohm, H. Thermo-mechanical properties of soft candy: Application of time-temperature superposition to mimic response at high deformation rates. Food Biophys. 2018, 13, 11–17. [Google Scholar] [CrossRef]
- McCulloch, E.; MacBeath, A.; Lucas, M. A finite element model for ultrasonic cutting of toffee. Appl. Mech. Mater. 2006, 5–6, 519–526. [Google Scholar] [CrossRef]
- Kohyama, K.; Takada, A.; Sakurai, N.; Hayakawa, F.; Yoshiaki, H. Tensile test of cabbage leaves for quality evaluation of shredded cabbage. Food Sci. Technol. Res. 2008, 14, 337–344. [Google Scholar] [CrossRef]
- Schab, D.; Zahn, S.; Rohm, H. Development of a caramel-based viscoelastic reference material for cutting tests at different rates. Materials 2021, 14, 3798. [Google Scholar] [CrossRef]
- Standard 527-1; Plastics—Determination of Tensile Properties—Part 1: General Principles. International Standardization Organization: Geneva, Switzerland, 2019.
- Dowling, N.E. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture and Fatigue; Pearson Education Limited: Harlow, Essex, UK, 2013. [Google Scholar]
- Ma, Z.C.; Zhao, H.W.; Wang, K.T.; Zhou, X.Q.; Hu, X.L.; Lu, S.; Cheng, H.B. Note: Investigation on the influences of gripping methods on elastic modulus by a miniature tensile device and in situ verification. Rev. Sci. Instr. 2013, 84, 066102. [Google Scholar] [CrossRef]
- McCulloch, E. Experimental and Finite Element Modeling of Ultrasonic Cutting of Food. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2008. Available online: https://theses.gla.ac.uk/264/ (accessed on 14 June 2021).
- Rojo, F.J.; Vincent, J.F.V. Fracture properties of potato crisps. Int. J. Food Sci. Technol. 2008, 43, 752–760. [Google Scholar] [CrossRef]
- Quinn, J.B.; Quinn, G.D. A practical and systematic review of Weibull statistics for reporting strengths of dental materials. Dent. Mater. 2010, 26, 135–147. [Google Scholar] [CrossRef] [Green Version]
- Aarseth, K.A.; Prestløkken, E. Mechanical properties of feed pellets: Weibull analysis. Biosyst. Eng. 2003, 84, 349–361. [Google Scholar] [CrossRef]
- Guinea, G.V.; Rojo, F.J.; Elices, M. Brittle failure of dry spaghetti. Eng. Fail. Anal. 2004, 11, 705–714. [Google Scholar] [CrossRef]
- Romero de Ávila, M.D.; Escudero, R.; Ordóñez, J.A.; Cambero, M.I. Weibull analysis characterizes the breaking properties of dry-cured ham slices. Meat Sci. 2014, 97, 451–458. [Google Scholar] [CrossRef]
- Işıklı, N.D.; Şenol, B.; Çoksöyler, N. Some physical and mechanical properties of roasted Zerun wheat. J. Food Sci. Technol. 2014, 51, 1990–1997. [Google Scholar] [CrossRef] [Green Version]
- Łysiak, G. Fracture toughness of pea: Weibull analysis. J. Food Eng. 2007, 83, 436–443. [Google Scholar] [CrossRef]
- Moore, P.; Booth, G. Failure modes and analysis in metals. In The Welding Engineer’s Guide to Fracture and Fatigue; Moore, P., Booth, G., Eds.; Woodhead Publishing: Sawston, UK, 2015; pp. 95–110. [Google Scholar]
- Schuldt, S.; Boden, L.; Schneider, Y.; Rohm, H. Pre-crack cutting properties of viscoelastic food models. J. Food Eng. 2016, 169, 272–277. [Google Scholar] [CrossRef]
- Wagoner, T.B.; Luck, P.J.; Foegeding, E.A. Caramel as a model system for evaluating the roles of mechanical properties and oral processing on sensory perception of texture. J. Food Sci. 2016, 81, S736–S744. [Google Scholar] [CrossRef]






| Condition A | Condition B | Condition C | |
|---|---|---|---|
| Length l0 | 90 | 45 | 90 |
| Tensile velocity [mm/min] | 1000 | 1000 | 2500 |
| Extension rate [1/mm] | 11.1 | 22.2 | 27.8 |
| Fracture stress [MPa] 1 | - | 1.66 b ± 0.07 | 1.69 b ± 0.07 |
| Tensile strength [MPa] 1 | 1.42 a ± 0.02 | - |
| Tensile Velocity [mm/min] | 6.53–7.20 g/100 g Moisture | 7.22–7.91 g/100 g Moisture | ||
|---|---|---|---|---|
| σ0 [MPa] | mW [–] | σ0 [MPa] | mW [–] | |
| 500 | 1.62 | 5.93 | 1.10 | 3.12 |
| 750 | 1.67 | 7.64 | 1.30 | 4.07 |
| 1000 | 1.70 | 7.88 | 1.41 | 4.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schab, D.; Tiedemann, L.; Rohm, H.; Zahn, S. Application of a Tensile Test Method to Identify the Ductile-Brittle Transition of Caramel. Foods 2022, 11, 3218. https://doi.org/10.3390/foods11203218
Schab D, Tiedemann L, Rohm H, Zahn S. Application of a Tensile Test Method to Identify the Ductile-Brittle Transition of Caramel. Foods. 2022; 11(20):3218. https://doi.org/10.3390/foods11203218
Chicago/Turabian StyleSchab, Dennis, Lydia Tiedemann, Harald Rohm, and Susann Zahn. 2022. "Application of a Tensile Test Method to Identify the Ductile-Brittle Transition of Caramel" Foods 11, no. 20: 3218. https://doi.org/10.3390/foods11203218
APA StyleSchab, D., Tiedemann, L., Rohm, H., & Zahn, S. (2022). Application of a Tensile Test Method to Identify the Ductile-Brittle Transition of Caramel. Foods, 11(20), 3218. https://doi.org/10.3390/foods11203218






