A New Perspective to Tribocharging: Could Tribocharging Lead to the Development of a Non-Destructive Approach for Process Monitoring and Quality Control of Powders?
Abstract
:1. Introduction
2. Background Theory
3. Materials and Methods
3.1. Materials
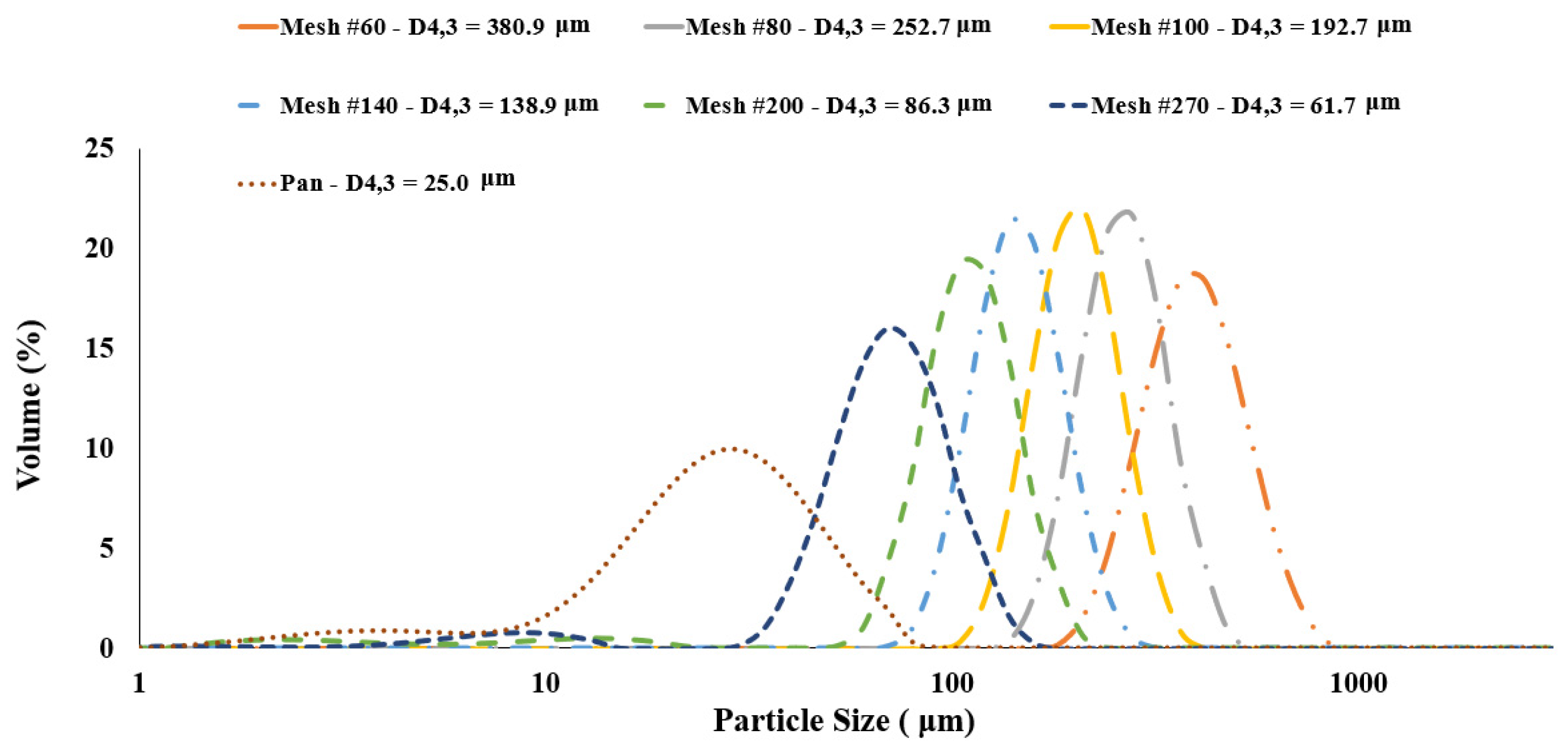
3.2. Sieving
3.3. Analytical Methods
3.4. Charge Measurements
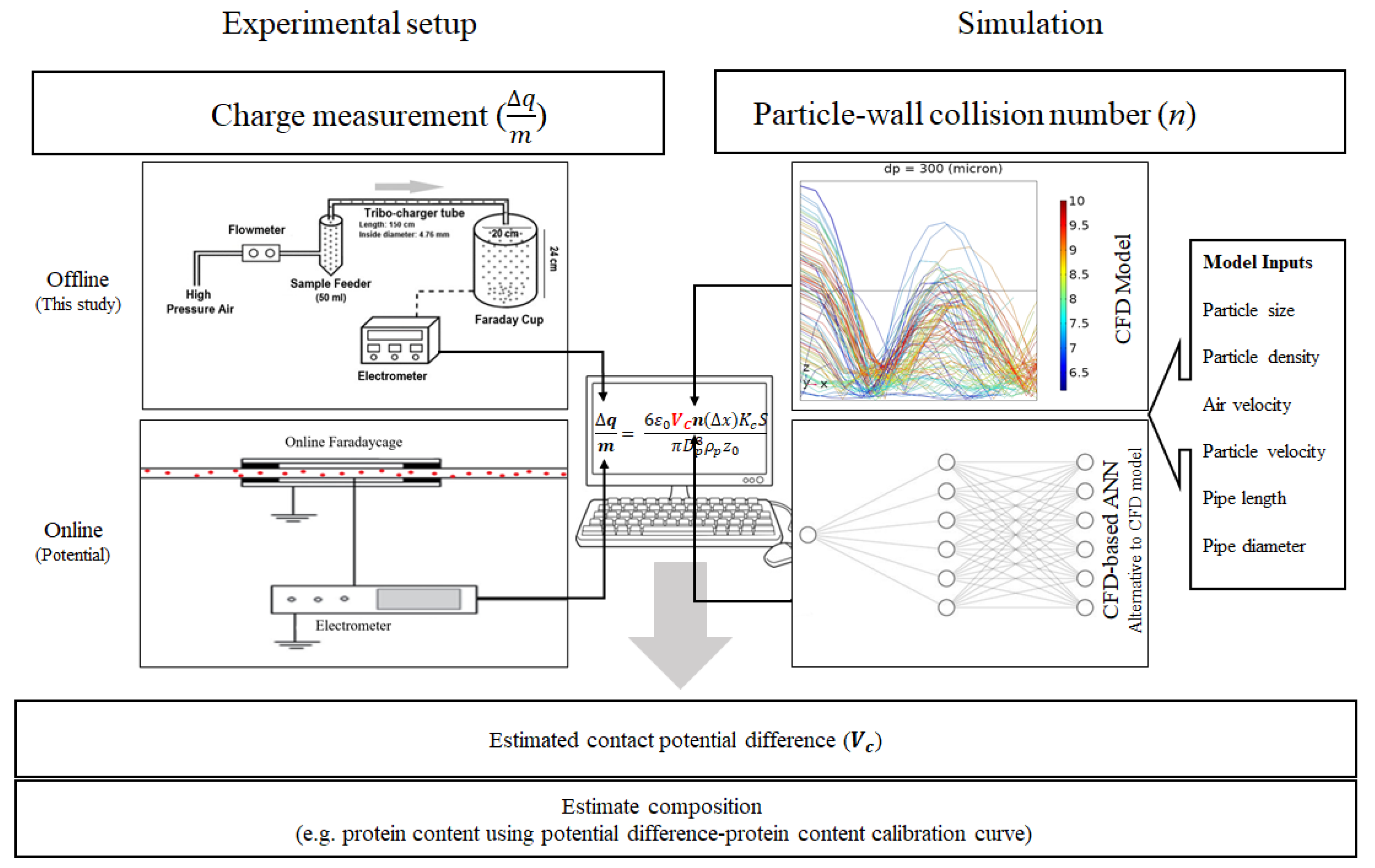
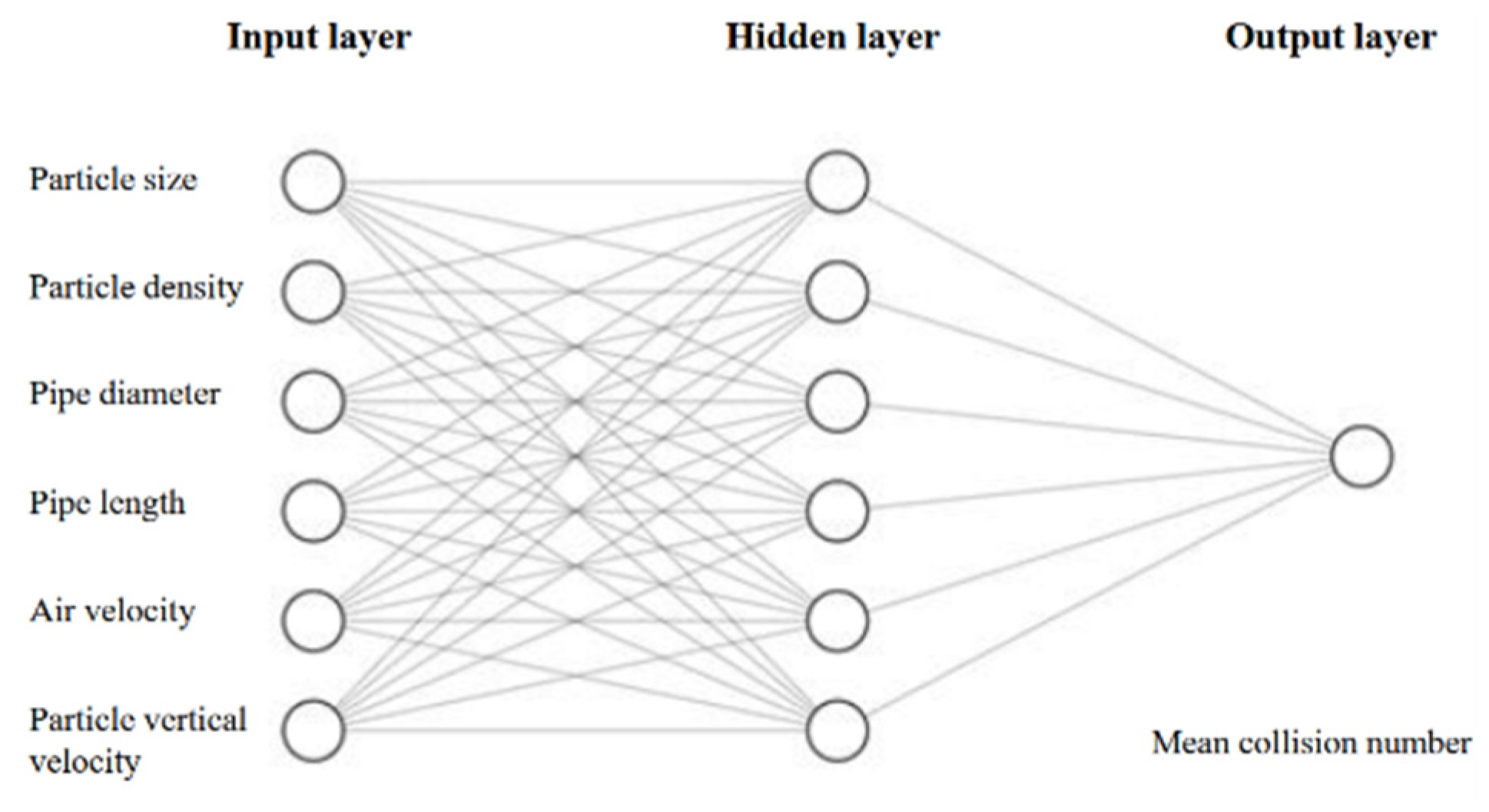
3.5. Computational Fluid Dynamics and Artificial Neural Networks
4. Results and Discussion
4.1. Experimental Results (Characterization of All Sieved Fractions in Terms of Partice Size, Protein Content and Charge-to-Mass Ratio)
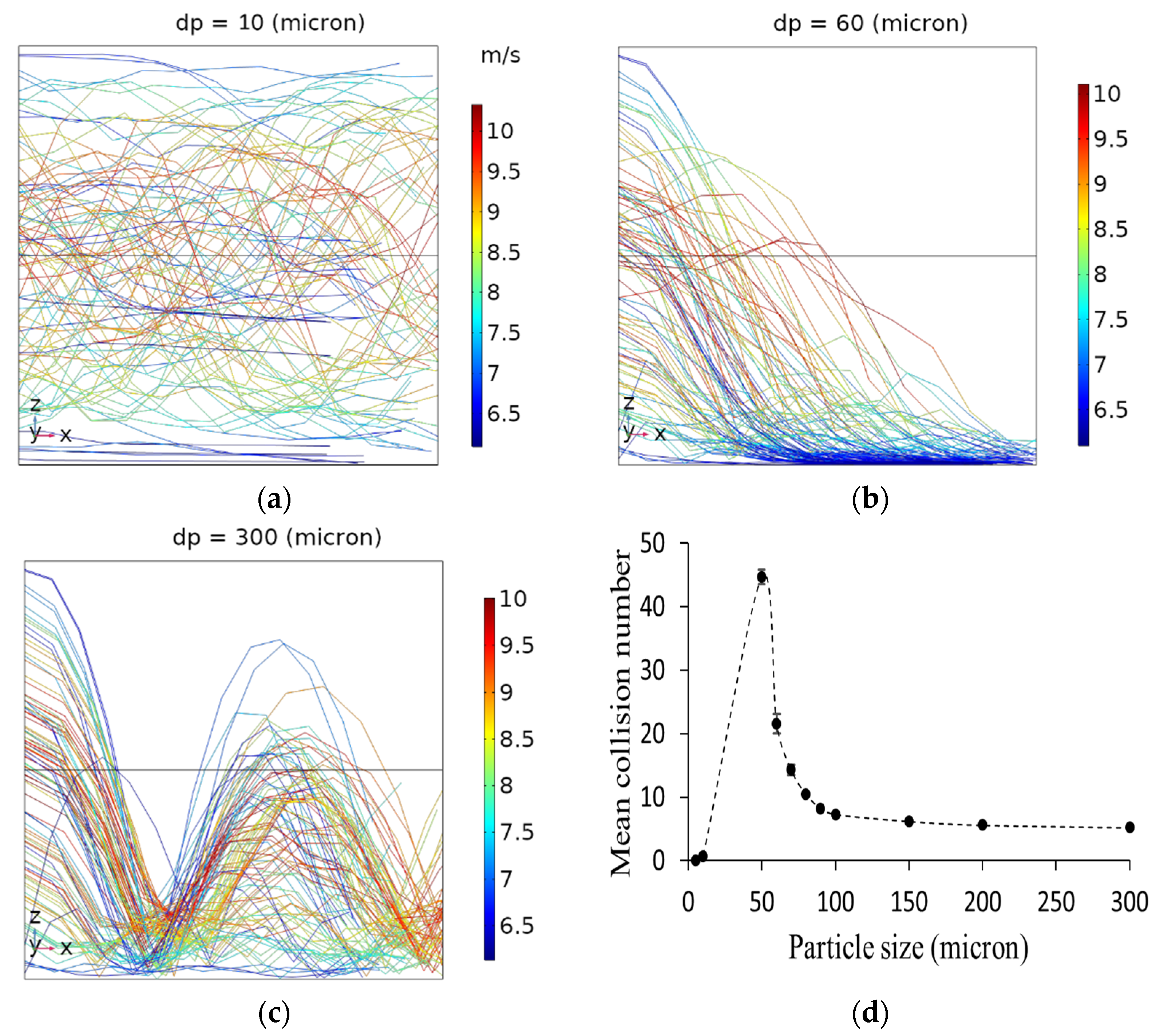
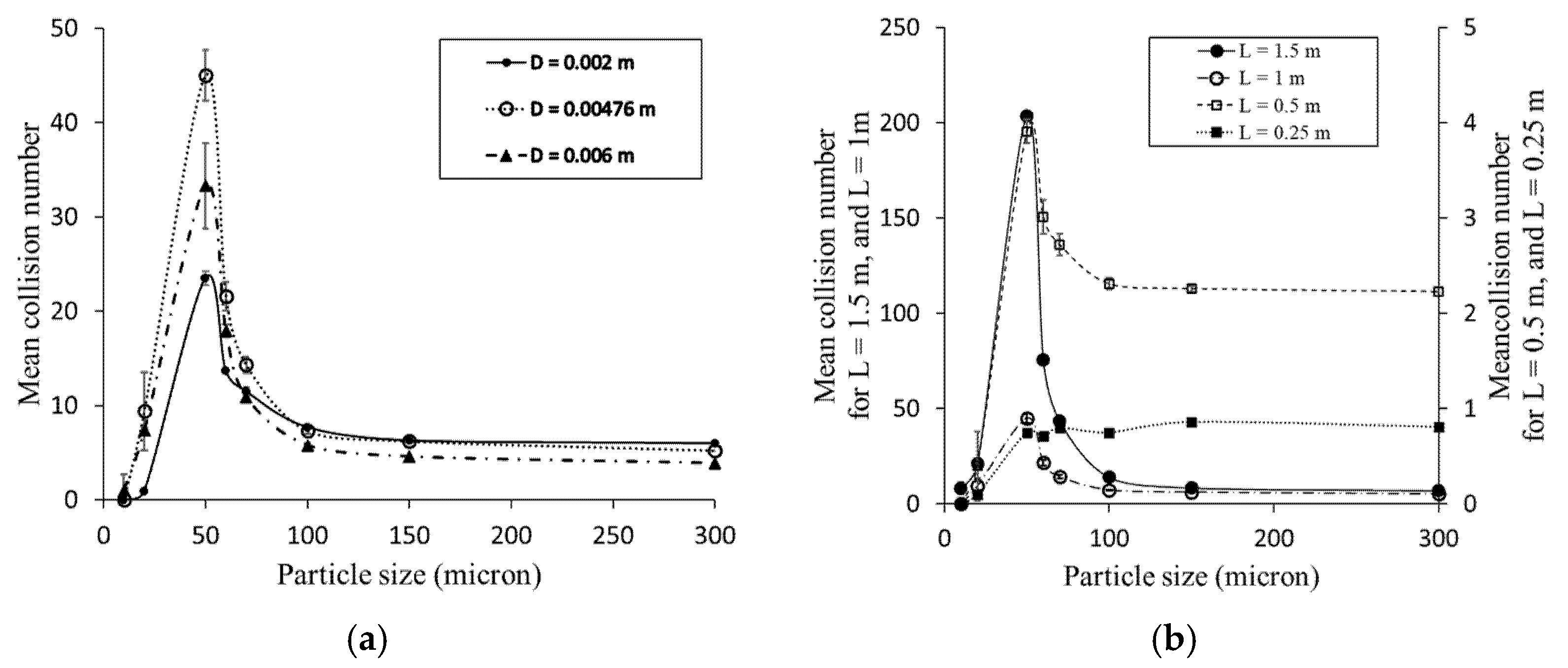
4.2. Influence of Particle Size on Particle-Wall Collision Numbers
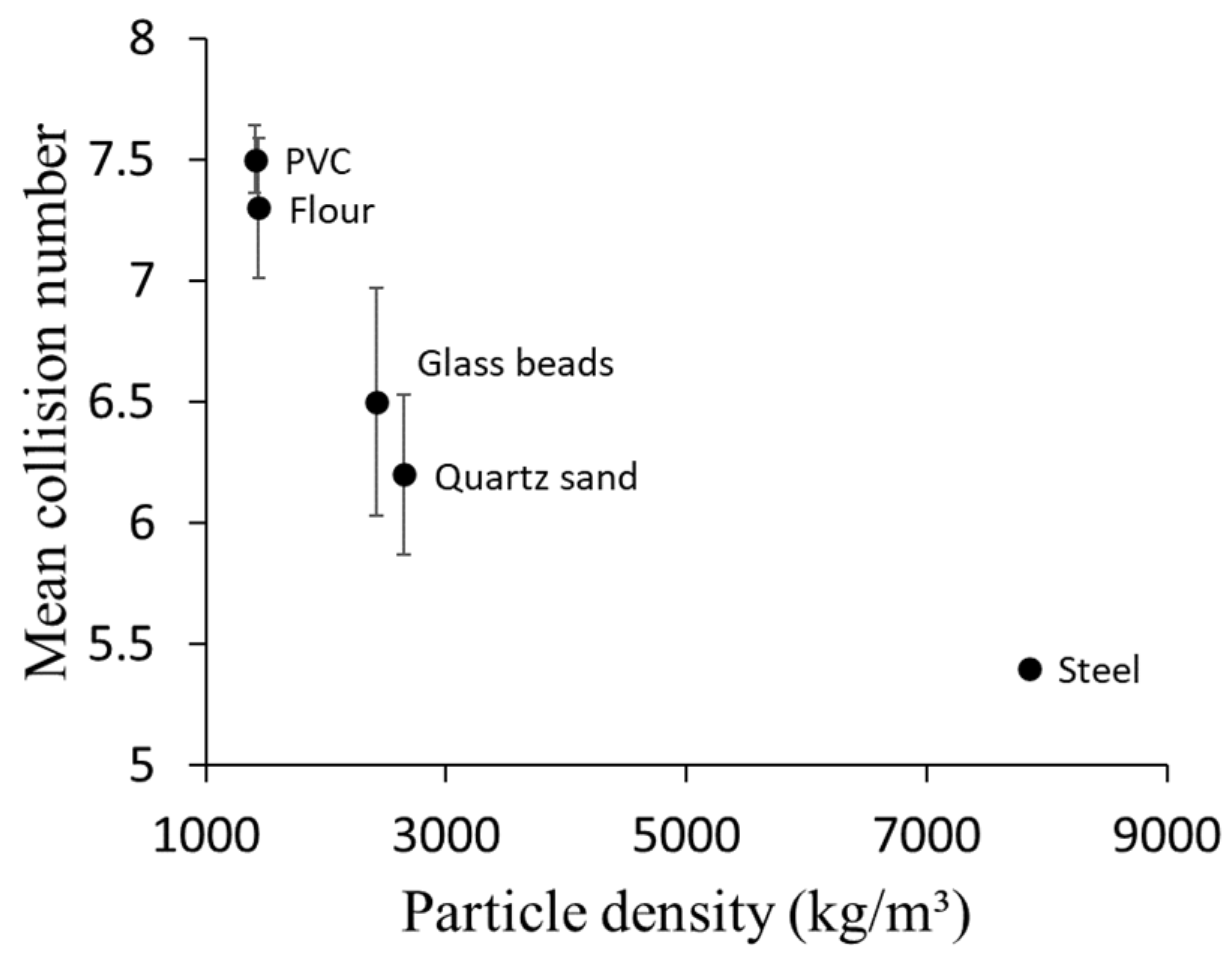
4.3. Influence of Particle Density on Particle-Wall Collision Numbers
4.4. Influence of Pipe Diameter and Length on Particle-Wall Collision Numbers
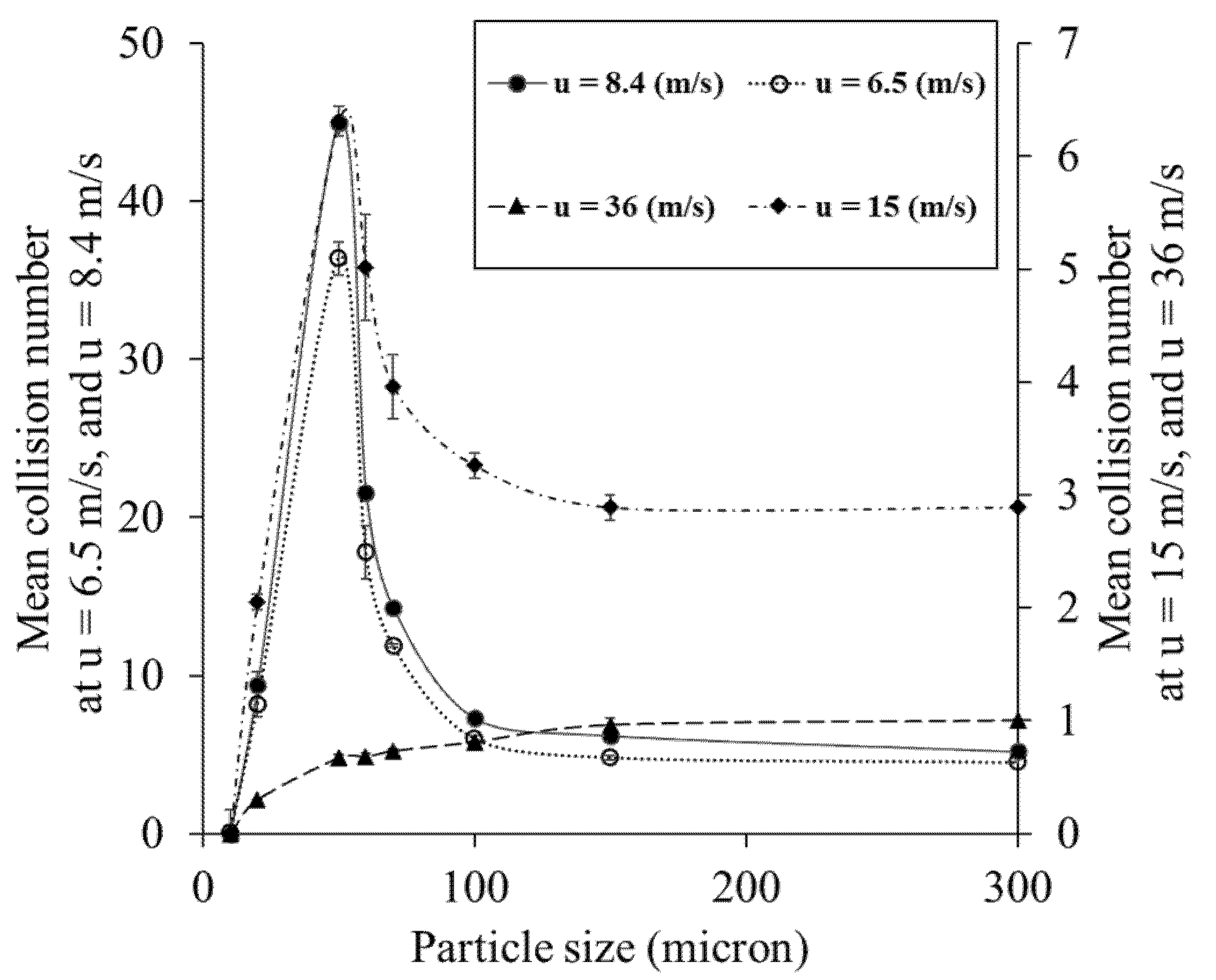
4.5. Influence of Air Velocity on Particle-Wall Collision Numbers
4.6. Neural Network Performance
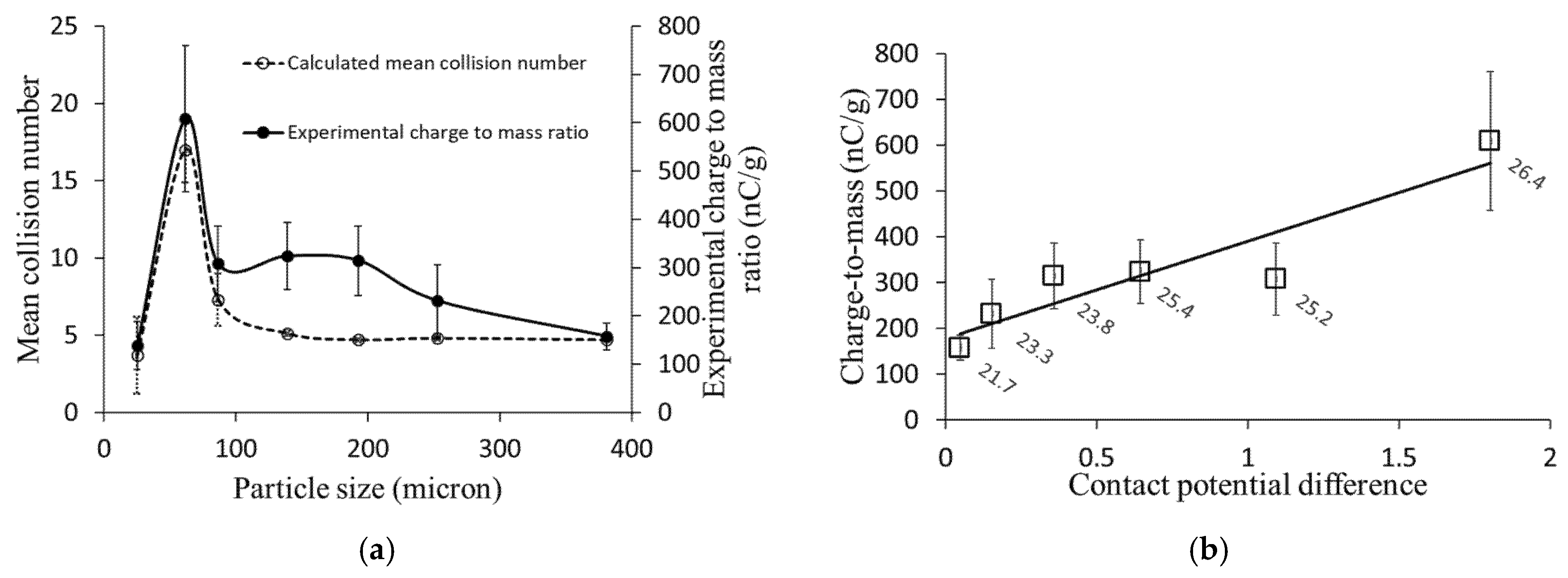
4.7. Correlation of Experimentally Measured Charge with Calculated Collision Numbers
4.8. Influence of Powder Composition on Charging Behavior
5. Limitations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Matsusaka, S.; Maruyama, H.; Matsuyama, T.; Ghadiri, M. Triboelectric charging of powders: A review. Chem. Eng. Sci. 2010, 65, 5781–5807. [Google Scholar] [CrossRef] [Green Version]
- Lim, T.S.E.; Lim, E.; Tay, W.Q.; Cruz, D.A.; Wong, S.Y. Triboelectric charging of 3-in-1 coffee mixes: Formulation and fouling. J. Food Process Eng. 2021, 44, e13890. [Google Scholar] [CrossRef]
- Pu, Y.; Mazumder, M.; Cooney, C. Effects of Electrostatic Charging on Pharmaceutical Powder Blending Homogeneity. J. Pharm. Sci. 2009, 98, 2412–2421. [Google Scholar] [CrossRef]
- Hi, M.A.; Nourafkan, E.; Hassanpour, A. A review of current techniques for the evaluation of powder mixing. Adv. Powder Technol. 2018, 29, 1525–1549. [Google Scholar] [CrossRef]
- Hao, T.; Tukianen, J.; Nivorozhkin, A.; Landrau, N. Probing pharmaceutical powder blending uniformity with electrostatic charge measurements. Powder Technol. 2013, 245, 64–69. [Google Scholar] [CrossRef]
- Schuck, P.; Dolivet, A.; Jeantet, R. Analytical Methods for Food and Dairy Powders; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Vitelli, M.; Mehrtash, H.; Assatory, A.; Tabtabaei, S.; Legge, R.L.; Rajabzadeh, A.R. Rapid and non-destructive determination of protein and starch content in agricultural powders using near-infrared and fluorescence spectroscopy, and data fusion. Powder Technol. 2021, 381, 620–631. [Google Scholar] [CrossRef]
- Yu, L.X. Pharmaceutical Quality by Design: Product and Process Development, Understanding, and Control. Pharm. Res. 2008, 25, 781–791. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Munir, M.T.; Yu, W.; Young, B.R. A Review Towards Hyperspectral Imaging for Real-Time Quality Control of Food Products with an Illustrative Case Study of Milk Powder Production. Food Bioprocess Technol. 2020, 13, 739–752. [Google Scholar] [CrossRef]
- Fotovat, F.; Bi, X.T.; Grace, J.R. Electrostatics in gas-solid fluidized beds: A review. Chem. Eng. Sci. 2017, 173, 303–334. [Google Scholar] [CrossRef]
- Amyotte, P. An Introduction to Dust Explosions: Understanding the Myths and Realities of Dust Explosions for a Safer Workplace; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Chowdhury, F.; Sowinski, A.; Ray, M.; Passalacqua, A.; Mehrani, P. Charge generation and saturation on polymer particles due to single and repeated particle-metal contacts. J. Electrost. 2018, 91, 9–15. [Google Scholar] [CrossRef]
- Assatory, A.; Vitelli, M.; Rajabzadeh, A.R.; Legge, R.L. Dry fractionation methods for plant protein, starch and fiber enrichment: A review. Trends Food Sci. Technol. 2019, 86, 340–351. [Google Scholar] [CrossRef]
- Tabtabaei, S.; Jafari, M.; Rajabzadeh, A.R.; Legge, R.L. Solvent-free production of protein-enriched fractions from navy bean flour using a triboelectrification-based approach. J. Food Eng. 2016, 174, 21–28. [Google Scholar] [CrossRef]
- Tabtabaei, S.; Jafari, M.; Rajabzadeh, A.R.; Legge, R.L. Development and optimization of a triboelectrification bioseparation process for dry fractionation of legume flours. Sep. Purif. Technol. 2016, 163, 48–58. [Google Scholar] [CrossRef]
- Tabtabaei, S.; Vitelli, M.; Rajabzadeh, A.R.; Legge, R. Analysis of protein enrichment during single- and multi-stage tribo-electrostatic bioseparation processes for dry fractionation of legume flour. Sep. Purif. Technol. 2017, 176, 48–58. [Google Scholar] [CrossRef]
- Tabtabaei, S.; Konakbayeva, D.; Rajabzadeh, A.R.; Legge, R.L. Functional properties of navy bean (Phaseolus vulgaris) protein concentrates obtained by pneumatic tribo-electrostatic separation. Food Chem. 2019, 283, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Jafari, M.; Rajabzadeh, A.R.; Tabtabaei, S.; Marsolais, F.; Legge, R.L. Physicochemical characterization of a navy bean (Phaseolus vulgaris) protein fraction produced using a solvent-free method. Food Chem. 2016, 208, 35–41. [Google Scholar] [CrossRef] [PubMed]
- Basset, C.; Kedidi, S.; Barakat, A. Chemical- and Solvent-Free Mechanophysical Fractionation of Biomass Induced by Tribo-Electrostatic Charging: Separation of Proteins and Lignin. ACS Sustain. Chem. Eng. 2016, 4, 4166–4173. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, J.; de Wit, M.; Boom, R.M.; Schutyser, M.A. Lupine protein enrichment by milling and electrostatic separation. Innov. Food Sci. Emerg. Technol. 2016, 33, 596–602. [Google Scholar] [CrossRef]
- Laurentie, J.; Traoré, P.; Dascalescu, L. Discrete element modeling of triboelectric charging of insulating materials in vibrated granular beds. J. Electrost. 2013, 71, 951–957. [Google Scholar] [CrossRef]
- Dwari, R.K.; Rao, K.H. Dry beneficiation of coal—A review. Miner. Process. Extr. Met. Rev. 2007, 28, 177–234. [Google Scholar] [CrossRef]
- Crowe, C.T.; Schwarzkopf, J.D.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Masuda, H.; Matsusaka, S.; Akiba, S.; Shimomura, H. Electrification of Fine Particles in Gas-Solids Pipe Flow. KONA Powder Part. J. 1998, 16, 216–222. [Google Scholar] [CrossRef] [Green Version]
- Itakura, T.; Masuda, H.; Ohtsuka, C.; Matsusaka, S. The contact potential difference of powder and the tribo-charge. J. Electrost. 1996, 38, 213–226. [Google Scholar] [CrossRef]
- Masuda, H.; Komatsu, T.; Iinoya, K. The static electrification of particles in gas-solids pipe flow. AIChE J. 1976, 22, 558–564. [Google Scholar] [CrossRef]
- Matsusaka, S.; Ghadiri, M.; Masuda, H. Electrification of an elastic sphere by repeated impacts on a metal plate. J. Phys. D Appl. Phys. 2000, 33, 2311–2319. [Google Scholar] [CrossRef]
- Watanabe, H.; Ghadiri, M.; Matsuyama, T.; Ding, Y.L.; Pitt, K.G.; Maruyama, H.; Matsusaka, S.; Masuda, H. Triboelectrification of pharmaceutical powders by particle impact. Int. J. Pharm. 2007, 334, 149–155. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ema, A.; Yasuda, D.; Tanoue, K.-I.; Masuda, H. Tribo-charge and rebound characteristics of particles impact on inclined or rotating metal target. Powder Technol. 2003, 135, 2–13. [Google Scholar] [CrossRef]
- Tanoue, K.-I.; Tanaka, H.; Kitano, H.; Masuda, H. Numerical simulation of tribo-electrification of particles in a gas–solids two-phase flow. Powder Technol. 2001, 118, 121–129. [Google Scholar] [CrossRef]
- Matsusaka, S.; Masuda, H. Electrostatics of particles. Adv. Powder Technol. 2003, 14, 143–166. [Google Scholar] [CrossRef]
- Elghobashi, S. Particle-laden turbulent flows: Direct simulation and closure models. Appl. Sci. Res. 1991, 48, 301–314. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, Z. A Drag Coefficient Correlation. Z. Ver. Deutsch. Ing. 1935, 77, e323. [Google Scholar]
- Swiniarski, R. Introduction to Neural Networks. In Neural Networks World; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar] [CrossRef]
- Anochi, J.A.; Velho, H.F.D.C. Optimization of Feedforward Neural Network by Multiple Particle Collision Algorithm. In Proceedings of the IEEE SSCI 2014–2014 IEEE Symposium Series on Computational Intelligence—FOCI 2014: 2014 IEEE Symposium on Foundations of Computational Intelligence, Orlando, FL, USA, 9–12 December 2014. [Google Scholar] [CrossRef]
- Ramchoun, H.; Idrissi, M.A.J.; Ghanou, Y.; Ettaouil, M. Multilayer Perceptron: Architecture Optimization and Training. Int. J. Interact. Multimed. Artif. Intell. 2016, 4, 26. [Google Scholar] [CrossRef]
- Rajabzadeh, A.R.; Zendehboudi, S.; Lohi, A.; Elkamel, A. Colloidal interaction and connectionist modelling of protein osmotic pressure and the effect of physicochemical properties. Can. J. Chem. Eng. 2013, 91, 1621–1631. [Google Scholar] [CrossRef]
- Chan, L.; Zahtila, T.; Ooi, A.; Philip, J. Transport of particles in a turbulent rough-wall pipe flow. J. Fluid Mech. 2021, 908, A1–A22. [Google Scholar] [CrossRef]
- Sommerfeld, M. Analysis of collision effects for turbulent gas–particle flow in a horizontal channel: Part I. Particle transport. Int. J. Multiph. Flow 2003, 29, 675–699. [Google Scholar] [CrossRef]
- Karsoliya, S. Approximating Number of Hidden layer neurons in Multiple Hidden Layer BPNN Architecture. Int. J. Eng. Trends Technol. 2012, 3, 714–717. [Google Scholar]
- Liu, Y.; Starzyk, J.A.; Zhu, Z. Optimizing Number of Hidden Neurons in Neural Networks. In Proceedings of the IASTED International Conference on Artificial Intelligence and Applications, AIA, Innsbruck, Austria, 12–14 February 2007. [Google Scholar]
- Rivals, I.; Personnaz, L. A Statistical Procedure for Determining the Optimal Number of Hidden Neurons of a Neural Model. In Proceedings of the Second International Symposium on Neural Computation (NC), Berlin, Germany, 23–26 May 2000; pp. 14–17. [Google Scholar]
- Fnaiech, F.; Najim, M. A New Feedforward Neural Network Hidden Layer Neuron Pruning Algorithm. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal, Salt Lake City, UT, USA, 7–11 May 2001; Volume 2. [Google Scholar] [CrossRef]
- Shin-Ike, K. A Two Phase Method for Determining the Number of Neurons in the Hidden Layer of a 3-Layer Neural Network. In Proceedings of the SICE Annual Conference, Taipei, Taiwan, 18–21 August 2010. [Google Scholar]
- Biegaj, K.W.; Rowland, M.G.; Lukas, T.M.; Heng, J.Y.Y. Surface Chemistry and Humidity in Powder Electrostatics: A Comparative Study between Tribocharging and Corona Discharge. ACS Omega 2017, 2, 1576–1582. [Google Scholar] [CrossRef] [Green Version]
- Mazumder, M.; Sims, R.; Biris, A.; Srirama, P.; Saini, D.; Yurteri, C.; Trigwell, S.; De, S.; Sharma, R. Twenty-first century research needs in electrostatic processes applied to industry and medicine. Chem. Eng. Sci. 2006, 61, 2192–2211. [Google Scholar] [CrossRef] [Green Version]
- Dodbiba, G.; Fujita, T. Progress in Separating Plastic Materials for Recycling. Phys. Sep. Sci. Eng. 2004, 13, 165–182. [Google Scholar] [CrossRef] [Green Version]
- Pearse, M.; Hickey, T. The separation of mixed plastics using a dry, triboelectric technique. Resour. Recover. Conserv. 1978, 3, 179–190. [Google Scholar] [CrossRef]
- Żenkiewicz, M.; Żuk, T.; Markiewicz, E. Triboelectric series and electrostatic separation of some biopolymers. Polym. Test. 2015, 42, 192–198. [Google Scholar] [CrossRef]
- Yang, J.; Wang, H.; Zhang, G.; Bai, X.; Zhao, X.; He, Y. Recycling organics from non-metallic fraction of waste printed circuit boards by a novel conical surface triboelectric separator. Resour. Conserv. Recycl. 2019, 146, 264–269. [Google Scholar] [CrossRef]
- Landauer, J.; Foerst, P. Triboelectric separation of a starch-protein mixture—Impact of electric field strength and flow rate. Adv. Powder Technol. 2018, 29, 117–123. [Google Scholar] [CrossRef]
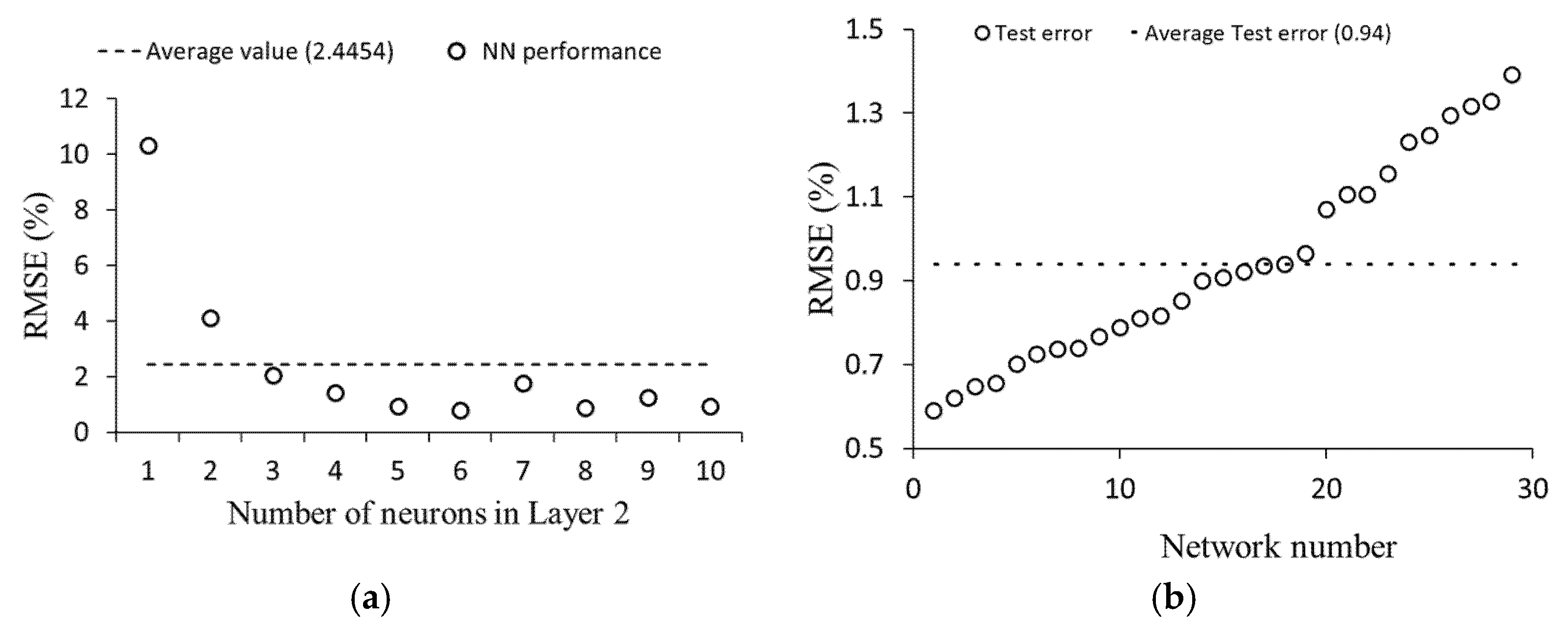
| Parameter | Range |
|---|---|
| Network inputs | |
| Particle size (micron) | 10–600 |
| Particle density (kg/m3) | 1410–7850 |
| Pipe diameter (m) | 0.002–0.006 |
| Pipe length (m) | 0.25–1.5 |
| Average air velocity (m/s) | 6.5–36 |
| Particle vertical velocity (m/s) | 0–1.2 |
| Network output | |
| Particle-wall mean collision number | 0.6–80 |
| Sieved Fractions (Mesh Numbers) | Mean Particle Diameter (D43, µm) | Protein Content (wt%) | Charge-to-Mass Ratio (nC/g) |
|---|---|---|---|
| No. 60 | 380.9 ± 9.9 | 21.7 ± 0.9 | 157.9 ± 27.8 |
| No. 80 | 252.7 ± 1.5 | 23.3 ± 0.2 | 231.2 ± 74.9 |
| No. 100 | 192.7 ± 0.5 | 23.8 ± 0.7 | 314.5 ± 71.6 |
| No. 140 | 138.9 ± 0.1 | 25.4 ± 0.7 | 323.8 ± 69.1 |
| No. 200 | 86.3 ± 0.1 | 25.2 ± 0.4 | 307.8 ± 78.3 |
| No. 270 | 61.7 ± 0.0 | 26.4 ± 0.8 | 608.8 ± 151.3 |
| Pan (<53 μm) | 25.0 ± 0.0 | 14.2 ± 0.1 | 138.2 ± 49.5 |
| Material | Density (kg/m3) |
|---|---|
| Flour | 1440 |
| PVC | 1410 |
| Glass beads | 2420 |
| Quartz sand | 2650 |
| Steel | 7850 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehrtash, H.; Konakbayeva, D.; Tabtabaei, S.; Srinivasan, S.; Rajabzadeh, A.R. A New Perspective to Tribocharging: Could Tribocharging Lead to the Development of a Non-Destructive Approach for Process Monitoring and Quality Control of Powders? Foods 2022, 11, 693. https://doi.org/10.3390/foods11050693
Mehrtash H, Konakbayeva D, Tabtabaei S, Srinivasan S, Rajabzadeh AR. A New Perspective to Tribocharging: Could Tribocharging Lead to the Development of a Non-Destructive Approach for Process Monitoring and Quality Control of Powders? Foods. 2022; 11(5):693. https://doi.org/10.3390/foods11050693
Chicago/Turabian StyleMehrtash, Hadi, Dinara Konakbayeva, Solmaz Tabtabaei, Seshasai Srinivasan, and Amin Reza Rajabzadeh. 2022. "A New Perspective to Tribocharging: Could Tribocharging Lead to the Development of a Non-Destructive Approach for Process Monitoring and Quality Control of Powders?" Foods 11, no. 5: 693. https://doi.org/10.3390/foods11050693
APA StyleMehrtash, H., Konakbayeva, D., Tabtabaei, S., Srinivasan, S., & Rajabzadeh, A. R. (2022). A New Perspective to Tribocharging: Could Tribocharging Lead to the Development of a Non-Destructive Approach for Process Monitoring and Quality Control of Powders? Foods, 11(5), 693. https://doi.org/10.3390/foods11050693








