Simulated and Verification of Mass and Heat Transfer Coupled Model of Jujube Slices Dried by Hot Air Combined with Radio Frequency Heat Treatment at Different Drying Stages
Abstract
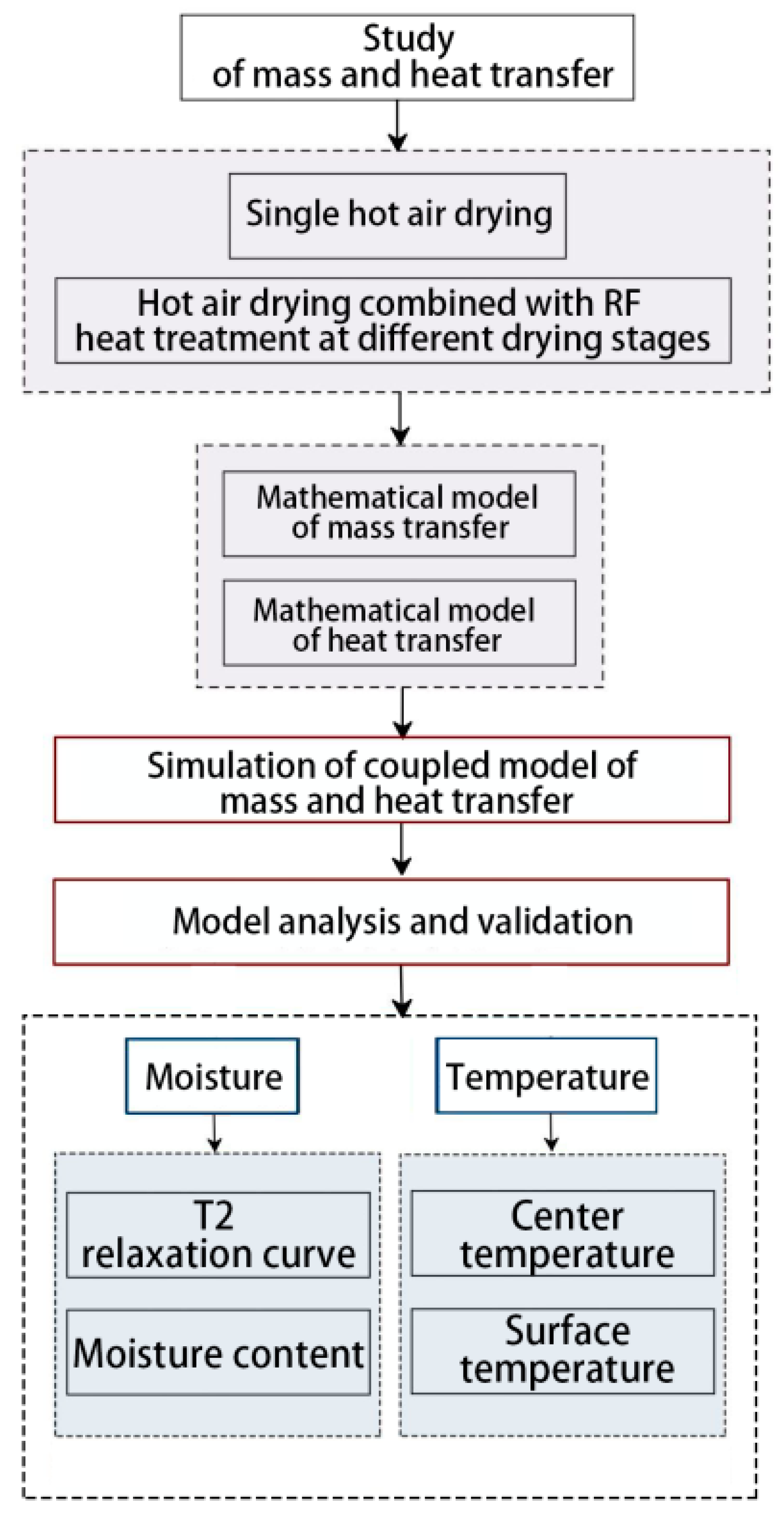
:1. Introduction
2. Materials and Methods
2.1. Preparation of Sample
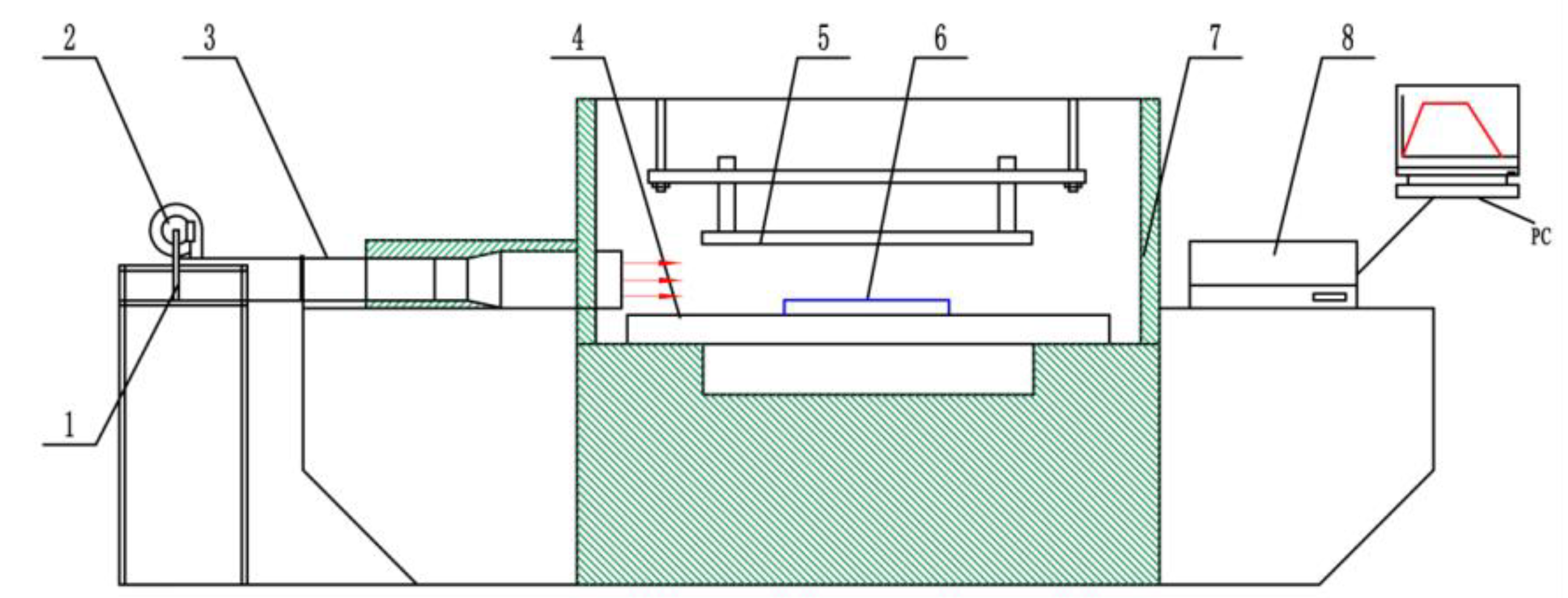
2.2. Experimental Equipment
| Equipment | Model and Manufacturer |
|---|---|
| RF drying system (equipped with hot air drying system) | SO-6F (frequency of 27.12 MHz, rated output power of 6 kW), Monga Strayfield Private Limited, Monga, India. As shown in Figure 2 |
| electronic balance | BSM220.4,Shanghai Zhuojing Electronic Technology Co., LTD., Shanghai, China) |
| fiber optic thermometer | HQ-FTS-I9C01, Xi ‘an Herch Opto Electronic Technology Co., LTD., Xi’an, China) |
| freezer | BCD-267G, Hisense Rongsheng Freezer Co., LTD., Foshan, China) |
| differential scanning calorimeter | DSC214 Polyma, NETZSCH, Bavaria, Germany |
| thermal characteristics analyzer | KD2pro, Beijing Gaolitei Technology Co., LTD., Beijing, China |
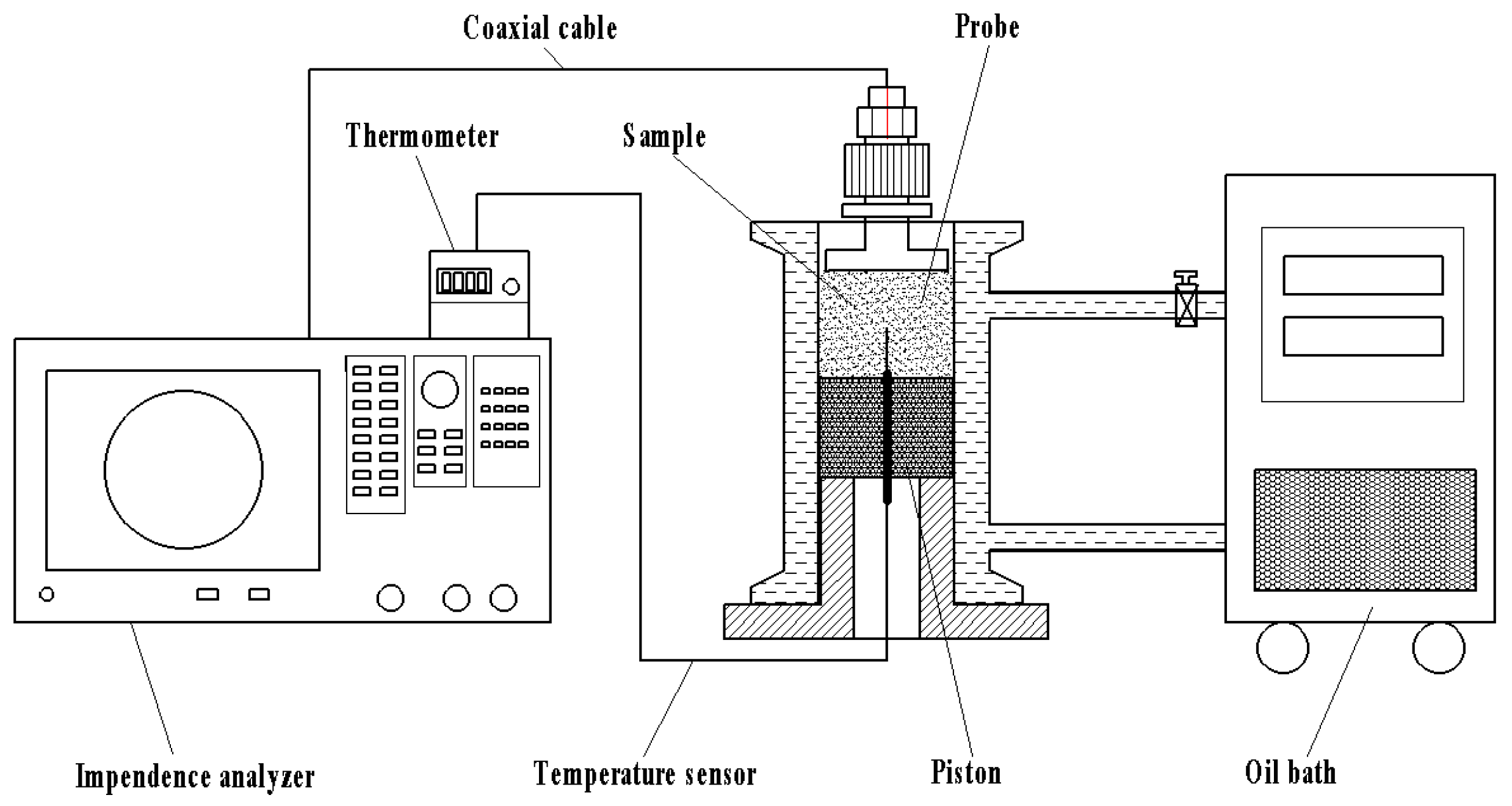
| terminal open-circuit coaxial probe dielectric characteristics measurement system | E4991B, Keysight Technologies Malaysia Sdn Bhd, Penang, Malaysia. As shown in Figure 3 |
| water bath kettle | RC-HH-2, Beijing Ruicheng Yongchuang Technology Co., LTD., Beijing, China |
| infrared camera | RSE 600, Fluke Corporation, Washington, P.O. Box 9090 Everett, WA 98206-9090 U.S.A. |
2.3. Establishment of Mathematical Models
2.3.1. Mass and Heat Transfer
2.3.2. Governing Equations of the RF Heating Process
2.3.3. Boundary Equation
2.4. Determination of Model Parameters
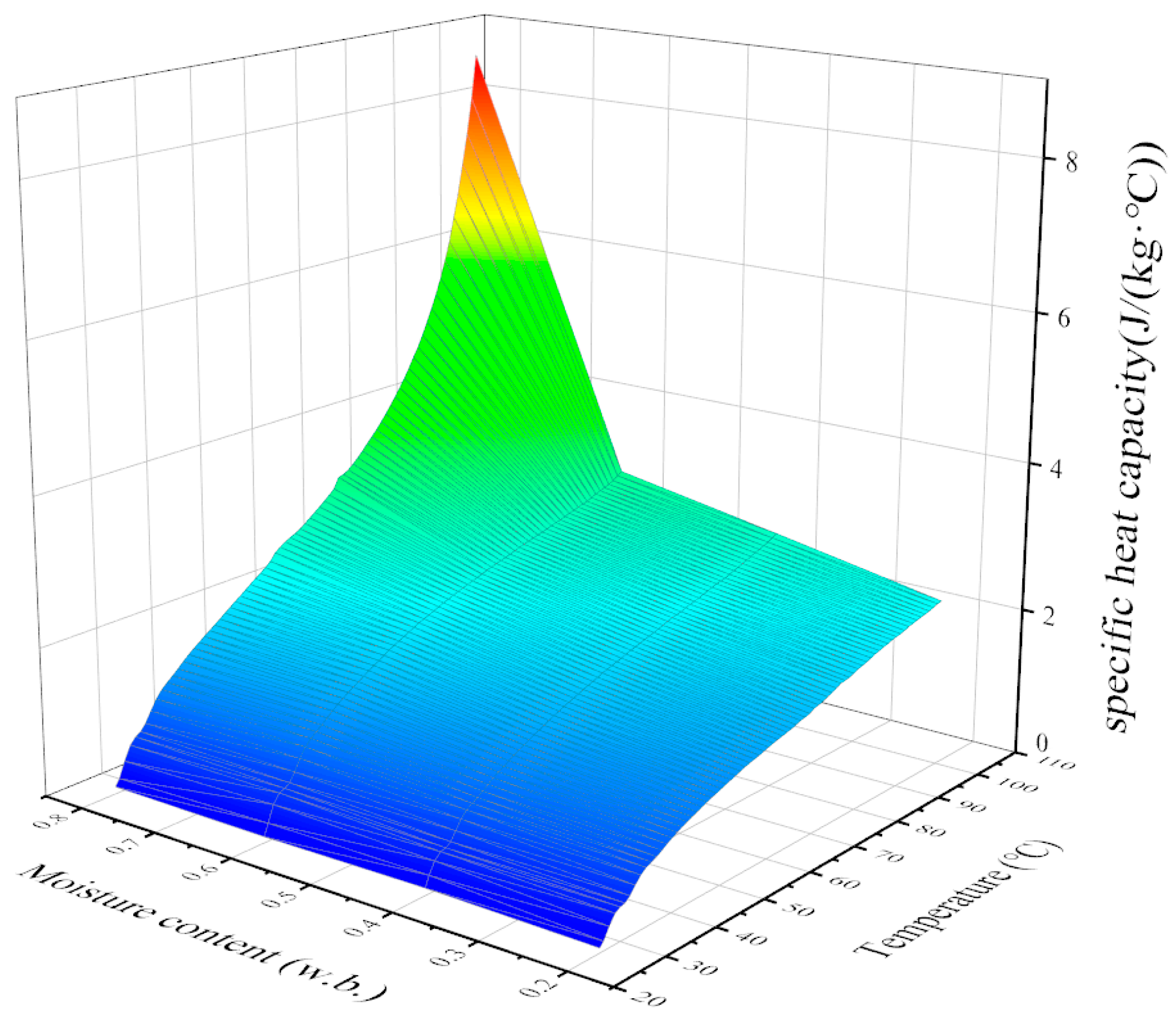
2.4.1. Specific Heat Capacity
2.4.2. Thermal Conductivity
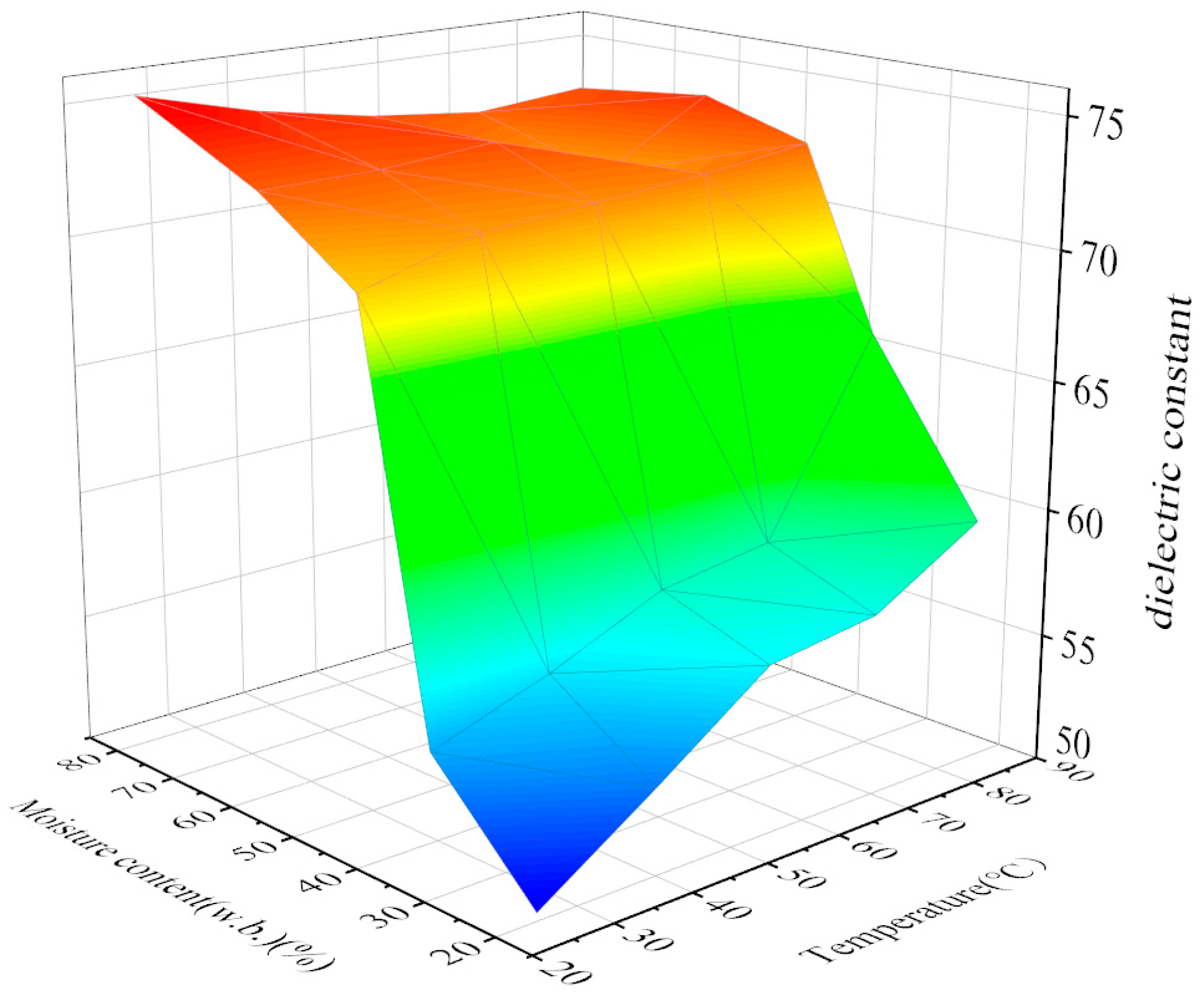
2.4.3. Dielectric Properties
2.4.4. Effective Moisture Diffusion Coefficient
2.4.5. Mass Transfer Coefficient
2.4.6. Convective Heat Transfer Coefficient
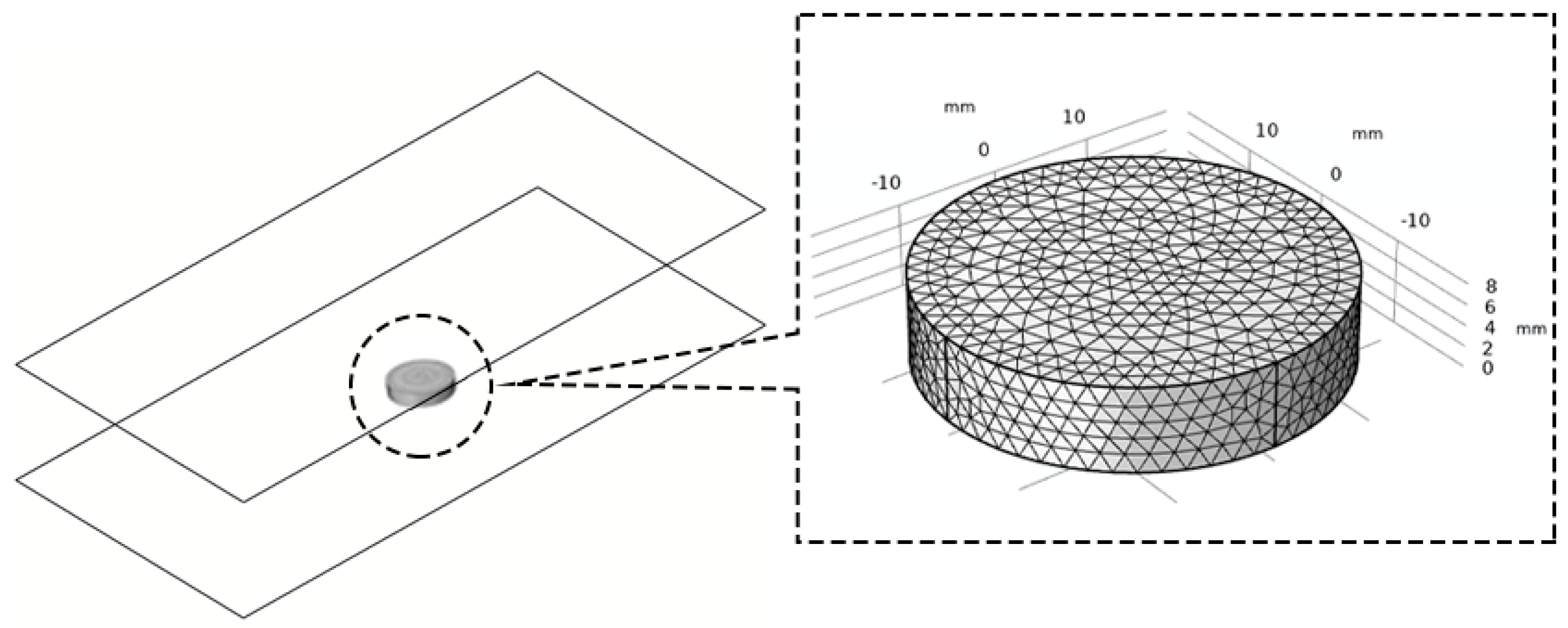
2.5. Development of Finite Element Model
2.5.1. Development of Geometric Model
2.5.2. Model Assumption
- (1)
- All two phases (liquid, solid) in the food sample were continuous media;
- (2)
- The jujube slice was a cylinder, and no morphological changes occured during drying;
- (3)
- The initial moisture content and initial temperature of jujube slices were uniform, and evaporation occurred on the upper surface of the sample;
- (4)
- The moisture is present only in liquid and vapor form;
- (5)
- Diffusion is the main mechanism by which moisture migrates from inside the material to the surface;
- (6)
- The jujube slice samples were isotropic;
- (7)
- The characteristics of jujube slice thermal, physical characteristics, and dielectric properties.
2.5.3. Resolution of Simulation Model
2.6. Model Verification
2.6.1. Moisture Content Detection
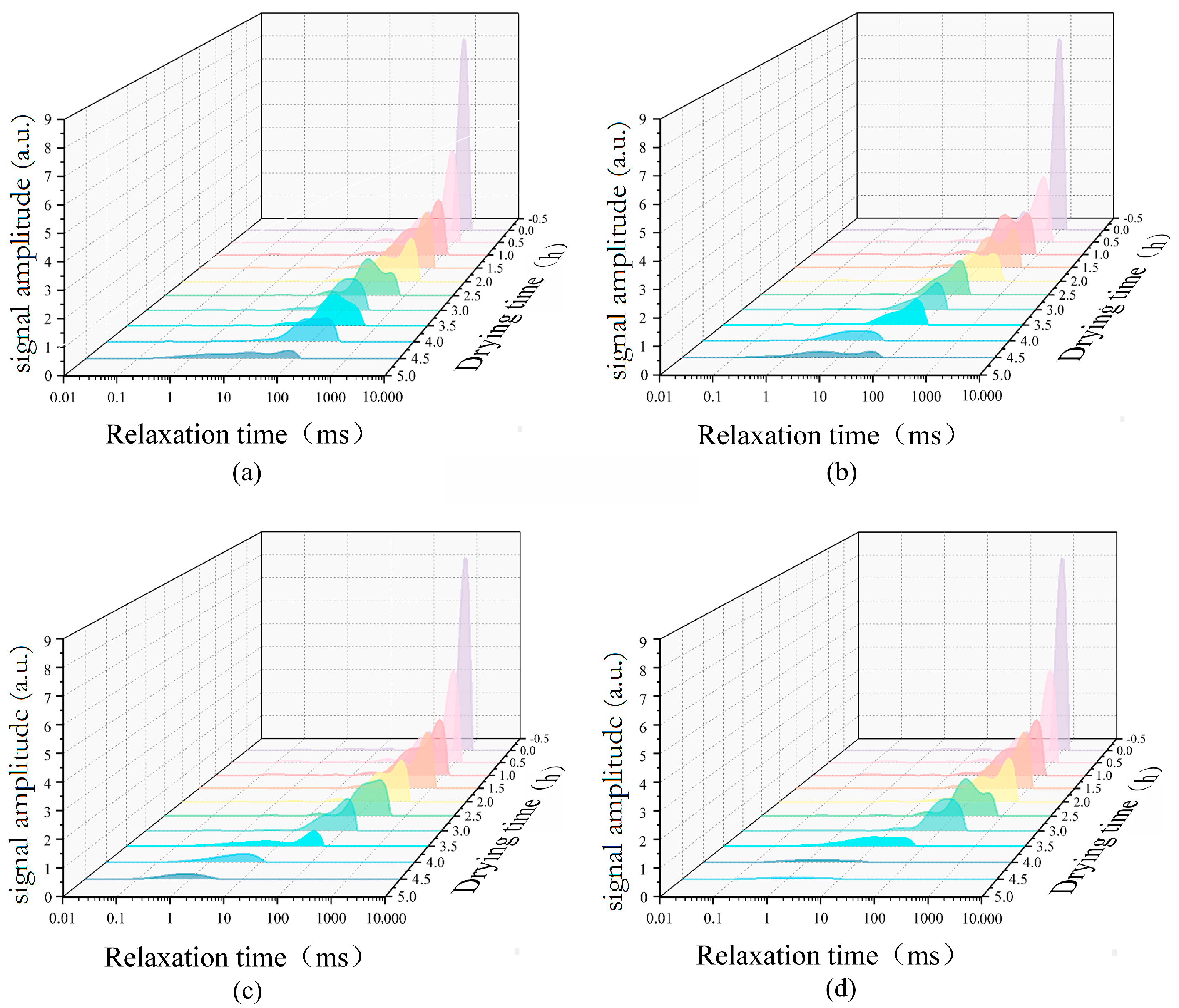
2.6.2. Nuclear Magnetic Signal Acquisition of Moisture of Jujube Slice
2.6.3. Center Temperature Detection
2.6.4. Surface Temperature Detection
3. Results and Discussion
3.1. Specific Heat Capacity Analysis
3.2. Thermal Conductivity Analysis
3.3. Dielectric Properties Analysis
3.4. Moisture Analysis
3.5. Nuclear Magnetic Signal Analysis
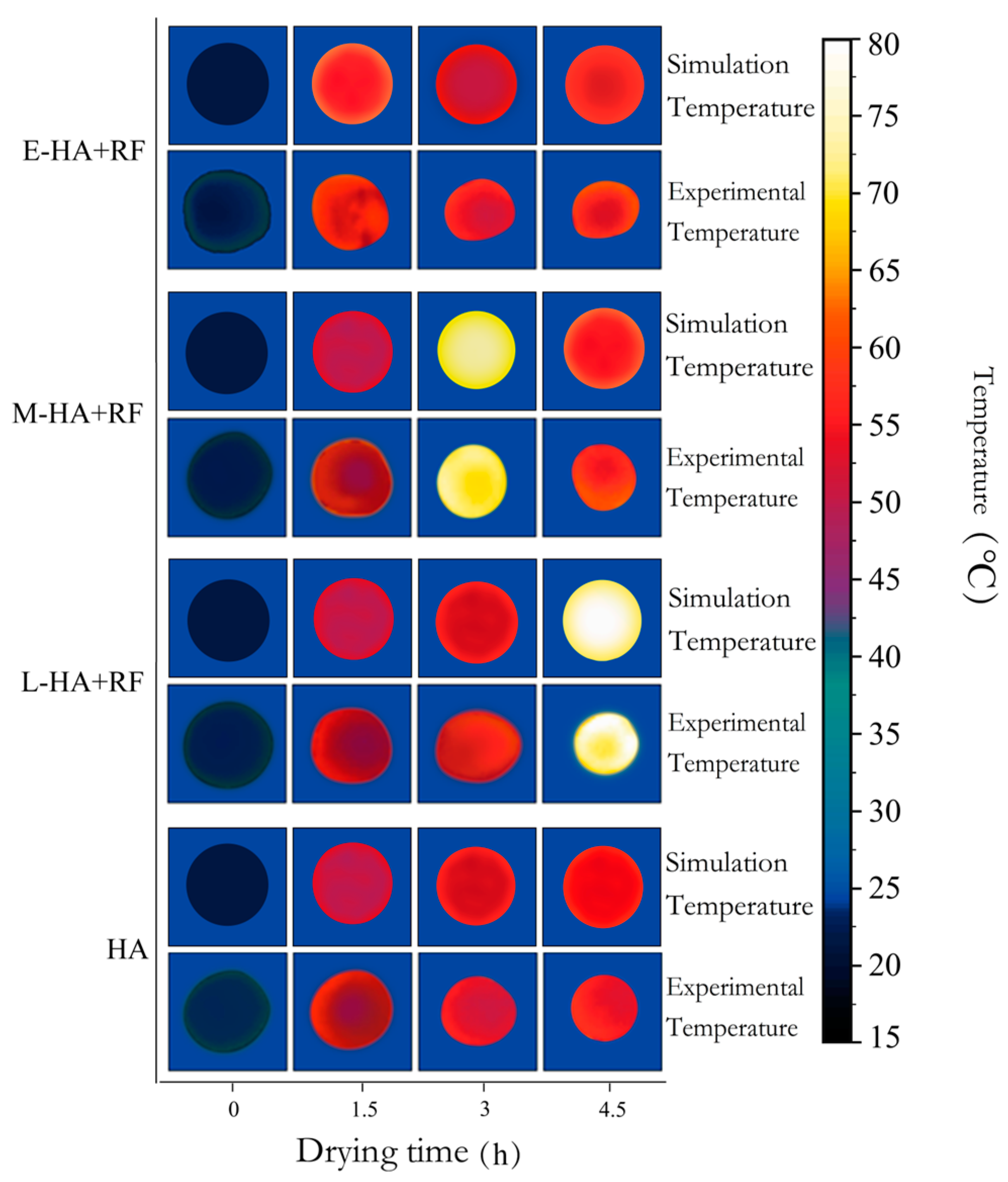
3.6. Surface Temperature
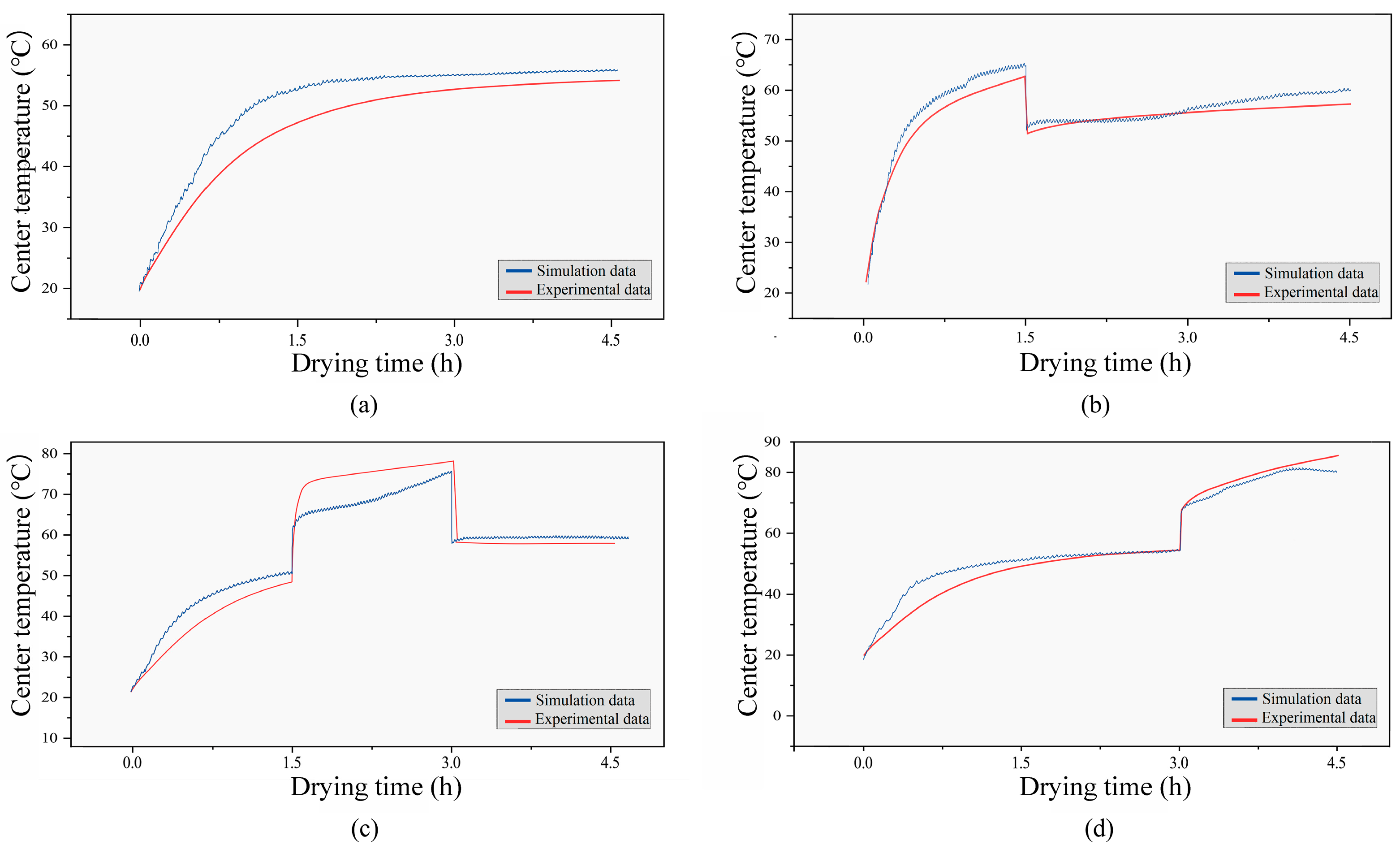
3.7. Center Temperature
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, W.; Zhao, D.; Fan, Y.; Wang, C.; Liu, Z. Comparison of the Nutrient Quality, Stable Isotope and Multi-Element Characteristics of Xinjiang Jujube for Origin Traceability. J. Nucl. Agric. Sci. 2021, 35, 1099–1112. [Google Scholar]
- Orikasa, T.; Wu, L.; Shiina, T.; Tagawa, A. Drying characteristics of kiwifruit during hot air drying. J. Food Eng. 2008, 85, 303–308. [Google Scholar] [CrossRef]
- Damayanti, W.; Tang, Y.; Jing, P.; Liao, M.; Jiao, S. Study on Hot Air-Assisted Radio Frequency Drying Technology of Rough Rice and Associated Quality. Storage Process 2021, 21, 79–86. [Google Scholar]
- Ling, Z.; Ren, G.; Duan, X.; Lu, Y.; Chen, X. Design and analysis of radio frequency dryer for small particles (containing powder). Food Mach. 2019, 35, 99–103. [Google Scholar]
- Yin, J.; Gong, C.; Tang, Y.; Jing, P.; Jiao, S. Mathematical modeling of vitamin C thermal degradation kinetics in carrot cubes during hot air-assisted radio frequency drying. J. Food Saf. Qual. 2021, 12, 1357–1361. [Google Scholar]
- Yao, X.; Zang, Y.; Gu, J.; Ding, H.; Niu, Y.; Zheng, X.; Zhu, R.; Wang, Q. Microstructure Analysis and Quality Evaluation of Jujube Slices Dried by Hot Air Combined with Radio Frequency Heat Treatment at Different Drying Stages. Foods 2022, 11, 3086. [Google Scholar] [CrossRef]
- Jayapragasam, P.; Le Bideau, P.; Loulou, T. Luikov’s Analytical Solution with Complex Eigenvalues in Intensive Drying. Transp. Porous Media 2019, 130, 923–946. [Google Scholar] [CrossRef]
- Wang, K.; Li, J.; Peng, F.; Liu, Y.; Ma, Q.; Li, M.; Xu, H. Effects of Radio Frequency Treatment on Short- and Medium-Wavelength Infrared Drying Kinetics and Quality Characteristics of Red Jujubes. Food Sci. 2020, 41, 117–123. [Google Scholar]
- Zhou, X.; Xu, R.Z.; Zhang, B.H.; Pei, S.; Liu, Q.Q.; Ramaswamy, H.S.; Wang, S.J. Radio Frequency-Vacuum Drying of Kiwifruits: Kinetics, Uniformity, and Product Qualit. Food Bioprocess Technol. 2018, 11, 2094–2109. [Google Scholar]
- Wang, X.; Kang, C.; Wu, Z.; Li, Y.; Xu, S.; Yang, M. Simulation and experiment of temperature uniformity of Erzhi Pills during hotair drying process. Chin. Tradit. Herb. Drugs 2020, 51, 1226–1232. [Google Scholar]
- Liu, Y.; Tang, J.; Mao, Z.; Mah, J.-H.; Jiao, S.; Wang, S. Quality and mold control of enriched white bread by combined radio frequency and hot air treatment. J. Food Eng. 2011, 104, 492–498. [Google Scholar] [CrossRef]
- Lian, M.; Huang, L.; Duan, X. Quality change and moisture distribution of kiwifruit during FD-MVD. Food Ferment. Ind. 2020, 46, 162–168. [Google Scholar]
- Corey, M.; Kerr, W.; Mulligan, J.; Lavelli, V. Phytochemical stability in dried apple and green tea functional products as related to moisture properties. LWT-Food Sci. Technol. 2011, 44, 67–74. [Google Scholar] [CrossRef]
- Topcam, H.; Gogus, F.; Ozbek, H.N.; Elik, A.; Yanik, D.K.; Dalgic, A.C.; Erdogdu, F. Hot air-assisted radio frequency drying of apricots: Mathematical modeling study for process design. J. Food Sci. 2022, 87, 764–779. [Google Scholar] [CrossRef]
- Aversa, M.; Curcio, S.; Calabro, V.; Iorio, G. An analysis of the transport phenomena occurring during food drying process. J. Food Eng. 2007, 78, 922–932. [Google Scholar] [CrossRef]
- Farinu, A.; Baik, O.-D. Thermal properties of sweet potato with its moisture content and temperature. Int. J. Food Prop. 2007, 10, 703–719. [Google Scholar] [CrossRef] [Green Version]
- Joardder MU, H.; Kumar, C.; Karim, M.A. Multiphase transfer model for intermittent microwave-convective drying of food: Considering shrinkage and pore evolution. Int. J. Multiph. Flow 2017, 95, 101–119. [Google Scholar]
- Kumar, C.; Joardder MU, H.; Farrell, T.W.; Millar, G.J.; Karim, M.A. Mathematical model for intermittent microwave convective drying of food materials. Dry. Technol. 2016, 34, 962–973. [Google Scholar] [CrossRef] [Green Version]
- Nejadi, J.; Nikbakht, A.M. Numerical Simulation of Corn Drying in a Hybrid Fluidized Bed-Infrared Dryer. J. Food Process Eng. 2017, 40, e12373. [Google Scholar] [CrossRef]
- Onwude, D.I.; Hashim, N.; Abdan, K.; Janius, R.; Chen, G. Numerical modeling of radiative heat and mass transfer for sweet potato during drying. J. Food Process. Preserv. 2018, 42, e13741. [Google Scholar] [CrossRef]
- Ruiz-Lopez Ii Cordova, A.V.; Rodriguez-Jimenes, G.C.; Garcia-Alvarado, M.A. Moisture and temperature evolution during food drying: Effect of variable properties. J. Food Eng. 2004, 63, 117–124. [Google Scholar] [CrossRef]
- Solomon, A.B.; Fanta, S.W.; Delele, M.A.; Vanierschot, M. Modeling and simulation of heat and mass transfer in an Ethiopian fresh injera drying process. Heliyon 2021, 7, e06201. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Wang, S. Recent developments in radio frequency drying for food and agricultural products using a multi-stage strategy: A review. Crit. Rev. Food Sci. Nutr. 2023, 63, 2654–2671. [Google Scholar] [PubMed]
- Song, S.; Wu, X.; Chen, Q.; Zhang, M.; Hu, X. Comparison of Halogen Analyzer Method and Oven Method for Determining the Moisture Content of Different Foods. Mod. Food 2021, 1, 171–173+180. [Google Scholar]
- Kumar, C.; Joardder, M.; Farrell, T.; Karim, M. Investigation of intermittent microwave convective drying (IMCD) of food materials by a coupled 3D electromagnetics and multiphase model. Dry. Technol. 2018, 36, 736–750. [Google Scholar] [CrossRef]
- Onwude, D.I.; Hashim, N.; Abdan, K.; Janius, R.; Chen, G. Modelling the mid-infrared drying of sweet potato: Kinetics, mass and heat transfer parameters, and energy consumption. Heat Mass Transf. 2018, 54, 2917–2933. [Google Scholar]
- Birla, S.L.; Wang, S.; Tang, J. Computer simulation of radio frequency heating of model fruit immersed in moisture. J. Food Eng. 2008, 84, 270–280. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.; Xie, W.; Zheng, Z.; Fan, B.; Yang, D. Simulation and experimental study of radio frequency heating of low-moisture maize kernels. Trans. Chin. Soc. Agric. Eng. 2021, 37, 11–17. [Google Scholar]
- Jiang, D.; Wang, W.; Wang, S.; Lei, D.; Liu, Y.; Xiao, H.; Wu, M.; Gao, Z.; Zheng, Z. Coupled modeling and heat and mass transfer analysis of white radish slices dried by infrared radiation combined hot air drying. Trans. Chin. Soc. Agric. Eng. 2022, 38, 314–323. [Google Scholar]
- Song, R.; Zhang, F.; Yang, W.; Li, S.; Hao, D.; Yao, B. Dynamic modeling and simulation of potato microwave drying. J. Hunan Agric. Univ. (Nat. Sci.) 2018, 44, 204–209. [Google Scholar]
- Meng, J.; Jiang, J.; Zheng, Z.; Deng, L.; Wang, J.; Xue, L.; Han, Z.; Wang, H.; Xiao, H. Effects of three drying technologies on drying kinetics and quality attributes of yam slices. Chin. Tradit. Herb. Drugs 2019, 50, 2575–2582. [Google Scholar]
- Qian, J.; Zhang, Q.; Wang, J.; Fang, X.; Zhang, W.; Gao, Z.; Liu, Y.; Xiao, H. Effects of three drying technologies on drying characteristics and quality attributes of jujube crisps. Trans. Chin. Soc. Agric. Eng. 2016, 32, 259–265. [Google Scholar]
- Liu, Q.; Wang, Q. Effects of Short- and Medium-wave Infrared Radiation Drying on Drying Characteristics. Nutr. Qual. Antioxid. Act. Mulberry 2021, 42, 39–45. [Google Scholar]
- Shorstkii, I.; Sosnin, M.; Smetana, S.; Toepfl, S.; Parniakov, O.; Wiktor, A. Correlation of the cell disintegration index with Luikov’s heat and mass transfer parameters for drying of pulsed electric field (PEF) pretreated plant materials. J. Food Eng. 2022, 316, 110822. [Google Scholar] [CrossRef]
- Dincer, I.; Hussain, M. Development of a new Biot number and lag factor correlation for drying applications. Int. J. Heat Mass Transf. 2004, 47, 653–658. [Google Scholar] [CrossRef]
- Ju, H.; Zhao, H.; Zhang, J.; Zhang, W.; Yu, X.; Wang, J.; Gao, Z.; Xiao, H. Drying characteristics of Chaenomeles sinensis with different drying methods based on Dincer model. Chin. Tradit. Herb. Drugs 2020, 51, 3911–3921. [Google Scholar]
- Kumar, C.; Millar, G.J.; Karim, M.A. Effective Diffusivity and Evaporative Cooling in Convective Drying of Food Material. Dry. Technol. 2015, 33, 227–237. [Google Scholar] [CrossRef] [Green Version]
- Thuwapanichayanan, R.; Prachayawarakorn, S.; Soponronnarit, S. Heat and moisture transport behaviour and quality of chopped garlic undergoing different drying methods. J. Food Eng. 2014, 136, 34–41. [Google Scholar] [CrossRef]
- Yuan, Y.; Tan, L.; Xu, Y.; Yuan, Y.; Dong, J. Numerical and experimental study on drying shrinkage-deformation of apple slices during process of heat-mass transfer. Int. J. Therm. Sci. 2019, 136, 539–548. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, X. Radio frequency-vacuum drying of kiwifruits: Kinetics, uniformity and product quality. In Proceedings of the 21st International Drying Symposium (IDS), Valencia, Spain, 11–14 September 2018. [Google Scholar]
- Chen, X.; Liu, Y.; Zhang, R.; Zhu, H.; Li, F.; Yang, D.; Jiao, Y. Radio Frequency Drying Behavior in Porous Media: A Case Study of Potato Cube with Computer Modeling. Foods 2022, 11, 3279. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, S.; Yang, C.; Zang, Y.; Li, Y.; Gu, J.; Ding, H.; Yao, X.; Zhu, R.; Wang, Q.; Dong, W.; et al. Simulated and Verification of Mass and Heat Transfer Coupled Model of Jujube Slices Dried by Hot Air Combined with Radio Frequency Heat Treatment at Different Drying Stages. Foods 2023, 12, 3025. https://doi.org/10.3390/foods12163025
Cao S, Yang C, Zang Y, Li Y, Gu J, Ding H, Yao X, Zhu R, Wang Q, Dong W, et al. Simulated and Verification of Mass and Heat Transfer Coupled Model of Jujube Slices Dried by Hot Air Combined with Radio Frequency Heat Treatment at Different Drying Stages. Foods. 2023; 12(16):3025. https://doi.org/10.3390/foods12163025
Chicago/Turabian StyleCao, Shuaitao, Chenyan Yang, Yongzhen Zang, Yang Li, Jiangwei Gu, Haiyang Ding, Xuedong Yao, Rongguang Zhu, Qiang Wang, Wancheng Dong, and et al. 2023. "Simulated and Verification of Mass and Heat Transfer Coupled Model of Jujube Slices Dried by Hot Air Combined with Radio Frequency Heat Treatment at Different Drying Stages" Foods 12, no. 16: 3025. https://doi.org/10.3390/foods12163025
APA StyleCao, S., Yang, C., Zang, Y., Li, Y., Gu, J., Ding, H., Yao, X., Zhu, R., Wang, Q., Dong, W., & Huang, Y. (2023). Simulated and Verification of Mass and Heat Transfer Coupled Model of Jujube Slices Dried by Hot Air Combined with Radio Frequency Heat Treatment at Different Drying Stages. Foods, 12(16), 3025. https://doi.org/10.3390/foods12163025




