A Systematical Rheological Study of Maize Kernel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Drying of Maize Kernels
2.2.1. Natural Drying (ND)
2.2.2. Hot Air/Vacuum Drying (HVD)
2.3. Sample Preparation
2.4. Stress Relaxation Tests
2.5. Creep Tests
2.6. Time–Temperature Superposition
2.7. Statistical Analysis
3. Results and Discussion
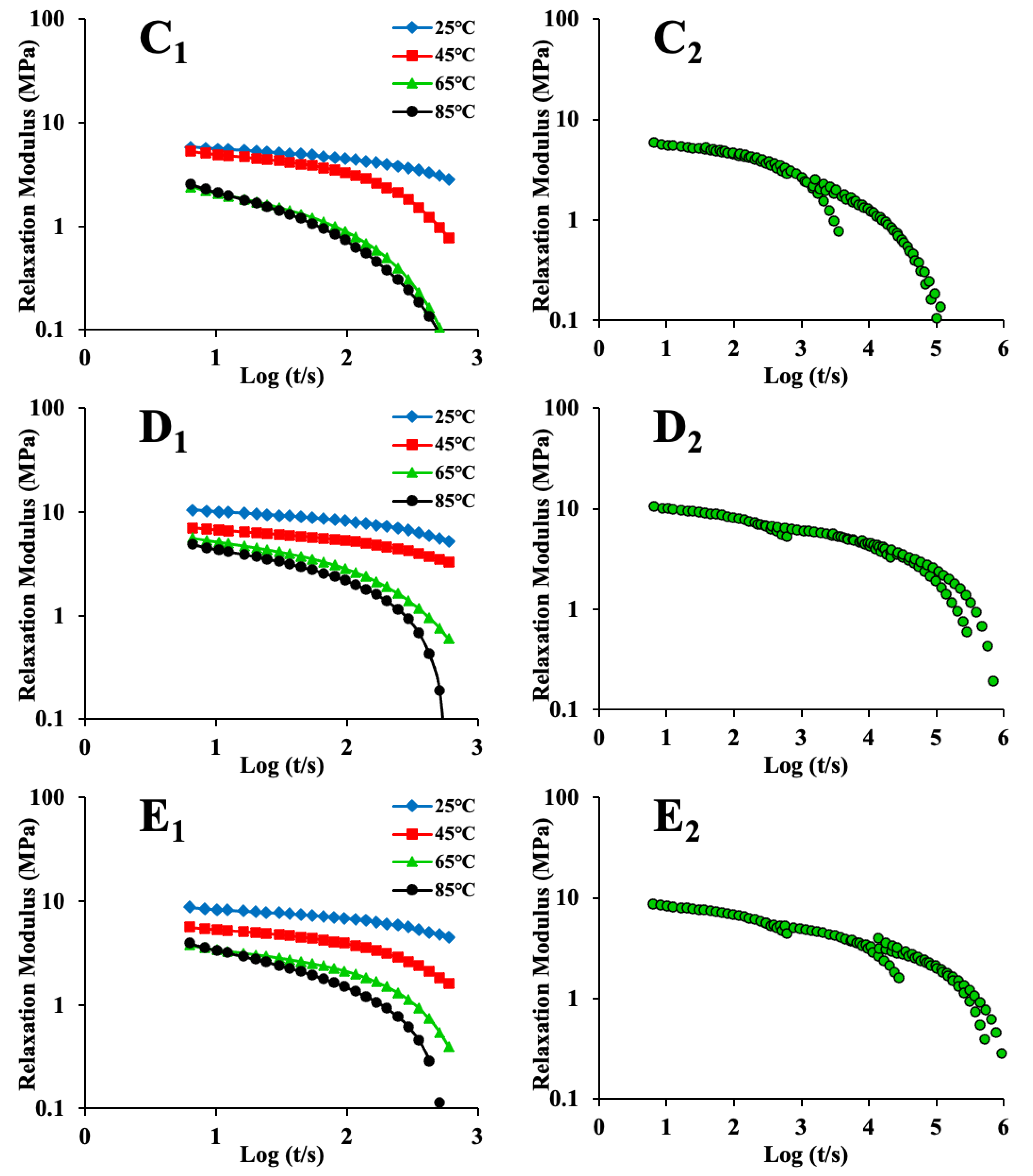
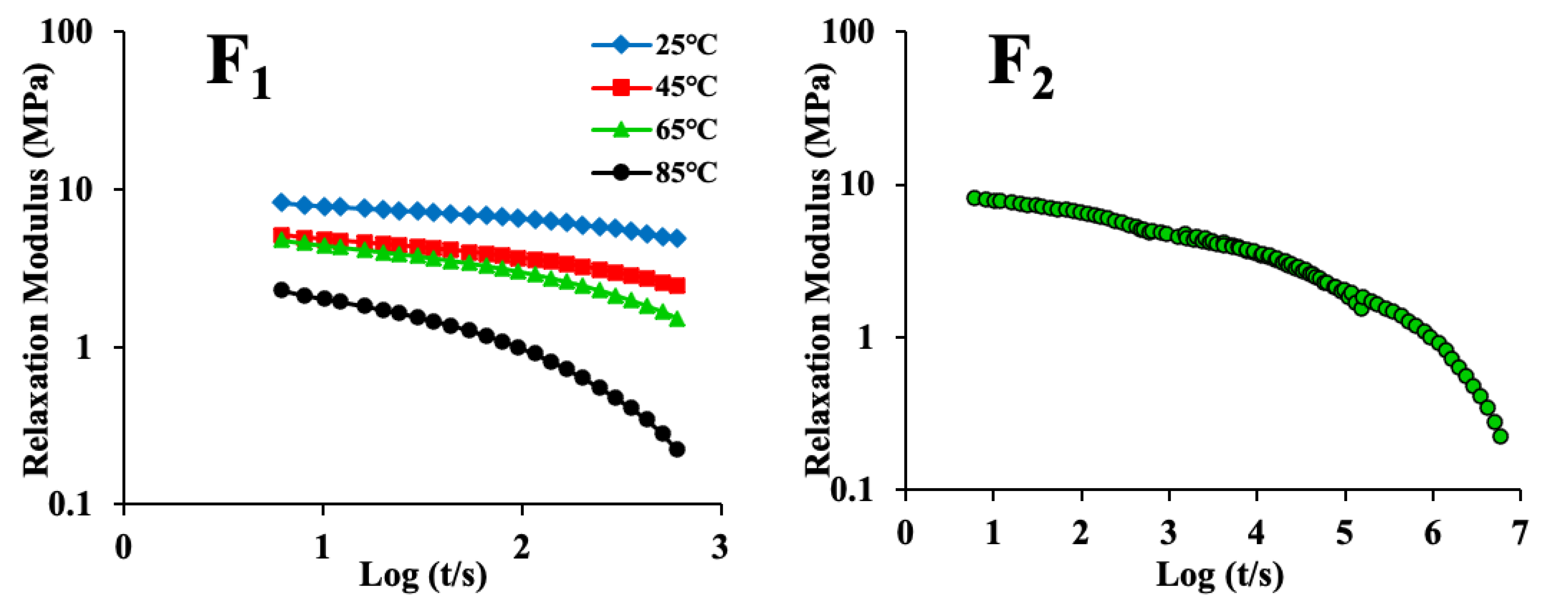
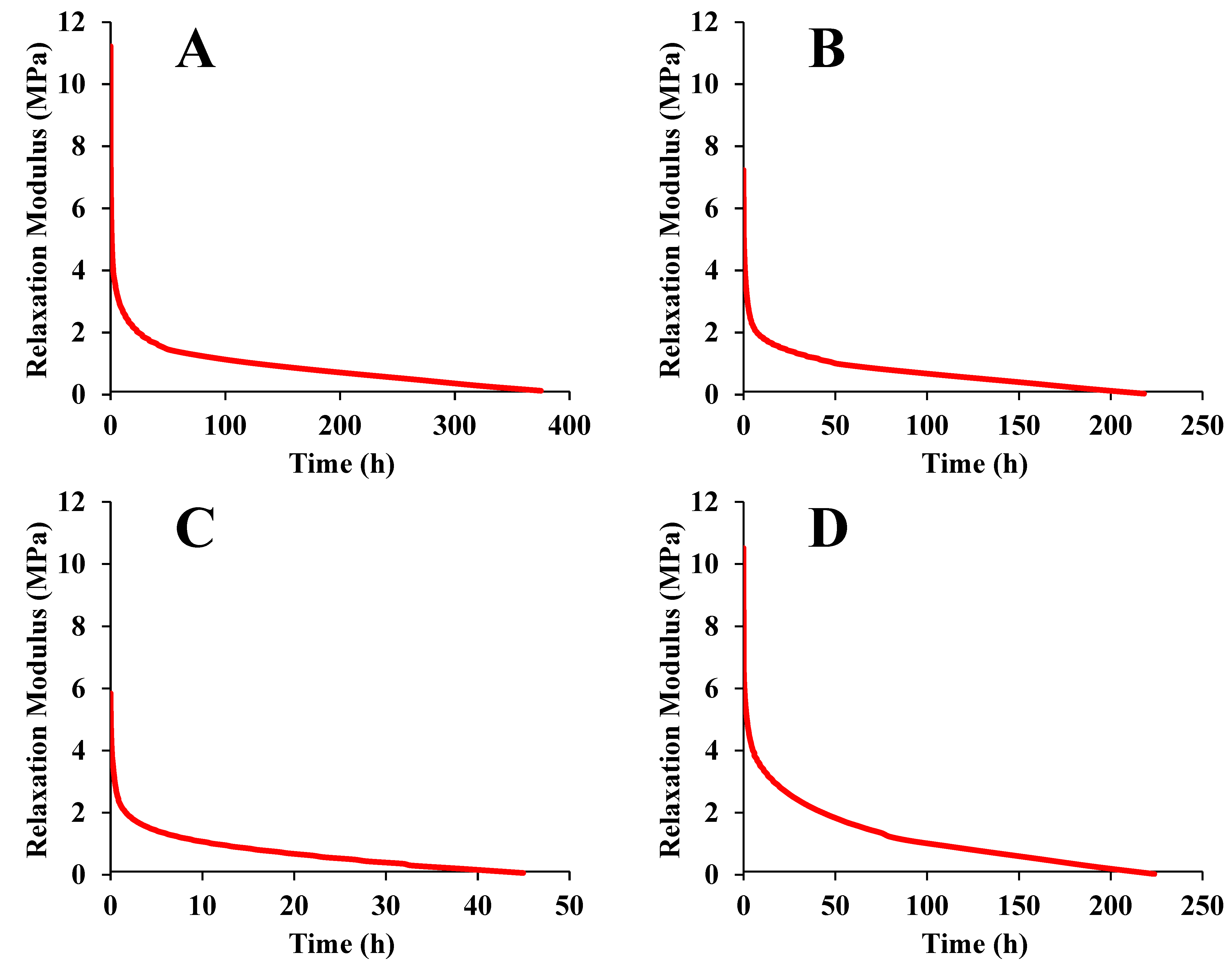
3.1. Analysis of Stress Relaxation Behavior
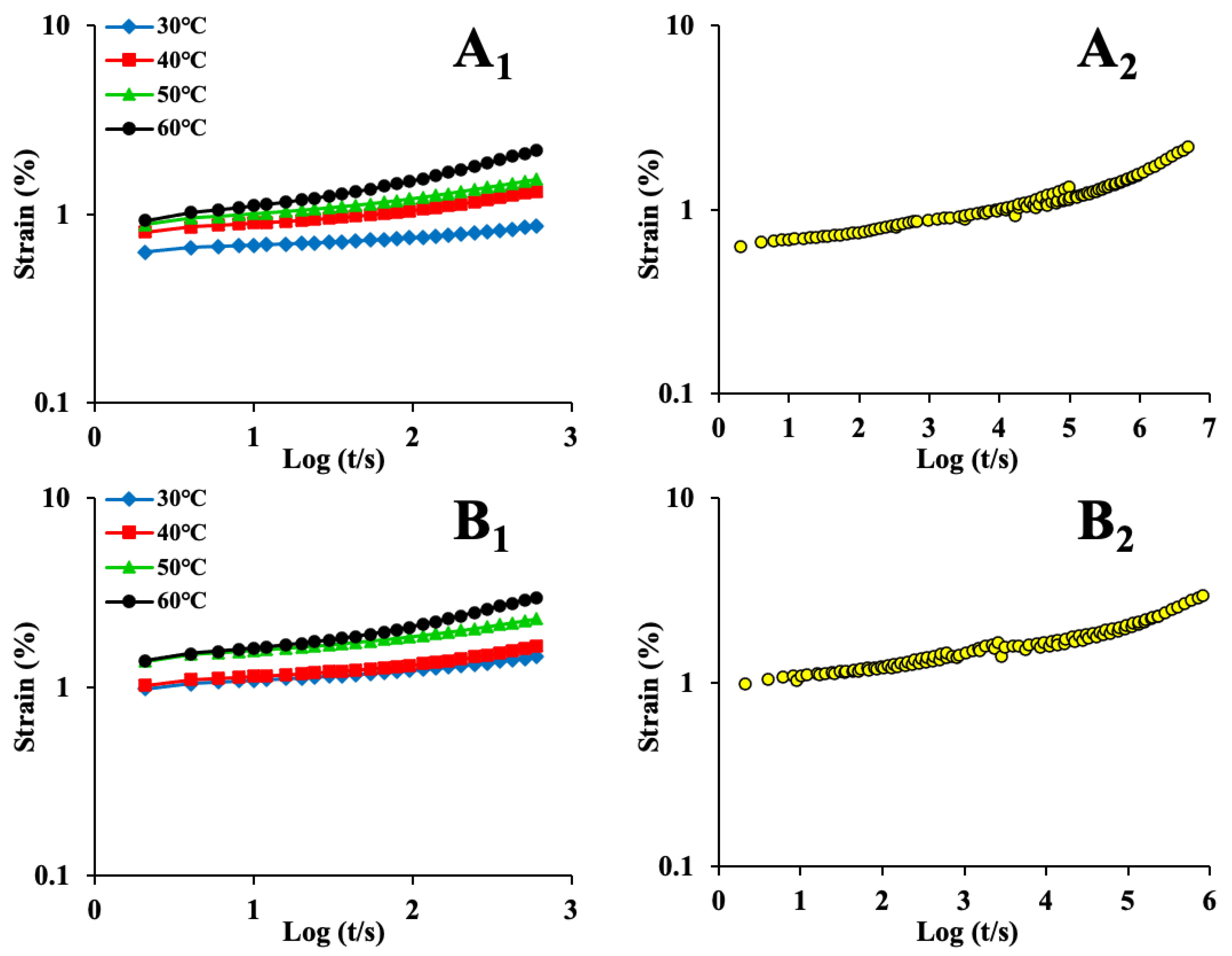
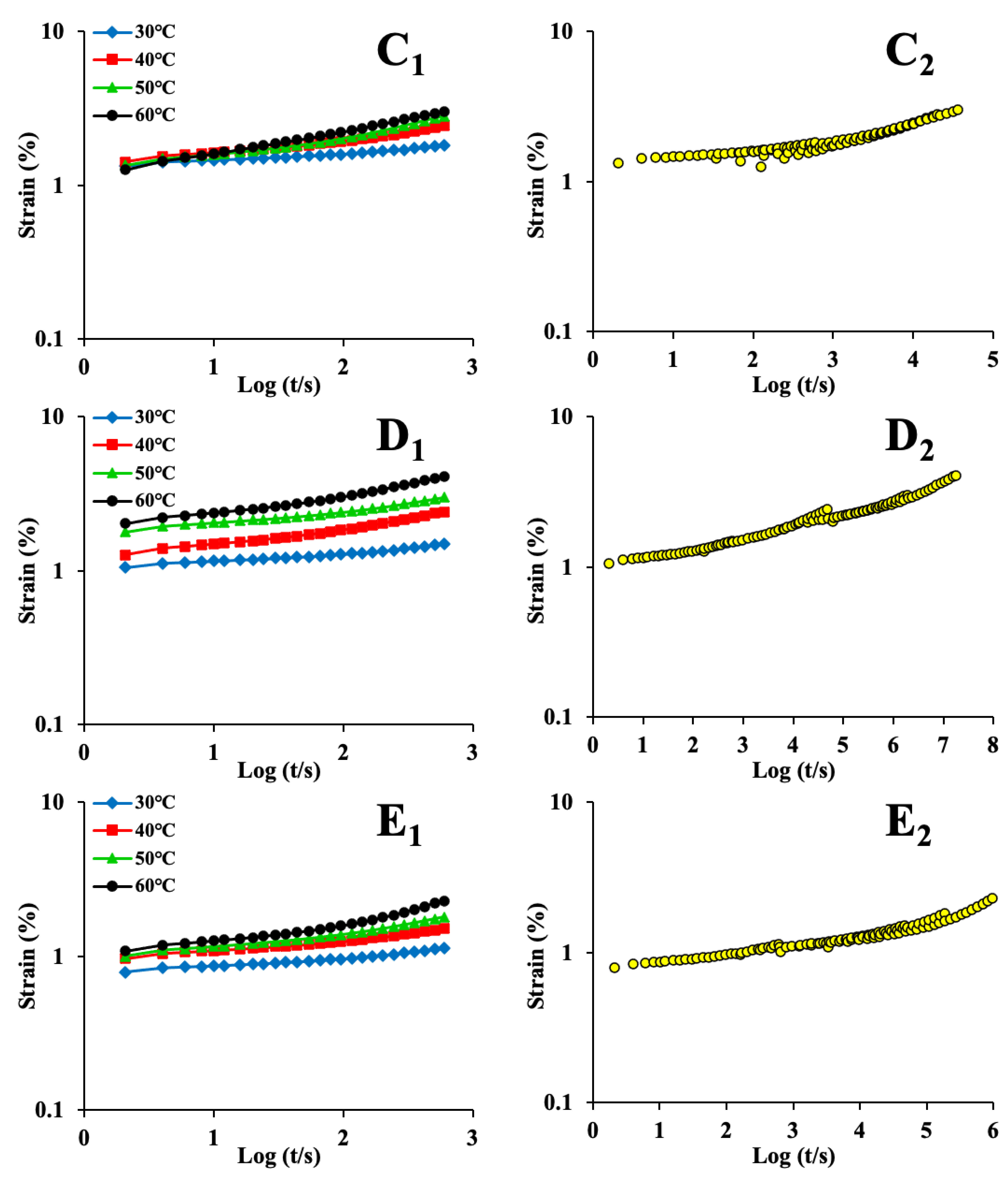
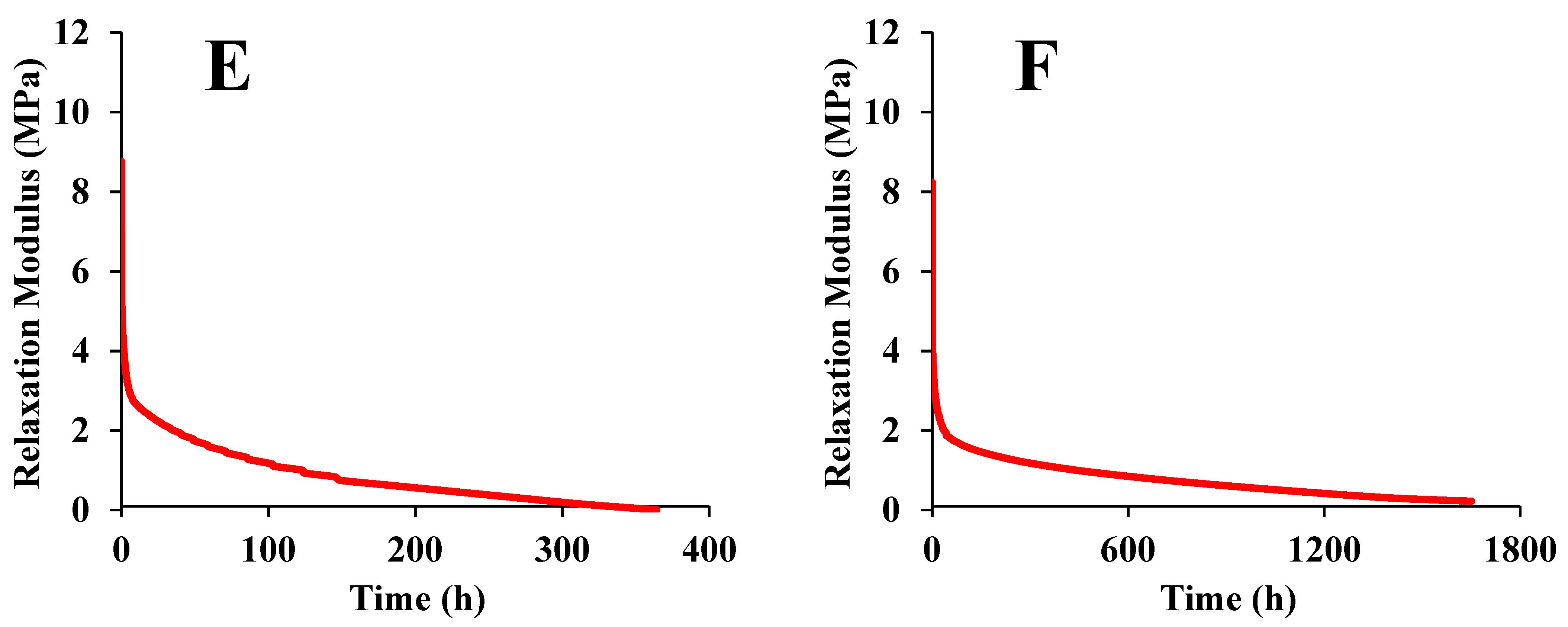
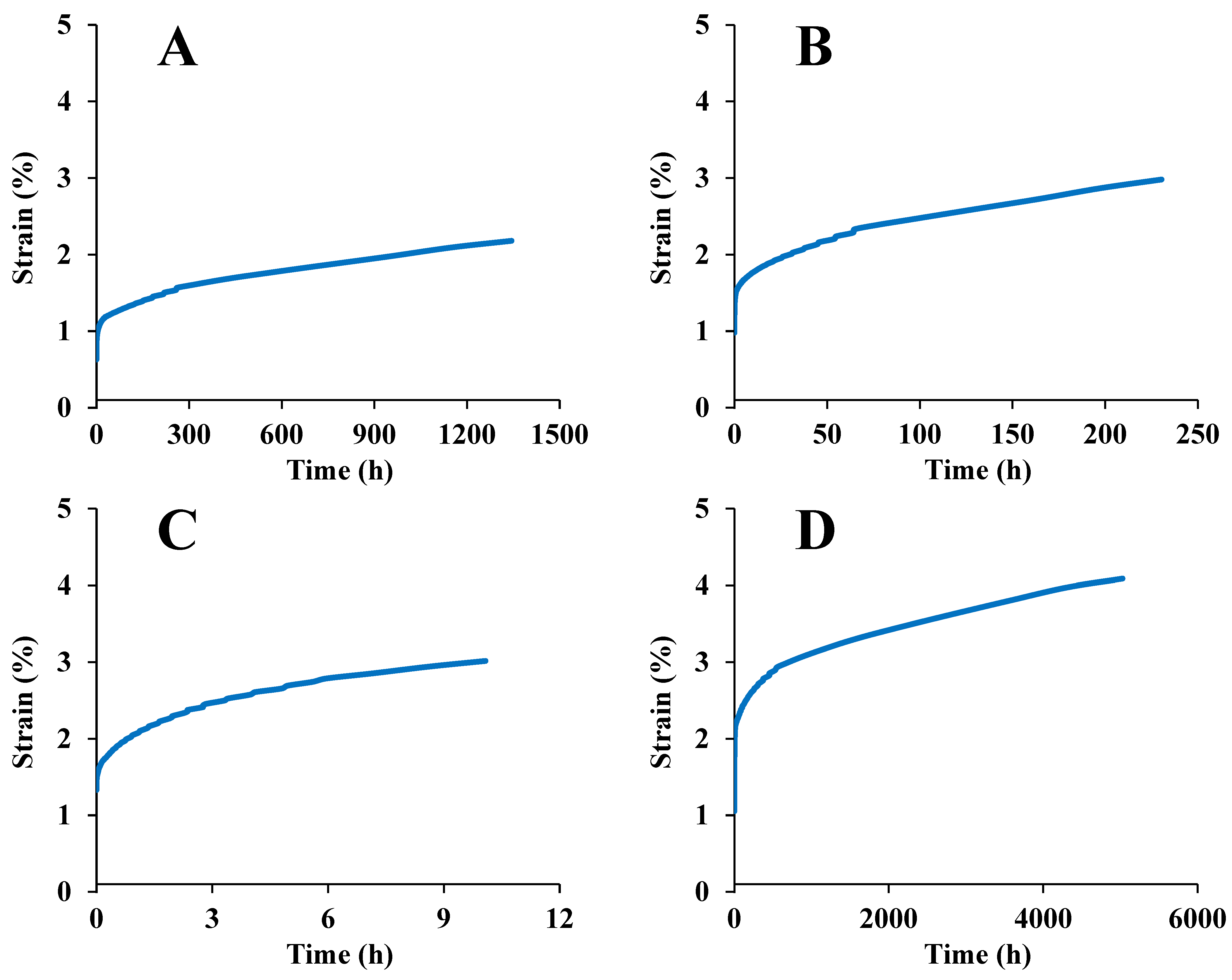
3.2. Analysis of Creep Behavior
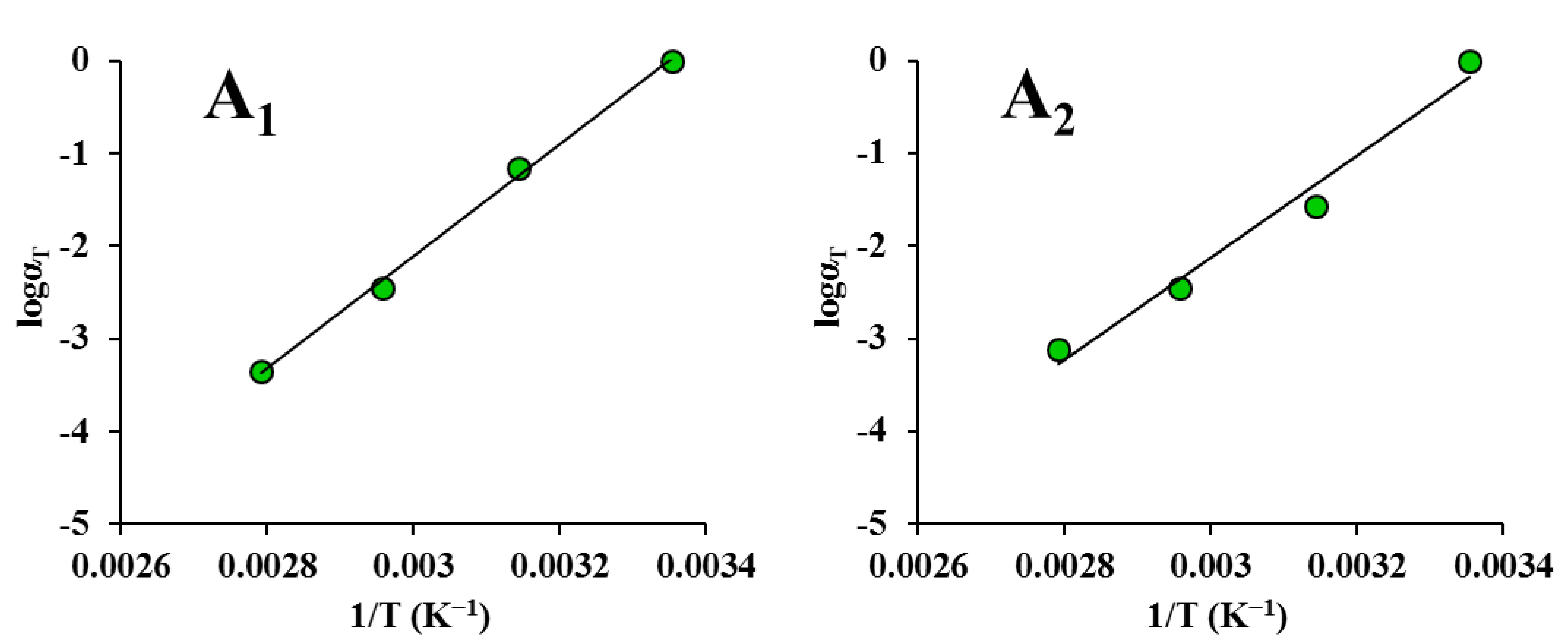
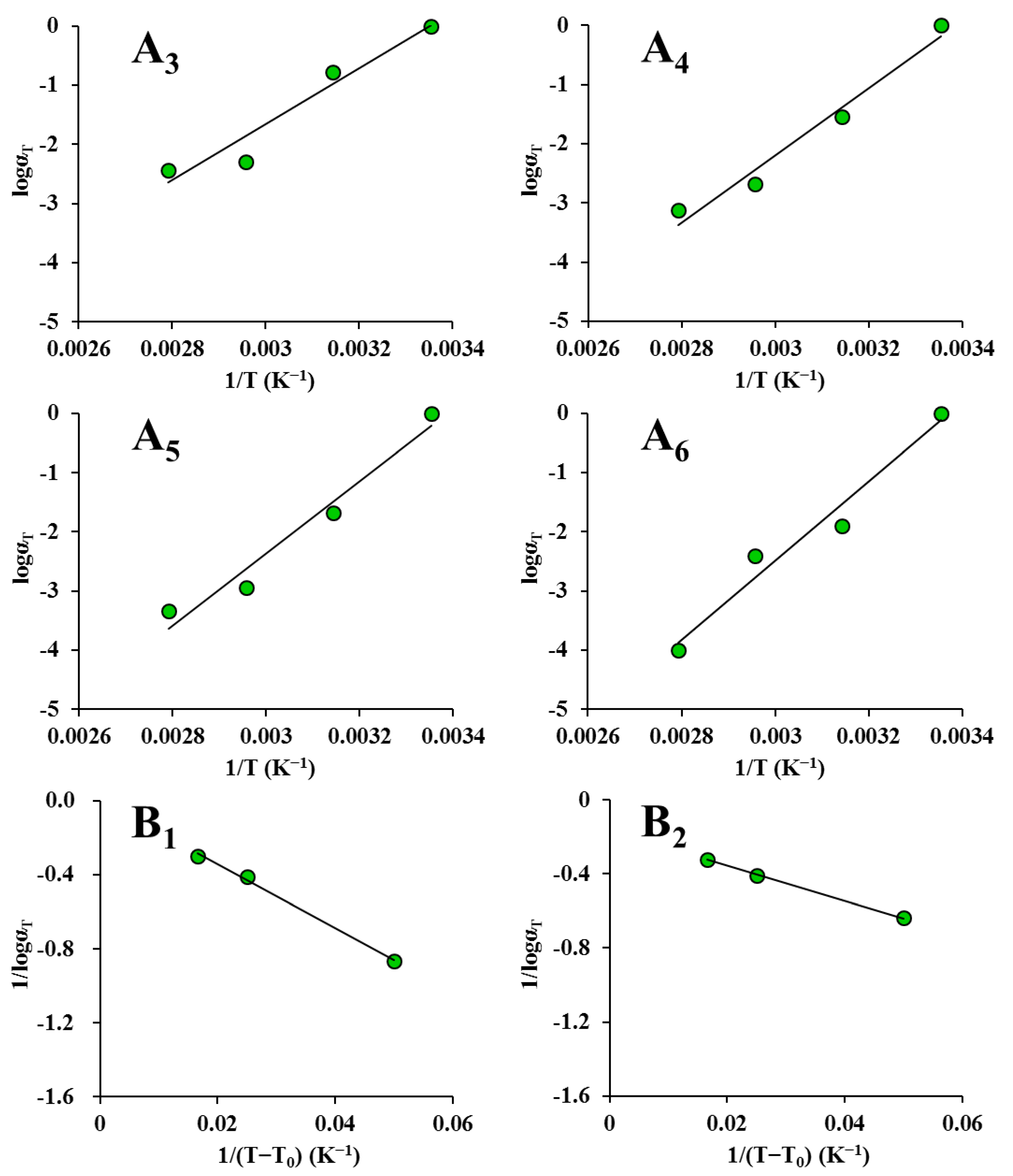
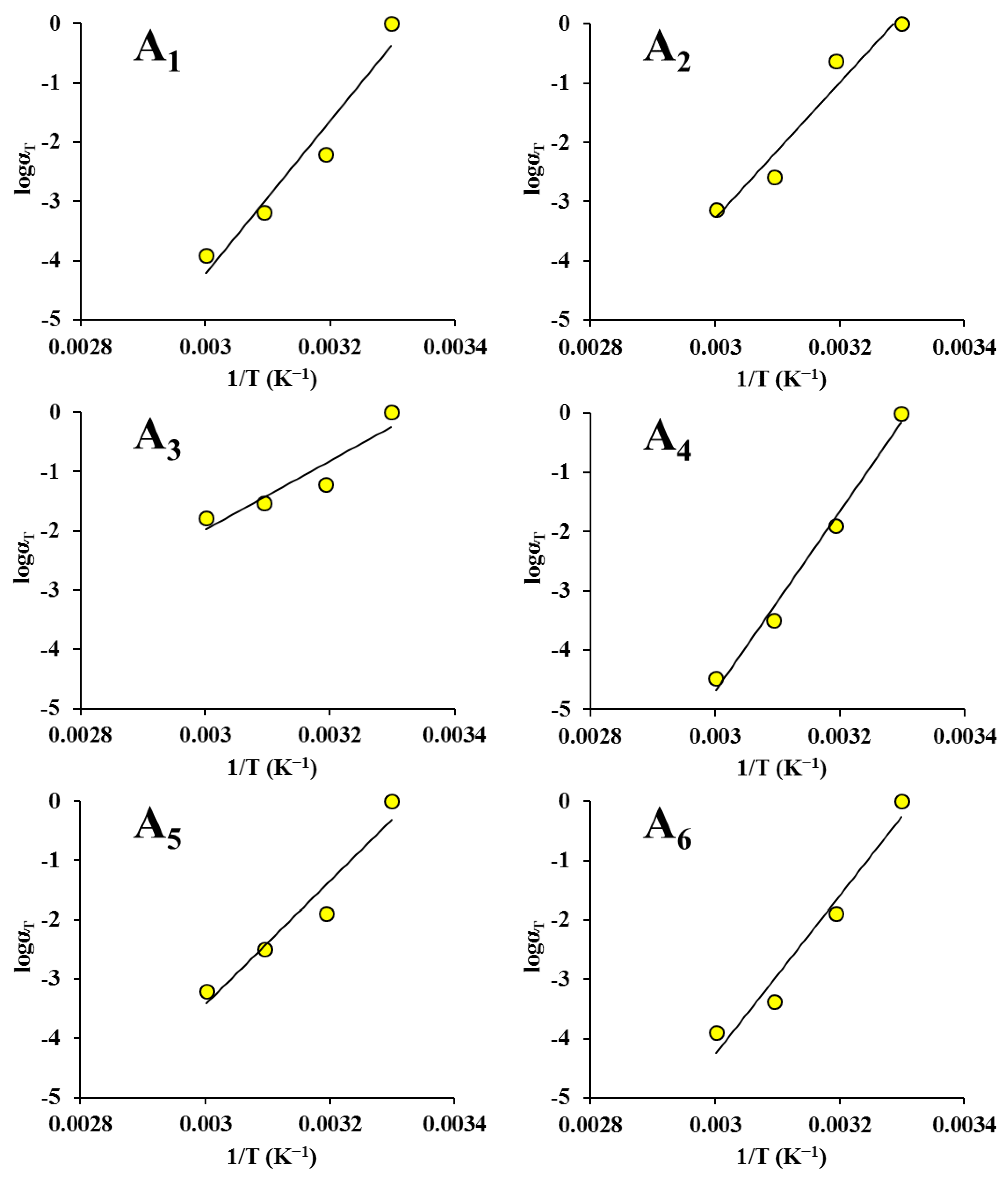
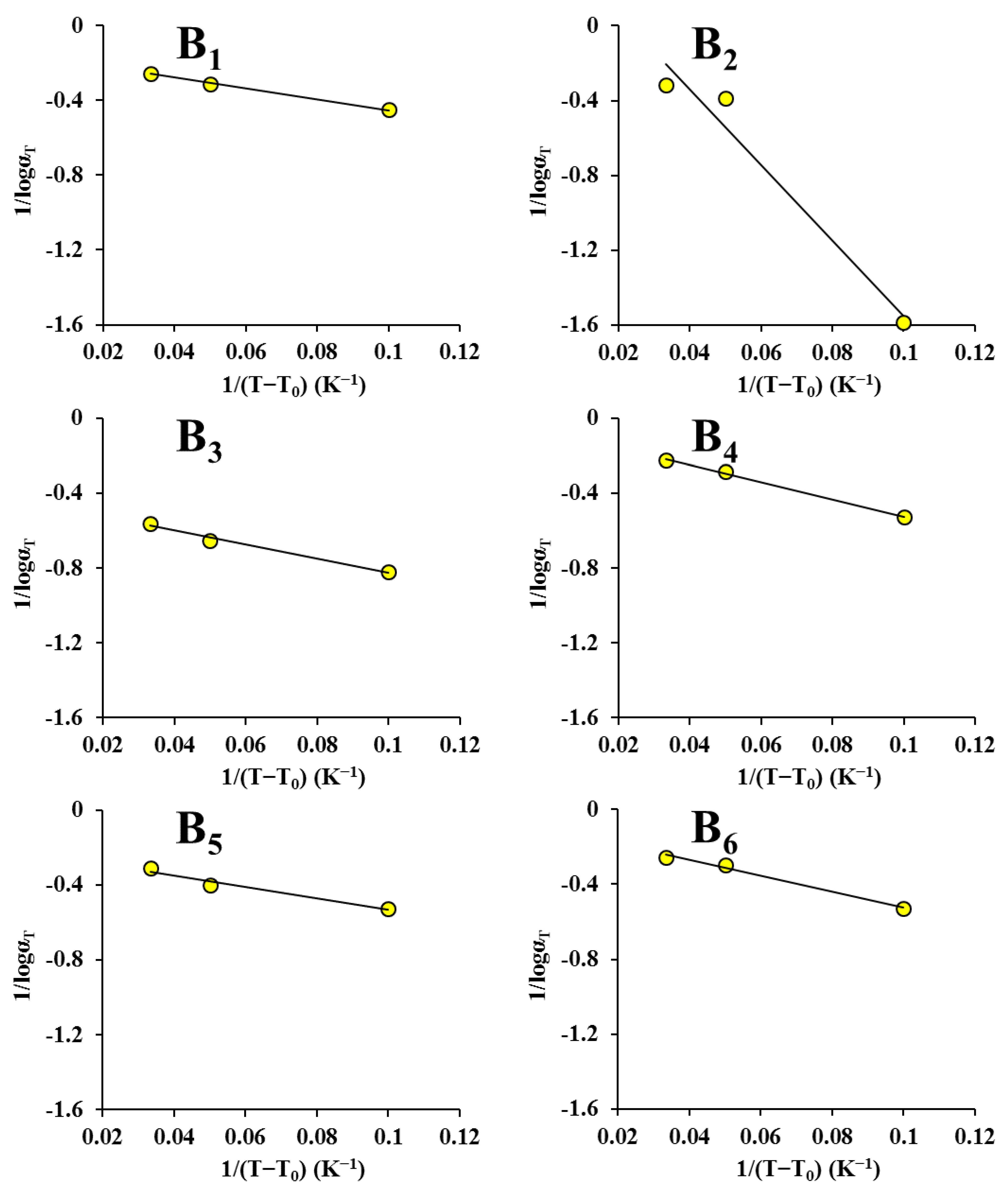
3.3. Applicability of Time-Temperature Superposition
3.4. Long-Period Stress Relaxation and Creep Response
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, J.; Xing, F.; Wang, C.; Zeng, X.; Zou, Q. Investigation and development of maize fused network analysis with multi-omics. Plant Physiol. Biochem. 2019, 141, 380–387. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wang, Y.; Xue, J.; Xie, R.; Wang, K.; Zhao, R.; Liu, W.; Ming, B.; Hou, P.; Zhang, Z.; et al. Allocation of maize varieties according to temperature for use in mechanical kernel harvesting in Ningxia, China. Int. J. Agric. Biol. Eng. 2021, 14, 20–28. [Google Scholar] [CrossRef]
- Bradford, K.J.; Dahal, P.; Van Asbrouck, J.; Kunusoth, K.; Bello, P.; Thompson, J.; Wu, F. The dry chain: Reducing postharvest losses and improving food safety in humid climates. Trends Food Sci. Technol. 2018, 71, 84–93. [Google Scholar] [CrossRef]
- Bazyma, L.A.; Guskov, V.P.; Basteev, A.V.; Lyashenko, A.M.; Lyakhno, V.; Kutovoy, V.A. The investigation of low temperature vacuum drying processes of agricultural materials. J. Food Eng. 2006, 74, 410–415. [Google Scholar] [CrossRef]
- Maskan, M. Microwave/air and microwave finish drying of banana. J. Food Eng. 2000, 44, 71–78. [Google Scholar] [CrossRef]
- Arévalo-Pinedo, A.; Murr, F.E.X. Kinetics of vacuum drying of pumpkin (Cucurbita maxima): Modeling with shrinkage. J. Food Eng. 2006, 76, 562–567. [Google Scholar] [CrossRef]
- Onwude, D.I.; Hashim, N.; Chen, G. Recent advances of novel thermal combined hot air drying of agricultural crops. Trends Food Sci. Technol. 2016, 57, 132–145. [Google Scholar] [CrossRef]
- Essex, E. Objective measurements for texture in foods. J. Texture Stud. 1969, 1, 19–37. [Google Scholar] [CrossRef]
- Waananen, K.M.; Okos, M.R. Stress-relaxation properties of yellow-dent corn kernels under uniaxial loading. Trans. ASAE 1992, 35, 1249–1258. [Google Scholar] [CrossRef]
- Ravanbod, R.; Torkaman, G.; Esteki, A. Biotribological and biomechanical changes after experimental haemarthrosis in the rabbit knee. Haemophilia 2011, 17, 124–133. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Wang, L.; Li, D.; Huang, Z.; Adhikari, B.; Chen, X.D. The stress-relaxation behavior of rice as a function of time, moisture and temperature. Int. J. Food Eng. 2017, 13, 20160162. [Google Scholar] [CrossRef]
- Li, Q.; Li, D.; Wang, L.; Özkan, N.; Mao, Z. Dynamic viscoelastic properties of sweet potato studied by dynamic mechanical analyzer. Carbohyd. Polym. 2010, 79, 520–525. [Google Scholar] [CrossRef]
- Abedi, F.M.; Takhar, P.S. Stress relaxation properties of bananas during drying. J. Texture Stud. 2022, 53, 146–156. [Google Scholar] [CrossRef] [PubMed]
- Ditudompo, S.; Takhar, P.S.; Ganjyal, G.M.; Hanna, M.A. The effect of temperature and moisture on the mechanical properties of extruded cornstarch. J. Texture Stud. 2013, 44, 225–237. [Google Scholar] [CrossRef]
- Ozturk, O.K.; Takhar, P.S. Physical and viscoelastic properties of carrots during drying. J. Texture Stud. 2020, 51, 532–541. [Google Scholar] [CrossRef]
- Shahgholi, G.; Latifi, M.; Jahanbakhshi, A. Potato creep analysis during storage using experimental measurement and finite element method (FEM). J. Food Process Eng. 2020, 43, e13522. [Google Scholar] [CrossRef]
- Lin, C.; He, G.; Liu, J.; Pan, L.; Liu, S.; Li, J.; Guo, S. Construction and non-linear viscoelastic properties of nano-structure polymer bonded explosives filled with graphene. Compos. Sci. Technol. 2018, 160, 152–160. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980; p. 273. [Google Scholar]
- Xu, Y. Creep behavior of natural fiber reinforced polymer composites. Ph.D. Thesis, Louisiana State University, Baton Rouge, LA, USA, 2009. [Google Scholar]
- Vaidyanathan, T.K.; Vaidyanathan, J. Validity of predictive models of stress relaxation in selected dental polymers. Dent. Mater. 2015, 31, 799–806. [Google Scholar] [CrossRef]
- Kontogiorgos, V. Linear viscoelasticity of gluten: Decoupling of relaxation mechanisms. J. Cereal Sci. 2017, 75, 286–295. [Google Scholar] [CrossRef]
- Koutsomichalis, A.; Kalampoukas, T.; Mouzakis, D.E. Mechanical testing and modeling of the time–temperature superposition response in hybrid fiber reinforced composites. Polymers 2021, 13, 1178. [Google Scholar] [CrossRef]
- Amjadi, M.; Fatemi, A. Creep behavior and modeling of high-density polyethylene (HDPE). Polym. Test. 2021, 94, 107031. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Rajesh, P.; Srikavya, B.; Rathore, D.K.; Prusty, R.K.; Ray, B.C. Creep behaviour prediction of multi-layer graphene embedded glass fiber/epoxy composites using time-temperature superposition principle. Compos. Part A Appl. Sci. Manuf. 2018, 107, 507–518. [Google Scholar] [CrossRef]
- Xue, C.; Gao, H.; Hu, Y.; Hu, G. Experimental test and curve fitting of creep recovery characteristics of modified graphene oxide natural rubber and its relationship with temperature. Polym. Test. 2020, 87, 106509. [Google Scholar] [CrossRef]
- Sheng, S.; Wang, L.; Li, D.; Mao, Z.; Adhikari, B. Viscoelastic behavior of maize kernel studied by dynamic mechanical analyzer. Carbohyd. Polym. 2014, 112, 350–358. [Google Scholar] [CrossRef]
- Wang, Z.D.; Zhao, X.X. Modeling and characterization of viscoelasticity of PI/SiO2 nanocomposite films under constant and fatigue loading. Mater. Sci. Eng. A 2008, 486, 517–527. [Google Scholar] [CrossRef]
- Tajvidi, M.; Falk, R.H.; Hermanson, J.C. Time–temperature superposition principle applied to a kenaf-fiber/high-density polyethylene composite. J. Appl. Polym. Sci. 2005, 97, 1995–2004. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Q.; Lei, Y.; Yao, F. Creep behavior of bagasse fiber reinforced polymer composites. Bioresour. Technol. 2010, 101, 3280–3286. [Google Scholar] [CrossRef]
- Jabbar, A.; Militký, J.; Madhukar Kale, B.; Rwawiire, S.; Nawab, Y.; Baheti, V. Modeling and analysis of the creep behavior of jute/green epoxy composites incorporated with chemically treated pulverized nano/micro jute fibers. Ind. Crop. Prod. 2016, 84, 230–240. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Z.; Li, Y.; Huang, P.; Chen, Q.; Fu, S. Tensile creep behavior of short-carbon-fiber reinforced polyetherimide composites. Compos. Part B Eng. 2021, 212, 108717. [Google Scholar] [CrossRef]
- Rajan, S.; Sutton, M.A.; Wehbe, R.; Gurdal, Z.; Kidane, A.; Emri, I. Characterization of viscoelastic bending stiffness of uncured carbon-epoxy prepreg slit tape. Compos. Struct. 2021, 275, 114295. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Lv, W.; Li, D.; Wang, L. Freeze-thaw and ultrasound pretreatment before microwave combined drying affects drying kinetics, cell structure and quality parameters of Platycodon grandiflorum. Ind. Crop. Prod. 2021, 164, 113391. [Google Scholar] [CrossRef]
- Qiao, J.; Wu, Y.; Li, L. Effect of filler content on the stress relaxation behavior of fly ash/polyurea composites. Polym. Test. 2020, 81, 106168. [Google Scholar] [CrossRef]
- Zhao, N.; Li, B.; Zhu, Y.; Li, D.; Wang, L. Viscoelastic analysis of oat grain within linear viscoelastic region by using dynamic mechanical analyzer. Int. J. Food Eng. 2020, 16, 20180350. [Google Scholar] [CrossRef]
- Ozturk, O.K.; Takhar, P.S. Stress relaxation behavior of oat flakes. J. Cereal Sci. 2017, 77, 84–89. [Google Scholar] [CrossRef]
- Sozer, N.; Dalgic, A.C. Modelling of rheological characteristics of various spaghetti types. Eur. Food Res. Technol. 2007, 225, 183–190. [Google Scholar] [CrossRef]
- Khan, M.; Nagy, S.A.; Karim, M.A. Transport of cellular water during drying: An understanding of cell rupturing mechanism in apple tissue. Food Res. Int. 2018, 105, 772–781. [Google Scholar] [CrossRef]
- Wang, J.; Mujumdar, A.S.; Deng, L.Z.; Gao, Z.J.; Xiao, H.W.; Raghavan, G. High-humidity hot air impingement blanching alters texture, cell-wall polysaccharides, water status and distribution of seedless grape. Carbohydr. Polym 2018, 194, 9–17. [Google Scholar] [CrossRef]
- Ozturk, O.K.; Singh Takhar, P. Selected physical and viscoelastic properties of strawberries as a function of heated-air drying conditions. Dry. Technol. 2019, 37, 1833–1843. [Google Scholar] [CrossRef]
- Sandhu, J.S.; Takhar, P.S. Effect of frying parameters on mechanical properties and microstructure of potato disks. J. Texture Stud. 2015, 46, 385–397. [Google Scholar] [CrossRef]
- Zhu, Y.; Fu, N.; Li, D.; Wang, L.; Chen, X.D. Physical and viscoelastic properties of different moisture content highland barley kernels. Int. J. Food Eng. 2017, 13, 20170186. [Google Scholar] [CrossRef]
- Ornaghi, H.L.; Monticeli, F.M.; Neves, R.M.; Zattera, A.J.; Cioffi, M.O.H.; Voorwald, H.J.C. Effect of stacking sequence and porosity on creep behavior of glass/epoxy and carbon/epoxy hybrid laminate composites. Compos. Commun. 2020, 19, 210–219. [Google Scholar] [CrossRef]
- Hao, A.; Chen, Y.; Chen, J.Y. Creep and recovery behavior of kenaf/polypropylene nonwoven composites. J. Appl. Polym. Sci. 2014, 131, 8864–8874. [Google Scholar] [CrossRef]
- Militký, J.; Jabbar, A. Comparative evaluation of fiber treatments on the creep behavior of jute/green epoxy composites. Compos. Part B Eng. 2015, 80, 361–368. [Google Scholar] [CrossRef]
- Ahmed, J. Optimization of high-pressure-assisted xanthan gum dispersions for the maximization of rheological moduli: Application of time-pressure/ temperature superposition principle. Food Hydrocolloid. 2022, 122, 107080. [Google Scholar] [CrossRef]
- Mateyawa, S.; Xie, D.F.; Truss, R.W.; Halley, P.J.; Nicholson, T.M.; Shamshina, J.L.; Rogers, R.D.; Boehm, M.W.; Mcnally, T. Effect of the ionic liquid 1-ethyl-3-methylimidazolium acetate on the phase transition of starch: Dissolution or gelatinization? Carbohyd. Polym. 2013, 94, 520–530. [Google Scholar] [CrossRef] [PubMed]
- Kontogiorgos, V.; Shah, P.; Bills, P. Influence of supramolecular forces on the linear viscoelasticity of gluten. Rheol. Acta 2016, 55, 187–195. [Google Scholar] [CrossRef]
- Ahmed, J. Effect of pressure, concentration and temperature on the oscillatory rheology of guar gum dispersions: Response surface methodology approach. Food Hydrocolloid. 2021, 113, 106554. [Google Scholar] [CrossRef]
- Nakada, M.; Miyano, Y.; Cai, H.; Kasamori, M. Prediction of long-term viscoelastic behavior of amorphous resin based on the time-temperature superposition principle. Mech. Time Depend. Mat. 2011, 15, 309–316. [Google Scholar] [CrossRef]
- Yusoff, N.I.M.; Jakarni, F.M.; Nguyen, V.H.; Hainin, M.R.; Airey, G.D. Modelling the rheological properties of bituminous binders using mathematical equations. Constr. Build. Mater. 2013, 40, 174–188. [Google Scholar] [CrossRef]
- Singh, A.P.; Lakes, R.S.; Gunasekaran, S. Viscoelastic characterization of selected foods over an extended frequency range. Rheol. Acta 2006, 46, 131–142. [Google Scholar] [CrossRef]
- Sun, S.; Song, Y.; Zheng, Q. Morphology and mechanical properties of thermo-molded bioplastics based on glycerol-plasticized wheat gliadins. J. Cereal Sci. 2008, 48, 613–618. [Google Scholar] [CrossRef]
- Ahmed, J. Applicability of time–temperature superposition principle: Dynamic rheology of mung bean starch blended with sodium chloride and sucrose—Part 2. J. Food Eng. 2012, 109, 329–335. [Google Scholar] [CrossRef]
- Herum, F.L.; Mensah, J.K.; Barre, H.J.; Majidzadeh, K. Viscoelastic behavior of soybeans due to temperature and moisture content. Trans. ASAE 1979, 22, 1219–1224. [Google Scholar] [CrossRef]
- Meza, B.E.; Verdini, R.A.; Rubiolo, A.C. Temperature dependency of linear viscoelastic properties of a commercial low-fat soft cheese after frozen storage. J. Food Eng. 2012, 109, 475–481. [Google Scholar] [CrossRef]
- Altay, F.; Gunasekaran, S. Rheological evaluation of gelatin–xanthan gum system with high levels of co-solutes in the rubber-to-glass transition region. Food Hydrocolloid. 2012, 28, 141–150. [Google Scholar] [CrossRef]
- Contreras Mateus, M.D.; López López, M.T.; Ariza-León, E.; Chaves Guerrero, A. Rheological implications of the inclusion of ferrofluids and the presence of uniform magnetic field on heavy and extra-heavy crude oils. Fuel 2021, 285, 119184. [Google Scholar] [CrossRef]
- Yildiz, M.E.; Kokini, J.L. Determination of Williams–Landel–Ferry constants for a food polymer system: Effect of water activity and moisture content. J. Rheol. 2001, 45, 903–912. [Google Scholar] [CrossRef]
- Altay, F.; Gunasekaran, S. Mechanical spectra and calorimetric evaluation of gelatin–xanthan gum systems with high levels of co-solutes in the glassy state. Food Hydrocolloid. 2013, 30, 531–540. [Google Scholar] [CrossRef]
- Peleg, M. On the use of the WLF model in polymers and foods. Crit. Rev. Food Sci. 1992, 32, 59–66. [Google Scholar] [CrossRef]
- Li, M.; Li, D.; Wang, L.; Adhikari, B. Creep behavior of starch-based nanocomposite films with cellulose nanofibrils. Carbohyd. Polym. 2015, 117, 957–963. [Google Scholar] [CrossRef]
- Shi, A.; Wang, L.; Li, D.; Adhikari, B. Characterization of starch films containing starch nanoparticles. Part 2: Viscoelasticity and creep properties. Carbohyd. Polym. 2013, 96, 602–610. [Google Scholar] [CrossRef]
- Laplante, G.; Lee-Sullivan, P. Moisture effects on FM300 structural film adhesive: Stress relaxation, fracture toughness, and dynamic mechanical analysis. J. Appl. Polym. Sci. 2005, 95, 1285–1294. [Google Scholar] [CrossRef]
- Ngai, K.L.; Rajagopal, A.K.; Teitler, S. Slowing down of relaxation in a complex system by constraint dynamics. J. Chem. Phys. 1988, 88, 5086–5094. [Google Scholar] [CrossRef]
- Enrione, J.I.; Sáez, C.; López, D.; Skurtys, O.; Acevedo, C.; Osorio, F.; Macnaughtan, W.; Hill, S. Structural relaxation of salmon gelatin films in the glassy state. Food Bioprocess Technol. 2012, 5, 2446–2453. [Google Scholar] [CrossRef]
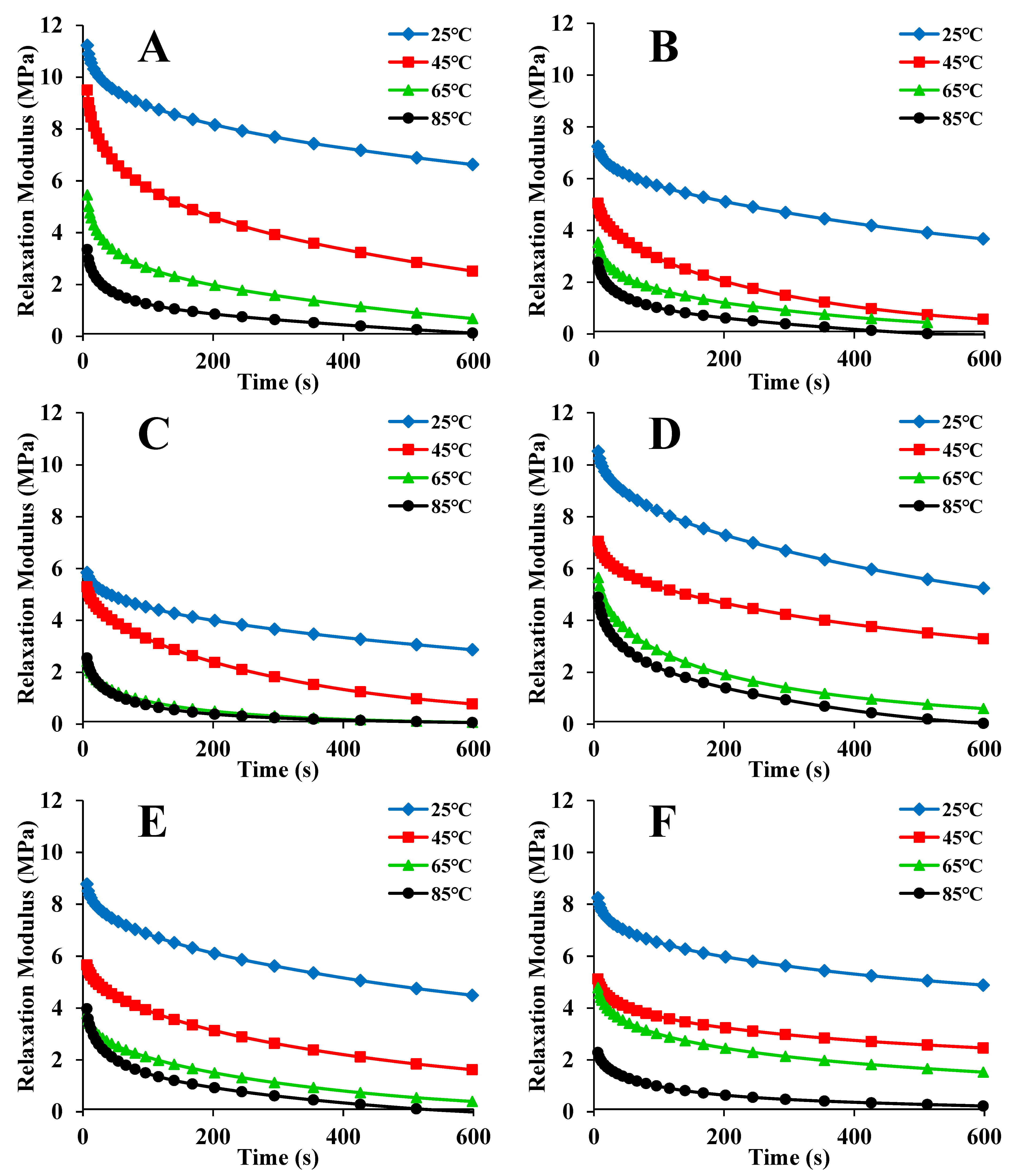
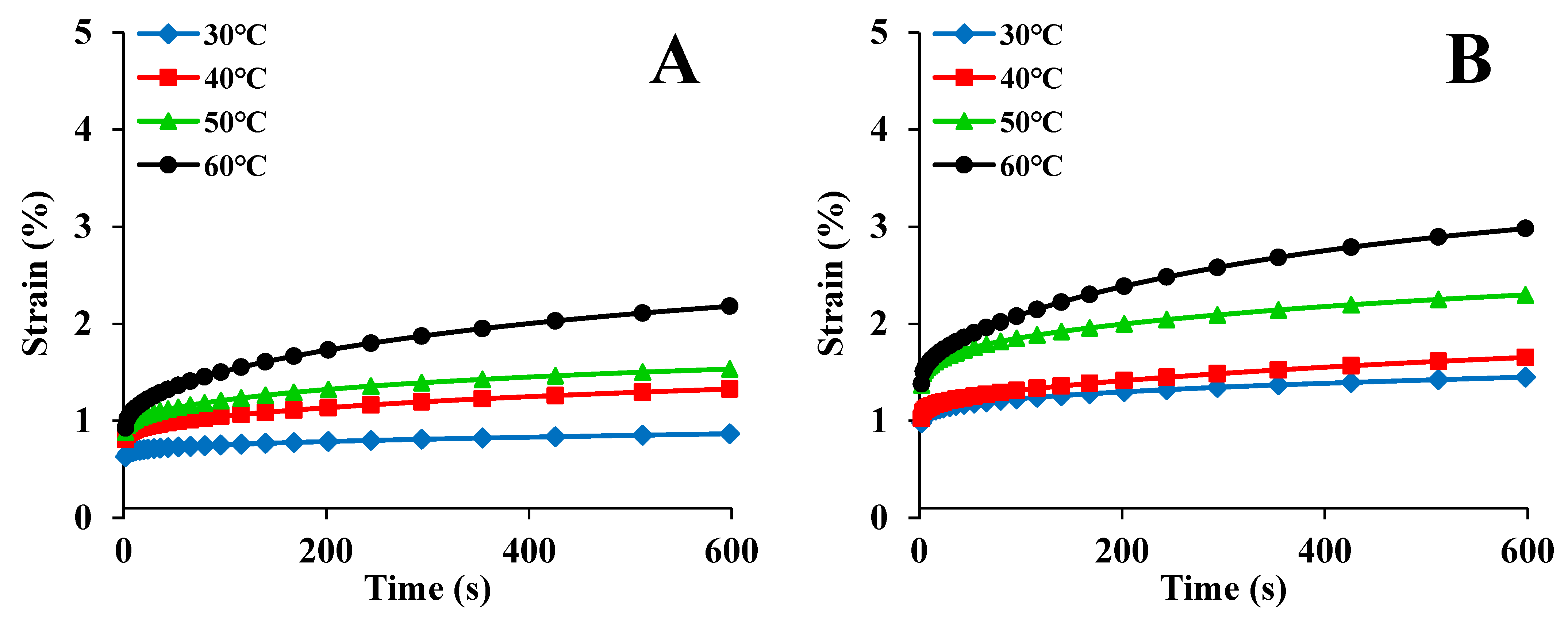
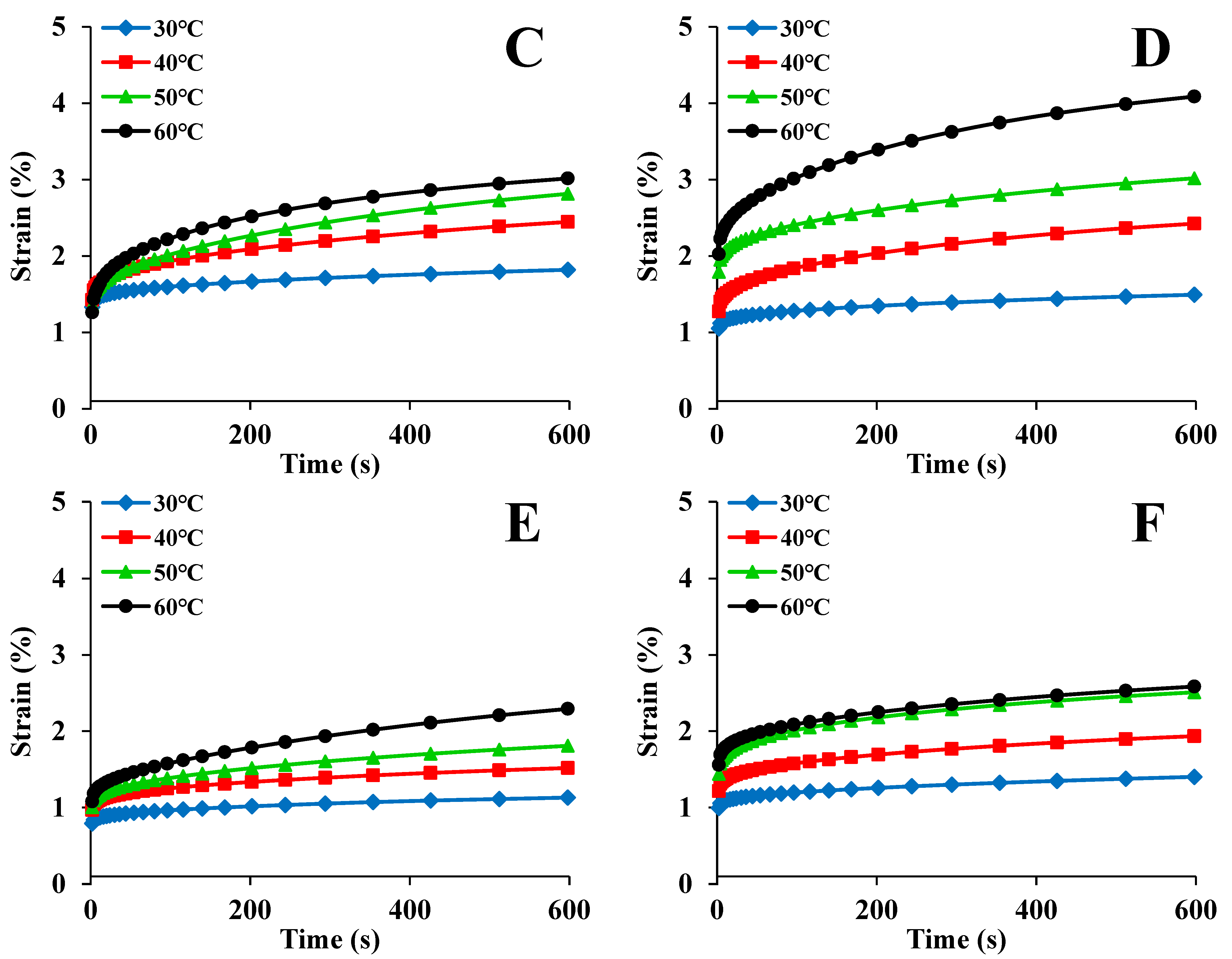
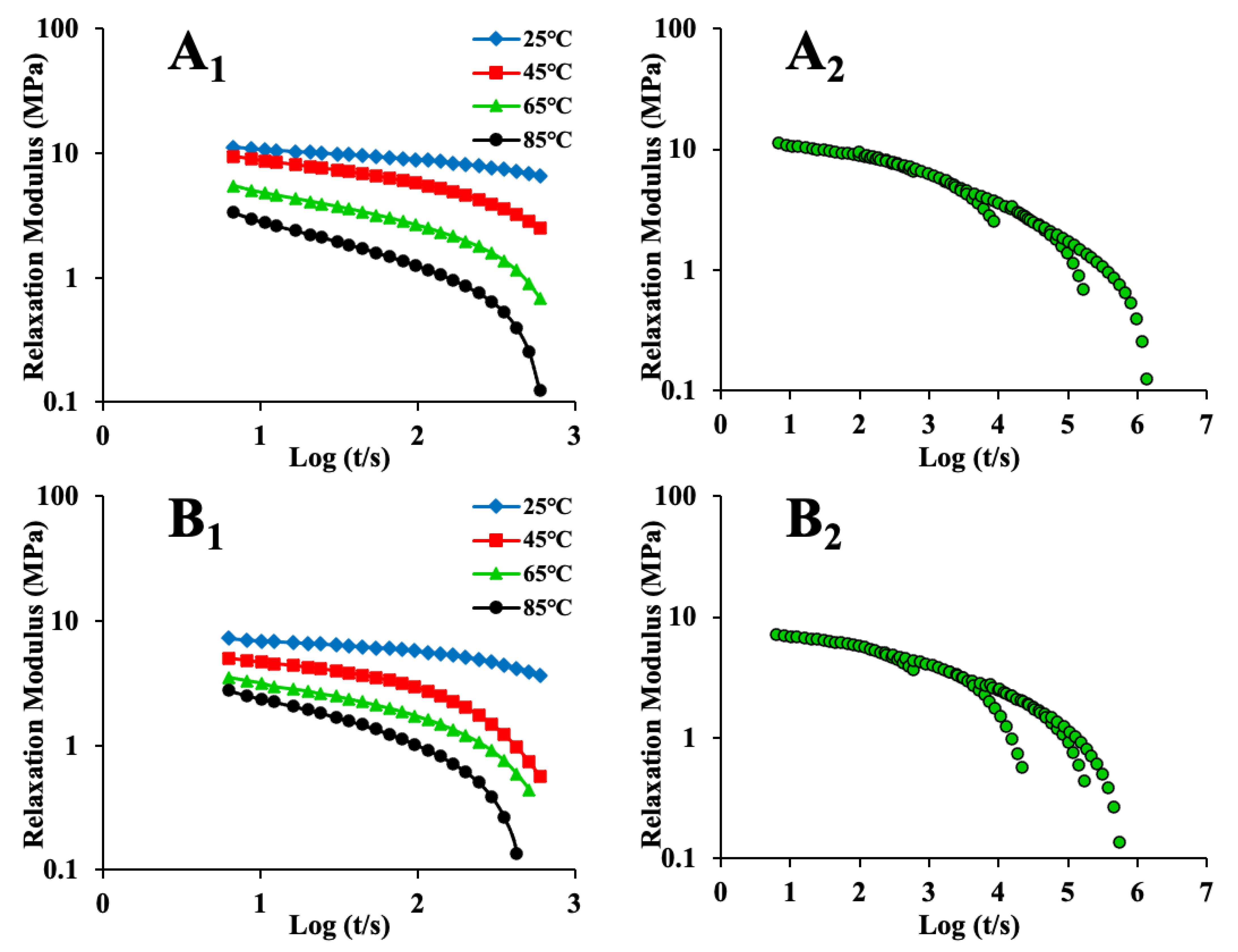



| Drying Condition | T (°C) | E1 (MPa) | τ (s) | E0 (Mpa) | R2 |
|---|---|---|---|---|---|
| ND | 25 | 3.893 | 155.324 | 6.894 | 0.970 |
| 45 | 5.934 | 127.648 | 3.024 | 0.973 | |
| 65 | 3.855 | 101.195 | 1.150 | 0.960 | |
| 85 | 2.580 | 70.449 | 0.502 | 0.949 | |
| HVD 35 °C | 25 | 3.349 | 231.258 | 3.609 | 0.982 |
| 45 | 4.180 | 168.697 | 0.631 | 0.989 | |
| 65 | 2.265 | 122.905 | 0.674 | 0.971 | |
| 85 | 2.337 | 87.183 | 0.203 | 0.964 | |
| HVD 45 °C | 25 | 2.715 | 198.521 | 2.915 | 0.982 |
| 45 | 4.308 | 194.858 | 0.738 | 0.990 | |
| 65 | 2.045 | 82.344 | 0.208 | 0.977 | |
| 85 | 2.237 | 56.494 | 0.225 | 0.976 | |
| HVD 55 °C | 25 | 4.893 | 211.059 | 5.252 | 0.983 |
| 45 | 3.368 | 187.663 | 3.374 | 0.980 | |
| 65 | 4.495 | 118.842 | 0.866 | 0.984 | |
| 85 | 4.144 | 119.810 | 0.359 | 0.973 | |
| HVD 65 °C | 25 | 3.896 | 206.480 | 4.516 | 0.981 |
| 45 | 3.848 | 204.399 | 1.597 | 0.989 | |
| 65 | 2.994 | 163.361 | 0.506 | 0.980 | |
| 85 | 3.269 | 86.022 | 0.364 | 0.962 | |
| HVD 75 °C | 25 | 2.867 | 154.009 | 5.058 | 0.974 |
| 45 | 2.260 | 129.410 | 2.635 | 0.974 | |
| 65 | 2.791 | 124.449 | 1.743 | 0.976 | |
| 85 | 1.803 | 87.104 | 0.367 | 0.980 |
| Drying Condition | T (°C) | E1 (MPa) | E2 (MPa) | η2 (MPa s) | η1 (MPa s) | τ (s) | ε’ (∞) (×10−6 s−1) | R2 |
|---|---|---|---|---|---|---|---|---|
| ND | 30 | 12.366 | 93.513 | 2123.752 | 3.343 × 104 | 22.711 | 2.393 | 0.986 |
| 40 | 9.459 | 44.621 | 1960.307 | 1.500 × 104 | 43.932 | 5.335 | 0.991 | |
| 50 | 8.550 | 29.893 | 1429.997 | 1.362 × 104 | 47.837 | 5.874 | 0.991 | |
| 60 | 8.037 | 15.943 | 884.383 | 6667.172 | 55.472 | 11.999 | 0.995 | |
| HVD 35 °C | 30 | 7.874 | 44.399 | 1249.639 | 1.758 × 104 | 28.146 | 4.551 | 0.986 |
| 40 | 7.510 | 39.770 | 1249.193 | 1.169 × 104 | 31.410 | 6.846 | 0.991 | |
| 50 | 5.546 | 21.809 | 782.902 | 9165.199 | 35.898 | 8.729 | 0.989 | |
| 60 | 5.392 | 12.599 | 869.341 | 5301.574 | 69.001 | 15.090 | 0.995 | |
| HVD 45 °C | 30 | 5.860 | 42.303 | 822.937 | 1.662 × 104 | 19.453 | 4.813 | 0.982 |
| 40 | 5.346 | 21.779 | 685.719 | 7719.949 | 31.485 | 10.363 | 0.990 | |
| 50 | 5.511 | 15.600 | 752.968 | 5336.196 | 48.267 | 14.992 | 0.993 | |
| 60 | 5.858 | 9.698 | 377.393 | 5333.766 | 38.915 | 14.999 | 0.990 | |
| HVD 55 °C | 30 | 7.352 | 50.190 | 1277.306 | 1.815 × 104 | 25.449 | 4.409 | 0.985 |
| 40 | 5.876 | 18.000 | 778.471 | 7273.839 | 43.248 | 10.998 | 0.991 | |
| 50 | 4.255 | 18.021 | 530.068 | 6427.004 | 29.414 | 12.447 | 0.988 | |
| 60 | 3.671 | 9.550 | 512.969 | 4199.839 | 53.714 | 19.048 | 0.992 | |
| HVD 65 °C | 30 | 9.741 | 65.245 | 2054.107 | 2.380 × 104 | 31.483 | 3.361 | 0.987 |
| 40 | 7.926 | 39.079 | 1085.328 | 1.463 × 104 | 27.773 | 5.467 | 0.987 | |
| 50 | 7.549 | 28.880 | 1011.784 | 9554.119 | 35.034 | 8.373 | 0.991 | |
| 60 | 6.956 | 22.999 | 957.637 | 5738.029 | 41.638 | 13.942 | 0.994 | |
| HVD 75 °C | 30 | 7.816 | 57.858 | 1335.159 | 1.856 × 104 | 23.076 | 4.311 | 0.986 |
| 40 | 6.288 | 30.236 | 975.934 | 1.119 × 104 | 32.277 | 7.149 | 0.988 | |
| 50 | 5.263 | 18.040 | 602.605 | 8122.873 | 33.404 | 9.849 | 0.988 | |
| 60 | 4.896 | 20.384 | 621.951 | 7975.713 | 30.512 | 10.030 | 0.988 |
| Equation | Parameters | Drying Condition | |||||
|---|---|---|---|---|---|---|---|
| ND | HVD 35 °C | HVD 45 °C | HVD 55 °C | HVD 65 °C | HVD 75 °C | ||
| WLF | C1 | 14.990 | 5.995 | 8.406 | 7.174 | 7.758 | 5.882 |
| C2 (K) | 191.700 | 56.655 | 134.400 | 72.001 | 71.984 | 43.807 | |
| R2 | 0.997 | 0.999 | 0.953 | 0.992 | 0.986 | 0.857 | |
| Arrhenius | Ea | 126.900 | 124.200 | 90.860 | 117.300 | 126.600 | 134.800 |
| R2 | 0.997 | 0.959 | 0.934 | 0.967 | 0.960 | 0.963 |
| Equation | Parameters | Drying Condition | |||||
|---|---|---|---|---|---|---|---|
| ND | HVD 35 °C | HVD 45 °C | HVD 55 °C | HVD 65 °C | HVD 75 °C | ||
| WLF | C1 | 6.127 | 32.020 | 2.226 | 15.873 | 4.435 | 9.671 |
| C2 (K) | 17.771 | 257.500 | 8.346 | 73.297 | 13.647 | 40.668 | |
| R2 | 0.998 | 0.963 | 0.985 | 0.998 | 0.966 | 0.989 | |
| Arrhenius | Ea | 250.599 | 220.498 | 111.035 | 292.645 | 199.302 | 255.960 |
| R2 | 0.932 | 0.945 | 0.870 | 0.987 | 0.936 | 0.955 |
| Equation | Parameters | Drying Condition | |||||
|---|---|---|---|---|---|---|---|
| ND | HVD 35 °C | HVD 45 °C | HVD 55 °C | HVD 65 °C | HVD 75 °C | ||
| Generalized Maxwell equation | E1 (MPa) | 4.449 | 2.543 | 1.118 | 2.326 | 2.297 | 1.753 |
| E2 (MPa) | 2.802 | 1.796 | 1.674 | 3.555 | 2.763 | 3.166 | |
| E3 (MPa) | 2.858 | 2.573 | 2.923 | 4.050 | 3.253 | 2.485 | |
| τ1 (s) | 2177.795 | 4704.469 | 55.148 | 8945.749 | 5866.535 | 8.865 × 105 | |
| τ2 (s) | 123.826 | 1.676 × 105 | 2.760 × 104 | 1.604 × 105 | 2.716 × 105 | 242.832 | |
| τ3(s) | 8.286 × 104 | 155.342 | 821.170 | 143.129 | 146.080 | 2.284 × 104 | |
| E0 (MPa) | 0.668 | 0.095 | 0.095 | 0.322 | 0.172 | 0.365 | |
| R2 | 0.994 | 0.980 | 0.990 | 0.992 | 0.987 | 0.996 | |
| Kohlrausch–Williams–Watts (KWW) equation | E0 (MPa) | 16.501 | 10.670 | 7.847 | 13.554 | 14.006 | 12.593 |
| τ | 1059.509 | 958.363 | 798.541 | 3888.804 | 791.291 | 1602.291 | |
| β | 0.194 | 0.191 | 0.271 | 0.187 | 0.149 | 0.145 | |
| R2 | 0.992 | 0.978 | 0.984 | 0.974 | 0.978 | 0.995 |
| Equation | Parameters | Drying Condition | |||||
|---|---|---|---|---|---|---|---|
| ND | HVD 35 °C | HVD 45 °C | HVD 55 °C | HVD 65 °C | HVD 75 °C | ||
| Burgers equation | E1 (MPa) | 10.244 | 6.968 | 5.251 | 6.081 | 8.161 | 6.503 |
| E2 (MPa) | 17.795 | 13.754 | 11.929 | 7.081 | 18.004 | 11.459 | |
| η2 (MPa s) | 4.317 × 105 | 2.145 × 104 | 3.291 × 104 | 1.142 × 105 | 1.789 × 105 | 1.821 × 105 | |
| η1 (MPa s) | 3.389 × 107 | 4.294 × 106 | 3.126 × 105 | 6.964 × 107 | 8.018 × 106 | 4.386 × 107 | |
| R2 | 0.951 | 0.956 | 0.966 | 0.950 | 0.946 | 0.922 | |
| Two-parameter power law equation | a | 0.005 | 0.008 | 0.010 | 0.008 | 0.006 | 0.009 |
| b | 0.088 | 0.083 | 0.097 | 0.088 | 0.080 | 0.067 | |
| R2 | 0.905 | 0.932 | 0.879 | 0.970 | 0.912 | 0.970 | |
| Findley power law equation | a | 2.418 × 10−4 | 0.001 | 2.829 × 10−4 | 0.003 | 4.020 × 10−4 | 0.003 |
| b | 0.263 | 0.254 | 0.392 | 0.148 | 0.254 | 0.113 | |
| ε0 | 0.007 | 0.010 | 0.014 | 0.008 | 0.008 | 0.007 | |
| R2 | 0.978 | 0.977 | 0.974 | 0.982 | 0.974 | 0.976 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, S.; Shi, A.; Xing, J. A Systematical Rheological Study of Maize Kernel. Foods 2023, 12, 738. https://doi.org/10.3390/foods12040738
Sheng S, Shi A, Xing J. A Systematical Rheological Study of Maize Kernel. Foods. 2023; 12(4):738. https://doi.org/10.3390/foods12040738
Chicago/Turabian StyleSheng, Shaoyang, Aimin Shi, and Junjie Xing. 2023. "A Systematical Rheological Study of Maize Kernel" Foods 12, no. 4: 738. https://doi.org/10.3390/foods12040738
APA StyleSheng, S., Shi, A., & Xing, J. (2023). A Systematical Rheological Study of Maize Kernel. Foods, 12(4), 738. https://doi.org/10.3390/foods12040738






