Optimization Function for Determining Optimal Dose Range for Beef and Seed Potato Irradiation
Abstract
1. Introduction
2. Materials and Methods
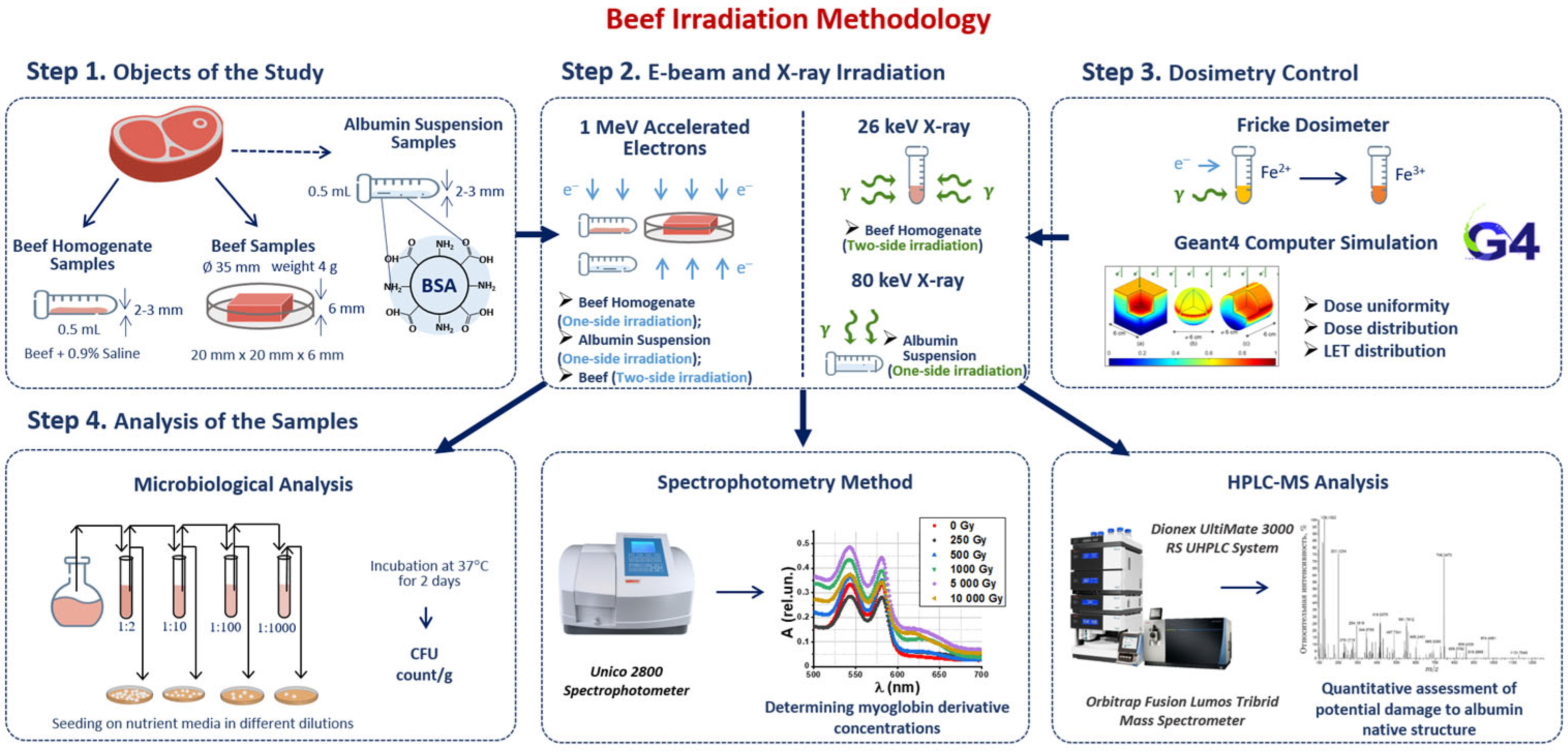
2.1. Beef Irradiation Methodology to Find Optimal Dose Range for Beef Irradiation
2.1.1. Objects of This Study
2.1.2. Research Stages
2.1.3. Electron Beam Irradiation
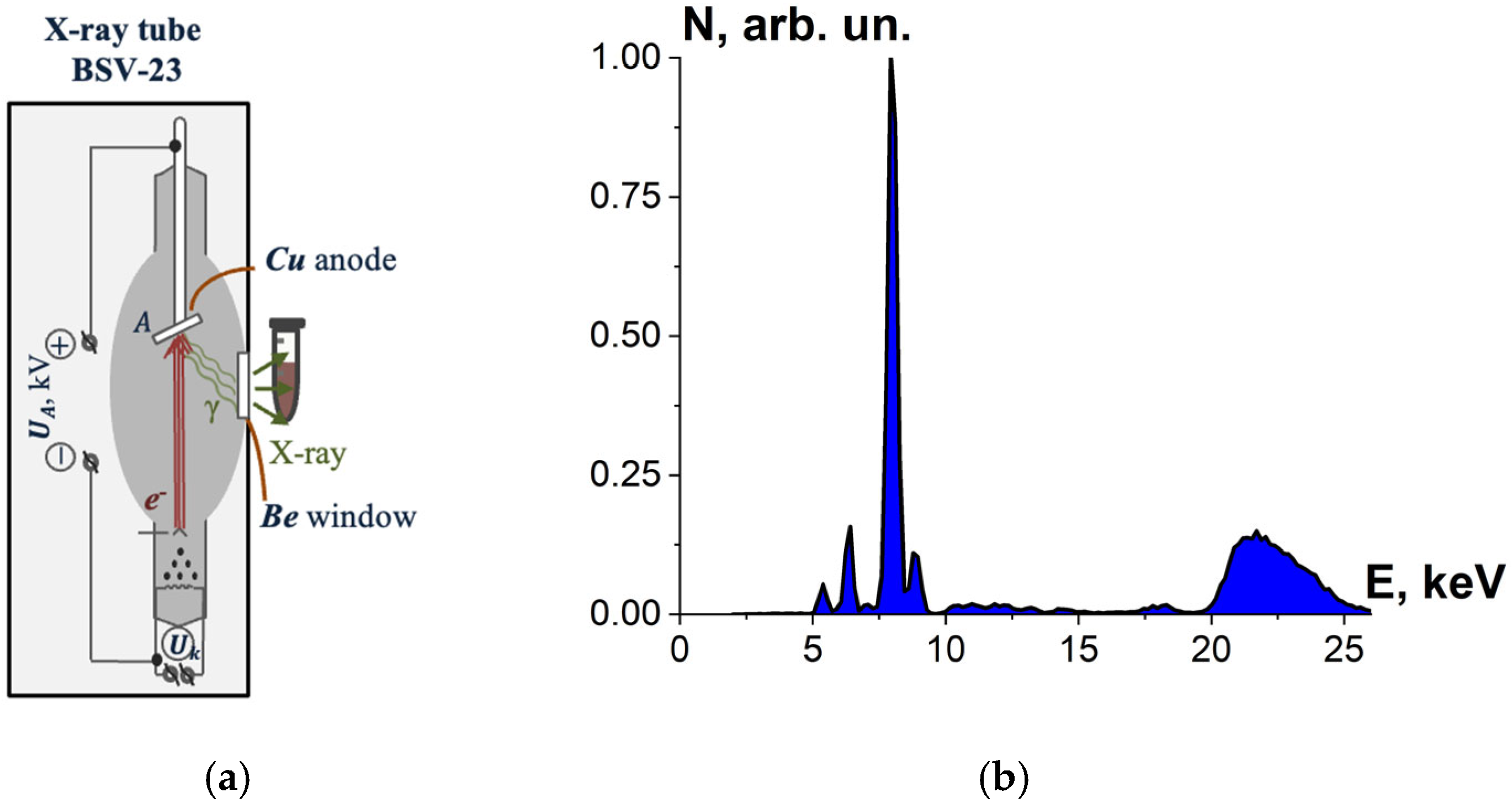
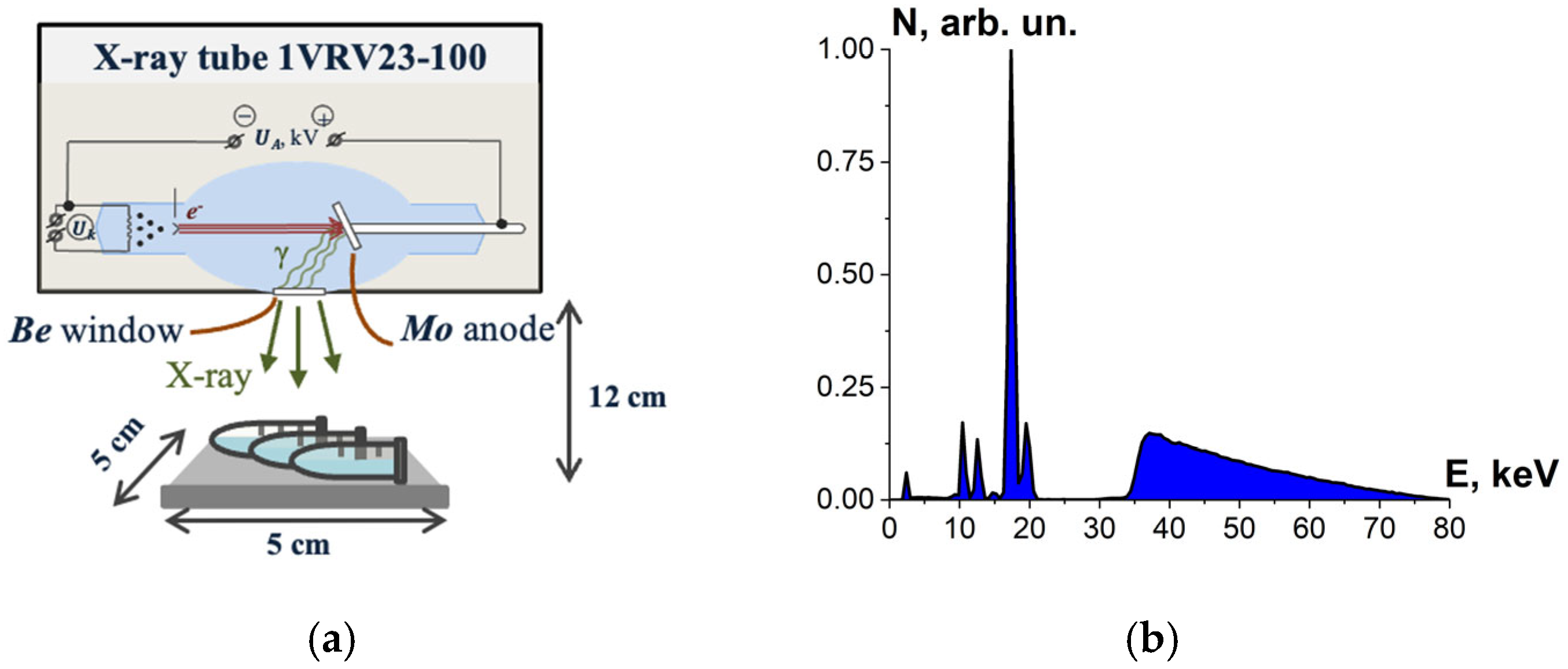
2.1.4. X-Ray Irradiation
2.1.5. Dosimetry Control
2.1.6. GEANT 4 Computer Simulation to Determine Dose Uniformity and Linear Energy Transfer in Irradiated Sample
2.1.7. Microbiological Analysis of Beef Homogenate
2.1.8. Spectrophotometry Method to Determine the Concentration of Myoglobin Derivatives in Beef
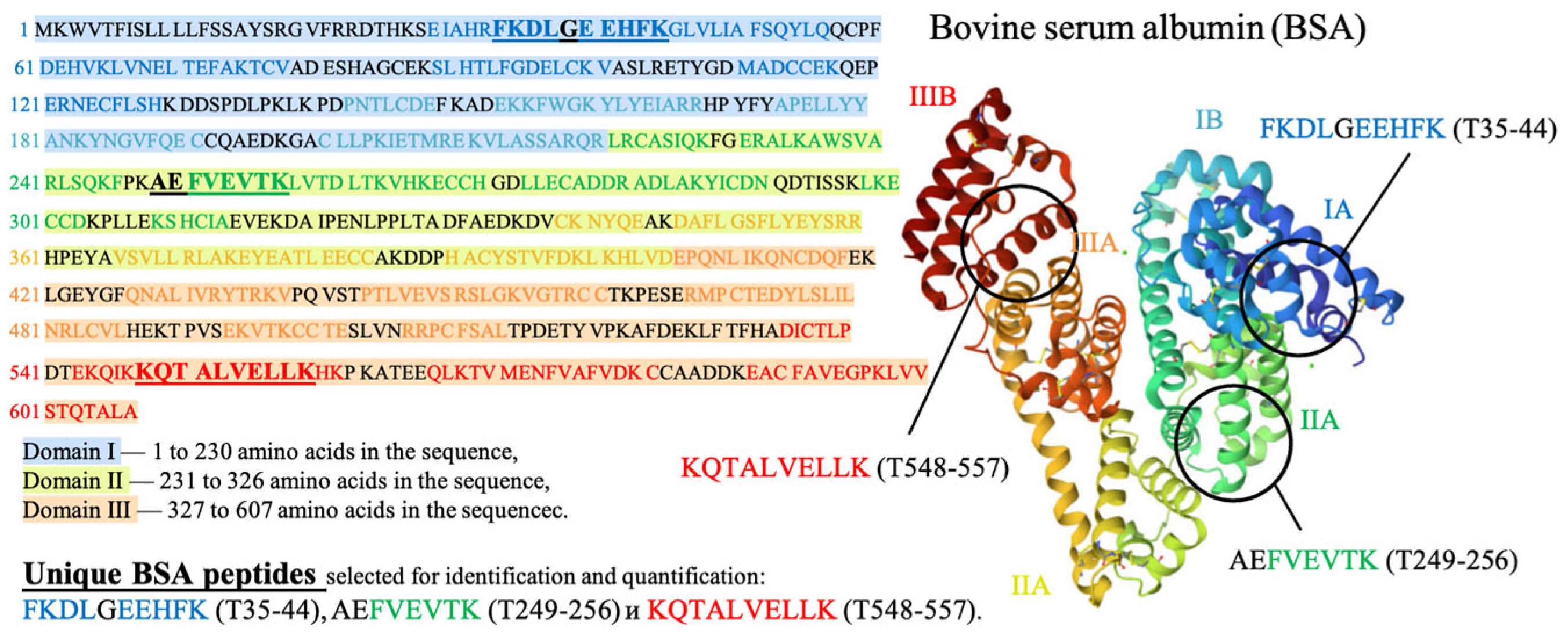
2.1.9. HPLC-MS Method to Assess the Potential Damage to Native Structure of Bovine Serum Albumin
2.2. Potato Pre-Planting Irradiation Methodology to Find the Optimal Dose Range
2.2.1. Objects of This Study
2.2.2. Research Stages
2.2.3. Low-Energy Electron Beam Irradiation of Seed Potato Tubers
2.2.4. Estimation of the Dose Absorbed by the Tubers During Irradiation
2.2.5. Low-Energy Electron Beam Irradiation of Phytopathogen
2.2.6. Estimation of the Dose Absorbed by Phytopathogens During Irradiation
2.2.7. Potato Productivity Analysis
2.2.8. Analysis of Phytosanitary Condition of New Crop Tubers
2.2.9. Estimation of the Diameters of Phytopathogen Colonies
3. Results and Discussion
3.1. Factors Influencing Food Irradiation Efficiency
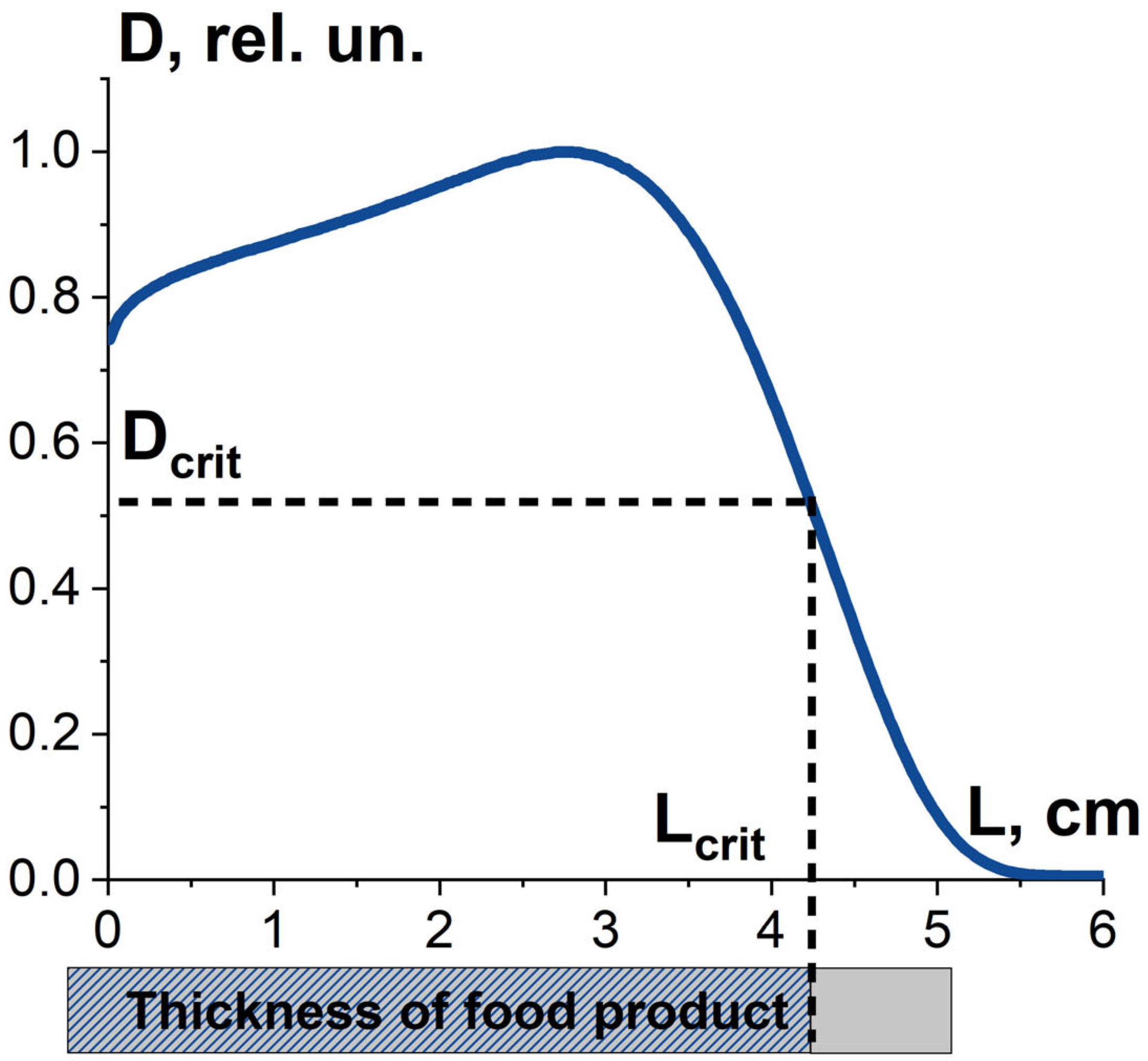
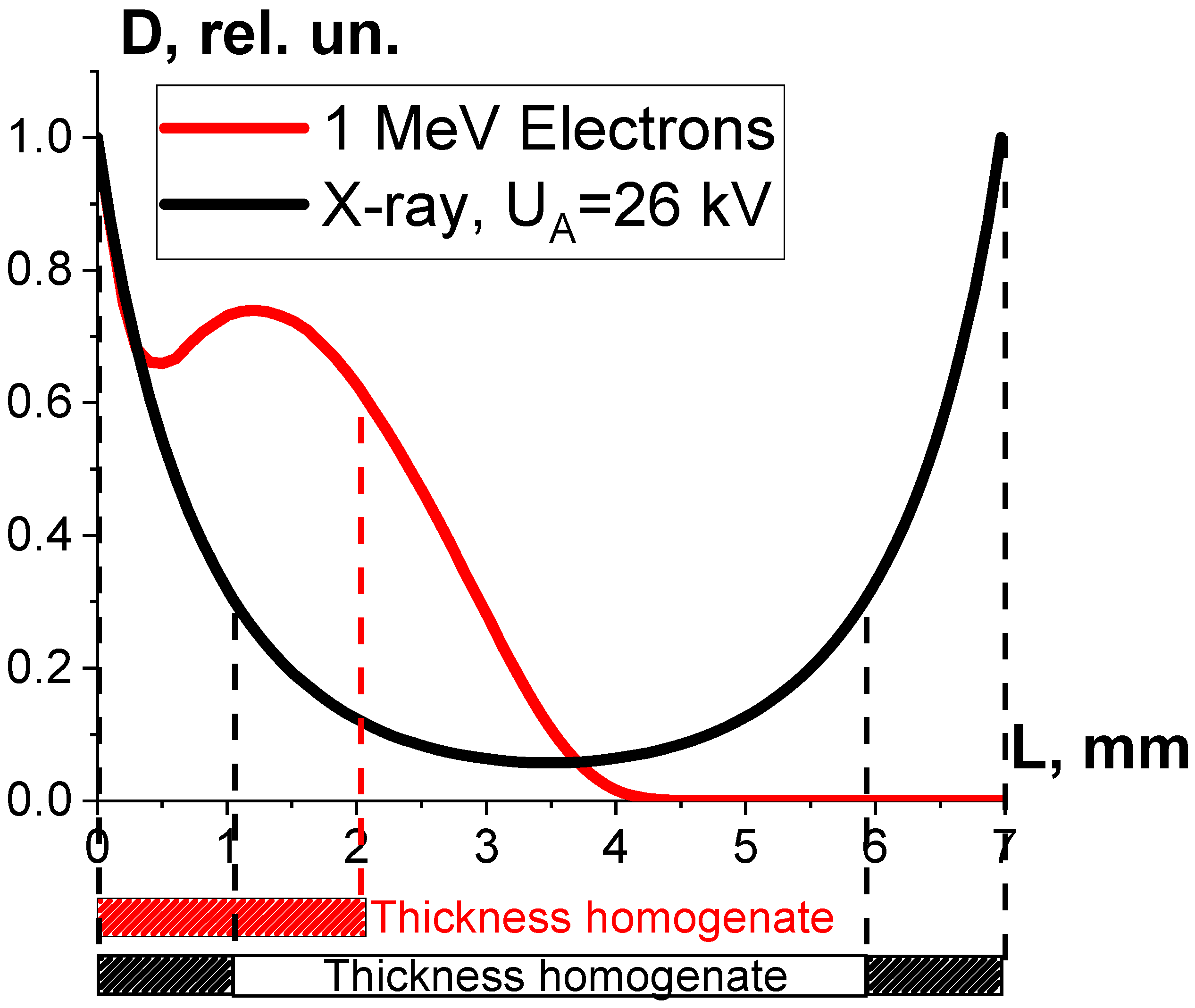
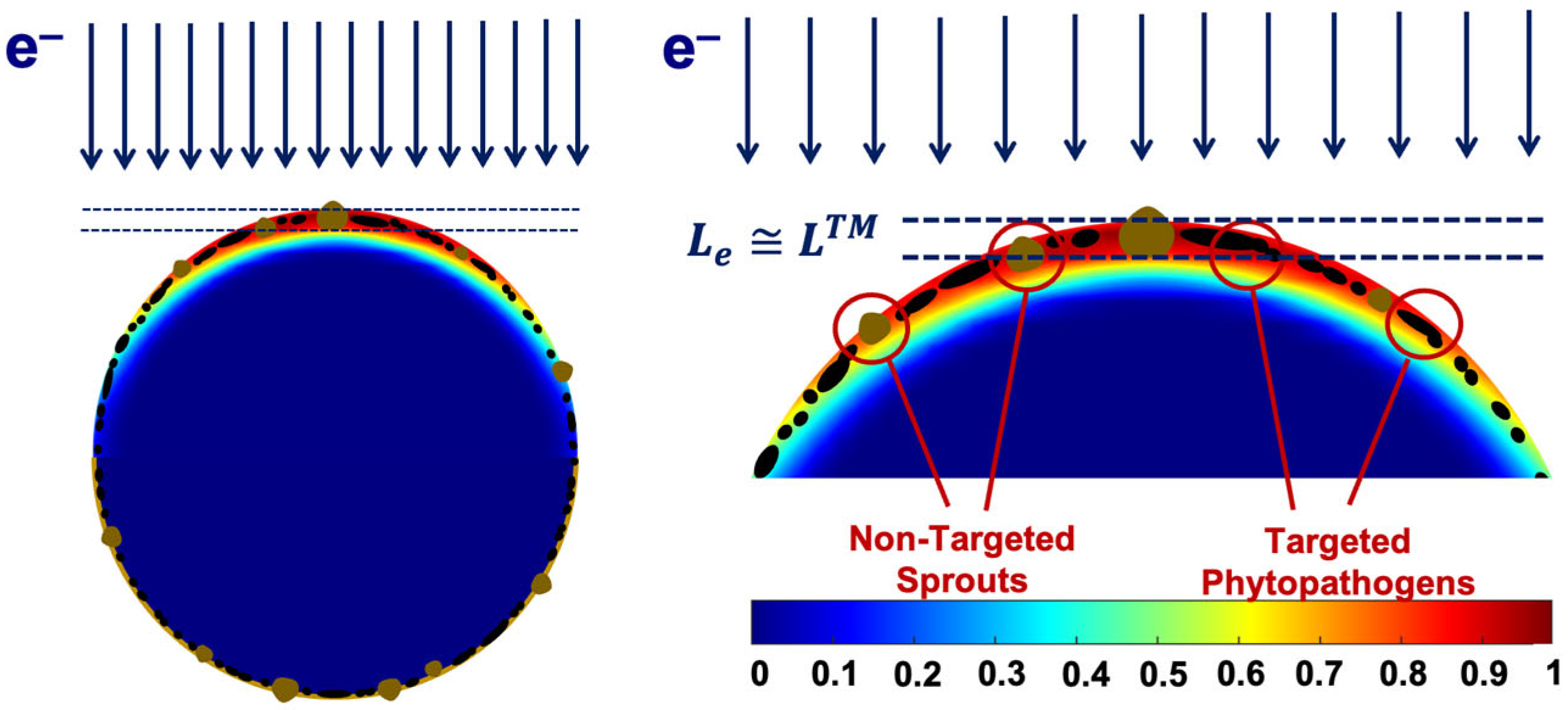
3.1.1. Factor K1 and Irradiation Dose Uniformity
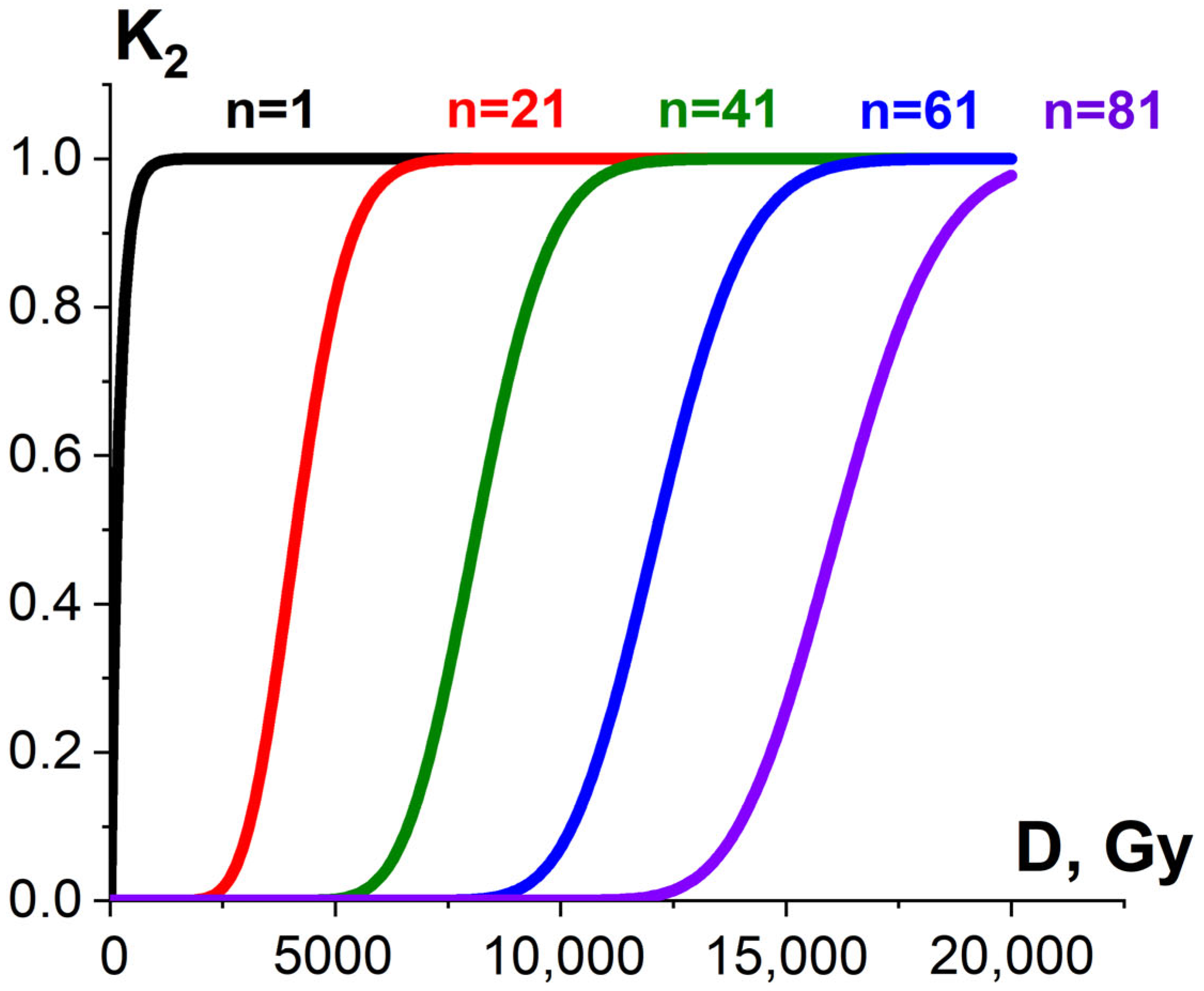
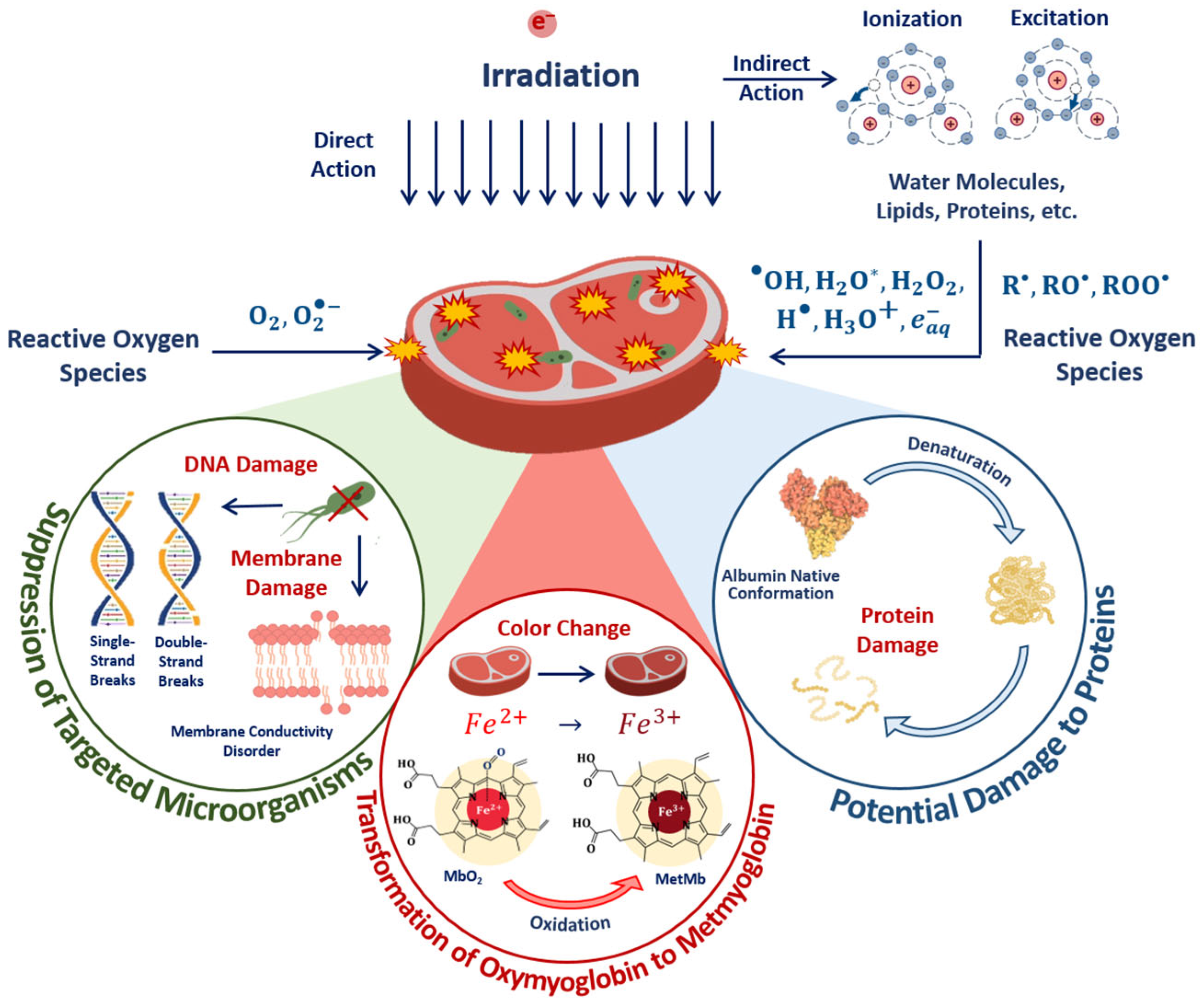
3.1.2. Factor K2 and Probability of Irradiation Hitting Pathogens and Surrounding Molecules
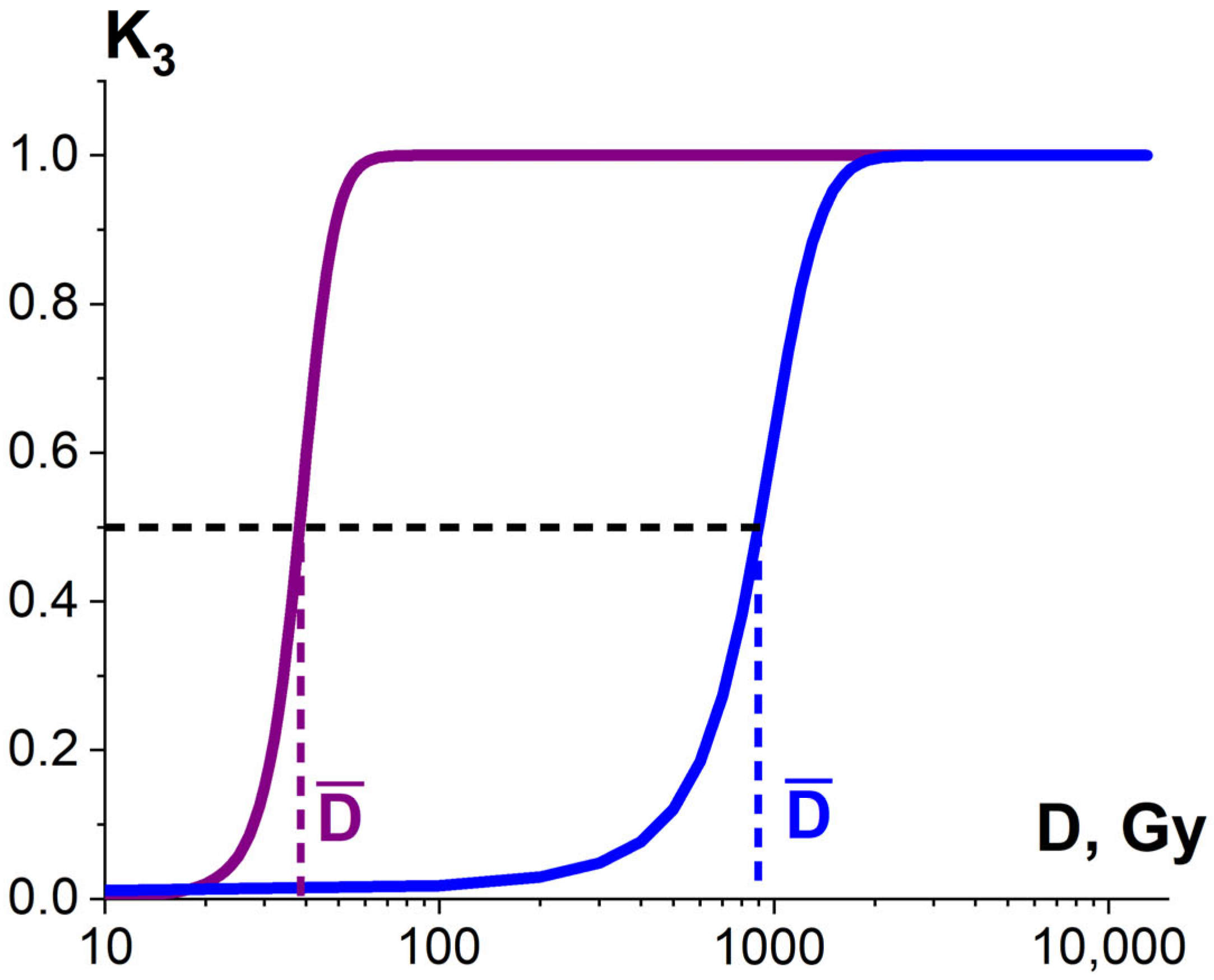
3.1.3. Factor K3 and Heterogenic Radiosensitivity of Pathogens and Surrounding Molecules
3.2. The Influence of K1, K2, K3 Factors on Pathogen Inactivation and Damage to Proteins
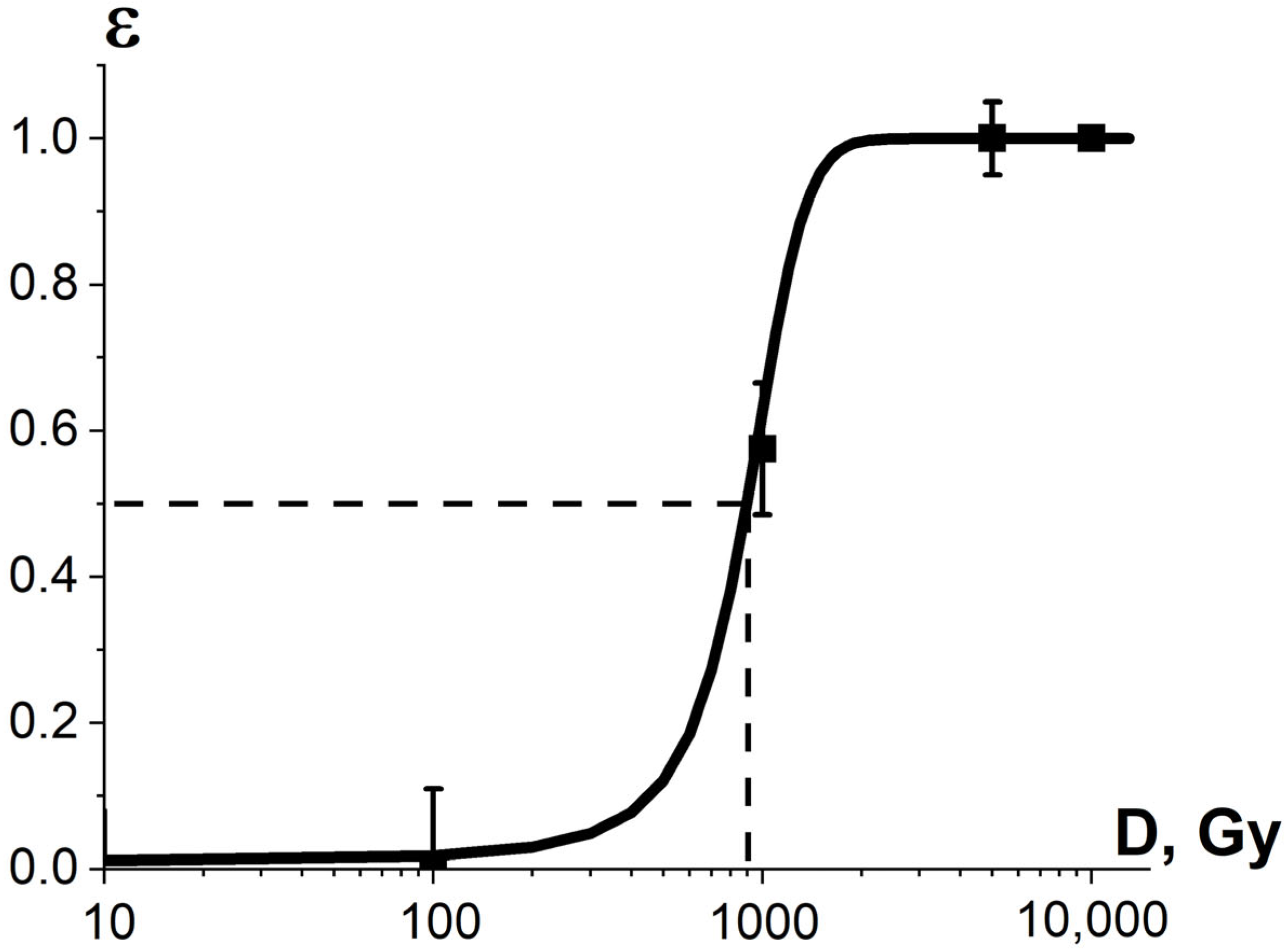
3.2.1. Factor K1 and Pathogen Suppression Efficiency
3.2.2. Factor K3 and Efficiency of Phytopathogen Suppression
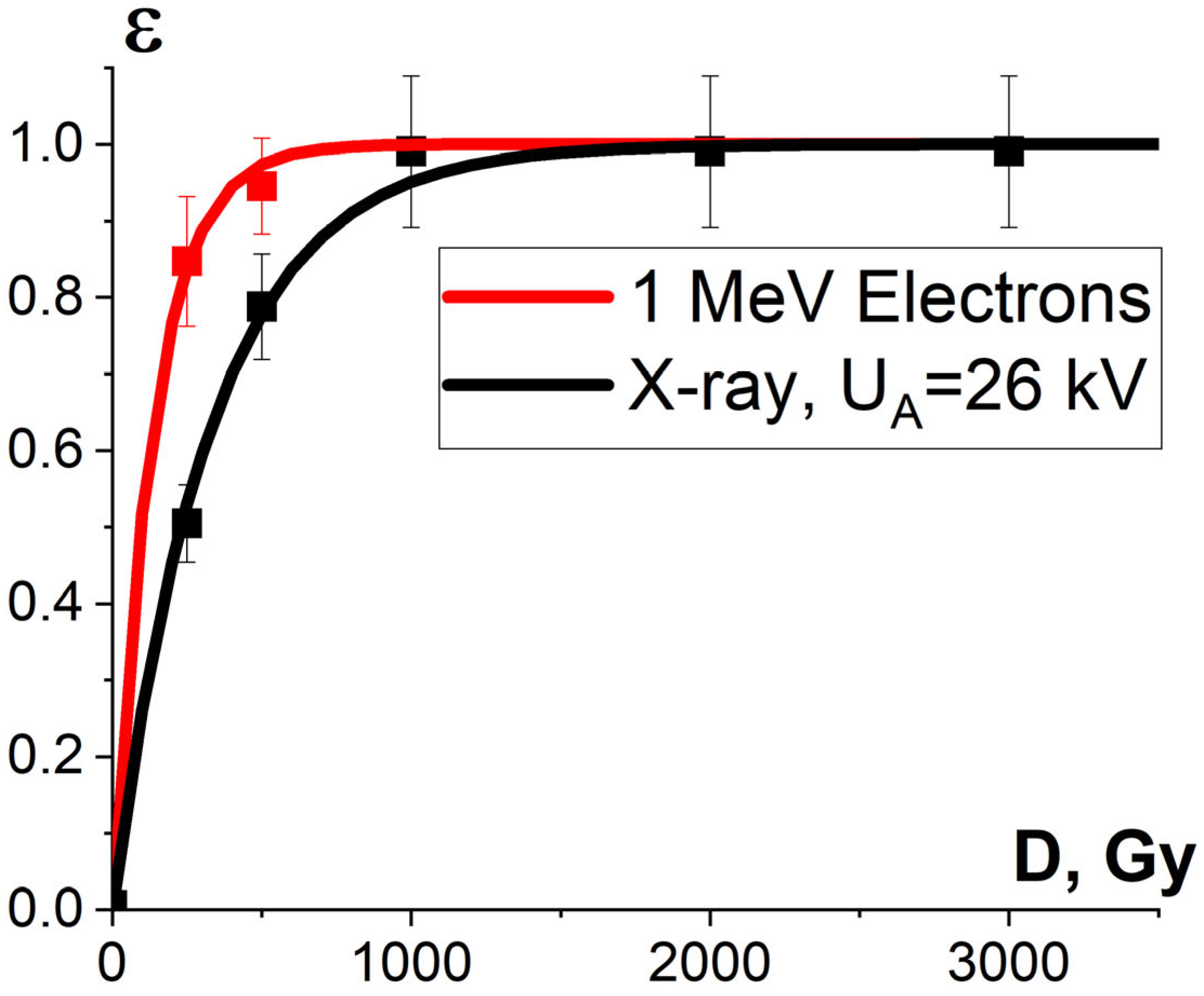
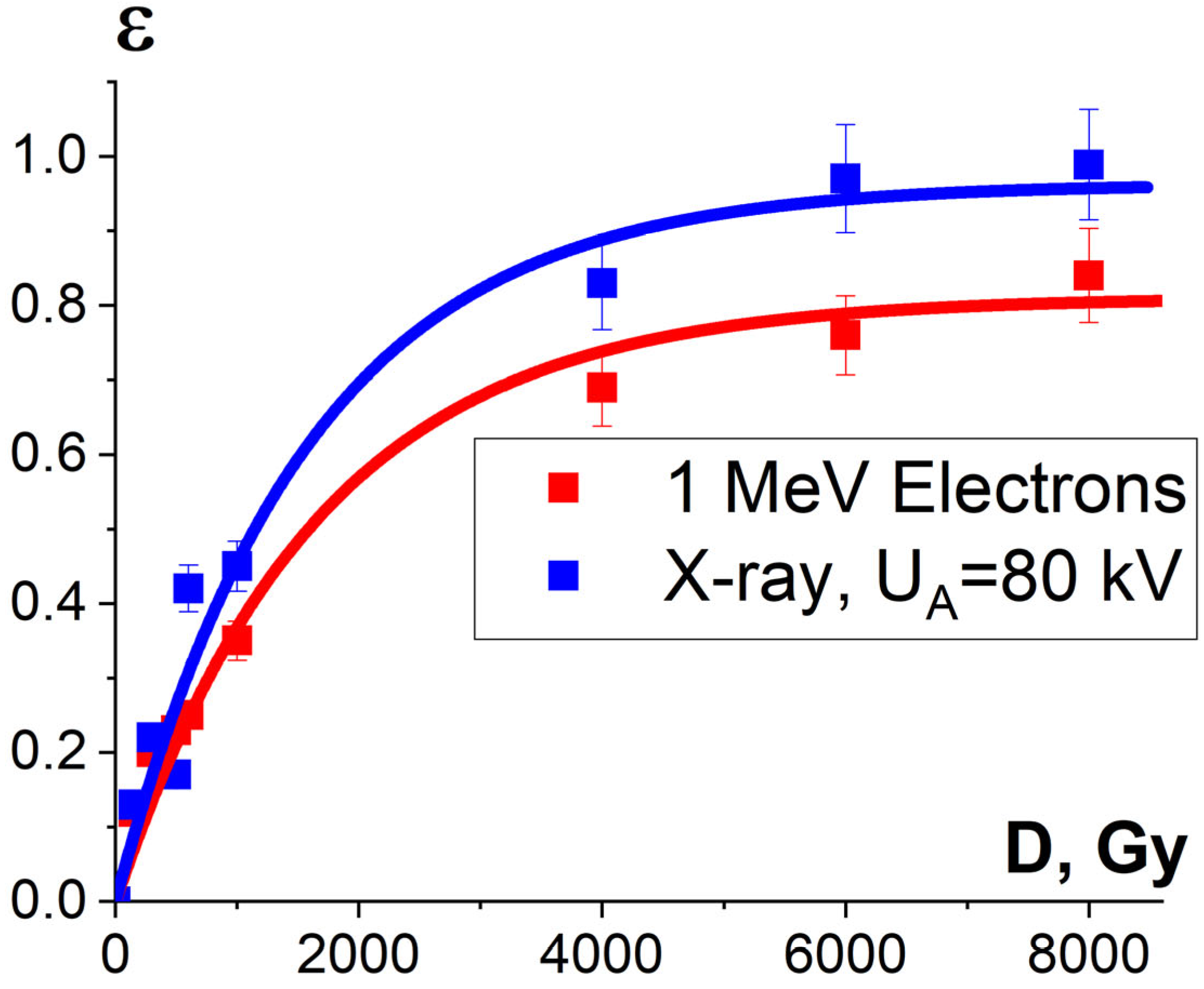
3.2.3. Factor K2 and Damage to Protein Native Structure
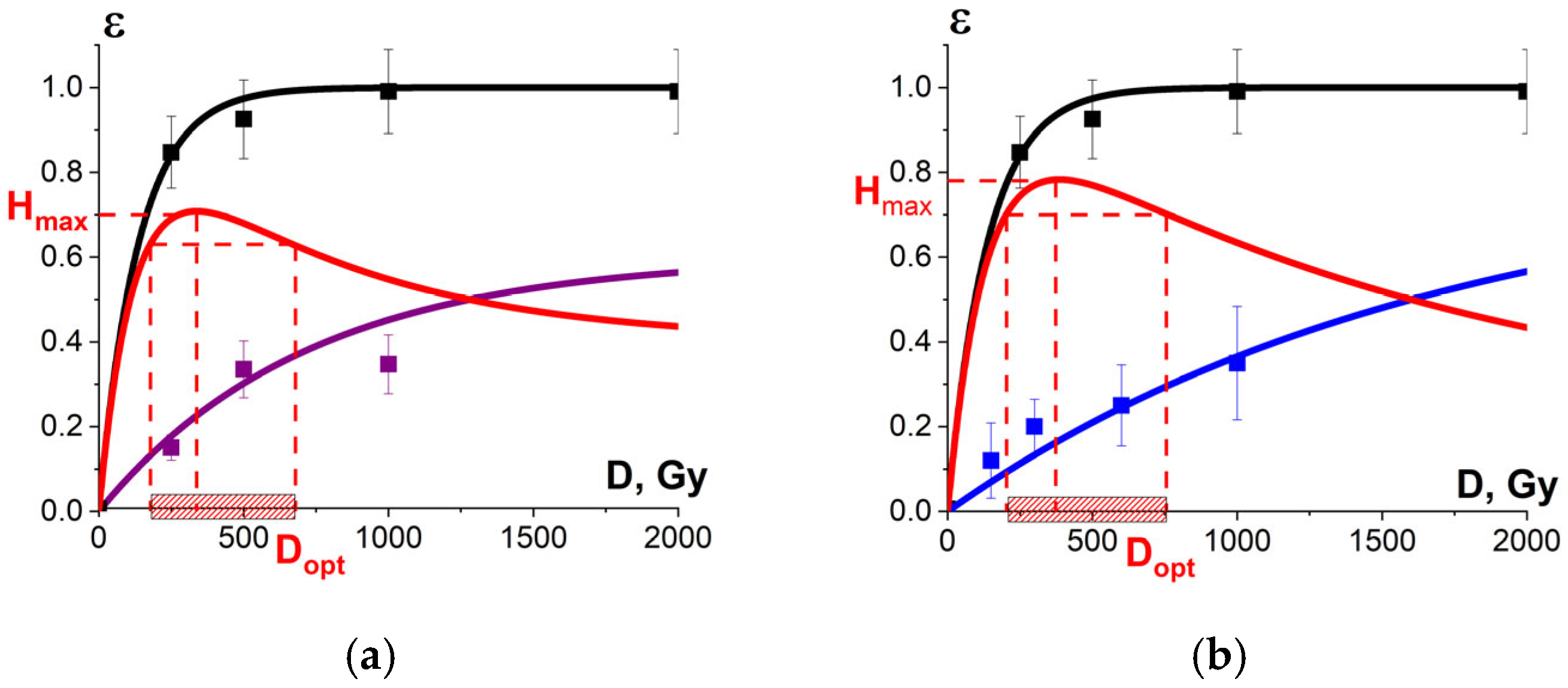
3.3. Optimization Function to Increase Food Irradiation Efficiency
3.3.1. Optimal Dose Range for Beef Irradiation
3.3.2. Optimal Dose Range for Seed Potato Irradiation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Number of Viable Cells, CFU/g and Averaged over Six Consecutive Calculation Repetitions | ||
|---|---|---|
| Dose, Gy | E-Beam | X-Ray |
| 0 | (1.0 ± 0.2) × 104 | (1.0 ± 0.2) × 104 |
| 250 | (0.15 ± 0.03) × 104 | (0.5 ± 0.13) × 104 |
| 500 | (0.05 ± 0.014) × 104 | (0.21 ± 0.03) × 104 |
| 1000 | (0.018 ± 0.003) × 104 | (0.020 ± 0.007) × 104 |
| 2000 | (0.014 ± 0.002) × 104 | (0.021 ± 0.002) × 104 |
| 3000 | (0.019 ± 0.003) × 104 | (0.009 ± 0.005) × 104 |
| Dose, Gy | Diameter of Fungi Colonies, mm |
|---|---|
| 0 | 40.1 ± 3.2 |
| 100 | 40.3 ± 4.4 |
| 1000 | 16.9 ± 3.6 |
| 5000 | 0 |
| 10,000 | 0 |
| Concentration of Peptide, % | |||
|---|---|---|---|
| Dose, Gy | X-Ray | Dose, Gy | E-Beam |
| 0 | 99.0 ± 0.9 | 0 | 100 ± 1.0 |
| 150 | 87.3 ± 1.6 | 150 | 88.0 ± 0.9 |
| 300 | 78.1 ± 1.2 | 300 | 80.0 ± 1.5 |
| 450 | 83.5 ± 3.1 | 600 | 75.0 ± 1.8 |
| 600 | 58.4 ± 3.3 | 1000 | 65.0 ± 2.6 |
| 1000 | 55.9 ± 6.2 | 4000 | 31.0 ± 5.0 |
| 4000 | 17.3 ± 7.2 | 8000 | 16.0 ± 6.0 |
| 6000 | 3.0 ± 7.4 | - | - |
| 8000 | 1.1 ± 0.1 | - | - |
| Dose, Gy | Metmyoglobin Concentration, % |
|---|---|
| 0 | 100 |
| 250 | 84.9 ± 3.0 |
| 500 | 66.5 ± 6.7 |
| 1000 | 65.3 ± 6.9 |
| 5000 | 55.8 ± 8.8 |
| 10,000 | 50.0 ± 10.0 |
| Dose, Gy | Potato Yield, tons/hectare |
|---|---|
| 0 | 26.5 ± 2.7 |
| 20 | 24.7 ± 3.8 |
| 40 | 20.7 ± 2.6 |
| 100 | 7.7 ± 1.8 |
| 150 | 3.0 ± 1.6 |
| 200 | 0 |
References
- Innovating Radiation Processing of Food with Low Energy Beams from Machine Sources. Available online: https://www.iaea.org/projects/crp/d61025 (accessed on 29 September 2024).
- Joint FAO/IAEA Centre of Nuclear Techniques in Food and Agriculture. Available online: https://www.fao.org/agriculture/fao-iaea-nuclear-techniques/en (accessed on 29 September 2024).
- Indiarto, R.; Irawan, A.N.; Subroto, E. Meat Irradiation: A Comprehensive Review of Its Impact on Food Quality and Safety. Foods 2023, 12, 1845. [Google Scholar] [CrossRef] [PubMed]
- Chernyaev, A. Radiation Technologies. Science. National Economy. Medicine; Moscow University Press: Moscow, Russia, 2019; ISBN 978-5-19-011409-6. [Google Scholar]
- Chmielewski, A.G. Radiation Technologies: The Future Is Today. Radiat. Phys. Chem. 2023, 213, 111233. [Google Scholar] [CrossRef]
- Indiarto, R.; Pratama, A.W.; Sari, T.I.; Theodora, H.C. Food Irradiation Technology: A Review of The Uses and Their Capabilities. Int. J. Eng. Trends Technol. 2020, 68, 91–98. [Google Scholar] [CrossRef]
- Farkas, J.; Ehlermann, D.A.E.; Mohácsi-Farkas, C. Food Technologies: Food Irradiation. In Encyclopedia of Food Safety; Elsevier: Amsterdam, The Netherlands, 2014; pp. 178–186. [Google Scholar]
- González, G.S.; Cova, M.C.; Lires, C.; Horak, C.; Gómez, B.; Narvaiz, P. A Highly Nutritive Bread, Developed and Gamma Irradiated to Serve in Disaster Relief or as an Emergency Ration. Food Control 2017, 72, 338–344. [Google Scholar] [CrossRef]
- Watkins, P.; Knoerzer, K.; Ferlazzo, M.L.; Banati, R.B.; Adorno, P.; Stockham, K.; Stobaus, T. Infant Milk Powder After γ-Irradiation and Accelerated Storage as an Indicator for Space Food Stability. Adv. Astronaut. Sci. Technol. 2023, 6, 117–132. [Google Scholar] [CrossRef]
- Mohácsi-Farkas, C. Food Irradiation: Special Solutions for the Immuno-Compromised. Radiat. Phys. Chem. 2016, 129, 58–60. [Google Scholar] [CrossRef]
- CODEX STAN 106-1983; Codex General Standard for Irradiated Foods. Codex Alimentarius Commission: Rome, Italy, 2003.
- Derakhshan, Z.; Oliveri Conti, G.; Heydari, A.; Hosseini, M.S.; Mohajeri, F.A.; Gheisari, H.; Kargar, S.; Karimi, E.; Ferrante, M. Survey on the Effects of Electron Beam Irradiation on Chemical Quality and Sensory Properties on Quail Meat. Food Chem. Toxicol. 2018, 112, 416–420. [Google Scholar] [CrossRef]
- Brewer, S. Irradiation Effects on Meat Color—A Review. Meat Sci. 2004, 68, 1–17. [Google Scholar] [CrossRef]
- Ali, S.; Alsayeqh, A.F. Review of Major Meat-Borne Zoonotic Bacterial Pathogens. Front. Public Health 2022, 10, 1045599. [Google Scholar] [CrossRef]
- Valero, A.; Pérez-Rodríguez, F.; Carrasco, E.; Fuentes-Alventosa, J.M.; García-Gimeno, R.M.; Zurera, G. Modelling the Growth Boundaries of Staphylococcus aureus: Effect of Temperature, PH and Water Activity. Int. J. Food Microbiol. 2009, 133, 186–194. [Google Scholar] [CrossRef]
- Noor, R.; Islam, Z.; Munshi, S.; Rahman, F. Influence of Temperature on Escherichia coli Growth in Different Culture Media. J. Pure Appl. Microbiol. 2013, 7, 899–904. [Google Scholar]
- Medveďová, A.; Valík, Ľ.; Studeničová, A. The Effect of Temperature and Water Activity on the Growth of Staphylococcus aureus. Czech J. Food Sci. 2009, 27, SII28–SII35. [Google Scholar] [CrossRef]
- Matejčeková, Z.; Spodniaková, S.; Dujmić, E.; Liptáková, D.; Valík, Ľ. Modelling Growth of Lactobacillus plantarum as a Function of Temperature: Effects of Media. J. Food Nutr. Res. 2019, 58, 125–134. [Google Scholar]
- Xylia, P.; Chrysargyris, A.; Botsaris, G.; Skandamis, P.; Tzortzakis, N. Salmonella Enteritidis Survival in Different Temperatures and Nutrient Solution PH Levels in Hydroponically Grown Lettuce. Food Microbiol. 2022, 102, 103898. [Google Scholar] [CrossRef]
- Rodrigo, D.; Rosell, C.M.; Martinez, A. Risk of Bacillus Cereus in Relation to Rice and Derivatives. Foods 2021, 10, 302. [Google Scholar] [CrossRef]
- Wijtes, T.; McClure, P.J.; Zwietering, M.H.; Roberts, T.A. Modelling Bacterial Growth of Listeria Monocytogenes as a Function of Water Activity, PH and Temperature. Int. J. Food Microbiol. 1993, 18, 139–149. [Google Scholar] [CrossRef]
- Zwietering, M.H.; Wijtzes, T.; Rombouts, F.M.; Riet, K. A Decision Support System for Prediction of Microbial Spoilage in Foods. J. Ind. Microbiol. 1993, 12, 324–329. [Google Scholar] [CrossRef]
- Begum, T.; Follett, P.A.; Hossain, F.; Christopher, L.; Salmieri, S.; Lacroix, M. Microbicidal Effectiveness of Irradiation from Gamma and X-Ray Sources at Different Dose Rates against the Foodborne Illness Pathogens Escherichia coli, Salmonella typhimurium and Listeria monocytogenes in Rice. LWT 2020, 132, 109841. [Google Scholar] [CrossRef]
- Rajkowski, K.T.; Niebuhr, S.E.; Dickson, J. Effect of Gamma or Beta Radiation on Salmonella DT 104 in Ground Pork. J. Food Prot. 2006, 69, 1430–1433. [Google Scholar] [CrossRef]
- Jeong, S.-G.; Kang, D.-H. Inactivation of Escherichia coli O157:H7, Salmonella typhimurium, and Listeria monocytogenes in Ready-to-Bake Cookie Dough by Gamma and Electron Beam Irradiation. Food Microbiol. 2017, 64, 172–178. [Google Scholar] [CrossRef]
- Munir, M.T.; Mtimet, N.; Guillier, L.; Meurens, F.; Fravalo, P.; Federighi, M.; Kooh, P. Physical Treatments to Control Clostridium Botulinum Hazards in Food. Foods 2023, 12, 1580. [Google Scholar] [CrossRef] [PubMed]
- Mostafa Abd El-Aal, H.A.H. Lipid Peroxidation End-Products as a Key of Oxidative Stress: Effect of Antioxidant on Their Production and Transfer of Free Radicals. In Lipid Peroxidation; InTech: Penang, Malaysia, 2012. [Google Scholar]
- Domínguez, R.; Pateiro, M.; Gagaoua, M.; Barba, F.J.; Zhang, W.; Lorenzo, J.M. A Comprehensive Review on Lipid Oxidation in Meat and Meat Products. Antioxidants 2019, 8, 429. [Google Scholar] [CrossRef] [PubMed]
- Jo, Y.; An, K.-A.; Arshad, M.S.; Kwon, J.-H. Effects of E-Beam Irradiation on Amino Acids, Fatty Acids, and Volatiles of Smoked Duck Meat during Storage. Innov. Food Sci. Emerg. Technol. 2018, 47, 101–109. [Google Scholar] [CrossRef]
- Bliznyuk, U.; Borshchegovskaya, P.; Bolotnik, T.; Ipatova, V.; Kozlov, A.; Nikitchenko, A.; Mezhetova, I.; Chernyaev, A.; Rodin, I.; Kozlova, E. Volatile Compound Markers in Beef Irradiated with Accelerated Electrons. Molecules 2024, 29, 940. [Google Scholar] [CrossRef]
- Cieśla, K.; Roos, Y.; Głuszewski, W. Denaturation Processes in Gamma Irradiated Proteins Studied by Differential Scanning Calorimetry. Radiat. Phys. Chem. 2000, 58, 233–243. [Google Scholar] [CrossRef]
- Li, Z.; Chu, S.; Wang, P.; Gao, S.; Li, S.; Yu, X. Effects of Irradiation Treatment on Protein Structure and Digestion Characteristics of Seed-Watermelon (Citrullus lanatus Var.) Kernel Protein. Food Sci. Biotechnol. 2020, 29, 1201–1211. [Google Scholar] [CrossRef]
- Zong, W.; Gouda, M.; Cai, E.; Wang, R.; Xu, W.; Wu, Y.; Munekata, P.E.S.; Lorenzo, J.M. The Antioxidant Phytochemical Schisandrin A Promotes Neural Cell Proliferation and Differentiation after Ischemic Brain Injury. Molecules 2021, 26, 7466. [Google Scholar] [CrossRef]
- Brown, A.V.; Bliznyuk, U.A.; Borshchegovskaya, P.Y.; Ipatova, V.S.; Khmelevsky, O.Y.; Chernyaev, A.P.; Ananyeva, I.A.; Rodin, I.A. High-Performance Liquid Chromatography—Mass Spectrometry Study of the Effect of Accelerated Electrons on the Structure of Bovine Serum Albumin. Inorg. Mater. 2024. [Google Scholar] [CrossRef]
- Chulikova, N.; Malyuga, A.; Borshchegovskaya, P.; Zubritskaya, Y.; Ipatova, V.; Chernyaev, A.; Yurov, D.; Zolotov, S.; Nikitchenko, A.; Bliznyuk, U.; et al. Electron Beam Irradiation to Control Rhizoctonia Solani in Potato. Agriculture 2023, 13, 1221. [Google Scholar] [CrossRef]
- Etemadinasab, H.; Zahedi, M.; Ramin, A.-A.; Kadivar, M.; Shirmardi, S. pezhman Effects of Electron Beam Irradiation on Physicochemical, Nutritional Properties and Storage Life of Five Potato Cultivars. Radiat. Phys. Chem. 2020, 177, 109093. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, S.; Wang, F.; Long, T.; Chen, B.; Wang, D.; Gao, P. The Effect of Electron Beam Irradiation on the Microbial Stability and Quality Characteristics of Vacuum-packaged Ready-to-eat Potato. J. Food Process. Preserv. 2022, 46, e16829. [Google Scholar] [CrossRef]
- Weinert, N.; Meincke, R.; Gottwald, C.; Heuer, H.; Schloter, M.; Berg, G.; Smalla, K. Bacterial Diversity on the Surface of Potato Tubers in Soil and the Influence of the Plant Genotype. FEMS Microbiol. Ecol. 2010, 74, 114–123. [Google Scholar] [CrossRef] [PubMed]
- Danyo, E.K.; Ivantsova, M.; Selezneva, I. Ionizing Radiation Effects on Microorganisms and Its Applications in the Food Industry. Foods Raw Mater. 2023, 12, 1–12. [Google Scholar] [CrossRef]
- Jung, K.-W.; Lim, S.; Bahn, Y.-S. Microbial Radiation-Resistance Mechanisms. J. Microbiol. 2017, 55, 499–507. [Google Scholar] [CrossRef]
- Krasavin, E.; Kozubek, S. Mutagenic Effect of Radiation with Different LET; Energoatomizdat: Moscow, Russia, 1991. [Google Scholar]
- Belousov, A.; Krusanov, G.; Chernyaev, A. Contribution of Secondary Particles to the Depth Distribution of Absorbed Dose by Photon Irradiation. Mem. Fac. Phys. Lomonosov Mosc. State Univ. 2018, 5, 1850801-1–1850801-6. [Google Scholar]
- Bliznyuk, U.; Avdyukhina, V.; Borshchegovskaya, P.; Bolotnik, T.; Ipatova, V.; Nikitina, Z.; Nikitchenko, A.; Rodin, I.; Studenikin, F.; Chernyaev, A.; et al. Effect of Electron and X-Ray Irradiation on Microbiological and Chemical Parameters of Chilled Turkey. Sci. Rep. 2022, 12, 750. [Google Scholar] [CrossRef]
- Waje, C.K.; Jun, S.Y.; Lee, Y.K.; Kim, B.N.; Han, D.H.; Jo, C.; Kwon, J.H. Microbial Quality Assessment and Pathogen Inactivation by Electron Beam and Gamma Irradiation of Commercial Seed Sprouts. Food Control 2009, 20, 200–204. [Google Scholar] [CrossRef]
- Kim, T.-K.; Hwang, K.-E.; Ham, Y.-K.; Kim, H.-W.; Paik, H.-D.; Kim, Y.-B.; Choi, Y.-S. Interactions between Raw Meat Irradiated by Various Kinds of Ionizing Radiation and Transglutaminase Treatment in Meat Emulsion Systems. Radiat. Phys. Chem. 2020, 166, 108452. [Google Scholar] [CrossRef]
- Hashim, M.S.; Yusop, S.M.; Rahman, I.A. The Impact of Gamma Irradiation on the Quality of Meat and Poultry: A Review on Its Immediate and Storage Effects. Appl. Food Res. 2024, 4, 100444. [Google Scholar] [CrossRef]
- Spectrophotometer UV-3000. Available online: https://istina.msu.ru/equipment/card/615320740/ (accessed on 29 September 2024).
- Zijlstra, W.G.; Buursma, A. Spectrophotometry of Hemoglobin: Absorption Spectra of Bovine Oxyhemoglobin, Deoxyhemoglobin, Carboxyhemoglobin, and Methemoglobin. Comp. Biochem. Physiol. B Biochem. Mol. Biol. 1997, 118, 743–749. [Google Scholar] [CrossRef]
- Kozlova, E.; Sherstyukova, E.; Sergunova, V.; Kozlov, A.; Gudkova, O.; Inozemtsev, V.; Chernysh, A. The Toxic Influence of Excess Free Iron on Red Blood Cells in the Biophysical Experiment: An In Vitro Study. J. Toxicol. 2022, 2022, 7113958. [Google Scholar] [CrossRef] [PubMed]
- Lina Potato Type. Available online: http://www.kartofel.org/cultivars/main_cult/opisaniya2016/lina.htm (accessed on 29 September 2024).
- Sorokin, O. Applied Statistics on the Computer; State Unitary Enterprise Editorial and Printing Association of the Siberian Branch of the Russian Academy of Agricultural Sciences: Krasnobsk, Russia, 2004. [Google Scholar]
- Kudryashov, Y. Radiation Biophysics (Ionizing Radiation); Victor, M., Mikhail, L., Eds.; Fizmatlit: Moscow, Russia, 2004. [Google Scholar]
- Cebrián, G.; Condón, S.; Mañas, P. Physiology of the Inactivation of Vegetative Bacteria by Thermal Treatments: Mode of Action, Influence of Environmental Factors and Inactivation Kinetics. Foods 2017, 6, 107. [Google Scholar] [CrossRef] [PubMed]
- Yousefi, N.; Abbasi, S. Food Proteins: Solubility & Thermal Stability Improvement Techniques. Food Chem. Adv. 2022, 1, 100090. [Google Scholar] [CrossRef]
- Alizadeh, E.; Orlando, T.M.; Sanche, L. Biomolecular Damage Induced by Ionizing Radiation: The Direct and Indirect Effects of Low-Energy Electrons on DNA. Annu. Rev. Phys. Chem. 2015, 66, 379–398. [Google Scholar] [CrossRef]
- Han, J.; Wang, Y.; Wang, Y.; Hao, S.; Zhang, K.; Tian, J.; Jin, Y. Effect of Changes in the Structure of Myoglobin on the Color of Meat Products. Food Mater. Res. 2024, 4, e011. [Google Scholar] [CrossRef]







| Session Number | Total Time of Irradiation from Two Sides, s | Beam Current, µA | Charge on the Plate Qexp, nC | Absorbed Dose D, Gy |
|---|---|---|---|---|
| 1 | 32 ± 1 | 0.10 ± 0.01 | 2070 ± 40/2070 ± 40 | 20.0 ± 0.4 |
| 2 | 50 ± 1 | 0.10 ± 0.01 | 4120 ± 70/4080 ± 70 | 40 ± 1 |
| 3 | 100 ± 1 | 0.10 ± 0.01 | 10,170 ± 200/10,240 ± 200 | 100 ± 2 |
| 4 | 150 ± 1 | 0.10 ± 0.01 | 15,430 ± 300/15,220 ± 300 | 150 ± 3 |
| 5 | 200 ± 1 | 0.10 ± 0.01 | 20,320 ± 400/20,360 ± 400 | 200 ± 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozlova, E.; Bliznyuk, U.; Chernyaev, A.; Borshchegovskaya, P.; Braun, A.; Ipatova, V.; Zolotov, S.; Nikitchenko, A.; Chulikova, N.; Malyuga, A.; et al. Optimization Function for Determining Optimal Dose Range for Beef and Seed Potato Irradiation. Foods 2024, 13, 3729. https://doi.org/10.3390/foods13233729
Kozlova E, Bliznyuk U, Chernyaev A, Borshchegovskaya P, Braun A, Ipatova V, Zolotov S, Nikitchenko A, Chulikova N, Malyuga A, et al. Optimization Function for Determining Optimal Dose Range for Beef and Seed Potato Irradiation. Foods. 2024; 13(23):3729. https://doi.org/10.3390/foods13233729
Chicago/Turabian StyleKozlova, Elena, Ulyana Bliznyuk, Alexander Chernyaev, Polina Borshchegovskaya, Arcady Braun, Victoria Ipatova, Sergey Zolotov, Alexander Nikitchenko, Natalya Chulikova, Anna Malyuga, and et al. 2024. "Optimization Function for Determining Optimal Dose Range for Beef and Seed Potato Irradiation" Foods 13, no. 23: 3729. https://doi.org/10.3390/foods13233729
APA StyleKozlova, E., Bliznyuk, U., Chernyaev, A., Borshchegovskaya, P., Braun, A., Ipatova, V., Zolotov, S., Nikitchenko, A., Chulikova, N., Malyuga, A., Zubritskaya, Y., Bolotnik, T., Oprunenko, A., Kozlov, A., Beklemishev, M., Yagudina, R., & Rodin, I. (2024). Optimization Function for Determining Optimal Dose Range for Beef and Seed Potato Irradiation. Foods, 13(23), 3729. https://doi.org/10.3390/foods13233729






