A Quantitative Risk Assessment Model for Listeria monocytogenes in Ready-to-Eat Smoked and Gravad Fish
Abstract
:1. Introduction
2. Materials and Methods
2.1. Exposure Assessment
2.1.1. Contaminated Lots of Pre-Fillet Fish
| Country | Product | Sample Size, n | Positive Enrichment, s | Prevalence (%) | Source * |
|---|---|---|---|---|---|
| Finland | Raw rainbow trout | 35 | 0 | 0.00 | Autio et al. [33] |
| Brazil | Raw salmon | 255 | 105 | 41.2 | Cruz et al. [34] |
| Ireland | Raw salmon | 60 | 17 | 28.3 | Dass [29] |
| Italy | Raw salmon | 21 | 5 | 23.8 | Di Ciccio et al. [35] |
| Finland | Raw fish | 45 | 2 | 4.40 | Markkula et al. [36] |
| Fish before processing | 212 | 9 | 4.20 | ||
| Poland | Incoming salmon | 46 | 2 | 4.34 | Medrala et al. [37] |
| Incoming seatrout | 26 | 4 | 15.4 | ||
| Finland | Raw fish | 18 | 2 | 11.1 | Miettinen et al. [38] |
| Norway | Salmon pre filleting | 24 | 4 | 16.6 | Rorvik et al. [39] |
| Denmark | Raw fish | 12 | 0 | 0.00 | Vogel et al. [40] |
| Raw fish | 18 | 0 | 0.00 |
2.1.2. Storage of Pre-Fillet Fish
2.1.3. Filleting of Raw Fish
2.1.4. Holding-Off Time of Fish Fillets
2.1.5. Brining or Salting of Fish Fillets (Relevant to Smoked Fish)
2.1.6. Smoking and Maturation of Salted Fish Fillets (Relevant to Smoked Fish)
2.1.7. Smearing of Fish Fillets with Ingredients (Relevant to Gravad Fish)
2.1.8. Maceration or Curing of Fish Fillets (Relevant to Gravad Fish)
2.1.9. Slicing of Processed Fish Fillets
2.1.10. Packaging of Processed Fish Slices
2.1.11. Within-Lot Testing
2.1.12. Cold Chain
2.1.13. Home Storage
2.1.14. Portioning Before Consumption
2.2. Hazard and Risk Characterisation
2.3. QRA Model’s Ouputs
2.4. QRA Model’s Functionality: Reference and What-If Scenarios
- (a)
- Reference, constituted by the baseline scenarios of the three RTE seafood products, with parameter values supported as much as possible by current data and, in their absence, by reasonable assumptions.
- (b)
- Reduction of L. monocytogenes prevalence in a lot of incoming fish, assessed by setting the parameter of the Beta distribution regarding prevalence to half its original value (0.437).
- (c)
- Reduction in cross-contamination during filleting, assessed by assuming that filleting knives are cleaned/disinfected after filleting every fish, and therefore setting the parameter InitSlicer of the function sfSlicer() to zero.
- (d)
- Absence of contamination during salting or smearing of fish fillets, represented by a zero probability of contamination during brine injection (PccBrine = 0%) for smoked brined fish and zero probability of contamination during smearing with salt or curing agents (PccSmear = 0%) for both smoked dry-salted fish and gravad fish.
- (e)
- Application of protective cultures when processing fish fillets, represented by an increase in the mean lot concentration of LAB in RTE seafood after packaging () by 5 log10 CFU/g. Therefore, the minimum (), mode (), and maximum () parameters defining the Pert distribution regarding were set to 4.00, 5.28, and 6.60 log10 CFU/g, respectively, for the RTE products.
- (f)
- Lower home storage temperature, represented by a decrease of 1.5 °C in the mode and maximum storage temperature at home (TempHome mode = 5.5 and TempHome max = 11.4).
2.5. QRA Model’s Implementation
3. Results and Discussion
3.1. Reference Scenario and Comparison with Other QRA Models
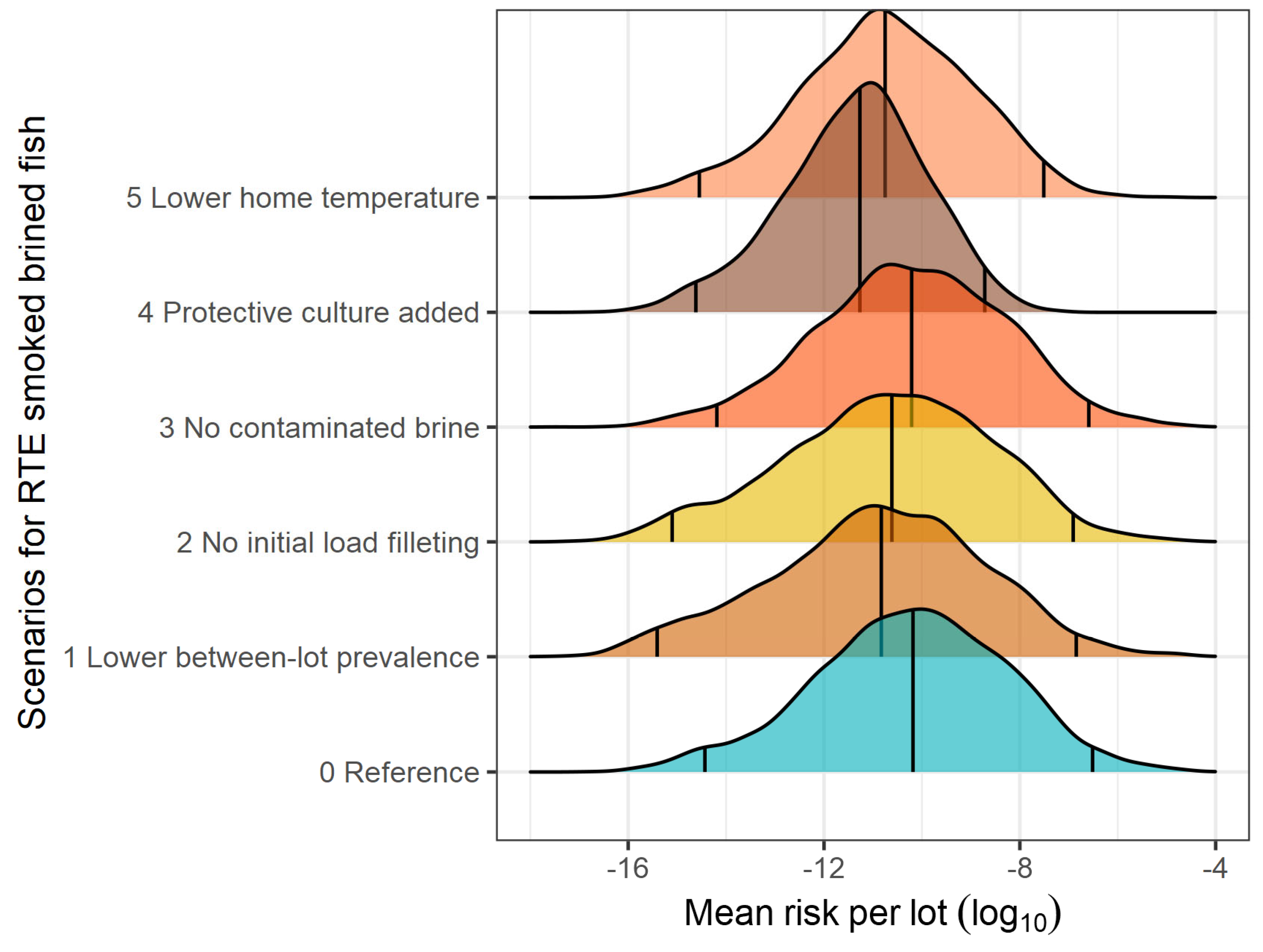
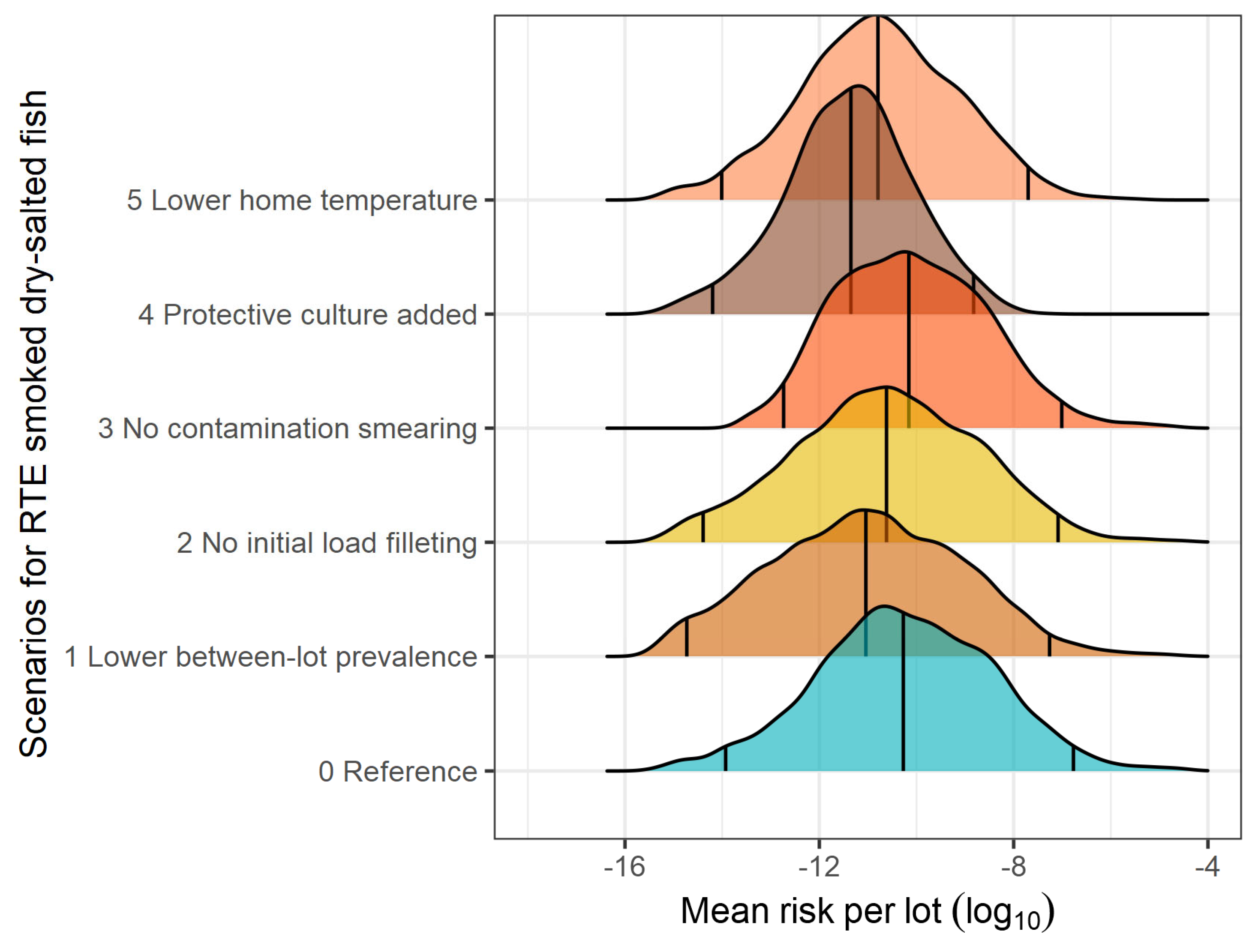
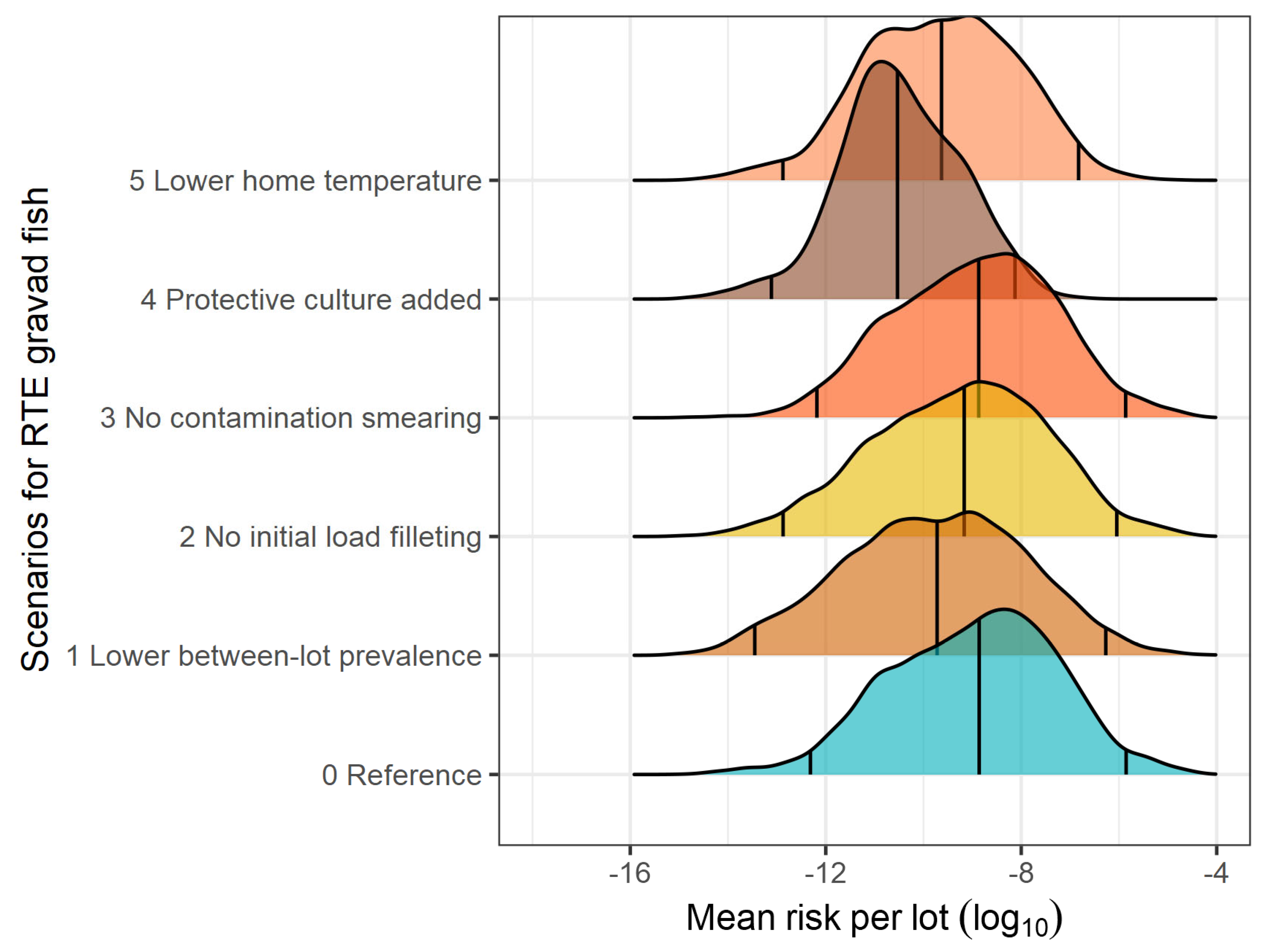
3.2. What-If Scenarios
4. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. The Function Lot2LotGen
Appendix A.2. The Function sfGrowthLDP
Appendix A.3. The Function sfRawFishStorage
Appendix A.4. The Function sfSlicer
Appendix A.5. The Function sfBriningCC
Appendix A.6. The Function sfSmearingCC
Appendix A.7. The Function sfBrineORsaltCC
Appendix A.8. The Function sfSmoking
Appendix A.9. The Function sfMaceration
Appendix A.10. The Function sfTesting
Appendix A.11. The Function sfMejlholmDalgaard
Appendix A.12. The Function sfMejlholmDalgaardLAB
Appendix A.13. The Function sfGrowthJameson
Appendix A.14. The Function sfCharacteristics
Appendix A.15. The Function sfColdChain
Appendix A.16. The Function sfPortioning
References
- Dass, S.C.; Cummins, E.J.; Abu-Ghannam, N. Prevalence and typing of Listeria monocytogenes strains in retail vacuum-packed cold-smoked salmon in the Republic of Ireland. J. Food Saf. 2010, 31, 21–27. [Google Scholar] [CrossRef]
- Domenech, E.; Amoros, J.A.; Martorell, S.; Escriche, I. Safety assessment of smoked fish related to Listeria monocytogenes prevalence using risk management metrics. Food Control 2012, 25, 233–238. [Google Scholar] [CrossRef]
- Jami, M.; Ghanbari, M.; Zunabovic, M.; Domig, K.J.; Kneifel, W. Listeria monocytogenes in aquatic food products—A review. Compr. Rev. Food Sci. Food Saf. 2014, 13, 798–813. [Google Scholar] [CrossRef]
- Klaeboe, H.; Rosef, O.; Saebo, M. Longitudinal studies on Listeria monocytogenes and other Listeria species in two salmon processing plants. Int. J. Environ. Health Res. 2005, 15, 71–77. [Google Scholar] [CrossRef] [PubMed]
- Rotariu, O.; Thomas, D.J.I.; Goodburn, K.E.; Hutchison, M.L.; Strachan, N.J.C. Smoked salmon industry practices and their association with Listeria monocytogenes. Food Control 2014, 35, 284–292. [Google Scholar] [CrossRef]
- Szymczak, B.; Szymczak, M.; Trafiałek, J. Prevalence of Listeria species and L. monocytogenes in ready-to-eat foods in the West Pomeranian region of Poland: Correlations between the contamination level, serogroups, ingredients, and producers. Food Microbiol. 2020, 91, 103532. [Google Scholar] [CrossRef]
- Skjerdal, T.; Reitehaug, E.; Eckner, K. Development of performance objectives for Listeria monocytogenes contaminated salmon (Salmo salar) intended used as sushi and sashimi based on analysis of naturally contaminated samples. Int. J. Food Microbiol. 2014, 184, 8–13. [Google Scholar] [CrossRef]
- Félix, B.; Sevellec, Y.; Palma, F.; Douarre, P.E.; Felten, A.; Radomski, N.; Mallet, L.; Blanchard, Y.; Leroux, A.; Soumet, C.; et al. A European-wide dataset to uncover adaptive traits of Listeria monocytogenes to diverse ecological niches. Sci. Data 2022, 9, 190. [Google Scholar] [CrossRef]
- EFSA. The European Union One Health 2022 Zoonoses Report. EFSA J. 2023, 21, e8442. [Google Scholar] [CrossRef]
- Haas, C.N.; Rose, J.B.; Gerba, C.P. Quantitative Microbial Risk Assessment; Wiley: New York, NY, USA, 1999. [Google Scholar]
- EFSA. The public health risk posed by Listeria monocytogenes in frozen fruit and vegetables including herbs, blanched during processing. EFSA Panel of Biological Hazards (BIOHAZ). EFSA J. 2020, 8, 6092. [Google Scholar] [CrossRef]
- ECDC. Surveillance and Disease Data for Listeriosis. European Centre for Disease Prevention and Control. Available online: https://www.ecdc.europa.eu/en/all-topics-z/listeriosis/surveillance-and-disease-data/eu-summary-reports (accessed on 15 June 2022).
- Lachman, R.; Halbedel, S.; Luth, S.; Holzer, A.; Adier, M.; Pietzka, A.; Al Dahouk, S.; Stark, K.; Flieger, A.; Kieta, S.; et al. Invasive listeriosis outbreaks and salmon products: A genomic, epidemiological study. Emerg. Microbes Infect. 2022, 11, 1308–1315. [Google Scholar] [CrossRef] [PubMed]
- ECDC-EFSA. Prolonged Multi-Country Outbreak of Listeria monocytogenes ST173 Linked to Consumption of Fish Products—19 June 2024; European Centre for Disease Prevention and Control, European Food Safety Authority: Rome, Italy, 2024; ISBN 978-92-9498-726-6. [Google Scholar] [CrossRef]
- IFSAC. IFSAC. Interagency Food Safety Analytics Collaboration. Foodborne Illness Source Attribution Estimates for 2021 for Salmonella, Escherichia coli O157, and Listeria monocytogenes Using Multi-Year Outbreak Surveillance Data, United States. GA and D.C.: U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, Food and Drug Administration, U.S. Department of Agriculture’s Food Safety and Inspection. Available online: https://www.cdc.gov/ifsac/media/pdfs/P19-2021-report-TriAgency-508.pdf (accessed on 9 January 2024).
- EFSA BIOHAZ Panel; Ricci, A.; Allende, A.; Bolton, D.; Chemaly, M.; Davies, R.; Escámez, P.S.F.; Girones, R.; Herman, L.; Koutsoumanis, K. Scientific Opinion on the Listeria monocytogenes contamination of ready-to-eat foods and the risk for human health in the EU. EFSA J. 2018, 16, 5134. [Google Scholar] [CrossRef]
- Leclercq, A.; Kooh, P.; Augustin, J.C.; Guillier, L.; Thébault, A.; Cadavez, V.; Gonzales-Barron, U.; Sanaa, M. Risk factors for sporadic listeriosis: A systematic review and meta-analysis. Microb. Risk Anal. 2021, 17, 100128. [Google Scholar] [CrossRef]
- Gonzales-Barron, U.; Cadavez, V.; De Oliveira Mota, J.; Guillier, L.; Sanaa, M. A critical review of risk assessment models for Listeria monocytogenes in seafood. Foods 2024, 13, 716. [Google Scholar] [CrossRef]
- Pouillot, R.; Miconnet, N.; Afchain, A.-L.; Delignette-Muller, M.L.; Beaufort, A.; Rosso, L.; Denis, J.-B.; Cornu, M. Quantitative risk assessment of Listeria monocytogenes in French cold-smoked salmon: I. Quantitative exposure assessment. Risk Anal. 2007, 27, 683–700. [Google Scholar] [CrossRef]
- Pouillot, R.; Goulet, V.; Delignette-Muller, M.L.; Mahé, A.; Cornu, M. Quantitative risk assessment of Listeria monocytogenes in French cold-smoked salmon: II. Risk characterization. Risk Anal. 2009, 29, 806–819. [Google Scholar] [CrossRef]
- Fritsch, L.; Guillier, L.; Augustin, J.C. Next generation quantitative microbiological risk assessment: Refinement of the cold smoked salmon-related listeriosis risk model by integrating genomic data. Microb. Risk Anal. 2018, 10, 20–27. [Google Scholar] [CrossRef]
- Chen, R.; Orsis, R.H.; Guariglia-Oropeza, V.; Wiedmann, M. Development of a modeling tool to assess ad reduce regulatory ad recall risks for cold-smoked salmon due to Listeria monocytogenes contamination. J. Food Prot. 2022, 85, 1335–1354. [Google Scholar] [CrossRef]
- FDA-FSIS. Quantitative Assessment of Relative Risk to Public Health from Foodborne Listeria monocytogenes among Selected Categories of Ready-to-Eat Foods; FDA-FSIS: Washington, DC, USA, 2003; pp. 1–541. [Google Scholar]
- Pérez-Rodríguez, F.; Carrasco, E.; Bover-Cid, S.; Joffré, A.; Valero, A. Closing gaps for performing a risk assessment on Listeria monocytogenes in ready-to-eat (RTE) foods: Activity 2, a quantitative risk characterization on L. monocytogenes in RTE foods; starting from the retail stage. EFSA Support. Publ. 2017, 14, 1252E. [Google Scholar] [CrossRef]
- Lindqvist, R.; Westöö, A. Quantitative risk assessment for Listeria monocytogenes in smoked or gravad salmon and rainbow trout in Sweden. Int. J. Food Microbiol. 2000, 58, 181–196. [Google Scholar] [CrossRef]
- FAO-WHO. Risk Assessment of Listeria monocytogenes in Ready-to-Eat Foods: Technical Report; World Health Organization and Food and Agriculture Organization of the United Nations: Geneve, Switzerland, 2004; pp. 1–269. [Google Scholar]
- Garrido, V.; García-Jalón, I.; Vitas, A.; Sanaa, M. Listeriosis risk assessment: Simulation modelling and “what if” scenarios applied to consumption of ready-to-eat products in a Spanish population. Food Control 2010, 21, 231–239. [Google Scholar] [CrossRef]
- Gospavic, R.; Haque, M.; Leroi, F.; Popov, V.; Lauzon, H. Quantitative microbial risk assessment for Listeria monocytogenes in cold smoked salmon. WIT Trans. Inf. Commun. Technol. 2010, 43, PI563–PI572. [Google Scholar]
- Dass, S. Exposure Assessment of Listeria monocytogenes in Vacuum Packed Cold-Smoked Salmon in the Republic of Ireland. Ph.D. Thesis, Technological University Dublin, Dublin, Ireland, 2011. [Google Scholar]
- Pasonen, P.; Ranta, J.; Tapanainen, H.; Valsta, L.; Tuominen, P. Listeria monocytogenes risk assessment on cold smoked and salt-cured fishery products in Finland—A repeated exposure model. Int. J. Food Microbiol. 2019, 304, 97–105. [Google Scholar] [CrossRef] [PubMed]
- FAO-WHO. Joint FAO/WHO Expert Meeting on Microbiological Risk Assessment of Listeria monocytogenes in Foods: Summary and Conclusions; WHO HQ: Geneva, Switzerland, 2023. [Google Scholar]
- Nauta, M. The modular process risk model (MPRM): A structural approach to food chain exposure assessment. In Microbial Risk Analysis of Foods; Schaffner, D.W., Doyle, M.P., Eds.; ASM Press: Washington, DC, USA, 2008; pp. 99–136. [Google Scholar]
- Autio, T.; Hielm, S.; Miettinen, M.; Sjoberg, A.-M.; Aarnisalo, K.; Bjorkroth, J.; Mattila-Sandholm, T.; Korkeala, H. Sources of Listeria monocytogenes contamination in a cold-smoked rainbow trout processing plant detected by pulsed-field gel electrophoresis typing. Appl. Environ. Microbiol. 1999, 65, 150–155. [Google Scholar] [CrossRef] [PubMed]
- Cruz, C.D.; Silvestre, F.A.; Kinoshita, E.M.; Landgraf, M.; Franco, B.D.G.M.; Destro, M.T. Epidemiological survey of Listeria monocytogenes in a gravlax salmon processing line. Braz. J. Microbiol. 2008, 39, 375–383. [Google Scholar] [CrossRef]
- Di Ciccio, P.; Meloni, D.; Festino, A.R.; Conter, M.; Zanardi, E.; Ghidini, S.; Vergara, A.; Mazzette, R.; Ianieri, A. Longitudinal study on the sources of Listeria monocytogenes contamination in cold-smoked salmon and its processing environment in Italy. Int. J. Food Microbiol. 2012, 158, 79–84. [Google Scholar] [CrossRef]
- Markkula, A.; Autio, T.; Lunden, J.; Korkeala, H. Raw and processed fish show identical Listeria monocytogenes genotypes with pulsed-field gel electrophoresis. J. Food Prot. 2005, 68, 1228–1231. [Google Scholar] [CrossRef]
- Medrala, D.; Dabrowski, W.; Czekajlo-Kolodziej, U.; Daczkowska-Kozon, E.; Koronkiewcz, A.; Augustynowicz, E.; Manzano, M. Persistence of Listeria monocytogenes strains isolated from products in a Polish fish-processing plant over a 1-year period. Food Microbiol. 2003, 20, 715–724. [Google Scholar] [CrossRef]
- Miettinen, H.; Aarnisalo, K.; Salo, S.; Sjoberg, A. Evaluation of surface contamination and the presence of Listeria monocytogenes in fish processing factories. J. Food Prot. 2001, 64, 635–639. [Google Scholar] [CrossRef]
- Rorvik, L.M.; Caugant, D.A.; Yndestad, M. Contamination patter of Listeria monocytogenes and other Listeria spp. in a salmon slaughterhouse and smoked salmon processing plant. Int. J. Food Microbiol. 1995, 25, 19–27. [Google Scholar] [CrossRef]
- Vogel, B.; Huss, H.; Ojeniyi, B.; Ahrens, P.; Gram, L. Elucidation of Listeria monocytogenes contamination routes in cold-smoked salmon processing plants detected by DNA-based typing methods. Appl. Environ. Microbiol. 2001, 67, 2586–2595. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, B. Statistical Aspects of the Microbiological Examination of Foods, 3rd ed.; Elsevier Science: Amsterdam, The Netherlands, 2016; 336p, ISBN 9780128039731. [Google Scholar]
- Jia, Z.; Bai, W.; Li, X.; Fang, T.; Li, C. Assessing the growth of Listeria monocytogenes in salmon with or without the competition of background microflora—A one-step kinetic analysis. Food Control 2020, 114, 107139. [Google Scholar] [CrossRef]
- Hoelzer, K.; Pouillot, R.; Gallagher, D.; Silverman, M.B.; Kause, J.; Dennis, S. Estimation of Listeria monocytogenes transfer coefficients and efficacy of bacterial removal through cleaning and sanitation. Int. J. Food Microbiol. 2012, 157, 267–277. [Google Scholar] [CrossRef]
- Aarnisalo, K.; Sheen, S.; Raaska, L.; Tamplin, M. Modelling transfer of Listeria monocytogenes during slicing of ‘gravad’ salmon. Int. J. Food Microbiol. 2007, 118, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Gudbjornsdottir, B.; Suihko, M.L.; Gustavsson, P.; Thorkelsson, G.; Salo, S.; Sjoberg, A.M.; Niclasen, O.; Bredholt, S. The incidence of Listeria monocytogenes in meat, poultry and seafood plants in the Nordic countries. Food Microbiol. 2004, 21, 217–225. [Google Scholar] [CrossRef]
- Gudmundsdottir, S.; Gudbjornsdottir, B.; Lauzon, H.; Einarsson, H.; Kristinsson, K.; Kristjansson, M. Tracing Listeria monocytogenes isolates from cold-smoked salmon and its processing environment in Iceland using pulsed-field gel electrophoresis. Int. J. Food Microbiol. 2005, 101, 41–51. [Google Scholar] [CrossRef]
- Eklund, M.W.; Poysky, F.T.; Paranjpye, R.N.; Lashbrook, L.C.; Peterson, M.E.; Pelory, G.A. Incidence and sources of Listeria monocytogenes in cold-smoked fishery products and processing plants. J. Food Prot. 1995, 58, 502–508. [Google Scholar] [CrossRef]
- Porsby, C.H.; Vogel, B.F.; Mohr, M.; Gram, L. Influence of processing steps in cold-smoked salmon production on survival and growth of persistent and presumed non-persistent Listeria monocytogenes. Int. J. Food Microbiol. 2008, 122, 287–295. [Google Scholar] [CrossRef]
- Neunlist, M.R.; Ralazamahaleo, M.; Cappelier, J.-M.; Besnard, V.; Federighi, M.; Leroi, F. Effect of salting and cold-smoking process on the culturability, viability and virulence of Listeria monocytogenes strain Scott A. J. Food Prot. 2005, 68, 85–91. [Google Scholar] [CrossRef]
- Lopes, S.M.; Carmo da Silva, D.; Tondo, E.C. Survival of Listeria monocytogenes in gravlax salmon (Salmo salar) recipe. Int. J. Gastron. Food Sci. 2023, 34, 100836. [Google Scholar] [CrossRef]
- Mejlholm, O.; Dalgaard, P. Modeling and predicting the growth boundary of Listeria monocytogenes in lightly preserved seafood. J. Food Prot. 2007, 70, 70–84. [Google Scholar] [CrossRef] [PubMed]
- Mejlholm, O.; Dalgaard, P. Modeling and predicting the growth of lactic acid bacteria in lightly preserved seafood and their inhibiting effect on Listeria monocytogenes. J. Food Prot. 2007, 70, 2485–2497. [Google Scholar] [CrossRef] [PubMed]
- Mejlholm, O.; Dalgaard, P. Development and validation of an extensive growth and growth boundary model for Listeria monocytogenes in lightly preserved and ready-to-eat shrimp. J. Food Prot. 2009, 72, 2132–2143. [Google Scholar] [CrossRef] [PubMed]
- Mejlholm, O.; Dalgaard, P. Development and validation of an extensive growth and growth boundary model for psychrotolerant Lactobacillus spp. in seafood and meat products. Int. J. Food Microbiol. 2013, 167, 244–260. [Google Scholar] [CrossRef]
- Mejlholm, O.; Dalgaard, P. Modelling and predicting the simultaneous growth of Listeria monocytogenes and psychrotolerand lactic acid bacteria in processed seafood and mayonnaise-based seafood salads. Food Microbiol. 2015, 46, 1–14. [Google Scholar] [CrossRef]
- Mejlholm, O.; Gunvig, A.; Borggaard, C.; Blom-Hanssen, J.; Mellefont, L.; Ross, T.; Leroi, F.; Else, T.; Visser, D.; Dalgaard, P. Predicting growth rates and growth boundary of Listeria monocytogenes—An international validation study with focus on processed and ready-to-eat meat and seafood. Int. J. Food Microbiol. 2010, 141, 137–150. [Google Scholar] [CrossRef]
- Gimenez, B.; Dalgaard, P. Modelling and predicting the simultaneous growth of Listeria monocytogenes and spoilage microorganisms in cold-smoked salmon. J. Appl. Microbiol. 2004, 96, 96–109. [Google Scholar] [CrossRef]
- Møller, C.O.A.; Ilg, Y.; Aabo, S.; Christensen, B.B.; Dalgaard, P.; Hansen, T.B. Effect of natural microbiota on growth of Salmonella spp. in fresh pork—A predictive microbiology approach. Food Microbiol. 2013, 34, 284–295. [Google Scholar] [CrossRef]
- Nauta, M. Microbiological risk assessment models for partitioning and mixing during food handling. Int. J. Food Microbiol. 2005, 100, 311–322. [Google Scholar] [CrossRef]
- Svanevik, C.S.; Lunestad, B.T.; Storesund, J. Listeria monocytogenes in Salmonid Slaughter Facilities—Screening Program for the Norwegian Food Safety Authority; Report Series: Rapport fra havforskningen 2021-45; Institute of Marine Research: Oslo, Norway, 2021; IMR: 2021; ISSN 1893-4536. Project No.: 15600. [Google Scholar]
- Gonzales-Barron, U.; Cadavez, V.; Thebault, A.; Kooh, P. The Pathogens-in-Foods Database (PIF) (Version 1). Zenodo, 2021. Available online: https://pif.esa.ipb.pt/ (accessed on 10 January 2024). [CrossRef]
- Daelman, J.; Membré, J.M.; Jacxsens, L.; Vermeulen, A.; Devlieghere, F.; Uyttendaele, M. A quantitative microbiological exposure assessment model for Bacillus cereus in REPFEDs. Int. J. Food Microbiol. 2013, 166, 433–449. [Google Scholar] [CrossRef]
- Peiris, I.P.; Lopez-Valladares, G.; Parihar, V.S.; Helmersson, S.; Barbuddhe, S.; Tham, W.; Danielsson-Tham, M.-L. Gravad (Gravlax) and cold-smoked salmon, still a potential source of listeriosis. J. Foodserv. 2009, 20, 15–20. [Google Scholar] [CrossRef]
- FDA. FDA-iRISK 4.2 Food Safety Modeling Tool: Technical Document; U.S. Food and Drug Administration, U.S. Department of Agriculture: Washington, USA, 2021. [Google Scholar]
- Leistner, L. Basic aspects of food preservation by hurdle technology. Int. J. Food Microbiol. 2000, 55, 181–186. [Google Scholar] [CrossRef] [PubMed]
- Maqsood, S.; Benjakul, S.; Shahidi, F. Emerging role of phenolic compounds as natural food additives in fish and fish products. Crit. Rev. Food Sci. Nutr. 2012, 53, 162–179. [Google Scholar] [CrossRef] [PubMed]
- Niedziela, J.-C.; MacRae, M.; Ogden, I.D.; Nesvadba, P. Control of Listeria monocytogenes in salmon; antimicrobial effect of salting, smoking and specific smoke compounds. LWT—Food Sci. Technol. 1998, 31, 155–161. [Google Scholar] [CrossRef]
- Wiernasz, N.; Leroi, F.; Chevalier, F.; Cornet, J.; Cardinal, M.; Rohloff, J.; Passerini, D.; Skırnisdóttir, S.; Pilet, M.F. Salmon gravlax biopreservation with lactic acid bacteria: A polyphasic approach to assessing the impact on organoleptic properties, microbial ecosystem and volatilome composition. Front. Microbiol. 2020, 10, 3103. [Google Scholar] [CrossRef]
- Chen, B.Y.; Pyla, R.; Kim, T.J.; Silva, J.L.; Jung, Y.S. Prevalence and contamination patterns of Listeria monocytogenes in catfish processing environment and fresh fillets. Food Microbiol. 2010, 27, 645–652. [Google Scholar] [CrossRef]
- WHO. Statistical Aspects of Microbiological Criteria Related to Foods: A Risk Managers Guide; Microbiological Risk Assessment series 24; World Health Organization & Food and Agriculture Organization of the United Nations: Geneve, Switzerland, 2016; p. 120. Available online: https://iris.who.int/bitstream/handle/10665/249531/9789241565318–eng.pdf?sequence=1 (accessed on 20 January 2024).
- Couvert, O.; Pinon, A.; Bergis, H.; Bourdichon, F.; Carlin, F.; Cornu, M.; Denis, C.; Gnanou, B.; Guillier, L.; Jamet, E.; et al. Validation of a stochastic modelling approach for Listeria monocytogenes growth in refrigerated foods. Int. J. Food Microbiol. 2010, 144, 236–242. [Google Scholar] [CrossRef]
- Wiernasz, N.; Gigout, F.; Cardinal, M.; Cornet, J.; Rohloff, J.; Courcoux, P.; Vigneau, E.; Skírnisdottír, S.; Passerini, D.; Pilet, M.-F.; et al. Effect of the manufacturing process on the microbiota, organoleptic properties and volatilome of three salmon-based products. Foods 2021, 10, 2517. [Google Scholar] [CrossRef]
- Hwang, C.-A.; Sheen, S. Modeling the growth characteristics of Listeria monocytogenes and native microflora in smoked salmon. J. Food Sci. 2009, 74, M125–M130. [Google Scholar] [CrossRef]
- Orozco, L.N. The Occurrence of Listeria monocytogenes and Microbiological Quality of Cold Smoked and Gravad Fish on the Iceland Retail Market; Report, Fisheries Training Programme; The United Nations University: Reykjavic, Iceland, 2000; p. 30. [Google Scholar]
- Leblanc, I.; Leroi, F.; Hartke, A.; Auffray, Y. Do stress encountered during the smoked salmon process influence the survival of the spoiling bacterium Shewanella putrefaciens? Lett. Appl. Microbiol. 2000, 30, 437–442. [Google Scholar] [CrossRef]
- Endrikat, S.; Gallagher, D.; Pouillot, R.; Hicks Quesenberry, H.; Labarre, D.; Schroeder, C.M.; Kause, J. A comparative risk assessment for Listeria monocytogenes in prepackaged versus retail-sliced deli meat. J. Food Prot. 2010, 73, 612–619. [Google Scholar] [CrossRef] [PubMed]
- Marc, L. Développement d’un Modèle Modulaire Décrivant L’effet des Interactions Entre les Facteurs Environnementaux sur les Aptitudes de Croissance de Listeria. Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, 2001. [Google Scholar]
- Pouillot, R.; Delignette-Muller, M.L. Evaluating variability and uncertainty separately in microbial quantitative risk assessment using two R packages. Int. J. Food Microbiol. 2010, 142, 330–340. [Google Scholar] [CrossRef] [PubMed]
- Pouillot, R.; Kiermeier, A.; Guillier, L.; Cadavez, V.; Sanaa, M. Updated Parameters for Listeria monocytogenes Dose–Response Model Considering Pathogen Virulence and Age and Sex of Consumer. Foods 2024, 13, 751. [Google Scholar] [CrossRef] [PubMed]
- Pouillot, R.; Gallagher, D.; Tang, J.; Hoelzer, K.; Kause, J.; Dennis, S.B. Listeria monocytogenes in retail delicatessens: An interagency risk assessment-model and baseline results. J. Food Prot. 2015, 78, 134–145. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 15 September 2023).
- Hartemink, R.; Georgsson, F. Incidence of Listeria species in seafood and seafood salads. Int. J. Food Microbiol. 1991, 12, 189–195. [Google Scholar] [CrossRef]
- Pelroy, G.A.; Peterson, M.E.; Holland, P.J.; Eklund, M.W. Inhibition of Listeria monocytogenes in cold-process (smoked) salmon by sodium lactate. J. Food Prot. 1994, 57, 108–113. [Google Scholar] [CrossRef]
- Kang, J.; Stasiewicz, M.J.; Murray, D.; Boor, K.J.; Wiedmann, M.; Bergholz, T.M. Optimization of combinations of bactericidal and bacteriostatic treatments to control Listeria monocytogenes on cold-smoked salmon. Int. J. Food Microbiol. 2014, 179, 1–9. [Google Scholar] [CrossRef]
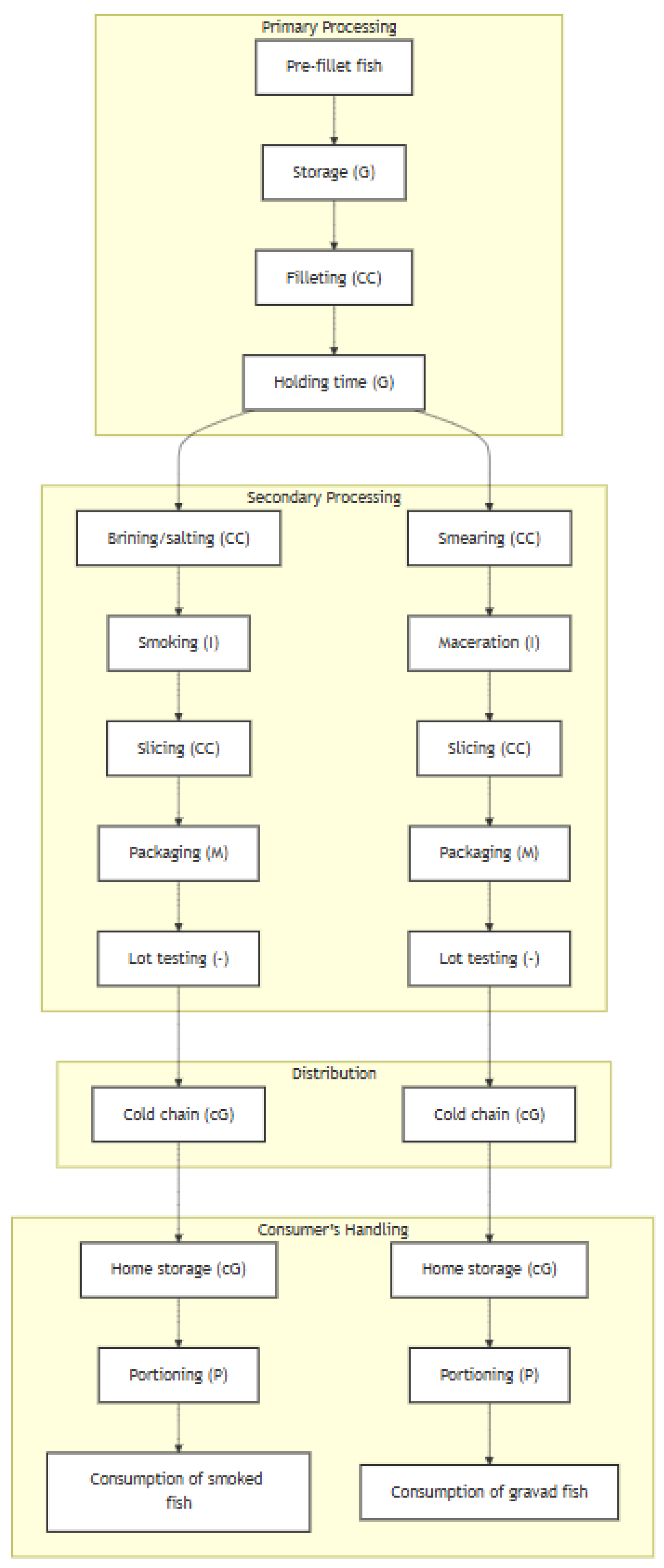
| Module | Stage | Microbial Process | Assumptions | Sources | Function in R |
|---|---|---|---|---|---|
| Primary processing | Generation of contaminated lots of pre-fillet (pre-processed) fish | None | LM prevalence in fish units is modelled from data found in incoming fish sampled at primary processing. Since LM numbers in incoming fish were generally low (<10 CFU/g), LM concentration in fish was calculated from the expected proportion of non-zeroes under a Poisson distribution. | Autio et al. [33], Cruz et al. [34], Dass [29], Di Ciccio et al. [35], Markkula et al. [36], Medrala et al. [37], Miettinen et al. [38], Rorvik et al. [39], Vogel et al. [40], Jarvis [41] | Lot2LotGen() |
| Storage | Growth | LM in pre-filleted fish is assumed to follow the kinetics of a cocktail of CICC 21632 (serotype 1/2a), CICC 21633 (serotype 1/2a), CICC 21635 (serotype 4b), and CICC 21639 (serotype 1/2a) LM inoculated in raw salmon flesh. Lag phase is considered. | Jia et al. [42] | sfRawFishStorage(), served by sfGrowthLDP() | |
| Filleting | Cross-contamination | LM is transferred to the fillets during the slicing process of the raw whole fish using a compartmental model defined by two variability distributions: “a”, the transfer rate between slicer blade (or filleting knife) and product, and “e”, the transfer rate from the original contamination to the slicing system. Distribution parameters were obtained from published data. | Hoelzer et al. [43], Aarnisalo et al. [44] | sfSlicer() | |
| Holding-off time | Growth | The same predictive microbiology model as in Storage, yet the LM growth and the exhaustion of the lag phase were followed up in this stage. | Jia et al. [42] | sfRawFishStorage(), served by sfGrowthLDP() | |
| Secondary processing | Brining or salting (smoked fish) | Cross-contamination | Fish fillets can be salted either through brine injection or by dry salting. Internal contamination by brining may occur during the injection of saline solution due to brine containers or the brine itself serving as reservoirs for LM, at a given probability. For dry-salted fillets, it is assumed that external contamination can occur during the procedure of smearing salt on fish fillets if surfaces are contaminated with LM, at a given probability. A published distribution for LM transfer rate is assumed. | Gudbjornsdottir et al. [45], Gudmundsdottir et al. [46] Hoelzer et al. [43] | sfBrineORsaltCC(), served by sfBriningCC() and sfSmearingCC() |
| Smoking and maturation (smoked fish) | Inactivation | Salting, drying, and smoking produce a slight reduction in LM, which is different if fish fillets were brine-injected or dry-salted. The LM log10 reduction in brine-injected fish fillets was assumed to be that of the combined results of inoculation experiments in smoked salmon, first salted through brine injection, and then submitted to cycles of cold-smoking between 6 and 8 h until a total maturation time of 18–24 h. The LM log10 reduction in dry-salted fish was assumed to be that of the combined results of inoculation experiments on the surface of dry-salted salmon, determined before and after a total maturation time between 18 and 24 h. | Eklund et al. [47], Porsby et al. [48] Eklund et al. [47], Porsby et al. [48], Neunlist et al. [49] | sfSmoking() | |
| Smearing (gravad fish) | Cross-contamination | During smearing of fish fillets with salt, sugar, and spices, external contamination can occur if surfaces are contaminated with LM, at a given probability. A published distribution for LM transfer rate is assumed. | Hoelzer et al. [43] | sfSmearingCC() | |
| Maceration (gravad fish) | Inactivation | The maceration of fish smeared with gravlax curing agents is assumed to reduce the populations of LM, according to the results of a study where inoculated raw salmon was smeared with salt, brown sugar, black pepper, and dill and left to macerate at 4.5 °C for 72 h. | Lopes et al. [50] | sfMaceration() | |
| Slicing | Cross-contamination | The same compartmental model as in Filleting, but used to produce slices from smoked or gravad fish fillets. | Hoelzer et al. [43], Aarnisalo et al. [44] | sfSlicer() | |
| Packaging | Mixing | No cross-contamination is assumed during packaging. Consecutive slices of recently-sliced RTE smoked or gravad fish are gathered into packages of end-product. | - | sfPackaging() | |
| Within-lot testing | None | At a given probability, any lot of RTE smoked or gravad fish can be subjected to sampling and testing, according to a two-class or three-class microbiological sampling plan. | - | sfTesting() | |
| Distribution | Cold chain | Growth | LM in smoked or gravad fish, as affected by populations of lactic acid bacteria (LAB), are assumed to grow during the various cold chain logistics stages, including transportation to retail, display at retail, and transportation to home. Specific growth rates for LM and LAB are estimated from secondary models, using validated kinetic parameters. LM numbers follow an extended Jameson-effect competition model, which uses an interaction Gamma parameter. | Mejlholm and Dalgaard [51,52,53,54,55], Mejlholm et al. [56] Gimenez et al. [57], Moller et al. [58] | sfColdChain(), served by sfMejlholmDalgaard(), sfMejlholmDalgaardLAB(), sfGrowthJameson() |
| Consumer’s handling | Home storage | Growth | The same as in Cold chain, following up the growth. | Mejlholm and Dalgaard [51,52,53,54,55], Mejlholm et al. [56], Gimenez et al. [57], Moller et al. [58] | sfColdChain(), served by sfMejlholmDalgaard(), sfMejlholmDalgaardLAB(), sfGrowthJameson() |
| Portioning | Partitioning | The consumer is assumed to take a number of RTE fish slices from the pack. LM cells present in a contaminated pack are assumed to be moderately clustered within the package. | Nauta [59] | sfPortioning() |
| Type of Salting | Source | Conditions of Smoking and Maturation | Before Treatment (log10 CFU/g) | After Treatment (log10 CFU/g) | Reduction (log10 CFU/g) |
|---|---|---|---|---|---|
| Brine injection | Porsby et al. [48] | Cold smoking, 24 °C in cycles of 6 h | 3.00 ± 0.3 | 2.50 ± 1.1 | 0.50 |
| 3.30 ± 0.4 | 1.80 ± 0.9 | 1.50 | |||
| 2.90 ± 0.2 | 1.00 ± 0.0 | 1.90 | |||
| 3.30 ± 0.1 | 1.80 ± 0.6 | 1.50 | |||
| 3.00 ± 0.1 | 1.10 ± 0.3 | 1.90 | |||
| Elkund et al. [47] | Cold smoking, 17–21 °C × 18 h | 2.36 | 1.41 | 0.95 | |
| 3.34 | 2.63 | 0.71 | |||
| Cold smoking, 22–30 °C × 18 h | 2.11 | 2.34 | −0.23 | ||
| 3.28 | 3.38 | −0.10 | |||
| 4.57 | 4.49 | 0.08 | |||
| Dry-salting | Porsby et al. [48] | Cold smoking, 24 °C in cycles of 6 h | 3.30 ± 0.2 | 1.30 ± 0.7 | 1.80 |
| 3.10 ± 0.2 | 1.40 ± 0.7 | 1.70 | |||
| Neunlist et al. [49]) | Liquid smoking and maturing, 4 °C × 24 h | 5.70 | 4.70 | 1.00 | |
| Elkund et al. [47] | Cold smoking, 17–21 °C × 18 h | 2.04 | 0.83 | 1.21 | |
| 2.56 | 1.11 | 1.45 | |||
| Cold smoking, 22–30 °C ×18 h | 0.11 | −0.39 | 0.50 | ||
| 1.04 | 0.54 | 0.50 | |||
| 2.42 | 1.84 | 0.58 |
| Type of Parameter | Parameter | Definition (Unit) | Value or Distribution | Source |
|---|---|---|---|---|
| Relative to kinetic parameters of LM in RTE seafood | Optimum growth rate of LM (h−1) | 0.419 | Mejlholm and Dalgaard [51] | |
| MPDLM | Maximum population density of LM (log10 CFU/g) | MPDLM min = 6.60 MPDLM mode = 7.36 MPDLM max = 8.20 MPDLM ~ Pert (MPDLM min, MPDLM mode, MPDLM max) | Pérez-Rodríguez et al. [24] | |
| h0 LM | Parameter regarding the initial physiological state of LM (-) | μh0 = 2.8 σh0 = 4.6 h0 LM ~ Normal (μh0, σh0), h0 > 0 | Couvert et al. [71]: q0 then obtained by (1/(exp(h0)−1)) | |
| Relative to kinetic parameters of LAB in RTE seafood | Optimum growth rate of LAB (h−1) | 0.583 | Mejlholm and Dalgaard [54] | |
| MPDLAB | Maximum population density of LAB (log10 CFU/g) | MPDLAB min = 8.0 MPDLAB mode = 8.5 MPDLAB max = 9.0 MPDLAB ~ Pert (MPDLAB min, MPDLAB mode, MPDLABM max) | MPDLAB min from Mejlholm and Dalgaard [54] | |
| q0 LAB | Parameter regarding the initial physiological state of LAB (-) | ln q0 LABmin = −12 ln q0 LABmode = 2.73 ln q0 LABmax = 1.26 q0 LAB~exp{ Pert (ln q0 LABmin, ln q0 LABmode, ln q0 LABmax)} | Couvert et al. [71] | |
| Relative to smoked fish characteristics | Between-lot mean concentration of LAB in smoked fish after packaging (log10 CFU/g) | = −1.00 = 0.28 = 1.60 ~ Pert (, | Wiernasz et al. [72] | |
| pHSF | pH of smoked fish (-) | pHminSF = 5.8 pHmodeSF = 6.1 pHmaxSF = 6.5 pHSF~Pert (pHminSF, pHmodeSF, pHmaxSF) | pHminSF from Mejlholm and Dalgaard [51] pHmodeSF from Porsby et al. [48] pHmaxSF from Hwang and Sheen [73] | |
| NaClSF | NaCl content in smoked fish (% wb) | NaClminSF = 1.5 NaClmodeSF = 3.4 NaClmaxSF = 5.3 NaClSF~Pert (NaClminSF, NaClmodeSF, NaClmaxSF) | NaClminSF from FAO-WHO [26] NaClmodeSF from Porsby et al. [48], Mejlholm and Dalgaard [51], FAO-WHO [26], and Orozco [74] NaClmaxSF from Mejlholm and Dalgaard [51] | |
| PheSF | Phenol compound in smoked fish (ppm) | PheminSF = 5 PhemodeSF = 10 PhemaxSF = 22 PheSF~Pert (PheminSF, PhemodeSF, PhemaxSF) | PheminSF from Leblanc et al. [72] PhemodeSF from Hwang and Sheen [73], Porsby et al. [48], Mejlholm and Dalgaard [51], FAO/WHO [26], Leblanc et al. [75], and Eklund et al. [47] PhemaxSF from Porsby et al. [48] | |
| CO2 equi SF | CO2 concentration at equilibrium in the packaging of smoked fish (fraction) | CO2equi SF min = 0.25 CO2equi SF mode = 0.25 CO2equi SF max = 0.30 CO2equi SF~Pert (CO2equi SF min, CO2equi SF mode, CO2equi SF max) | Mejlholm and Dalgaard [51] | |
| Others: NitSF, LAtot GF, AAtot SF, BAtot SF, CAtot SF, DAtot SF, SAtot SF | Nitrites concentration (ppm) and lactic acid, acetic acid, benzoic acid, citric acid, diacetate, lactic acid, and sorbic acid concentrations in water phase (ppm) | Allow for minimum, mode, and maximum for each compound to be sampled from Pert distribution. Values of zero set to all. | ||
| Relative to gravad fish characteristics | Between-lot mean concentration of LAB in gravad fish after packaging (log10 CFU/g) | = −1.00 = 0.28 = 1.60 ~ Pert (, | Wiernacz et al. [72] | |
| pHGF | pH of gravad fish (-) | pHminGF = 6.1 pHmodeGF = 6.2 pHmaxGF = 6.3 pHSF~Pert (pHminSF, pHmodeSF, pHmaxSF) | Mejlholm and Dalgaard [51] and Orozco [74] | |
| NaClGF | NaCl content in gravad fish (% wb) | NaClminGF = 3.0 NaClmodeGF = 3.2 NaClmaxGF = 3.4 NaClGF~Pert (NaClminGF, NaClmodeGF, NaClmaxGF) | Mejlholm and Dalgaard [51] and Aarnisalo et al. [44] | |
| PheGF | Phenol compound in gravad fish (ppm) | PheminSF = 0 PhemodeSF = 0 PhemaxSF = 5 PheGF~Pert (PheminGF, PhemodeGF, PhemaxGF) | Mejlholm and Dalgaard [51] | |
| CO2 equi GF | CO2 concentration at equilibrium in the packaging of gravad fish (fraction) | CO2equi GF min = 0.25 CO2equi GF mode = 0.25 CO2equi GF max = 0.30 CO2equi GF~Pert (CO2equi SF min, CO2equi SF mode, CO2equi SF max) | Mejlholm and Dalgaard [51] | |
| Others: NitGF, LAtot GF, AAtot GF, BAtot GF, CAtot GF, DAtot GF, SAtot GF | Nitrite concentration and lactic acid, acetic acid, benzoic acid, citric acid, diacetate, lactic acid, and sorbic acid concentrations in water phase (ppm) | Allow for minimum, mode and maximum for each compound to be sampled from Pert distribution. Values of zero set to all. | - | |
| Relative to cold chain distribution | timeCC | Time elapsed between end of production and arrival of the product at home (h) | timeCC min = 12 timeCC mode = 144 timeCC max = 720 timeCC~Pert (timeCC min, timeCC mode, timeCC max) | FDA-FSIS [23] |
| TempCC | Average temperature between end of production and arrival of the product at home (°C) | TempCC min = 0.28 TempCC mode = 4.60 TempCC max = 7.00 TempCC~Pert (TempCC min, TempCC mode, TempCC max) | From Normal (4.6, 2.2) °C in Pouillot et al. [20] | |
| CorTimeTempCC | Correlation between time and temperature during cold chain | −0.16 | Pouillot et al. [19] | |
| Relative to home storage | TimeHome | Storage time at home (h) | TimeHome min = 0.73 TimeHome mode = 70 TimeHome max = 840 for smoked fish and 528 for gravad fish TimeHome ~ Pert (timeHome min, timeHome mode, timeHome max) | Minimum and mode values from Weibull (shape = 1.14, scale = 18.39) days in Endrikat et al. [76] Maximum is best guess: 35 days for smoked fish and 22 days for gravad fish |
| TempHome | Storage temperature at home (°C) | TempHome min = 1.12 TempHome mode = 7.0 TempHome max = 12.9 TempCC~Pert (TempHome min, TempHome mode, TempHome max) | From Normal (7, 3) °C in Pouillot et al. [20] | |
| CorTimeTempHome | Correlation between time and temperature at home storage | −0.12 | Pouillot et al. [19] |
| Scenario | Mean Counts (CFU/g) in Contaminated Lots (Mean, Median, [95% CI]) | Prevalence of Contaminated Lots | Prevalence of Contaminated Packs | P (N > 10 CFU/g in a Contaminated Pack) * |
|---|---|---|---|---|
| Smoked brined fish | ||||
| Reference | 0.0028; 0.0017 [1.18 × 10−4–0.0130] | 0.3870 | 0.0814 | 0 |
| Lower prevalence of contaminated lots | 0.0023; 0.0014 [9.49 × 10−5–0.0097] | 0.2343 | 0.0497 | 0 |
| No initial load on filleting knives | 0.0023; 0.0012 [7.69 × 10−5–0.0117] | 0.3298 | 0.0652 | 0 |
| No contamination during brining | 0.0028; 0.0017 [1.20 × 10−4–0.0129] | 0.3767 | 0.0792 | 0 |
| Addition of LAB culture | 0.0028; 0.0017 [1.18 × 10−4–0.0130] | 0.3870 | 0.0814 | 0 |
| Lower home storage temperature | 0.0028; 0.0017 [1.18 × 10−4–0.0130] | 0.3870 | 0.0814 | 0 |
| Smoked dry-salted fish | ||||
| Reference | 0.0021; 0.0013 [1.28 × 10−4–0.0095] | 0.3443 | 0.0649 | 0 |
| Lower prevalence of contaminated lots | 0.0016; 0.0009 [7.18 × 10−5–0.0072] | 0.1611 | 0.0311 | 0 |
| No initial load on filleting knives | 0.0018; 0.0010 [8.71 × 10−5–0.0085] | 0.2927 | 0.0512 | 0 |
| No contamination during smearing | 0.0012; 0.0005 [3.58 × 10−5–0.0063] | 0.3554 | 0.0406 | 0 |
| Addition of LAB culture | 0.0021; 0.0013 [1.28 × 10−4–0.0095] | 0.3443 | 0.0649 | 0 |
| Lower home storage temperature | 0.0021; 0.0013 [1.28 × 10−4–0.0095] | 0.3443 | 0.0649 | 0 |
| Gravad fish | ||||
| Reference | 0.0029; 0.0020 [4.25 × 10−4–0.0102] | 0.5215 | 0.1114 | 0 |
| Lower prevalence of contaminated lots | 0.0022; 0.0016 [2.66 × 10−4–0.0080] | 0.3124 | 0.0542 | 0 |
| No initial load on filleting knives | 0.0023; 0.0016 [2.41 × 10−4–0.0091] | 0.4521 | 0.0886 | 0 |
| No contamination during smearing | 0.0026/0.0018 [3.97 × 10−4–0.0100] | 0.5031 | 0.1137 | 0 |
| Addition of LAB culture | 0.0029; 0.0020 [4.25 × 10−4–0.0102] | 0.5215 | 0.1114 | 0 |
| Lower home storage temperature | 0.0029; 0.0020 [4.25 × 10−4–0.0102] | 0.5215 | 0.1114 | 0 |
| Scenario | Counts (CFU/g) in Any Serving (Mean, Median, [95% CI]) | Prevalence of Contaminated Servings | P (N > 10 CFU/g in a Contaminated Serving) | P (N > 100 CFU/g in a Contaminated Serving) |
|---|---|---|---|---|
| Smoked brined fish | ||||
| Reference | 103.6; 0.00 [0–0.2261] | 0.0459 | 0.0122 | 0.0040 |
| Lower prevalence of contaminated lots | 103.4; 0.00 [0–0.0605] | 0.0267 | 0.0110 | 0.0037 |
| No initial load on filleting knives | 76.39; 0.00 [0–0.1195] | 0.0453 | 0.0111 | 0.0035 |
| No contamination during brining | 100.9; 0.00 [0–0.2139] | 0.0444 | 0.0120 | 0.0039 |
| Addition of LAB culture | 0.0548; 0.00 [0–0.0886] | 0.0416 | 0.0021 | 0.0002 |
| Lower home storage temperature | 6.4923; 0.00 [0–0.0994] | 0.0413 | 0.0064 | 0.0016 |
| Smoked dry-salted fish | ||||
| Reference | 125.9; 0.00 [0–0.1197] | 0.0352 | 0.0100 | 0.0032 |
| Lower prevalence of contaminated lots | 58.58; 0.00 [0–0.0206] | 0.0165 | 0.0082 | 0.0027 |
| No initial load on filleting knives | 104.0; 0.00 [0–0.0642] | 0.0274 | 0.0092 | 0.0029 |
| No contamination during smearing | 74.26; 0.00 [0–0.0763] | 0.0210 | 0.0060 | 0.0019 |
| Addition of LAB culture | 0.0340; 0.00 [0–0.0508] | 0.0320 | 0.0015 | 8.1 x 10−5 |
| Lower home storage temperature | 3.8733; 0.00 [0–0.0567] | 0.0318 | 0.0052 | 0.0012 |
| Gravad fish | ||||
| Reference | 162.6; 0.00 [0–3.3787] | 0.0735 | 0.0260 | 0.0104 |
| Lower prevalence of contaminated lots | 85.84; 0.00 [0–0.4191] | 0.0353 | 0.0213 | 0.0085 |
| No initial load on filleting knives | 124.9; 0.00 [0–1.8050] | 0.0579 | 0.0237 | 0.0094 |
| No contamination during smearing | 156.5; 0.00 [0–3.3617] | 0.0744 | 0.0255 | 0.0101 |
| Addition of LAB culture | 0.2100; 0.00 [0–0.4503] | 0.0660 | 0.0057 | 0.0005 |
| Lower home storage temperature | 12.486; 0.00 [0–1.0267] | 0.0675 | 0.0157 | 0.0052 |
| Scenario | Mean | Median | 2.5 pct | 97.5 pct | 99.5 pct | log10 RR |
|---|---|---|---|---|---|---|
| Smoked brined fish | ||||||
| Reference | 9.751 × 10−8 | 6.572 × 10−11 | 3.693 × 10−15 | 3.064 × 10−7 | 3.836 × 10−6 | - |
| Lower prevalence of contaminated lots | 8.778 × 10−8 | 1.478 × 10−11 | 3.911 × 10−16 | 1.422 × 10−7 | 2.881 × 10−6 | 0.05 |
| No initial load on filleting knives | 6.920 × 10−8 | 2.431 × 10−11 | 7.494 × 10−16 | 1.233 × 10−7 | 2.272 × 10−6 | 0.15 |
| No contamination during brining | 9.272 × 10−8 | 6.164 × 10−11 | 6.477 × 10−15 | 2.566 × 10−7 | 3.287 × 10−6 | 0.02 |
| Addition of LAB culture | 2.718 × 10−10 | 5.399 × 10−12 | 2.409 × 10−15 | 1.918 × 10−9 | 8.972 × 10−9 | 2.55 |
| Lower home temperature | 1.112 × 10−8 | 1.769 × 10−11 | 2.842× 10−15 | 3.082 × 10−8 | 2.113 × 10−7 | 0.94 |
| Smoked dry-salted fish | ||||||
| Reference | 9.634 × 10−8 | 5.352 × 10−11 | 1.183 × 10−14 | 1.703 × 10−7 | 4.087 × 10−6 | - |
| Lower prevalence of contaminated lots | 5.113 × 10−8 | 9.071 × 10−12 | 1.868 × 10−15 | 5.483 × 10−8 | 1.513 × 10−6 | 0.28 |
| No initial load on filleting knives | 7.428 × 10−8 | 2.415 × 10−11 | 4.059 × 10−15 | 8.223 × 10−8 | 2.386 × 10−6 | 0.11 |
| No contamination during smearing | 5.984 × 10−8 | 6.953 × 10−11 | 1.835 × 10−13 | 9.772 × 10−8 | 2.608 × 10−6 | 0.20 |
| Addition of LAB culture | 1.693 × 10−10 | 4.462 × 10−12 | 6.363 × 10−15 | 1.502 × 10−9 | 5.888 × 10−9 | 2.76 |
| Lower home temperature | 6.899 × 10−9 | 1.607 × 10−11 | 9.780 × 10−15 | 1.991 × 10−8 | 1.817 × 10−7 | 1.14 |
| Gravad fish | ||||||
| Reference | 2.086 × 10−7 | 1.376 × 10−9 | 4.863 × 10−13 | 1.402 × 10−6 | 9.436 × 10−6 | - |
| Lower prevalence of contaminated lots | 1.133 × 10−7 | 1.900 × 10−10 | 3.531 × 10−14 | 5.372 × 10−7 | 3.815 × 10−6 | 0.27 |
| No initial load on filleting knives | 1.623 × 10−7 | 6.810 × 10−10 | 1.344 × 10−13 | 9.013 × 10−7 | 7.841 × 10−6 | 0.10 |
| No contamination during smearing | 2.037 × 10−7 | 1.347 × 10−9 | 6.725 × 10−13 | 1.368 × 10−6 | 1.036 × 10−5 | 0.01 |
| Addition of LAB culture | 1.019 × 10−9 | 2.940 × 10−11 | 7.731 × 10−14 | 7.457 × 10−9 | 2.977 × 10−8 | 2.31 |
| Lower home temperature | 2.761 × 10−8 | 2.343 × 10−10 | 1.328 × 10−13 | 1.500 × 10−7 | 9.657 × 10−7 | 0.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzales-Barron, U.; Pouillot, R.; Skjerdal, T.; Carrasco, E.; Teixeira, P.; Stasiewicz, M.J.; Hasegawa, A.; De Oliveira Mota, J.; Guillier, L.; Cadavez, V.; et al. A Quantitative Risk Assessment Model for Listeria monocytogenes in Ready-to-Eat Smoked and Gravad Fish. Foods 2024, 13, 3831. https://doi.org/10.3390/foods13233831
Gonzales-Barron U, Pouillot R, Skjerdal T, Carrasco E, Teixeira P, Stasiewicz MJ, Hasegawa A, De Oliveira Mota J, Guillier L, Cadavez V, et al. A Quantitative Risk Assessment Model for Listeria monocytogenes in Ready-to-Eat Smoked and Gravad Fish. Foods. 2024; 13(23):3831. https://doi.org/10.3390/foods13233831
Chicago/Turabian StyleGonzales-Barron, Ursula, Régis Pouillot, Taran Skjerdal, Elena Carrasco, Paula Teixeira, Matthew J. Stasiewicz, Akio Hasegawa, Juliana De Oliveira Mota, Laurent Guillier, Vasco Cadavez, and et al. 2024. "A Quantitative Risk Assessment Model for Listeria monocytogenes in Ready-to-Eat Smoked and Gravad Fish" Foods 13, no. 23: 3831. https://doi.org/10.3390/foods13233831
APA StyleGonzales-Barron, U., Pouillot, R., Skjerdal, T., Carrasco, E., Teixeira, P., Stasiewicz, M. J., Hasegawa, A., De Oliveira Mota, J., Guillier, L., Cadavez, V., & Sanaa, M. (2024). A Quantitative Risk Assessment Model for Listeria monocytogenes in Ready-to-Eat Smoked and Gravad Fish. Foods, 13(23), 3831. https://doi.org/10.3390/foods13233831








