Development of a Theoretical Model for the Price Formation of Agri-Food Products in the Food Supply Chain: A Slovenian Case Study
Abstract
:1. Introduction
1.1. Literature Review
1.2. Hypothesis of the Study
- (a)
- We assume that the economic models developed will successfully identify the dispersion of the different types of costs that affect the pricing of food.
- (b)
- We assume that the results of the elasticity of food price development in relation to cost changes in the food chains will follow meaningful and current trends in cost development in agricultural production and the processing industry.
- (c)
- We assume that with the results obtained at the micro and macro levels, we will be able to contribute to the innovation to understand the sensitivity of each sector in the food chains and that these results will be useful for the timely development of new support measures in the agricultural sector.
2. Materials and Methods
2.1. Selection of the Appropriate Type of the Model
2.2. Specification of the PRICE/PRICE Econometric Sub-Model—Basic Model
2.3. Specification of the Econometric Model CONSUMPTION/PRICE—Test Model
- -
- Consumer price index for cereals and cereal products; meat; milk, cheese and eggs;
- -
- Inflation index;
- -
- Average monthly gross wages in Slovenia;
- -
- Employed population in Slovenia.
- The annual domestic consumption data for cereals, meat and milk were used as the basis for all 12 months (same data for all 12 months);
- The weighting value for each individual month was calculated by adding the monthly index changes (in %) of all 4 included factors;
- We multiplied the two data from points 1 and 2 and subtracted the product from the data from point 1;
- The final difference from point 3 was divided by the product of point 3;
- We added the resulting quotient with the value −1 and obtained the difference, which represents the monthly change in consumption;
- We multiplied the difference from point 5 by the data from point 1 and obtained the monthly consumption data.
2.4. Summary of the Theoretical Explanation of the Combination of Two Models (Basic and Test Models)
2.5. Testing Model Approaches
- -
- VIF = 1: No multicollinearity (the variable is not correlated with other independent variables).
- -
- 1 < VIF ≤ 5: Moderate multicollinearity, generally acceptable.
- -
- VIF > 5: High multicollinearity, may need to be investigated.
- -
- VIF > 10: Very high multicollinearity, problematic and the variable may need to be removed or treated (e.g., by regularisation or dimensionality reduction).
3. Results
3.1. Theoretical Model of Price Formation—Cereal Sector
3.1.1. Econometric Sub-Models for the Primary Sector (Combination of the PRICE/PRICE and CONSUMPTION/PRICE Models)
3.1.2. Econometric Sub-Models for the Secondary Sector (Combination of the PRICE/PRICE and CONSUMPTION/PRICE Models)
3.1.3. Econometric Sub-Models for the Tertiary Sector (Combination of the PRICE/PRICE and CONSUMPTION/PRICE Models)
3.2. Theoretical Model of Price Formation—Meat Sector
3.2.1. Econometric Sub-Models for the Primary Sector (Combination of the PRICE/PRICE and CONSUMPTION/PRICE Models)
3.2.2. Econometric Sub-Models for the Secondary Sector (Combination of the PRICE/PRICE and CONSUMPTION/PRICE Models)
3.2.3. Econometric Sub-Models for the Tertiary Sector (Combination of the PRICE/PRICE and CONSUMPTION/PRICE Models)
3.3. Theoretical Model of Price Formation—Dairy Sector
3.3.1. Econometric Sub-Models for the Primary Sector (Combination of the PRICE/PRICE and CONSUMPTION/PRICE Models)
3.3.2. Econometric Sub-Models for the Secondary Sector (Combination of the PRICE/PRICE and CONSUMPTION/PRICE Models)
3.3.3. Econometric Sub-Models for the Tertiary Sector (Combination of the PRICE/PRICE and CONSUMPTION/PRICE Models)
4. Discussion
- (1)
- Updating databases that would help to understand the distribution of costs in the cereal and dairy chain (mainly in the processing industry phase).
- (2)
- Creation of centralised databases for the collection of non-confidential data that would contribute to a comprehensive understanding of the functioning of agri-food systems. Information on prices, costs and profit margins throughout the value chain can help to better and more quickly identify market failures. Information on the determinants of prices, costs and margins can help develop policies to address market failures and increase competitiveness.
- (3)
- Regular monitoring of prices at the level of the individual agricultural and food sectors. The shorter the information delay and the more detailed the information, the faster governments receive a signal about disruptions that negatively affect the efficient market balance in a specific market. Furthermore, policy makers can intervene in inefficient markets by providing value chain actors with market information that is otherwise difficult to obtain.
- (4)
- After further analyses, the results obtained could lead to the development of mitigation measures in case of major changes at the level of individual agricultural and food sectors.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


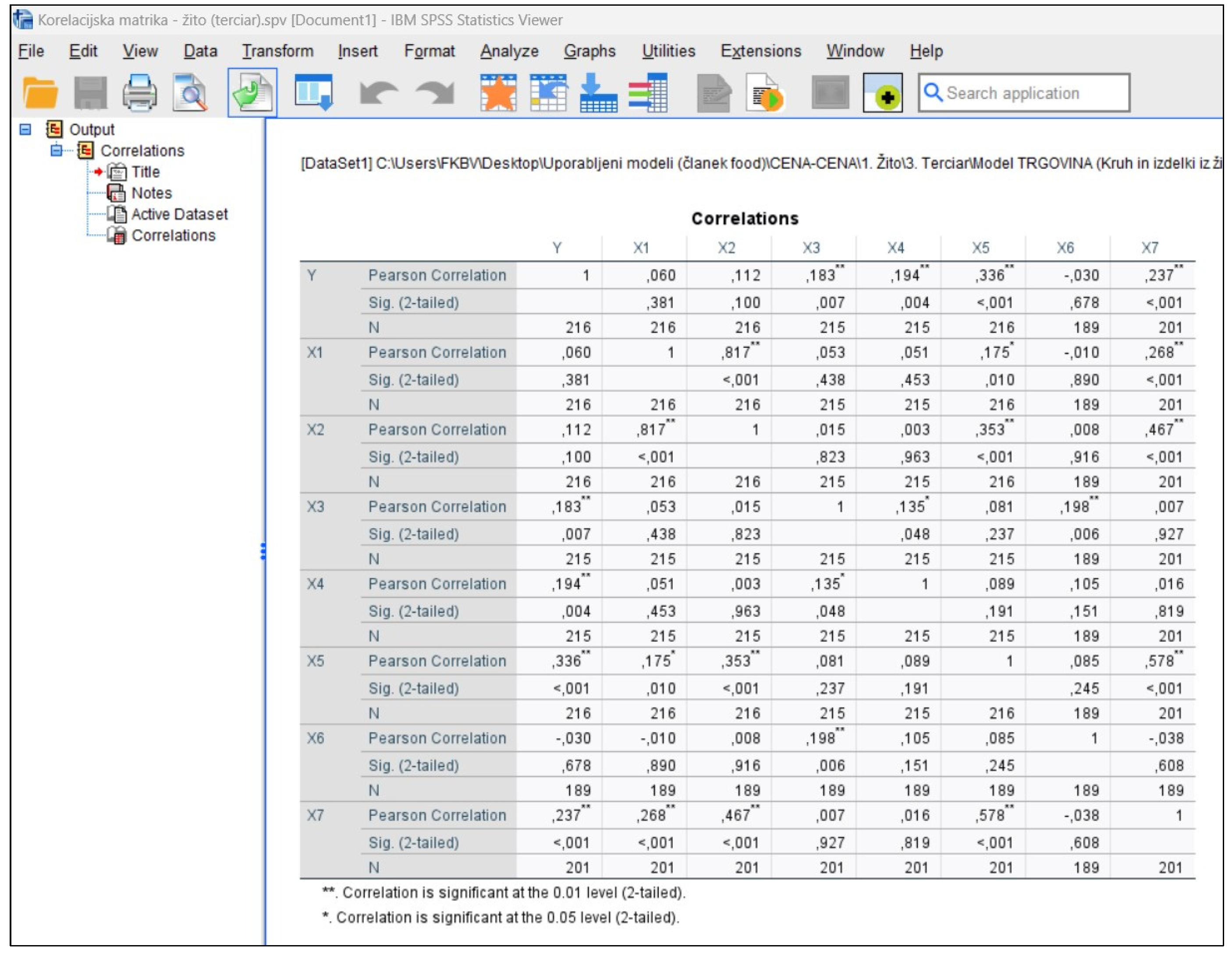
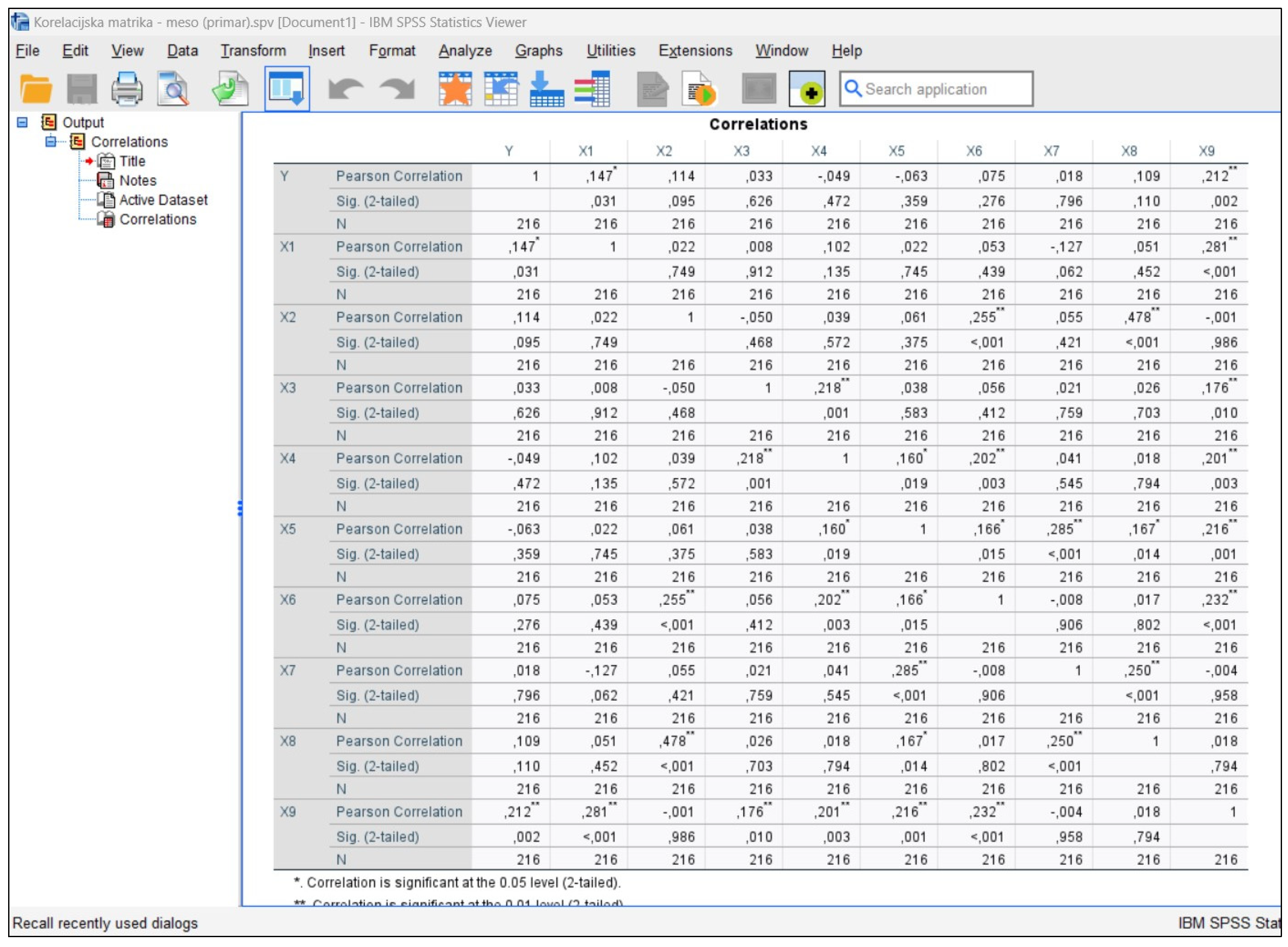

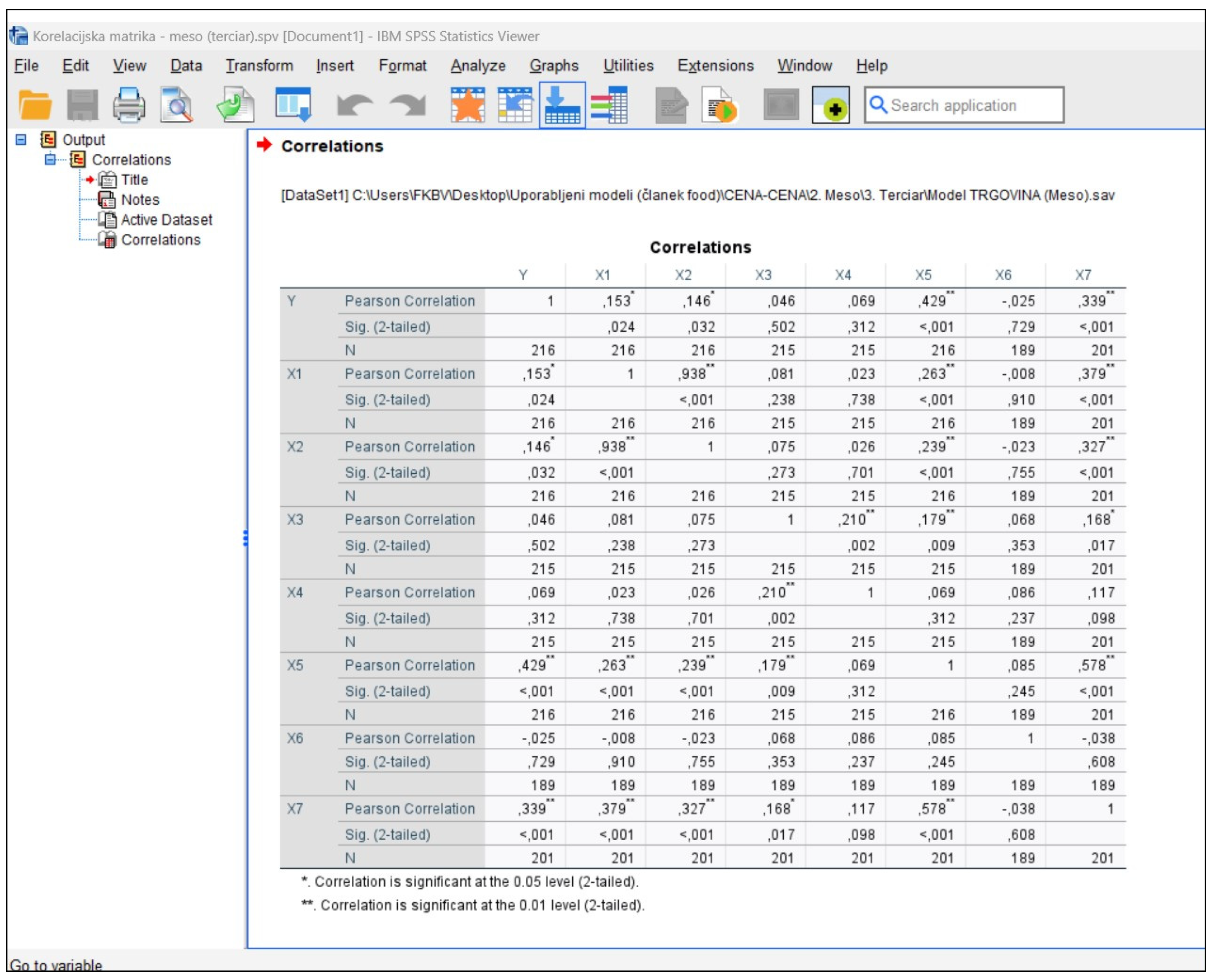
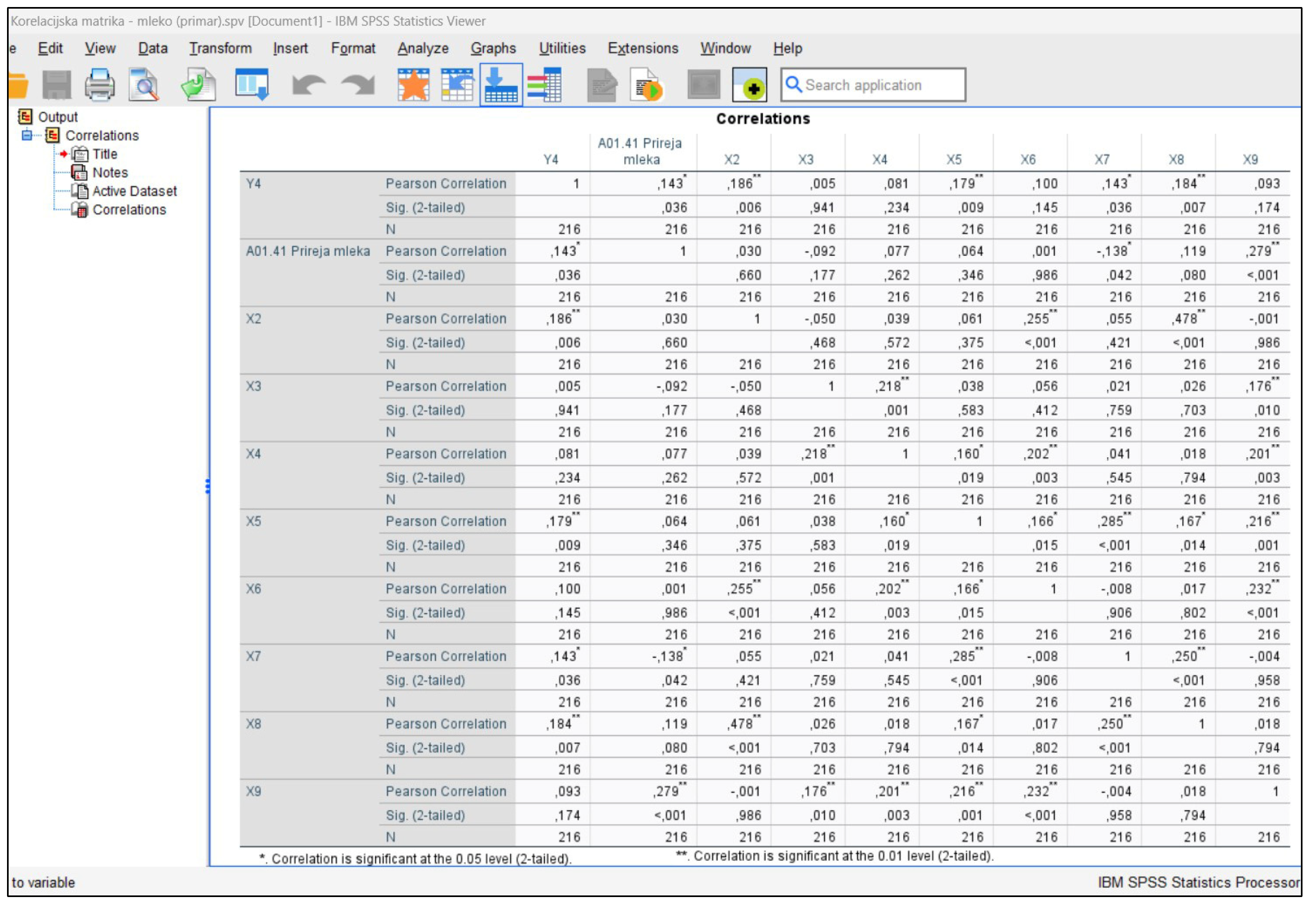


References
- Carbone, A. Food supply chains: Coordination governance and other shaping forces. Agric. Food Econ. 2017, 5, 3. [Google Scholar] [CrossRef]
- Djekic, I.; Batlle-Bayer, L.; Bala, A.; Fullana-i-Palmer, P.; Jambrak, A.R. Role of the food supply chain stakeholders in achieving UN SDGs. Sustainability 2021, 13, 9095. [Google Scholar] [CrossRef]
- Fagioli, F.F.; Rocchi, L.; Paolotti, L.; Słowiński, R.; Boggia, A. From the farm to the agri-food system: A multiple criteria framework to evaluate extended multi-functional value. Ecol. Indic. 2017, 79, 91–102. [Google Scholar] [CrossRef]
- Krysanov, D.; Varchenko, O. Agro-food chains: Key issues of creation and development. Econ. Forecast. 2017, i, 72–91. [Google Scholar]
- Zakic, N.; Bozilovic, S.; Sijakovic, I. Analysis and upgrading of value chain. Ekon. J. Econ. Theory Pract. Soc. Issues 2018, 64, 1–15. [Google Scholar] [CrossRef]
- Cucagna, M. Value Creation in the Agri-Food Value Chain. Doctoral Dissertation, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2014. Available online: https://hdl.handle.net/2142/50474 (accessed on 15 November 2024).
- Firlej, K.; Stanuch, M. Food chain price differences–theoretical and methodological aspects. Roczniki 2022, 2022, 54–66. [Google Scholar] [CrossRef]
- Santeramo, F.G.; Jelliffe, J.; Hoekman, B. Agri-food value chains and the global food dollar: The role of trade and services. Food Policy 2024, 127, 102706. [Google Scholar] [CrossRef]
- Dahal, B.; Kimmerer, C.; Hailu, G. Value added to agricultural commodities. In Future Food Systems; Academic Press: Cambridge, MA, USA, 2024; pp. 89–107. [Google Scholar] [CrossRef]
- Olayemi, W.A.; Olatidoye, O.P. Understanding the Agribusiness Model and Agricultural Value Chain (Africa). In Agripreneurship and the Dynamic Agribusiness Value Chain; Springer Nature Singapore: Singapore, 2024; pp. 257–272. [Google Scholar] [CrossRef]
- Gizaw, D.; Myrland, Ø.; Xie, J. Asymmetric price transmission in a changing food supply chain. Aquac. Econ. Manag. 2021, 25, 89–105. [Google Scholar] [CrossRef]
- Čechura, L.; Jaghdani, T.J. Market imperfections within the European wheat value chain: The case of France and the United Kingdom. Agriculture 2021, 11, 838. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, S. Research on Price Formation Based on Resource Optimization Allocation. Sustainability 2024, 16, 5129. [Google Scholar] [CrossRef]
- Crespi, J.M.; MacDonald, J.M. Concentration in food and agricultural markets. In Handbook of Agricultural Economics; Elsevier: Amsterdam, The Netherlands, 2022; Volume 6, pp. 4781–4843. [Google Scholar] [CrossRef]
- Hernández, M.A.; Espinoza, A.; Berrospi, M.L.; Deconinck, K.; Swinnen, J.; Vos, R. The Role of Market Concentration in the Agrifood Industry; International Food Policy Research Institute: Washington, DC, USA, 2023; Volume 2168. [Google Scholar]
- de Vries, J.R.; Turner, J.A.; Finlay-Smits, S.; Ryan, A.; Klerkx, L. Trust in agri-food value chains: A systematic review. Int. Food Agribus. Manag. Rev. 2023, 26, 175–197. [Google Scholar] [CrossRef]
- Sexton, R.J. Market power, misconceptions, and modern agricultural markets. Am. J. Agric. Econ. 2013, 95, 209–219. [Google Scholar] [CrossRef]
- Assefa, T.T.; Meuwissen, M.P.; Oude Lansink, A.G. Price volatility transmission in food supply chains: A literature review. Agribusiness 2015, 31, 3–13. [Google Scholar] [CrossRef]
- Isakson, S.R. Food and finance: The financial transformation of agro-food supply chains. In New Directions in Agrarian Political Economy; Routledge: London, UK, 2017; pp. 109–136. [Google Scholar]
- LloYd, T. Forty years of price transmission research in the food industry: Insights, challenges and prospects. J. Agric. Econ. 2017, 68, 3–21. [Google Scholar] [CrossRef]
- Karikallio, H.; Arovuori, K.; Pyykkonen, P. Vertical price formation in the Finnish food chain. In Proceedings of the European Association of Agricultural Economists (EAAE), Chania, Greece, 3–6 September 2009. [Google Scholar] [CrossRef]
- Diab, S.; Karaki, M.B. Do increases in gasoline prices cause higher food prices? Energy Econ. 2023, 127, 107066. [Google Scholar] [CrossRef]
- Lundberg, C.; Skolrud, T.; Adrangi, B.; Chatrath, A. Oil price pass through to agricultural commodities. Am. J. Agric. Econ. 2021, 103, 721–742. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, S.; Lopez, C.; Chen, H.; Lu, H.; Mangla, S.K.; Elgueta, S. Risk analysis of the agri-food supply chain: A multi-method approach. Int. J. Prod. Res. 2020, 58, 4851–4876. [Google Scholar] [CrossRef]
- Awokuse, T.; Lim, S.; Santeramo, F.; Steinbach, S. Robust policy frameworks for strengthening the resilience and sustainability of agri-food global value chains. Food Policy 2024, 127, 102714. [Google Scholar] [CrossRef]
- Bunte, F.; Bolhuis, J.; de Bont, C.; Jukema, G.; Kuiper, E. Pricing of food products. Memorandum 2009, 9, 74. Available online: https://www.acm.nl/sites/default/files/old_download/documenten/nma/LEI_Pricing_of_Food_products.pdf (accessed on 20 November 2024).
- Oosterkamp, E.B.; Logatcheva, K.; van Galen, M.A.; Georgiev, E.S. Food Price Monitoring and Observatories: An Exploration of Costs and Effects; Summary and Executive Summary. LEI. 2012. Available online: https://www.researchgate.net/publication/283312093_Food_price_monitoring_and_observatories_an_exploration_of_costs_and_effects_Summary_and_Executive_Summary (accessed on 20 November 2024).
- Masten, I.; Feldin, A.; Kuhar, A.; Polanec, S.; Rednak, M.; Volk, T. Analysis of the Design and Price Monitoring Model Along the Food Supply Chain: Final Report on the Results of the Research Work Carried Out on the Project Within the Framework of the Targeted Research Program (CRP) “Let’s Secure Food for Tomorrow”; V5–1119; University of Ljubljana, Faculty of Economics: Ljubljana, Slovenia, 2014. [Google Scholar]
- Canning, P. A Revised and Expanded food Dollar Series: A Better Understanding of our Food Costs; Economic Research Report; United States Department of Agriculture: Washington, DC, USA, 2011; Volume 114. [Google Scholar] [CrossRef]
- Pavić, L.; Turk, J.; Grgić, I.; Prišenk, J. Impact Analysis of the Young Farmers’ Support Program on Slovenian Dairy Sector Development Using Econometric Modeling Approach. Agronomy 2020, 10, 429. [Google Scholar] [CrossRef]
- Prišenk, J.; Turk, J. Assessment of Concept between Rural Development Challenges and Local Food Systems: A Combination between Multi-Criteria Decision Analysis and Econometric Modelling Approach. Sustainability 2022, 14, 3477. [Google Scholar] [CrossRef]
- Prišenk, J.; Turk, J.; Pažek, K.; Rozman, Č.; Borec, A.; Zidar, N. An Assessment of Food Value Chains to Identify Gaps and Make Recommendations for Further Development: A Slovenian Case Study. Agriculture 2024, 14, 502. [Google Scholar] [CrossRef]
- Akkaya, M. Vector Autoregressive Model and Analysis. In Handbook of Research on Emerging Theories, Models, and Applications of Financial Econometrics; Springer: Cham, Switzerland, 2021; pp. 197–214. [Google Scholar]
- Gujarati, D.N.; Porter, D.C. Basic Econometrics, 5th ed.; McGraw-Hill Education: Boston, MA, USA, 2008; 944p. [Google Scholar]
- Cucagna, M.E.; Goldsmith, P.D. Value adding in the agri-food value chain. Int. Food Agribus. Manag. Rev. 2018, 21, 293–316. [Google Scholar] [CrossRef]
- Bertazzoli, A.; Ghelfi, R.; Rivaroli, S.; Samoggia, A. Value sharing and food system dynamics for milk, tomato, and cereals food chains. Int. J. Food Syst. Dyn. 2010, 1, 330–341. [Google Scholar] [CrossRef]
- EconPort—Factors Affecting Supply. Available online: http://www.econport.org/content/handbook/supply/changeSupply.html (accessed on 6 December 2024).
- Hobbs, J.E. Food supply chains during the COVID-19 pandemic. Can. J. Agric. Econ./Rev. Can. D’agroeconomie 2020, 68, 171–176. [Google Scholar] [CrossRef]
- Aday, S.; Aday, M.S. Impact of COVID-19 on the food supply chain. Food Qual. Saf. 2020, 4, 167–180. [Google Scholar] [CrossRef]
- Keating, B.A.; Herrero, M.; Carberry, P.S.; Gardner, J.; Cole, M.B. Food wedges: Framing the global food demand and supply challenge towards 2050. Glob. Food Secur. 2014, 3, 125–132. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Gupta, A.S. What role did rising demand play in driving food prices up? South Asian J. Macroecon. Public Financ. 2017, 6, 59–81. [Google Scholar] [CrossRef]
- Kumari, A. Identifying Factors Affecting Food Inflation in India: A Review of Literature. Pac. Bus. Rev. Int. 2023, 15, 38–49. [Google Scholar]
- Mudrak, R.; Nyzhnyk, I.; Lagodiienko, V.; Lagodiienko, N. Impact of seasonal production on the dynamics of prices for meat and dairy products in Ukraine. TEM J. 2019, 8, 1159. [Google Scholar] [CrossRef]
- Samal, A.; Ummalla, M.; Goyari, P. The impact of macroeconomic factors on food price inflation: An evidence from India. Future Bus. J. 2022, 8, 15. [Google Scholar] [CrossRef]
- Lagi, M.; Bar-Yam, Y.; Bertrand, K.Z.; Bar-Yam, Y. Accurate market price formation model with both supply-demand and trend-following for global food prices providing policy recommendations. Proc. Natl. Acad. Sci. USA 2015, 112, E6119–E6128. [Google Scholar] [CrossRef] [PubMed]
- Kartal, M.T.; Depren, Ö. Asymmetric relationship between global and national factors and domestic food prices: Evidence from Turkey with novel nonlinear approaches. Financ. Innov. 2023, 9, 11. [Google Scholar] [CrossRef]
- Ulussever, T.; Ertuğrul, H.M.; Kılıç Depren, S.; Kartal, M.T.; Depren, Ö. Estimation of impacts of global factors on world food prices: A comparison of machine learning algorithms and time series econometric models. Foods 2023, 12, 873. [Google Scholar] [CrossRef]
- Adeleke, M.A.; Awodumi, O.B. Modelling time and frequency connectedness among energy, agricultural raw materials and food markets. J. Appl. Econ. 2022, 25, 644–662. [Google Scholar] [CrossRef]
- Derindag, O.F.; Chang, B.H.; Gohar, R.; Wong, W.K.; Bhutto, N.A. Food prices response to global and national factors: Evidence beyond asymmetry. Cogent Econ. Financ. 2023, 11, 2187128. [Google Scholar] [CrossRef]
- Ben Hassen, T.; El Bilali, H. Impacts of the Russia-Ukraine war on global food security: Towards more sustainable and resilient food systems? Foods 2022, 11, 2301. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Nasreen, S.; Shahbaz, M.; Hammoudeh, S. Time-frequency causality and connectedness between international prices of energy, food, industry, agriculture and metals. Energy Econ. 2020, 85, 104529. [Google Scholar] [CrossRef]
- Milford, A.B.; Le Mouël, C.; Bodirsky, B.L.; Rolinski, S. Drivers of meat consumption. Appetite 2019, 141, 104313. [Google Scholar] [CrossRef]
- Rehman, F.U.; Khan, D. The determinants of food price inflation in Pakistan: An econometric analysis. Adv. Econ. Bus. 2015, 3, 571–576. [Google Scholar] [CrossRef]
- Gohar, R.; Bagadeem, S.; Chang, B.H.; Zong, M. Do the income and price changes affect consumption in the emerging 7 countries? Empirical evidence using quantile ARDL model. Ann. Financ. Econ. 2022, 17, 2250024. [Google Scholar] [CrossRef]
- Cedrez, C.B.; Chamberlin, J.; Hijmans, R.J. Seasonal, annual, and spatial variation in cereal prices in Sub-Saharan Africa. Glob. Food Secur. 2020, 26, 100438. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, C.L.; Christiaensen, L.; Kaminski, J. Food price seasonality in Africa: Measurement and extent. Food Policy 2017, 67, 119–132. [Google Scholar] [CrossRef] [PubMed]
- Gričar, S.; Bojnec, Š.; Turk, J.; Rozman, Č. Application of Time Series Methodology to the Example of Tourist Prices; University of Primorska Press: Koper, Slovenia, 2016. [Google Scholar]
- Kramer, L. Investopedia. How Does the Law of Supply and Demand Affect Prices? Available online: https://www.investopedia.com/ask/answers/033115/how-does-law-supply-and-demand-affect-prices.asp (accessed on 6 December 2024).
- Fernando, J. Investopedia. Law of Supply and Demand in Economics: How It Works. Available online: https://www.investopedia.com/terms/l/law-of-supply-demand.asp (accessed on 6 December 2024).
- Dean, E.; Elardo, J.; Green, M.; Wilson, B.; Berger, S. Demand, Supply, and Equilibrium in Markets for Goods and Services. In Principles of Economics: Scarcity and Social Provisioning, 2nd ed.; Rice University: Houston, TX, USA, 2020; Available online: https://openoregon.pressbooks.pub/socialprovisioning2/chapter/4-1-demand-supply-and-equilibrium-in-markets-for-goods-and-services/ (accessed on 3 December 2024).
- Changes in Supply: Increase and Decrease of Supply. Available online: https://www.toppr.com/guides/business-economics/determination-of-prices/changes-in-supply/ (accessed on 6 December 2024).
- Vafaei, N.; Ribeiro, R.A.; Camarinha-Matos, L.M. Data normalisation techniques in decision making: Case study with TOPSIS method. Int. J. Inf. Decis. Sci. 2018, 10, 19–38. [Google Scholar] [CrossRef]
- Lees, N.; Nuthall, P.; Wilson, M.M.J. Relationship quality and supplier performance in food supply chains. Int. Food Agribus. Manag. Rev. 2020, 23, 425–445. [Google Scholar] [CrossRef]
- Bellemare, M.F. The Use and Misuse of R-Squared. 2015. Available online: https://marcfbellemare.com/wordpress/10793 (accessed on 7 January 2025).
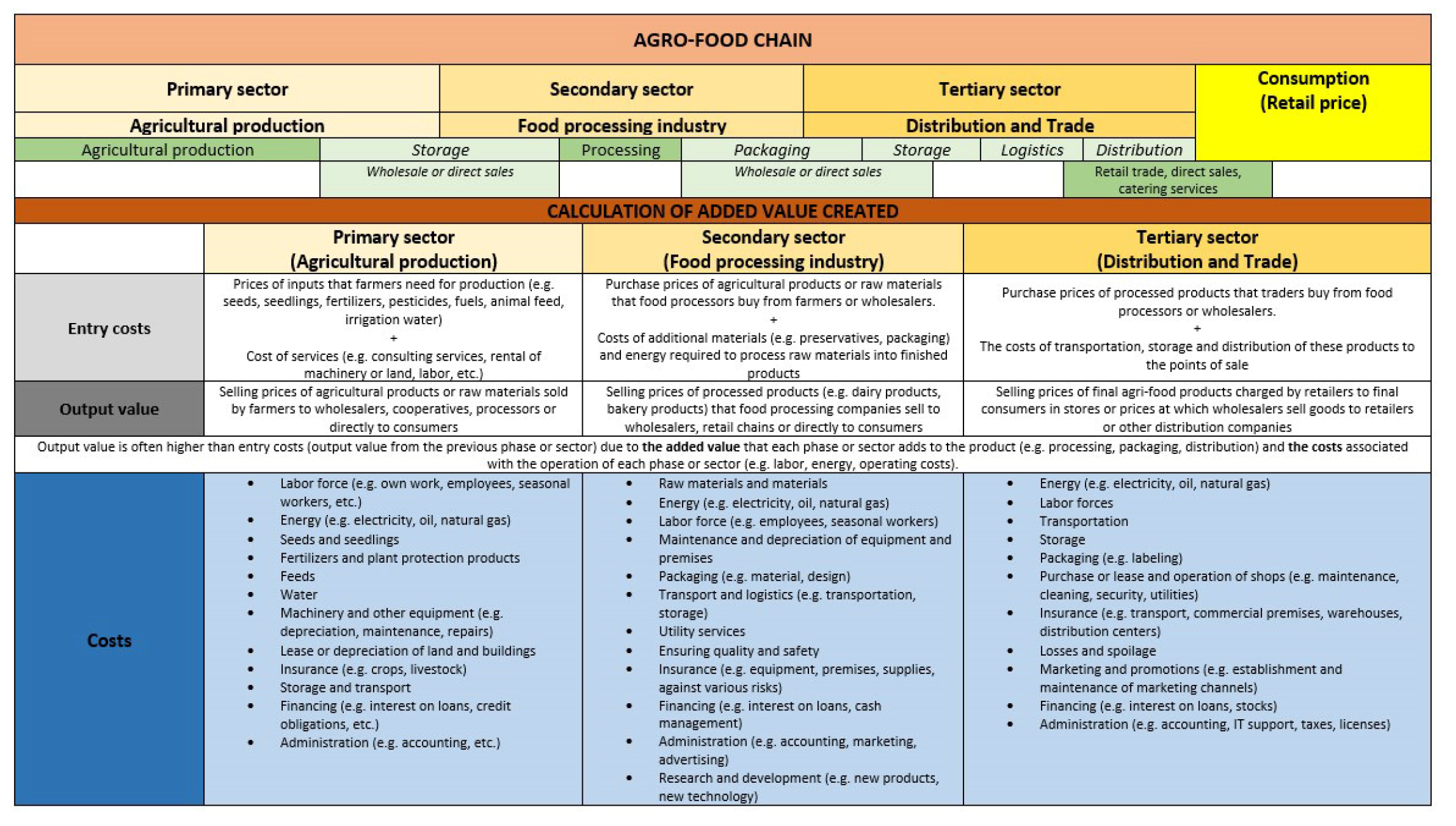
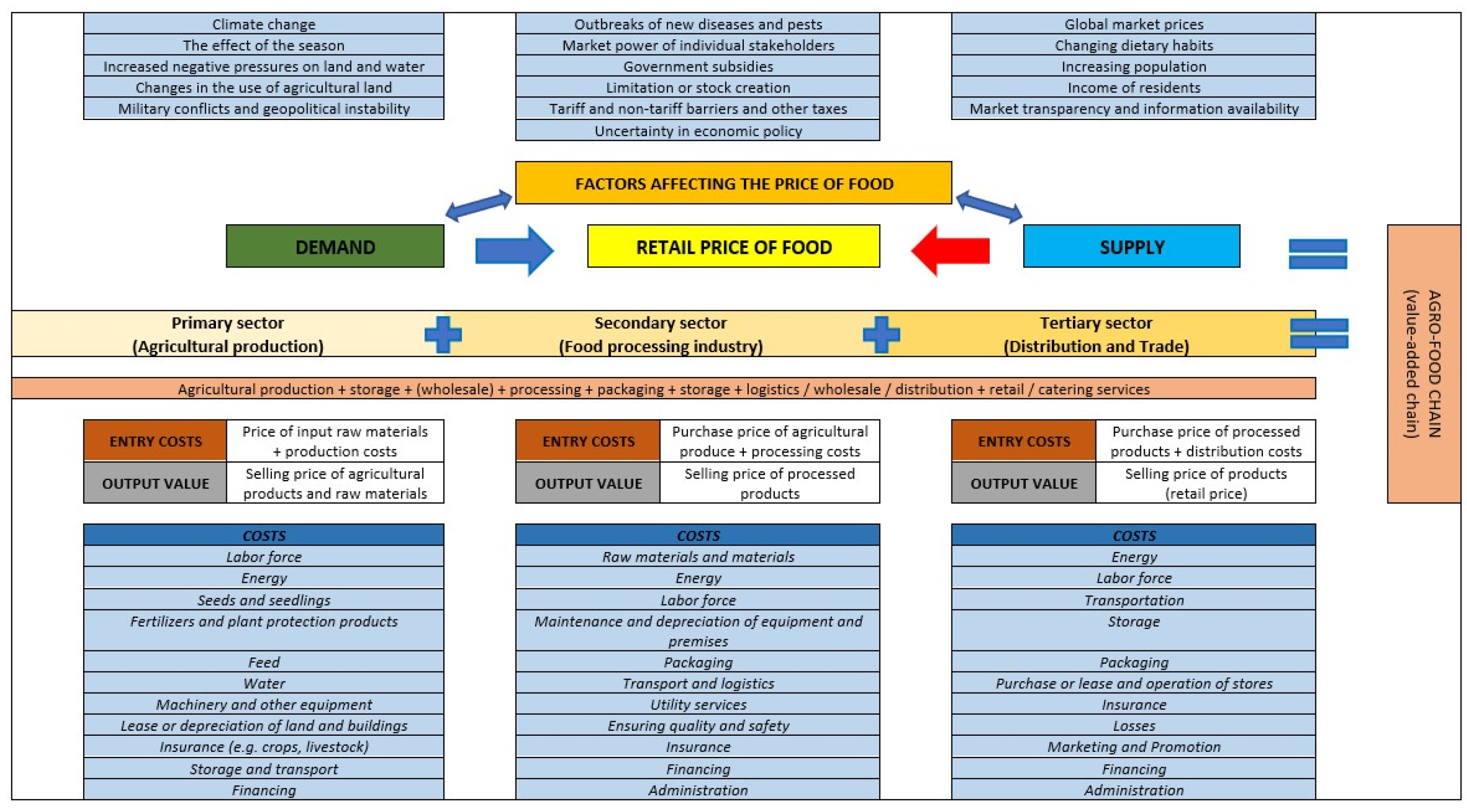
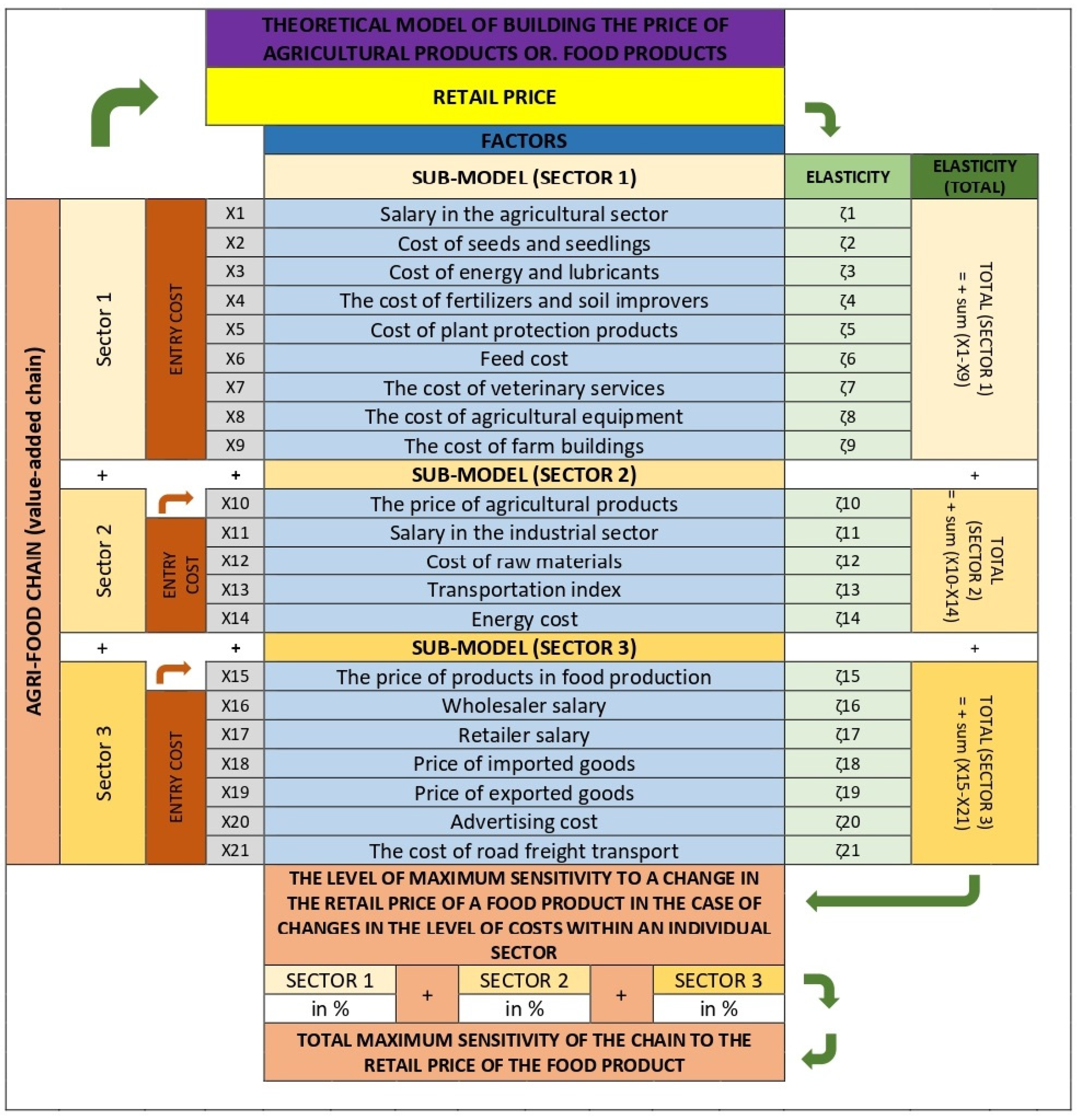
| Scenario | VAR Models | Standard Econometric Models |
|---|---|---|
| Purpose | To model and analyse dynamic, interdependent relationships among multiple variables. | To estimate causal relationships or quantify the effect of independent variables on a dependent variable. |
| Dynamic Systems | Use when variables are interdependent and influence each other over time. | Use when the goal is to estimate the effect of specific variables on an outcome. |
| Forecasting | Well suited for multivariate time series forecasting. | Use simpler time series models for univariate forecasting. |
| Causal Analysis | Not ideal for causal inference. | Best for testing hypotheses about causal relationships. |
| Focus | Dynamic interrelationships and feedback effects. | Elasticity and proportional relationships. |
| Outputs | Coefficients, impulse response functions (IRFs), forecast error variance decomposition. | Elasticities of the dependent variable with respect to independent variables. |
| Examples | Economic indicators (GDP, inflation, interest rates). | Demand analysis, cost functions, production functions. |
| Results of Adf Test—Example of Cereal Sector | ||||
|---|---|---|---|---|
| ADF Statistic | p-Value | Number of Observations Used | Critical Values | |
| Primary Sector | ||||
| Y | −4.635 | 0.000 | 210 | 1%: −3.461878735881654 5%: −2.875403665910809 10%: −2.574159410430839 |
| X1 | −0.476 | 0.897 | 201 | 1%: −3.4633090972761744 5%: −2.876029332045744 10%: −2.5744932593252643 |
| X2 | −5.556 | 0.000 | 212 | 1%: −3.4615775784078466 5%: −2.875271898983725 10%: −2.5740891037735847 |
| X3 | −6.704 | 0.000 | 211 | 1%: −3.46172743446274 5%: −2.8753374677799957 10%: −2.574124089081557 |
| X4 | −9.894 | 0.000 | 215 | 1%: −3.461136478222043 5%: −2.875078880098608 10%: −2.5739861168199027 |
| X5 | −13.930 | 0.000 | 215 | 1%: −3.461136478222043 5%: −2.875078880098608 10%: −2.5739861168199027 |
| X6 | −4.042 | 0.001 | 211 | 1%: −3.46172743446274 5%: −2.8753374677799957 10%: −2.574124089081557 |
| X7 | −15.063 | 0.000 | 215 | 1%: −3.461136478222043 5%: −2.875078880098608 10%: −2.5739861168199027 |
| X8 | −3.109 | 0.026 | 202 | 1%: −3.4631437906252636 5%: −2.8759570379821047 10%: −2.574454682874228 |
| Secondary sector | ||||
| Y | −3.088 | 0.027 | 152 | 1%: −3.474120870218417 5%: −2.880749791423677 10%: −2.5770126333102494 |
| X1 | −10.527 | 0.000 | 147 | 1%: −3.4756368462466662 5%: −2.8814104466172608 10%: −2.5773652982553568 |
| X2 | −0.705 | 0.846 | 143 | 1%: −3.4769274060112707 5%: −2.8819726324025625 10%: −2.577665408088415 |
| X3 | −4.111 | 0.001 | 155 | 1%: −3.4732590518613002 5%: −2.880374082105334 10%: −2.5768120811654525 |
| X4 | −2.578 | 0.098 | 143 | 1%: −3.4769274060112707 5%: −2.8819726324025625 10%: −2.577665408088415 |
| X5 | −11.574 | 0.000 | 154 | 1%: −3.473542528196209 5%: −2.880497674144038 10%: −2.576878053634677 |
| Tertiary sector | ||||
| Y | −6.294 | 3.533 ×10−8 | 185 | 1%: −3.4662005731940853 5%: −2.8772932777920364 10%: −2.575167750182615 |
| X1 | −1.182 | 0.681 | 175 | 1%: −3.4682803641749267 5%: −2.8782017240816327 10%: −2.5756525795918366 |
| X2 | 0.610 | 0.988 | 176 | 1%: −3.4680615871598537 5%: −2.8781061899535128 10%: −2.5756015922004134 |
| X3 | −4.030 | 0.001 | 176 | 1%: −3.4680615871598537 5%: −2.8781061899535128 10%: −2.5756015922004134 |
| X4 | −6.051 | 1.275 × 10−7 | 176 | 1%: −3.4680615871598537 5%: −2.8781061899535128 10%: −2.5756015922004134 |
| X5 | −4.378 | 0.000 | 187 | 1%: −3.465811691080702 5%: −2.877123351472649 10%: −2.5750770662586864 |
| X6 | −2.793 | 0.059 | 179 | 1%: −3.4674201432469816 5%: −2.877826051844538 10%: −2.575452082332012 |
| X7 | −1.292 | 0.633 | 173 | 1%: −3.4687256239864017 5%: −2.8783961376954363 10%: −2.57575634100705 |
| Sector/Type of the Model | PRICE/PRICE | CONSUMPTION/PRICE |
|---|---|---|
| Cereal primary sector | LIN—2.34 | LOG—1.97 |
| Cereal secondary sector | LIN—2.17 | LIN-LOG—2.08 |
| Cereal tertiary sector | LIN—2.27 | LOG—1.99 |
| Meat primary sector | LOG-LIN—1.84 | LOG-LIN—2.10 |
| Meat secondary sector | LIN—1.79 | LOG—2.27 |
| Meat tertiary sector | LIN—2.10 | LOG—2.15 |
| Dairy primary sector | LOG-LIN—1.90 | LIN-LOG—2.04 |
| Dairy secondary sector | LIN—1.89 | LIN-LOG—2.04 |
| Dairy tertiary sector | LOG-LIN—2.25 | LOG—1.98 |
| PRICE/PRICE MODELS | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Independent Variable | Cereal Primary Sector | Cereal Secondary Sector | Cereal Tertiary Sector | Meat Primary Sector | Meat Secondary Sector | Meat Tertiary Sector | Dairy Primary Sector | Dairy Secondary Sector | Dairy Tertiary Sector |
| X1 | 1.074 | 1.048 | 2.531 | 1.121 | 1.237 | 7.537 | 1.179 | 1.255 | 4.729 |
| X2 | 1.431 | 2.786 | 3.110 | 1.437 | 2.413 | 7.195 | 1.438 | 2.391 | 5.186 |
| X3 | 1.095 | 1.165 | 1.077 | 1.082 | 1.388 | 1.109 | 1.108 | 1.240 | 1.070 |
| X4 | 1.128 | 2.803 | 1.050 | 1.129 | 2.498 | 1.094 | 1.129 | 2.753 | 1.114 |
| X5 | 1.114 | 1.093 | 1.674 | 1.193 | 1.045 | 1.614 | 1.194 | 1.048 | 1.650 |
| X6 | 1.221 | 1.064 | 1.203 | 1.033 | 1.209 | 1.032 | |||
| X7 | 1.366 | 1.954 | 1.177 | 1.824 | 1.196 | 1.820 | |||
| X8 | 1.205 | 1.442 | 1.470 | ||||||
| X9 | 1.238 | 1.253 | |||||||
| CONSUMPTION/PRICE MODELS | |||||||||
| Independent Variable | Cereal Primary Sector | Cereal Secondary Sector | Cereal Tertiary Sector | Meat Primary Sector | Meat Secondary Sector | Meat Tertiary Sector | Dairy Primary Sector | Dairy Secondary Sector | Dairy Tertiary Sector |
| X1 | 1.049 | 1.034 | 2.590 | 1.152 | 1.299 | 6.594 | 1.216 | 1.068 | 3.905 |
| X2 | 1.428 | 2.479 | 3,110 | 1.439 | 2.174 | 6.233 | 1.395 | 1.549 | 3.928 |
| X3 | 1.109 | 1.157 | 1.058 | 1.084 | 1.409 | 1.139 | 1.127 | 1.113 | 1.107 |
| X4 | 1.134 | 2.468 | 1.048 | 1.285 | 2.322 | 1.136 | 1.103 | 1.524 | 1.127 |
| X5 | 1.111 | 1.073 | 1.689 | 1.221 | 1.032 | 1.780 | 1.228 | 1.066 | 1.121 |
| X6 | 1.233 | 1.045 | 1.283 | 1.064 | 1.201 | 1.039 | |||
| X7 | 1.369 | 2.034 | 1.181 | 1.901 | 1.260 | 1.037 | |||
| X8 | 1.226 | 1.514 | 1.404 | ||||||
| X9 | 1.361 | 1.177 | |||||||
| Type of the Formulation | Equations |
|---|---|
| LIN | Yb = 77.433 + 0.00002172 * X1b + 0.198 * X2 − 0.008 * X3 − 0.002 * X4 − 0.163 * X5 + 0.139 * X6 − 0.129 * X7 + 0.193 * X8 |
| LOG-LIN | LNYb = 4.384 + 4.403 × 10−7 * X1b + 0.002 * X2 − 0.00008049 * X3 − 0.00001408 * X4 − 0.002 * X5 + 0.001 * X6 − 0.001 * X7 + 0.002 * X8 |
| LIN-LOG | Yb = −3.612 − 0.061 * lnX1b + 20.475 * lnX2 − 1.005 * lnX3 − 0.084 * lnX4 – 16.303 * lnX5 + 13.318 * lnX6 – 13.788 * lnX7 + 20.026 * lnX8 |
| LOG | LNYb = 3.588 + 0 * lnX1b + 0.194 * lnX2 − 0.01 * lnX3 + 0 * lnX4 − 0.161 * lnX5 + 0.127 * lnX6 − 0.126 * lnX7 + 0.198 * lnX8 |
| Elasticities in the PRICE/PRICE Model (Primary Sector) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | |
| LIN | 0.00 | 0.20 | −0.01 | 0.00 | −0.16 | 0.14 | −0.13 | 0.19 | / |
| Elasticities of the CONSUMPTION/PRICE Model (Primary Sector) | |||||||||
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | |
| LOG | 0.07 | 1.06 | 4.69 | −3.34 | 7.57 | −1.03 | 7.32 | −14.14 | / |
| Type of the Formulation | Equations |
|---|---|
| LIN | Yb = 74.66 − 0.01 * X1b + 0.0 * X2b + 0.261 * X3 + 0.176 * X4 − 0.004 * X5 |
| LOG-LIN | LNYb = 4.354 − 0.00009806 * X1b − 0.000004145 * X2b + 0.003 * X3 + 0.002 * X4 − 0.0000416 * X5 |
| LIN-LOG | Yb = − 15.191 − 1.088 * lnX1b − 0.265 * lnX2b + 26,267 * lnX3 + 1.298 * lnX4 − 0.291 * lnX5 |
| LOG | LNYb = 3.463 − 0.011 * lnX1b − 0.003 * lnX2b + 0.26 * lnX3 + 0.013 * lnX4 − 0.003 * lnX5 |
| Elasticities in the PRICE/PRICE Model (Secondary Sector) | |||||
|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | |
| LIN | −0.01 | 0.00 | 0.26 | 0.01 | 0.00 |
| Elasticities of the CONSUMPTION/PRICE Model (Secondary Sector) | |||||
| X1 | X2 | X3 | X4 | X5 | |
| LIN-LOG | 3.02 | −5.33 | 293.44 | −3.28 | −5.88 |
| Type of the Formulation | Equations |
|---|---|
| LIN | Yb = 48.445 + 0.0 * X1b + 0.00001864 * X2b + 0.008 * X3b + 0.007 * X4b + 0.509 * X5 − 0.073 * X6 + 0.069 * X7 |
| LOG-LIN | LNYb = 4.112 − 0.000002909 * X1b + 5,334E−07 * X2b + 0.00007896 * X3b + 0.00007673 * X4b + 0.005 * X5 − 0.001 * X6 + 0.001 * X7 |
| LIN-LOG | Yb = − 152.208 − 0.634 * lnX1b − 0.059 * lnX2b + 0.614 * lnX3b + 0.631 * lnX4b + 53,903 * lnX5 – 5.967 * lnX6 + 6.725 * lnX7 |
| LOG | LNYb = 2.182 − 0.006 * lnX1b + 0.0 * lnX2b + 0.006 * lnX3b + 0.007 * lnX4b + 0.51 * lnX5 − 0.058 * lnX6 + 0.072 * lnX7 |
| Elasticities in the PRICE/PRICE Model (Tertiary Sector) | |||||||
|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | |
| LIN | 0.00 | 0.00 | 0.01 | 0.01 | 0.51 | −0.07 | 0.07 |
| Elasticities of the CONSUMPTION/PRICE Model (Tertiary Sector) | |||||||
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | |
| LOG | 0.17 | 0.20 | 0.68 | 0.03 | −4,36 | −10.73 | −11.66 |
| Maximum Sensitivity for Price Changes in Agricultural Products in the Event of Cost Changes in a Single Sector (Calculated Weights—in %) | ||
|---|---|---|
| Primary Sector | Secondary Sector | Tertiary Sector |
| 51.2 | 2.2 | 46.6 |
| Type of the Formulation | Equations |
|---|---|
| LIN | Yc = 63.953 + 0.001 * X1c + 0.044 * X2 + 0.006 * X3 − 0.018 * X4 − 0.114 * X5 + 0.013 * X6 + 0.032 * X7 + 0.097 * X8 + 0.295 * X9 |
| LOG-LIN | LNYc = 4.252 + 0.000005029 * X1c + 0.0 * X2 + 0.00006107 * X3 + 0.0 * X4 − 0.001 * X5 − 0.0 * X6 + 0.0 * X7 + 0.001 * X8 + 0.003 * X9 |
| LIN-LOG | Yc = − 68.485 + 0.603 * lnX1c + 4,436 * lnX2 + 0.522 * lnX3 − 1.565 * lnX4 − 11.767 * lnX5 + 1.27 * lnX6 + 3.421 * lnX7 + 10.095 * lnX8 + 29,288 * lnX9 |
| LOG | LNYc = 2.955 + 0.006 * lnX1c + 0.045 * lnX2 + 0.005 * lnX3 − 0.016 * lnX4 − 0.116 * lnX5 + 0.012 * lnX6 + 0.034 * lnX7 + 0.098 * lnX8 + 0.287 * lnX9 |
| Elasticities in the PRICE/PRICE Model (Primary Sector) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | |
| LOG-LIN | 0.01 | 0.00 | 0.01 | 0.00 | −0.10 | 0.00 | 0.00 | 0.10 | 0.30 |
| Elasticities of the CONSUMPTION/PRICE Model (Primary Sector) | |||||||||
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | |
| LOG-LIN | 0.00 | 3.41 | −3.01 | 1.21 | −2.11 | 2.81 | 1.50 | 8.52 | −4.51 |
| Type of the Formulation | Equations |
|---|---|
| LIN | Yc = 62.017 − 0.062 * X1c − 0.001 * X2c + 0.439 * X3 + 0.181 * X4 + 0.002 * X5 |
| LOG-LIN | LNYc = 4.235 − 0.001 * X1c − 0.000008301 * X2c + 0.004 * X3 + 0.002 * X4 + 0.00001291 * X5 |
| LIN-LOG | Yc = − 69.344 – 6.371 * lnX1c − 0.951 * lnX2c + 43,756 * lnX3 + 1.485 * lnX4 + 0.249 * lnX5 |
| LOG | LNYc = 2.956 − 0.063 * lnX1c − 0.01 * lnX2c + 0.428 * lnX3 + 0.015 * lnX4 + 0.002 * lnX5 |
| Elasticities in the PRICE/PRICE Model (Secondary Sector) | |||||
|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | |
| LIN | −0.06 | −0.01 | 0.44 | 0.01 | 0.00 |
| Elasticities of the CONSUMPTION/PRICE Model (Secondary Sector) | |||||
| X1 | X2 | X3 | X4 | X5 | |
| LOG | 6.89 | 2.00 | −1.57 | −1.56 | 0.59 |
| Type of the Formulation | Equations |
|---|---|
| LIN | Yc = 38.508 − 0.001 * X1c + 0.001 * X2c − 0.01 * X3c + 0.009 * X4c + 0.568 * X5 − 0.037 * X6 + 0.093 * X7 |
| LOG-LIN | LNYc = 4.000 − 0.00001188 * X1c + 0.000008777 * X2c − 0.00009817 * X3c + 0.00008861 * X4c + 0.006 * X5 + 0.0 * X6 + 0.001 * X7 |
| LIN-LOG | Yc = − 184.493 − 1.432 * lnX1c + 0.806 * lnX2c − 1.072 * lnX3c + 0.884 * lnX4c + 57,242 * lnX5 – 3.566 * lnX6 + 9.348 * lnX7 |
| LOG | LNYc = 1.804 − 0.014 * lnX1c + 0.008 * lnX2c − 0.011 * lnX3c + 0.008 * lnX4c + 0.566 * lnX5 − 0.036 * lnX6 + 0.09 * lnX7 |
| Elasticities in the PRICE/PRICE Model (Tertiary Sector) | |||||||
|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | |
| LIN | −0.01 | 0.01 | −0.01 | 0.01 | 0.57 | −0.04 | 0.09 |
| Elasticities of the CONSUMPTION/PRICE Model (Tertiary Sector) | |||||||
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | |
| LOG | 0.16 | 1.10 | −2.74 | −0.65 | 6.11 | −5.67 | −13.22 |
| Maximum Sensitivity for Price Changes in Agricultural Products in the Event of Cost Changes in a Single Sector (Calculated Weights—in %) | ||
|---|---|---|
| Primary Sector | Secondary Sector | Tertiary Sector |
| 32.7 | 55.2 | 12.1 |
| Type of the Formulation | Equations |
|---|---|
| LIN | Yd = 54.589 + 0.001 * X1d + 0.095 * X2 + 0.002 * X3 + 0.007 * X4 + 0.113 * X5 + 0.016 * X6 + 0.086 * X7 + 0.097 * X8 + 0.027 * X9 |
| LOG-LIN | LNYd = 4.166 + 0.000009831 * X1d + 0.001 * X2 + 0.00001766 * X3 + 0.00006249 * X4 + 0.001 * X5 + 0.0 * X6 + 0.001 * X7 + 0.001 * X8 + 0.0 * X9 |
| LIN-LOG | Yd = − 122.215 +1.241 * lnX1d + 9,489 * lnX2 + 0.11 * lnX3 + 0.986 * lnX4 + 11.188 * lnX5 + 1.687 * lnX6 + 9,587 * lnX7 + 10.474 * lnX8 + 2.842 * lnX9 |
| LOG | LNYd = 2.456 + 0.012 * lnX1d + 0.093 * lnX2 + 0.001 * lnX3 + 0.009 * lnX4 + 0.105 * lnX5 + 0.017 * lnX6 + 0.094 * lnX7 + 0.097 * lnX8 + 0.031 * lnX9 |
| Elasticities in the PRICE/PRICE Model (Primary Sector) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | |
| LOG-LIN | 0.01 | 0.10 | 0.00 | 0.01 | 0.10 | 0.00 | 0.10 | 0.10 | 0.00 |
| Elasticities of the CONSUMPTION/PRICE Model (Primary Sector) | |||||||||
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | |
| LIN-LOG | −60.70 | 313.53 | 177.59 | 65.43 | −38.54 | −61.22 | −101.77 | −1105.87 | −2340.50 |
| Type of the Formulation | Equations |
|---|---|
| LIN | Yd = 94.7 + 0.023 * X1d + 0.0 * X2d + 0.002 * X3 + 0.306 * X4 + 0.01 * X5 |
| LOG-LIN | LNYd = 4.552 + 0.0 * X1d − 0.000002038 * X2d + 0.00003454 * X3 + 0.003 * X4 + 0.0 * X5 |
| LIN-LOG | Yd = 66.901 + 3.349 * lnX1d − 0.053 * lnX2d + 1.702 * lnX3 + 2.231 * lnX4 + 1.303 * lnX5 |
| LOG | LNYd = 4.273 + 0.033 * lnX1d − 0.001 * lnX2d + 0.018 * lnX3 + 0.022 * lnX4 + 0.013 * lnX5 |
| Elasticities in the PRICE/PRICE Model (Secondary Sector) | |||||
|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | |
| LIN | 0.02 | 0.00 | 0.00 | 0.02 | 0.01 |
| Elasticities of the CONSUMPTION/PRICE model (secondary sector) | |||||
| X1 | X2 | X3 | X4 | X5 | |
| LIN-LOG | 2182.746 | −320.970 | 4182.105 | −360.963 | −334.491 |
| Type of the Formulation | Equations |
|---|---|
| LIN | Yd = 8.966 + 0.001 * X1d − 0.001 * X2a − 0.005 * X3d − 0.01 * X4d + 0.976 * X5 + 0.061 * X6 − 0.108 * X7 |
| LOG-LIN | LNYd = 3.72 + 0.00000777 * X1d − 0.00001275 * X2a − 0.00003787 * X3d + 0.0 * X4d + 0.009 * X5 + 0.001 * X6 − 0.001 * X7 |
| LIN-LOG | Yd = − 322.039 + 1.143 * lnX1d − 1.645 * lnX2a − 0.617 * lnX3d − 0.946 * lnX4d + 97,436 * lnX5 + 6.308 * lnX6 – 9.828 * lnX7 |
| LOG | LNYd = 0.5 + 0.011 * lnX1d − 0.016 * lnX2a − 0.005 * lnX3d − 0.01 * lnX4d + 0.943 * lnX5 + 0.06 * lnX6 − 0.09 * lnX7 |
| Elasticities in the PRICE/PRICE Model (Tertiary Sector) | |||||||
|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | |
| LOG-LIN | 0.01 | −0.01 | 0.00 | 0.00 | 0.90 | 0.10 | −0.10 |
| Elasticities of the CONSUMPTION/PRICE Model (Tertiary Sector) | |||||||
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | |
| LOG | 1.56 | −0.53 | −0.71 | 1.72 | −3.59 | −6.65 | −4.777 |
| Maximum Sensitivity for Price Changes in Agricultural Products in the Event of Cost Changes in a Single Sector (Calculated Weights—in %) | ||
|---|---|---|
| Primary Sector | Secondary Sector | Tertiary Sector |
| 23.3 | 2.6 | 74.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prišenk, J.; Zidar, N.; Turk, J. Development of a Theoretical Model for the Price Formation of Agri-Food Products in the Food Supply Chain: A Slovenian Case Study. Foods 2025, 14, 415. https://doi.org/10.3390/foods14030415
Prišenk J, Zidar N, Turk J. Development of a Theoretical Model for the Price Formation of Agri-Food Products in the Food Supply Chain: A Slovenian Case Study. Foods. 2025; 14(3):415. https://doi.org/10.3390/foods14030415
Chicago/Turabian StylePrišenk, Jernej, Nejc Zidar, and Jernej Turk. 2025. "Development of a Theoretical Model for the Price Formation of Agri-Food Products in the Food Supply Chain: A Slovenian Case Study" Foods 14, no. 3: 415. https://doi.org/10.3390/foods14030415
APA StylePrišenk, J., Zidar, N., & Turk, J. (2025). Development of a Theoretical Model for the Price Formation of Agri-Food Products in the Food Supply Chain: A Slovenian Case Study. Foods, 14(3), 415. https://doi.org/10.3390/foods14030415






