A Fuzzy Logic-Based Algorithm to Solve the Slot Planning Problem in Container Vessels
Abstract
:1. Introduction
- Thousands of loading/unloading moves are required for large container vessels [17].
- The proposed algorithms should be fast with a runtime of less than 10 min, to cope with the last-minute load list changes. This is a practical requirement from the shipping companies to evaluate different forecast scenarios for the load list for the upcoming ports in the vessel’s route [7].
- The stowage coordinators have limited time to produce the stowage plans [18].
- The complex interactions between the low-level stacking rules, the high-level stress limits and the stability requirements of the vessel impose a trade-off between minimizing the overstowage and making use of the span of the quay cranes. In the meantime, overstowage is considered as container blockage that can lead to unnecessary additional movements of the containers during the loading/unloading operations [18].
- Single-phase approaches [23]:This approach represents the structure of the vessel as a set of slots and consists of formulating a model to describe the whole stowage problem at once to minimize the overstowage. Most of these approaches have a common denominator, is to sacrifice model accuracy (e.g., doesn’t consider the vessel’s stability, or only a very simplified representation is used such as weight distribution) to achieve scalability.In this case the input data consists of the overall list of Containers-To-Load (CTLAll Vessel) onto the vessel (presented in a transportation matrix: the number of containers loaded and unloaded in each port in the vessel’s route). In addition to vessel characteristics (mostly treating the vessel as rectangular bays rather than the true vessel’s configuration). Due to the problem simplification, this approach cannot guarantee obtaining optimal solution for application requirement if used on commercial sized vessel in a reasonable time [24]
- This approach classifies the constraints and objectives into high-level and low-level
- High-level constraints and objectives:These include vessel stability and balancing requirement that is essential for seaworthiness [2], (including the draft, trim, metacentric height (GM), and stress moments such as shear, bending and torsion, in addition to satisfying the weight and volume capacity limits as well as capacity limits of the different container types of the bays) [18]. The common objectives are the minimization of hatch overstowage (minimize the number of containers on deck that need to be removed in order to gain access to containers below deck) and crane make-span.
- Low-level constraints and objectives:These are mainly the shipping line stacking rules that concern the way each container is loaded into a position on the vessel. These rules include but not limited to that the weight and height capacities are satisfied, and that reefers (refrigerated containers) are assigned to positions with a power supply. The objective reflects the rules of thumb of stowage coordinators (explained later) to obtain stowage plans that are robust to fluctuations in the forecasted demands [18].
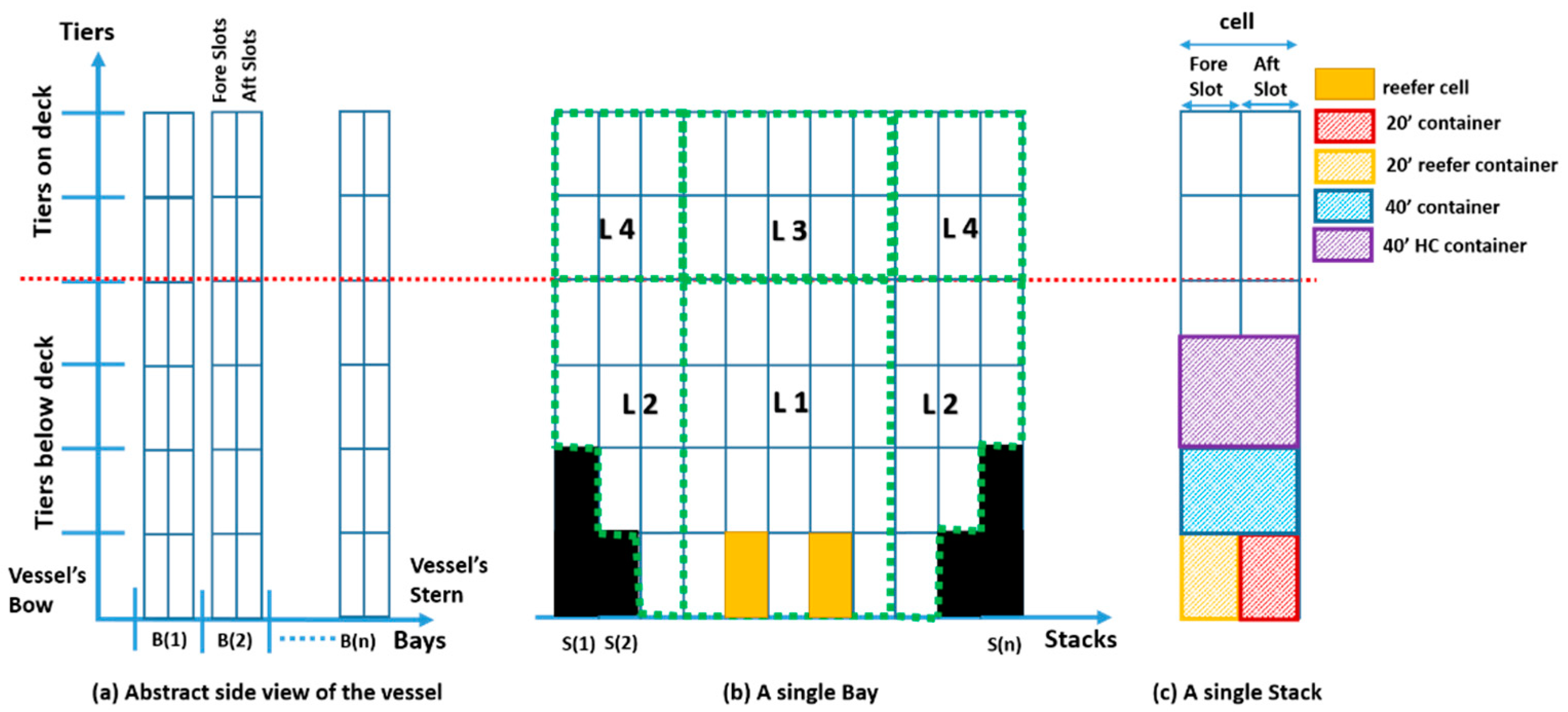
- The size; ISO containers are normally 8′ wide, height (8′6′′ and 9′6′′), length (20′, 40′ and 45′);
- The weight;
- The Discharge Port or Port Of Destination (POD) (i.e., where it would be unloaded);
- Whether the container is refrigerated and needs an electric power supply (i.e., reefer container); and
- Other special containers must be placed according to a complex set of separation rules, for example, containers with dangerous goods (IMO containers) and pallet-wide containers which are slightly wider.
- The assigned containers to a certain stack must be stacked on top of each other (i.e., no container can physically hang in the air).
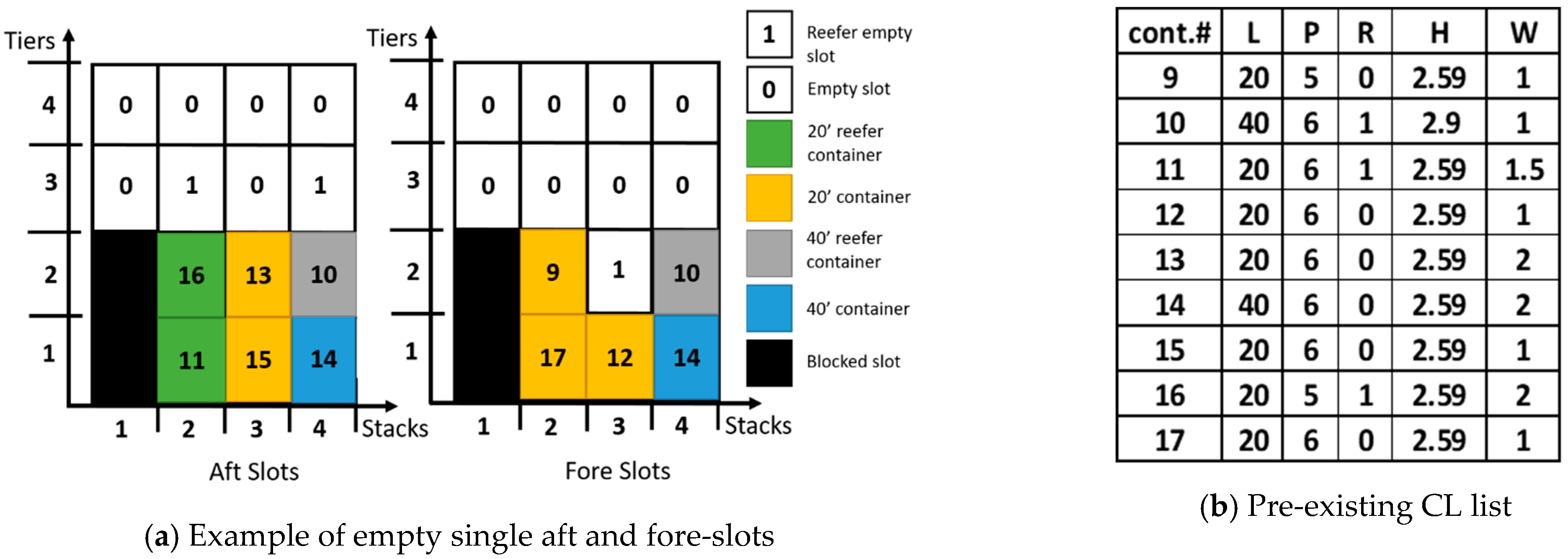
- A cell must be either empty or fully loaded and should satisfy the length constraints (i.e., the two slots are occupied by two 20′ containers or one 40′ container ==> Hence, the number of 20′ containers must be even).
- 20′ containers are forbidden to be stowed above a 40′ container.
- A 20′/40′ reefer container must be placed in a slot/cell that has access to a power plug, respectively.
- The sum of the weights and heights of the allocated containers must conform to the stack weight and height limits.
- Already existing containers cannot be reallocated.
- using fewer stacks and fewer PODs within a stack in the current port
- increasing the available space in a location
- reducing the possibility of overstowage in the downstream ports
- Increasing the number of reefer containers to be loaded in the downstream ports.
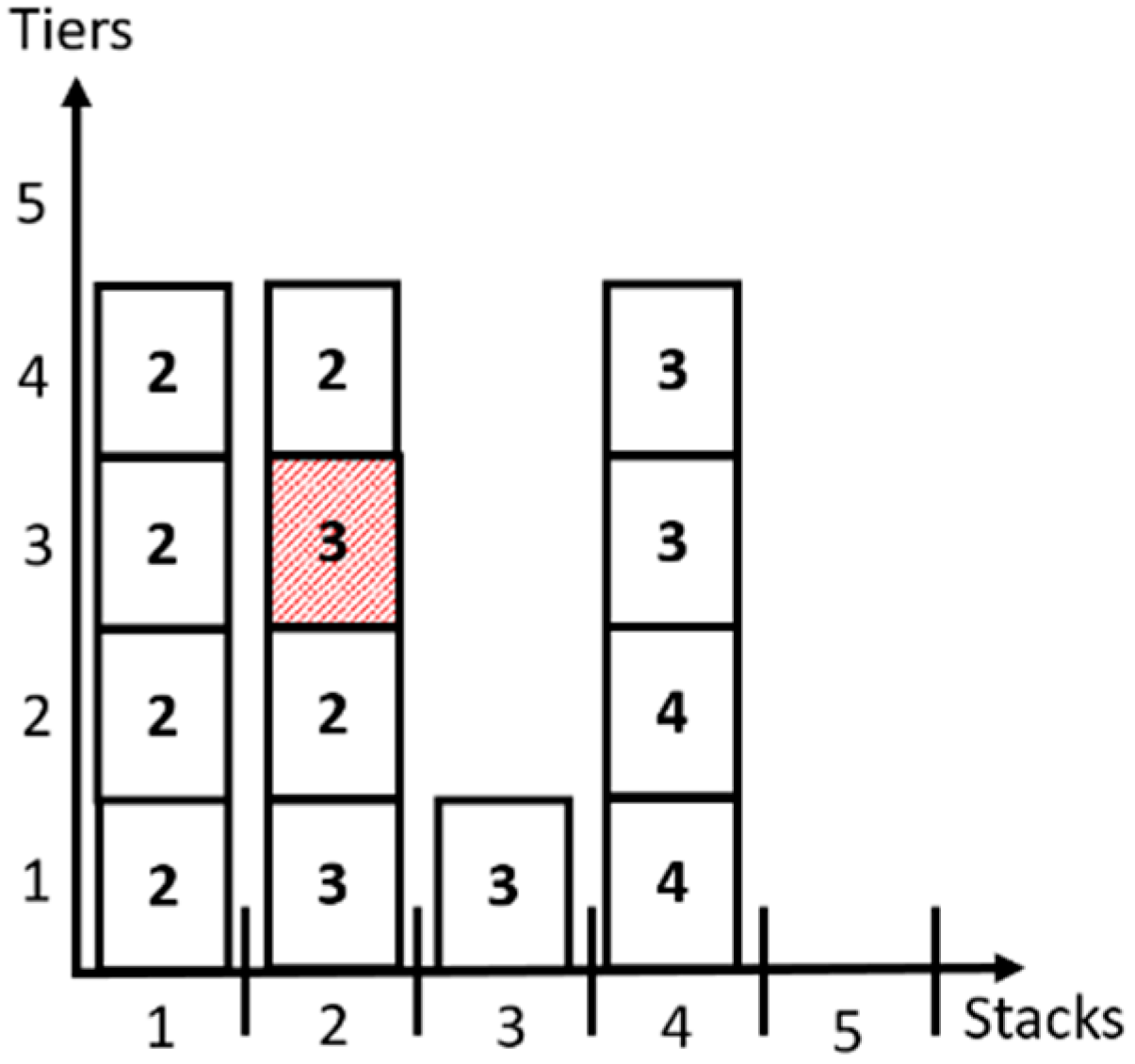
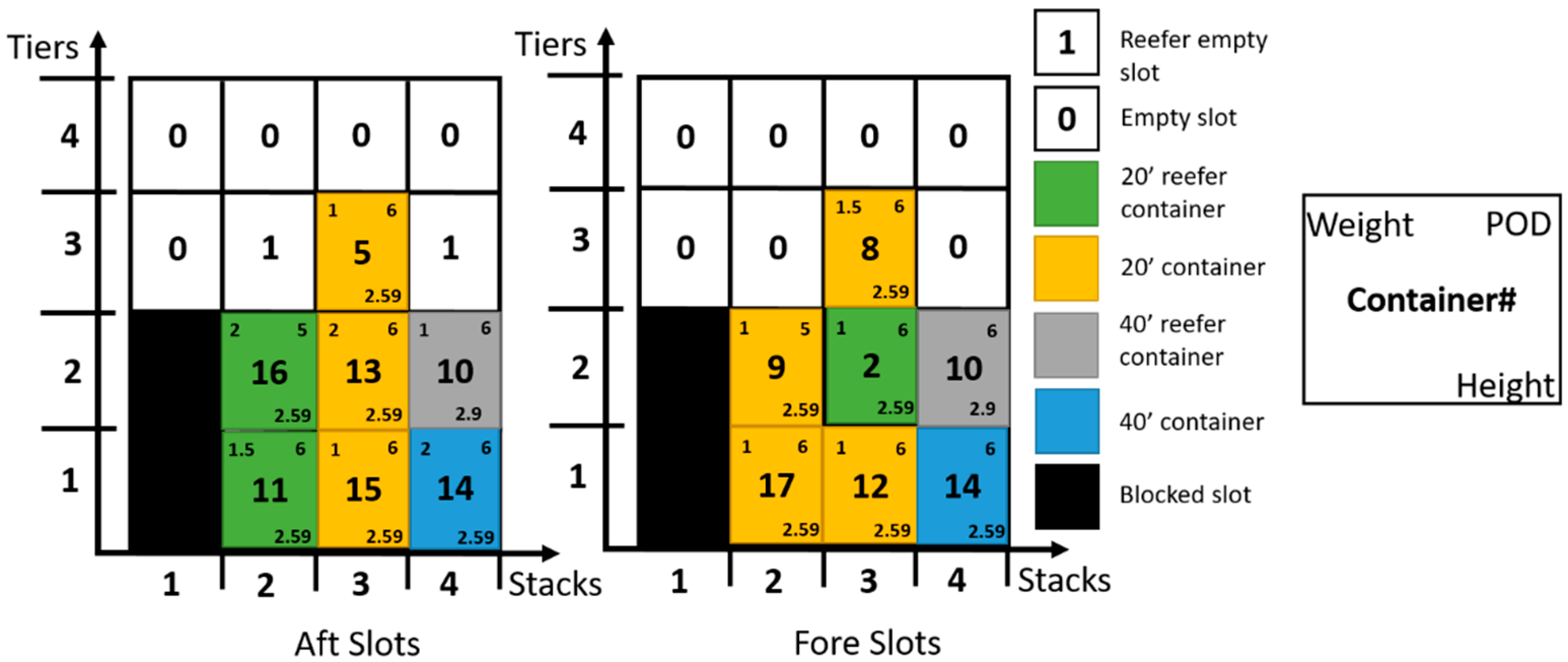
- Overstowage is minimized. An over-stowed container is a container that has a POD further than any of the containers, which are located beneath it as shown in the second stack in Figure 3. A penalty of POS = 100 units is paid for each over-stowed container.
- Having containers of different PODs within the same stack is minimized. A penalty of PDP = 20 units is paid for each POD that is included within a stack. For example, in Figure 3, the total penalty is 120 for the four stacks is added to the objective function.
- The number of non-empty stacks (i.e., used stack) is minimized. A penalty of PS = 10 units is paid if there is at least one container located in a stack. For example, in Figure 3, the total penalty is 40 for the four occupied stacks added to the objective function.
- Locating a non-reefer container in a reefer cell is minimized. A penalty of PR = 5 units is paid for each reefer slot that is occupied with a non-reefer container is added to the objective function.
2. Literature Review
2.1. The Single-Phase Approach
2.2. The Decomposition Approach
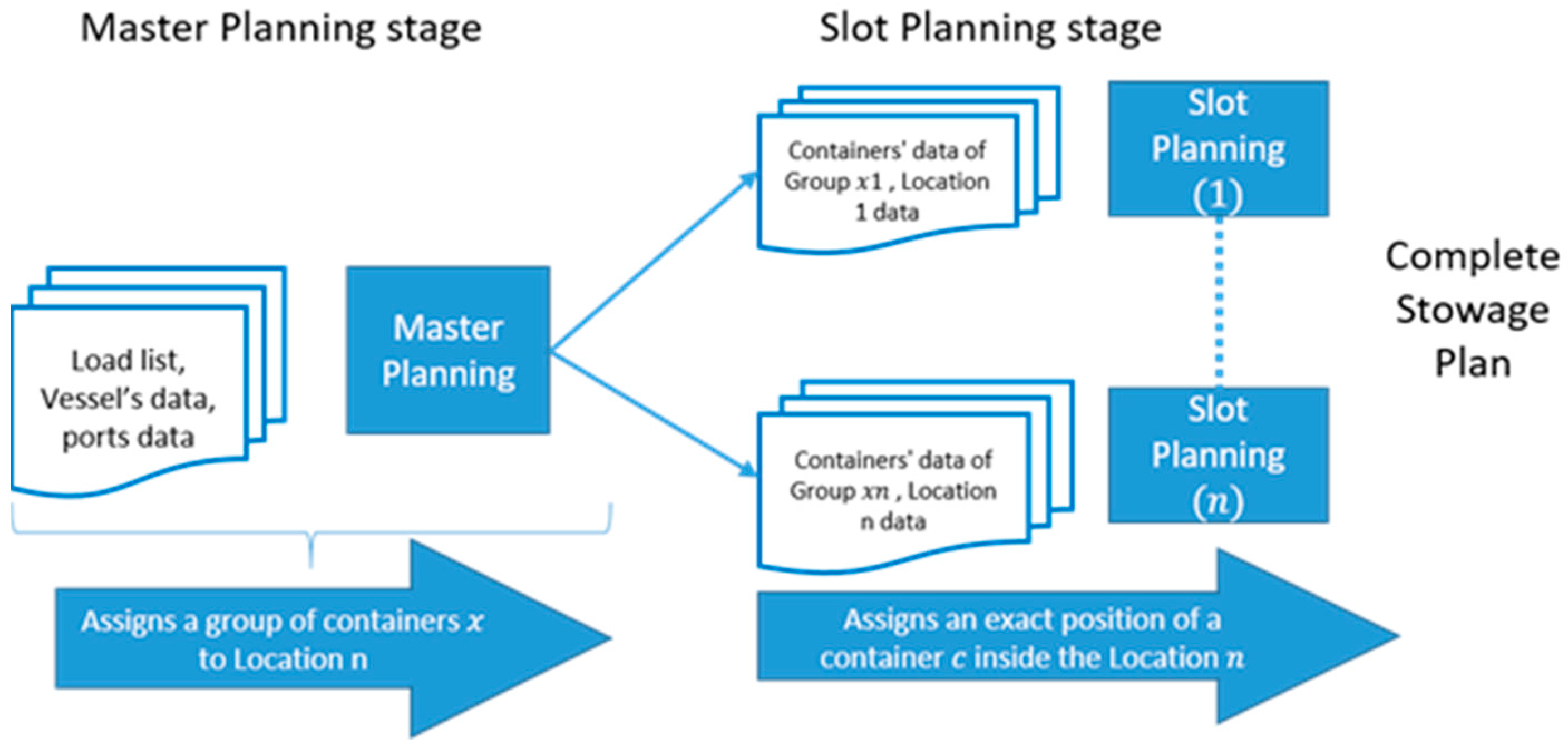
2.2.1. The Master Planning Phase
2.2.2. The Slot Planning Phase
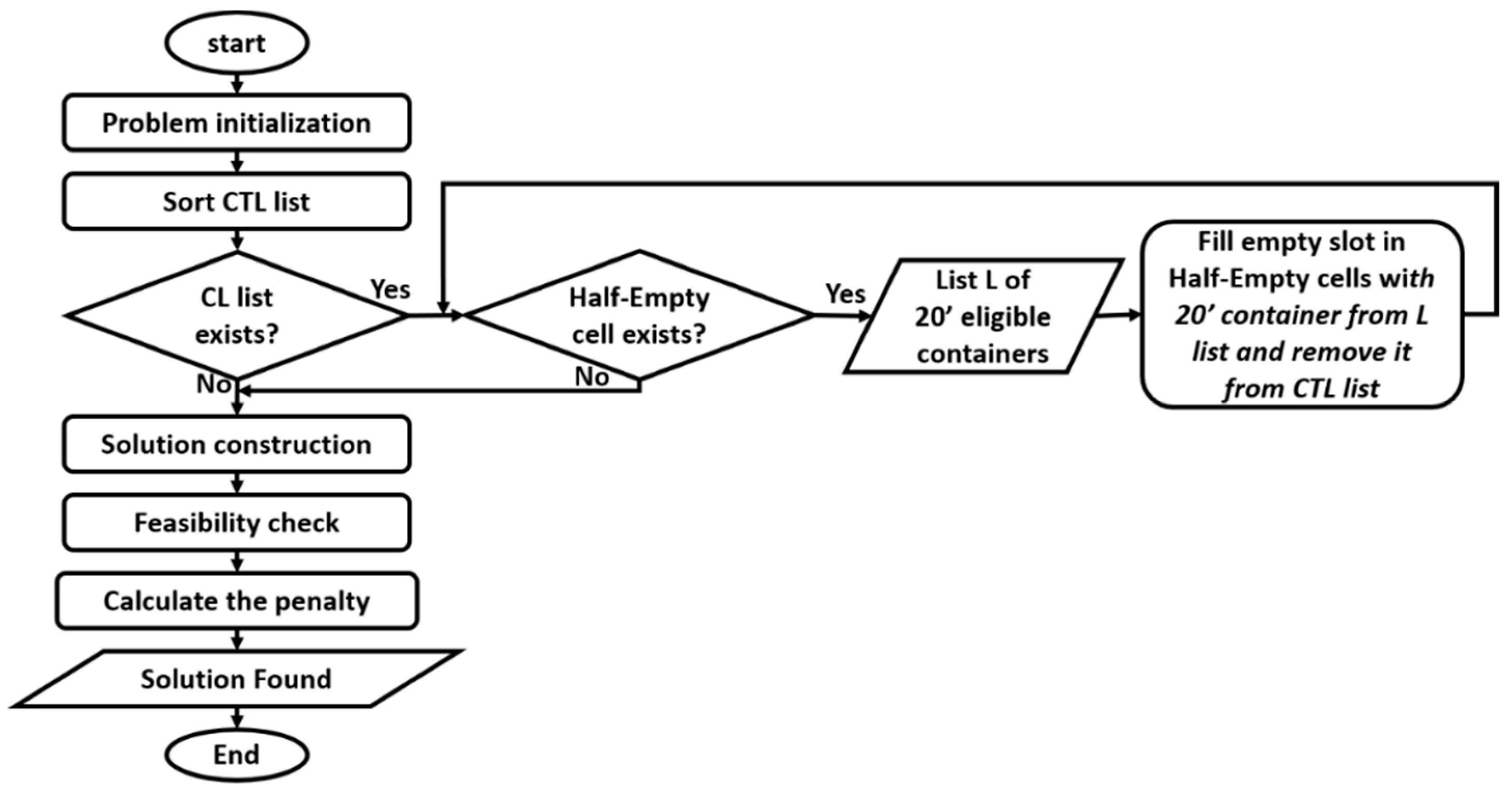
3. Proposed Methodology
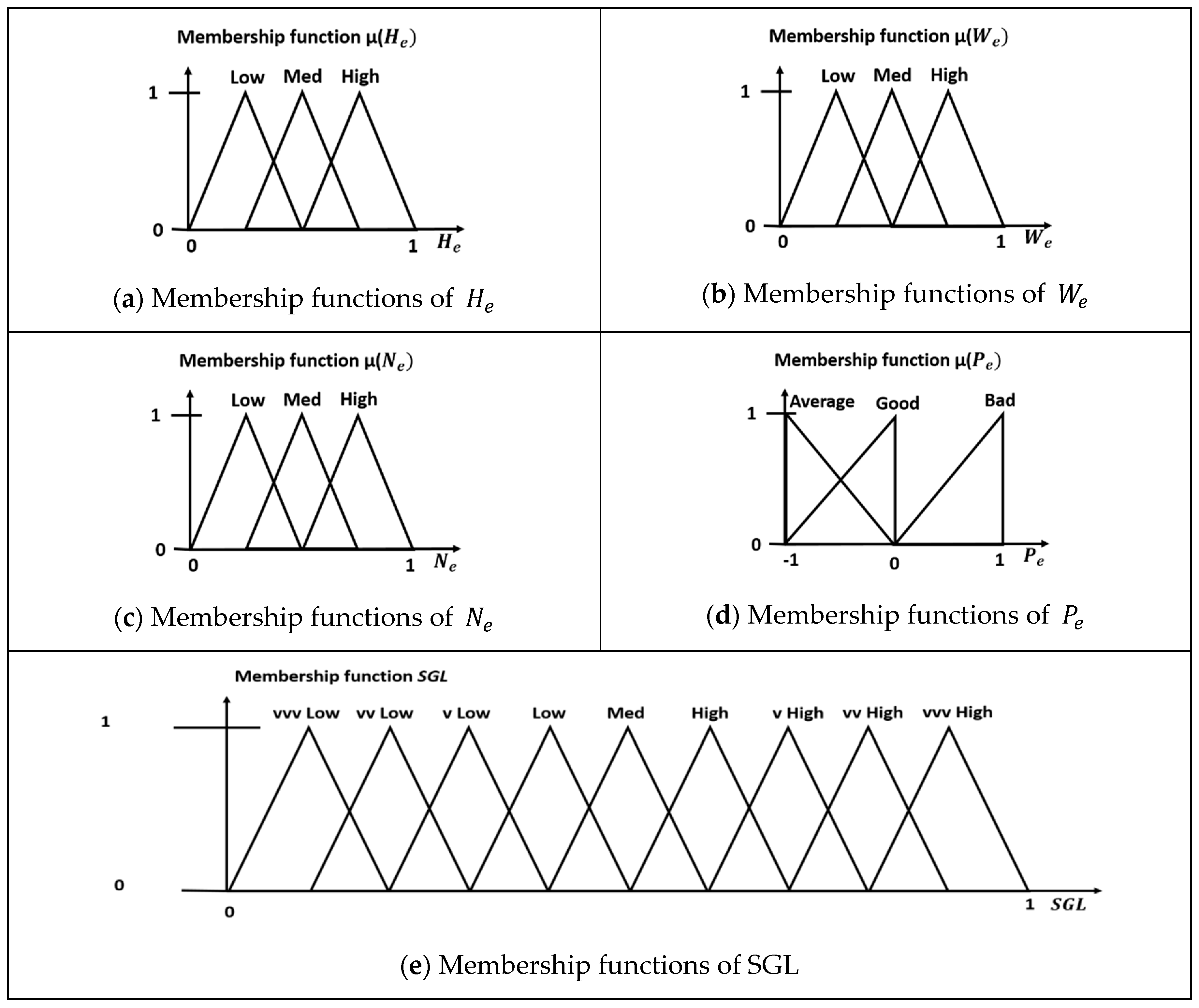
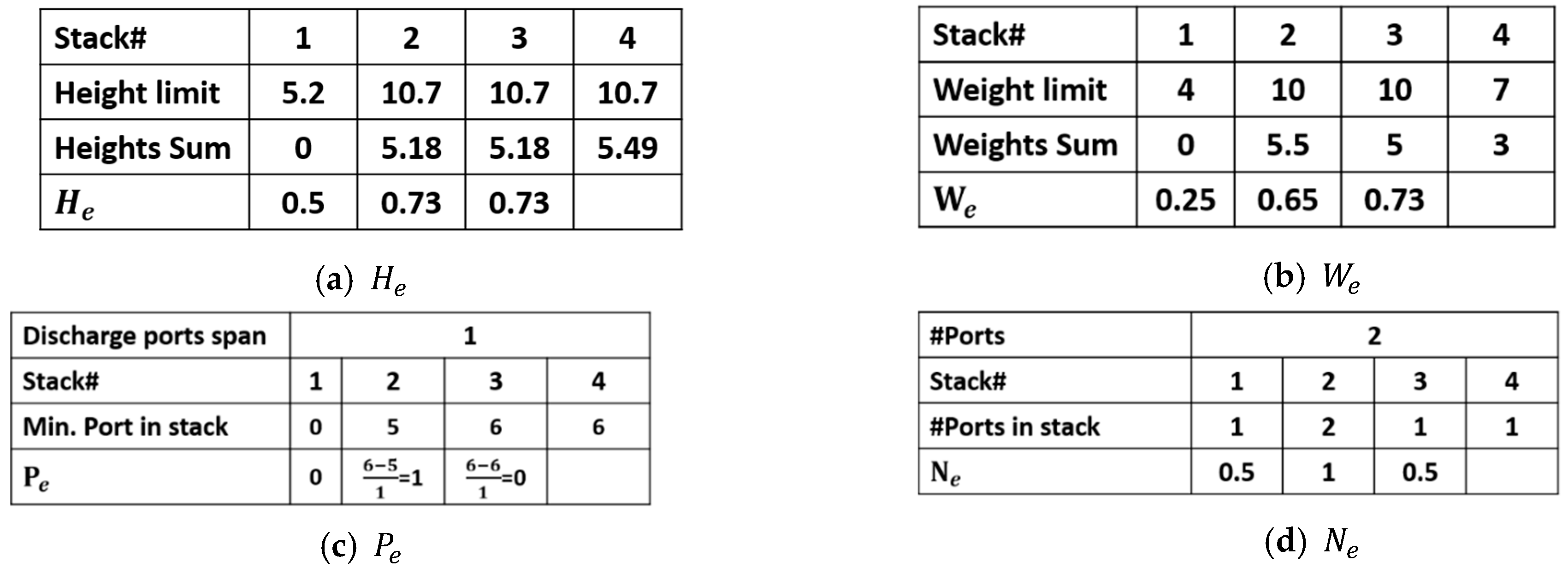
- Height eligibility ()
- Weight eligibility ()
- Number of ports eligibility ()
- Port eligibility ()
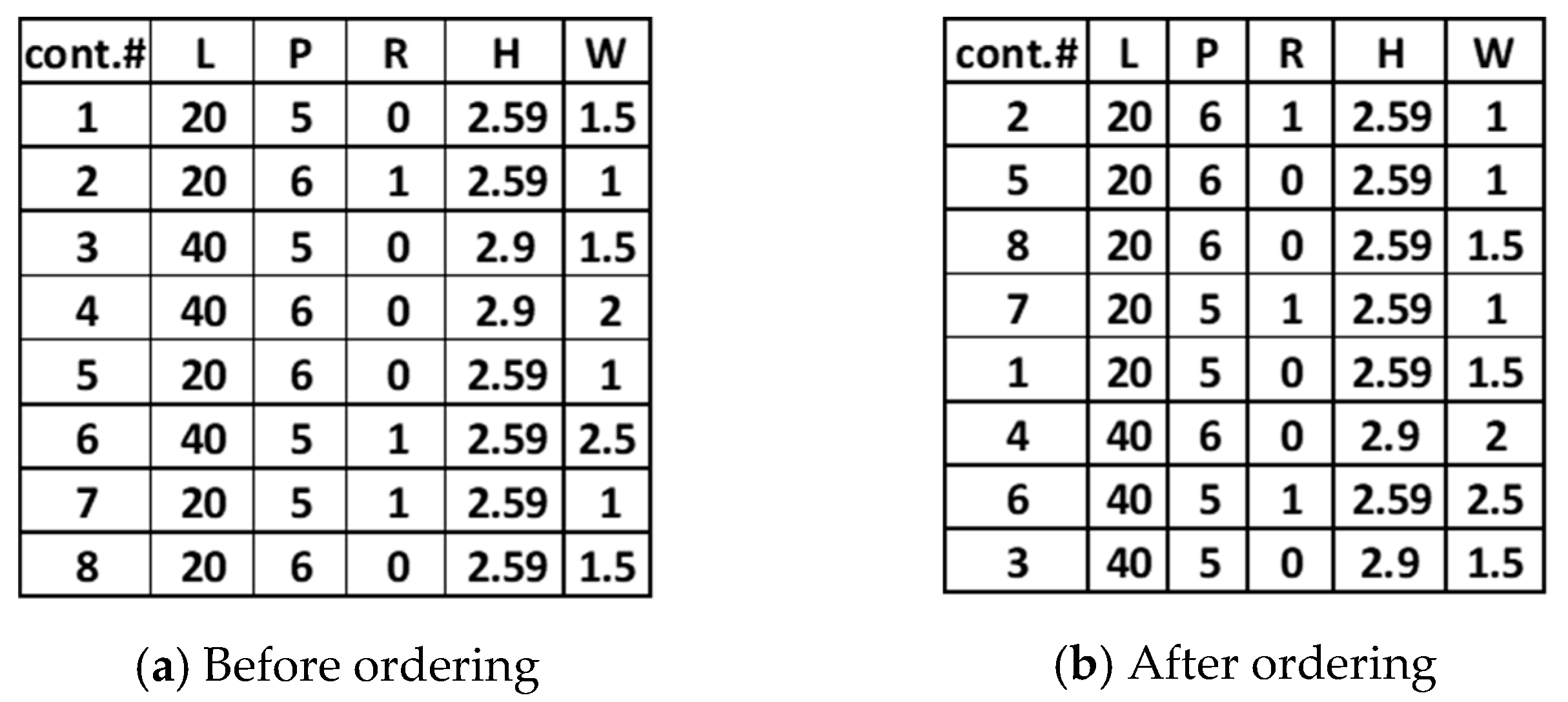
- Sort input Containers-To-Load (CTL) List as depicted in Section 3.1
- Fill empty slots in half-empty cells with 20′ containers from the CTL list as will be presented in Section 3.2
- Perform the Solution Construction with all necessary iteration as will be described in Section 3.3
- Compute the Feasibility Check and Penalty Calculation for the solution obtained above as will be discussed in Section 3.4
3.1. Sort Containers-to-Load (CTL) List
3.2. Fill Empty Slots in Half-Empty Cells with 20′ Containers from the CTL List
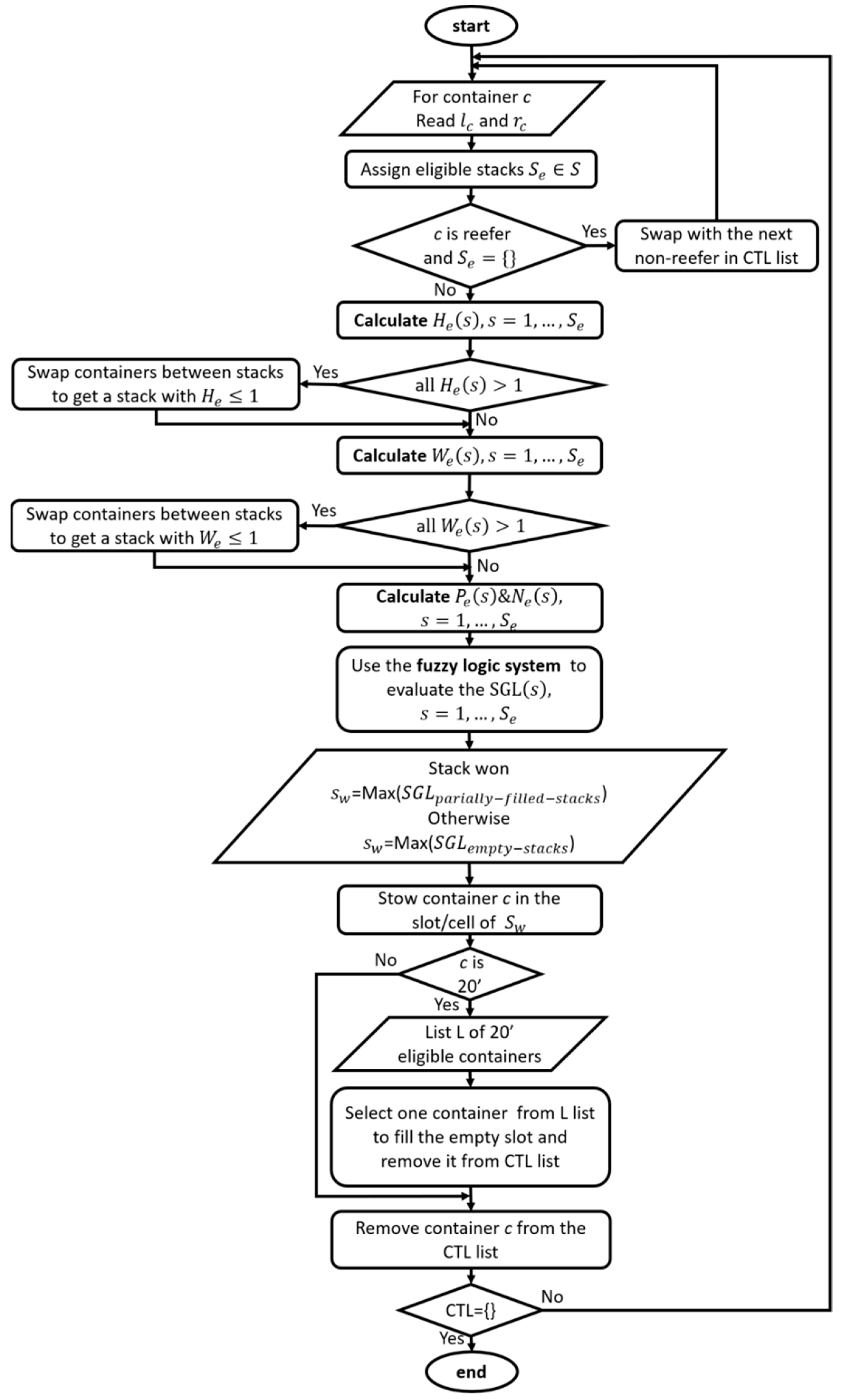
3.3. Solution Construction
- Assign eligible stacks
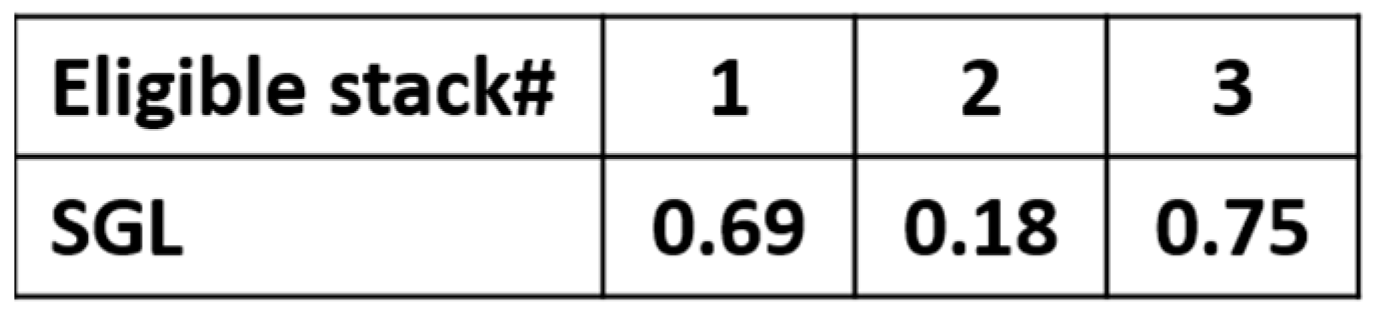
- Variables/Output Calculations: calculate the four variables of the slot planning fuzzy logic system ((, , and ) and use the fuzzy Mamdani fuzzy logic system to evaluate the output (SGL) for each stack
- Container Stowage: stow the container to the slot/cell and remove that container from the CTL list
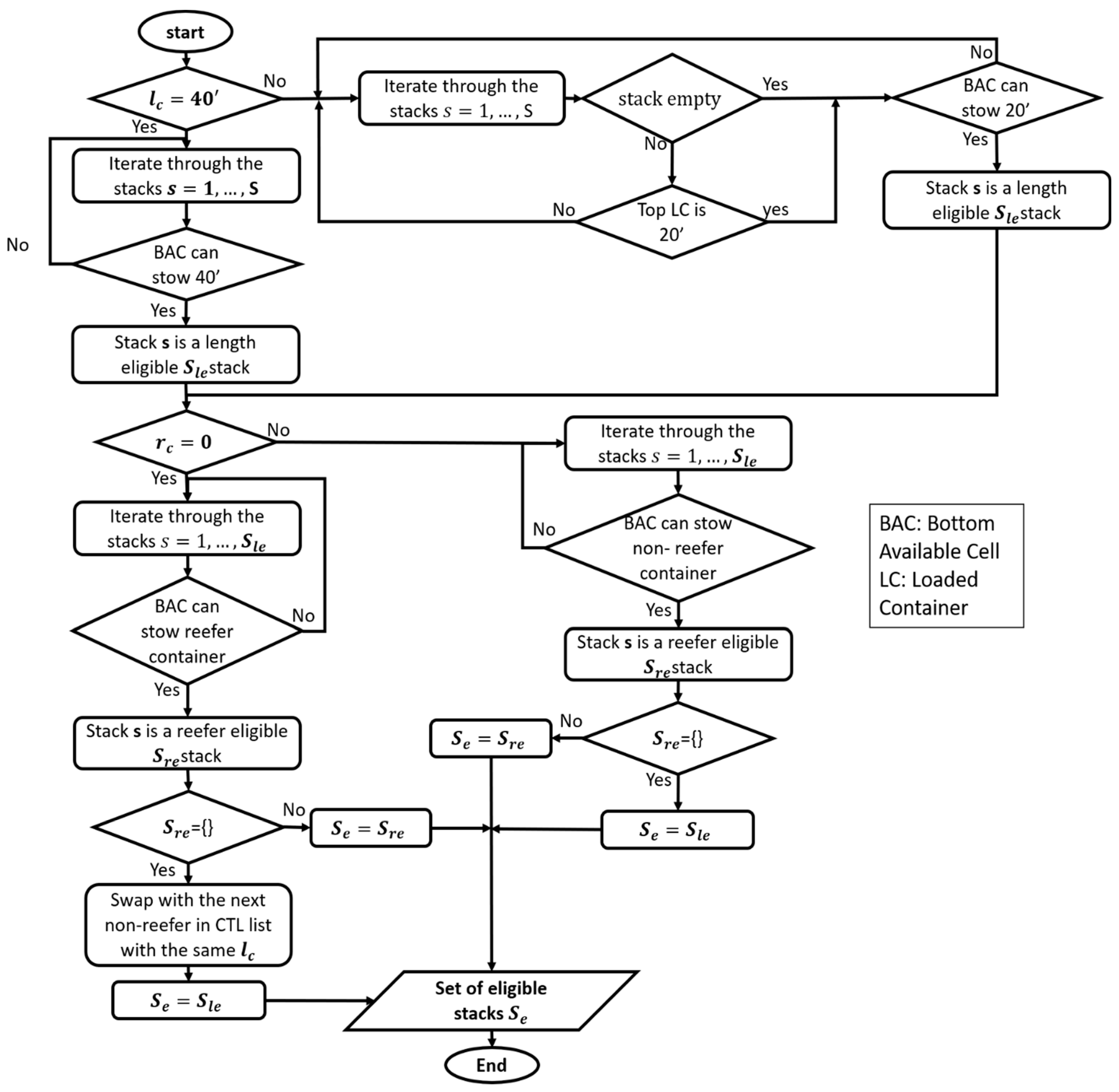
3.3.1. Assign Eligible Stacks
3.3.2. Variables/Output Calculations
- Height eligibility
- Weight eligibility
- Port eligibility
- Number of ports eligibility
3.3.3. Container Stowage
3.4. Feasibility Check and Penalty Calculation
4. Results and Discussion
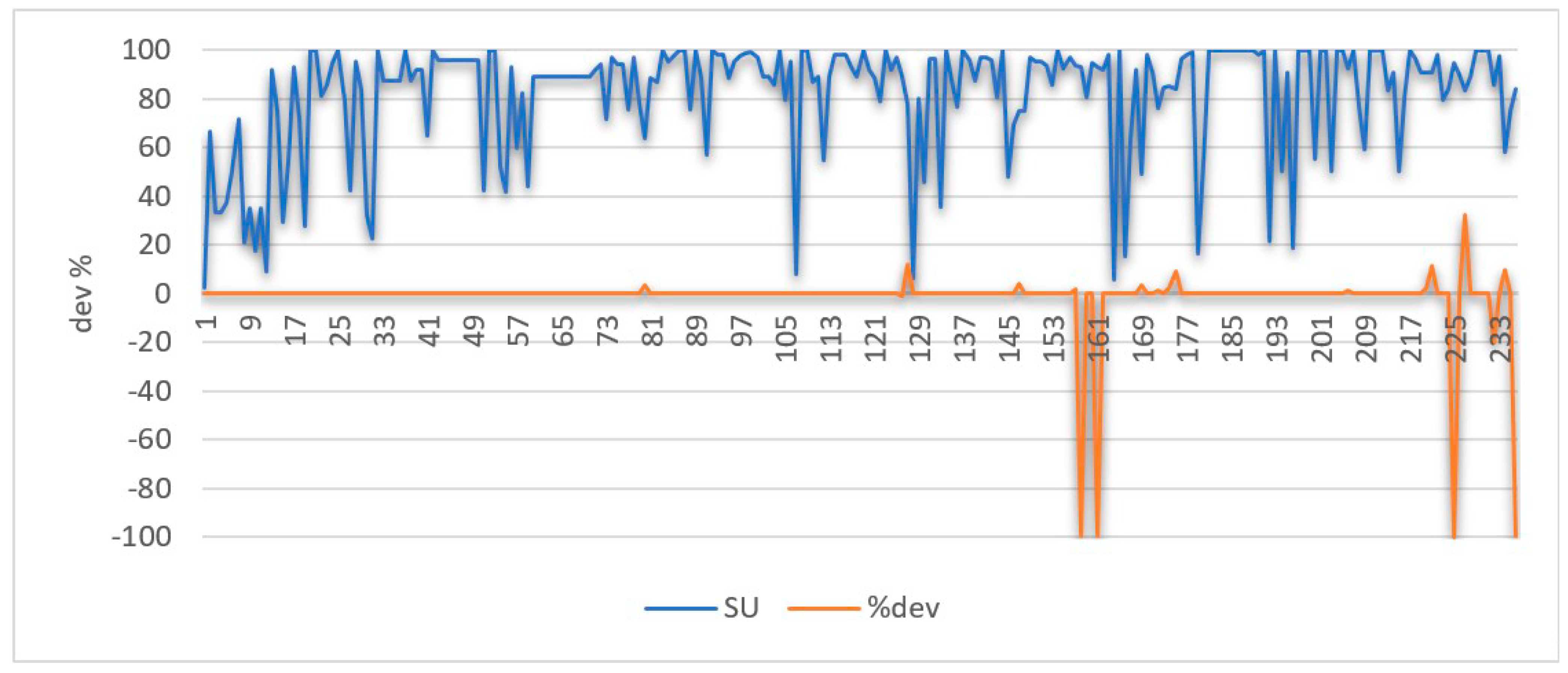
- The first category includes 222 instances of the 236 benchmark instances presented in Figure 16. Among these instances, four of which yielded tighter upper-bound that was reached by Integer Programming models of either Parreño et al. [2] or Delgado et al. [7]. The proposed results yielded improvements in these four instances of (99.5%, 99.5%, 20% and 99.7%) over the upper-bound of Delgado et al. [7]. All four instances have an average improvement of 80% for the four instances.
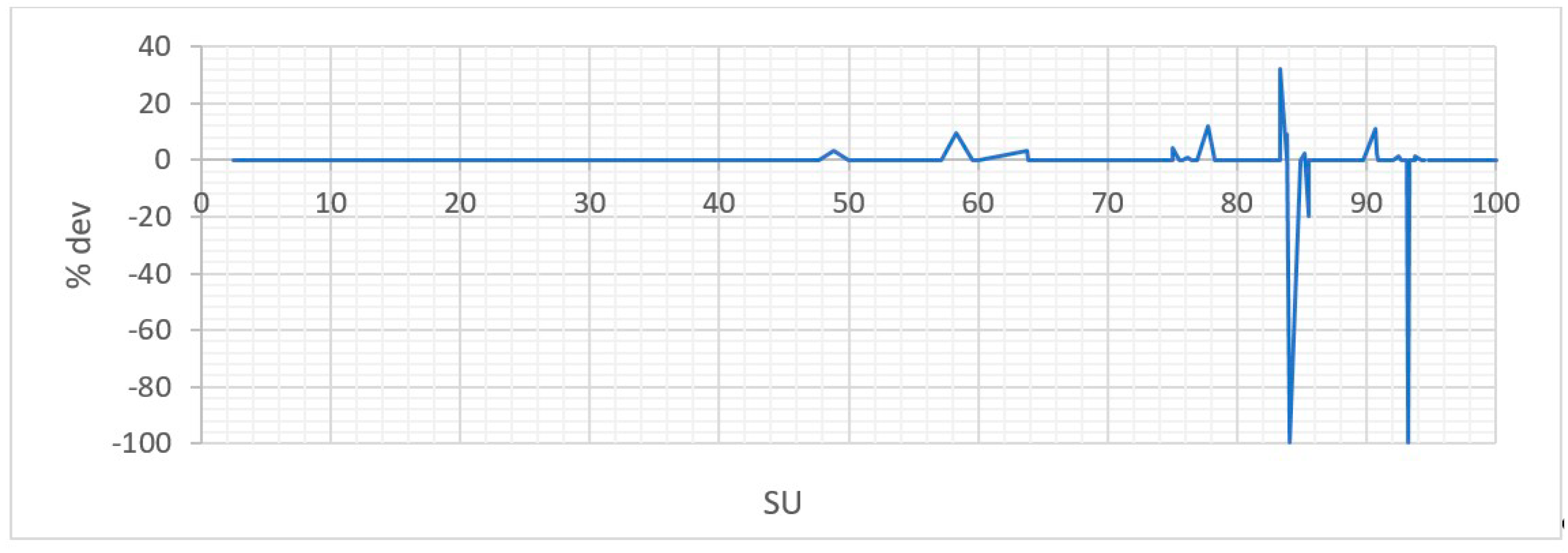
- The second category includes 13 instances. These instances do not have an optimum solution. As shown in Figure 16, the minimum, maximum and average percentage deviations from the optimum solution were 1.1%, 32%, and 7.2%, respectively.
- ○
- It is important to note that for nine instances out of these 13 instances, the only contributor to the deviation from the optimal solution was the reefer penalty (with an average of 3%). These instances belong to six different groups.
- ○
- After investigation, it was found that these instances had either, no to very few reefer containers to load. On the other hand, the location had a very high capacity of reefer slots. In these instances, if the relative difference between the number of reefer containers to load and the number of reefer cells in the location decreases, worse results are more likely to be achieved. These instances had an average Space Utilization percentage of 80%.
- ○
- Four of these nine instances belong to a group of instances that have no reefer containers but, in these locations, there exist a high number of reefer slots relating to the location’s dimension ranging from 8 to 64. These four instances have an average number of reefer slots that is equal to 25 and have a high number of HC containers regarding the number of the 40′ containers. In addition to having an average available capacity and utilization of 92 slots and 88%, respectively.
- ○
- Two instances of the 13 instances have an unnecessary stack opened to stow a single container. This is because the algorithm chooses the eligible stacks according to the reefer characteristics of the container to load. Given that at one stage of execution, this was the only stack that had the same reefer characteristic of the container to load, subsequently, this stack was opened.
- ○
- The algorithm also failed to find the optimum solution in the only instance of four port of destinations. The algorithm failed to perform better port clustering and yielded a deviation of 12% from the optimum solution.
- ○
- The worst case belonged to group #11 with a deviation value of 32% because of the overstowage penalty.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stahlbock, R.; Steenken, D. Container terminal operation and operations research—A classification and literature review. In Container Terminals and Automated Transport Systems: Logistics Control Issues and Quantitative Decision Support; Springer: Berlin/Heidelberg, Germany, 2005; pp. 3–49. [Google Scholar]
- Parreno, F.; Pacino, D.; Alvarez-Valdes, R. A GRASP algorithm for the container stowage slot planning problem. Transp. Res. Part E Logist. Transp. Rev. 2016, 94, 141–157. [Google Scholar] [CrossRef] [Green Version]
- Lun, Y.H.V.; Lai, K.-H.; Cheng, T.C. Investigation of the influences of ‘transport complex economy’ and political risk on freight transport growth. Int. J. Logist. Res. Appl. 2011, 14, 285–296. [Google Scholar] [CrossRef]
- Tanaka, S.; Voß, S. An exact algorithm for the block relocation problem with a stowage plan. Eur. J. Oper. Res. 2019, 279, 767–781. [Google Scholar] [CrossRef]
- Maritime Shipping and International Trade. 2021. Available online: https://porteconomicsmanagement.org/pemp/contents/part1/maritime-shipping-and-international-trade/world-container-throughput/ (accessed on 20 January 2021).
- Bilican, M.S.; Evren, R.; Karatas, M. A Mathematical Model and Two-Stage Heuristic for the Container Stowage Planning Problem with Stability Parameters. IEEE Access 2020, 8, 113392–113413. [Google Scholar] [CrossRef]
- Delgado, A.; Jensen, R.M.; Janstrup, K.H.; Rose, T.H.; Andersen, K.H. A Constraint Programming model for fast optimal stowage of container vessel bays. Eur. J. Oper. Res. 2012, 220, 251–261. [Google Scholar] [CrossRef]
- Monaco, M.F.; Sammarra, M.; Sorrentino, G. The Terminal-Oriented Ship Stowage Planning Problem. Eur. J. Oper. Res. 2014, 239, 256–265. [Google Scholar] [CrossRef]
- Pacino, D.; Delgado, A.; Jensen, R.M.; Bebbington, T. Fast Generation of Near-Optimal Plans for Eco-Efficient Stowage of Large Container Vessels. In Proceedings of the International Conference on Computational Logistics, Hamburg, Germany, 19–22 September 2011; Volume 6971, pp. 286–301. [Google Scholar] [CrossRef] [Green Version]
- Shi, W.; Li, K.X. Themes and tools of maritime transport research during 2000–2014. Marit. Policy Manag. 2016, 44, 151–169. [Google Scholar] [CrossRef]
- Fazi, S. A decision-support framework for the stowage of maritime containers in inland shipping. Transp. Res. Part E Logist. Transp. Rev. 2019, 131, 1–23. [Google Scholar] [CrossRef]
- Parthibaraj, C.S.; Palaniappan, P.; Gunasekaran, A.; Subramanian, N. Multi-agent system with iterative auction mechanism for master bay plan problem in marine logistics. Marit. Policy Manag. 2017, 44, 705–726. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Ji, S.; Zheng, L. Solving inland container ship stowage planning problem on full route through a two-phase approach. Int. J. Shipp. Transp. Logist. 2020, 12, 65. [Google Scholar] [CrossRef]
- Korach, A.; Brouer, B.D.; Jensen, R.M. Matheuristics for slot planning of container vessel bays. Eur. J. Oper. Res. 2020, 282, 873–885. [Google Scholar] [CrossRef]
- Wang, N.; Yu, L.; Yu, L.; Ke, S. Optimization of Containership Stowage in Circular Route Based on Greedy Algorithm. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; pp. 146–150. [Google Scholar] [CrossRef]
- Cohen, M.W.; Coelho, V.N.; Dahan, A. Container Vessel Stowage Planning System Using Genetic Algorithm. In Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10199, pp. 557–572. [Google Scholar]
- Wilson, I.D.; Roach, P.A. Container stowage planning: A methodology for generating computerised solutions. J. Oper. Res. Soc. 2000, 51, 1248–1255. [Google Scholar] [CrossRef]
- Pacino, D.; Jensen, R.M. Fast Slot Planning Using Constraint-Based Local Search. In IAENG Transactions on Engineering Technologies: Special Issue of the International MultiConference of Engineers and Computer Scientists 2012; Yang, G.-C., Ao, S.-I., Huang, X., Castillo, O., Eds.; Springer: Dordrecht, The Netherlands, 2013; Volume 186, pp. 49–63. [Google Scholar]
- Ambrosino, D.; Sciomachen, A. Using a Bin Packing Approach for Stowing Hazardous Containers into Containerships. In Optimized Packings with Applications; Fasano, G., Ed.; Springer: Cham, Switzerland, 2015; Volume 105, pp. 1–18. [Google Scholar]
- Ambrosino, D.; Anghinolfi, D.; Paolucci, M.; Sciomachen, A. A new three-step heuristic for the Master Bay Plan Problem. Marit. Econ. Logist. 2009, 11, 98–120. [Google Scholar] [CrossRef]
- Ambrosino, D.; Anghinolfi, D.; Paolucci, M.; Sciomachen, A. An Experimental Comparison of Different Heuristics for the Master Bay Plan Problem. In Proceedings of the 9th International Symposium on Experimental Algorithms, Naples, Italy, 20–22 May 2010; pp. 314–325. [Google Scholar] [CrossRef]
- Expósito-izquierdo, C.; Melián-batista, B.; Moreno-vega, J.M. A Review of Soft Computing Techniques in Maritime Logistics and Its Related Fields. In Soft Computing Based Optimization and Decision Models, Studies in Fuzziness and Soft Computing; Springer: Cham, Switzerland, 2018; Volume 360, pp. 1–23. [Google Scholar]
- De Azevedo, A.T.; De Arruda, E.F.; Salles-Neto, L.; Chaves, A.A.; Moretti, A.C. Solution of the 3D Stochastic Stowage Planning for Container Ships through Representation by Rules. In Proceedings of the Fourth International Workshop on Knowledge Discovery, Knowledge Management and Decision Support, Mazatlan, Mexico, 6–8 November 2013; pp. 120–129. [Google Scholar] [CrossRef] [Green Version]
- Araújo, E.J.; Chaves, A.; Salles-Neto, L.; De Azevedo, A.T. Pareto clustering search applied for 3D container ship loading plan problem. Expert Syst. Appl. 2016, 44, 50–57. [Google Scholar] [CrossRef]
- Pacino, D. An LNS Approach for Container Stowage Multi-port Master Planning. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2013; Volume 8197, pp. 35–44. [Google Scholar] [CrossRef]
- Gheith, M.; Eltawil, A.B.; Harraz, N.A. Solving the container pre-marshalling problem using variable length genetic algorithms. Eng. Optim. 2015, 48, 687–705. [Google Scholar] [CrossRef]
- Güven, C.; Eliiyi, D.T. Modelling and optimisation of online container stacking with operational constraints. Marit. Policy Manag. 2018, 46, 201–216. [Google Scholar] [CrossRef]
- Avriel, S.; Penn, M.; Shpirer, M.; Witteboon, N. Stowage planning for container ships to reduce the number of shifts. Ann. Oper. Res. 1998, 76, 55–71. [Google Scholar] [CrossRef]
- Dubrovsky, O.; Levitin, G.; Penn, M. A Genetic Algorithm with a Compact Solution Encoding for the Container Ship Stowage Problem. J. Heuristics 2002, 8, 585–599. [Google Scholar] [CrossRef]
- Ding, D.; Chou, M.C. Stowage planning for container ships: A heuristic algorithm to reduce the number of shifts. Eur. J. Oper. Res. 2015, 246, 242–249. [Google Scholar] [CrossRef]
- Rahsed, D.M.; Gheith, M.S.; Eltawil, A.B. A Rule-based Greedy Algorithm to Solve Stowage Planning Problem. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; pp. 437–441. [Google Scholar]
- Roberti, R.; Pacino, D. A Decomposition Method for Finding Optimal Container Stowage Plans. Transp. Sci. 2018, 52, 1444–1462. [Google Scholar] [CrossRef]
- De Azevedo, A.T.; Ribeiro, C.M.; De Sena, G.J.; Chaves, A.A.; Neto, L.L.S.; Moretti, A.C. Solving the 3D container ship loading planning problem by representation by rules and beam search. In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems, Algarve, Portugal, 4–6 February 2012; pp. 132–141. [Google Scholar] [CrossRef]
- De Azevedo, A.T.; Ribeiro, C.M.; De Sena, G.J.; Chaves, A.; Neto, L.L.S.; Moretti, A.C. Solving the 3D container ship loading planning problem by representation by rules and meta-heuristics. Int. J. Data Anal. Tech. Strat. 2014, 6, 228–260. [Google Scholar] [CrossRef]
- De Azevedo, A.C.; de Arruda, A.T.; Neto, E.F.; Chaves, L.L.S.; Moretti, A.A. On the application of participatory learning system for solving the 3d loading and unloading containers in port terminals for multiple scenarios. Rev. Pesqui. Nav. Brasília 2015, 27, 57–68. [Google Scholar]
- Azevedo, A.T.; Salles-Neto, L.; Chaves, A.; Moretti, A.C. Solving the 3D stowage planning problem integrated with the quay crane scheduling problem by representation by rules and genetic algorithm. Appl. Soft Comput. 2018, 65, 495–516. [Google Scholar] [CrossRef]
- Lee, Z.Q.; Fan, R.; Hsu, W.-J. Towards Real-Time Automated Stowage Planning—Optimizing Constraint Test Ordering. In Proceedings of the International Conference on Computational Logistics, Lisbon, Portugal, 7–9 September 2016; pp. 175–189. [Google Scholar] [CrossRef]
- Lee, Z.Q.; Fan, R.; Hsu, W.-J. A Near-Optimal Algorithm for Constraint Test Ordering in Automated Stowage Planning. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1298–1308. [Google Scholar] [CrossRef]
- Wilson, I.; Roach, P. Principles of Combinatorial Optimization Applied to Container-Ship Stowage Planning. J. Heuristics 1999, 5, 403–418. [Google Scholar] [CrossRef]
- Kang, J.-G.; Kim, Y.-D. Stowage planning in maritime container transportation. J. Oper. Res. Soc. 2002, 53, 415–426. [Google Scholar] [CrossRef]
- Pacino, D.; Delgado, A.; Jensen, R.M.; Bebbington, T. An Accurate Model for Seaworthy Container Vessel Stowage Planning with Ballast Tanks. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2012; Volume 7555, pp. 17–32. [Google Scholar] [CrossRef]
- Ambrosino, D.; Paolucci, M.; Sciomachen, A. Experimental evaluation of mixed integer programming models for the multi-port master bay plan problem. Flex. Serv. Manuf. J. 2015, 27, 263–284. [Google Scholar] [CrossRef]
- Ambrosino, D.; Paolucci, M.; Sciomachen, A. Computational evaluation of a MIP model for multi-port stowage planning problems. Soft Comput. 2015, 21, 1753–1763. [Google Scholar] [CrossRef]
- Ambrosino, D.; Paolucci, M.; Sciomachen, A. A MIP Heuristic for Multi Port Stowage Planning. Transp. Res. Procedia 2015, 10, 725–734. [Google Scholar] [CrossRef] [Green Version]
- Delgado, A.; Jensen, R.M.; Schulte, C. Generating Optimal Stowage Plans for Container Vessel Bays. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2009; Volume 5732, pp. 6–20. [Google Scholar] [CrossRef]
- Pacino, D.; Jensen, R. A Local Search Extended Heuristic for Stowing Under Deck Locations of Container Vessels. In Proceedings of the ODYSSEUS 2009—The 4th International Workshop on Freight Transportation and Logistics, Cesme-Izmir, Turkey, 26–29 May 2009; pp. 1–3. [Google Scholar]
- Pacino, D.; Jensen, R.M. Constraint-Based Local Search for Container Stowage Slot Planning. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2012; Volume 2, pp. 1467–1472. [Google Scholar]
- Ries, J.; González-Ramírez, R.G.; Miranda, P.A. A Fuzzy Logic Model for the Container Stacking Problem at Container Terminals. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2014; Volume 8760, pp. 93–111. [Google Scholar] [CrossRef] [Green Version]
- Valdes-Gonzalez, H.; Reyes-Bozo, L.; Vyhmeister, E.; Salazar, J.L.; Sepúlveda-Rojas, J.P.; Mosca-Arestizábal, M. Container stacking revenue management system: A fuzzy-based strategy for Valparaiso port. DYNA 2015, 82, 38–45. [Google Scholar] [CrossRef]
- Rekik, I.; Elkosantini, S. A multi agent system for the online container stacking in seaport terminals. J. Comput. Sci. 2019, 35, 12–24. [Google Scholar] [CrossRef]
- Atef, S.; Ismail, N.; Eltawil, A.B. A new fuzzy logic based approach for optimal household appliance scheduling based on electricity price and load consumption prediction. Adv. Build. Energy Res. 2021, 1–19. [Google Scholar] [CrossRef]
- Xia, M.; Li, Y.; Shen, Y.; Zhao, N. Loading Sequencing Problem in Container Terminal with Deep Q-Learning. J. Coast. Res. 2020, 103, 817–821. [Google Scholar] [CrossRef]
- Aghda, S.A.F.; Mirfakhraei, M. Improved routing in dynamic environments with moving obstacles using a hybrid Fuzzy-Genetic algorithm. Futur. Gener. Comput. Syst. 2020, 112, 250–257. [Google Scholar] [CrossRef]
- Voloshyn, A.; Gnatienko, G.; Drobot, E. Fuzzy Membership Functions in a Fuzzy Decision Making Problem. Int. J. Inf. Theor. Appl. 2003, 10, 243–247. [Google Scholar]
- Wang, C. A Study of Membership Functions on Mamdani-Type Fuzzy Inference System for Industrial Decision-Making. Master’s Thesis, Lehigh University, Bethlehem, PA, USA, 2015. [Google Scholar]



| Sets | |
|---|---|
| Set of 20′ containers | |
| Set of 40′ containers | |
| Penalties | |
| POS | Penalty for each Over-Stowed container |
| PDP | Penalty for each Ports of Discharge (PODs) within a stack |
| PS | Penalty for an open Stack |
| PR | Penalty for stowing a non-reefer container in a Reefer cell/slot |
| Decision Variables | |
| is an overstowing container or not | |
| or not | |
| is empty or not | |
| or not | |
| Group | No. of Inst. | Capacity (TEU) | No. of Containers (TEU) | 40′ | 20′ | HC | R | No. of Destination Ports | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Avg. | Min. | Max. | Avg. | 1 | 2 | ≥3 | ||||||
| 1 | 13 | 16 | 116 | 63 | 8 | 116 | 54 | √ | 13 | |||||
| 2 | 22 | 8 | 168 | 68 | 8 | 136 | 52 | √ | 22 | |||||
| 3 | 13 | 30 | 124 | 74 | 8 | 124 | 68 | √ | √ | 13 | ||||
| 4 | 78 | 6 | 208 | 79 | 2 | 202 | 63 | √ | √ | 78 | ||||
| 5 | 36 | 38 | 176 | 97 | 8 | 170 | 81 | √ | √ | √ | 36 | |||
| 6 | 15 | 42 | 172 | 73 | 16 | 74 | 46 | √ | √ | √ | 15 | |||
| 7 | 14 | 72 | 204 | 147 | 24 | 202 | 117 | √ | √ | √ | √ | 14 | ||
| 8 | 14 | 40 | 148 | 96 | 40 | 136 | 87 | √ | √ | √ | 14 | |||
| 9 | 17 | 44 | 220 | 124 | 36 | 200 | 111 | √ | √ | √ | √ | 15 | 2 | |
| 10 | 8 | 72 | 176 | 122 | 10 | 156 | 93 | √ | √ | √ | 6 | 2 | ||
| 11 | 6 | 48 | 176 | 101 | 28 | 148 | 84 | √ | √ | √ | √ | 3 | 3 | |
| Grp# | #Inst | Fuzzy | GRASP(1 s) | CBLS | CP(10 s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| %Sol | %Opt | T(s) | %Sol | %Opt | T(s) | %Sol | %Opt | T(s) | %Sol | %Opt | T(s) | ||
| 1 | 13 | 100 | 100 | 4.52 | 100 | 100 | 6.3 | 100 | 59 | 0.1 | 100 | 100 | 0.1 |
| 2 | 22 | 100 | 95 | 8.12 | 100 | 100 | 15.4 | 100 | 77 | 3.6 | 91 | 91 | 21.6 |
| 3 | 13 | 100 | 100 | 5.1 | 100 | 100 | 7.8 | 100 | 92 | 0.5 | 100 | 100 | 0.5 |
| 4 | 78 | 100 | 100 | 28.32 | 100 | 99 | 37.3 | 100 | 92 | 6 | 99 | 99 | 19.7 |
| 5 | 36 | 100 | 94 | 16.41 | 100 | 94 | 22.3 | 97 | 58 | 7.1 | 92 | 92 | 39 |
| 6 | 15 | 100 | 93 | 4.68 | 100 | 100 | 6 | 93 | 80 | 1.2 | 100 | 100 | 5.4 |
| 7 | 14 | 100 | 71 | 6.66 | 100 | 93 | 9 | 93 | 79 | 2.3 | 64 | 64 | 53.5 |
| 8 | 14 | 100 | 100 | 6.4 | 100 | 100 | 6.1 | 93 | 43 | 1.5 | 93 | 93 | 10.5 |
| 9 | 17 | 94 | 82 | 8.69 | 94 | 82 | 12.3 | 94 | 47 | 5.2 | 88 | 88 | 36.5 |
| 10 | 8 | 100 | 88 | 3.33 | 100 | 100 | 4.8 | 100 | 88 | 0.7 | 100 | 100 | 0.7 |
| 11 | 6 | 100 | 67 | 2.56 | 100 | 83 | 3.2 | 50 | 17 | 1.3 | 83 | 83 | 10.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashed, D.; Eltawil, A.; Gheith, M. A Fuzzy Logic-Based Algorithm to Solve the Slot Planning Problem in Container Vessels. Logistics 2021, 5, 67. https://doi.org/10.3390/logistics5040067
Rashed D, Eltawil A, Gheith M. A Fuzzy Logic-Based Algorithm to Solve the Slot Planning Problem in Container Vessels. Logistics. 2021; 5(4):67. https://doi.org/10.3390/logistics5040067
Chicago/Turabian StyleRashed, Dalia, Amr Eltawil, and Mohamed Gheith. 2021. "A Fuzzy Logic-Based Algorithm to Solve the Slot Planning Problem in Container Vessels" Logistics 5, no. 4: 67. https://doi.org/10.3390/logistics5040067
APA StyleRashed, D., Eltawil, A., & Gheith, M. (2021). A Fuzzy Logic-Based Algorithm to Solve the Slot Planning Problem in Container Vessels. Logistics, 5(4), 67. https://doi.org/10.3390/logistics5040067






