Carbon Emissions Effect on Vendor-Managed Inventory System Considering Displaced Re-Start-Up Production Time
Abstract
:1. Introduction
1.1. Research Motivation
1.2. Research Background
1.3. Literature Review
2. Research Contribution
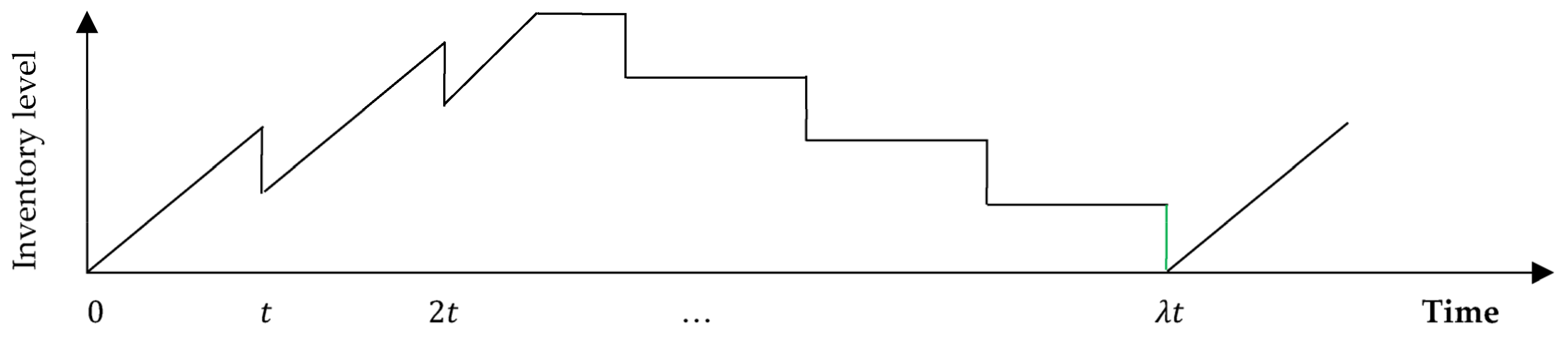
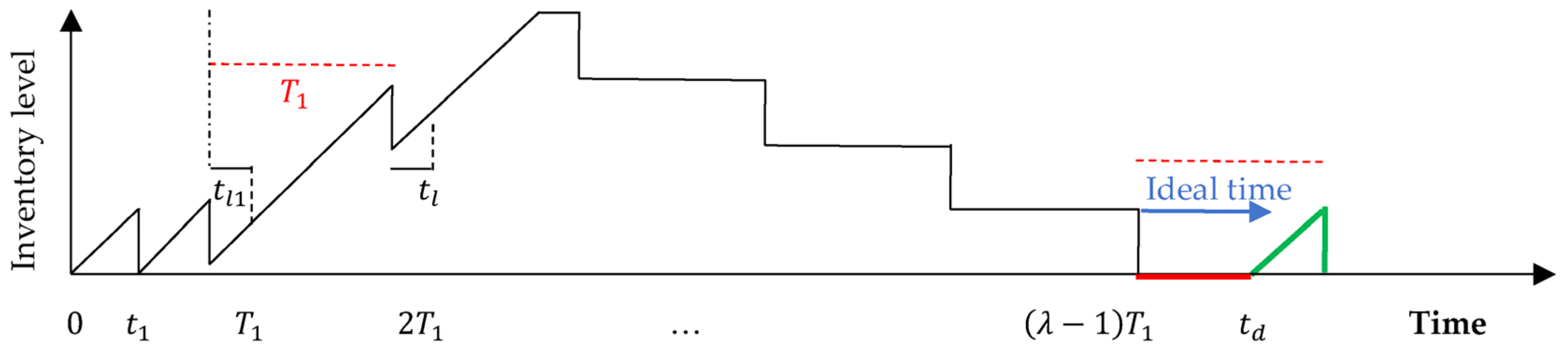
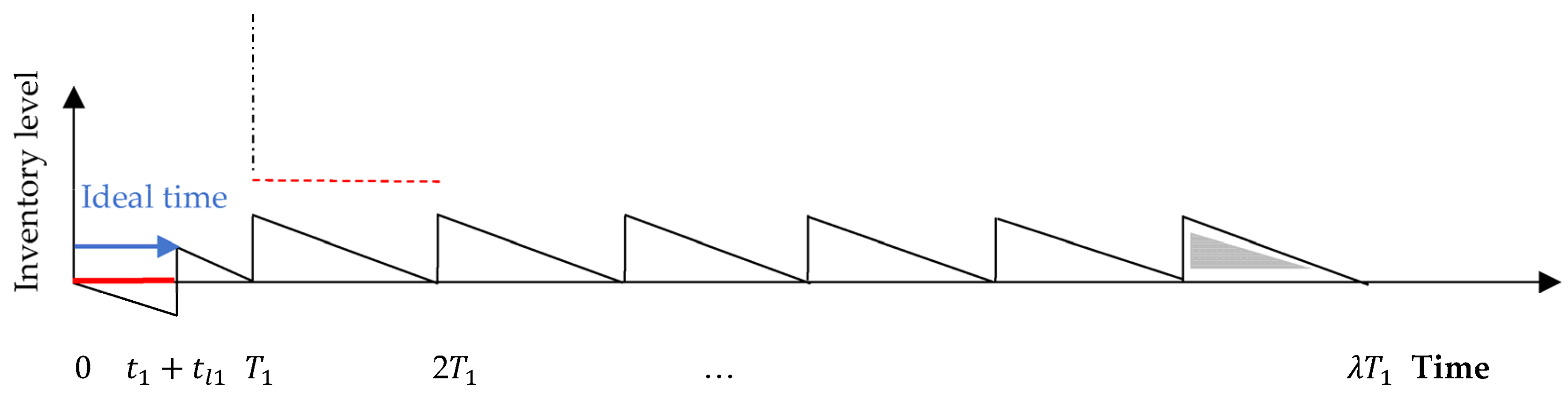
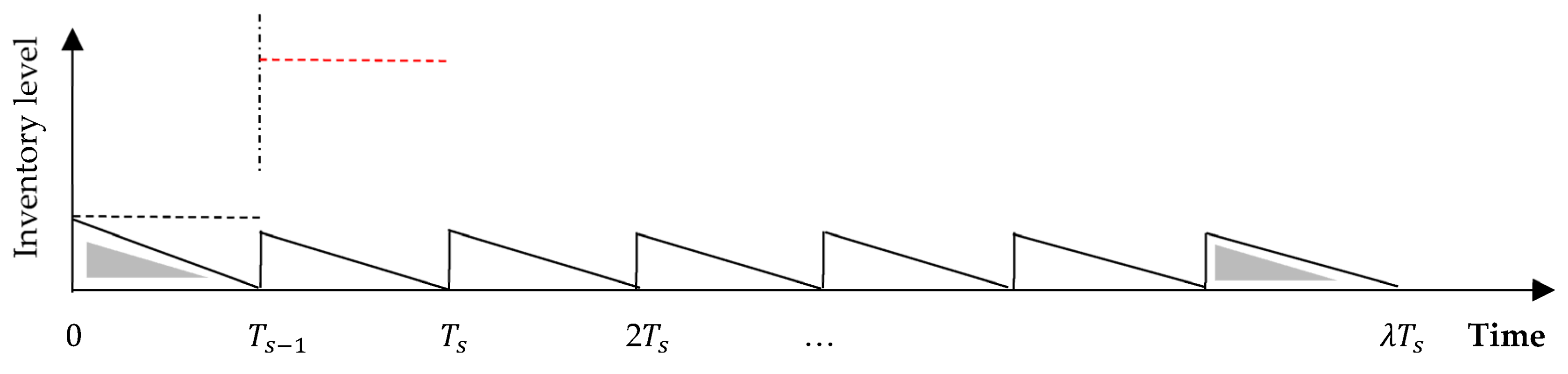
3. Formulation of the Joint Model
3.1. Notations
3.2. Assumptions
- A single item is manufactured at a rate (units/unit time).
- The demand is consumed at rate (units/unit time).
- No capacity restrictions are assumed, i.e., both the vendor and buyer have unlimited storage capacity.
- Any replenishment, ordered at the reorder point, reaches the buyer’s warehouse just prior to the end of that period. However, in the first period of the first cycle, where no items have been manufactured yet, i.e., the buyer’s inventory is zero, the first replenishment, ordered at the beginning of the first period delivers once it has been produced, from which it will arrive to the buyer’s warehouse after a transportation time, . In this case, shortages are allowed and fully backordered by time .
- In the first cycle, , which guarantees that the second lot will reach the buyer’s warehouse no later than time .
3.3. The Mathematical Model
3.3.1. Total Cost Function for the First Cycle under a Centralized Scenario
3.3.2. Total Cost Function for Subsequent Cycles under a Centralized Scenario
4. Numerical Examples
4.1. Example 1
4.2. Example 2
4.3. Example 3
5. Model Overview and Managerial Insights
6. Discussion
7. Conclusions and Further Research
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Solution Procedure
Appendix C
Solution Procedure
References
- Alamri, A.A. A Sustainable Closed-Loop Supply Chains Inventory Model Considering Optimal Number of Remanufacturing Times. Sustainability 2023, 15, 9517. [Google Scholar] [CrossRef]
- Alamri, A.A. Exploring the Effect of the First Cycle on the Economic Production Quantity Repair and Waste Disposal Model. Appl. Math. Model. 2021, 89, 519–540. [Google Scholar] [CrossRef]
- Benjaafar, S.; Li, Y.; Daskin, M. Carbon Footprint and the Management of Supply Chains: Insights from Simple Models. IEEE Trans. Autom. Sci. Eng. 2012, 10, 99–116. [Google Scholar] [CrossRef]
- Wang, X.J.; Choi, S.H. Impacts of Carbon Emission Reduction Mechanisms on Uncertain Make-To-Order Manufacturing. Int. J. Prod. Res. 2016, 54, 3311–3328. [Google Scholar] [CrossRef]
- EPA. Carbon Pollution from Transportation. U.S. Environmental Protection Agency. 2022. Available online: https://www.epa.gov/transportation-air-pollution-and-climate-change/carbon-pollution-transportation#transportation (accessed on 17 July 2023).
- Jaber, M.Y.; Zolfaghari, S. Quantitative Models for Centralised Supply Chain Coordination. In Supply Chains: Theory and Applications; InTech Open: Rijeka, Croatia, 2008; pp. 307–338. [Google Scholar]
- Glock, C.H. The Joint Economic Lot Size Problem: A Review. Int. J. Prod. Econ. 2012, 135, 671–686. [Google Scholar] [CrossRef]
- Rekik, Y.; Syntetos, A.; Jemai, Z. An E-Retailing Supply Chain Subject to Inventory Inaccuracies. Int. J. Prod. Econ. 2015, 167, 139–155. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Glock, C.H.; El Saadany, A.M.A. Supply Chain Coordination with Emissions Reduction Incentives. Int. J. Prod. Res. 2013, 51, 69–82. [Google Scholar] [CrossRef]
- Lippman, S.A. Economic Order Quantities and Multiple Set-up Costs. Manag. Sci. 1971, 18, 39–47. [Google Scholar] [CrossRef]
- Konur, D. Carbon Constrained Integrated Inventory Control and Truckload Transportation with Heterogeneous Freight Trucks. Int. J. Prod. Econ. 2014, 153, 268–279. [Google Scholar] [CrossRef]
- Venkatachalam, S.; Narayanan, A. Efficient Formulation and Heuristics for Multi-Item Single Source Ordering Problem with Transportation Cost. Int. J. Prod. Res. 2016, 54, 4087–4103. [Google Scholar] [CrossRef]
- Damert, M.; Feng, Y.; Zhu, Q.; Baumgartner, R.J. Motivating Low-Carbon Initiatives among Suppliers: The Role of Risk and Opportunity Perception. Resour. Conserv. Recycl. 2018, 136, 276–286. [Google Scholar] [CrossRef]
- Das, C.; Jharkharia, S. Low Carbon Supply Chain: A State-of-the-Art Literature Review. J. Manuf. Technol. Manag. 2018, 29, 398–428. [Google Scholar] [CrossRef]
- Banerjee, A. A Joint Economic-lot-size Model for Purchaser and Vendor. Decis. Sci. 1986, 17, 292–311. [Google Scholar] [CrossRef]
- Dong, Y.; Xu, K. A Supply Chain Model of Vendor Managed Inventory. Transp. Res. E Logist. Transp. Rev. 2002, 38, 75–95. [Google Scholar] [CrossRef]
- Devy, N.L.; Ai, T.J.; Astanti, R.D. A Joint Replenishment Inventory Model with Lost Sales. IOP Conf. Ser. Mater. Sci. Eng. 2018, 337, 12018. [Google Scholar] [CrossRef]
- Utama, D.M.; Santoso, I.; Hendrawan, Y.; Dania, W.A.P. Integrated Procurement-Production Inventory Model in Supply Chain: A Systematic Review. Oper. Res. Perspect. 2022, 9, 100221. [Google Scholar] [CrossRef]
- Nugroho, A.; Wee, H.M. Supply Chain Coordination under Vendor Managed Inventory System Considering Carbon Emission for Imperfect Quality Deteriorating Items. In Proceedings of the 9th International Conference on Operations and Supply Chain Management, Ho Chi Minh City, Vietnam, 15 December 2019; pp. 15–18. [Google Scholar]
- Bai, Q.; Jin, M.; Xu, X. Effects of Carbon Emission Reduction on Supply Chain Coordination with Vendor-Managed Deteriorating Product Inventory. Int. J. Prod. Econ. 2019, 208, 83–99. [Google Scholar] [CrossRef]
- Goyal, S.K. An Integrated Inventory Model for a Single Supplier-Single Customer Problem. Int. J. Prod. Res. 1977, 15, 107–111. [Google Scholar] [CrossRef]
- Goyal, S.K. “A Joint Economic-lot-size Model for Purchaser and Vendor”: A Comment. Decis. Sci. 1988, 19, 236–241. [Google Scholar] [CrossRef]
- Gunasekaran, A.; Irani, Z.; Papadopoulos, T. Modelling and Analysis of Sustainable Operations Management: Certain Investigations for Research and Applications. J. Oper. Res. Soc. 2014, 65, 806–823. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Soleymanfar, V.R.; Govindan, K. Sustainable Economic Production Quantity Models for Inventory Systems with Shortage. J. Clean. Prod. 2018, 174, 1011–1020. [Google Scholar] [CrossRef]
- Montabon, F.; Pagell, M.; Wu, Z. Making Sustainability Sustainable. J. Supply Chain. Manag. 2016, 52, 11–27. [Google Scholar] [CrossRef]
- Wahab, M.I.M.; Mamun, S.M.H.; Ongkunaruk, P. EOQ Models for a Coordinated Two-Level International Supply Chain Considering Imperfect Items and Environmental Impact. Int. J. Prod. Econ. 2011, 134, 151–158. [Google Scholar] [CrossRef]
- Hua, G.; Cheng, T.C.E.; Wang, S. Managing Carbon Footprints in Inventory Management. Int. J. Prod. Econ. 2011, 132, 178–185. [Google Scholar] [CrossRef]
- Wangsa, I. Greenhouse Gas Penalty and Incentive Policies for a Joint Economic Lot Size Model with Industrial and Transport Emissions. Int. J. Ind. Eng. Comput. 2017, 8, 453–480. [Google Scholar]
- Gautam, P.; Kishore, A.; Khanna, A.; Jaggi, C.K. Strategic Defect Management for a Sustainable Green Supply Chain. J. Clean. Prod. 2019, 233, 226–241. [Google Scholar] [CrossRef]
- Bazan, E.; Jaber, M.Y.; Zanoni, S. Supply Chain Models with Greenhouse Gases Emissions, Energy Usage and Different Coordination Decisions. Appl. Math. Model. 2015, 39, 5131–5151. [Google Scholar] [CrossRef]
- Halat, K.; Hafezalkotob, A. Modeling Carbon Regulation Policies in Inventory Decisions of a Multi-Stage Green Supply Chain: A Game Theory Approach. Comput. Ind. Eng. 2019, 128, 807–830. [Google Scholar] [CrossRef]
- Ghosh, A.; Jha, J.K.; Sarmah, S.P. Optimal Lot-Sizing under Strict Carbon Cap Policy Considering Stochastic Demand. Appl. Math. Model. 2017, 44, 688–704. [Google Scholar] [CrossRef]
- Hariga, M.; As’ad, R.; Shamayleh, A. Integrated Economic and Environmental Models for a Multi Stage Cold Supply Chain under Carbon Tax Regulation. J. Clean. Prod. 2017, 166, 1357–1371. [Google Scholar] [CrossRef]
- Ganesh Kumar, M.; Uthayakumar, R. Modelling on Vendor-Managed Inventory Policies with Equal and Unequal Shipments under GHG Emission-Trading Scheme. Int. J. Prod. Res. 2019, 57, 3362–3381. [Google Scholar] [CrossRef]
- Chen, X.; Benjaafar, S.; Elomri, A. The Carbon-Constrained EOQ. Oper. Res. Lett. 2013, 41, 172–179. [Google Scholar] [CrossRef]
- Saga, R.S.; Jauhari, W.A.; Laksono, P.W.; Dwicahyani, A.R. Investigating Carbon Emissions in a Production-Inventory Model under Imperfect Production, Inspection Errors and Service-Level Constraint. Int. J. Logist. Syst. Manag. 2019, 34, 29–55. [Google Scholar] [CrossRef]
- Zanoni, S.; Mazzoldi, L.; Jaber, M.Y. Vendor-Managed Inventory with Consignment Stock Agreement for Single Vendor–Single Buyer under the Emission-Trading Scheme. Int. J. Prod. Res. 2014, 52, 20–31. [Google Scholar] [CrossRef]
- Huang, Y.-S.; Fang, C.-C.; Lin, Y.-A. Inventory Management in Supply Chains with Consideration of Logistics, Green Investment and Different Carbon Emissions Policies. Comput. Ind. Eng. 2020, 139, 106207. [Google Scholar] [CrossRef]
- Malik, A.I.; Kim, B.S. A Constrained Production System Involving Production Flexibility and Carbon Emissions. Mathematics 2020, 8, 275. [Google Scholar] [CrossRef]
- Astanti, R.D.; Daryanto, Y.; Dewa, P.K. Low-Carbon Supply Chain Model under a Vendor-Managed Inventory Partnership and Carbon Cap-and-Trade Policy. J. Open Innov. Technol. Mark. Complex. 2022, 8, 30. [Google Scholar] [CrossRef]
- Turken, N.; Geda, A.; Takasi, V.D.G. The Impact of Co-Location in Emissions Regulation Clusters on Traditional and Vendor Managed Supply Chain Inventory Decisions. Ann. Oper. Res. 2021, 1–50. [Google Scholar] [CrossRef]
- Sarkar, B.; Saren, S. Product Inspection Policy for an Imperfect Production System with Inspection Errors and Warranty Cost. Eur. J. Oper. Res. 2016, 248, 263–271. [Google Scholar] [CrossRef]
- Rad, M.A.; Khoshalhan, F.; Glock, C.H. Optimal Production and Distribution Policies for a Two-Stage Supply Chain with Imperfect Items and Price-and Advertisement-Sensitive Demand: A Note. Appl. Math. Model. 2018, 57, 625–632. [Google Scholar] [CrossRef]
- Kim, M.-S.; Kim, J.-S.; Sarkar, B.; Sarkar, M.; Iqbal, M.W. An Improved Way to Calculate Imperfect Items during Long-Run Production in an Integrated Inventory Model with Backorders. J. Manuf. Syst. 2018, 47, 153–167. [Google Scholar] [CrossRef]
- De Giovanni, P.; Karray, S.; Martín-Herrán, G. Vendor Management Inventory with Consignment Contracts and the Benefits of Cooperative Advertising. Eur. J. Oper. Res. 2019, 272, 465–480. [Google Scholar] [CrossRef]
- Phan, D.A.; Vo, T.L.H.; Lai, A.N.; Nguyen, T.L.A. Coordinating Contracts for VMI Systems under Manufacturer-CSR and Retailer-Marketing Efforts. Int. J. Prod. Econ. 2019, 211, 98–118. [Google Scholar] [CrossRef]
- Ben-Daya, M.; As’ad, R.; Nabi, K.A. A Single-Vendor Multi-Buyer Production Remanufacturing Inventory System under a Centralized Consignment Arrangement. Comput. Ind. Eng. 2019, 135, 10–27. [Google Scholar] [CrossRef]
- Tarhini, H.; Karam, M.; Jaber, M.Y. An Integrated Single-Vendor Multi-Buyer Production Inventory Model with Transshipments between Buyers. Int. J. Prod. Econ. 2020, 225, 107568. [Google Scholar] [CrossRef]
- Dey, O.; Giri, B.C. A New Approach to Deal with Learning in Inspection in an Integrated Vendor-Buyer Model with Imperfect Production Process. Comput. Ind. Eng. 2019, 131, 515–523. [Google Scholar] [CrossRef]
- Giri, B.C.; Chakraborty, A.; Maiti, T. Consignment Stock Policy with Unequal Shipments and Process Unreliability for a Two-Level Supply Chain. Int. J. Prod. Res. 2017, 55, 2489–2505. [Google Scholar] [CrossRef]
- Jauhari, W.A.; Sofiana, A.; Kurdhi, N.A.; Laksono, P.W. An Integrated Inventory Model for Supplier-Manufacturer-Retailer System with Imperfect Quality and Inspection Errors. Int. J. Logist. Syst. Manag. 2016, 24, 383–407. [Google Scholar]
- Khan, M.; Hussain, M.; Cárdenas-Barrón, L.E. Learning and Screening Errors in an EPQ Inventory Model for Supply Chains with Stochastic Lead Time Demands. Int. J. Prod. Res. 2017, 55, 4816–4832. [Google Scholar] [CrossRef]
- Pal, S.; Mahapatra, G.S. A Manufacturing-Oriented Supply Chain Model for Imperfect Quality with Inspection Errors, Stochastic Demand under Rework and Shortages. Comput. Ind. Eng. 2017, 106, 299–314. [Google Scholar] [CrossRef]
- Tiwari, S.; Kazemi, N.; Modak, N.M.; Cárdenas-Barrón, L.E.; Sarkar, S. The Effect of Human Errors on an Integrated Stochastic Supply Chain Model with Setup Cost Reduction and Backorder Price Discount. Int. J. Prod. Econ. 2020, 226, 107643. [Google Scholar] [CrossRef]
- Jaggi, C.K.; Tiwari, S.; Shafi, A.A. Effect of Deterioration on Two-Warehouse Inventory Model with Imperfect Quality. Comput. Ind. Eng. 2015, 88, 378–385. [Google Scholar] [CrossRef]
- Bouchery, Y.; Ghaffari, A.; Jemai, Z.; Tan, T. Impact of Coordination on Costs and Carbon Emissions for a Two-Echelon Serial Economic Order Quantity Problem. Eur. J. Oper. Res. 2017, 260, 520–533. [Google Scholar] [CrossRef]
- Kazemi, N.; Abdul-Rashid, S.H.; Ghazilla, R.A.R.; Shekarian, E.; Zanoni, S. Economic Order Quantity Models for Items with Imperfect Quality and Emission Considerations. Int. J. Syst. Sci. Oper. Logist. 2018, 5, 99–115. [Google Scholar] [CrossRef]






| No | Authors | First Cycle | Independent Cycles | Adjustable Parameters | Emissions | Carbon Regulations |
|---|---|---|---|---|---|---|
| 1 | Wahab et al. [26] | Transportation | Carbon tax | |||
| 2 | Gautam et al. [29] | Transportation | Carbon tax | |||
| 3 | Hariga et al. [33] | Storage, Transportation | Carbon tax | |||
| 4 | Bazan et al. [30] | Production, Transportation | Carbon tax, Penalty | |||
| 5 | Ghosh et al. [32] | Production | Carbon tax, Carbon cap | |||
| 6 | Zanoni et al. [37] | Production | Carbon tax, Penalty | |||
| 7 | Konur [11] | Transportation | Carbon cap | |||
| 8 | Wangsa [28] | Production | Carbon tax, Penalty | |||
| 9 | Astanti et al. [40] | Production, Transportation | Carbon tax | |||
| 10 | Saga et al. [36] | Production | Carbon tax, Penalty | |||
| 11 | Jaber et al. [9] | Production | Carbon tax, Penalty | |||
| 12 | Bouchery [56] | Transportation | Carbon tax | |||
| 13 | Malik and Kim. [39] | Production | Carbon tax | |||
| 14 | Kumar and Uthayakumar [34] | Production | Carbon tax, Penalty | |||
| 15 | The proposed model | Production, Transportation, Storage | Carbon tax, Carbon cap |
| Order quantity for the first cycle (subsequent cycles) | |
| The time to produce units in the first cycle (subsequent cycles) | |
| The time elapsed to deliver the first shipment of size in the first cycle | |
| The time elapsed to deliver the shipment of size , where | |
| The time to consume units | |
| The time to consume units (the last lot that was delivered from the previous cycle) | |
| The time for the first cycle (subsequent cycles) | |
| The idle time before production re-start-up time for subsequent cycles | |
| Buyer’s demand rate (units/unit time) | |
| Energy consumed while storing the items in buyer’s warehouse (kWh/unit/unit time) | |
| Energy consumed while storing the items in vendor’s warehouse (kWh/unit/unit time) | |
| CO2 emissions from electricity (ton CO2/kWh) | |
| Vendor’s production rate (units/unit time) | |
| CO2 emissions from production (ton CO2/unit) | |
| Fixed transportation cost ($/truck) | |
| Maximum capacity for the truck (units/truck) | |
| Number of trucks required to deliver the lot size | |
| Fixed transportation cost per unit, where ; | |
| Product’s weight (ton/unit) | |
| Distance between the vendor and the buyer (km) | |
| Distance between the freight and the vendor (km) | |
| Fuel consumption for truckload (liters/km/ton) | |
| Fuel consumption for an empty truck (liters/km) | |
| CO2 emissions from truck fuel (ton CO2/liter) | |
| Variable transportation cost related to fuel consumption ($/liter) | |
| The total amount of CO2 emissions generated by the system (ton CO2/unit) | |
| CO2 emissions cap (ton CO2) | |
| Buyer’s CO2 emissions tax ($/ton CO2) | |
| Vendor’s CO2 emissions tax ($/ton CO2) | |
| Vendor’s CO2 emissions tax for transportation ($/ton CO2) | |
| Unit production cost | |
| Vendor’s set-up cost | |
| Buyer’s ordering cost | |
| Vendor’s holding cost | |
| Buyer’s holding cost | |
| Vendor’s investment cost that renders an item green | |
| CO2 emissions from production subject to investment (ton CO2/unit), where | |
| Vendor’s coordination multiplier |
| 1.44 | 1.44 | 0.0005 | 8000 | 1.4 | 600 |
| kWh/unit/month | kWh/unit/month | ton CO2/kWh | units/month | ton CO2/unit | USD/truck |
| 500 | 1.5 | 0.01 | 80 | 300 | 0.75 |
| units/truck | USD/unit | ton/unit | km | km | USD/liter |
| 0.064 | 0.32 | 0.0026 | 5000 | 5 | 3 |
| liters/km/ton | liters/km | ton CO2/liter | tonCO2/month | USD/unit/month | USD/unit/month |
| 800 | 2.5 | 2.5 | 2.5 | 3000 | 0.08 |
| USD/setup | USD/ton CO2 | USD/ton CO2 | USD/ton CO2 | units/month | month |
| 50 | 1200 | 400 | |||
| USD/unit | USD/setup | USD/order |
| First Cycle | Mixed Policy | % Saving | |||||
|---|---|---|---|---|---|---|---|
| With investment | 1285 | 2 | 2 | 3219 | 163,696 | 2.26% | |
| Without investment | 1091 | 2 | 2 | 4202 | 167,477 | ||
| Subsequent Cycles | |||||||
| With investment | 1032 | 2 | 2 | 3219 | 165,910 | 2.94% | |
| Without investment | 1411 | 1 | 3 | 4202 | 170,927 |
| Subsequent Cycles | Mixed Policy | % Saving | |||||
|---|---|---|---|---|---|---|---|
| With investment | 647 | 5 | 1 | 3219 | 165,432 | 0.29% | |
| Without investment | 641 | 4 | 1 | 4202 | 169,473 | 0.85% |
| Parameter | First Cycle | Mixed Policy | % Saving | |||||
|---|---|---|---|---|---|---|---|---|
| With investment | 1473 | 2 | 3 | 3219 | 164,166 | 1.63% | ||
| Without investment | 2074 | 1 | 4 | 4202 | 166,890 | |||
| Subsequent Cycles | ||||||||
| With investment | 1191 | 2 | 2 | 3219 | 164,921 | 2.19% | ||
| Without investment | 1009 | 2 | 2 | 4202 | 168,610 | |||
| First Cycle | ||||||||
| With investment | 1091 | 2 | 2 | 3219 | 162,561 | 2.21% | ||
| Without investment | 1292 | 1 | 2 | 4202 | 166,232 | |||
| Subsequent Cycles | ||||||||
| With investment | 1411 | 1 | 3 | 3219 | 166,011 | 0.85% | ||
| Without investment | 1004 | 1 | 2 | 4202 | 167,422 | |||
| First Cycle | ||||||||
| With investment | 1822 | 1 | 3 | 1878 | 104,679 | 4.00% | ||
| Without investment | 1493 | 1 | 3 | 2801 | 109,037 | |||
| Subsequent Cycles | ||||||||
| With investment | 1508 | 1 | 3 | 1879 | 105,998 | 3.25% | ||
| Without investment | 1234 | 1 | 2 | 2802 | 109,557 | |||
| First Cycle | ||||||||
| With investment | 1371 | 2 | 2 | 2818 | 162,185 | 3.12% | ||
| Without investment | 1091 | 2 | 2 | 4202 | 167,477 | |||
| Subsequent Cycles | ||||||||
| With investment | 1102 | 2 | 2 | 2818 | 164,520 | 3.75% | ||
| Without investment | 1411 | 1 | 3 | 4202 | 170,927 | |||
| First Cycle | ||||||||
| With investment | 2223 | 1 | 4 | 3219 | 163,818 | 2.27% | ||
| Without investment | 1824 | 1 | 3 | 4202 | 167,617 | |||
| Subsequent Cycles | ||||||||
| With investment | 1796 | 1 | 3 | 3219 | 165,859 | 2.70% | ||
| Without investment | 1469 | 1 | 3 | 4202 | 170,457 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alamri, A.A. Carbon Emissions Effect on Vendor-Managed Inventory System Considering Displaced Re-Start-Up Production Time. Logistics 2023, 7, 67. https://doi.org/10.3390/logistics7040067
Alamri AA. Carbon Emissions Effect on Vendor-Managed Inventory System Considering Displaced Re-Start-Up Production Time. Logistics. 2023; 7(4):67. https://doi.org/10.3390/logistics7040067
Chicago/Turabian StyleAlamri, Adel A. 2023. "Carbon Emissions Effect on Vendor-Managed Inventory System Considering Displaced Re-Start-Up Production Time" Logistics 7, no. 4: 67. https://doi.org/10.3390/logistics7040067
APA StyleAlamri, A. A. (2023). Carbon Emissions Effect on Vendor-Managed Inventory System Considering Displaced Re-Start-Up Production Time. Logistics, 7(4), 67. https://doi.org/10.3390/logistics7040067






