The Radiation-Specific Components Generated in the Second Step of Sequential Reactions Have a Mountain-Shaped Function

Abstract

A mathematical model for radiation hormesis below 100 mSv has previously been reported, but the origins of the formula used in the previous report were not provided. In the present paper, we first considered a sequential reaction model with identical rate constants. We showed that the function of components produced in the second step of this model agreed well with the previously reported function. Furthermore, in a general sequential reaction model with different rate constants, it was mathematically proved that the function representing the component produced in the second step is always mountain-shaped: the graph has a peak with one inflection point on either side, and such a component may induce radiation hormesis.

1. Introduction

Cancer is a disease that afflicts people worldwide, and there is no specific cure for it. Cancer is generated by various causes, including radiation exposure. When the radiation dose is 100 mSv or higher, the cancer incidence probability is proportional to the radiation dose [1,2]. However, it is difficult to statistically evaluate the cancer incidence probability at doses of less than 100 mSv; that is, it is unclear how the cancer incidence probability increases or decreases with a radiation dose in this range [1,3,4,5,6,7,8,9,10]. The management of radiation risks is based on the hypotheses that radiation is dangerous to living organisms even at low doses and that the cancer incidence probability is proportional to a radiation dose below 100 mSv as well (linear non-threshold theory: LNT). However, there are doubts as to whether the LNT model is valid at low doses, and the phenomenon of radiation hormesis, in which radiation is beneficial to living organisms, has also been reported [11,12,13]. Therefore, it may be possible to clarify the truth at low doses by adding biological findings at the molecular–cellular level and mathematical models [11,14,15,16,17,18,19,20,21,22].

The radiation adaptive response has been reported as a phenomenon related to low dose [23,24,25,26,27,28,29,30], and the term “inhibition effect (R(x))” used in previous papers is not strictly equivalent to the adaptive response but is defined as the element that theoretically leads to radiation-specific hormesis-coupled LNT [31,32]. In addition, a hunchback-shaped graph has been proposed to describe components involved in the radiation adaptive response (Figure 1A) [33,34,35]. If such an increasing/decreasing component contributes to radiation hormesis, the cancer incidence probability must be greater than zero at 0 mSv (Figure 1C) [31,36,37,38,39]. In other words, the causes of cancer development in this case are not limited to radiation, and factors other than radiation [28,29] must be involved, for example, reactive oxygen species.

On the other hand, for cancers caused solely by radiation, the cancer incidence probability must be zero when the radiation dose is 0 mSv [31]. Moreover, if the components are generated solely by radiation, R(0) must be zero [31]. Therefore, R(x) with a mountain-shaped graph, as shown in Figure 1B, is required for the existence of a radiation hormesis effect (Figure 1E) [31]. If the R(x) of Figure 1A is used, the cancer incidence probability mathematically has negative values (Figure 1D), and it is impossible for the cancer incidence probability to have negative values. In Figure 1B, unlike Figure 1A, there is one inflection point in the region 0 < x < x₀. In this paper, the mathematical equation used previously [31,32] is derived from the concept of chemical kinetics in Section 2, and a more general model is discussed in Section 3 and Section 4.

2. Generative Model Fitted to the Previously-Reported Equation

As one R(x) with a mountain-shaped graph (Figure 1B), Equation (1) has previously been used [31]. The maximum hormesis effect can be produced when n is 2 (Equation (2)) [31]. In fact, Fornalski [40,41,42,43,44] used Equations (1) and (2) as a function to show a radiation adaptive response. In this section, what model Equation (2) can be derived from is discussed.

$$R\left(x\right)=x^n{e}^{-ax}$$

(1)

$$R\left(x\right)=x^2{e}^{-ax}$$

(2)

Usually, in reaction kinetics using differential equations, each component quantity is given as a function of time. Considering that the dose x is proportional to time if the dose rate is constant, each component quantity can be expressed as a function of dose x. Here, the reaction model of Scheme 1 is considered. In this scheme, the raw material P decomposes to produce Q, Q further decomposes to produce R, and R decomposes to another substance. In addition, when the component amount of each factor increases or decreases only with the dose of radiation, differential Equations (3)–(5) hold. All rate constants are the same, and the rate constant, a, is positive. Defining the initial quantity of P(x) as a positive number, P₀, and solving these equations produces Equation (6). The obtained Equation (6) has the same form as Equation (2). This means that the component R produced in the second step of the sequential reaction is a candidate for the component that induces the hormesis effect.

$$\frac{dP}{dx}=-aP$$

(3)

$$\frac{dQ}{dx}=aP-aQ$$

(4)

$$\frac{dR}{dx}=aQ-aR$$

(5)

$$R\left(x\right)=\frac{1}{2}{P}_0{a}^2{x}^2{e}^{-ax}$$

(6)

3. Considerations Using a General Model

In the previous section, it was shown that the component R in Scheme 1 obeys Equation (2). However, it is not usual that the three reaction rate constants are exactly the same. Therefore, we should consider a general model in which each reaction constant is different (Scheme 2). By solving the differential Equations (3), (7), and (8) in the same way as in Section 2, Equation (9) is obtained in accordance with a previous report [45]. Note that P₀, a, b, and c are positive.

$$\frac{dQ}{dx}=aP-bQ$$

(7)

$$\frac{dR}{dx}=bQ-cR$$

(8)

$$R\left(x\right)=P_0\frac{-ab}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}\left\{\left(b-c\right)e^{-ax}+\left(c-a\right)e^{-bx}+\left(a-b\right)e^{-cx}\right\}$$

(9)

In Scheme 2, Q(x) can be easily derived mathematically to have a graph with the hunchbacked shape, as shown in Figure 1A; so, the component Q cannot induce the hormesis effect considered in this paper. On the other hand, if Equation (9) has a mountain-shaped graph (Figure 1B), as in Equation (2), then the component R is the candidate factor we desire. Therefore, in the next section, the shape of R(x) in Scheme 2 will be considered mathematically.

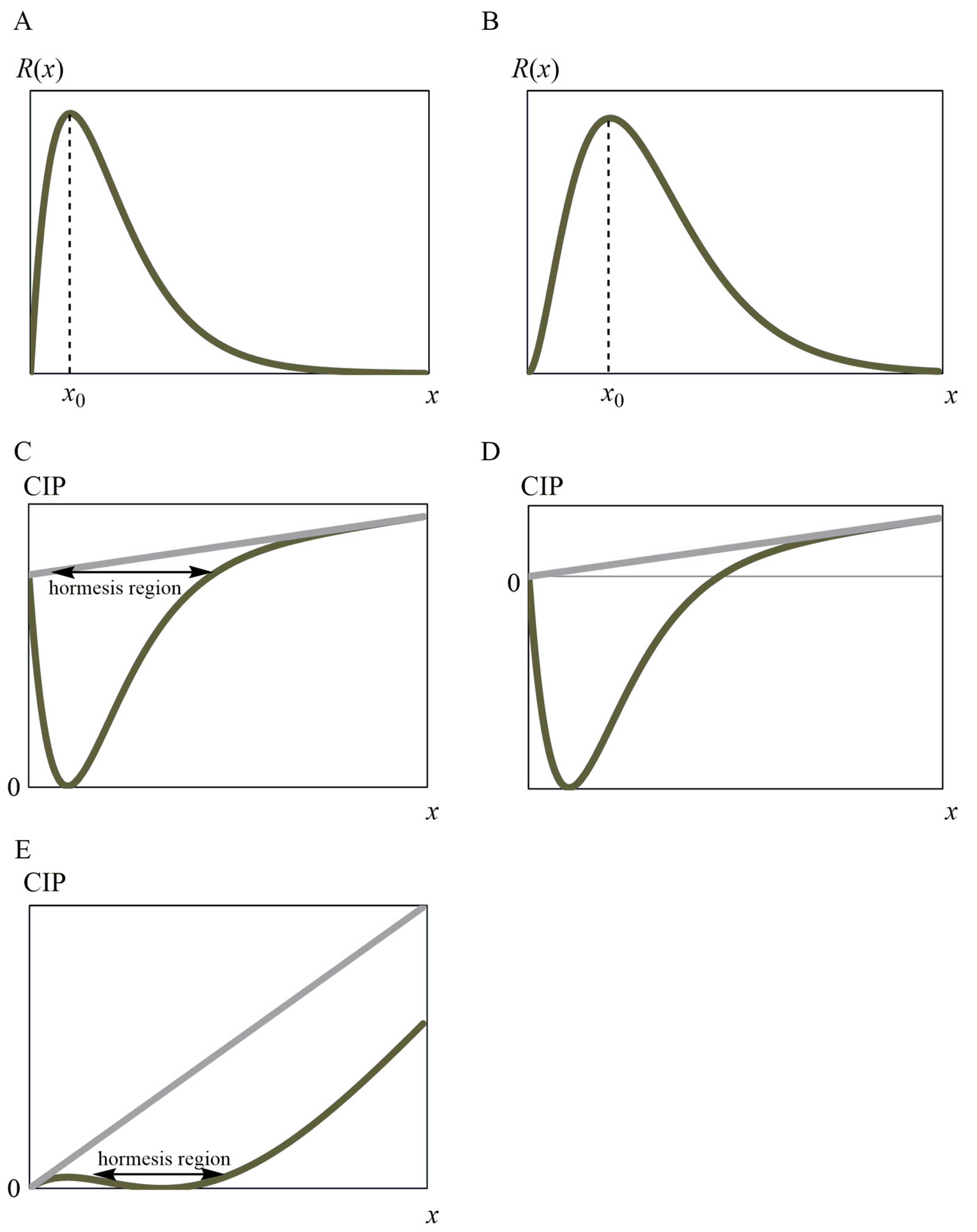
4. Shape of R(x) in Scheme 2: Proof That Equation (9) Has a Mountain-Shaped Graph as in Figure 1B

4.1. First-Order Differentiation

To prove that the graph of Equation (9) is mountain-shaped (Figure 1B), an increase/decrease in R(x) is considered. Consider function f(x) defined in Equation (10). Since P₀, a, b, and c are positive, abP₀ is always positive. For R(x)/abP₀, a, b, and c can be treated symmetrically. Therefore, it is not necessary to consider all of a > b > c, a > c > b, b > a > c, b > c > a, c > a > b, and c > b > a but only one of these cases mathematically. That is, there is no loss of generality in considering b > c > a for R(x)/abP₀. In this case, since −1/(a − b)(b − c)(c − a) is positive, we consider an increase/decrease in f(x).

$$f\left(x\right) :=\left(b-c\right)e^{-ax}+\left(c-a\right)e^{-bx}+\left(a-b\right)e^{-cx}$$

(10)

Differentiation of f(x) leads to Equation (11).

$$\frac{df}{dx}=e^{-ax}\left\{a\left(c-b\right)+b\left(a-c\right)e^{\left(a-b\right)x}+c\left(b-a\right)e^{\left(a-c\right)x}\right\}$$

(11)

Next, we consider the function g(x) defined in Equation (12); note that the sign of g(x) for a given x is the same as that of df/dx.

$$g\left(x\right) :=a\left(c-b\right)+b\left(a-c\right)e^{\left(a-b\right)x}+c\left(b-a\right)e^{\left(a-c\right)x}$$

(12)

Differentiation of g(x) gives Equation (13).

$$\frac{dg}{dx}=\left(c-a\right)\left(b-a\right)e^{ax}\left(b{e}^{-bx}-c{e}^{-cx}\right)$$

(13)

Since we have assumed b > c > a, Equation (14) must hold for dg/dx to be nonnegative.

$$b{e}^{-bx}-c{e}^{-cx}\ge 0$$

(14)

Solving Equation (14) yields Equation (15), which also defines x₁.

$$x\le \frac{\ln \frac{b}{c}}{b-c}=: x_1$$

(15)

From Equation (12), the following values are obtained when x is 0 and when x is infinite.

$$g\left(0\right)=0$$

(16)

$$g\left(\infty \right)=a\left(c-b\right)<0$$

(17)

Summarizing the above, a derivative sign chart of g(x) is presented in

Table 1. The derivative sign chart of g(x).

$x$	$0$	$\cdots$	$x_1$	$\cdots$	$\infty$
$\frac{dg}{dx}$		$+$	$0$	$-$
$g\left(x\right)$	$0$	$up$		$down$	$-$

.

From the signs in Table 1, there is only one value of x for which g(x) is zero. If such a value of x is defined as x₂, Equation (18) holds. This x₂ is larger than x₁, and thus the signs of df/dx are derived from the signs of g(x), which in turn give us the signs of dR/dx (

Table 2. The signs of df/dx and dR/dx.

$x$	$0$	$\cdots$	$x_2$	$\cdots$	$\infty$
$\frac{df}{dx}$	$0$	$+$	$0$	$-$
$\frac{dR}{dx}$	$0$	$+$	$0$	$-$

).

$$g\left(x_2\right)=0$$

(18)

4.2. Second-Order Differentiation

Further differentiation of Equation (11) yields Equation (19).

$$\frac{d^{2}f}{d{x}^2}=e^{-ax}\left\{a^2\left(b-c\right)+b^2\left(c-a\right)e^{\left(a-b\right)x}+c^2\left(a-b\right)e^{\left(a-c\right)x}\right\}$$

(19)

Considering the function h(x) defined in Equation (20), we see that the sign of h(x) at a given x is the same as that of d²f/dx².

$$h\left(x\right) :=a^2\left(b-c\right)+b^2\left(c-a\right)e^{\left(a-b\right)x}+c^2\left(a-b\right)e^{\left(a-c\right)x}$$

(20)

Differentiation of h(x) produces Equation (21).

$$\frac{dh}{dx}=\left(c-a\right)\left(b-a\right)e^{ax}\left(c^2{e}^{-cx}-b^2{e}^{-bx}\right)$$

(21)

Since we have assumed b > c > a, Equation (22) must hold for dh/dx to be nonnegative.

$$c^2{e}^{-cx}-b^2{e}^{-bx}\ge 0$$

(22)

Solving Equation (22) yields Equation (23). Using the definition in Equation (15), we can also express the relation in Equation (15) using x₁.

$$x\ge 2\frac{\ln \frac{b}{c}}{b-c}=2x_1$$

(23)

From Equation (20), the following values are obtained when x is 0 and when x is infinite.

$$h\left(0\right)=\left(b-c\right)\left(b-a\right)\left(c-a\right)>0$$

(24)

$$h\left(\infty \right)=a^2\left(b-c\right)>0$$

(25)

A derivative sign chart of h(x) summarizing the above is presented in

Table 3. The derivative sign chart of h(x) without h(2x₁).

$x$	$0$	$\cdots$	$2x_1$	$\cdots$	$\infty$
$\frac{dh}{dx}$		$-$	$0$	$+$
$h\left(x\right)$	$+$	$down$	$\left(unknown\right)$	$up$	$+$

.

It remains necessary to find the sign of h(2x₁). Substituting 2x₁ for x in Equation (20), we obtain Equation (26).

$$h\left(2x_1\right)=a^2\left(b-c\right)+b^2\left(c-a\right)e^{2\left(a-b\right)x_1}+c^2\left(a-b\right)e^{2\left(a-c\right)x_1}$$

(26)

Equation (27) is obvious from Equations (22) and (23). Substituting Equation (27) into Equation (26) and rearranging, we obtain Equation (28).

$$c^2{e}^{-2c{x}_1}-b^2{e}^{-2b{x}_1}=0$$

(27)

$$h\left(2x_1\right)=\left(b-c\right)\left(a+b{e}^{\left(a-b\right)x_1}\right)\left(a-b{e}^{\left(a-b\right)x_1}\right)$$

(28)

Once the sign of m(x₁), defined by Equation (29), is known, the sign of h(2x₁) is clear.

$$m\left(x_1\right) :=a-b{e}^{\left(a-b\right)x_1}$$

(29)

Applying Equation (15) to Equation (29), we can obtain Equation (30).

$$m\left(x_1\right) :=a-b^{\frac{a-c}{b-c}}{c}^{\frac{b-a}{b-c}}$$

(30)

Next, we consider the function p(k) defined by Equation (31). Note that p(k) decreases monotonically with k for k > 0.

$$p\left(k\right)=\frac{\ln k}{k-1}\hspace{1em}(k>0)$$

(31)

We recall that a is positive. The assumption b > c > a implies that b/a > c/a; so, the monotonicity of Equation (31) implies that Equation (32) holds.

$$\frac{\ln \frac{b}{a}}{\frac{b}{a}-1}<\frac{\ln \frac{c}{a}}{\frac{c}{a}-1}$$

(32)

Rearranging Equation (32), we can obtain Equation (33); so, m(x₁) is negative.

$$a-b^{\frac{a-c}{b-c}}{c}^{\frac{b-a}{b-c}}<0$$

(33)

Hence, h(2x₁) is negative, and we can update Table 3 as

Table 4. The full derivative sign chart of h(x).

$x$	$0$	$\cdots$	$2x_1$	$\cdots$	$\infty$
$\frac{dh}{dx}$		$-$	$0$	$+$
$h\left(x\right)$	$+$	$down$	$-$	$up$	$+$

.

From the signs in Table 4, there are two values of x for which h(x) is zero. The x value in the range 0 < x < 2x₁ is defined as x₃ and that in the range 2x₁ < x is defined as x₄, expressed as Equations (34) and (35), respectively. We then derive the signs of d²f/dx² from those of h(x), which are the same as those of d²R/dx² (

Table 5. The signs of d²f/dx² and d²R/dx².

$x$	$0$	$\cdots$	$x_3$	$\cdots$	$x_4$	$\cdots$
$\frac{d^{2}f}{d{x}^2}$		$+$	$0$	$-$	$0$	$+$
$\frac{d^{2}R}{d{x}^2}$		$+$	$0$	$-$	$0$	$+$

).

$$h\left(x_3\right)=0$$

(34)

$$h\left(x_4\right)=0$$

(35)

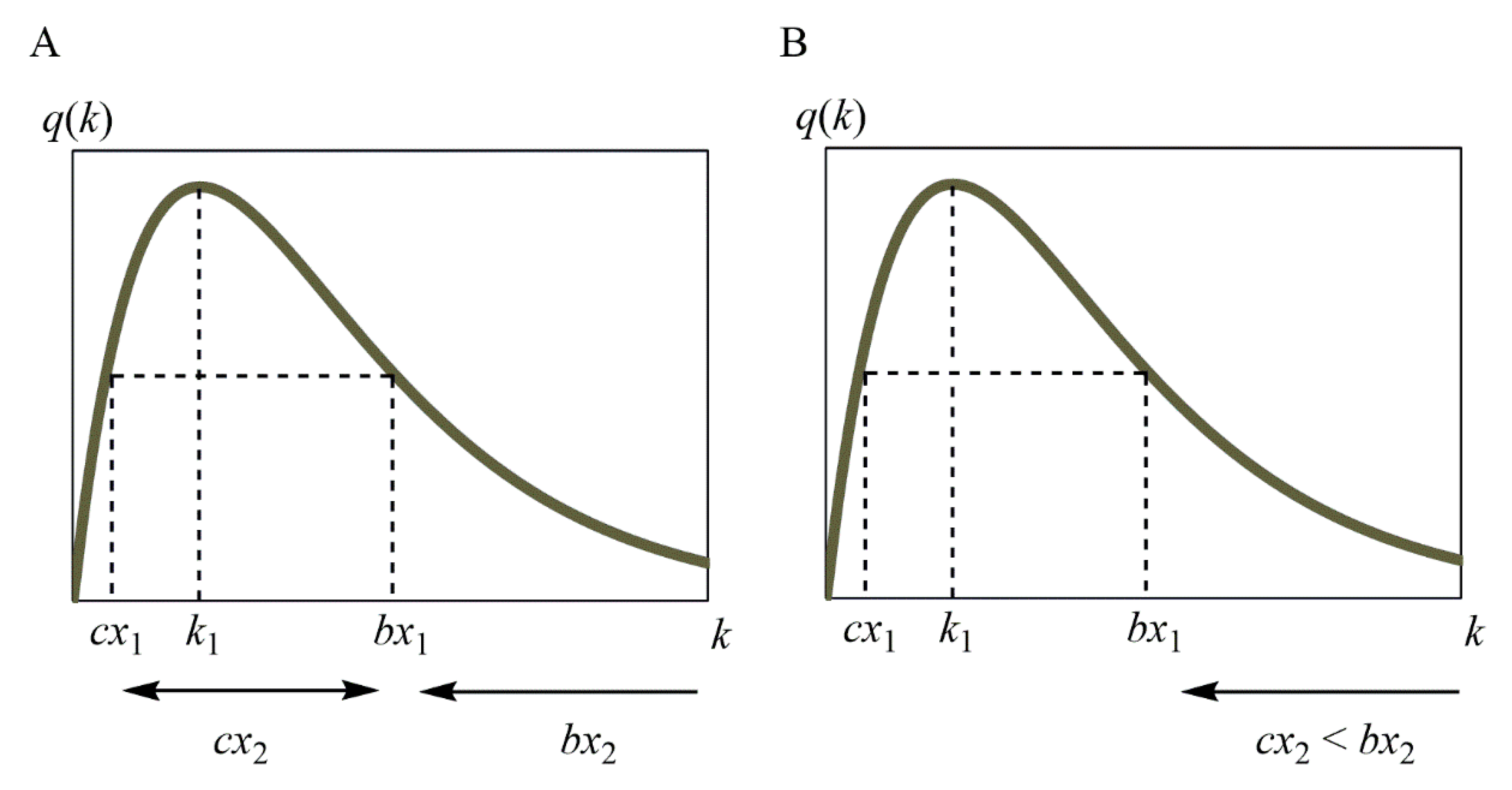
4.3. Increase/Decrease in R(x)

Using Table 2 and Table 5, we now consider the increase/decrease in f(x). Recall that x₃ < x₄. If d²f/dx²(x₂) > 0, then either (i) or (iii) below is correct, whereas if d²f/dx²(x₂) < 0, then (ii) is correct.

(i)

x₂ < x₃ < x₄;

(ii)

x₃ < x₂ < x₄;

(iii)

x₃ < x₄ < x₂.

Substituting x₂ for x, we obtain Equation (36) from Equation (11) and Equation (37) from Equation (19). For convenience, we define d²f/dx²(x₂) as u. We want to find the sign of u.

$$\frac{df}{dx}\left(x_2\right)=e^{-a{x}_2}\left\{a\left(c-b\right)+b\left(a-c\right)e^{\left(a-b\right)x_2}+c\left(b-a\right)e^{\left(a-c\right)x_2}\right\}=0$$

(36)

$$\frac{d^{2}f}{d{x}^2}\left(x_2\right)=e^{-a{x}_2}\left\{a^2\left(b-c\right)+b^2\left(c-a\right)e^{\left(a-b\right)x_2}+c^2\left(a-b\right)e^{\left(a-c\right)x_2}\right\}=:u$$

(37)

Substituting Equation (36) into Equation (37) gives Equation (38).

$$u=\left(c-a\right)\left(b-a\right)\left(b{e}^{-b{x}_2}-c{e}^{-c{x}_2}\right)$$

(38)

Next, we define v as in Equation (39). From the assumption b > c > a, the sign of v tells us the sign of u.

$$v :=b{e}^{-b{x}_2}-c{e}^{-c{x}_2}$$

(39)

From Equations (14) and (15), we can obtain Equation (40).

$$b{e}^{-b{x}_1}=c{e}^{-c{x}_1}$$

(40)

We multiply both sides of Equation (39) by x₂ and both sides of Equation (40) by x₁.

$$x_{2}v=b{x}_2{e}^{-b{x}_2}-c{x}_2{e}^{-c{x}_2}$$

(41)

$$b{x}_1{e}^{-b{x}_1}=c{x}_1{e}^{-c{x}_1}$$

(42)

Note that x₁ < x₂ and c < b; so, either (iv) or (v) below is correct.

(iv)

cx₁ < cx₂ < bx₁ < bx₂;

(v)

cx₁ < bx₁ < cx₂ < bx₂.

Now, we define q(k) as in Equation (43) and define k₁ as the maximizer of q(k).

$$q\left(k\right)=k{e}^{-k}\hspace{1em}\left(k\ge 0\right)$$

(43)

Considering Equation (42) and the increase/decrease in q(k), cx₁ is smaller and bx₁ is larger than k₁ in the graph shown in Figure 2. We now compare q(cx₁), q(bx₁), q(cx₂), and q(bx₂) for the cases in (iv) and (v).

Given cx₁ < cx₂ < bx₁ from (iv), we obtain q(cx₂) > q(bx₁) = q(cx₁). Moreover, q(bx₁) > q(bx₂) is established from bx₁ < bx₂. Therefore, q(cx₂) > q(bx₂) holds.

If instead we assume cx₁ < bx₁ < cx₂ < bx₂ as in (v), we obtain q(cx₁) = q(bx₁) > q(cx₂) > q(bx₂). Therefore, we have q(cx₂) > q(bx₂).

Thus, Equation (44) holds in both cases (iv) and (v).

$$c{x}_2{e}^{-c{x}_2}>b{x}_2{e}^{-b{x}_2}$$

(44)

From Equation (44), v is negative, and consequently, u is negative. Therefore, (ii) is correct. From the order x₃ < x₂ < x₄ and Table 2 and Table 5, the derivative sign chart of R(x) is as shown in

Table 6. The derivative sign chart of R(x).

$x$	$0$	$\cdots$	$x_3$	$\cdots$	$x_2$	$\cdots$	$x_4$	$\cdots$
$\frac{dR}{dx}$		$+$		$+$	$0$	$-$		$-$
$\frac{d^{2}R}{d{x}^2}$		$+$	$0$	$-$		$-$	$0$	$+$
$R\left(x\right)$	$0$	up, v		up, ^		down, ^		down, v

Note of Table 6: “v” means concave upward. “^” means concave downward.

. It is thus proved that Equation (9) is mountain-shaped, as shown in Figure 1B.

5. Conclusions and Implications

According to the proof described in Section 4, Equation (9) has a mountain-shaped graph with two inflection points. Therefore, Equation (9) can be used instead of Equation (2) for the radiation-specific component R that can induce the hormesis effect. In other words, in the case of cancer caused solely by radiation and in a general sequential reaction (Scheme 2) with different rate constants for each step, the component R that is produced in the second step may induce the radiation-specific hormesis effect at low doses. What we find in this paper is that at the present time there is no biophysical background other than Scheme 1 and Scheme 2 and only a theoretical mathematical approach for understanding Equations (2), (6), and (9). Therefore, this approach on some real data [46] should be used and tested. Furthermore, the exploration and overexpression of such a component may lead to the development of cancer-reducing therapeutic modalities.