Evaluation of the Interaction-Based Hazard Index Formula Using Data on Four Trihalomethanes from U.S. EPA’s Multiple-Purpose Design Study
Abstract
:1. Introduction
1.1. Hazard Index
1.2. HIINT
“Table 18. Effect of Lead on Arsenic: Neurological Toxicity for Oral Exposure
Table 19. Effect of Arsenic on Lead: Neurological Toxicity for Oral Exposure”.
2. Methods
2.1. Evaluation Approach
2.1.1. Simplified Scenario
2.1.2. Binary Mixture Evaluation
2.1.3. Quaternary Mixture Evaluation
2.2. THM Data Used for the Evaluation
2.2.1. Animals and Husbandry
2.2.2. Chemicals in the Mixtures Used for Evaluation of HIINT
2.2.3. Experimental Design
2.3. Calculation Approach
- (1)
- Conduct data quality analyses, perform dose–response modeling and select the best fitting model for each single, binary and quaternary THM dataset.
- (2)
- Obtain, for each binary mixture, the two components’ model estimates for their response-specific doses, i.e., the EDx (Dj) values for the endpoint of interest. Those component Dj values are estimated using the component-only data from the binary mixture study.
- (3)
- Use the component Dj values to estimate DADD2, which is the EDx[predicted] under dose addition using the harmonic mean formula (Section 2.3.3).
- (4)
- Obtain the observed DMIX2 estimates for the endpoint of interest by modeling the binary mixture data.
- (5)
- Calculate the binary interaction magnitude, MOBS. Because interaction is defined here as departure of the observed outcomes from the predicted outcomes under dose additivity, its magnitude is found by comparing DMIX2, the mixture EDx[observed], with DADD2, the mixture EDx[predicted] that is calculated from dose addition. Calculate the theoretical maximum interaction magnitude [M = (MOBS)1/g], where the g function is based on the component fractions and EDx values in the binary mixture.
- (6)
- Calculate and compare DADD4 and DINT4, the predicted mixture EDx values for the two quaternary mixture rays (CL and OZ mixtures), by setting HI = 1 and HIINT = 1, respectively.
- (7)
- Obtain DMIX4, the observed EDx estimates for the two quaternary mixture rays by modeling the data for each ray. Compare these with the DADD4 and DINT4 values for the two mixture rays.
- (8)
- To improve understanding of the potential for this evaluation, present some results in the context of the hazard index. Using exposure information from the quaternary mixture, calculate an HQ for each component, endpoint and mean Dj across the 8 studies. Use these HQ estimates to calculate the HI and the HIINT. (Note that the WOE score, B, is designated to be 1 or −1, as described earlier. Also note that to calculate HIINT for the quaternary mixture, the gij function is based on the component fractions of components i and j in that quaternary mixture.) Compare the HI and HIINT estimates for an assumed mixture dose = 1 mmol/kg/day. The results from this step show several significant digits to facilitate comparison across indices. In the final conclusions of an actual risk characterization, the HI and HIINT should be shown rounded to one significant digit.
- (9)
- Describe key uncertainties found during the analysis.
2.3.1. Component EDx Values
2.3.2. Binary Mixture EDx Values
2.3.3. Binary Interaction Magnitude
2.3.4. Quaternary Evaluation of EDx and Interaction Magnitude
3. Results
3.1. Application to the THM Data
3.1.1. Dj for the Components
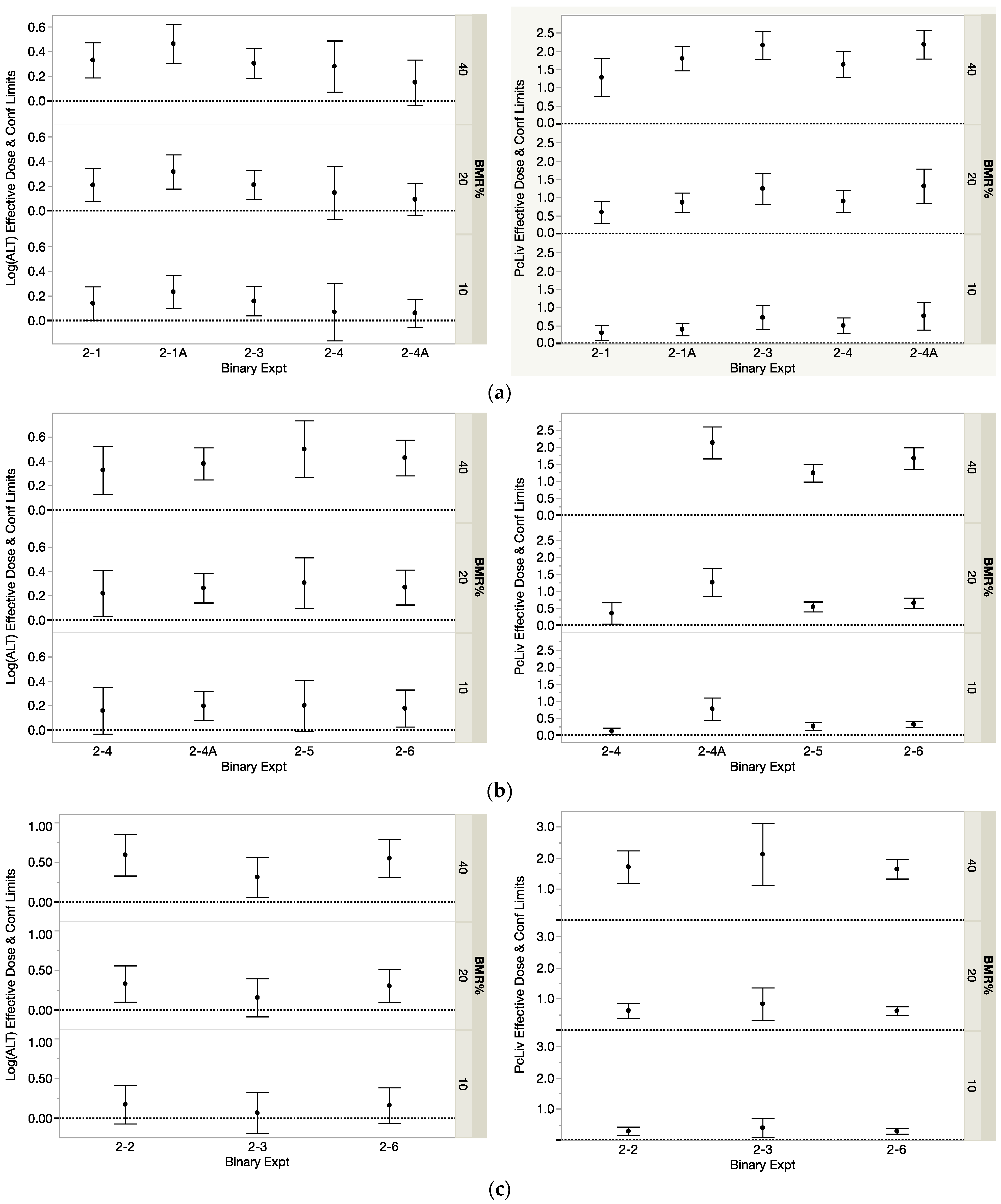
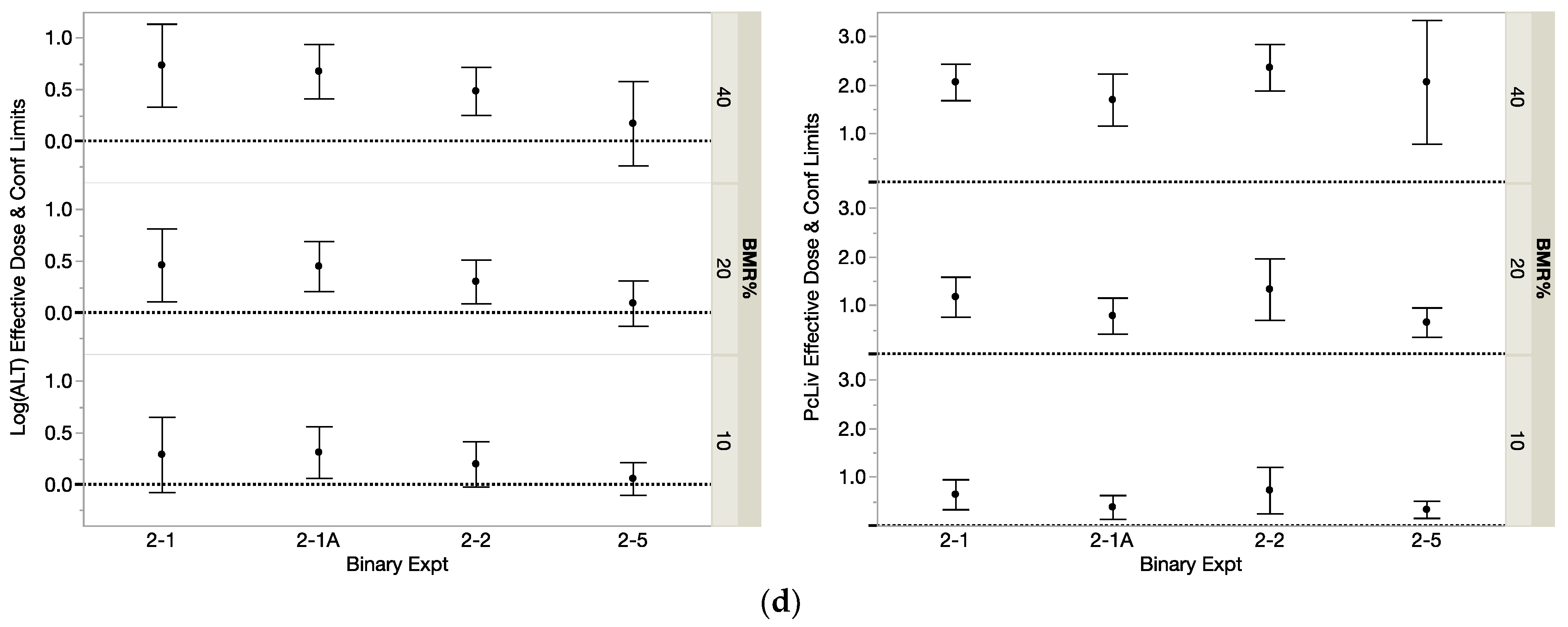
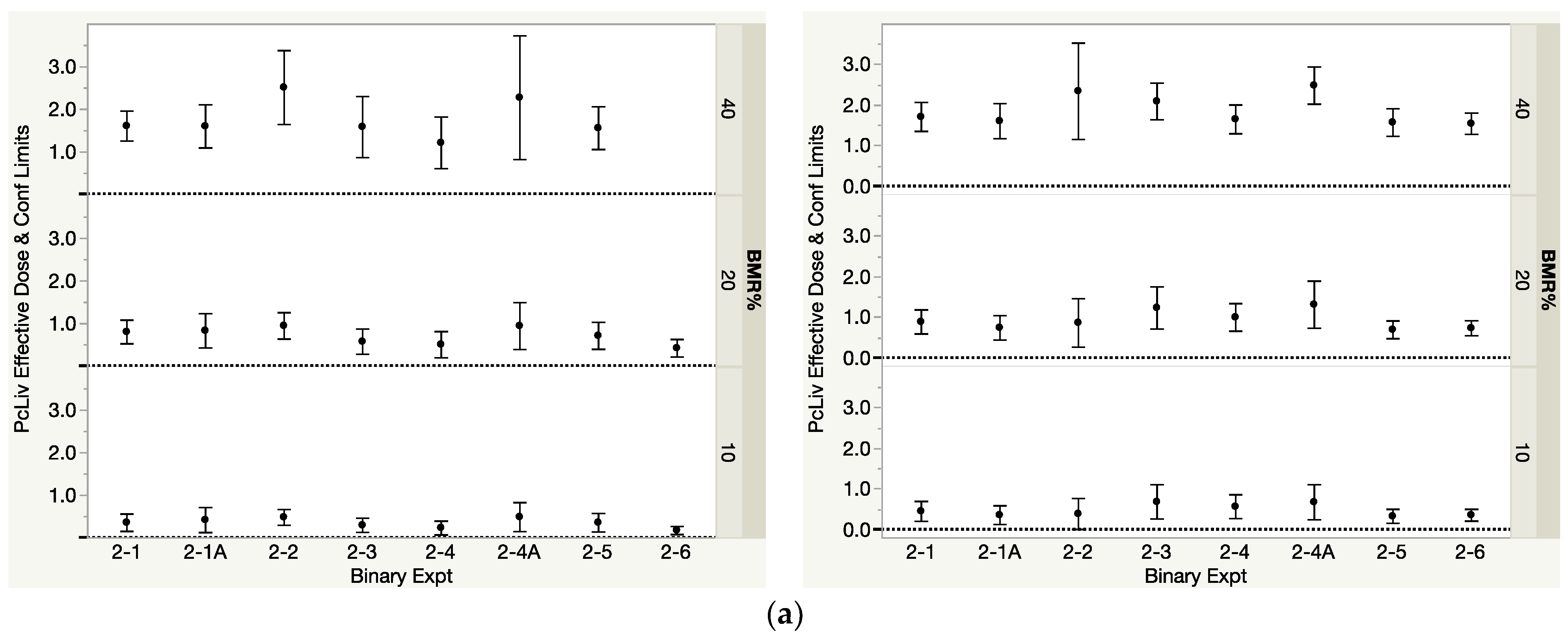
3.1.2. DMIX2 for the Binary Mixtures
3.1.3. Binary Interaction Magnitudes and Interaction Direction
3.1.4. Quaternary Mixture Predicted Indices and Predicted Effective Doses
3.1.5. HIINT Method and Results of Estimating the Theoretical M by Adjusting MOBS
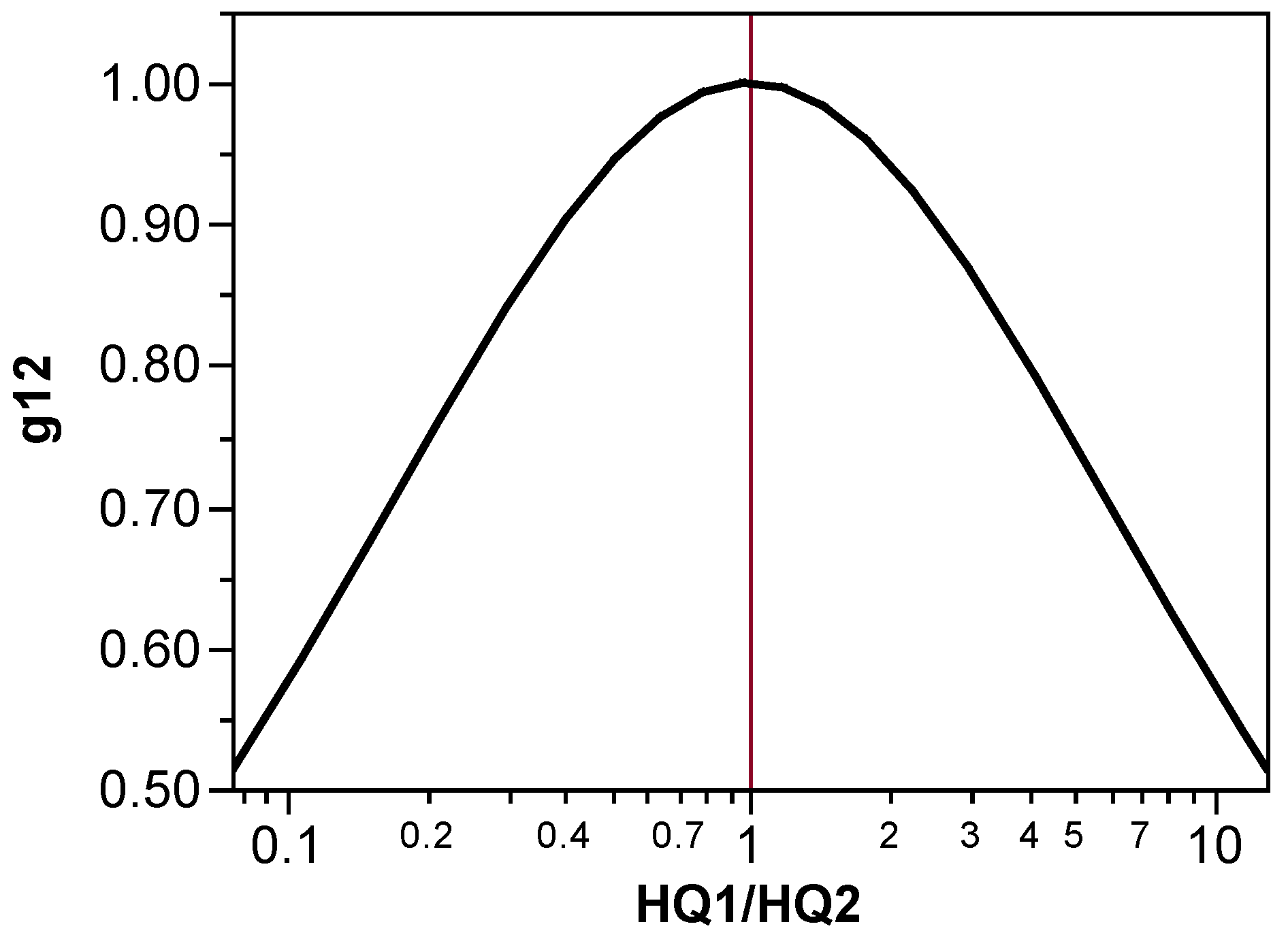
3.2. Evaluation of the Function g in the HIINT Formula
4. Discussion and Conclusions
4.1. Attributes and Improved Understanding of the HIINT Formula
4.2. Possible Improvements
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- U.S. EPA. Guidelines for the Health Risk Assessment of Chemical Mixtures; EPA/630/R-98/002; Risk Assessment Forum: Washington, DC, USA, 1986; p. 38.
- Kienzler, A.; Bopp, S.K.; van der Linden, S.; Berggren, E.; Worth, A. Regulatory assessment of chemical mixtures: Requirements, current approaches and future perspectives. Regul. Toxicol. Pharmacol. 2016, 80, 321–334. [Google Scholar] [CrossRef] [PubMed]
- Kortenkamp, A.; Backhaus, T.; Faust, M. State of the Art Report on Mixture Toxicity; University of London: London, UK, 2009; p. 391. [Google Scholar]
- Bopp, S.K.; Kienzler, A.; Richarz, A.-N.; van der Linden, S.C.; Paini, A.; Parissis, N.; Worth, A.P. Regulatory assessment and risk management of chemical mixtures: Challenges and ways forward. Crit. Rev. Toxicol. 2019, 49, 174–189. [Google Scholar] [CrossRef] [PubMed]
- U.S. EPA. Supplementary Guidance for Conducting Health Risk Assessment of Chemical Mixtures; EPA/630/R-00/002; Risk Assessment Forum: Washington, DC, USA, 2000; p. 209.
- U.S. EPA. Guidance on Cumulative Risk Assessment of Pesticide Chemicals That Have a Common Mechanism of Toxicity; Office of Pesticide Programs: Washington, DC, USA, 2002; p. 90.
- U.S. EPA. Developing Relative Potency Factors for Pesticide Mixtures: Biostatistical Analyses of Joint Dose-Response; EPA/600/R-03/052; Office of Research and Development, National Center for Environmental Assessment: Cincinnati, OH, USA; p. 115.
- U.S. EPA. Pesticide Cumulative Risk Assessment: Framework for Screening Analysis; EPA-HQ-OPP-2015-0422-0019; Office of Pesticide Programs: Washington, DC, USA, 2016; p. 17.
- U.S. EPA. Advances in Dose Addition for Chemical Mixtures: A White Paper; EPA/100/R-23/001; U.S. Environmental Protection Agency: Washington, DC, USA, 2023; p. 169.
- Hertzberg, R.C.; Mumtaz, M.M. Component-based risk assessment approaches with additivity and interactions. In Chemical Mixtures and Combined Chemical and Nonchemical Stressors: Exposure, Toxicity, Analysis, and Risk; Rider, C.V., Simmons, J.E., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 369–420. [Google Scholar]
- U.S. EPA. Risk Assessment Guidance for Superfund. Vol. 1. Human Health Evaluation Manual (Part A); EPA/540/1-89/002; Office of Solid Waste and Emergency Response: Washington, DC, USA, 1989; p. 271.
- ATSDR. Framework for Assessing Health Impacts of Multiple Chemicals and Other Stressors (Update); Agency for Toxic Substances and Disease Registry, U.S. Department of Health and Human Services, Public Health Service: Atlanta, GA, USA, 2018; p. 154.
- Hertzberg, R.C.; Teuschler, L.K. Evaluating quantitative formulas for dose-response assessment of chemical mixtures. Environ. Health Perspect. 2002, 110, 965–970. [Google Scholar] [CrossRef] [PubMed]
- Teuschler, L.K.; Gennings, C.; Stiteler, W.M.; Hertzberg, R.C.; Colman, J.T.; Thiyagarajah, A.; Lipscomb, J.C.; Hartley, W.R.; Simmons, J.E. A multiple-purpose design approach to the evaluation of risks from mixtures of disinfection by-products. Drug Chem. Toxicol. 2000, 23, 307–321. [Google Scholar] [CrossRef] [PubMed]
- Teuschler, L.K.; Gennings, C.; Hartley, W.R.; Carter, H.; Thiyagarajah, A.; Schoeny, R.; Cubbison, C. The interaction effects of binary mixtures of benzene and toluene on the developing heart of medaka (Oryzias latipes). Chemosphere 2005, 58, 1283–1291. [Google Scholar] [CrossRef] [PubMed]
- Teuschler, L.K.; Hertzberg, R.C.; McDonald, A.; Sey, Y.M.; Simmons, J.E. Evaluation of a Proportional Response Addition Approach to Mixture Risk Assessment and Predictive Toxicology Using Data on Four Trihalomethanes from the US EPA’s Multiple-Purpose Design Study. Toxics 2024, 12, 240. [Google Scholar] [CrossRef]
- Lin, Y.-J.; Ling, M.-P.; Chen, S.-C.; Chen, W.-Y.; Hsieh, N.-H.; Cheng, Y.-H.; You, S.-H.; Chou, W.-C.; Lin, M.-C.; Liao, C.-M. Mixture risk assessment due to ingestion of arsenic, copper, and zinc from milkfish farmed in contaminated coastal areas. Environ. Sci. Pollut. Res. 2017, 24, 14616–14626. [Google Scholar] [CrossRef] [PubMed]
- Omrane, F.; Gargouri, I.; Khadhraoui, M.; Elleuch, B.; Zmirou-Navier, D. Risk assessment of occupational exposure to heavy metal mixtures: A study protocol. BMC Public Health 2018, 18, 314. [Google Scholar] [CrossRef] [PubMed]
- Marx, C.; Mühlbauer, V.; Krebs, P.; Kuehn, V. Environmental risk assessment of antibiotics including synergistic and antagonistic combination effects. Sci. Total Environ. 2015, 524–525, 269–279. [Google Scholar] [CrossRef]
- Haddad, S.; Beliveau, M.; Tardif, R.; Krishnan, K. A PBPK Modeling-Based Approach to Account for Interactions in the Health Risk Assessment of Chemical Mixtures. Toxicol. Sci. 2001, 63, 125–131. [Google Scholar] [CrossRef]
- Niu, Z.; Zang, X.; Zhang, Y. Using physiologically based pharmacokinetic models to estimate the health risk of mixtures of trihalomethanes from reclaimed water. J. Hazard. Mater. 2015, 285, 190–198. [Google Scholar] [CrossRef]
- Ryker, S.J.; Small, M.J. Combining Occurrence and Toxicity Information to Identify Priorities for Drinking-Water Mixture Research. Risk Anal. 2008, 28, 653–666. [Google Scholar] [CrossRef]
- Kumari, M.; Kumar, A. Identification of component-based approach for prediction of joint chemical mixture toxicity risk assessment with respect to human health: A critical review. Food Chem. Toxicol. 2020, 143, 111458. [Google Scholar] [CrossRef] [PubMed]
- Simmons, J.E.; Teuschler, L.K.; Gennings, C.; Speth, T.; Richardson, S.; Miltner, R.; Narotsky, M.; Schenck, K.; Hunter, E., III; Hertzberg, R.C.; et al. Component-based and whole-mixture techniques for addressing the toxicity of drinking-water disinfection by-product mixtures. J. Toxicol. Environ. Health Part A 2004, 67, 741–754. [Google Scholar] [CrossRef]
- Villanueva, C.M.; Cordier, S.; Font-Ribera, L.; Salas, L.A.; Levallois, P. Overview of Disinfection By-products and Associated Health Effects. Curr. Environ. Health Rep. 2015, 2, 107–115. [Google Scholar] [CrossRef]
- ECHA. Guidance on the Biocidal Products Regulation Volume III Human Health—Assessment & Evaluation (Parts B + C); ECHA-17-R-01-EN; European Chemicals Agency: Helsinki, Finland, 2017; p. 427.
- Berenbaum, M.C. What is synergy? Pharmacol. Rev. 1989, 41, 93–141. [Google Scholar] [PubMed]
- Hoel, D.G. Statistical aspects of chemical mixtures. In Methods for Assessing the Effects of Mixtures of Chemicals; Vouk, V.B., Ed.; SCOPE (Series); Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Hertzberg, R.C.; Rice, G.E.; Teuschler, L.K. Methods for health risk assessment of combustion mixtures. In Hazardous Waste Incineration: Evaluating the Human Health and Environmental Risks; Roberts, S., Teaf, C., Bean, J., Eds.; CRC Press: Boca Raton, FL, USA, 1999; pp. 105–148. [Google Scholar]
- Boobis, A.; Budinsky, R.; Collie, S.; Crofton, K.; Embry, M.; Felter, S.; Hertzberg, R.; Kopp, D.; Mihlan, G.; Mumtaz, M.; et al. Critical analysis of literature on low-dose synergy for use in screening chemical mixtures for risk assessment. Crit. Rev. Toxicol. 2011, 41, 369–383. [Google Scholar] [CrossRef] [PubMed]
- Hertzberg, R.C.; MacDonell, M.M. Synergy and other ineffective mixture risk definitions. Sci. Total Environ. 2002, 288, 31–42. [Google Scholar] [CrossRef]
- Finney, D.J. Probit Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 1971. [Google Scholar]
- ATSDR. Interaction Profile for: Arsenic, Cadmium, Chromium, and Lead; Agency for Toxic Substances and Disease Registry, U.S. Department of Health and Human Services, Public Health Service: Atlanta, GA, USA, 2004; p. 181.
- Krasner, S.; McGuire, M.; Jacangelo, J.; Patania, N.; Reagan, K.; Aieta, E. The occurrence of disinfection byproducts in U.S. drinking water. J. Am. Water Work. Assoc. 1989, 81, 41–53. [Google Scholar] [CrossRef]
- Lilly, P.D.; Ross, T.M.; Pegram, R.A. Trihalomethane Comparative Toxicity: Acute Renal and Hepatic Toxicity of Chloroform and Bromodichloromethane Following Aqueous Gavage. Fundam. Appl. Toxicol. 1997, 40, 101–110. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Hertzberg, R.C.; Pan, Y.; Li, R.; Haber, L.T.; Lyles, R.H.; Herr, D.W.; Moser, V.C.; Simmons, J.E. A four-step approach to evaluate mixtures for consistency with dose addition. Toxicology 2013, 313, 134–144. [Google Scholar] [CrossRef] [PubMed]
- Mumtaz, M.; Durkin, P. A weight of evidence scheme for assessing interactions in chemical mixtures. Toxicol. Ind. Health 1992, 8, 377–406. [Google Scholar] [CrossRef] [PubMed]
- Dinse, G.E.; Umbach, D.M. Characterizing non-constant relative potency. Regul. Toxicol. Pharmacol. 2011, 60, 342–353. [Google Scholar] [CrossRef] [PubMed]
- ATSDR. Interaction Profiles for Toxic Substances. Available online: https://www.atsdr.cdc.gov/interactionprofiles/index.html (accessed on 16 April 2024).
- Lambert, J.C. Adverse Outcome Pathway ‘Footprinting’: A Novel Approach to the Integration of 21st Century Toxicology Information into Chemical Mixtures Risk Assessment. Toxics 2023, 11, 37. [Google Scholar] [CrossRef]
- Eccles, K.M.; Karmaus, A.L.; Kleinstreuer, N.C.; Parham, F.; Rider, C.V.; Wambaugh, J.F.; Messier, K.P. A geospatial modeling approach to quantifying the risk of exposure to environmental chemical mixtures via a common molecular target. Sci. Total Environ. 2023, 855, 158905. [Google Scholar] [CrossRef]
- Escher, S.E.; Partosch, F.; Konzok, S.; Jennings, P.; Luijten, M.; Kienhuis, A.; de Leeuw, V.; Reuss, R.; Lindemann, K.M.; Hougaard Bennekou, S. Development of a Roadmap for Action on New Approach Methodologies in Risk Assessment; EFSA Supporting Publication 19(6):EN-7241; European Food Safety Authority: Parma, Italy, 2022.



| Notation | Description |
|---|---|
| BMRx | Benchmark response value for PcLiv or for ALT, calculated as x% increase from the control mean value of that endpoint and used with inverse prediction to obtain the effective dose (EDx) for that endpoint; for ALT, the inverse prediction used Log(BMR) |
| Dj | EDx estimated by modeling the jth component |
| DMIX2, DMIX4 | EDx estimated by modeling the binary (MIX2) or quaternary (MIX4) mixture data |
| DADD2, DADD4 | EDx calculated for the mixture using dose addition and single chemical data for the binary (ADD2) or quaternary (ADD4) mixtures |
| DINT4 | EDx calculated for the mixture using the EPA interaction formula |
| πj | Dose fraction in the mixture for the jth component |
| HQj | Hazard quotient for the jth component, in this research, using animal data |
| HI | Additive hazard index |
| HIINT | Interaction-based HI |
| MOBS | Observed interaction magnitude calculated from binary data |
| Bjk | Binary weight of evidence score for the strength of evidence that chemical k will influence the toxicity of chemical j in humans; the sign of B indicates the direction of the interaction |
| fjk | Toxic hazard of the kth chemical relative to the total hazard from all chemicals potentially interacting with chemical j |
| gjk | Degree to which chemicals j and k are present in equitoxic amounts in the mixture; the HQj values used to calculate gjk depend on the component fractions of either the binary or quaternary mixture along with the component effective doses |
| Mjk | Theoretical maximum interaction magnitude |
| Category | Description | Greater Than Add | Less Than Add |
|---|---|---|---|
| I | Directly relevant to humans | 1.0 | −1.0 |
| II | Animal studies, but relevant | 0.75 | −0.5 |
| III | Plausible evidence, possibly not relevant because of different exposure route or use of in vitro data | 0.5 | 0.0 |
| IV | Additivity demonstrated or assumed because of poor data | 0.0 | 0.0 |
| Exp. ID a | Components Involved | Ratios Studied | Dosages Studied mmol/kg/day b | |
|---|---|---|---|---|
| 1:1 | Environmental | |||
| #2-1, #2-1A | CHCl3:BDCM | 1:1 | 2.7:1 | Single THMs individually at: 0.1, 1.0, 3.0 1:1 ratios mixtures at: 0.1, 1.0, 3.0 Environmentally relevant ratios mixtures at: 1.0, 3.0 |
| #2-2 | CHCl3:CHBr3 | 1:1 | 65:1 | |
| #2-3 | BDCM:CHBr3 | 1:1 | 24:1 | |
| #2-4, #2-4A | BDCM:CDBM | 1:1 | 2.4:1 | |
| #2-5 | CHCl3:CDBM | 1:1 | 6.5:1 | |
| #2-6 | CDBM:CHBr3 | 1:1 | 10:1 | |
| #4-2 | CHCl3:BDCM :CDBM:CHBr3 | Chlorination Ratio 0.319:0.342:0.290:0.049 Ozonation Ratio 0.655:0.187:0.129:0.029 (ratios apply to all three quaternary mixtures) | Each quaternary mixture studied at: 0.05, 1.5, 3.0 Each quaternary THM studied at one level: 0.76 (CDBM), 1.5 (other THMs) | |
| #4-3 | CHCl3:BDCM :CDBM:CHBr3 | |||
| #4-4 | CHCl3:BDCM :CDBM:CHBr3 | |||
| THM Modeled | Studied with | Binary Exp | PcLiv | Log(ALT) | ||||
|---|---|---|---|---|---|---|---|---|
| Dj10 | Dj20 | Dj40 | Dj10 | Dj20 | Dj40 | |||
| BDCM | CHCl3 | 2-1 | 0. 30 | 0.59 | 1.28 | 0.14 | 0.21 | 0.33 |
| BDCM | CHCl3 | 2-1A | 0.39 | 0.86 | 1.80 | 0.23 | 0.32 | 0.46 |
| 2-1, 2-1A Average | 0.34 | 0.73 | 1.54 | 0.19 | 0.26 | 0.40 | ||
| BDCM | CHBr3 | 2-3 | 0.72 | 1.24 | 2.16 | 0.16 | 0.21 | 0.30 |
| BDCM | CDBM | 2-4 | 0.50 | 0.89 | 1.63 | 0.07 | 0.14 | 0.28 |
| BDCM | CDBM | 2-4A | 0.76 | 1.31 | 2.19 | 0.06 | 0.09 | 0.15 |
| 2-4, 2-4A Average | 0.63 | 1.10 | 1.91 | 0.06 | 0.12 | 0.21 | ||
| BDCM Mean Dj | 0.53 | 0.98 | 1.81 | 0.13 | 0.19 | 0.31 | ||
| CDBM | BDCM | 2-4 | 0.12 | 0.35 | - | 0.16 | 0.22 | 0.33 |
| CDBM | BDCM | 2-4A | 0.77 | 1.26 | 2.13 | 0.20 | 0.26 | 0.38 |
| 2-4, 2-4A Average | 0.44 | 0.81 | 2.13 | 0.18 | 1.24 | 0.35 | ||
| CDBM | CHCl3 | 2-5 | 0.26 | 0.54 | 1.24 | 0.20 | 0.31 | 0.50 |
| CDBM | CHBr3 | 2-6 | 0.32 | 0.65 | 1.67 | 0.18 | 0.27 | 0.43 |
| CDBM Mean Dj | 0.36 | 0.70 | 1.68 | 0.18 | 0.26 | 0.41 | ||
| CHCl3 | BDCM | 2-1 | 0.64 | 1.18 | 2.06 | 0.29 | 0.46 | 0.73 |
| CHCl3 | BDCM | 2-1A | 0.38 | 0.79 | 1.70 | 0.31 | 0.45 | 0.68 |
| 2-1, 2-1A Average | 0.51 | 0.98 | 1.88 | 0.30 | 0.46 | 0.71 | ||
| CHCl3 | CHBr3 | 2-2 | 0.73 | 1.33 | 2.36 | 0.20 | 0.30 | 0.49 |
| CHCl3 | CDBM | 2-5 | 0.33 | 0.65 | 2.06 | 0.06 | 0.09 | 0.17 |
| CHCl3 Mean Dj | 0.52 | 0.99 | 2.05 | 0.21 | 0.33 | 0.52 | ||
| CHBr3 | CHCl3 | 2-2 | 0.29 | 0.62 | 1.71 | 0.18 | 0.33 | 0.59 |
| CHBr3 | BDCM | 2-3 | 0.40 | 0.84 | 2.12 | 0.07 | 0.16 | 0.32 |
| CHBr3 | CDBM | 2-6 | 0.29 | 0.62 | 1.64 | 0.16 | 0.30 | 0.55 |
| CHBr3 Mean Dj | 0.33 | 0.70 | 1.83 | 0.14 | 0.26 | 0.49 | ||
| (a) | |||||||
| THMs in Binary Mixture | Binary Exp | PcLiv | Log(ALT) | ||||
| DMIX210 | DMIX220 | DMIX210 | DMIX220 | DMIX210 | DMIX220 | ||
| BDCM, CHCl3 | 2-1 | 0.36 | 0.80 | 1.61 | 0.30 | 0.46 | 0.71 |
| BDCM, CHCl3 | 2-1A | 0.42 | 0.83 | 1.60 | 0.29 | 0.42 | 0.63 |
| 2-1, 2-1A Average | 0.39 | 0.82 | 1.60 | 0.29 | 0.44 | 0.67 | |
| CHCl3, CHBr3 | 2-2 | 0.48 | 0.95 | 2.51 | 0.19 | 0.34 | 0.59 |
| BDCM, CHBr3 | 2-3 | 0.30 | 0.58 | 1.59 | 0.14 | 0.20 | 0.30 |
| BDCM, CDBM | 2-4 | 0.23 | 0.51 | 1.21 | 0.12 | 0.17 | 0.26 |
| BDCM, CDBM | 2-4A | 0.49 | 0.94 | 2.27 | 0.09 | 0.13 | 0.21 |
| 2-4, 2-4A Average | 0.36 | 0.73 | 1.74 | 0.11 | 0.15 | 0.24 | |
| CDBM, CHCl3 | 2-5 | 0.36 | 0.71 | 1.56 | 0.10 | 0.18 | 0.33 |
| CDBM, CHBr3 | 2-6 | 0.18 | 0.42 | 3.16 | 0.26 | 0.41 | 0.66 |
| (b) | |||||||
| THMs in Binary Mixture | Binary Exp | PcLiv | Log(ALT) | ||||
| DMIX210 | DMIX220 | DMIX240 | DMIX210 | DMIX220 | DMIX240 | ||
| BDCM, CHCl3 | 2-1 | 0.46 | 0.89 | 1.71 | 0.17 | 0.27 | 0.44 |
| BDCM, CHCl3 | 2-1A | 0.36 | 0.75 | 1.61 | 0.31 | 0.51 | 0.82 |
| 2-1, 2-1A Average | 0.41 | 0.82 | 1.66 | 0.24 | 0.39 | 0.63 | |
| CHCl3, CHBr3 | 2-2 | 0.39 | 0.87 | 2.35 | 0.21 | 0.36 | 0.60 |
| BDCM, CHBr3 | 2-3 | 0.69 | 1.24 | 2.10 | 0.10 | 0.14 | 0.22 |
| BDCM, CDBM | 2-4 | 0.57 | 1.00 | 1.65 | 0.11 | 0.17 | 0.26 |
| BDCM, CDBM | 2-4A | 0.68 | 1.32 | 2.49 | 0.17 | 0.24 | 0.38 |
| 2-4, 2-4A Average | 0.62 | 1.16 | 2.07 | 0.14 | 0.21 | 0.32 | |
| CDBM, CHCl3 | 2-5 | 0.33 | 0.70 | 1.58 | 0.12 | 0.22 | 0.39 |
| CDBM, CHBr3 | 2-6 | 0.36 | 0.74 | 1.55 | 0.14 | 0.24 | 0.43 |
| Dataset a and Type of Dose | Observed 10% Dose | Predicted b (DADD210) | Mjk c | DADD2-DMIX2 | Direction d | |
|---|---|---|---|---|---|---|
| CHCl3 | 2-1,1A Dj | 0.51 | ||||
| 1:1 | 2-1,1A DMIX2 | 0.39 | 0.41 | 1.06 | 0.02 | additive |
| BDCM | 2-1,1A Dj | 0.34 | ||||
| CHCl3 | 2-2 Dj | 0.73 | ||||
| 1:1 | 2-2 DMIX2 | 0.48 | 0.42 | 1.18 | −0.06 | <additive |
| CHBr3 | 2-2 Dj | 0.29 | ||||
| BDCM | 2-3 Dj | 0.72 | ||||
| 1:1 | 2-3 DMIX2 | 0.30 | 0.51 | 1.78 | 0.21 | >additive |
| CHBr3 | 2-3 Dj | 0.40 | ||||
| BDCM | 2-4,4A Dj | 0.63 | ||||
| 1:1 | 2-4,4A DMIX2 | 0.36 | 0.52 | 1.45 | 0.16 | >additive |
| CDBM | 2-4,4A Dj | 0.44 | ||||
| CHCl3 | 2-5 Dj | 0.33 | ||||
| 1:1 | 2-5 DMIX2 | 0.36 | 0.29 | 1.23 | −0.07 | <additive |
| CDBM | 2-5 Dj | 0.26 | ||||
| CDBM | 2-6 Dj | 0.32 | ||||
| 1:1 | 2-6 DMIX2 | 0.18 | 0.30 | 1.71 | 0.12 | >additive |
| CHBr3 | 2-6 Dj | 0.29 | ||||
| Dataset | Mjk (10%) | Direction b (10%) | Mjk (20%) | Direction b (20%) | Mjk (40%) | Direction b (40%) | ||
|---|---|---|---|---|---|---|---|---|
| CHCl3:BDCM | 2-1,1A | 1:1 | 1.06 | 1.02 | 1.05 | |||
| CHCl3:CHBr3 | 2-2 | 1:1 | 1.18 | <add | 1.12 | <add | 1.27 | <add |
| BDCM:CHBr3 | 2-3 | 1:1 | 1.78 | >add | 1.76 | >add | 1.35 | >add |
| BDCM:CDBM | 2-4,4A | 1:1 | 1.45 | >add | 1.29 | >add | 1.15 | >add |
| CHCl3:CDBM | 2-5 | 1:1 | 1.23 | <add | 1.21 | <add | 1.01 | |
| CDBM:CHBr3 | 2-6 | 1:1 | 1.71 | >add | 1.50 | >add | 1.91 | <add |
| CHCl3:BDCM | 2-1,1A | Env | 1.11 | >add | 1.10 | >add | 1.07 | |
| CHCl3:CHBr3 | 2-2 | Env | 4.94 | >add | 3.24 | >add | 1.0004 | |
| BDCM:CHBr3 | 2-3 | Env | 1.03 | 1.04 | 1.08 | |||
| BDCM:CDBM | 2-4,4A | Env | 1.12 | <add | 1.17 | <add | 1.06 | |
| CHCl3:CDBM | 2-5 | Env | 1.04 | 1.14 | <add | 1.26 | >add | |
| CDBM:CHBr3 | 2-6 | Env | 1.27 | <add | 1.24 | <add | 1.14 | >add |
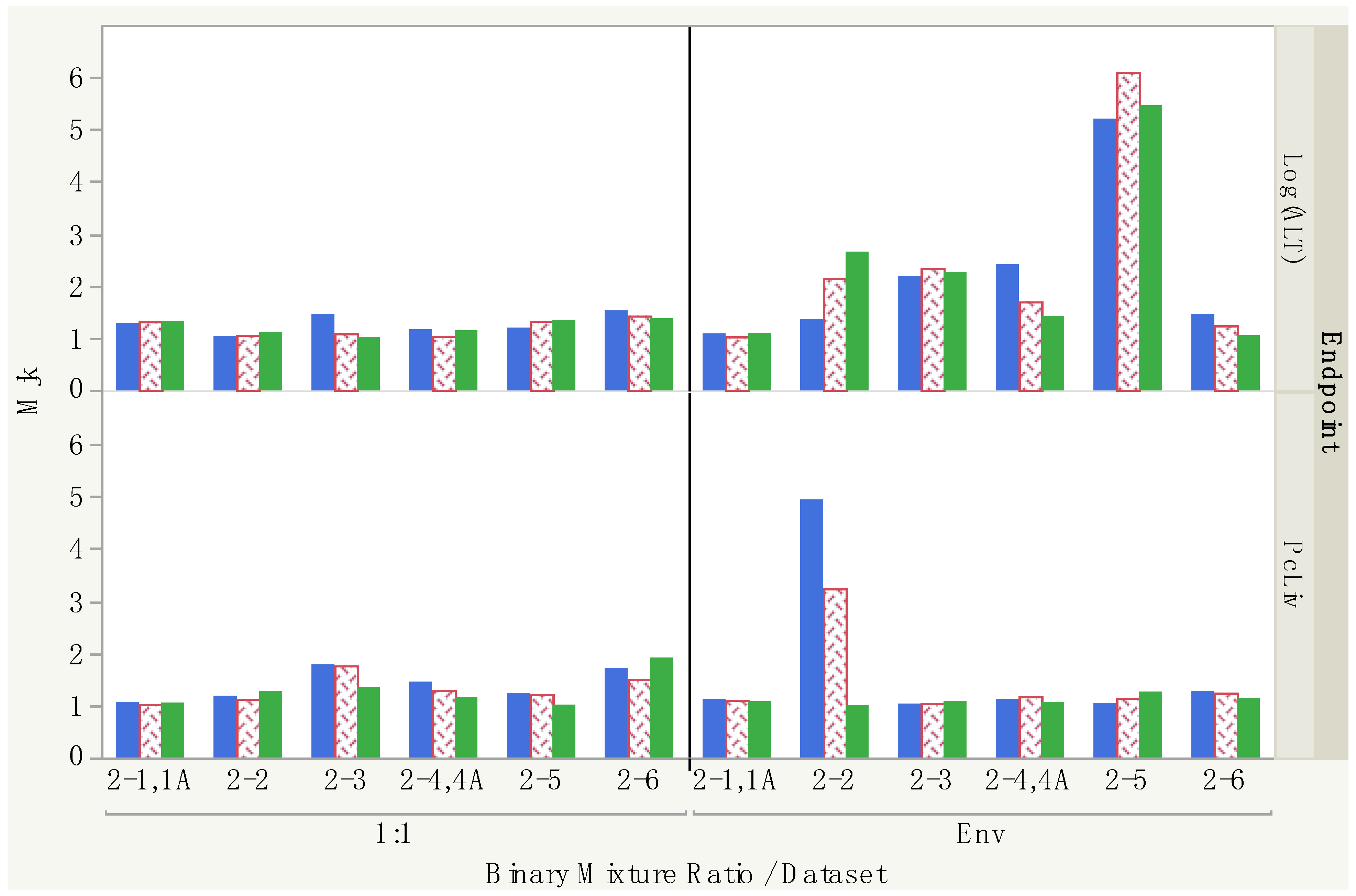
| Dataset | Mjk (10%) | Direction b (10%) | Mjk (20%) | Direction b (20%) | Mjk (40%) | Direction b (40%) | ||
|---|---|---|---|---|---|---|---|---|
| CHCl3:BDCM | 2-1,1A | 1:1 | 1.28 | <add | 1.32 | <add | 1.33 | <add |
| CHCl3:CHBr3 | 2-2 | 1:1 | 1.04 | 1.06 | 1.11 | <add | ||
| BDCM:CHBr3 | 2-3 | 1:1 | 1.46 | <add | 1.09 | 1.02 | ||
| BDCM:CDBM | 2-4,4A | 1:1 | 1.16 | <add | 1.04 | 1.14 | >add | |
| CHCl3:CDBM | 2-5 | 1:1 | 1.20 | <add | 1.33 | <add | 1.34 | <add |
| CDBM:CHBr3 | 2-6 | 1:1 | 1.53 | <add | 1.43 | <add | 1.37 | <add |
| CHCl3:BDCM | 2-1,1A | Env | 1.08 | 1.03 | 1.09 | |||
| CHCl3:CHBr3 | 2-2 | Env | 1.36 | <add | 2.15 | <add | 2.65 | <add |
| BDCM:CHBr3 | 2-3 | Env | 2.18 | >add | 2.34 | >add | 2.26 | >add |
| BDCM:CDBM | 2-4,4A | Env | 2.41 | <add | 1.70 | <add | 1.42 | <add |
| CHCl3:CDBM | 2-5 | Env | 5.20 | <add | 6.10 | <add | 5.46 | <add |
| CDBM:CHBr3 | 2-6 | Env | 1.46 | >add | 1.24 | >add | 1.05 | |
| Predicted Dose | Chlorination | Ozonation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PcLiv | Log(ALT) | PcLiv | Log(ALT) | |||||||||
| 10% | 20% | 40% | 10% | 20% | 40% | 10% | 20% | 40% | 10% | 20% | 40% | |
| DMIX4 a | 0.355 | 0.722 | 1.679 | 0.110 | 0.240 | 0.473 | 0.284 | 0.649 | 1.629 | 0.288 | 0.522 | 0.894 |
| DADD4 b | 0.455 | 0.865 | 1.837 | 0.166 | 0.249 | 0.393 | 0.492 | 0.926 | 1.938 | 0.185 | 0.281 | 0.444 |
| DINT4 (1:1) c | 0.396 | 0.797 | 1.741 | 0.197 | 0.279 | 0.427 | 0.479 | 0.937 | 1.892 | 0.220 | 0.339 | 0.540 |
| DINT4 (Env) c | 0.417 | 0.872 | 1.707 | 0.225 | 0.345 | 0.537 | 0.435 | 0.887 | 1.764 | 0.226 | 0.377 | 0.612 |
| Predicted Index | Chlorination | Ozonation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PcLiv | Log(ALT) | PcLiv | Log(ALT) | |||||||||
| 10% | 20% | 40% | 10% | 20% | 40% | 10% | 20% | 40% | 10% | 20% | 40% | |
| HI | 2.197 | 1.156 | 0.544 | 6.033 | 4.022 | 2.547 | 2.032 | 1.080 | 0.516 | 5.398 | 3.564 | 2.255 |
| HIINT (1:1) a | 2.524 | 1.254 | 0.574 | 5.067 | 3.579 | 2.344 | 2.086 | 1.067 | 0.529 | 4.546 | 2.988 | 1.851 |
| HIINT (Env) a | 2.396 | 1.147 | 0.586 | 4.440 | 2.895 | 1.863 | 2.299 | 1.128 | 0.567 | 4.420 | 2.653 | 1.634 |
| Binary Datasets | MOBS,jk | gjk | Mjk | Mjk Default | Quaternary Chlorination Results | ||
|---|---|---|---|---|---|---|---|
| Indices a | Doses b | ||||||
| CHCl3:BDCM | 2-1, 2-1A | 1.08 | 0.97 | 1.08 | 5 | HI = 6.033 HIINT = 4.921 using MOBS,jk HIINT = 4.440 using Mjk HIINT = 12.091 using default of Mjk = 5 | 0.166 for HI = 1 0.203 for HIINT = 1 using MOBS,jk 0.225 for HIINT = 1 using Mjk 0.083 for HIINT = 1 using default of Mjk = 5 |
| CHCl3:CHBr3 | 2-2 | 1.08 | 0.26 | 1.36 | 5 | ||
| BDCM:CHBr3 | 2-3 | 1.54 | 0.56 | 2.18 | 5 | ||
| BDCM:CDBM | 2-4, 2-4A | 1.81 | 0.67 | 2.41 | 5 | ||
| CHCl3:CDBM | 2-5 | 1.93 | 0.40 | 5.20 | 5 | ||
| CDBM:CHBr3 | 2-6 | 1.25 | 0.59 | 1.46 | 5 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hertzberg, R.C.; Teuschler, L.K.; McDonald, A.; Sey, Y.M.; Simmons, J.E. Evaluation of the Interaction-Based Hazard Index Formula Using Data on Four Trihalomethanes from U.S. EPA’s Multiple-Purpose Design Study. Toxics 2024, 12, 305. https://doi.org/10.3390/toxics12050305
Hertzberg RC, Teuschler LK, McDonald A, Sey YM, Simmons JE. Evaluation of the Interaction-Based Hazard Index Formula Using Data on Four Trihalomethanes from U.S. EPA’s Multiple-Purpose Design Study. Toxics. 2024; 12(5):305. https://doi.org/10.3390/toxics12050305
Chicago/Turabian StyleHertzberg, Richard C., Linda K. Teuschler, Anthony McDonald, Yusupha Mahtarr Sey, and Jane Ellen Simmons. 2024. "Evaluation of the Interaction-Based Hazard Index Formula Using Data on Four Trihalomethanes from U.S. EPA’s Multiple-Purpose Design Study" Toxics 12, no. 5: 305. https://doi.org/10.3390/toxics12050305
APA StyleHertzberg, R. C., Teuschler, L. K., McDonald, A., Sey, Y. M., & Simmons, J. E. (2024). Evaluation of the Interaction-Based Hazard Index Formula Using Data on Four Trihalomethanes from U.S. EPA’s Multiple-Purpose Design Study. Toxics, 12(5), 305. https://doi.org/10.3390/toxics12050305






