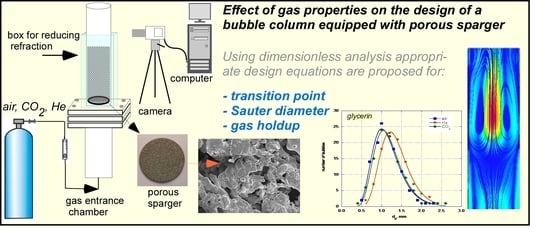
3.1. Bubble Size Distribution
Figure 3 illustrates typical bubble size distributions with the 40 μm sparger (
dc = 9 cm), for all gases studied and for a constant
UGS value. As expected [
4], the distributions are log-normal while regardless of the liquid phase only the low density He gas exhibits an observable effect on the bubble distribution curve. This can be attributed to the considerably lower momentum force exerted by the low density He gas (
Table 1). However, the value of mean Sauter diameter is not considerably affected by the type of gas but is mainly affected by the type of liquid phase employed (
Table 5).
In previous works in our lab [
4,
9], a correlation for predicting the Sauter mean diameter (
d32) based on dimensionless numbers was proposed. The same correlation can be used for predicting the mean Sauter diameter when different gases are employed provided that the constants of the correlation are suitably adjusted (Equation (4)).
where
We,
Re and
Fr are the Weber, Reynolds and Froude number respectively, based on gas superficial velocity and liquid phase properties and defined as:
In
Figure 4 it is shown that the proposed correlation (Equation (4)) can be used for predicting
d32 values with reasonable accuracy (i.e., ±15%) for all the gases employed.
3.2. Regime Transition
The transition point from homogeneous to heterogeneous regime is estimated by applying the drift flux analysis, which considers the relative motion of the two phases [
11]. The basic quantity is the drift flux,
j, is given by:
where
εG is the gas holdup and
UGS is the superficial gas velocity defined as:
where
QG is the gas flow rate and
A the column cross section. When the drift flux is plotted versus the gas holdup, the change in the slope of the curve indicates the transition from homogeneous to heterogeneous regime [
12].
The effect of the type of gas on regime transition is illustrated in
Figure 5. It is obvious that, only when the lower density gas, He, is employed, the homogeneous regime is extended to higher
j or equally
UGS values.
In previous papers [
9,
13], we have proposed a correlation (Equation (10)) for predicting the transition point that is based on dimensionless numbers and incorporates the physical properties of the liquid phase as well as the geometrical characteristics of the column and the porous sparger. This correlation has the general form:
where
Frtrans is the Froude number at the transition point and
Eo the Eotvos number based on
d32:
In view of the new results to incorporate the effect of type of gas, the ratio of gas density to that of air density is added. The new correlation is as follows:
The predicted UGS,trans values are in very good agreement, i.e., better than 15%, with the corresponding experimental data. The proposed correlation is suitable for predicting the transition point from homogeneous to heterogeneous regime.
3.3. Gas Holdup
In this section the effect of the various parameter on the gas holdup values is investigated. As it is expected, gas holdup increases with the gas velocity. The first part of the curve corresponds to the homogeneous regime, which is followed by a transition regime where the gas holdup slightly decreases. Finally, at the heterogeneous regime the gas holdup continues to increase, but with a lower slope than the homogeneous regime [
8].
Figure 6 shows the dependence of gas holdup on corresponding gas superficial velocity for the two bubble columns used. It is obvious from that by increasing the column diameter the gas holdup increases, especially for higher gas flow rates. However, the literature results concerning the effect of column diameter on gas holdup are contradictory. Some researchers report that the column diameter has no effect on gas holdup [
14,
15,
16,
17]. The above works concern bubble columns with diameter larger than 10 cm, where the gas distributor is a perforated plate.
Ruzicka et al. [
18] also state that the gas holdup is independent of column dimensions provided that the column diameter is larger than 10 cm, the column height is larger than 15 cm and the column height to diameter ratio is more than 5. On the other hand, some works report that the column diameter affects the gas holdup. Botton et al. [
19] report that gas holdup increases when the column diameter decreases, whereas Kumar et al. [
20] who conducted experiments in bubble columns with diameters larger than 10 cm, state that there is a continuous increase in the gas holdup with increasing column diameter. To the best of our knowledge, there are no experimental results concerning bubble columns with diameter less than 10 cm, equipped with fine porous sparger. Dhotre et al. [
21], who have numerically studied the effect of sparger type and height to diameter ratio on radial gas holdup profiles, report that for multipoint spargers, an increase of the column height to column diameter ratio results into marginal decrease of gas holdup. Obviously, when the column diameter decreases the wall effects become more intense.
Figure 7 presents typical effect of the type of gas on gas holdup. With increasing gas density gas holdup increases, e.g., helium that has a lower density exhibits lower values of gas holdup than air and CO
2. This behavior is attributed to the fact that, the lower density gas exerts a lower momentum force to an under-formation bubble (
Table 1). This observation agrees with other researchers [
22,
23] who also reported that gases of higher density produce higher gas holdup values, attributing this behavior on phenomena occurring during bubbles formation on the sparger. However, it is worth noticing that, even though the density of CO
2 is 50% higher than that of atmospheric air, for the lower gas superficial velocities both air and CO
2 exhibit almost the same behavior and only when the density decreases by more than 80% (i.e., for He)) a noticeable change is observed (
Figure 7).
In previous studies conducted in our lab [
8,
9,
13] a correlation for predicting the average gas holdup,
εG, was proposed based on dimensionless numbers. The equation has the general form:
where
Fr,
Ar and
Eo are the dimensionless Froude, Archimedes and Eotvos number respectively defined by:
the quantities
dc,
ds, are the column and the sparger diameter, while
dp is the mean pore size of the sparger material. The values of constants
c1 to
c7 depend on the of liquid phase. It was also proved [
8,
9,
10,
13] that the proposed correlations can predict hold up with reasonable accuracy, i.e., better than 15%.
However, in the ε
G prediction, the type of gas is not taken into account although the gas momentum affects bubble evolution (
Table 1). From
Figure 7, where the effect of gas type is presented, it is apparent that only the very low density gas He has has a measurable effect on gas holdup value. In case that the gas phase is other than air, it is necessary to introduce a term that incorporates the properties of the gas phase.
Based on the above, we have modified Equation (10) by introducing in the gas Reynolds number
ReG defined as:
The modified form of the proposed correlation is as follows:
where the constants of the correlation are given in
Table 6.
Figure 8 shows that the
εG values predicted by Equation (19) are in very good agreement (±15%) with the corresponding experimental data.