Using Discrete Multiphysics Modelling to Assess the Effect of Calcification on Hemodynamic and Mechanical Deformation of Aortic Valve
Abstract
:1. Introduction
2. Discrete Multiphysics
2.1. Smooth Particle Hydrodynamics
2.2. Lattice Spring Model (LSM)
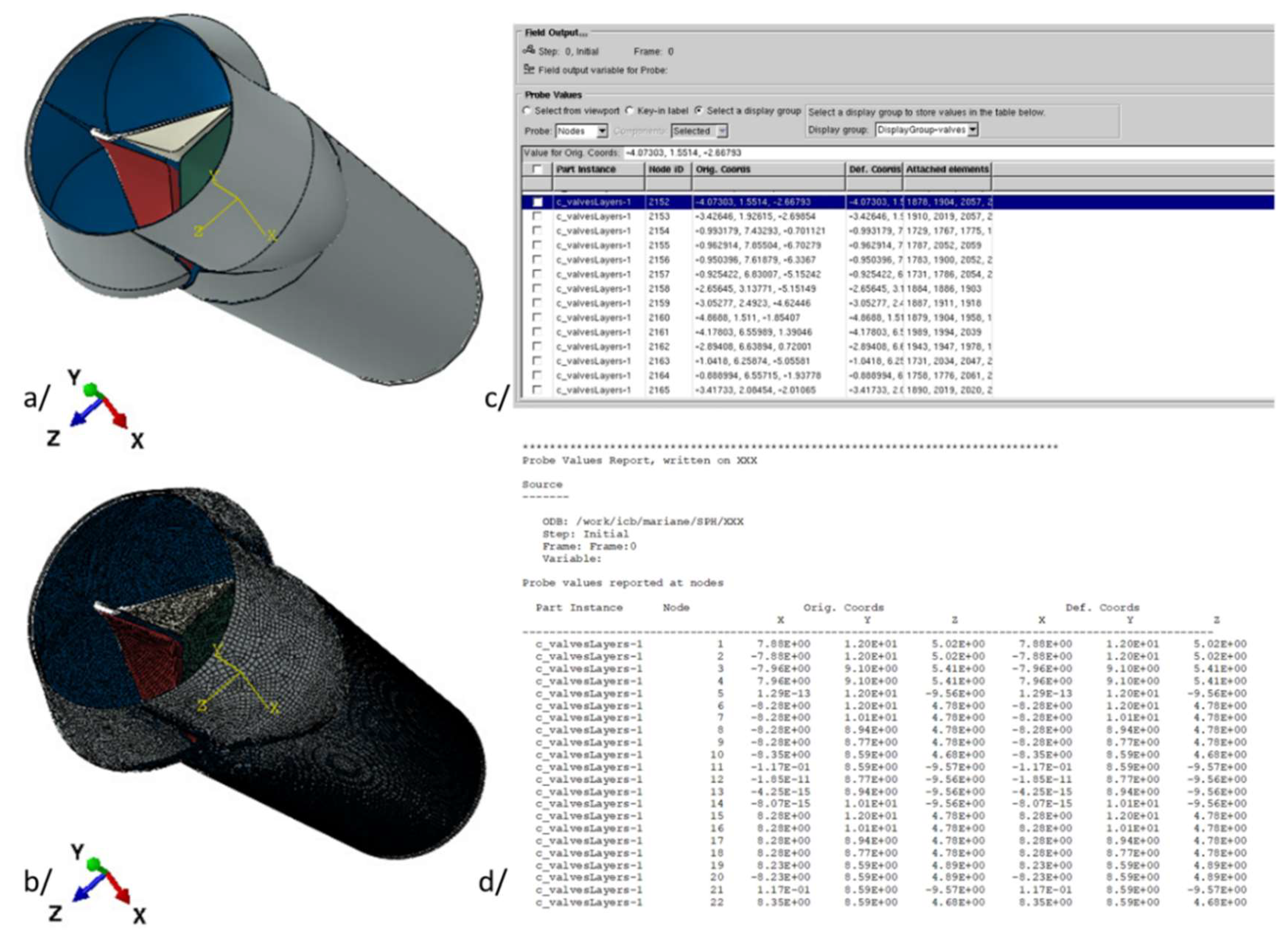
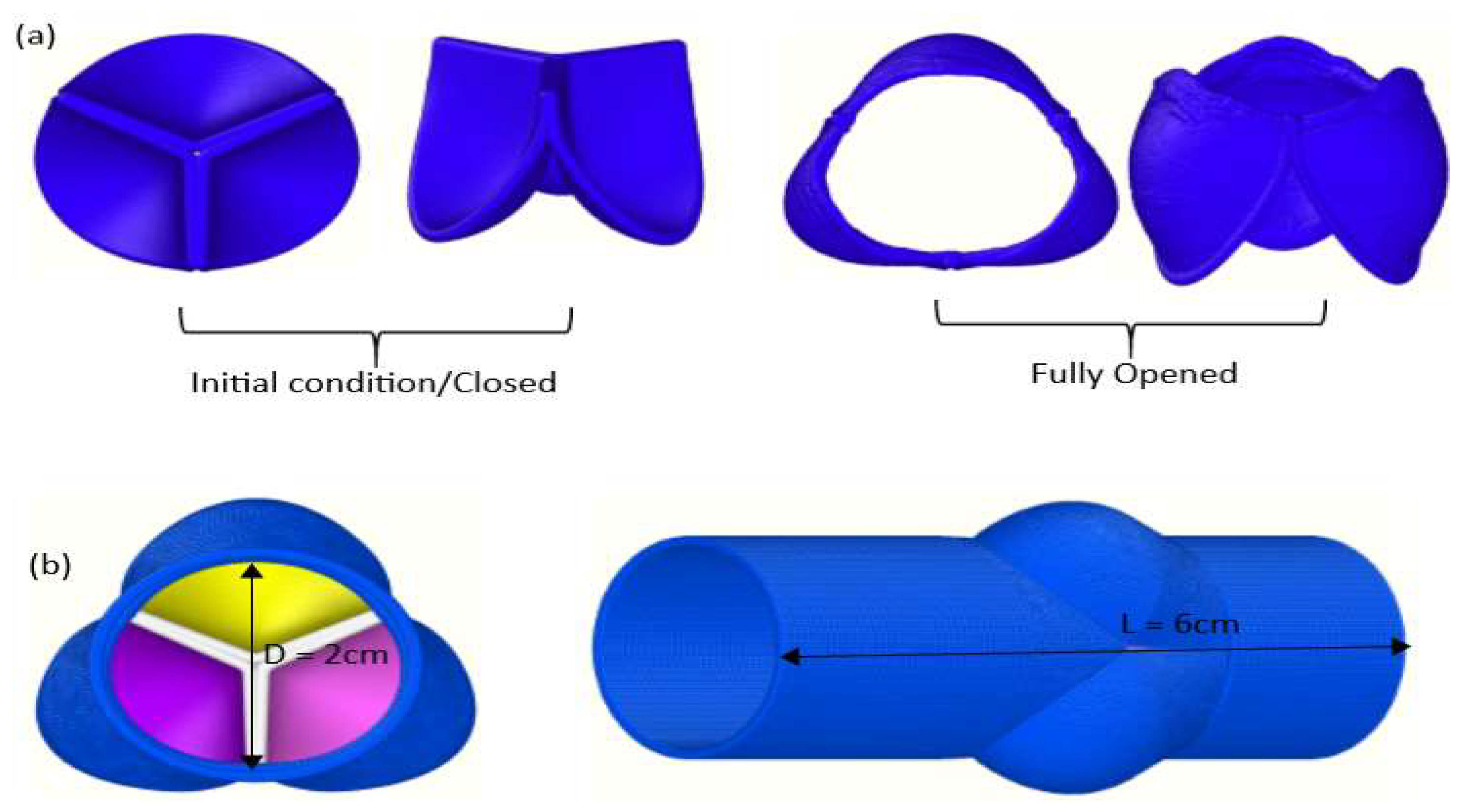
3. The Model
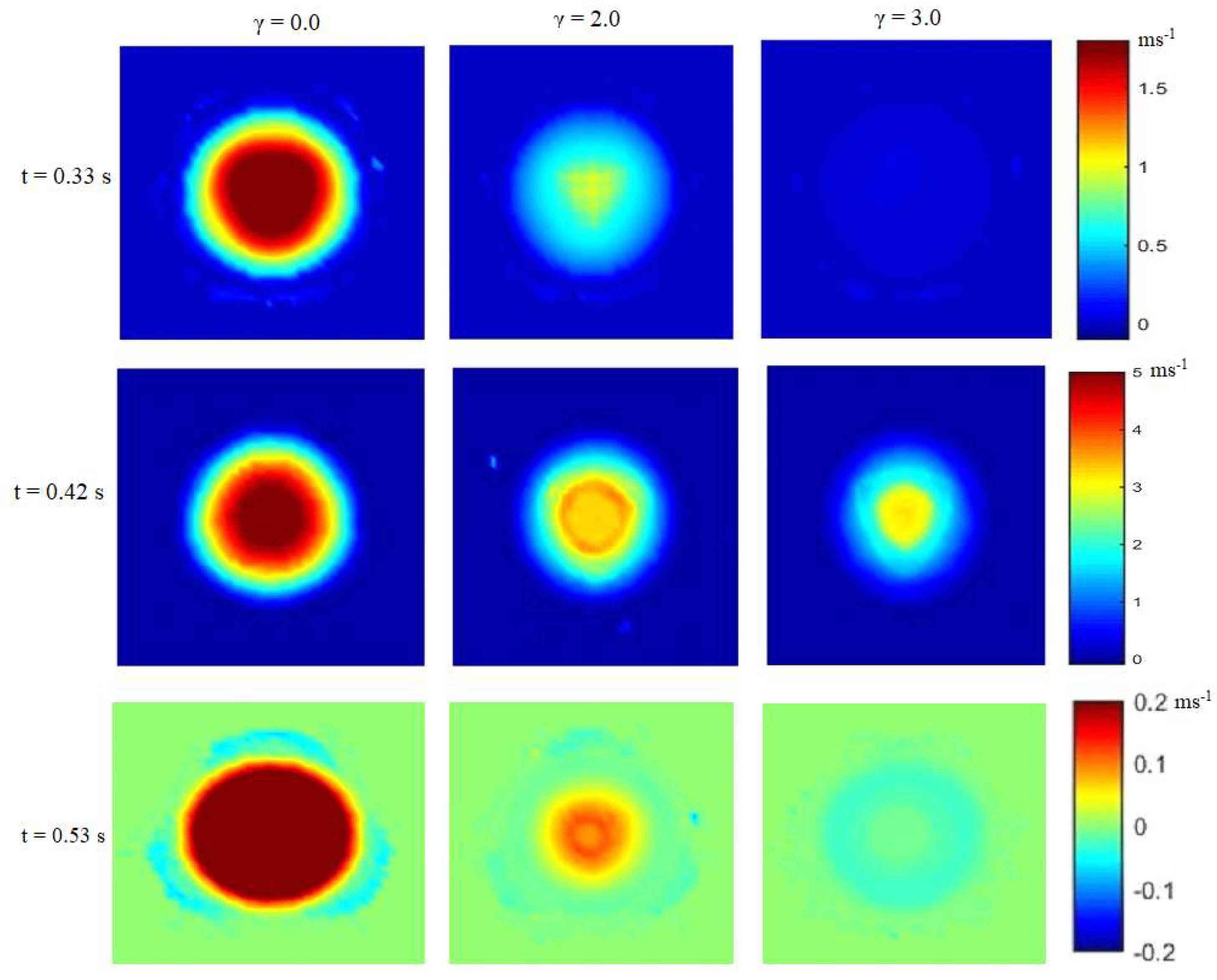
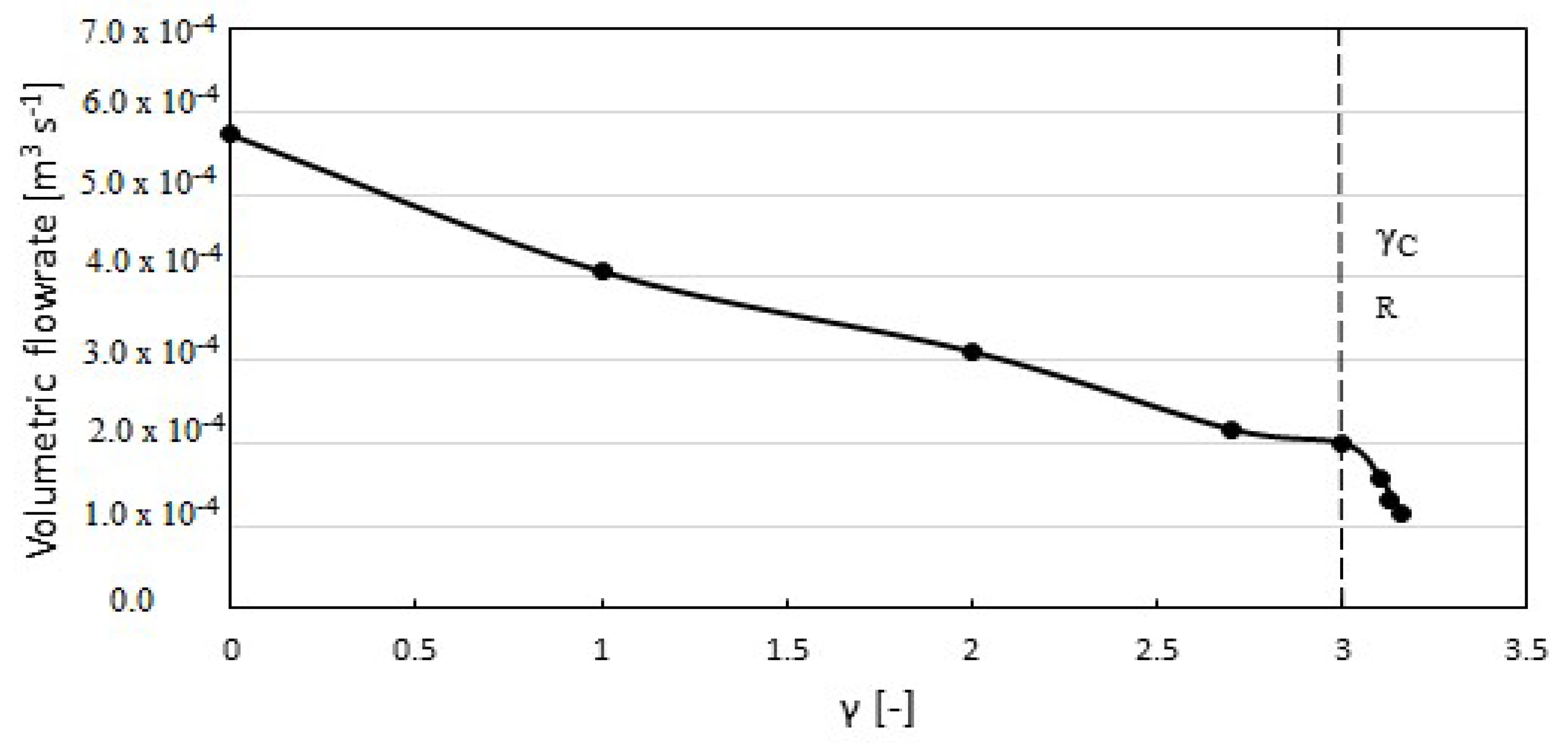
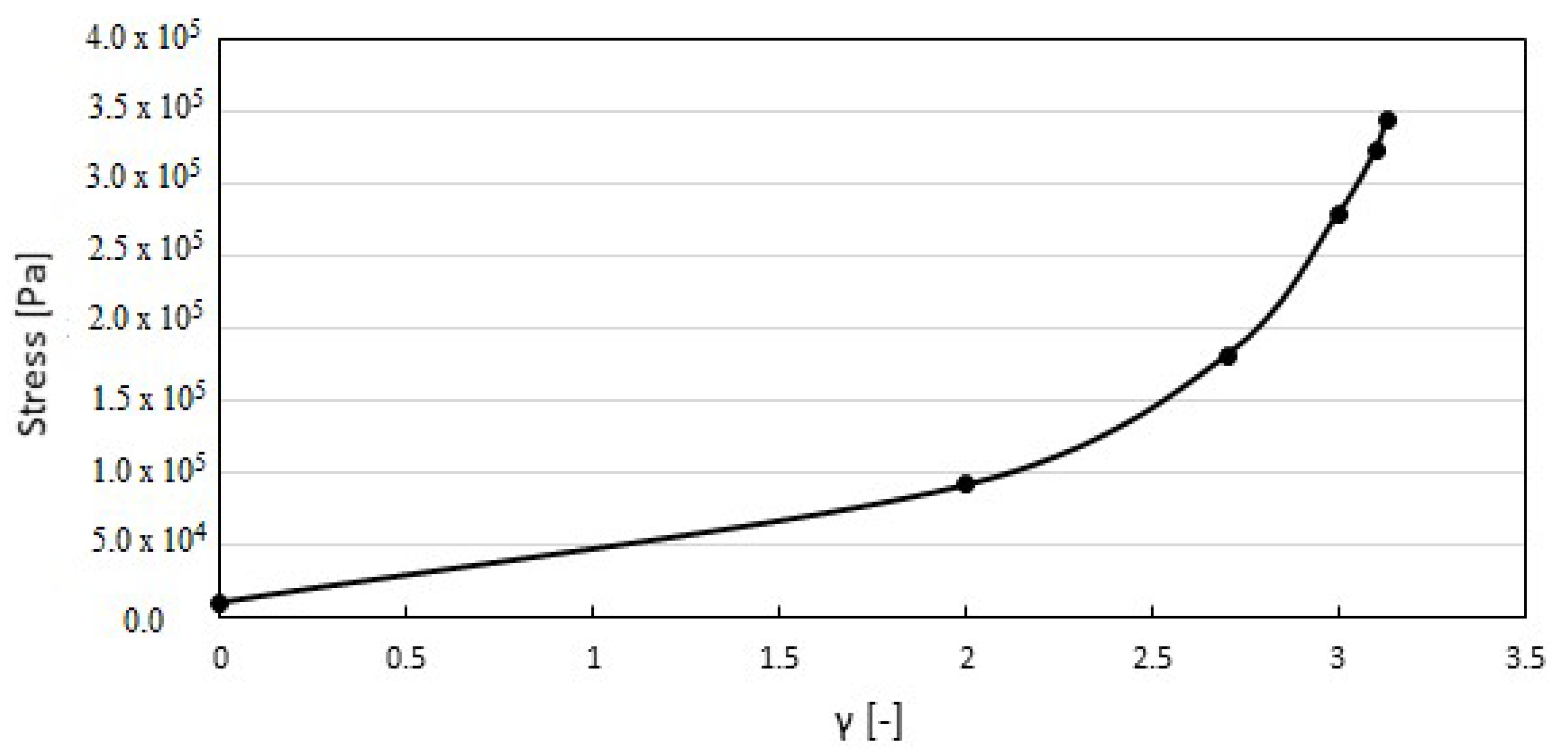
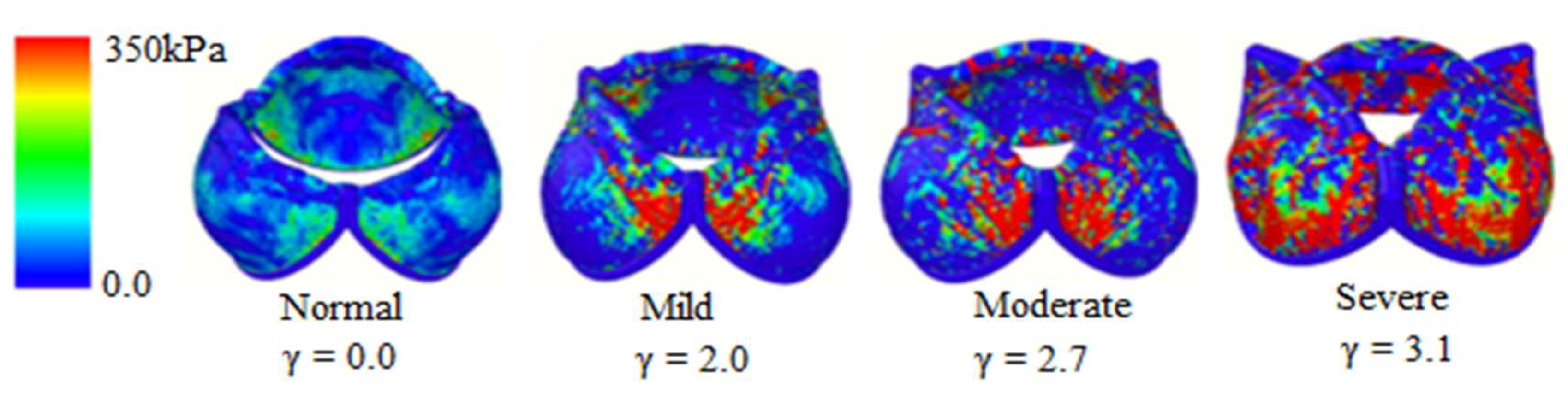
4. Results and Discussion
4.1. Stages of Calcification
4.2. Stress Distribution on the Membrane
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

- Creation or importation of the CAD geometry
- Writing of the data file
- Generation of the bond and coefficient files
- Implementation of the input file
References
- Fioretta, E.S.; Dijkman, P.E.; Emmert, M.Y.; Hoerstrup, S.P. The Future of Heart Valve Replacement: Recent Developments and Translational Challenges for Heart Valve Tissue Engineering: The Future of Heart Valve Replacement. J. Tissue Eng. Regen. Med. 2018, 12, e323–e335. [Google Scholar] [CrossRef] [PubMed]
- Amindari, A.; Saltik, L.; Kirkkopru, K.; Yacoub, M.; Yalcin, H.C. Assessment of Calcified Aortic Valve Leaflet Deformations and Blood Flow Dynamics Using Fluid-Structure Interaction Modeling. Inform. Med. Unlocked 2017, 9, 191–199. [Google Scholar] [CrossRef]
- Otto, C.M.; Prendergast, B. Aortic-Valve Stenosis—From Patients at Risk to Severe Valve Obstruction. N. Engl. J. Med. 2014, 371, 744–756. [Google Scholar] [CrossRef] [PubMed]
- Fedele, M.; Faggiano, E.; Dedè, L.; Quarteroni, A. A Patient-Specific Aortic Valve Model Based on Moving Resistive Immersed Implicit Surfaces. Biomech. Modeling Mechanobiol. 2017, 16, 1779–1803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Youssefi, P.; Gomez, A.; He, T.; Anderson, L.; Bunce, N.; Sharma, R.; Figueroa, C.A.; Jahangiri, M. Patient-Specific Computational Fluid Dynamics—Assessment of Aortic Hemodynamics in a Spectrum of Aortic Valve Pathologies. J. Thorac. Cardiovasc. Surg. 2017, 153, 8–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bluestein, D.; Einav, S. The Effect of Varying Degrees of Stenosis on the Characteristics of Turbulent Pulsatile Flow through Heart Valves. J. Biomech. 1995, 28, 915–924. [Google Scholar] [CrossRef]
- Hamid, M.S.; Sabbah, H.N.; Stein, P.D. Comparison of Finite Element Stress Analysis of Aortic Valve Leaflet Using Either Membrane Elements or Solid Elements. Comput. Struct. 1985, 20, 955–961. [Google Scholar] [CrossRef]
- Arjunon, S.; Rathan, S.; Jo, H.; Yoganathan, A.P. Aortic Valve: Mechanical Environment and Mechanobiology. Ann. Biomed. Eng. 2013, 41, 1331–1346. [Google Scholar] [CrossRef] [Green Version]
- Morganti, S.; Conti, M.; Aiello, M.; Valentini, A.; Mazzola, A.; Reali, A.; Auricchio, F. Simulation of Transcatheter Aortic Valve Implantation through Patient-Specific Finite Element Analysis: Two Clinical Cases. J. Biomech. 2014, 47, 2547–2555. [Google Scholar] [CrossRef]
- Lazaros, G.; Drakopoulou, M.I.; Tousoulis, D. Transaortic Flow in Aortic Stenosis: Stroke Volume Index versus Flow Rate. Cardiology 2018, 141, 71–73. [Google Scholar] [CrossRef]
- Ghasemi Bahraseman, H.; Mohseni Languri, E.; Yahyapourjalaly, N.; Espino, D.M. Fluid-Structure Interaction Modeling of Aortic Valve Stenosis at Different Heart Rates. Acta Bioeng. Biomech. 2016, 18, 11–20. [Google Scholar] [CrossRef]
- Alexiadis, A. The Discrete Multi-Hybrid System for the Simulation of Solid-Liquid Flows. PLoS ONE 2015, 10, e0124678. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alexiadis, A. A Smoothed Particle Hydrodynamics and Coarse-Grained Molecular Dynamics Hybrid Technique for Modelling Elastic Particles and Breakable Capsules under Various Flow Conditions: SPH-CGMD HYBRID. Int. J. Numer. Meth. Eng. 2014, 100, 713–719. [Google Scholar] [CrossRef]
- Alexiadis, A. A New Framework for Modelling the Dynamics and the Breakage of Capsules, Vesicles and Cells in Fluid Flow. Procedia IUTAM 2015, 16, 80–88. [Google Scholar] [CrossRef] [Green Version]
- Ariane, M.; Allouche, M.H.; Bussone, M.; Giacosa, F.; Bernard, F.; Barigou, M.; Alexiadis, A. Discrete Multi-Physics: A Mesh-Free Model of Blood Flow in Flexible Biological Valve Including Solid Aggregate Formation. PLoS ONE 2017, 12, e0174795. [Google Scholar] [CrossRef] [Green Version]
- Alexiadis, A.; Stamatopoulos, K.; Wen, W.; Batchelor, H.K.; Bakalis, S.; Barigou, M.; Simmons, M.J.H. Using Discrete Multi-Physics for Detailed Exploration of Hydrodynamics in an In Vitro Colon System. Comput. Biol. Med. 2017, 81, 188–198. [Google Scholar] [CrossRef]
- Ariane, M.; Vigolo, D.; Brill, A.; Nash, F.G.B.; Barigou, M.; Alexiadis, A. Using Discrete Multi-Physics for Studying the Dynamics of Emboli in Flexible Venous Valves. Comput. Fluids 2018, 166, 57–63. [Google Scholar] [CrossRef]
- Ariane, M.; Wen, W.; Vigolo, D.; Brill, A.; Nash, F.G.B.; Barigou, M.; Alexiadis, A. Modelling and Simulation of Flow and Agglomeration in Deep Veins Valves Using Discrete Multi Physics. Comput. Biol. Med. 2017, 89, 96–103. [Google Scholar] [CrossRef]
- Ariane, M.; Kassinos, S.; Velaga, S.; Alexiadis, A. Discrete Multi-Physics Simulations of Diffusive and Convective Mass Transfer in Boundary Layers Containing Motile Cilia in Lungs. Comput. Biol. Med. 2018, 95, 34–42. [Google Scholar] [CrossRef]
- Alexiadis, A. Deep Multiphysics: Coupling Discrete Multiphysics with Machine Learning to Attain Self-Learning in-Silico Models Replicating Human Physiology. Artif. Intell. Med. 2019, 98, 27–34. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Hackensack, NJ, USA, 2003. [Google Scholar]
- Kot, M.; Nagahashi, H.; Szymczak, P. Elastic Moduli of Simple Mass Spring Models. Vis. Comput. 2015, 31, 1339–1350. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed Particle Hydrodynamics: Theory and Application to Non-Spherical Stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A Numerical Approach to the Testing of the Fission Hypothesis. Astron. J. 1977, 82, 1013. [Google Scholar] [CrossRef]
- Hopp-Hirschler, M.; Shadloo, M.S.; Nieken, U. A Smoothed Particle Hydrodynamics Approach for Thermo-Capillary Flows. Comput. Fluids 2018, 176, 1–19. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Zainali, A.; Sadek, S.H.; Yildiz, M. Improved Incompressible Smoothed Particle Hydrodynamics Method for Simulating Flow around Bluff Bodies. Comput. Methods Appl. Mech. Eng. 2011, 200, 1008–1020. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Rahmat, A.; Yildiz, M. A Multiphase ISPH Method for Simulation of Droplet Coalescence and Electro-Coalescence. Int. J. Multiph. Flow 2018, 105, 32–44. [Google Scholar] [CrossRef]
- Schütt, M.; Stamatopoulos, K.; Simmons, M.J.H.; Batchelor, H.K.; Alexiadis, A. Modelling and Simulation of the Hydrodynamics and Mixing Profiles in the Human Proximal Colon Using Discrete Multiphysics. Comput. Biol. Med. 2020, 121, 103819. [Google Scholar] [CrossRef]
- Ji, S.; Chen, X.; Liu, L. Coupled DEM-SPH Method for Interaction between Dilated Polyhedral Particles and Fluid. Math. Probl. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Zhen, Z.; Zhang, H.; Li, Y.; Tang, X. Numerical Model of Oil Film Diffusion in Water Based on SPH Method. Math. Probl. Eng. 2019, 2019, 1–14. [Google Scholar] [CrossRef]
- Rahmat, A.; Barigou, M.; Alexiadis, A. Deformation and Rupture of Compound Cells under Shear: A Discrete Multiphysics Study. Phys. Fluids 2019, 31, 051903. [Google Scholar] [CrossRef]
- Tran-Duc, T.; Phan-Thien, N.; Khoo, B.C. A Smoothed Particle Hydrodynamics (SPH) Study of Sediment Dispersion on the Seafloor. Phys. Fluids 2017, 29, 083302. [Google Scholar] [CrossRef]
- Rahmat, A.; Tofighi, N.; Shadloo, M.S.; Yildiz, M. Numerical Simulation of Wall Bounded and Electrically Excited Rayleigh–Taylor Instability Using Incompressible Smoothed Particle Hydrodynamics. Colloids Surf. A Physicochem. Eng. Asp. 2014, 460, 60–70. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Yildiz, M. Numerical Modeling of Kelvin-Helmholtz Instability Using Smoothed Particle Hydrodynamics. Int. J. Numer. Meth. Engng. 2011, 87, 988–1006. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Restoring Particle Consistency in Smoothed Particle Hydrodynamics. Appl. Numer. Math. 2006, 56, 19–36. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Zainali, A.; Yildiz, M. Simulation of Single Mode Rayleigh–Taylor Instability by SPH Method. Comput. Mech. 2013, 51, 699–715. [Google Scholar] [CrossRef]
- Pazdniakou, A.; Adler, P.M. Lattice Spring Models. Transp. Porous. Med. 2012, 93, 243–262. [Google Scholar] [CrossRef]
- Lloyd, B.; Szekely, G.; Harders, M. Identification of Spring Parameters for Deformable Object Simulation. IEEE Trans. Visual. Comput. Graph. 2007, 13, 1081–1094. [Google Scholar] [CrossRef]
- Stevens, S.A.; Lakin, W.D.; Goetz, W. A Differentiable, Periodic Function for Pulsatile Cardiac Output Based on Heart Rate and Stroke Volume. Math. Biosci. 2003, 182, 201–211. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Bavo, A.M.; Rocatello, G.; Iannaccone, F.; Degroote, J.; Vierendeels, J.; Segers, P. Fluid-Structure Interaction Simulation of Prosthetic Aortic Valves: Comparison between Immersed Boundary and Arbitrary Lagrangian-Eulerian Techniques for the Mesh Representation. PLoS ONE 2016, 11, e0154517. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murgo, J.P.; Westerhof, N.; Giolma, J.P.; Altobelli, S.A. Aortic Input Impedance in Normal Man: Relationship to Pressure Wave Forms. Circulation 1980, 62, 105–116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blais, C.; Burwash, I.G.; Mundigler, G.; Dumesnil, J.G.; Loho, N.; Rader, F.; Baumgartner, H.; Beanlands, R.S.; Chayer, B.; Kadem, L.; et al. Projected Valve Area at Normal Flow Rate Improves the Assessment of Stenosis Severity in Patients With Low-Flow, Low-Gradient Aortic Stenosis: The Multicenter TOPAS (Truly or Pseudo-Severe Aortic Stenosis) Study. Circulation 2006, 113, 711–721. [Google Scholar] [CrossRef] [Green Version]
- Hammer, P.E.; Sacks, M.S.; del Nido, P.J.; Howe, R.D. Mass-Spring Model for Simulation of Heart Valve Tissue Mechanical Behavior. Ann. Biomed. Eng. 2011, 39, 1668–1679. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jermihov, P.N.; Jia, L.; Sacks, M.S.; Gorman, R.C.; Gorman, J.H.; Chandran, K.B. Effect of Geometry on the Leaflet Stresses in Simulated Models of Congenital Bicuspid Aortic Valves. Cardiovasc. Eng. Tech. 2011, 2, 48–56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Auricchio, F.; Conti, M.; Morganti, S.; Reali, A. Simulation of Transcatheter Aortic Valve Implantation: A Patient-Specific Finite Element Approach. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 1347–1357. [Google Scholar] [CrossRef] [PubMed]
- Kamimura, D.; Hans, S.; Suzuki, T.; Fox, E.R.; Hall, M.E.; Musani, S.K.; McMullan, M.R.; Little, W.C. Delayed Time to Peak Velocity Is Useful for Detecting Severe Aortic Stenosis. JAHA 2016, 5. [Google Scholar] [CrossRef]
- Saeed, S.; Senior, R.; Chahal, N.S.; Lønnebakken, M.T.; Chambers, J.B.; Bahlmann, E.; Gerdts, E. Lower Transaortic Flow Rate Is Associated with Increased Mortality in Aortic Valve Stenosis. JACC Cardiovasc. Imaging 2017, 10, 912–920. [Google Scholar] [CrossRef]
- Thubrikar, M.; Deck, J.; Aouad, J.; Nolan, S. Role of Mechanical Stress in Calcification of Aortic Bioprosthetic Valves. J. Thorac. Cardiovasc. Surg. 1983, 86, 115–125. [Google Scholar] [CrossRef]
- Huntley, G.D.; Thaden, J.J.; Alsidawi, S.; Michelena, H.I.; Maleszewski, J.J.; Edwards, W.D.; Scott, C.G.; Pislaru, S.V.; Pellikka, P.A.; Greason, K.L.; et al. Comparative Study of Bicuspid vs. Tricuspid Aortic Valve Stenosis. Eur. Heart J. Cardiovasc. Imaging 2018, 19, 3–8. [Google Scholar] [CrossRef]

| Parameters | Values |
|---|---|
| Number of SPH wall particle | 56,660 |
| Number of SPH fluid particle | 342,358 |
| Number of SPH leaflets | 19,725 |
| Mass of each particle (fluid) | 6.7 × 10−8 kg |
| Mass of each particle (Solid) | 14 × 10−8 kg |
| Smoothing length h | 1.0 × 10−3 m |
| Length L | 6 × 10−2 m |
| Diameter D | 2 × 10−2 m |
| Particle spacing l | 0.4 × 10−3 m |
| Fluid Density ρ | 1060 kg m−3 |
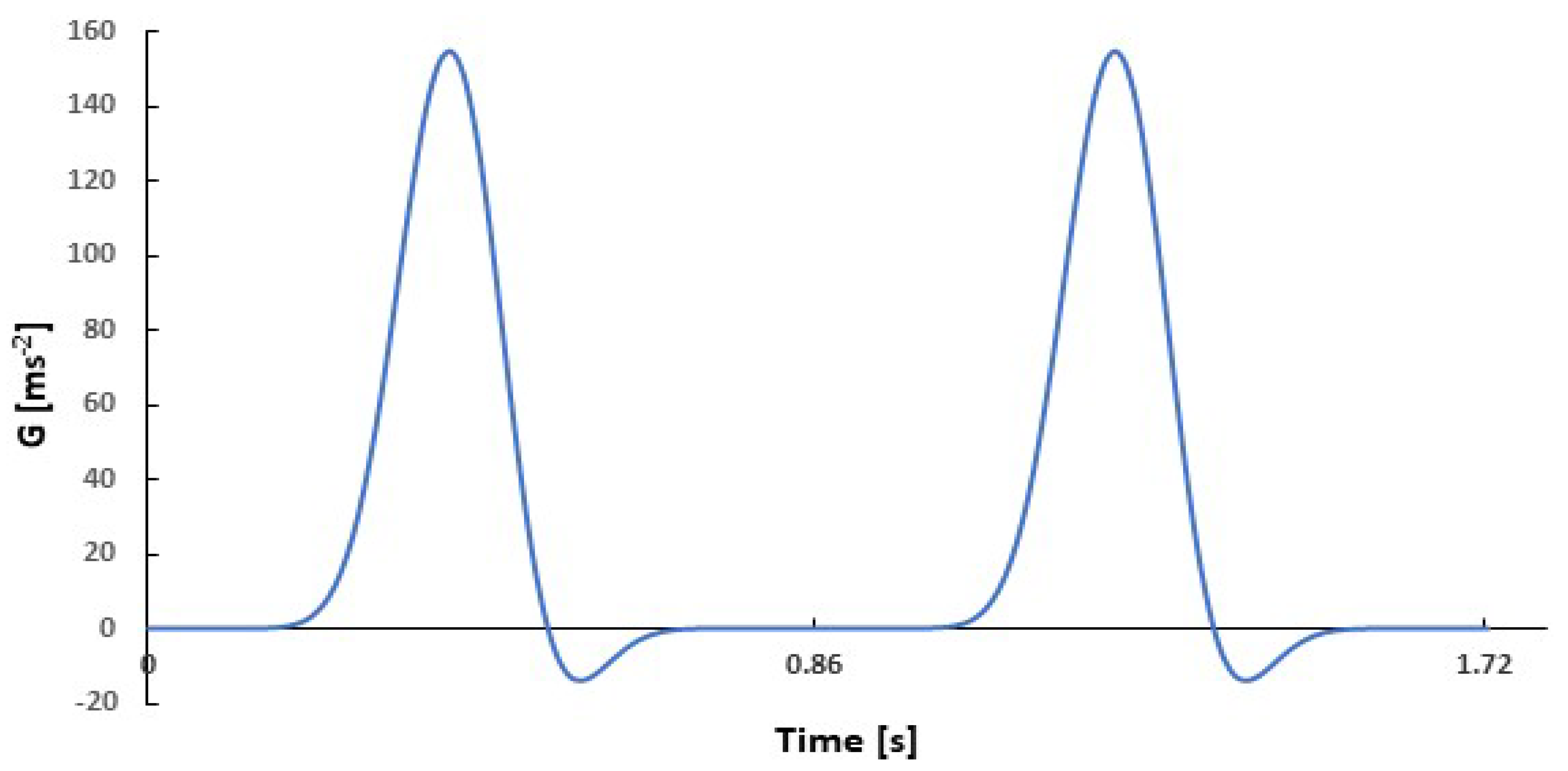
| Frequency f | 1.167 s−1 (70 beats min−1) |
| Pseudo-gravity G0 | 400 m s−2 |
| Viscosity μ | 0.003 Pa∙s |
| Elastic constant k | 10−14,500 N m−1 |
| Sound speed c0 | 16 m s−1 |
| Time step Δt | 1 × 10−6 s |
| Calcification | Maximum Orifice Diameter [cm] | Mean Flow × 10−4 [m3s−1] | Average Stress [kPa] |
|---|---|---|---|
| Normal (γ = 0.0) | 1.81 | 5.72 | 10.60 |
| Mild (γ = 2.0) | 1.41 | 3.21 | 91.68 |
| Moderate (γ = 2.7) | 1.29 | 2.17 | 181.61 |
| Severe (γ = 3.1) | 1.17 | 1.58 | 324.27 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, A.M.; Ariane, M.; Alexiadis, A. Using Discrete Multiphysics Modelling to Assess the Effect of Calcification on Hemodynamic and Mechanical Deformation of Aortic Valve. ChemEngineering 2020, 4, 48. https://doi.org/10.3390/chemengineering4030048
Mohammed AM, Ariane M, Alexiadis A. Using Discrete Multiphysics Modelling to Assess the Effect of Calcification on Hemodynamic and Mechanical Deformation of Aortic Valve. ChemEngineering. 2020; 4(3):48. https://doi.org/10.3390/chemengineering4030048
Chicago/Turabian StyleMohammed, Adamu Musa, Mostapha Ariane, and Alessio Alexiadis. 2020. "Using Discrete Multiphysics Modelling to Assess the Effect of Calcification on Hemodynamic and Mechanical Deformation of Aortic Valve" ChemEngineering 4, no. 3: 48. https://doi.org/10.3390/chemengineering4030048
APA StyleMohammed, A. M., Ariane, M., & Alexiadis, A. (2020). Using Discrete Multiphysics Modelling to Assess the Effect of Calcification on Hemodynamic and Mechanical Deformation of Aortic Valve. ChemEngineering, 4(3), 48. https://doi.org/10.3390/chemengineering4030048