Experimental Study and Numerical Simulation of Hydrodynamic Parameters of Tangential Swirlers
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
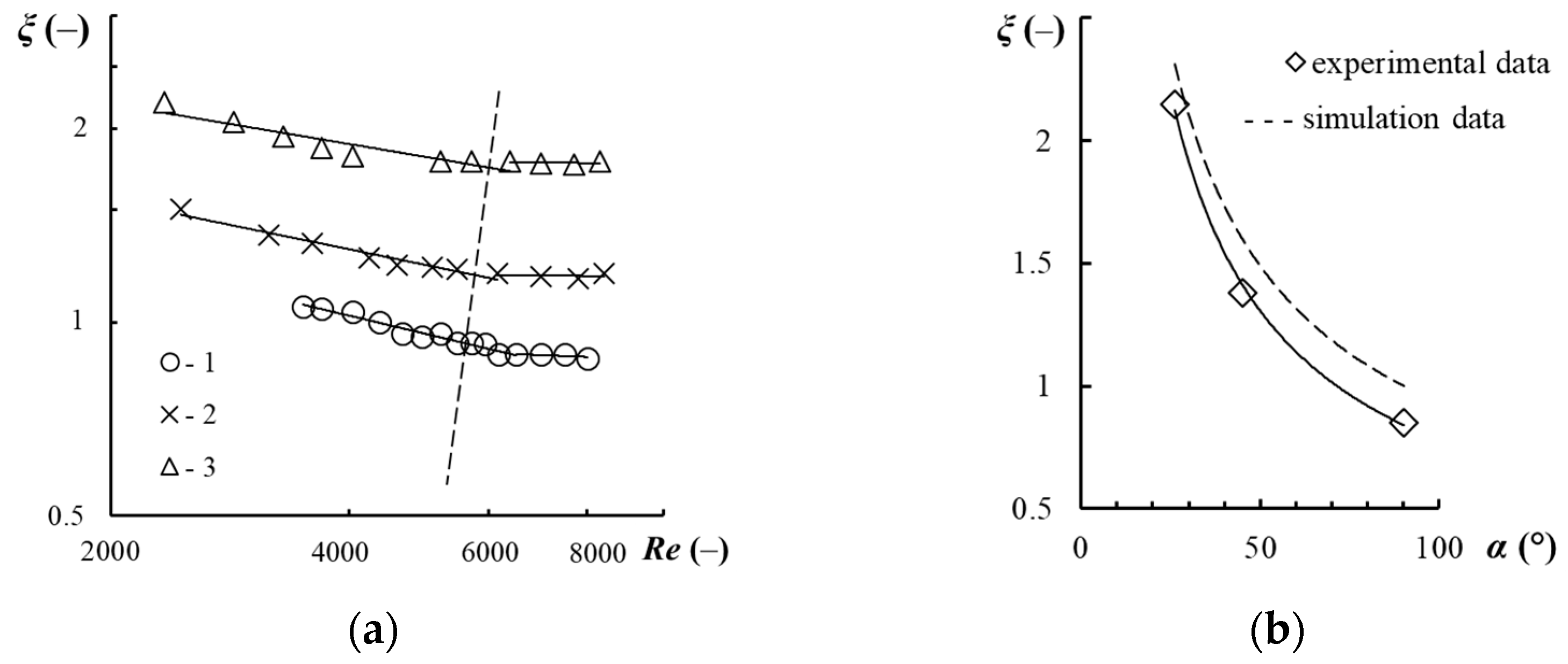
3.1. Swirler Resistance Comparison
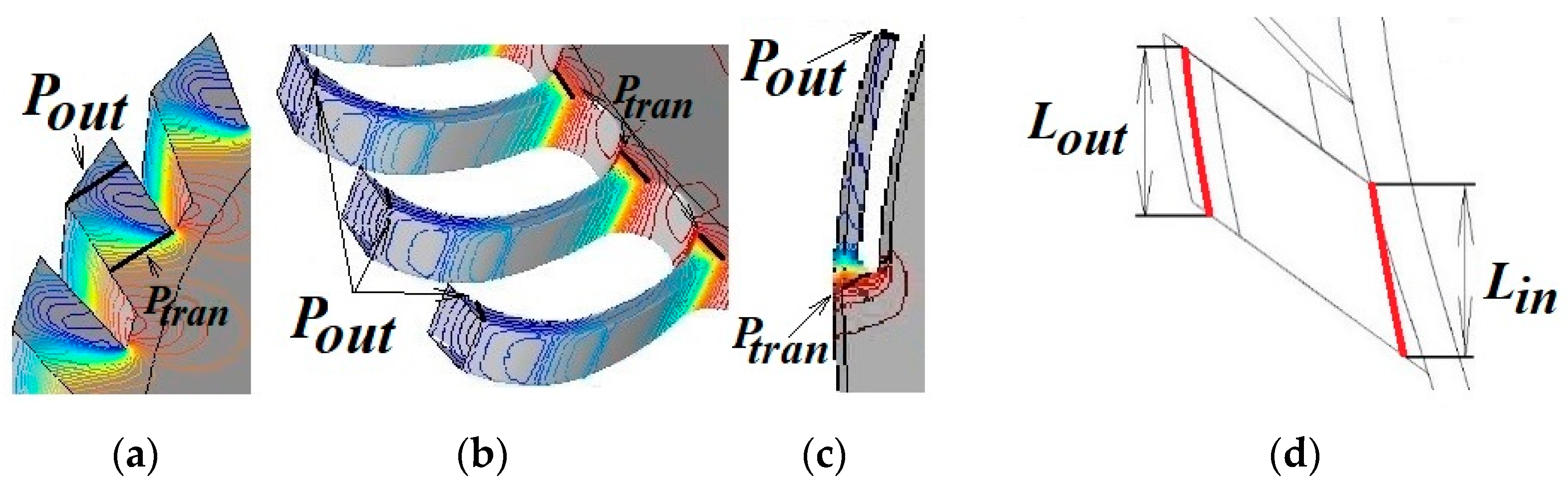
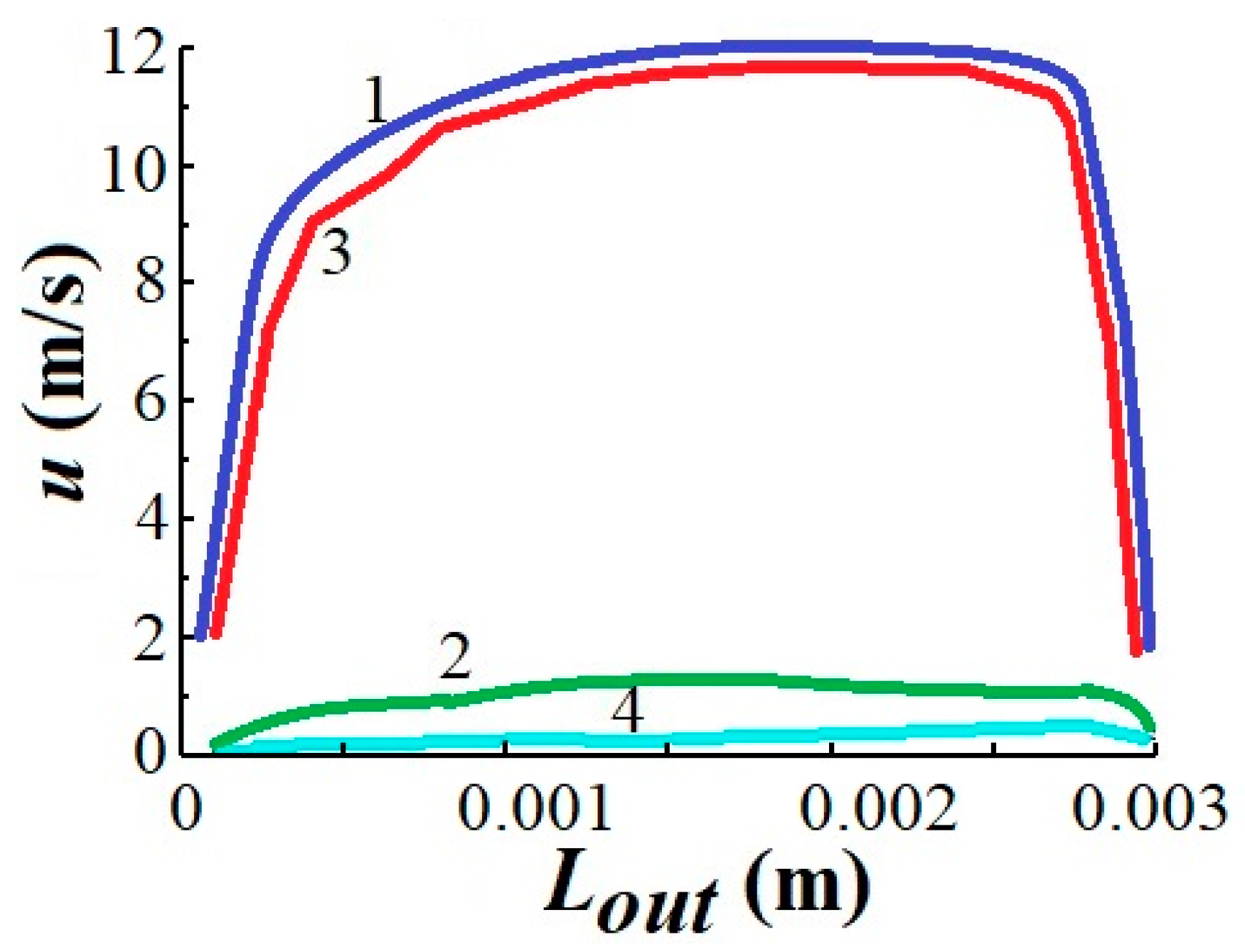
3.2. Gas Flow Modes in Swirler Channels
3.3. Effect of Channel Length on Swirler Resistance
3.4. Influence of the Channel Wall Slope Angle on Swirler Resistance
3.5. Influence of Channel Height and Number on Resistance Value
3.6. Effect of Channel Width on Resistance
3.7. Dependence for Estimating the Resistance Coefficient
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | rotation factor |
| b | width of the channel in the swirler (m) |
| D | diameter (m) |
| bubble dimensionless diameter | |
| Eu | Euler’s criterion |
| F | area of the swirler (m2) |
| f | total area of the channels (m2) |
| h | height of the channels in the swirler (m) |
| h+ | device dimensionless height |
| I, B, K | swirler design-dependent factors |
| J | share of the head loss |
| L | line of pressure reading (m) |
| l | length (m) |
| l+ | dimensionless distance from axis to layer boundary |
| m, q | degree |
| n | number of channels (pcs) |
| P | design pressure (Pa) |
| ΔP | pressure drop (Pa) |
| Re | Reynolds number of gas in the swirler’s channels |
| u | design gas velocity in the swirler’s channels (m/s) |
| average gas flow velocity in the swirler’s channels (m/s) | |
| α | channel slope angle (deg) |
| μ | coefficient of dynamic viscosity of the gas (Pa·s) |
| ξ | dimensionless resistance coefficient |
| density (kg/m3) | |
| φ | dimensionless gas content |
| ψ | minimum relative area (m) |
| Indices | |
| arc | arc |
| chan | channel |
| g | gas |
| g-l | gas-liquid |
| in | inlet |
| out | outer |
| p | total |
| s | swirler |
| st | stage |
| tran | transition area |
| w | working |
| y | tangential |
References
- Eldrainy, Y.A.; Ibrahim, M.F.A.; Jaafar, M.N.M. Investigation of radial swirler effect on flow pattern inside a gas turbine combustor. Mod. Appl. Sci. 2009, 3, 21–31. [Google Scholar] [CrossRef] [Green Version]
- Sandilya, P.; Rao, D.P.; Sharma, A.; Biswas, G. Gas-Phase Mass Transfer in a Centrifugal Contactor. Ind. Eng. Chem. Res. 2001, 40, 384–392. [Google Scholar] [CrossRef]
- Dmitrieva, O.S.; Dmitriev, A.V.; Nikolaev, A.N. Distribution of circulating water in the work area of a vortex chamber with disk atomizer for the purpose of increasing the efficiency of the cooling process. Chem. Pet. Eng. 2014, 50, 169–175. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, T.; Liu, Z.; Wang, S.; Gao, Y.; Wu, M. Mass Transfer in a Rotating Packed Bed: A Critical Review. Chem. Eng. Process. 2019, 139, 78–94. [Google Scholar] [CrossRef]
- Chen, Y.-S.; Lin, C.-C.; Liu, H.-S. Mass Transfer in a Rotating Packed Bed with Various Radii of the Bed. Ind. Eng. Chem. Res. 2005, 44, 7868–7875. [Google Scholar] [CrossRef]
- Sun, B.; Zou, H.; Chu, G.; Shao, L.; Zeng, Z.; Chen, J. Determination of Mass-Transfer Coefficient of CO2 in NH3 and CO2 Absorption by Materials Balance in a Rotating Packed Bed. Ind. Eng. Chem. Res. 2012, 51, 10949–10954. [Google Scholar] [CrossRef]
- Qian, Z.; Xu, L.; Cao, H.; Guo, K. Modeling Study on Absorption of CO2 by Aqueous Solutions of N-Methyldiethanolamine in Rotating Packed Bed. Ind. Eng. Chem. Res. 2009, 48, 9261–9267. [Google Scholar] [CrossRef]
- Chen, Q.-Y.; Chu, G.-W.; Luo, Y.; Sang, L.; Zhang, L.; Zou, H.-K.; Chen, J.-F. Polytetrafluoroethylene Wire Mesh Packing in a Rotating Packed Bed: Mass-Transfer Studies. Ind. Eng. Chem. Res. 2016, 55, 11606–11613. [Google Scholar] [CrossRef]
- Sun, B.-C.; Wang, X.-M.; Chen, J.-M.; Chu, G.-W.; Chen, J.-F.; Shao, L. Simultaneous Absorption of CO2 and NH3 into Water in a Rotating Packed Bed. Ind. Eng. Chem. Res. 2009, 48, 11175–11180. [Google Scholar] [CrossRef]
- Qian, Z.; Li, Z.-H.; Guo, K. Industrial Applied and Modeling Research on Selective H2S Removal Using a Rotating Packed Bed. Ind. Eng. Chem. Res. 2012, 51, 8108–8116. [Google Scholar] [CrossRef]
- Guo, K.; Wen, J.; Zhao, Y.; Wang, Y.; Zhang, Z.; Li, Z.; Qian, Z. Optimal Packing of a Rotating Packed Bed for H2S Removal. Environ. Sci. Technol. 2014, 48, 6844–6849. [Google Scholar] [CrossRef] [PubMed]
- Ovchinnikov, A.A. Dynamics of Two-Phase Swirling Turbulent Flows in Vortex Separators; New Knowledge: Kazan, Russia, 2005; 285p. [Google Scholar]
- Gurbanov, A.N. Highly efficient separation equipment for cleaning natural gas and oil refinery gases. Oilfield Bus./Oilfield Eng. 2017, 6, 46–51. [Google Scholar]
- Zamalieva, A.T.; Ziganshin, M.G. Improving the energy and environmental efficiency of gas cleaning systems at thermal power plants. Izv. TPU 2019, 330, 143–153. [Google Scholar] [CrossRef] [Green Version]
- Kharkov, V.V.; Nikolaev, A.N. Development and research of a vortex-type apparatus for concentrating fruit juices. Vestn. Kazan. Tekhnol. Univ. 2014, 14, 445–448. [Google Scholar]
- Eldrainy, Y.A.; Saqr, K.M.; Aly, H.S.; Jaafar, M.N.M. CFD insight of the flow dynamics in a novel swirler for gas turbine combustors. Int. Commun. Heat Mass Transf. 2009, 36, 936–941. [Google Scholar] [CrossRef]
- Jiao, W.Z.; Liu, Y.Z.; Qi, G.S. Gas Pressure Drop and Mass Transfer Characteristics in a Cross-flow Rotating Packed Bed with Porous Plate Packing. Ind. Eng. Chem. Res. 2010, 49, 3732–3740. [Google Scholar] [CrossRef]
- Wu, W.; Luo, Y.; Chu, G.-W.; Liu, Y.; Zou, H.-K.; Chen, J.-F. Gas Flow in a Multiliquid-Inlet Rotating Packed Bed: Three-Dimensional Numerical Simulation and Internal Optimization. Ind. Eng. Chem. Res. 2018, 57, 2031–2040. [Google Scholar] [CrossRef]
- Candel, S.; Durox, D.; Schuller, T.; Bourgouin, J.-F.; Moeck, J.P. Dynamics of Swirling Flames. Annu. Rev. Fluid Mech. 2014, 46, 147–173. [Google Scholar] [CrossRef]
- Palies, P.; Durox, D.; Schuller, T.; Candel, S. Experimental Study on the Effect of Swirler Geometry and Swirl Number on Flame Describing Functions. Combust. Sci. Technol. 2011, 183, 704–717. [Google Scholar] [CrossRef]
- Hu, H.B.; Wen, J.; Bao, L.Y.; Jia, L.B.; Song, D.; Song, B.W.; Pan, G.; Scaraggi, M.; Dini, D.; Xue, Q.J.; et al. Significant and stable drag reduction with air rings confined by alternated superhydrophobic and hydrophilic strips. Sci. Adv. 2017, 3, e1603288. [Google Scholar] [CrossRef] [Green Version]
- Wen, J.; Zhang, W.Y.; Ren, L.Z.; Bao, L.Y.; Dini, D.; Xi, H.D.; Hu, H.B. Controlling the number of vortices and torque in Taylor-Couette flow. J. Fluid Mech. 2020, 901, A30. [Google Scholar] [CrossRef]
- Deryagina, N.V.; Voinov, N.A.; Zemtsov, D.A.; Bogatkova, A.V. Hydrodynamics of the vortex tray. Therm. Sci. Eng. Prog. 2020, 18, 100524. [Google Scholar] [CrossRef]
- Litra, A.N.; Kunina, P.S.; Pavlenko, P.P. Study of the model of direct-flow centrifugal element. Gas Ind. 2009, 12, 17–19. [Google Scholar]
- Goldshtik, M.A. Transfer Processes in a Granular Layer; Publishing House of IT SB RAS: Novosibirsk, Russia, 2005; 358p. [Google Scholar]
- Laptev, U.G. Boundary Layer Models and Calculation of Heat and Mass Transfer Processes; Kazan University Product: Kazan, Russia, 2007; 500p. [Google Scholar]
- Voinov, N.A.; Zemtsov, D.A.; Zhukova, O.P.; Bogatkova, A.V. Hydraulic Resistance of Tangential Swirlers. Chem. Petrol. Eng. 2019, 55, 51–56. [Google Scholar] [CrossRef]
- Frolov, A.S.; Voinov, N.A.; Bogatkova, A.V.; Zemtsov, D.A.; Zhukova, O.P. Resistance of Tangential Swirlers with Rectilinear Channel Walls. Theor. Found. Chem. Eng. 2021, 55, 914–922. [Google Scholar] [CrossRef]
- Sheen, H.J.; Chen, W.J.; Jeng, S.Y.; Huang, T.L. Correlation of swirl number for a radial-type swirl generator. Exp. Therm. Fluid Sci. 1996, 12, 444–451. [Google Scholar] [CrossRef]
- Open Source Licensing Software OpenFOAM v1712. Available online: https://www.openfoam.com/news/main-news/openfoam-v1712 (accessed on 1 June 2022).
- Mitrofanova, O.V. Hydrodynamics and Heat Transfer in Swirling Flows in Channels with Swirlers (Analytical Review). High Temp. 2003, 41, 518–559. [Google Scholar] [CrossRef]
- Mitrofanova, O.V. Hydrodynamics and Heat Transfer of Swirling Flows in the Channels of Nuclear Power Plants; Fizmatlit: Moscow, Russia, 2010; 287p. [Google Scholar]

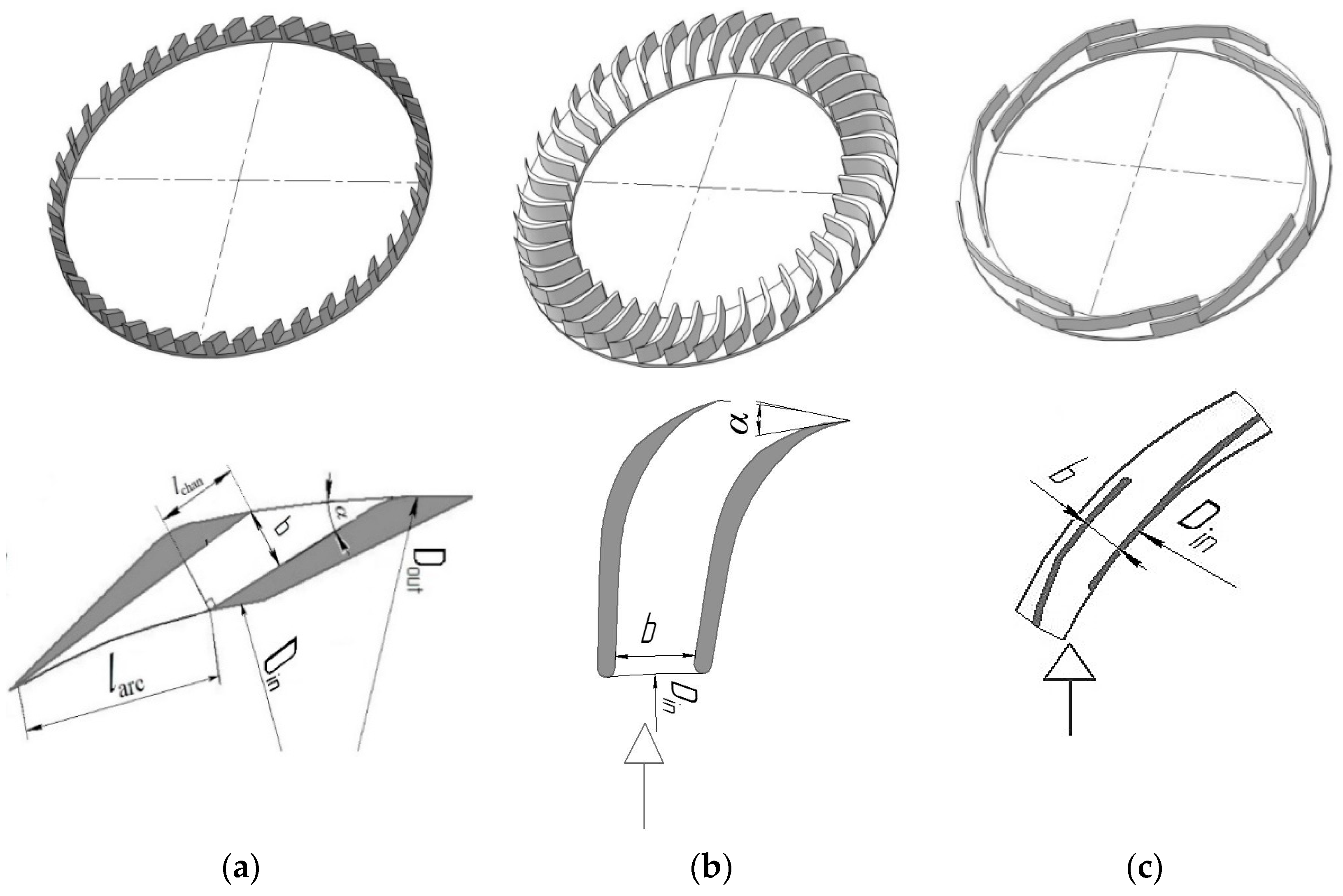












| No. Swirler | Figure | Dout (m) | Din (m) | h (m) | b (m) | n (pcs) | α (deg) | Channel Walls |
|---|---|---|---|---|---|---|---|---|
| 1 | Figure 1a | 0.065 | 0.005 | 0.0012 | 40 | - | straight | |
| 2 | 0.172 | 0.156 | 0.008 | 0.0030 | 40 | 26 | ||
| 3 | 0.180 | 0.150 | 0.008 | 0.0030 | 40 | 26 | ||
| 4 | 0.167 | 0.156 | 0.008 | 0.0050 | 25 | 26 | ||
| 5 | 0.174 | 0.156 | 0.010 | 0.0050 | 25 | 26 | ||
| 6 | 0.186 | 0.150 | 0.008 | 0.0050 | 25 | 26 | ||
| 7 | 0.170 | 0.114 | 0.010 | 0.0030 | 40 | 26 | ||
| 8 | 0.150 | 0.140 | 0.006 | 0.0040 | 40 | 26 | ||
| 9 | 0.186 | 0.176 | 0.005 | 0.0015 | 40 | 26 | ||
| 10 | 0.167 | 0.008 | 0.0030 | 40 | 45 | |||
| 11 | 0.150 | 0.008 | 0.0030 | 40 | 90 | |||
| 12 | Figure 1b | 0.150 | 0.108 | 0.004 | 0.0060 | 40 | 41 | profiled |
| 13 | 0.110 | 0.068 | 0.006 | 0.0035 | 40 | 28 | ||
| 14 | 0.170 | 0.128 | 0.003 | 0.0080 | 40 | 25 | ||
| 15 | 0.170 | 0.120 | 0.008 | 0.0035 | 40 | 26 | ||
| 16 | 0.170 | 0.120 | 0.016 | 0.0015 | 40 | 31 | ||
| 17 | Figure 1c | 0.130 | 0.008 | 0.0040 | 8 | 0 | annular | |
| 18 | 0.205 | 0.008 | 0.0030 | 8 | 0 | |||
| 19 | 0.170 | 0.008 | 0.0050 | 8 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Voinov, N.A.; Frolov, A.S.; Bogatkova, A.V.; Zemtsov, D.A. Experimental Study and Numerical Simulation of Hydrodynamic Parameters of Tangential Swirlers. ChemEngineering 2022, 6, 48. https://doi.org/10.3390/chemengineering6040048
Voinov NA, Frolov AS, Bogatkova AV, Zemtsov DA. Experimental Study and Numerical Simulation of Hydrodynamic Parameters of Tangential Swirlers. ChemEngineering. 2022; 6(4):48. https://doi.org/10.3390/chemengineering6040048
Chicago/Turabian StyleVoinov, Nikolai A., Alexander S. Frolov, Anastasiya V. Bogatkova, and Denis A. Zemtsov. 2022. "Experimental Study and Numerical Simulation of Hydrodynamic Parameters of Tangential Swirlers" ChemEngineering 6, no. 4: 48. https://doi.org/10.3390/chemengineering6040048
APA StyleVoinov, N. A., Frolov, A. S., Bogatkova, A. V., & Zemtsov, D. A. (2022). Experimental Study and Numerical Simulation of Hydrodynamic Parameters of Tangential Swirlers. ChemEngineering, 6(4), 48. https://doi.org/10.3390/chemengineering6040048






