Thermodynamics and Kinetics of the Reaction of Catalytic Dismutation of Chlorosilanes in the Vapor Phase in the Temperature Range of 353–393 K
Abstract
:1. Introduction
2. Results
2.1. Kinetic Analysis
2.2. Thermodynamics of Chlorosilanes Dismutation
2.3. Calculation of Equilibrium Concentrations Based on the Values of Keq
3. Discussion
4. Materials and Methods
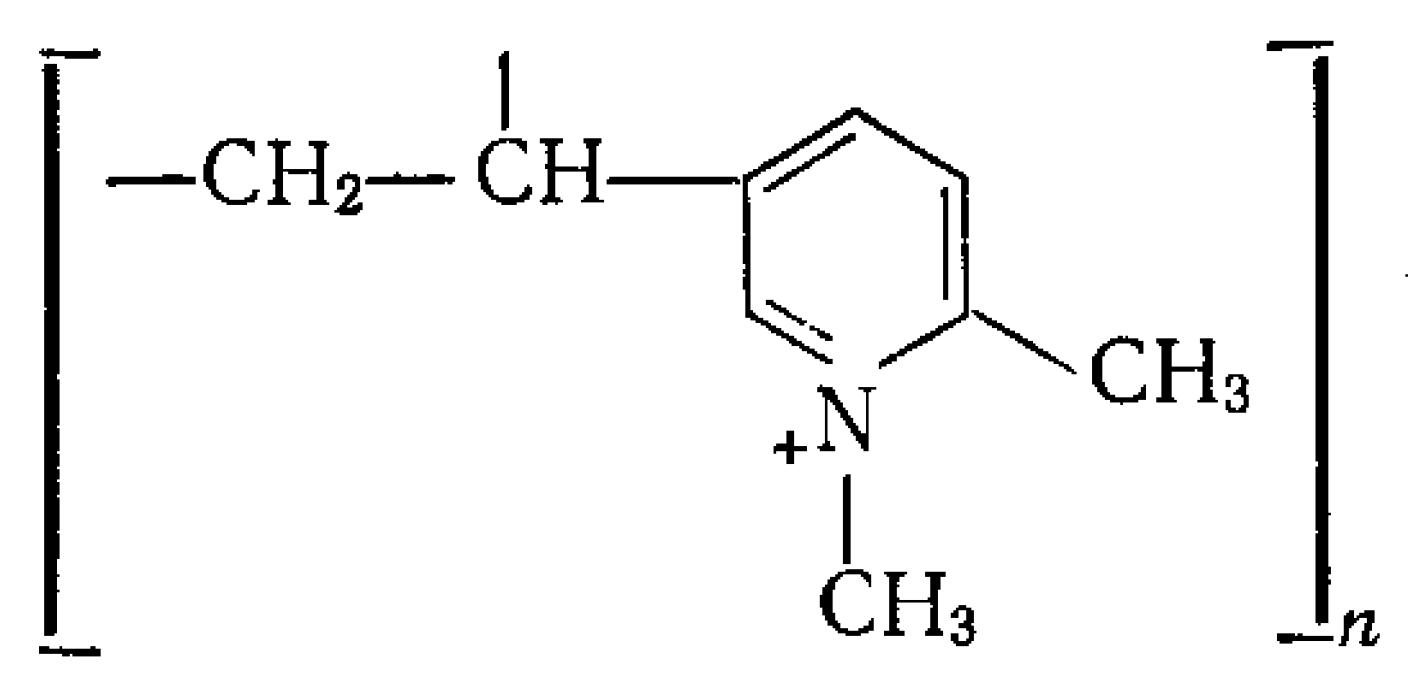
4.1. Reagents and Catalyst
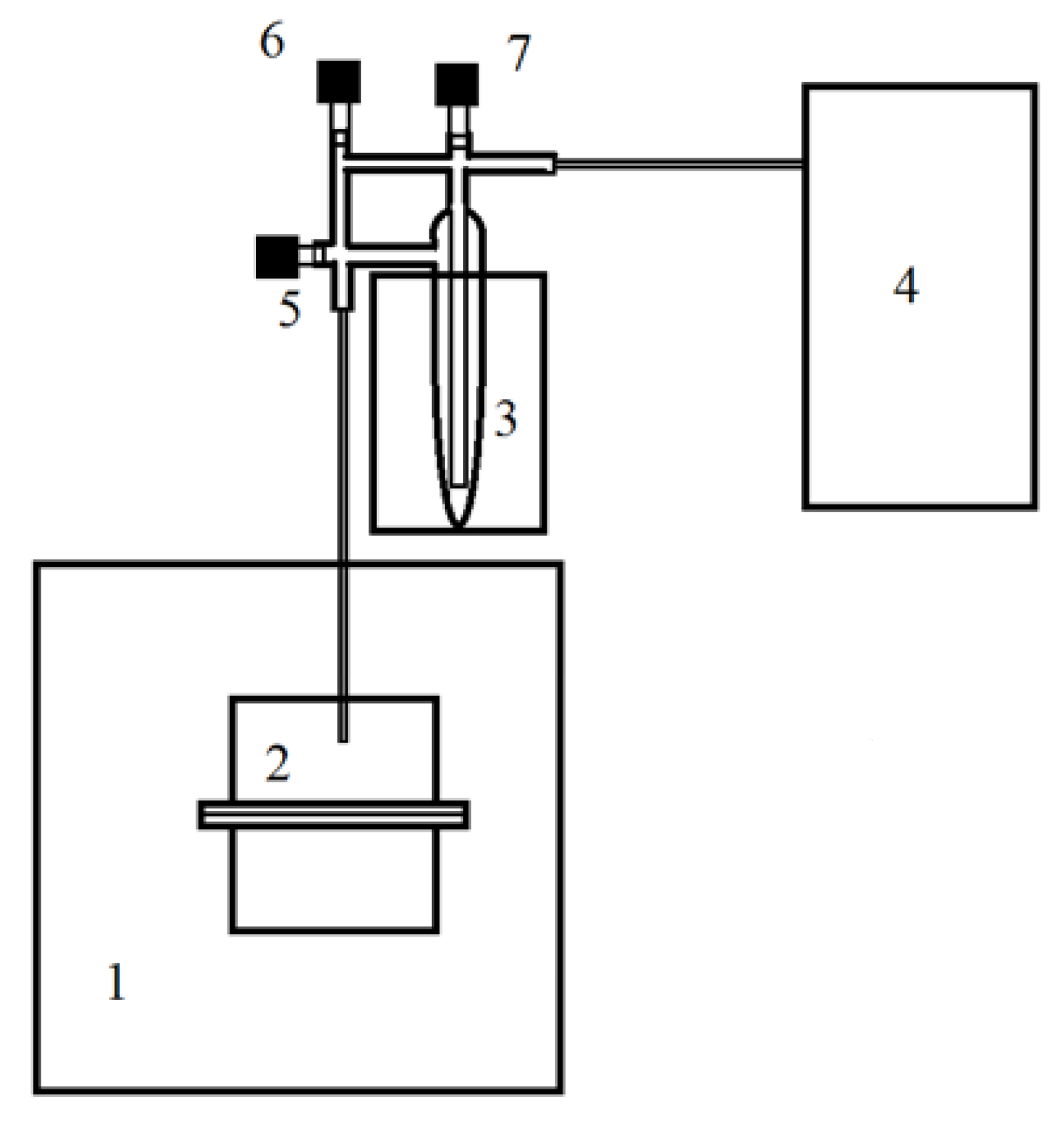
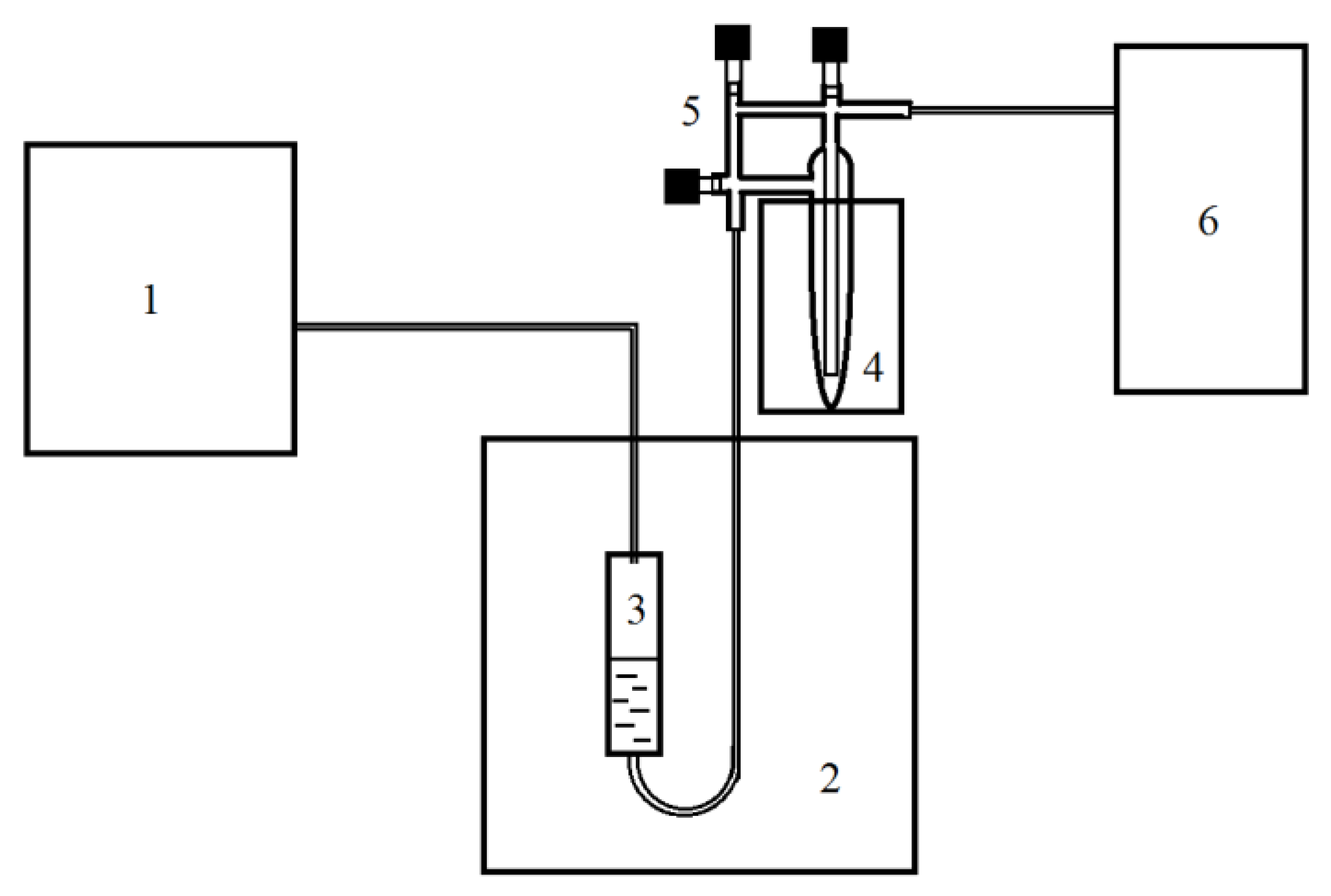
4.2. Design of Experiments
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. TS Dismutation

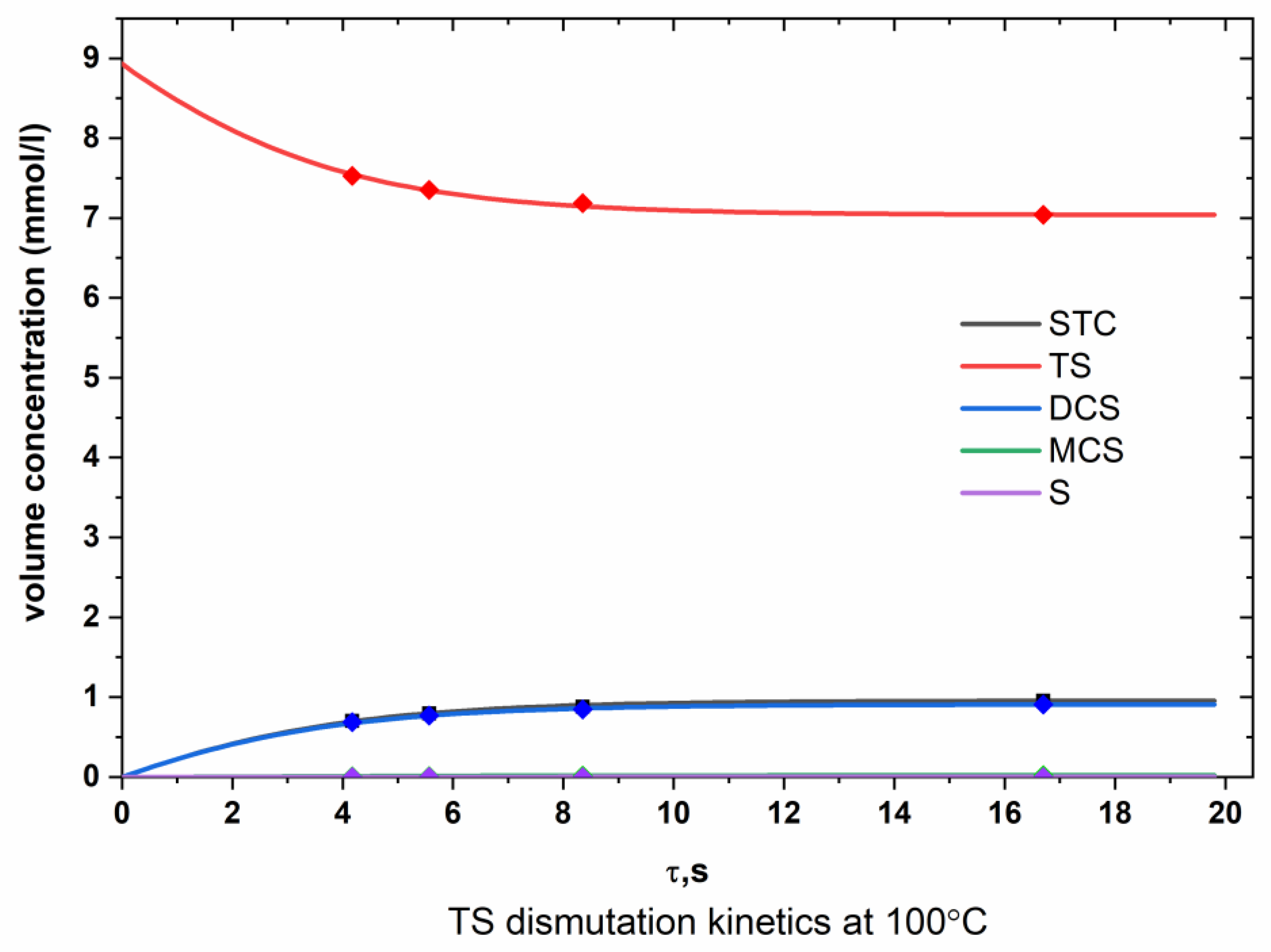
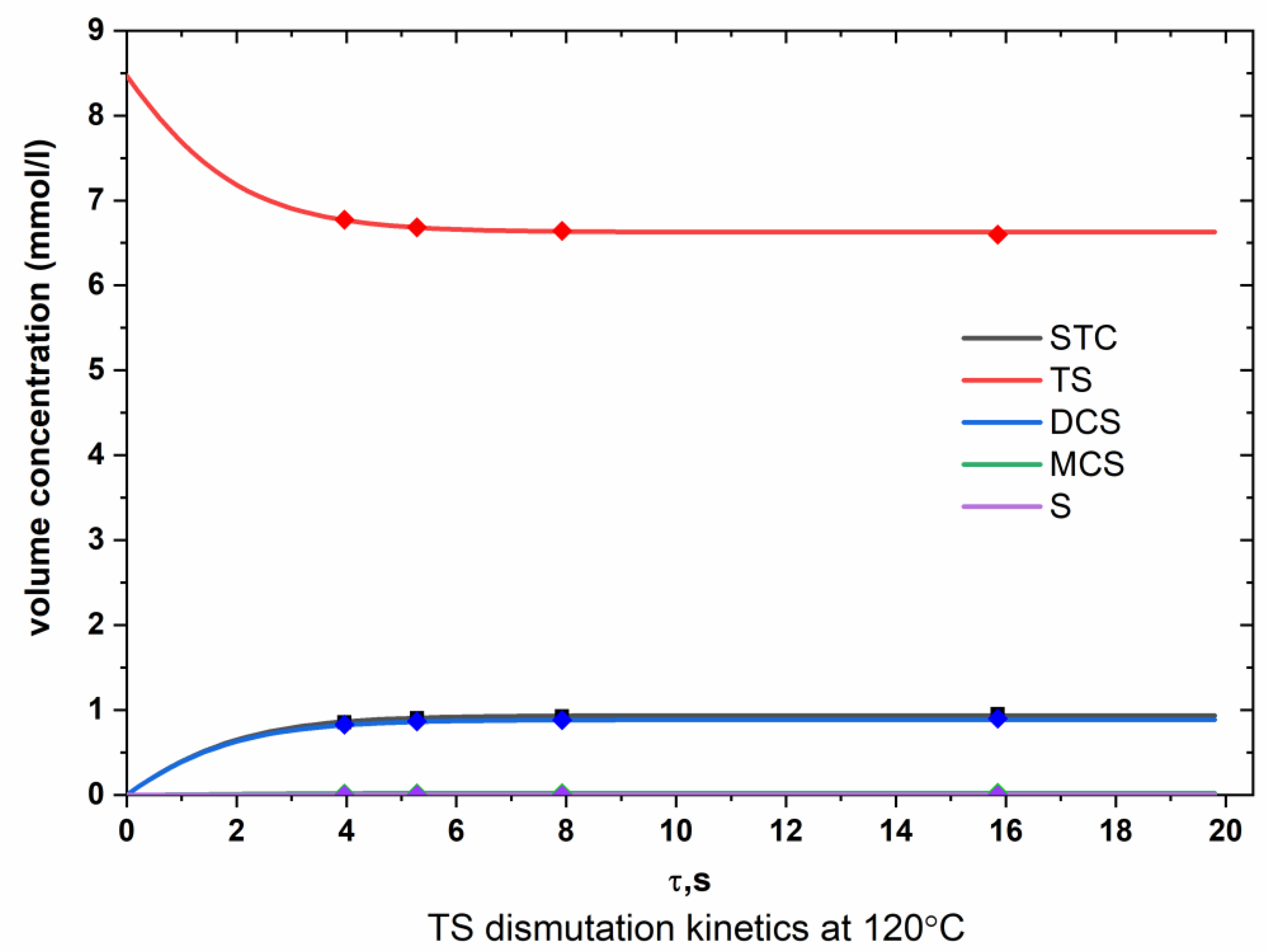
Appendix A.2. DCS Dismutation

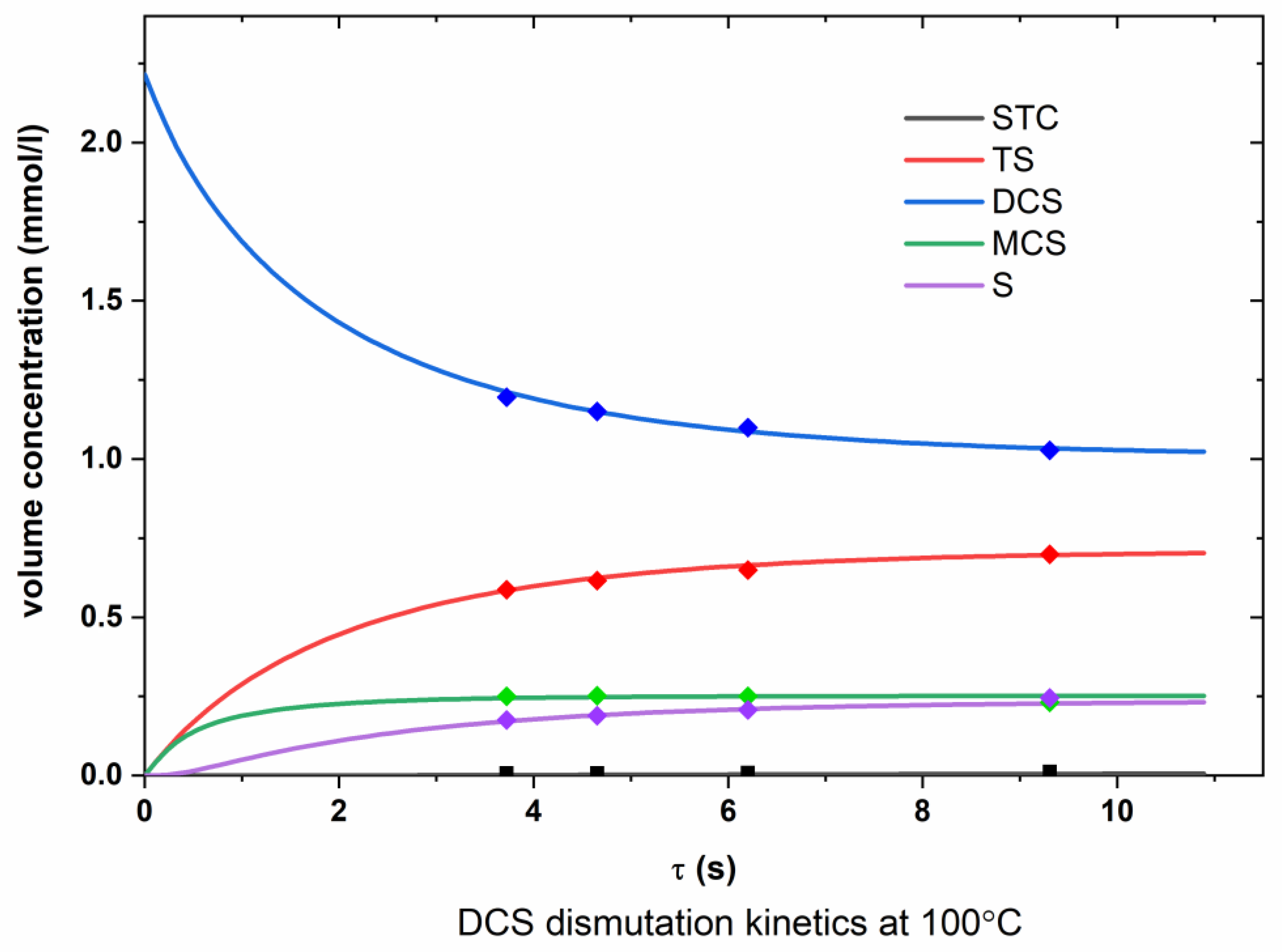
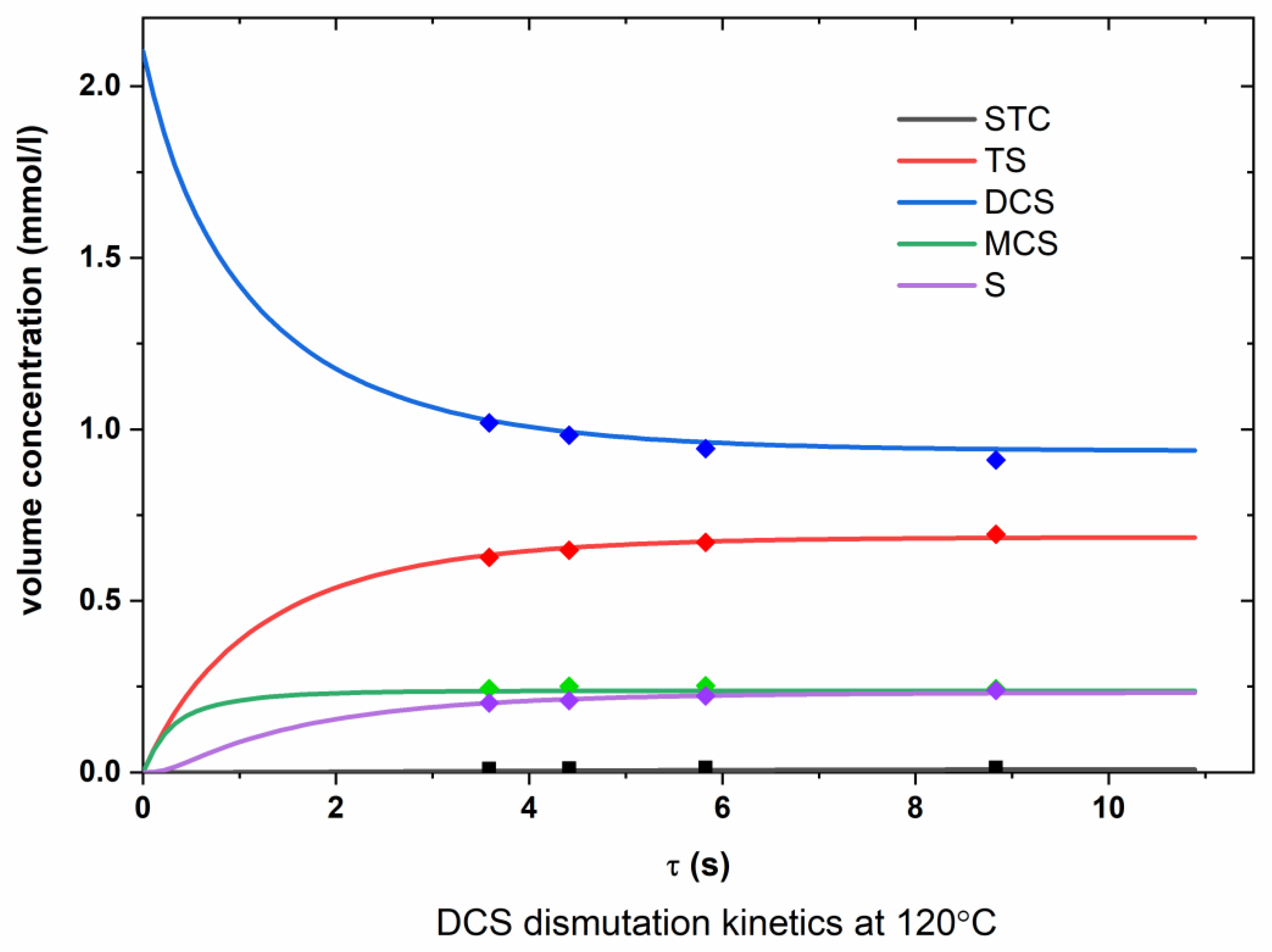
References
- Ahn, S.H.; Chun, D.M.; Chu, W.S. Perspective to Green Manufacturing and Applications. Int. J. Adv. Manuf. Technol. 2013, 14, 873–874. [Google Scholar] [CrossRef]
- Shah, A.V.; Meier, J.; Vallat-Sauvain, E.; Wyrsch, N.; Kroll, U.; Droz, C.; Graf, U. Material and solar cell research in microcrystalline silicon. Sol. Energ. Mat. Sol. 2003, 1, 469–491. [Google Scholar] [CrossRef]
- Eaglesham, D.J.; Cerullo, M. Dislocation-free stranski-krastanow growth of Ge on Si (100). Phys. Rev. Lett. 1990, 64, 1943–1947. [Google Scholar] [CrossRef] [PubMed]
- Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef]
- Bathey, B.R.; Cretella, M.C. Solar-grade silicon. J. Mater Sci. 2005, 17, 3877–3896. [Google Scholar] [CrossRef]
- Setty, H.S.N.; Yaws, C.L.; Martin, B.R.; Wangler, D.J. Method of Operating a Quartz Fluidized Bed Reactor for the Production of Silicon. US Patent No. 3963838, 15 June 1976. [Google Scholar]
- Iya, S.K.; Flagella, R.N.; Dipaolo, F.S. Heterogeneous decomposition of silane in a fixed bed reactor. J. Electrochem. Soc. 1982, 129, 1531–1535. [Google Scholar] [CrossRef]
- Zhang, P.; Duan, J.; Chen, G. Production of polycrystalline silicon from silane pyrolysis: A review of fines formation. Sol. Energy. 2018, 175, 44–53. [Google Scholar] [CrossRef]
- Vorotyntsev, V.M.; Mochalov, G.M.; Nipruk, O.V. Synthesis of monosilane by catalytic disproportionation of trichlorosilane in a reaction-distillation apparatus with recycle. Russ. J. Appl. Chem. 2001, 74, 621–625. [Google Scholar] [CrossRef]
- Matveev, A.K.; Mochalov, G.M.; Suvorov, S.S. Method of Obtaining Silane and Chlorosilanes. RU Patent No 2608523, 30 July 2015. [Google Scholar]
- Mehler, M. Electron. News 1984, 30, 54. [Google Scholar]
- Marin, G.; Lefort, M. Dismutation of Trichlorosilane. US Patent No 4018871A, 4 November 1975. [Google Scholar]
- O’Mara, W.C.; Herring, R.B.; Hunt, L.P. Handbook of Semiconductor Silicon Technology; Noyes Publications: Park Ridge, NJ, USA, 1990. [Google Scholar]
- Yasuda, K.; Okabe, T.H. Production processes of solar grade silicon based on metallothermic reduction. J. Jpn. Inst. Met. 2010, 74, 1–9. [Google Scholar] [CrossRef]
- Hou, Y.Q.; Xie, G.; Nie, Z.F.; Li, N. Direct current heating model for the Siemens. Adv. Mate Res. 2014, 881–883, 1805–1808. [Google Scholar]
- Jung, N.; Cho, K.D.; Lim, J.C.; Yoo, B.-R. Redistribution Catalyst and Methods for Its Preparation and Use to Convert Chlorosilicon Hydrides to Silane. US Patent No. 4613491, 23 September 1986. [Google Scholar]
- Erickson, C.E.; Wagner, G.H. Disproportionation of Silane Derivatives. US Patent No 2627451, 2 March 1953. [Google Scholar]
- Bakay, C.J. Verfahren zur herstellung von silan. Germany Patent No 2507864, 28 August 1975. [Google Scholar]
- Litteral, C.J. Disproportionation of Chlorosilane. US Patent No. 4113845, 12 September 1978. [Google Scholar]
- Devyatykh, G.G.; Panov, G.I.; Kharitonov, A.S. Investigation of the catalytic activity of resins. J. Inorg. Chem. 1987, 32, 1002–1005. [Google Scholar]
- Zubakova, L.B.; Tevlina, A.S.; Davankova, A.B. Sinteticheskie Ionoobmennye Materialy [Synthetic Ion-Exchange Materials]; Chemistry: Moscow, Russia, 1978. [Google Scholar]
- Kishankumar, K. Chlorosilane Disproportionation Process. US Patent No. 4395389, 26 July 1983. [Google Scholar]
- Morimoto, S. Process for the Disproportionation of Chlorosilanes. US Patent 4613489, 23 September 1986. [Google Scholar]
- Grishnova, N.D.; Gusev, A.V.; Moiseev, A.N.; Mochalov, G.M.; Balanovsky, N.V.; Kharitonov, T.N. Catalytic activity of anion-exchange resins in the trichlorosilane disproportionation reaction. J. Appl. Chem. 1999, 72, 1667–1672. [Google Scholar]
- Bailey, D.L.; Shafer, P.W.; Wagner, G.H. Disproportionation of Chlorosilanes Employing Amine-Type Catalysts. US Patent 2834648, 13 May 1958. [Google Scholar]
- Low Cost Solar Array Project. Feasibility of the Silane Process for Producing Semiconductor-Grade Silicon. Final Report, October 1975–March 1979; Union Carbide Corp.: Houston, TX, USA, 1979. [Google Scholar]
- Li, K.Y.; Huang, C.D. Redistribution reaction of trichlorosilane in a fixed-bed reactor. Ind. Eng. Chem. Res. 1988, 27, 1600–1606. [Google Scholar] [CrossRef]
- Hunt, L.P. Thermodynamic Equilibria in the Si-H-Cl and Si-H-Br Systems. J. Electrochem. Soc. 1988, 135, 206–209. [Google Scholar] [CrossRef]
- Ingle, W.M.; Peffley, M.S. Kinetics of the hydrogenation of silicon tetrachloride. J. Electrochem. Soc. 1985, 132, 1236–1240. [Google Scholar] [CrossRef]
- Walker, K.L.; Jardine, R.E.; Ring, M.A.; O’Neal, H.E. Mechanisms and kinetics of the thermal decompositions of trichlorosilane, dichlorosilane, and monochlorosilane. Int. J. Chem. Kinet. 1998, 30, 69–88. [Google Scholar] [CrossRef]
- Hogness, T.R.; Wilson, T.L.; Johnson, W.C. The thermal decomposition of silane. J. Amer. Chem. Soc. 1936, 58, 108–112. [Google Scholar] [CrossRef]
- Walch, S.P.; Dateo, C.E. Thermal decomposition pathways and rates for silane, chlorosilane, dichlorosilane, and trichlorosilane. J. Phys. Chem. A 2001, 105, 2015–2022. [Google Scholar] [CrossRef]
- Catoire, L.; Woiki, D.; Roth, P. Kinetics of the initiation step of the thermal decomposition of SiCl4. Int. J. Chem. Kinet. 1997, 29, 415–420. [Google Scholar] [CrossRef]
- Morachevsky, A.G.; Sladkov, I.B. Fiziko-Khimicheskie Svoistva Molekulyarnykh Neorganicheskikh Soedinenii (Eksperimental’nye Dannye i Metody Rascheta) [Physico-Chemical Properties of Molecular Inorganic Compounds (Experimental Data and Calculation Methods)]; Chemistry: St. Petersburg, Russia, 1996. [Google Scholar]
- Chase, M.W. NIST-JANAF Themochemical Tables, 4th ed.; American Institute of Physics: Woodbury, NY, USA, 1998; updated 19 February 2017. [Google Scholar]
- Stull, D.R.; Prophet, H. JÂNAF Thermochemical Tables; Office of Standard Reference Data, National Bureau of Standards: Washington, DC, USA, 1971.
- Maier, C.G.; Kelley, K.K. An equation for the representation of hightemperature heat content data. J. Am. Chem. Soc. 1932, 54, 3243–3246. [Google Scholar] [CrossRef]
- Vorotyntsev, A.; Markov, A.; Petukhov, A.; Atlaskina, M.; Atlaskin, A.; Kapinos, A.; Vorotyntsev, V.; Pryakhina, V. Catalytic disproportionation of chlorosilanes using imidazolium ionic liquids supported on polymer supports. Catal. Ind. 2021, 13, 1–11. [Google Scholar] [CrossRef]
- Blinov, I.A.; Belokhvostov, V.; Kossoy, A.; Mukhortov, D.; Kambur, M.; Lantratova, O.; Kurapova, E.S. Thermal Decomposition of Anion-Exchange Resin Based on Copolymer of 4-Vinylpyridine. Russ. J. Appl. Chem. 2016, 89, 554–558. [Google Scholar] [CrossRef]

| T, K | SiH3Cl | SiH2Cl2 | SiHCl3 | SiCl4 |
|---|---|---|---|---|
| 353 | 0.55 | 11.0 | 76 | 11.1 |
| 373 | 0.59 | 11.1 | 75 | 11.3 |
| 393 | 0.66 | 11.2 | 74 | 11.8 |
| Experiment Parameter | TS | DCS |
|---|---|---|
| Resin volume, ml | 4.6 | 4.0 |
| Atmospheric pressure, mm Hg | 760 | 760 |
| Bubbler temperature, K | 273 | 215.6 |
| Carrier gas consumption per bubbling, ml/min | 5, 10, 15, 20 | 10, 15, 20, 25 |
| Reactor temperature, K | 353, 373, 393 | 353, 373, 393 |
| T, K | Reaction | Keq | ||
|---|---|---|---|---|
| 353.0 | 1 | 2.02 | 142 | 1.42·10−2 |
| 2 | 42.6 | 199 | 2.14·10−1 | |
| 3 | 2800 | 1600 | 1.80 | |
| 373.0 | 1 | 3.02 | 173 | 1.75·10−2 |
| 2 | 81 | 460 | 1.76·10−1 | |
| 3 | 5300 | 3400 | 1.650 | |
| 393.0 | 1 | 6.32 | 336 | 1.88·10−2 |
| 2 | 143 | 770 | 1.86·10−1 | |
| 3 | 8100 | 5400 | 1.50 |
| Parameter | (1), dir. | (1), rev. | (2), dir. | (2), rev. | (3), dir. | (3), rev. |
|---|---|---|---|---|---|---|
| Ea, kJ/mol | 32.7 | 24.5 | 35.0 | 39.1 | 30.7 | 14 |
| T, K | Reactions | Kp | |||||
|---|---|---|---|---|---|---|---|
| [34] | [35] | [36] + [26] | [26] | Experiment (Static) | Experiment (Kinetics) | ||
| 353 | I | 1.2905 | 0.0134 | 0.0369 | 0.0208 | 0.021 ± 0.001 | 0.020 ± 0.007 |
| II | 0.0214 | 0.1259 | 0.1625 | 0.3586 | 0.35 ± 0.02 | 0.30 ± 0.07 | |
| III | 1.4127 | 0.6952 | 0.6986 | 1.6434 | 1.8 ± 0.3 | ||
| 373 | I | 1.4410 | 0.0158 | 0.0414 | 0.0233 | 0.022 ± 0.01 | 0.021 ± 0.005 |
| II | 0.0223 | 0.1331 | 0.1694 | 0.3731 | 0.360 ± 0.014 | 0.30 ± 0.08 | |
| III | 1.3918 | 0.6660 | 0.6692 | 1.5697 | 1.6 ± 0.1 | ||
| 393 | I | 1.5914 | 0.0185 | 0.0460 | 0.0258 | 0.024 ± 0.001 | 0.020 ± 0.005 |
| II | 0.0231 | 0.1399 | 0.1760 | 0.3867 | 0.39 ± 0.02 | 0.35 ± 0.05 | |
| III | 1.3742 | 0.6413 | 0.6442 | 1.5063 | 1.5 ± 0.1 | ||
| T, K | SiH4 | SiH3Cl | SiH2Cl2 | SiHCl3 | SiCl4 |
|---|---|---|---|---|---|
| Disproportionation of TS | |||||
| 353 [26] | 0.042 | 0.52 | 10.57 | 77.14 | 11.73 |
| 353 experiment statics | 0.55 ± 0.03 | 11.0 ± 0.4 | 76 ± 3 | 11.1 ± 0.4 | |
| 353 experiment kinetics | 0.03 ± 0.01 | 0.42 ± 0.12 | 10.5 ± 0.4 | 78 ± 3 | 11.4 ± 0.4 |
| 373 [26] | 0.05 | 0.59 | 10.97 | 76.08 | 12.31 |
| 373 experiment statics | 0.59 ± 0.02 | 11.1 ± 0.4 | 75 ± 3 | 11.3 ± 0.4 | |
| 373 experiment kinetics | 0.03 ± 1 | 0.4 ± 0.2 | 10.7 ± 0.4 | 77 ± 3 | 11.6 ± 0.8 |
| 393 [26] | 0.058 | 0.66 | 11.34 | 75.09 | 12.84 |
| 393 experiment statics | 0.66 ± 0.02 | 11.2 ± 0.4 | 74 ± 3 | 11.8 ± 0.4 | |
| 393 experiment kinetics | 0.04 ± 0.02 | 0.5 ± 0.2 | 10 ± 24 | 77 ± 3 | 11.5 ± 0.7 |
| Disproportionation of DHS | |||||
| 353 [26] | 10.24 | 15.55 | 38.8 | 34.7 | 0.65 |
| 353 experiment kinetics | 9 ± 2 | 15.2 ± 1.2 | 41 ± 3 | 33.2 ± 1.3 | 0.6 ± 0.7 |
| 373 [26] | 10.23 | 15.82 | 38.4 | 34.8 | 0.74 |
| 373 experiment kinetics | 9 ± 2 | 15.6 ± 0.5 | 41 ± 3 | 33 ± 2 | 0.6 ± 0.2 |
| 393 [26] | 10.22 | 16.06 | 38.0 | 34.8 | 0.82 |
| 393 experiment kinetics | 9 ± 2 | 17 ± 1 | 39 ± 2 | 34.2 ± 0.7 | 0.6 ± 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mochalov, G.; Stolmakov, Y.; Zhuchok, O. Thermodynamics and Kinetics of the Reaction of Catalytic Dismutation of Chlorosilanes in the Vapor Phase in the Temperature Range of 353–393 K. ChemEngineering 2023, 7, 13. https://doi.org/10.3390/chemengineering7010013
Mochalov G, Stolmakov Y, Zhuchok O. Thermodynamics and Kinetics of the Reaction of Catalytic Dismutation of Chlorosilanes in the Vapor Phase in the Temperature Range of 353–393 K. ChemEngineering. 2023; 7(1):13. https://doi.org/10.3390/chemengineering7010013
Chicago/Turabian StyleMochalov, Georgy, Yegor Stolmakov, and Olesya Zhuchok. 2023. "Thermodynamics and Kinetics of the Reaction of Catalytic Dismutation of Chlorosilanes in the Vapor Phase in the Temperature Range of 353–393 K" ChemEngineering 7, no. 1: 13. https://doi.org/10.3390/chemengineering7010013
APA StyleMochalov, G., Stolmakov, Y., & Zhuchok, O. (2023). Thermodynamics and Kinetics of the Reaction of Catalytic Dismutation of Chlorosilanes in the Vapor Phase in the Temperature Range of 353–393 K. ChemEngineering, 7(1), 13. https://doi.org/10.3390/chemengineering7010013






