One-Dimensional Modeling of Mass Transfer Processes in an Annular Centrifugal Contactor
Abstract
:1. Introduction
2. Methods and Materials
3. Results
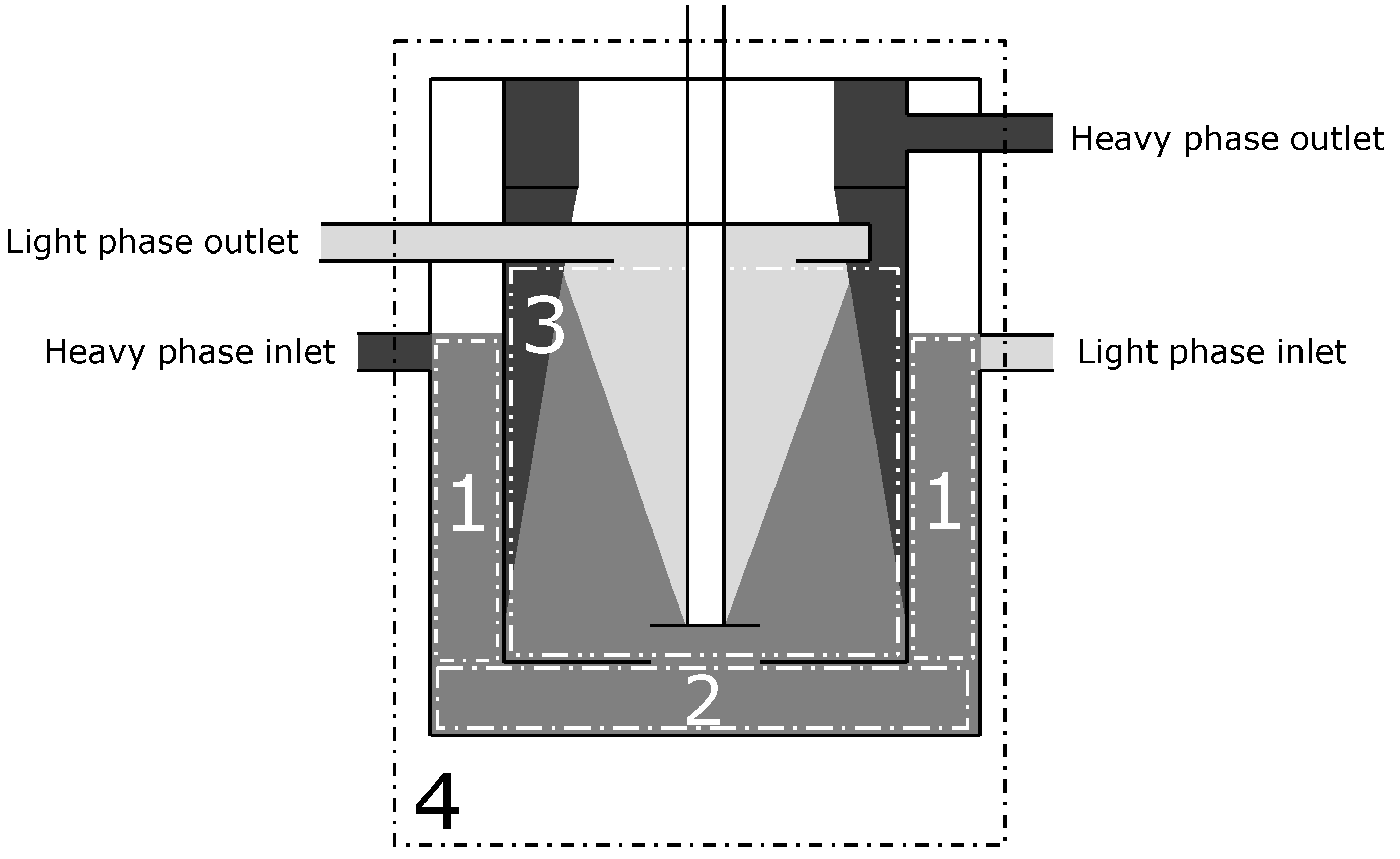
3.1. Definition of the Boundaries of the Balance Sheets
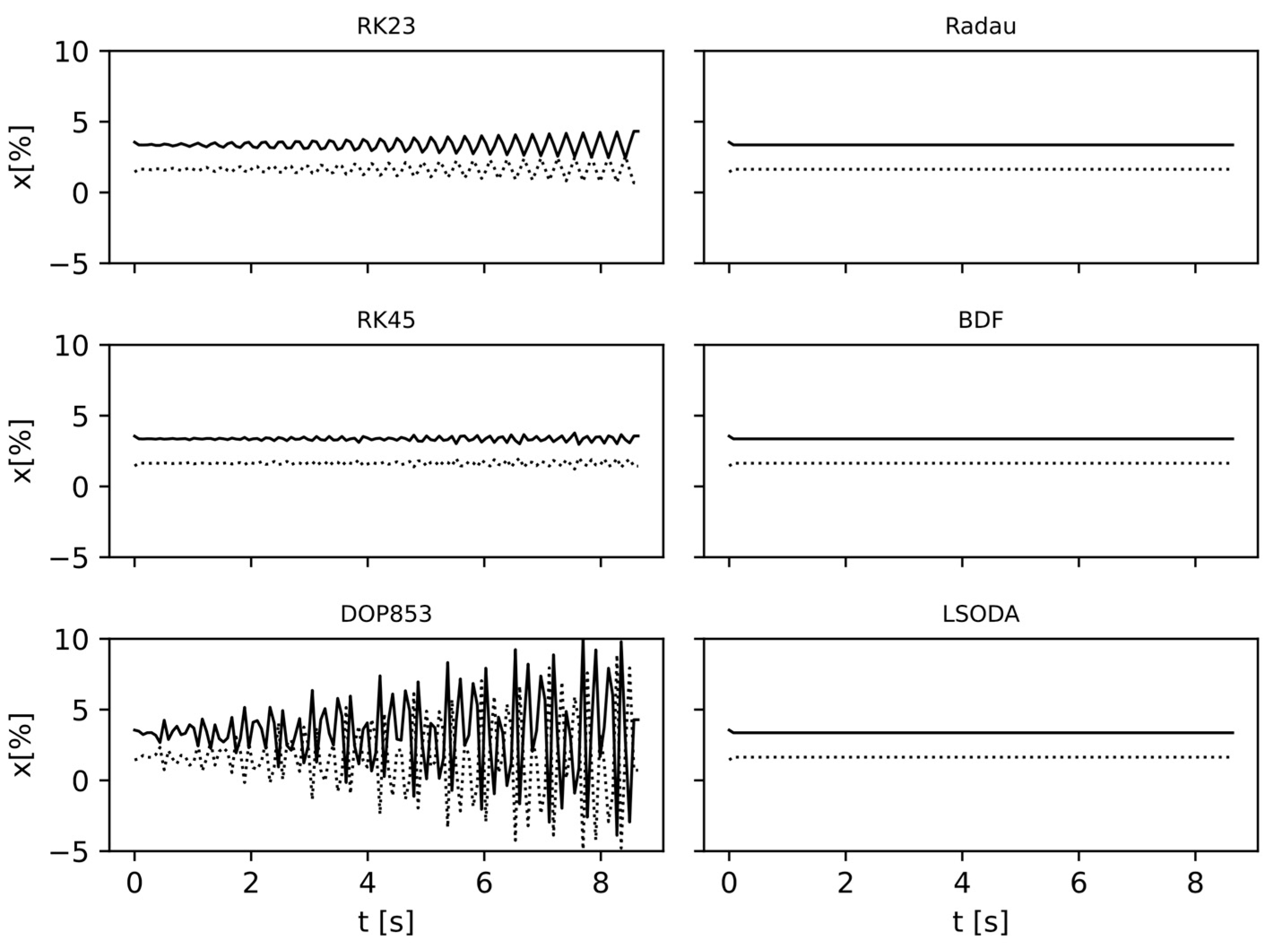
3.2. Creation of the Model Equations
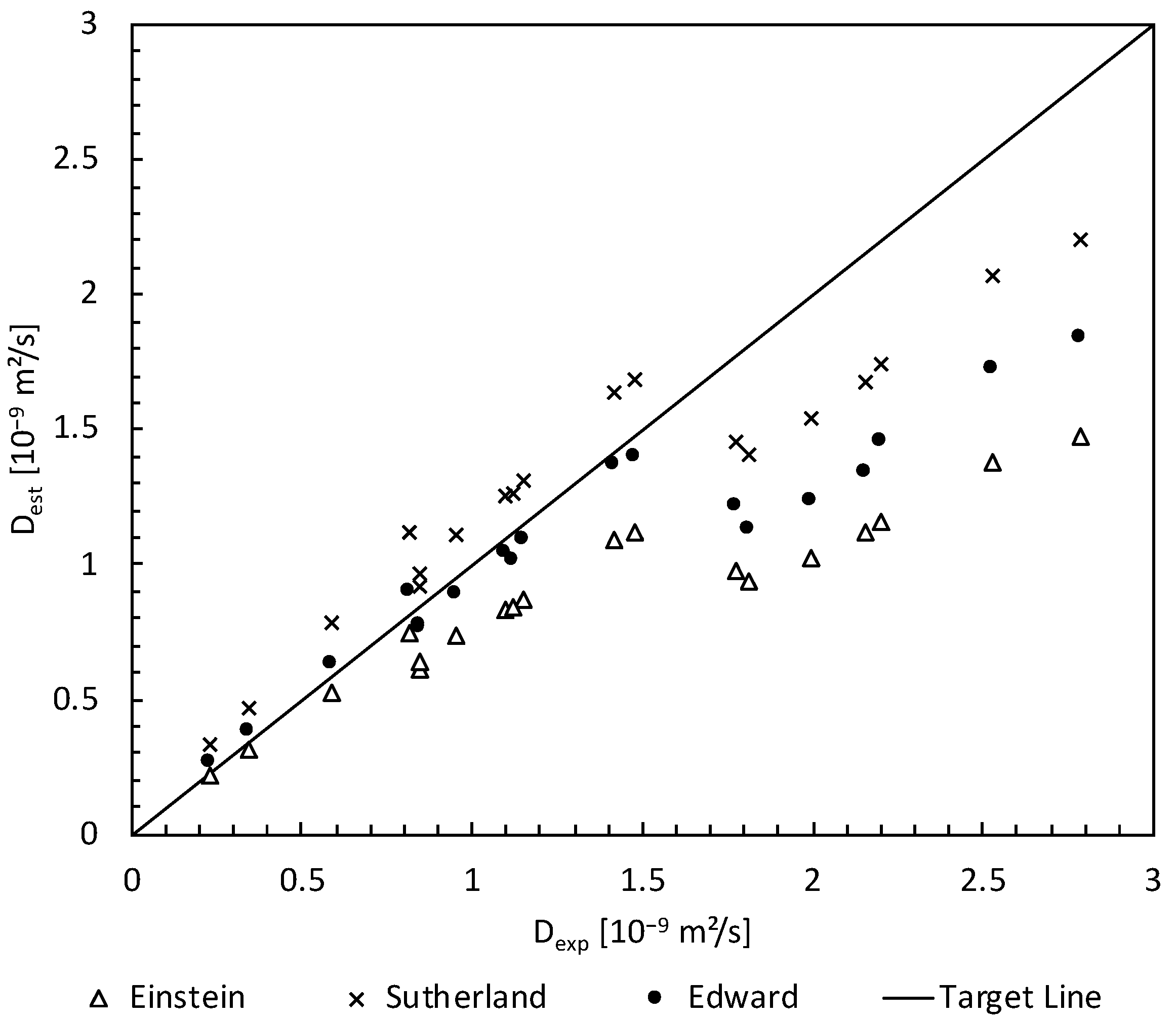
3.3. Estimation of Parameters Contributing to Mass Transfer
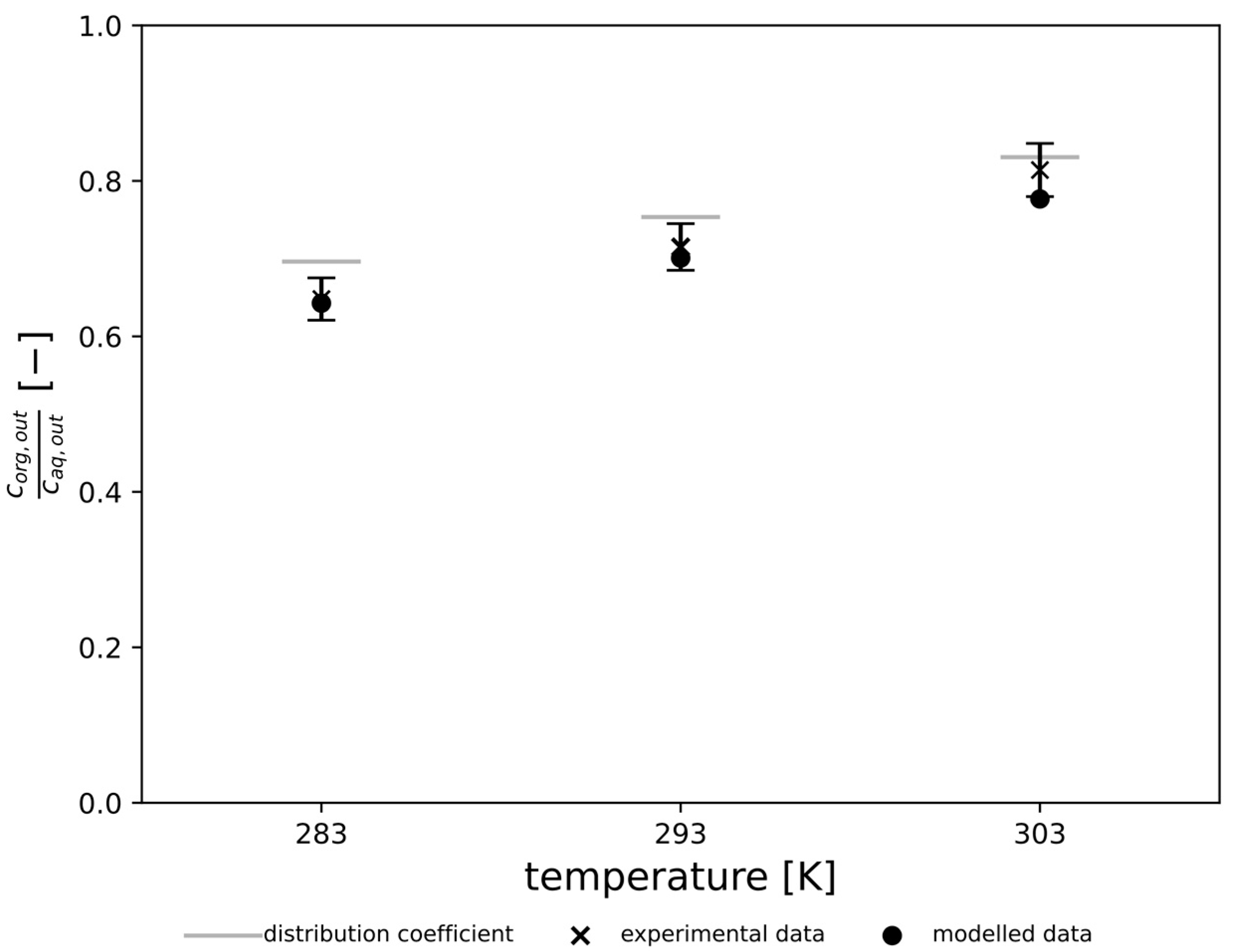
3.4. Validation of Simulated Results with Experimental Data
4. Model Validation and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hamamah, Z.A.; Grützner, T. Liquid-Liquid Centrifugal Contactors: Types and Recent Applications—A Review. ChemBioEng Rev. 2022, 9, 286–318. [Google Scholar] [CrossRef]
- Seyfang, B.C.; Klein, A.; Grützner, T. Extraction Centrifuges—Intensified Equipment Facilitating Modular and Flexible Plant Concepts. ChemEngineering 2019, 3, 17. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Du, C.; Yan, Z.; Duan, W.; Deng, J.; Luo, G. Liquid-liquid flow and mass transfer characteristics in a miniaturized annular centrifugal device. Chem. Eng. J. 2022, 431, 3. [Google Scholar] [CrossRef]
- Schuur, B.; Jansma, W.J.; Winkelman, J.G.M.; Heeres, H.J. Determination of the interfacial area of a continuous integrated mixer/separator (CINC) using a chemical reaction method. Chem. Eng. Process. 2008, 47, 1484–1491. [Google Scholar] [CrossRef] [Green Version]
- Kadam, B.D.; Joshi, J.B.; Koganti, S.B.; Patil, R.N. Dispersed phase hold-up, effective interfacial area and Sauter mean drop diameter in annular centrifugal extractors. Chem. Eng. Res. Des. 2009, 87, 1379–1389. [Google Scholar] [CrossRef]
- Nilsson, M. Combining Experiments and Simulations of Extraction Kinetics and Thermodynamics in Advanced Separation Processes for Used Nuclear Fuel; Technical Report; University of California: Irvine, CA, USA, 2018. [Google Scholar] [CrossRef] [Green Version]
- Patra, J.; Pandey, N.K.; Kamachi Muduli, U.; Natarajan, R.; Joshi, J.B. Hydrodynamic Study of Flow in the Rotor Region of Annular Centrifugal Contactors Using CFD Simulation. Chem. Eng. Commun. 2012, 200, 471–493. [Google Scholar] [CrossRef]
- Wardle, K.E. Hybrid Multiphase CFD Simulation for Liquid-Liquid Interfacial Area Prediction in Annular Centrifugal Contactors. Proc. Glob. 2013, 2013, 7650. [Google Scholar]
- Wardle, K.E.; Weller, H.G. Hybrid Multiphase CFD Solver for Coupled Dispersed/Segregated Flows in Liquid-Liquid Extraction. Int. J. Chem. Eng. 2013, 2013, 128936. [Google Scholar] [CrossRef]
- Misek, T.; Berger, R.; Schörter, J. Standard Test Systems for Liquid Extraction, 2nd ed.; European Federation of Chemical Engineering by Institution of Chemical Engineers: Rugby, UK, 1985. [Google Scholar]
- Berger, R.; Hampe, M.J.; Schröter, J. Neue Testsysteme für die Flüssig/Flüssig-Extraktion. Chem. Ing. Tech. 1992, 64, 1044–1046. [Google Scholar] [CrossRef]
- Duan, W.; Cao, S. Determination of the Liquid Hold-up Volume and the Interface Radius of an Annular Centrifugal Contactor using the Liquid-Fast-Separation Method. Chem. Eng. Commun. 2016, 203, 548–556. [Google Scholar] [CrossRef]
- Li, S.; Duan, W.; Chen, J.; Wang, J. CFD Simulation of Gas-Liquid-Liquid Three-Phase Flow in an Annular Centrifugal Contactor. Ind. Eng. Chem. Res. 2012, 51, 11245–11253. [Google Scholar] [CrossRef]
- Schuur, B.; Kraai, G.N.; Winkelman, J.G.M.; Heeres, H.J. Hydrodynamic features of centrifugal contactor separators: Experimental studies on liquid hold-up, residence time distribution, phase behavior and drop size distributions. Chem. Eng. Process. 2012, 55, 8–19. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Brauer, H. Unsteady State Mass Transfer trough the Interface of Spherical Particles—II: Discussion of results obtained by theoretical methods. Int. J. Heat Mass Transf. 1978, 21, 455–465. [Google Scholar] [CrossRef]
- Mersmann, A.; Kind, M.; Stichlmair, J. Thermische Verfahrenstechnik. Grundlagen und Methoden, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef] [Green Version]
- Stokes, G.G. On the Effect of the Internal Friction of Fluids on the Motion of Pendulums. Trans. Camb. Philos. Soc. 1851, 9, 8–106. [Google Scholar]
- Sutherland, W. A dynamical theory of diffusion for non-electrolytes and the molecular mass of albumin. Lond. Edinb. Dublin Philos. Mag. 1905, 9, 781–785. [Google Scholar] [CrossRef] [Green Version]
- Edward, J.T. Molecular volumes and the Stokes-Einstein equation. J. Chem. Educ. 1970, 47, 261–270. [Google Scholar] [CrossRef]
- Bondi, A. van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Westerterp, K.R.; Van Swaaij, W.P.M.; Beenackers, A.A.C.M. Chemical Reactor Design and Operation, 2nd ed.; Wiley: Chichester, UK, 1987. [Google Scholar]
- Haas, P.A. Turbulent dispersion of aqueous drops in organic liquids. AIChE J. 1987, 33, 987–995. [Google Scholar] [CrossRef]
- Clay, P.H. The mechanism of emulsion formation in turbulent flow. Proc. Ned. Akad. Wet. 1940, 43, 852–865. [Google Scholar]
- Calabrese, R.V.; Chang, T.P.K.; Dang, P.T. Drop breakup in turbulent stirred-tank contactors. Part I: Effect of dispersed-phase viscosity. AIChE J. 1986, 32, 657–666. [Google Scholar] [CrossRef] [Green Version]
- Hesketh, R.P.; Fraser Russell, T.W.; Etchells, A.W. Bubble size in horizontal pipelines. AIChE J. 1987, 33, 663–667. [Google Scholar] [CrossRef]
- Strehmel, K.; Weiner, R.; Podhaisky, H. Numerik Gewöhnlicher Differentialgleichungen. Nichtsteife, Steife und Differential-Algebraische Gleichungen, 2nd ed.; Vieweg+Teubner: Wiesbaden, Germany, 2012. [Google Scholar] [CrossRef]
- The SciPy Community. Scipy.Integrate.Solve_Ivp—SciPy v1.10.1 Manual. Available online: https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.solve_ivp.html#scipy.integrate.solve_ivp (accessed on 20 March 2023).
- Kraai, G.N.; Schuur, B.; van Zwol, F.; van de Bovenkamp, H.H.; Heeres, H.J. Novel highly integrated biodiesel production technology in a centrifugal contactor separator device. Chem. Eng. J. 2009, 154, 384–389. [Google Scholar] [CrossRef] [Green Version]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ritzler, P.M.; Weiss, C.K.; Seyfang, B.C. One-Dimensional Modeling of Mass Transfer Processes in an Annular Centrifugal Contactor. ChemEngineering 2023, 7, 59. https://doi.org/10.3390/chemengineering7040059
Ritzler PM, Weiss CK, Seyfang BC. One-Dimensional Modeling of Mass Transfer Processes in an Annular Centrifugal Contactor. ChemEngineering. 2023; 7(4):59. https://doi.org/10.3390/chemengineering7040059
Chicago/Turabian StyleRitzler, Peter M., Clemens K. Weiss, and Bernhard C. Seyfang. 2023. "One-Dimensional Modeling of Mass Transfer Processes in an Annular Centrifugal Contactor" ChemEngineering 7, no. 4: 59. https://doi.org/10.3390/chemengineering7040059
APA StyleRitzler, P. M., Weiss, C. K., & Seyfang, B. C. (2023). One-Dimensional Modeling of Mass Transfer Processes in an Annular Centrifugal Contactor. ChemEngineering, 7(4), 59. https://doi.org/10.3390/chemengineering7040059







