Parametric CFD Study of Spray Drying Chamber Geometry: Part I—Effects on Airflow Dynamics
Abstract
1. Introduction
2. Design of Experiments Methodology (DOE)
2.1. Objectives of the Numerical Experiment
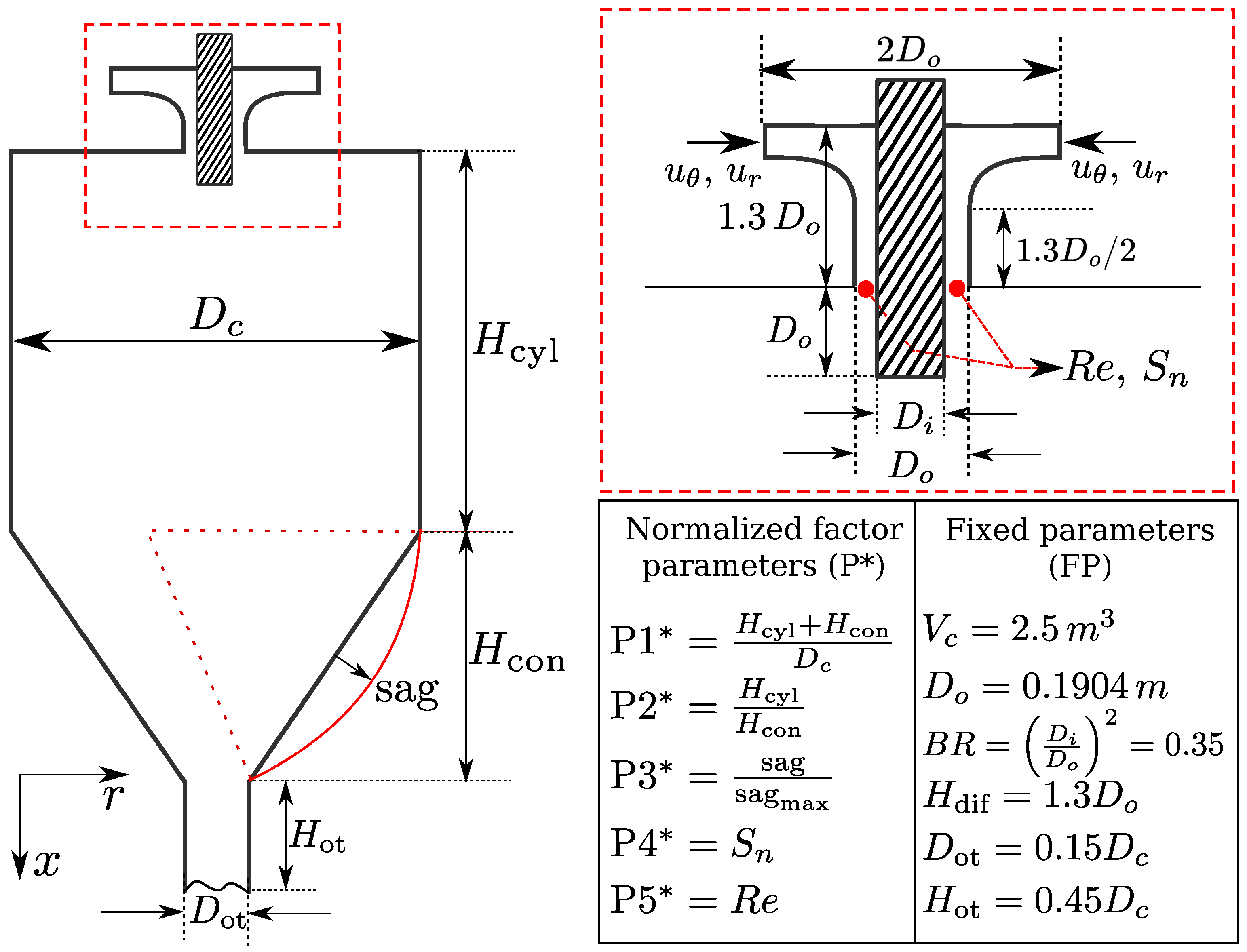
2.2. Parametrized Geometry of a Spray Drying Chamber
2.3. Factor Parameters
2.4. Ranges of Factor Parameters
2.5. Fixed (Held Constant) Parameters
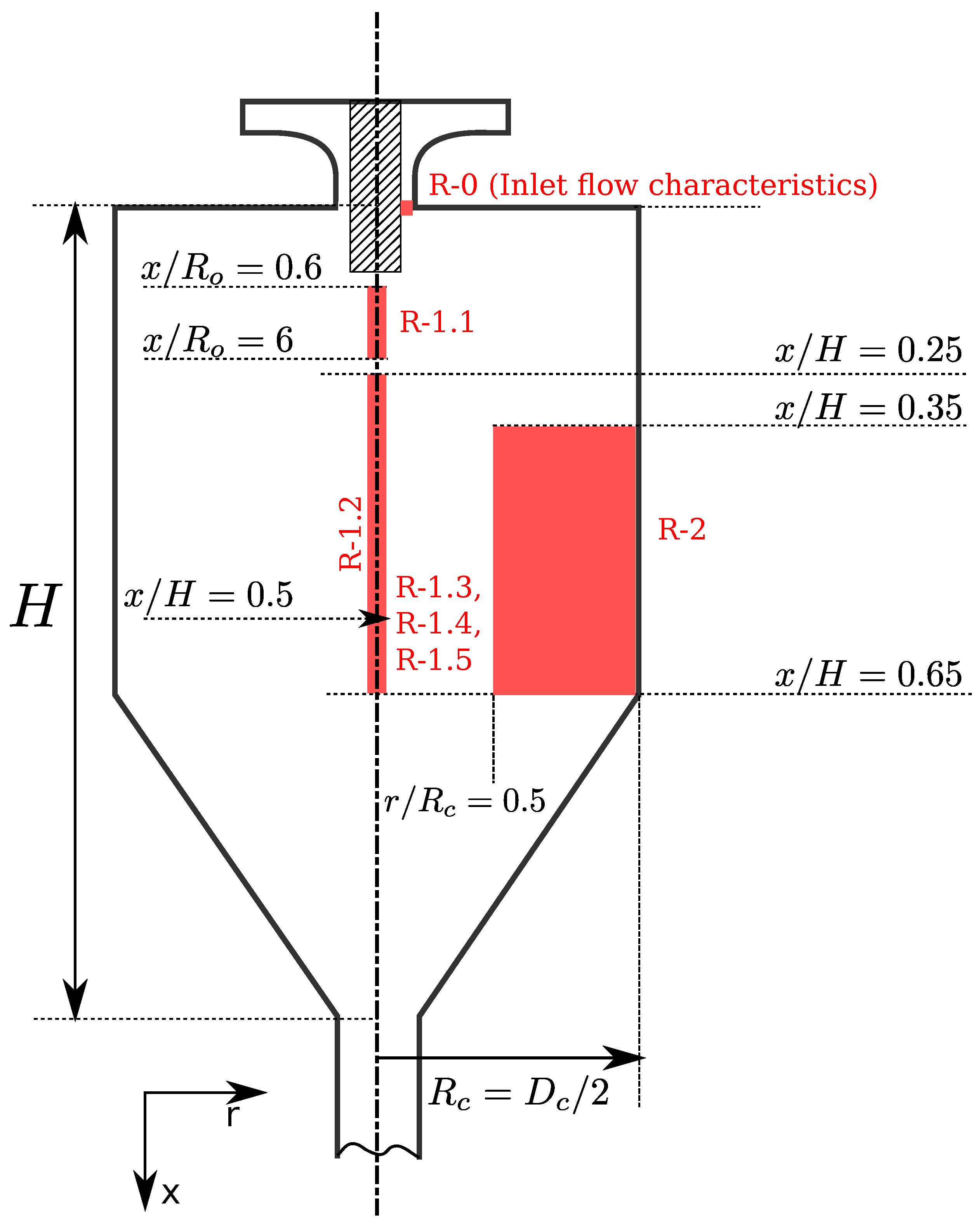
2.6. Response Variables
| Response Variables | |||
|---|---|---|---|
| Flow Region | Name | Description | Response Form and Location |
| Central jet (R1) | R-1.1 | Length of the internal recirculation vortex, described in [39,41] as part of the near-field of the jet. | and at |
| R-1.2 | Jet decay along the axis. It is affected by P4* [14]. May be affected by P5* [34]. | and at | |
| R-1.3 | Penetration of the jet in the drying chamber, normalized to the bulk velocity. It decreases as P4* increases P4* [14]. | at | |
| R-1.4 | Turbulence in the jet axis. | at and | |
| R-1.5 | Dominant frequency: R-1.5.1: frequency and R-1.5.2: amplitude, which are affected by P1* [34] and by P4* [15]. | R-1.5.1: at , R-1.5.2: Amplitude (m) at . | |
| External recirculation zone (R2) | R-2.1 | Recirculation strength. It may be related to wall shear stresses and particle–wall interactions [3]. It is affected by swirl (P4)* [28]. | in the axial direction in R2 |
| R-2.2 | Position of the recirculating flow. It may be affected by P5* [34]. | Position ( or ) of R-2.1 () (R-2.1) | |
| R-2.3 | Stability of recirculating flow. It may be related to P3* [13] and affects particle deposition on walls. It may also affect the detachment of dried particles [39]. | at predicted by R-2.2 | |
2.7. Nuisance Factors
2.8. Spreadsheet of Experiments
3. Numerical Methods and Computational Configuration
3.1. Governing Equations and Turbulence Modeling
3.2. Numerical Schemes and Methods
3.3. Adaptive Mesh Refinement (AMR)
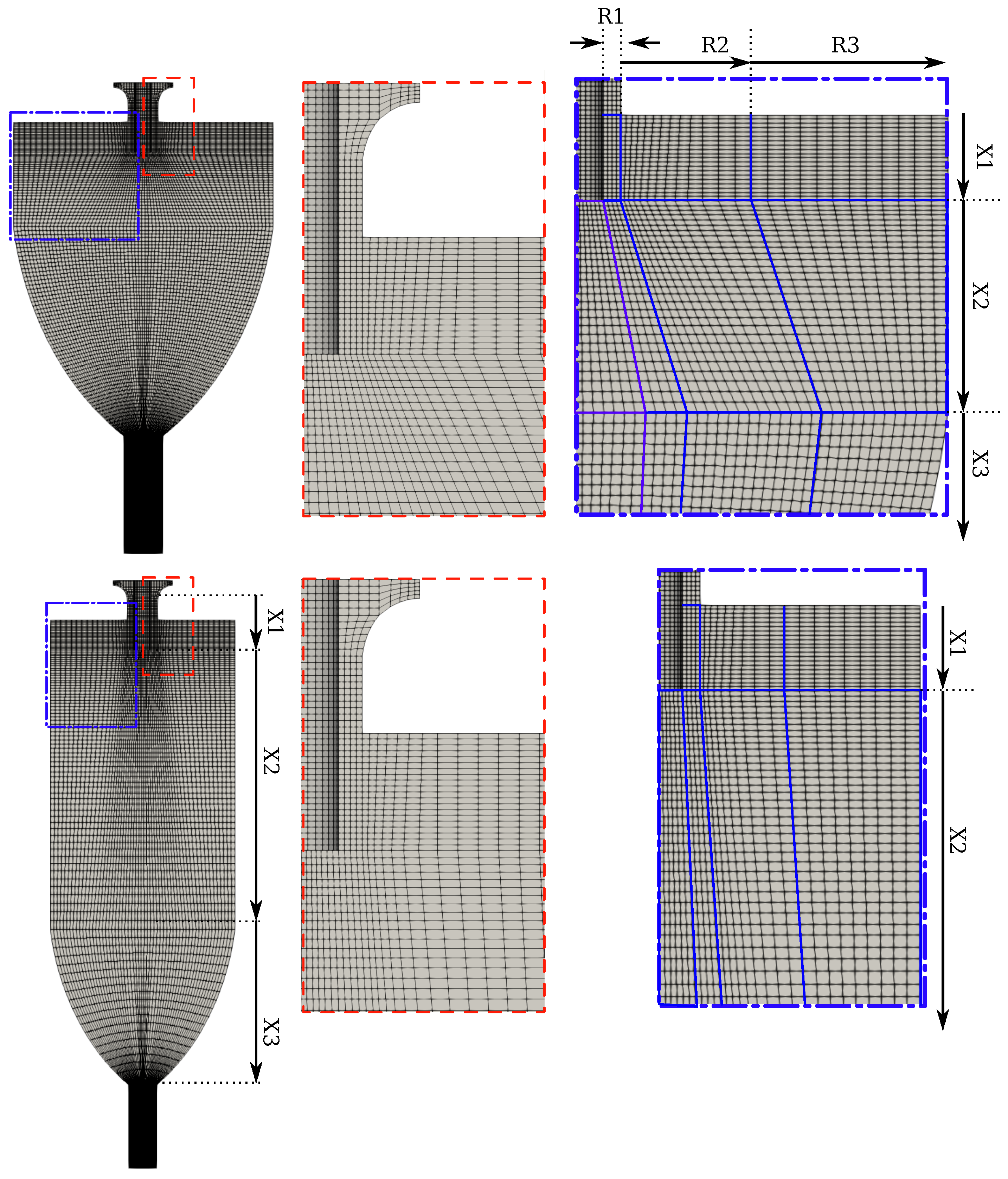
3.4. Grids
3.5. Base Computational Configuration
3.5.1. Boundary Conditions
3.5.2. Construction of the Computational Cases
- Reads the spreadsheet of experiments presented in Table 4 and a list of fixed parameters.
- Calculates the chamber dimensions for each case by an iterative procedure () and the position of the supporting vertices to create the conic-section of the chamber.
- Writes the mesh and boundary conditions configuration dictionaries.
- Writes the probe configuration file for each case, since some probe positions are relative to the chamber geometry.
3.5.3. Running Setup and Sampling of Data
3.5.4. Sampling and Post-Processing of Data
- The probes (12) located in R-0 were used to measure the axial velocity and swirl values at the entrance to the chamber. The collected data were used to calibrate the bulk velocity and swirl number at the discharge of the jet.
- The probes (61) located in R-1 zone were used to measure the response variables R-1.1 to R-1.5 and were located along the axial direction and . The probes in R-1.1 (20) were distributed from to and were used to capture information related to the recirculation vortex length. The probes in R-1.2 (40) were used to assess the decay of the jet ( at ) and were distributed from to . The last probe was located at and was used to determine the penetration of the jet (R-1.3) to measure the rms fluctuations of the axial velocity (R-1.4) and to calculate the dominant frequency of the jet (R-1.5).
- The probes (400) located in R-2 (recirculation zone) were arranged in a squared grid (20 × 20) from and . These ranges were considered sufficient to capture the principal features of the recirculation zone.
4. Results and Discussion
4.1. Computational Costs
4.2. Velocity Fields and Sampled Data
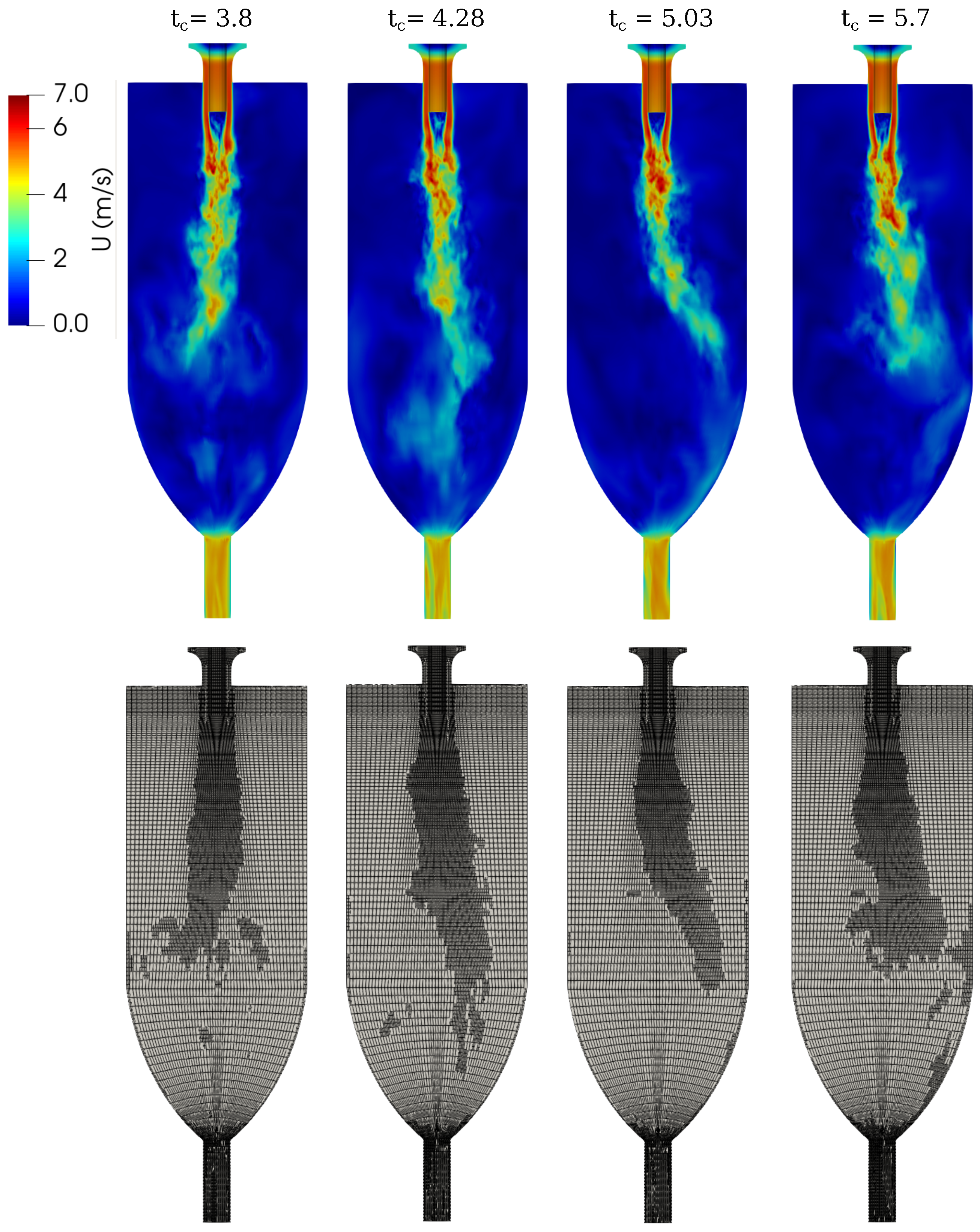
4.2.1. Velocity Fields and AMR
4.2.2. Examples of Sampled Data
4.3. Main Effects and Pareto Plots
4.3.1. R-1.1—Length of Internal Recirculation Vortex ( & )
4.3.2. R-1.2—Distance ( & ) for the Jet to Decay to 0.6
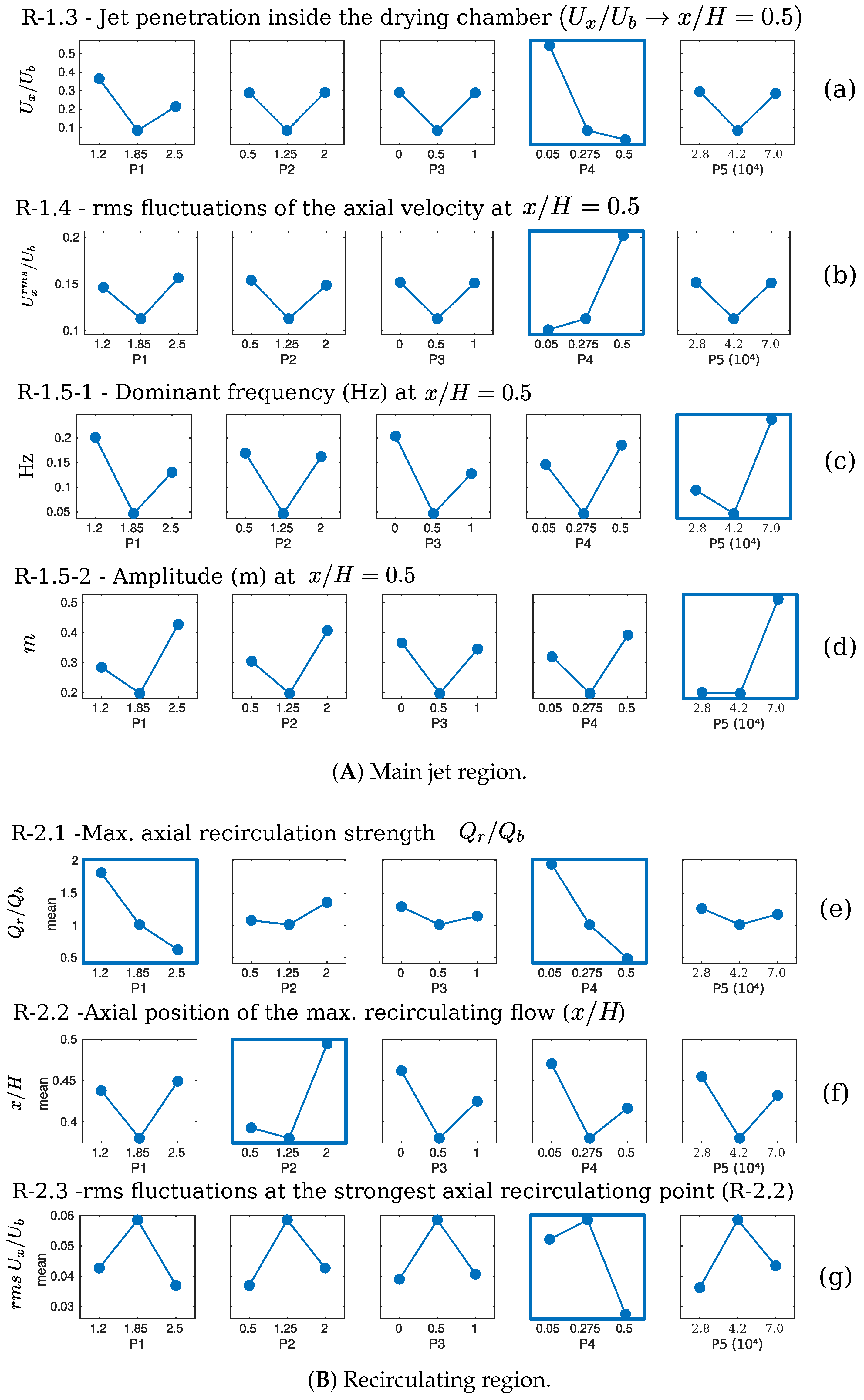
4.3.3. R-1.3—Jet Penetration Inside the Drying Chamber: Normalized Velocity ( at )
4.3.4. R-1.4—rms Fluctuations of the Axial Velocity at and at
4.3.5. R-1.5.1—Dominant Frequency (Hz) at the Normalized Position
4.3.6. R-1.5.2—Amplitude (m) of the Dominant Frequency
4.3.7. R-2.1—Maximum Axial Recirculation Strength ()
4.3.8. R-2.2—Axial Position of the Max. Recirculating Flow ( & )
4.3.9. R-2.3—rms Fluctuations of the Axial Velocity at the Recirculation Vortex (R-2.4—)
4.3.10. Spreadsheet of Main Effects
4.4. Curvature in the Response
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kieviet, F. Modelling Quality in Spray Drying. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 1997. [Google Scholar]
- Anandharamakrishnan, C.; Gimbun, J.; Stapley, A.G.F.; Rielly, C.D. A study of particle histories during spray drying using computational fluid dynamic simulations. Dry. Technol. 2010, 28, 566–576. [Google Scholar] [CrossRef][Green Version]
- Keshani, S.; Daud, W.R.W.; Nourouzi, M.; Namvar, F.; Ghasemi, M. Spray drying: An overview on wall deposition, process and modeling. J. Food Eng. 2015, 146, 152–162. [Google Scholar]
- Zbicinski, I. Modeling and scaling up of industrial spray dryers: A review. J. Chem. Eng. Jpn. 2017, 50, 757–767. [Google Scholar] [CrossRef]
- Huang, L.; Kumar, K.; Mujumdar, A. A parametric study of the gas flow patterns and drying performance of co-current spray dryer: Results of a computational fluid dynamics study. Dry. Technol. 2003, 21, 957–978. [Google Scholar] [CrossRef]
- Kadja, M.; Bergeles, G. Modelling of slurry droplet drying. Appl. Therm. Eng. 2003, 23, 829–844. [Google Scholar] [CrossRef]
- Roustapour, O.; Hosseinalipour, M.; Ghobadian, B.; Mohaghegh, F.; Azad, N. A proposed numerical–experimental method for drying kinetics in a spray dryer. J. Food Eng. 2009, 90, 20–26. [Google Scholar] [CrossRef]
- Wu, Z.; Mujumdar, A. A parametric study of spray drying of a solution in a pulsating high-temperature turbulent flow. Dry. Technol. 2006, 24, 751–761. [Google Scholar] [CrossRef]
- Phisut, N. Spray drying technique of fruit juice powder: Some factors influencing the properties of product. Int. Food Res. J. 2012, 19, 1297–1306. [Google Scholar]
- Fletcher, D.; Guo, B.; Harvie, D.; Langrish, T.; Nijdam, J.; Williams, J. What is important in the simulation of spray dryer performance and how do current CFD models perform? Appl. Math. Model. 2006, 30, 1281–1292. [Google Scholar] [CrossRef]
- Guo, B.; Langrish, T.; Fletcher, D.F. Simulation of turbulent swirl flow in an axisymmetric sudden expansion. AIAA J. 2001, 39, 96–102. [Google Scholar] [CrossRef]
- Huang, L.; Kumar, K.; Mujumdar, A. Use of computational fluid dynamics to evaluate alternative spray dryer chamber configurations. Dry. Technol. 2003, 21, 385–412. [Google Scholar] [CrossRef]
- Keshani, S.; Montazeri, M.H.; Daud, W.R.W.; Nourouzi, M.M. CFD modeling of air flow on wall deposition in different spray dryer geometries. Dry. Technol. 2015, 33, 784–795. [Google Scholar] [CrossRef]
- Langrish, T.; Williams, J.; Fletcher, D. Simulation of the effects of inlet swirl on gas flow patterns in a pilot-scale spray dryer. Chem. Eng. Res. Des. 2004, 82, 821–833. [Google Scholar] [CrossRef]
- Lebarbier, C.; Kockel, T.; Fletcher, D.; Langrish, T. Experimental measurement and numerical simulation of the effect of swirl on flow stability in spray dryers. Chem. Eng. Res. Des. 2001, 79, 260–268. [Google Scholar] [CrossRef]
- Woo, M.W.; Daud, W.R.W.; Mujumdar, A.S.; Wu, Z.; Talib, M.Z.M.; Tasirin, S.M. Non-swirling steady and transient flow simulations in short-form spray dryers. Chem. Prod. Process Model. 2009, 4, 20. [Google Scholar] [CrossRef]
- Anandharamakrishnan, C. Computational Fluid Dynamics Applications in Food Processing; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Woo, M.; Che, L.; Daud, W.R.W.; Mujumdar, A.; Chen, X. Highly swirling transient flows in spray dryers and consequent effect on modeling of particle deposition. Chem. Eng. Res. Des. 2012, 90, 336–345. [Google Scholar] [CrossRef]
- Pawar, S.K.; Abrahams, R.H.; Deen, N.G.; Padding, J.T.; van der Gulik, G.J.; Jongsma, A.; Innings, F.; Kuipers, J. An experimental study of dynamic jet behaviour in a scaled cold flow spray dryer model using PIV. Can. J. Chem. Eng. 2014, 92, 2013–2020. [Google Scholar] [CrossRef]
- Masters, K. Spray Drying Handbook; Longman Scientific & Technical: Iver, UK, 1991; ISBN 9780470217436. [Google Scholar]
- Mujumdar, A. Handbook of Industrial Drying; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Nijdam, J.J.; Guo, B.; Fletcher, D.F.; Langrish, T. Lagrangian and Eulerian models for simulating turbulent dispersion and coalescence of droplets within a spray. Appl. Math. Model. 2006, 30, 1196–1211. [Google Scholar] [CrossRef]
- Fletcher, D.; Langrish, T. Scale-adaptive simulation (SAS) modelling of a pilot-scale spray dryer. Chem. Eng. Res. Des. 2009, 87, 1371–1378. [Google Scholar] [CrossRef]
- Gutiérrez Suárez, J.A.; Galeano-Urueña, C.H.; Gómez-Mejía, A. Adaptive Mesh Refinement Strategies for Cost-Effective Eddy-Resolving Transient Simulations of Spray Dryers. ChemEngineering 2023, 7, 100. [Google Scholar] [CrossRef]
- Sommerfeld, M. Modelling requirements for CFD calculations of spray dryers. In Proceedings of the Jornada em Escoamentos multifásicos, Campinas, Brazil, 23–27 March 2015. [Google Scholar]
- Lampa, A.; Fritsching, U. Large Eddy Simulation of the spray formation in confinements. Int. J. Heat Fluid Flow 2013, 43, 26–34. [Google Scholar] [CrossRef]
- Gutiérrez Suárez, J.A.; Galeano-Urueña, C.H.; Gómez-Mejía, A. Low-Cost Eddy-Resolving Simulation in the Near-Field of an Annular Swirling Jet for Spray Drying Applications. ChemEngineering 2021, 5, 80. [Google Scholar] [CrossRef]
- Southwell, D.; Langrish, T. The effect of swirl on flow stability in spray dryers. Chem. Eng. Res. Des. 2001, 79, 222–234. [Google Scholar] [CrossRef]
- Coleman, D.E.; Montgomery, D.C. A systematic approach to planning for a designed industrial experiment. Technometrics 1993, 35, 1–12. [Google Scholar] [CrossRef]
- Rhew, R.D.; Parker, P.A. A parametric geometry computational fluid dynamics (CFD) study utilizing design of experiments (DOE). Am. Insitute Aeronaut. Astronaut. (AIAA) 2007, 1615, 2007. [Google Scholar]
- Carić, M. Concentrated and Dried Dairy Products; VCH Publishers Inc.: New York, NY, USA, 1994. [Google Scholar]
- Mujumdar, A.; Huang, L.; Chen, X. An overview of the recent advances in spray-drying. Dairy Sci. Technol. 2010, 90, 211–224. [Google Scholar] [CrossRef]
- García-Villalba, M.; Fröhlich, J.; Rodi, W. On inflow boundary conditions for large eddy simulation of turbulent swirling jets. In Proceedings of the 21st International Congress of Theoretical and Applied Mechanics, Warsaw, Poland, 15–21 August 2004. [Google Scholar]
- Pawar, S. Multiphase Flow in a Spray Dryer: Experimental and Computational Study. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2014. [Google Scholar]
- Huang, L.; Kumar, K.; Mujumdar, A. Simulation of a spray dryer fitted with a rotary disk atomizer using a three-dimensional computional fluid dynamic model. Dry. Technol. 2004, 22, 1489–1515. [Google Scholar] [CrossRef]
- Gutiérrez Suárez, J.A. Modelación CFD y validación Experimental del Proceso de Evaporación de Agua en un Secador por Aspersión. Master’s Thesis, Universidad Nacional de Colombia–Sede Bogotá–Facultad de Ingeniería–Ingeniería Mecánica, Bogotá, Colombia, 2015. [Google Scholar]
- Kieviet, F.; Kerkhof, P. Air flow, temperature and humidity patterns in a co-current spray dryer: Modelling and measurements. Dry. Technol. 1997, 15, 1763–1773. [Google Scholar] [CrossRef]
- Oakley, D. Spray dryer modeling in theory and practice. Dry. Technol. 2004, 22, 1371–1402. [Google Scholar] [CrossRef]
- Hammad, K.J.; Milanovic, I.; Al-Masoud, N. Characteristics of a Confined Annular Jet Flow Field. In Proceedings of the ASEE Northeast Section Conference 2013, Northfield, VT, USA, 14–16 March 2013. [Google Scholar]
- Southwell, D.; Langrish, T. Observations of flow patterns in a spray dryer. Dry. Technol. 2000, 18, 661–685. [Google Scholar] [CrossRef]
- Ko, N.; Chan, W. Similarity in the initial region of annular jets: Three configurations. J. Fluid Mech. 1978, 84, 641–656. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Davidson, L. Fluid Mechanics, Turbulent Flow and Turbulence Modeling; Lecture notes; Chalmers University of Technology: Gothenburg, Sweden, 2015. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 2006, 20, 181. [Google Scholar] [CrossRef]
- Travin, A.; Shur, M.; Strelets, M.; Spalart, P. Physical and numerical upgrades in the detached-eddy simulation of complex turbulent flows. In Advances in LES of Complex Flows; Springer: Dordrecht, The Netherlands, 2002; pp. 239–254. [Google Scholar] [CrossRef]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM®, 4th ed.; Holzmann CFD: Loeben, Germany, 2017. [Google Scholar]
- Moukalled, F.; Mangani, L.; Darwish, M. Temporal Discretization: The Transient Term. In The Finite Volume Method in Computational Fluid Dynamics; Springer: Cham, Switzerland, 2016; pp. 489–533. [Google Scholar] [CrossRef]
- Bathe, K.J.; Zhang, H. A mesh adaptivity procedure for CFD and fluid-structure interactions. Comput. Struct. 2009, 87, 604–617. [Google Scholar] [CrossRef]
- Culpo, M. Current Bottlenecks in the Scalability of OpenFOAM on Massively Parallel Clusters. PRACE White Paper to Appear on http://www. praceri. eu. 2011. Available online: https://www.google.com.hk/url?sa=t&source=web&rct=j&opi=89978449&url=https://prace-ri.eu/wp-content/uploads/Current_Bottlenecks_in_the_Scalability_of_OpenFOAM_on_Massively_Parallel_Clusters.pdf&ved=2ahUKEwj17sLrg6-KAxWy0jQHHax_JK0QFnoECBUQAQ&usg=AOvVaw1V7ePKvi4mgI2CWrmqrAHz (accessed on 16 December 2024).
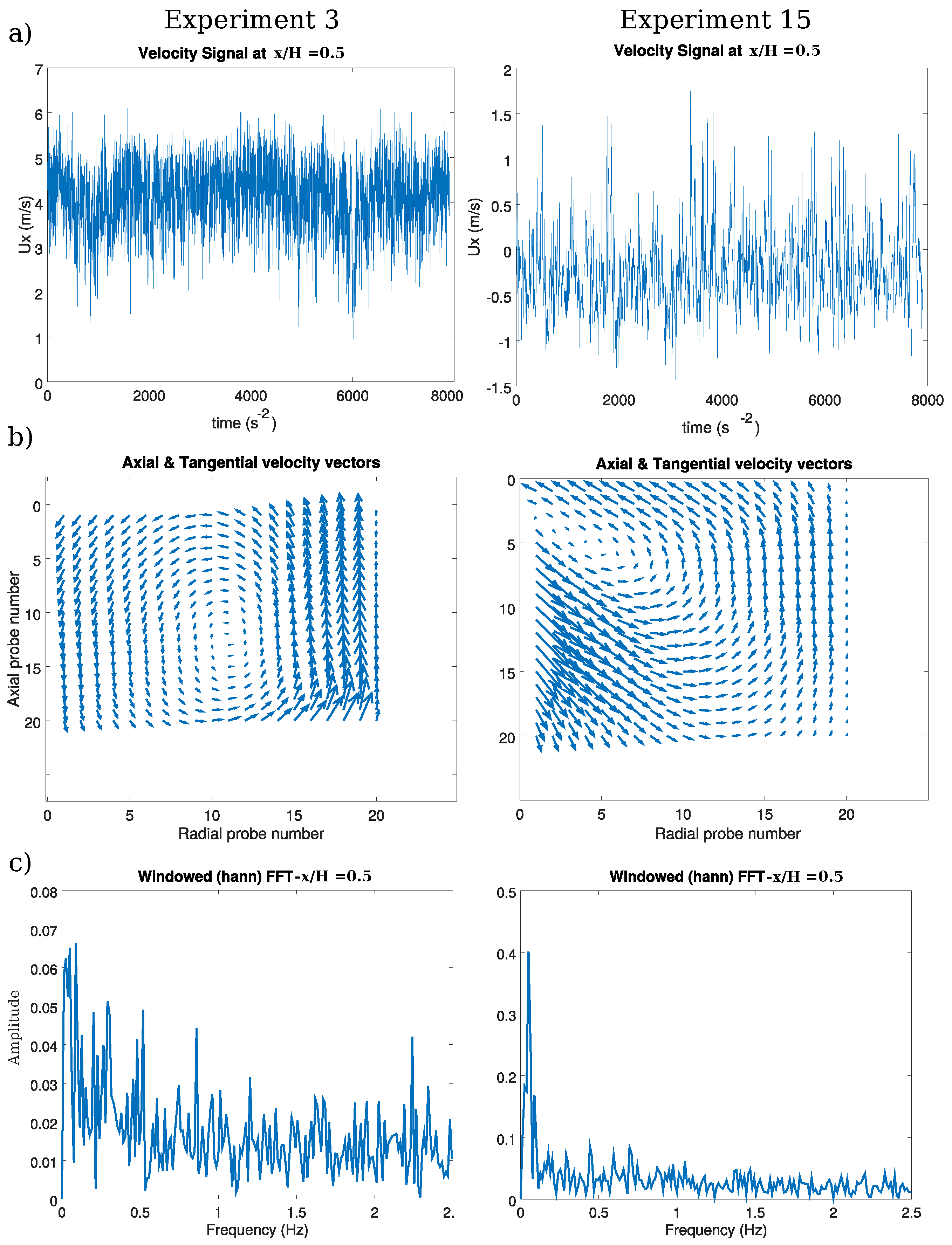
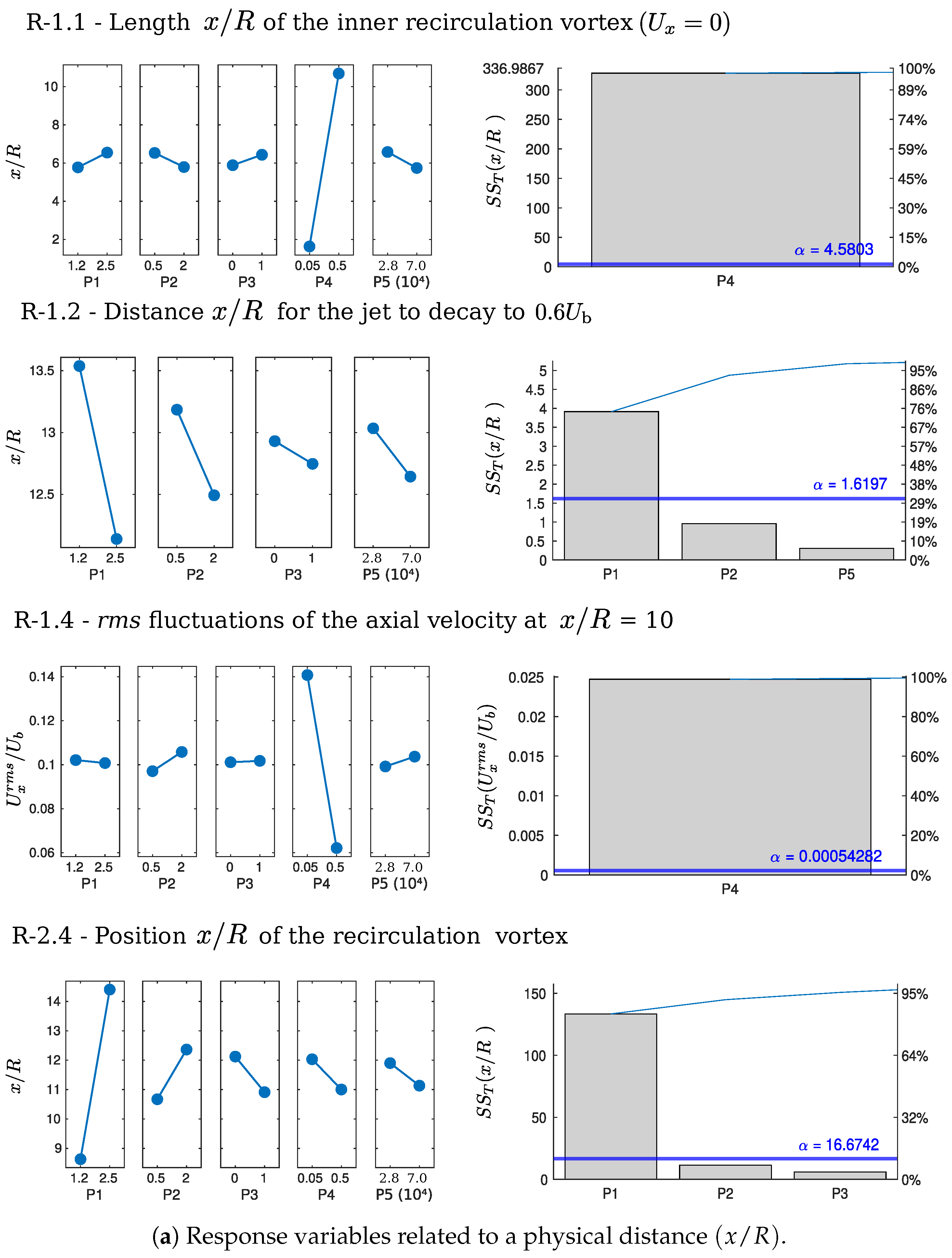
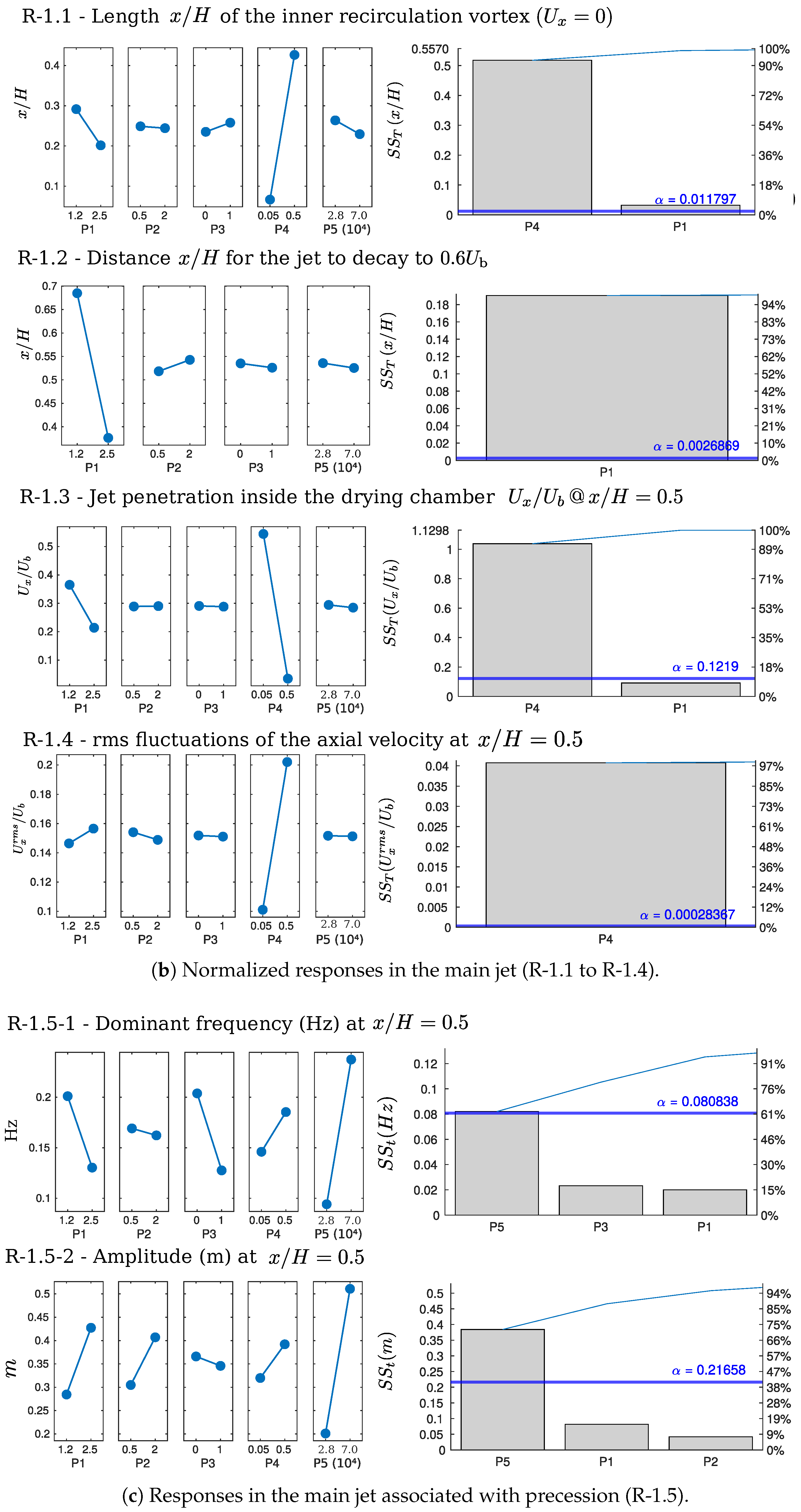
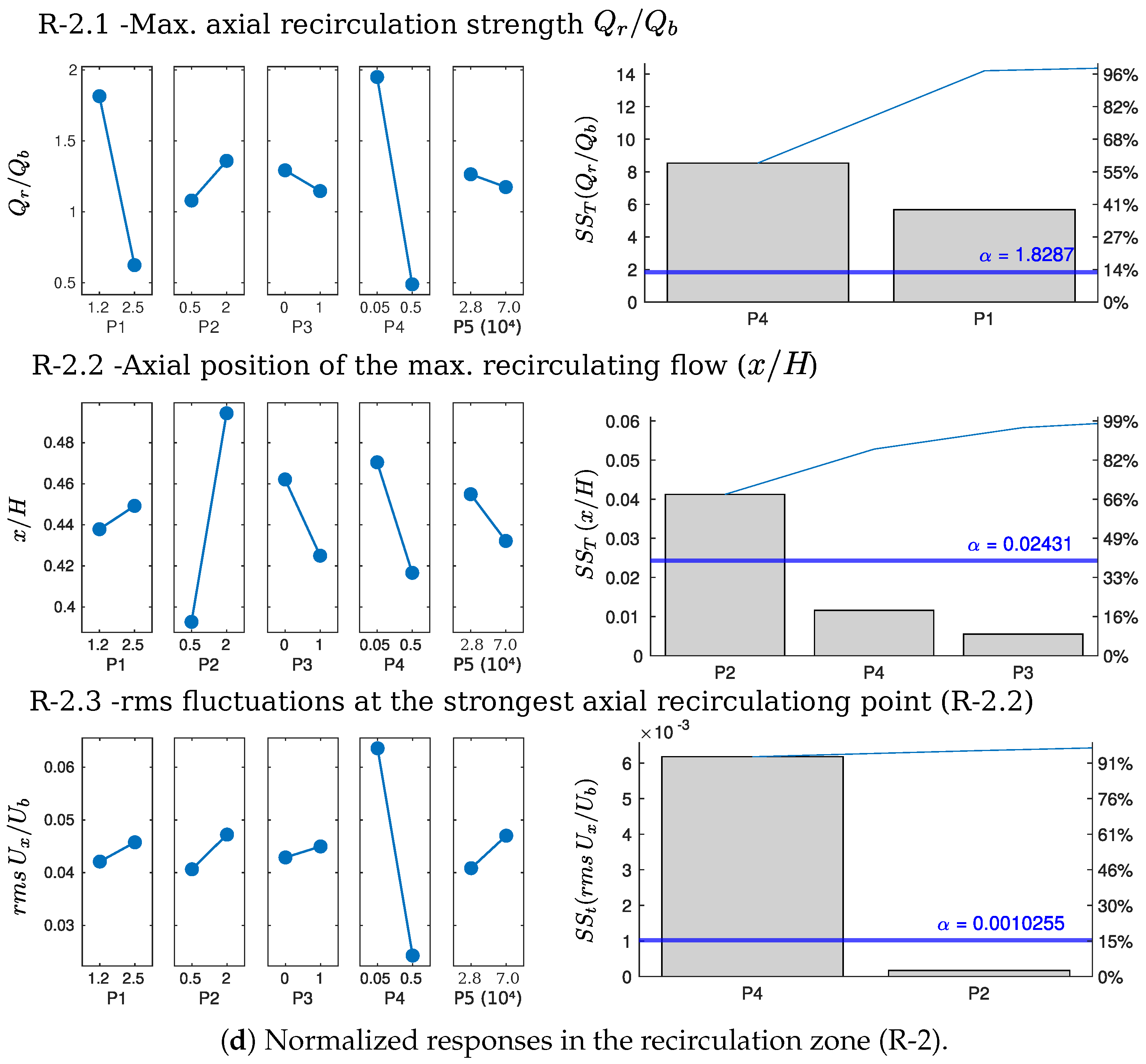
| Parameter | Middle Value | max. | min. |
|---|---|---|---|
| P1* | 1.68 | 2.5 | 1.2 |
| P2* | 1.60 | 2.0 | 0.5 |
| P3* | 1.75 | 1 | 0 |
| P4* | 0.25 | 0.5 | 0.05 |
| P5*() | 4.2 | 7.0 | 2.8 |
| Reference | P1* | P2* | P3* | P4* | (s) | P5*() |
|---|---|---|---|---|---|---|
| Kieviet and Kerkhof [37] | 1.68 | 1.16 | 0 | 0.09 | 19.73 | |
| Huang et al. [35] | 1.60 | 0.88 | 0 | 0 | 23.54 | |
| Woo et al. [16] | 1.75 | 0.67 | 0 | 0 | 8.60 | |
| Langrish et al. [14] | 2.01 | 1.56 | 0 | 0.45 | 14.36 | |
| Gutiérrez Suárez [36] | 1.77 | 1.15 | 0 | 0.10 | 10.25 | |
| Average | 1.76 | 1.08 | 0 | 0.13 | 15.30 | 4.2 |
| Maximum | 2.01 | 1.56 | 0 | 0.45 | 23.54 | 2.8 |
| Minimum | 1.60 | 0.67 | 0 | 0 | 8.60 | 7.0 |
| Experiment | P1* | P2* | P3* | P4* | P5* |
|---|---|---|---|---|---|
| 1 | 1.2 | 0.5 | 0 | 0.05 | 7.0 |
| 2 | 2.5 | 0.5 | 0 | 0.05 | 2.8 |
| 3 | 1.2 | 2 | 0 | 0.05 | 2.8 |
| 4 | 2.5 | 2 | 0 | 0.05 | 7.0 |
| 5 | 1.2 | 0.5 | 1 | 0.05 | 2.8 |
| 6 | 2.5 | 0.5 | 1 | 0.05 | 7.0 |
| 7 | 1.2 | 2 | 1 | 0.05 | 7.0 |
| 8 | 2.5 | 2 | 1 | 0.05 | 2.8 |
| 9 | 1.2 | 0.5 | 0 | 0.5 | 2.8 |
| 10 | 2.5 | 0.5 | 0 | 0.5 | 7.0 |
| 11 | 1.2 | 2 | 0 | 0.5 | 7.0 |
| 12 | 2.5 | 2 | 0 | 0.5 | 2.8 |
| 13 | 1.2 | 0.5 | 1 | 0.5 | 7.0 |
| 14 | 2.5 | 0.5 | 1 | 0.5 | 2.8 |
| 15 | 1.2 | 2 | 1 | 0.5 | 2.8 |
| 16 | 2.5 | 2 | 1 | 0.5 | 7.0 |
| 17 | 1.85 | 1.25 | 0.5 | 0.275 | 4.2 |
| Schemes | Description |
|---|---|
| Temporal terms | SUOE (Adams Moulton),second-order implicit. Described in Moukalled et al. [47]. |
| Gradient- | CDS (central differencing scheme) |
| Gradient- | Limited-CDS |
| Advective terms-div | Hybrid scheme, described in Gutiérrez Suárez et al. [27], Travin et al. [45] |
| RANS mode | LUD (linear upwind differencing) |
| LES mode | CDS (central differencing scheme) |
| Pressure–velocity coupling | PIMPLE algorithm, described in Holzmann [46]. |
| Flow Region | Main Jet Region (R1) | Recirculation Region (R2) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1.1* | 1.2* | 1.3* | 1.4* | 1.5.1* | 1.5.2* | 2.1* | 2.2* | 2.3* | |
| ine P1* | |||||||||
| P2* | |||||||||
| P3* | |||||||||
| P4* | |||||||||
| P5* | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez Suárez, J.A.; Galeano Urueña, C.H.; Gómez Mejía, A. Parametric CFD Study of Spray Drying Chamber Geometry: Part I—Effects on Airflow Dynamics. ChemEngineering 2025, 9, 5. https://doi.org/10.3390/chemengineering9010005
Gutiérrez Suárez JA, Galeano Urueña CH, Gómez Mejía A. Parametric CFD Study of Spray Drying Chamber Geometry: Part I—Effects on Airflow Dynamics. ChemEngineering. 2025; 9(1):5. https://doi.org/10.3390/chemengineering9010005
Chicago/Turabian StyleGutiérrez Suárez, Jairo Andrés, Carlos Humberto Galeano Urueña, and Alexánder Gómez Mejía. 2025. "Parametric CFD Study of Spray Drying Chamber Geometry: Part I—Effects on Airflow Dynamics" ChemEngineering 9, no. 1: 5. https://doi.org/10.3390/chemengineering9010005
APA StyleGutiérrez Suárez, J. A., Galeano Urueña, C. H., & Gómez Mejía, A. (2025). Parametric CFD Study of Spray Drying Chamber Geometry: Part I—Effects on Airflow Dynamics. ChemEngineering, 9(1), 5. https://doi.org/10.3390/chemengineering9010005







