Compound Climate Risk: Diagnosing Clustered Regional Flooding at Inter-Annual and Longer Time Scales
Abstract
1. Introduction
2. Data
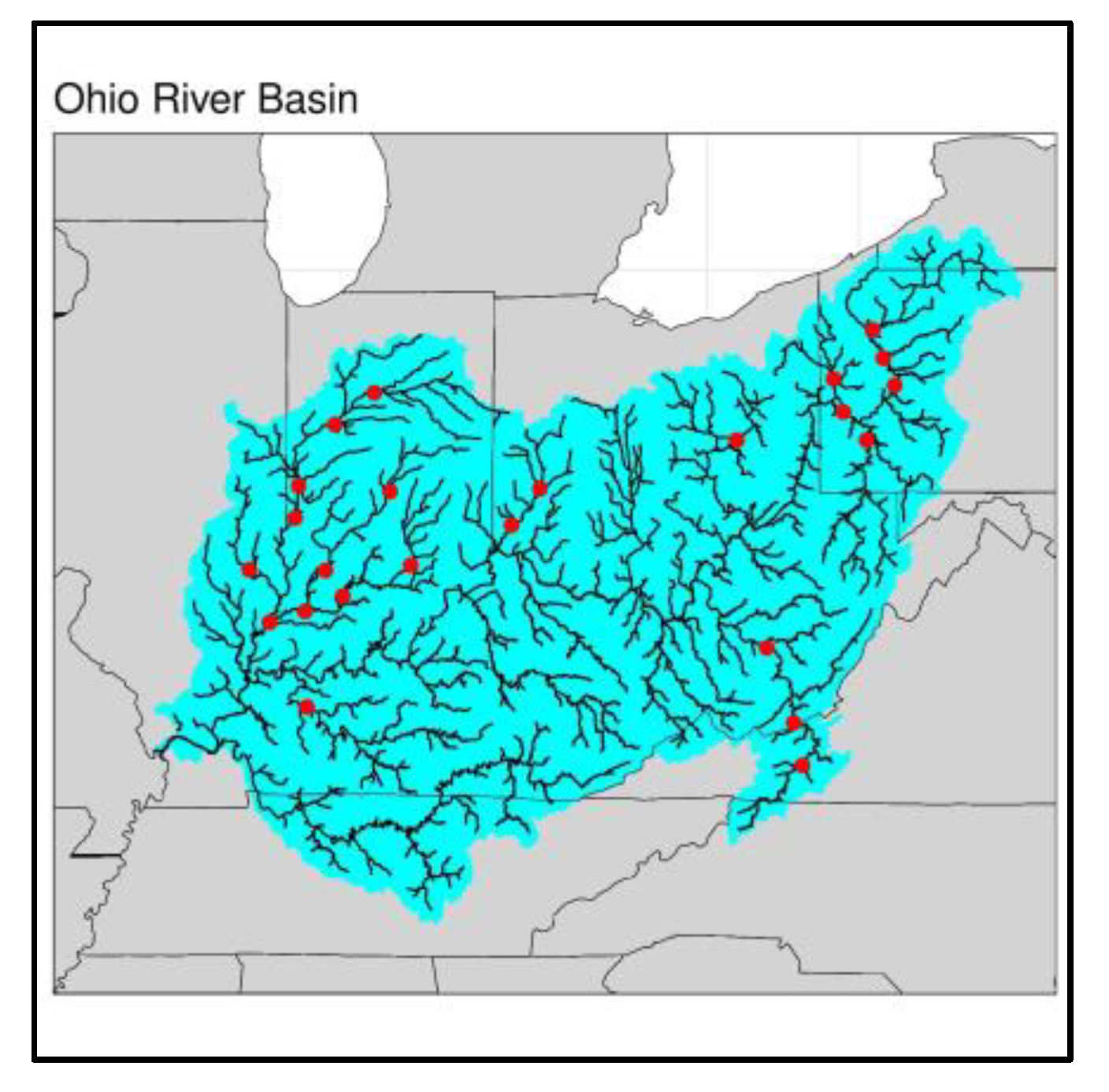
2.1. Streamflow Data
2.2. Climate Indices
3. Methods
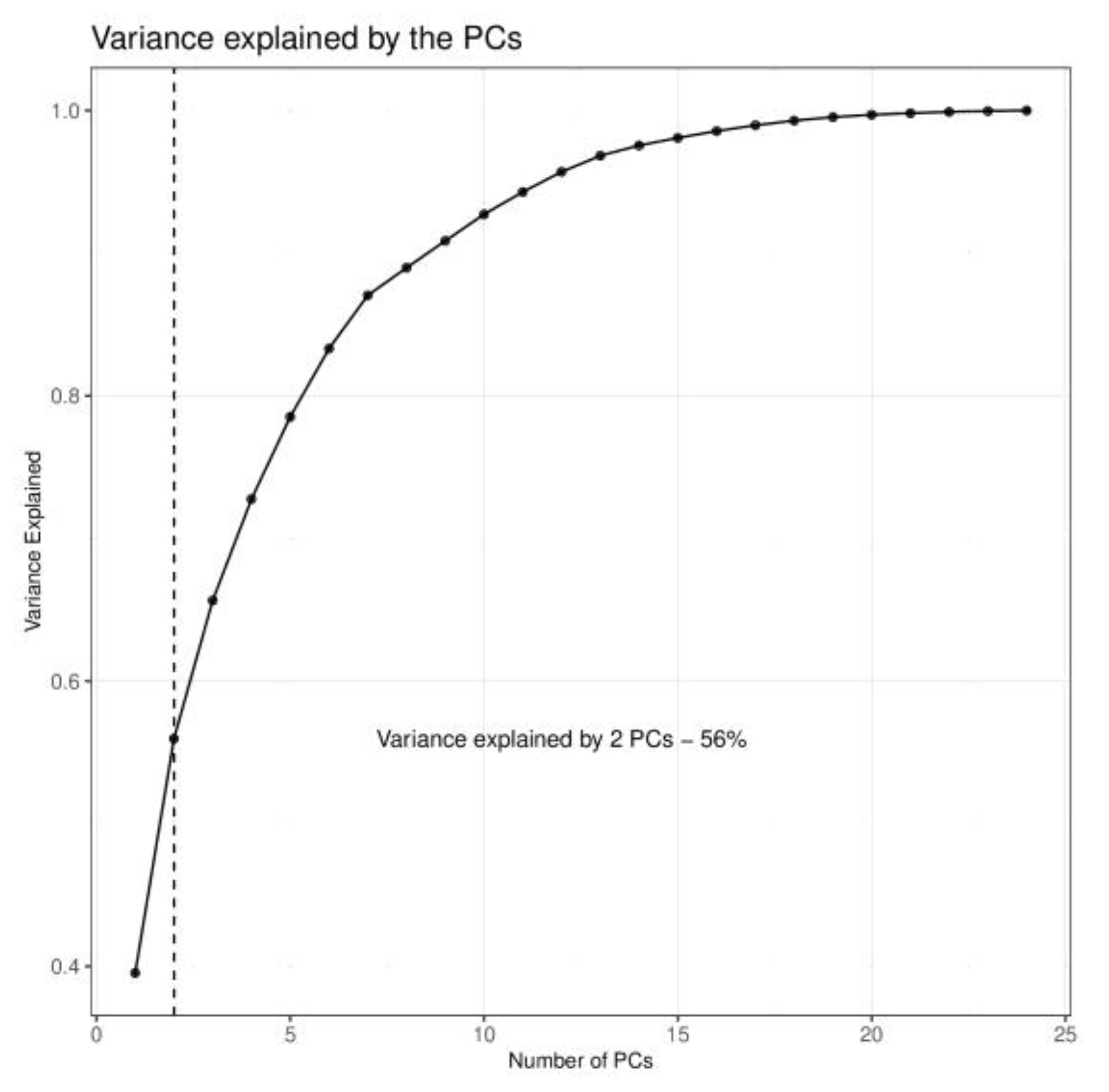
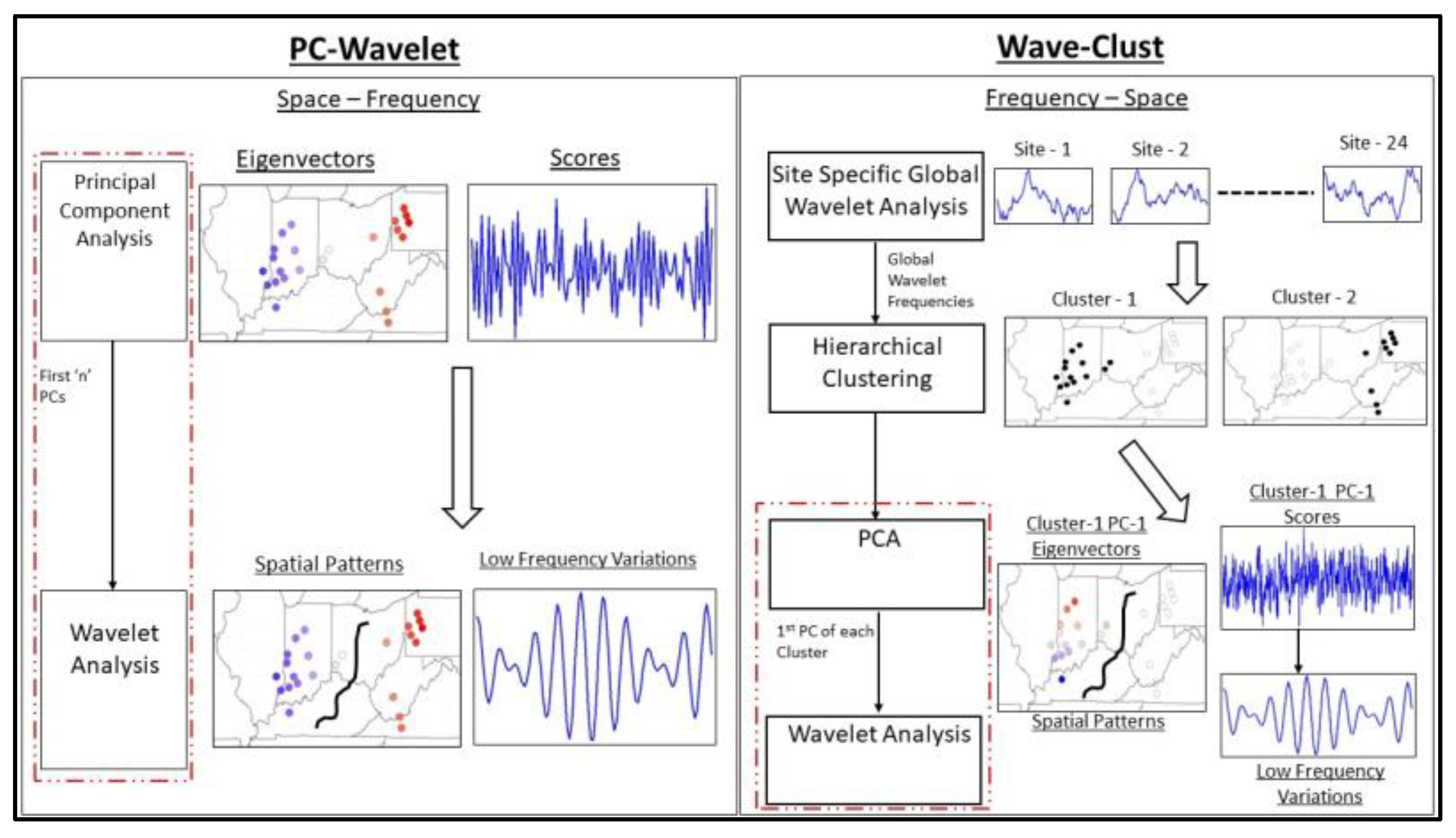
3.1. PC-Wavelet
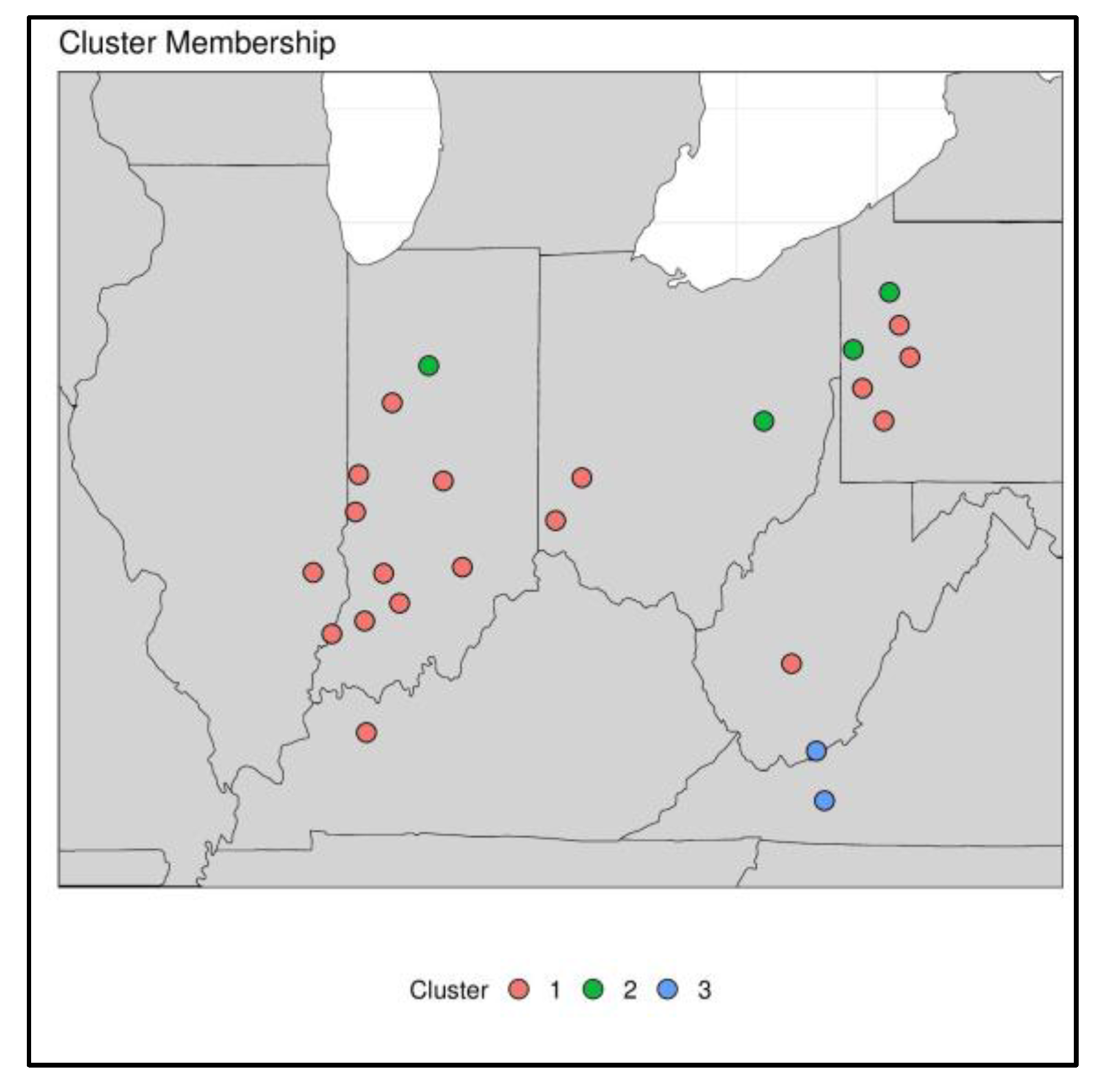
3.2. Wave-Clust
Wavelet Analysis
3.3. Diagnostic Analysis of the Role of Low Frequency Climate Variation
3.3.1. Correlation Analysis
3.3.2. Linear Regression with Regularization and Variable Selection
3.3.3. Non-Linear Regression
4. Results
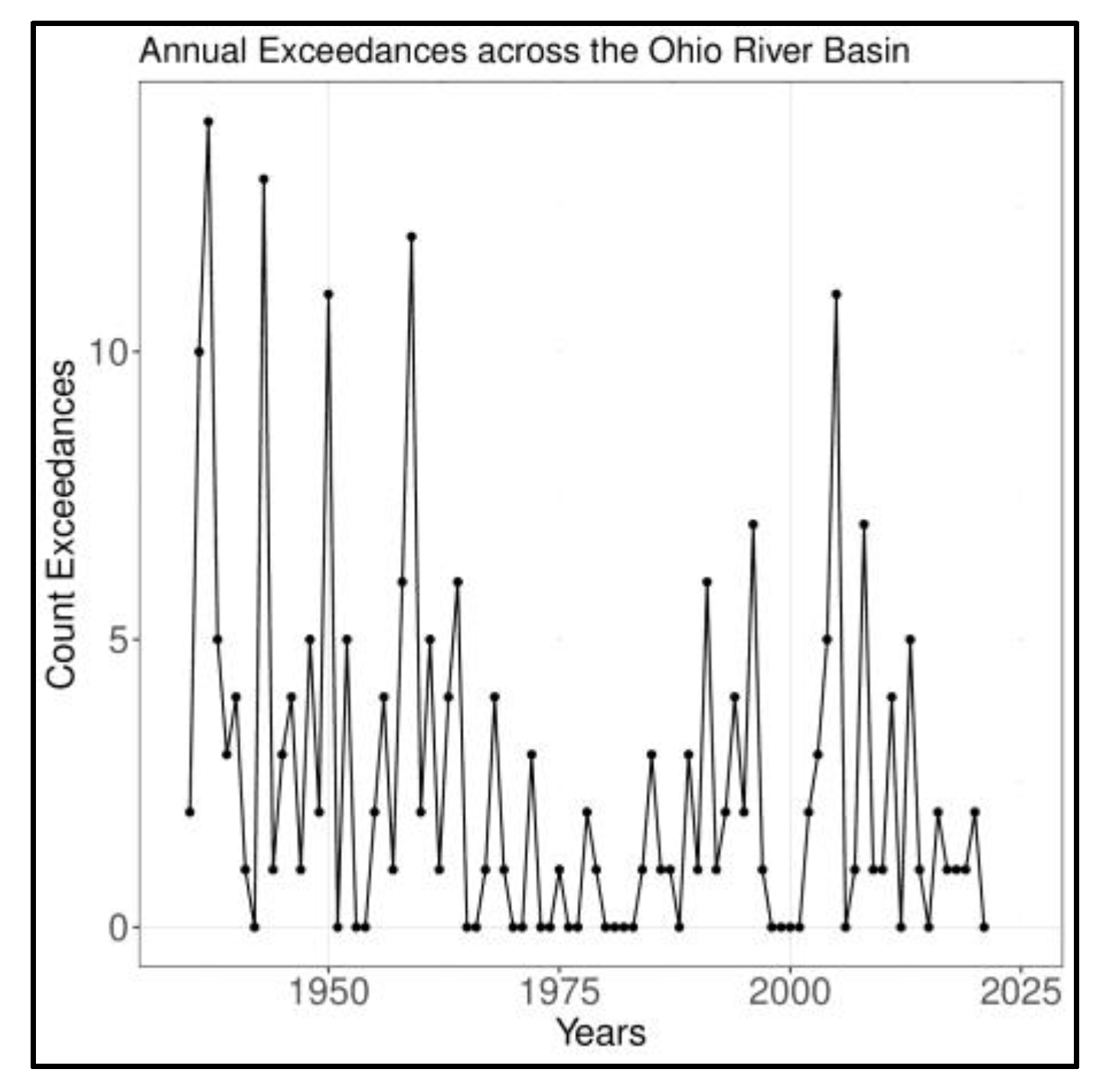
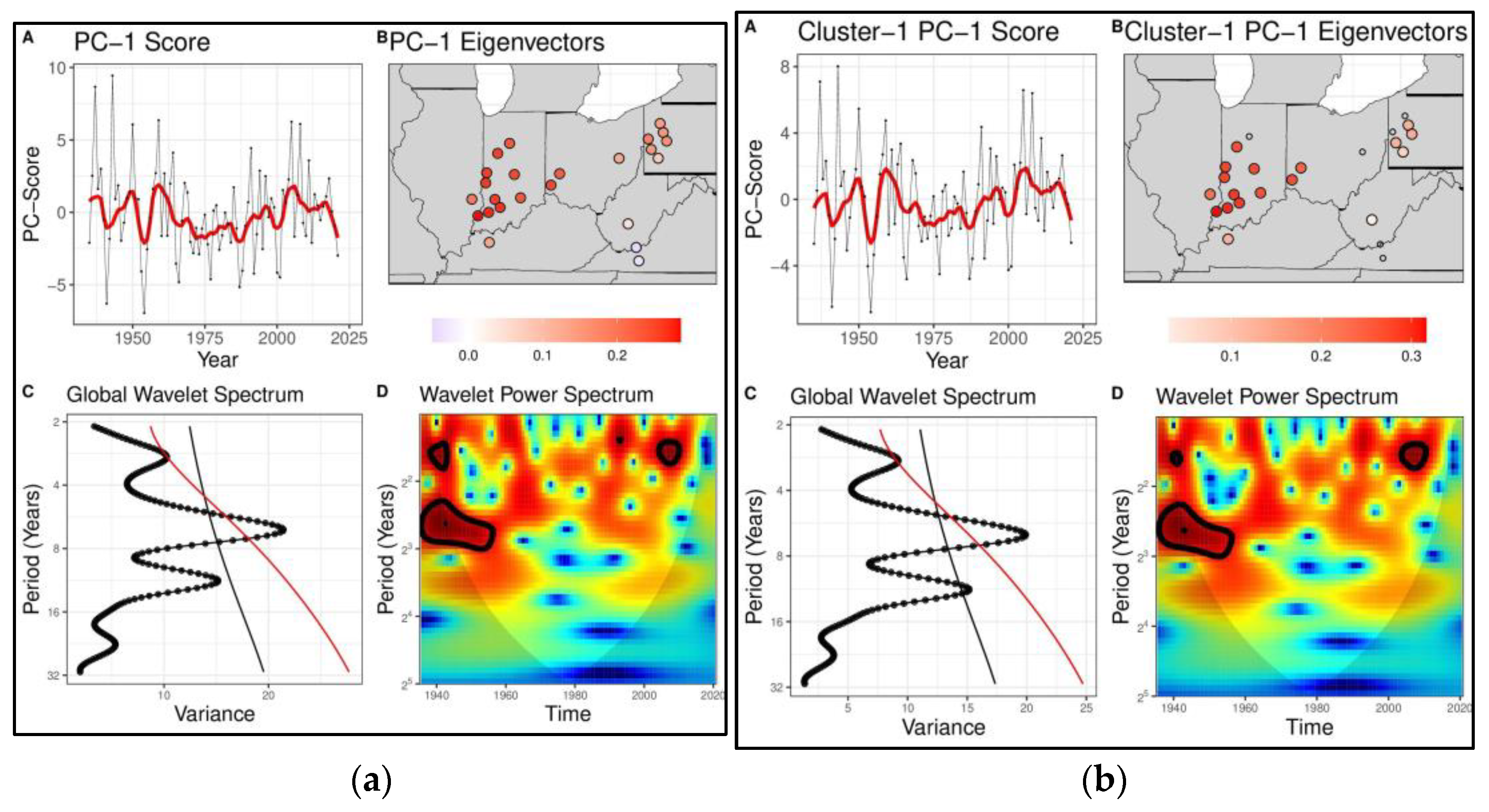
4.1. Diagnosis of Low Frequency Variations and Space-Time Signatures for the ORB
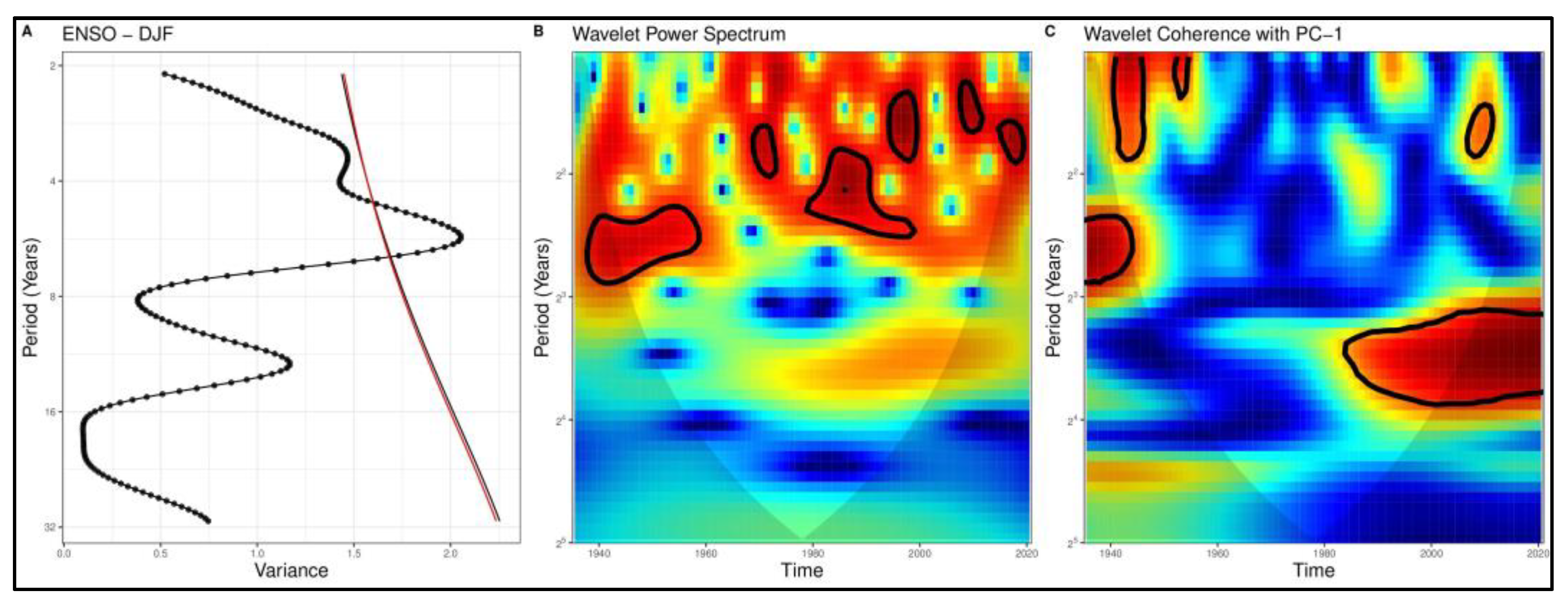
4.2. Diagnosis of Relations with Climate Indices
4.2.1. Correlation Analysis
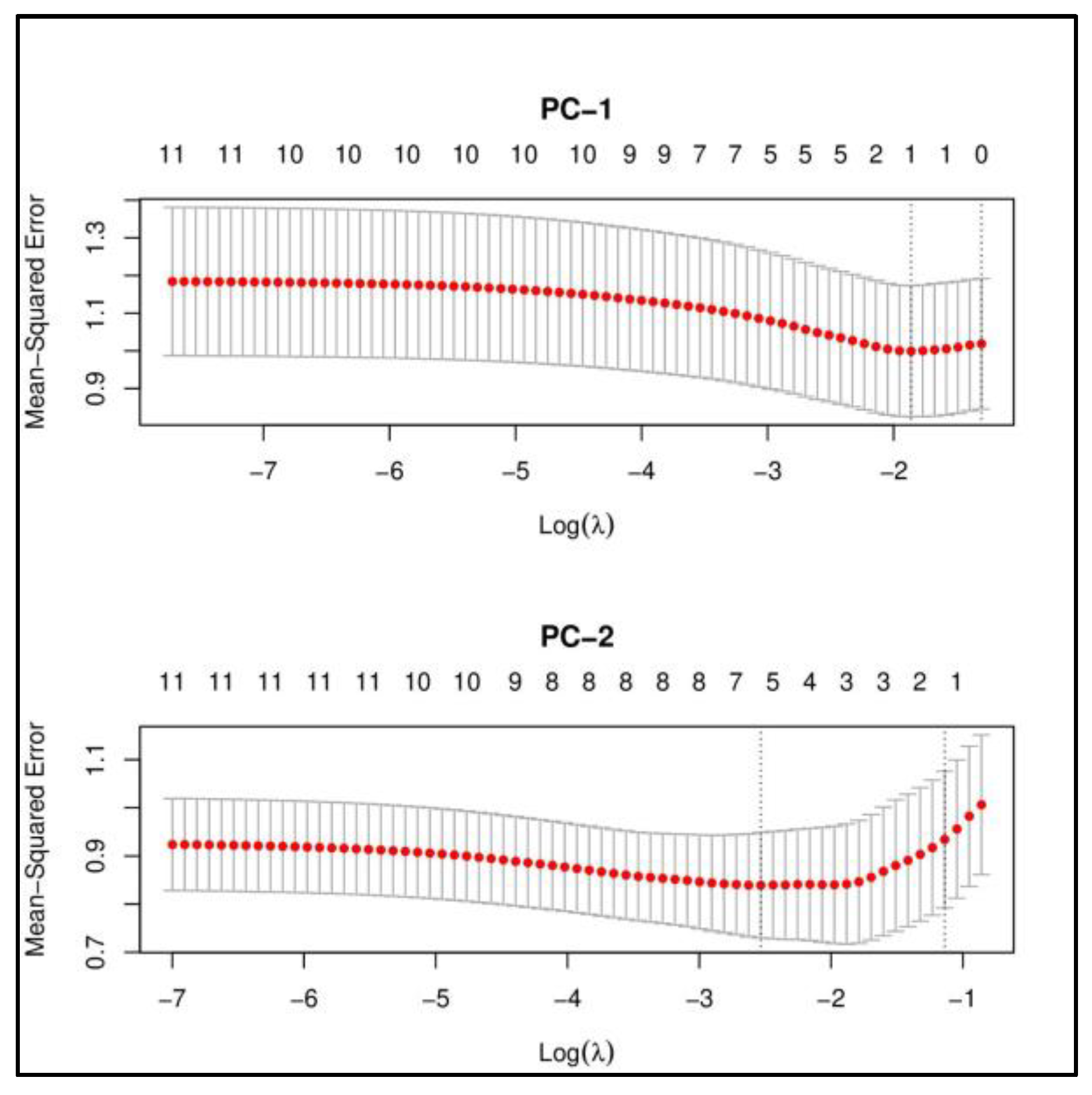
4.2.2. Linear Regression
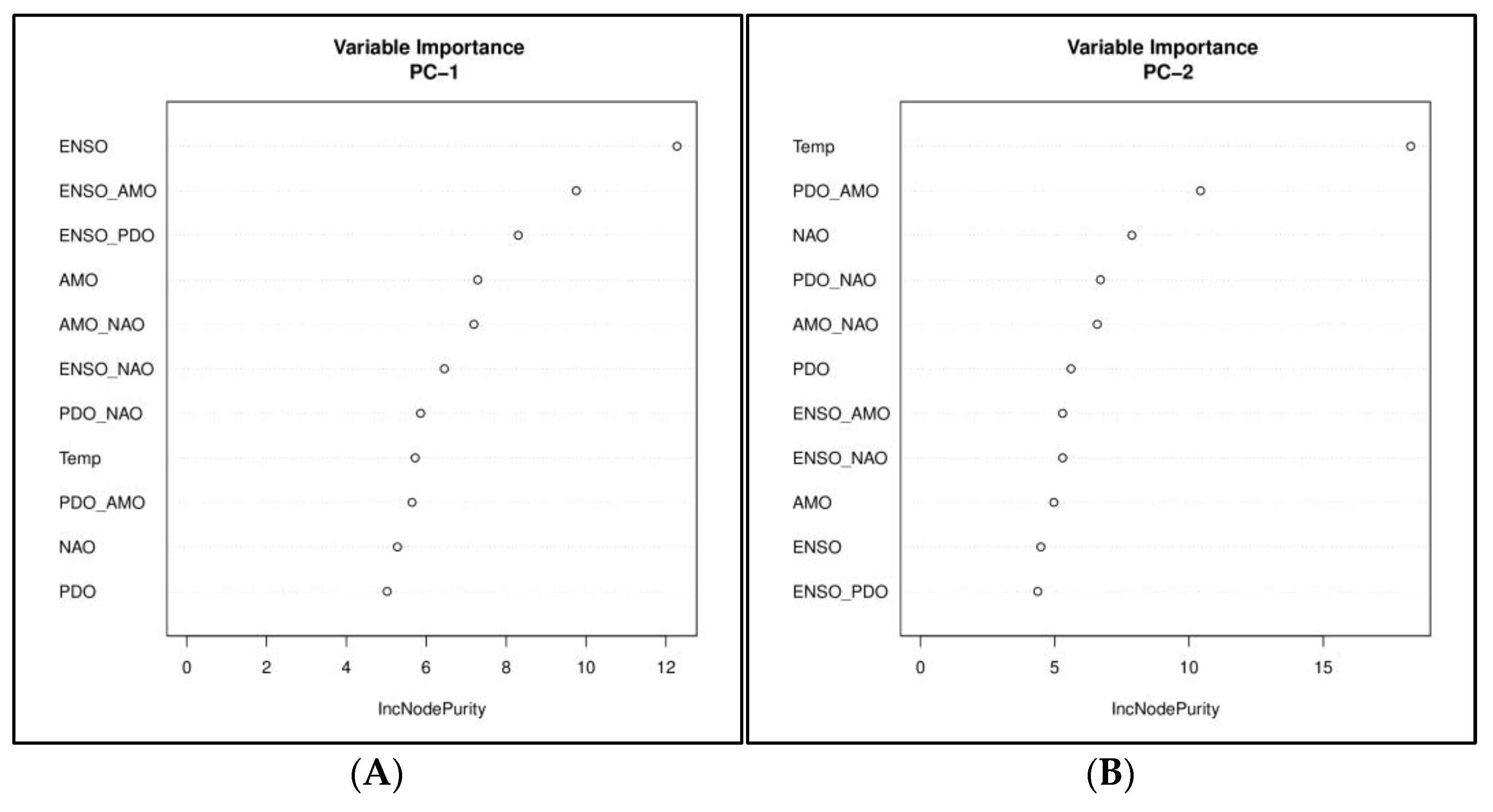
4.2.3. Non-Linear Regression
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Merz, B.; Blöschl, G.; Vorogushyn, S.; Dottori, F.; Aerts, J.C.J.H.; Bates, P.; Bertola, M.; Kemter, M.; Kreibich, H.; Lall, U.; et al. Causes, impacts and patterns of disastrous river floods. Nat. Rev. Earth Environ. 2021, 2, 592–609. [Google Scholar] [CrossRef]
- Pielke, R.A., Jr.; Gratz, J.; Landsea, C.W.; Collins, D.; Saunders, M.A.; Musulin, R. Normalized hurricane damage in the United States: 1900–2005. Nat. Hazards Rev. 2008, 9, 29–42. [Google Scholar] [CrossRef]
- Peduzzi, P.; Chatenoux, B.; Dao, H.; De Bono, A.; Herold, C.; Kossin, J.; Mouton, F.; Nordbeck, O. Global trends in tropical cyclone risk. Nat. Clim. Chang. 2012, 2, 289–294. [Google Scholar] [CrossRef]
- Merz, B.; Aerts, J.; Arnbjerg-Nielsen, K.; Baldi, M.; Becker, A.; Bichet, A.; Blöschl, G.; Bouwer, L.M.; Brauer, A.; Cioffi, F.; et al. Floods and climate: Emerging perspectives for flood risk assessment and management. Nat. Hazards Earth Syst. Sci. 2014, 14, 1921–1942. [Google Scholar] [CrossRef]
- Kemter, M.; Merz, B.; Marwan, N.; Vorogushyn, S.; Blöschl, G. Joint Trends in Flood Magnitudes and Spatial Extents across Europe. Geophys. Res. Lett. 2020, 47, e2020GL087464. [Google Scholar] [CrossRef] [PubMed]
- Bonnafous, L.; Lall, U.; Siegel, J. A water risk index for portfolio exposure to climatic extremes: Conceptualization and an application to the mining industry. Hydrol. Earth Syst. Sci. 2017, 21, 2075–2106. [Google Scholar] [CrossRef]
- Jain, S.; Lall, U. Floods in a changing climate: Does the past represent the future? Water Resour. Res. 2001, 37, 3193–3205. [Google Scholar] [CrossRef]
- Lun, D.; Fischer, S.; Viglione, A.; Blöschl, G. Detecting Flood-Rich and Flood-Poor Periods in Annual Peak Discharges across Europe. Water Resour. Res. 2020, 56, e2019WR026575. [Google Scholar] [CrossRef]
- Haraguchi, M.; Lall, U. Flood risks and impacts: A case study of Thailand’s floods in 2011 and research questions for supply chain decision making. Int. J. Disaster Risk Reduct. 2015, 14, 256–272. [Google Scholar] [CrossRef]
- Bonnafous, L.; Lall, U. Space-time clustering of climate extremes amplify global climate impacts, leading to fat-tailed risk. Nat. Hazards Earth Syst. Sci. 2021, 21, 2277–2284. [Google Scholar] [CrossRef]
- Swierczynski, T.; Brauer, A.; Lauterbach, S.; Martin-Puertas, C.; Dulski, P.; von Grafenstein, U.; Rohr, C. A 1600 yr seasonally resolved record of decadal-scale flood variability from the Austrian Pre-Alps. Geology 2012, 40, 1047–1050. [Google Scholar] [CrossRef]
- Meko, D.M.; Woodhouse, C.A. Tree-ring footprint of joint hydrologic drought in Sacramento and Upper Colorado river basins, western USA. J. Hydrol. 2005, 308, 196–213. [Google Scholar] [CrossRef]
- Ropelewski, C.F.; Halpert, M.S. Global and Regional Scale Precipitation Patterns Associated with the El Niño/Southern Oscillation. Mon. Weather Rev. 1987, 115, 1606–1626. [Google Scholar] [CrossRef]
- Ward, P.J.; Jongman, B.; Kummu, M.; Dettinger, M.D.; Weiland, F.C.S.; Winsemius, H.C. Strong influence of El Niño Southern Oscillation on flood risk around the world. Proc. Natl. Acad. Sci. USA 2014, 111, 15659–15664. [Google Scholar] [CrossRef]
- Ward, P.J.; Beets, W.; Bouwer, L.M.; Aerts, J.C.J.H.; Renssen, H. Sensitivity of river discharge to ENSO. Geophys. Res. Lett. 2010, 37, L12402. [Google Scholar] [CrossRef]
- Olsen, J.R.; Stedinger, J.R.; Matalas, N.C.; Stakhiv, E.Z. Climate Variability and Flood Frequency Estimation for the Upper Mississippi and Lower Missouri Rivers. JAWRA J. Am. Water Resour. Assoc. 1999, 35, 1509–1523. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific Interdecadal Climate Oscillation with Impacts on Salmon Production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1080. [Google Scholar] [CrossRef]
- Toomey, M.; Cantwell, M.; Colman, S.; Cronin, T.; Donnelly, J.; Giosan, L.; Heil, C.; Korty, R.; Marot, M.; Willard, D. The Mighty Susquehanna—Extreme Floods in Eastern North America During the Past Two Millennia. Geophys. Res. Lett. 2019, 46, 3398–3407. [Google Scholar] [CrossRef]
- Hodgkins, G.A.; Whitfield, P.H.; Burn, D.H.; Hannaford, J.; Renard, B.; Stahl, K.; Fleig, A.K.; Madsen, H.; Mediero, L.; Korhonen, J.; et al. Climate-driven variability in the occurrence of major floods across North America and Europe. J. Hydrol. 2017, 552, 704–717. [Google Scholar] [CrossRef]
- Stedinger, J.R., Jr.; Cohn, T.A.; Faber, B.A.; England, J.F.; Thomas, W.O., Jr.; Veilleux, A.G.; Kiang, J.E.; Mason, R.R., Jr. Guidelines for Determining Flood Flow Frequency—Bulletin 17C; U.S. Geological Survey: Reston, VA, USA, 2019. [Google Scholar]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Filho, F.D.A.S.; Lall, U. Seasonal to interannual ensemble streamflow forecasts for Ceara, Brazil: Applications of a multivariate, semiparametric algorithm. Water Resour. Res. 2003, 39, 1307. [Google Scholar] [CrossRef]
- Grantz, K.; Rajagopalan, B.; Clark, M.; Zagona, E. A technique for incorporating large-scale climate information in basin-scale ensemble streamflow forecasts. Water Resour. Res. 2005, 41, W10410. [Google Scholar] [CrossRef]
- Regonda, S.K.; Rajagopalan, B.; Clark, M.; Zagona, E. A multimodel ensemble forecast framework: Application to spring seasonal flows in the Gunnison River Basin. Water Resour. Res. 2006, 42, W09404. [Google Scholar] [CrossRef]
- Towler, E.; Rajagopalan, B.; Gilleland, E.; Summers, R.S.; Yates, D.; Katz, R. Modeling hydrologic and water quality extremes in a changing climate: A statistical approach based on extreme value theory. Water Resour. Res. 2010, 46, W11504. [Google Scholar] [CrossRef]
- Slater, L.J.; Anderson, B.; Buechel, M.; Dadson, S.; Han, S.; Harrigan, S.; Kelder, T.; Kowal, K.; Lees, T.; Matthews, T.; et al. Nonstationary weather and water extremes: A review of methods for their detection, attribution, and management. Hydrol. Earth Syst. Sci. 2021, 25, 3897–3935. [Google Scholar] [CrossRef]
- Schlef, K.E.; François, B.; Robertson, A.W.; Brown, C. A General Methodology for Climate-Informed Approaches to Long-Term Flood Projection—Illustrated with the Ohio River Basin. Water Resour. Res. 2018, 54, 9321–9341. [Google Scholar] [CrossRef]
- Lima, C.H.; Lall, U.; Troy, T.J.; Devineni, N. A climate informed model for nonstationary flood risk prediction: Application to Negro River at Manaus, Amazonia. J. Hydrol. 2015, 522, 594–602. [Google Scholar] [CrossRef]
- Brown, R.M. The Ohio River Floods of 1913. Bull. Am. Geogr. Soc. 1913, 45, 500–509. [Google Scholar] [CrossRef]
- NWS. Historic Ohio River Flood of 1937; National Weather Service: Silver Spring, MD, USA, 2022. [Google Scholar]
- NASA. When the Ohio River Floods. In NASA Applied Sciences; NASA: Washington, DC, USA, 2022. [Google Scholar]
- USGS. National Water Summary 1988–89—Hydrologic Events and Floods and Droughts; USGS Numbered Series 2375; U.S. Geological Survey: Reston, VA, USA, 1991. [Google Scholar] [CrossRef]
- Nakamura, J.; Lall, U.; Kushnir, Y.; Robertson, A.W.; Seager, R. Dynamical Structure of Extreme Floods in the U.S. Midwest and the United Kingdom. J. Hydrometeorol. 2013, 14, 485–504. [Google Scholar] [CrossRef]
- Robertson, A.W.; Kushnir, Y.; Lall, U.; Nakamura, J. Weather and Climatic Drivers of Extreme Flooding Events over the Midwest of the United States. In Extreme Events; American Geophysical Union (AGU): Washington, DC, USA, 2015; pp. 113–124. [Google Scholar] [CrossRef]
- Farnham, D.J.; Doss-Gollin, J.; Lall, U. Regional Extreme Precipitation Events: Robust Inference from Credibly Simulated GCM Variables. Water Resour. Res. 2018, 54, 3809–3824. [Google Scholar] [CrossRef]
- De Cicco, L.A.; Hirsch, R.M.; Lorenz, D.; Watkins, D. dataRetrieval. 2018. Available online: https://code.usgs.gov/water/dataRetrieval/-/tree/2.7.12 (accessed on 1 October 2022).
- NCAR. Overview: Climate Indices; NCAR: Boulder, CO, USA, 2022. [Google Scholar]
- Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. 2003, 108, 4407. [Google Scholar] [CrossRef]
- Zhang, Y.; Wallace, J.M.; Battisti, D.S. ENSO-like Interdecadal Variability: 1900–93. J. Clim. 1997, 10, 1004–1020. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Shea, D.J. Atlantic hurricanes and natural variability in 2005. Geophys. Res. Lett. 2006, 33, L12704. [Google Scholar] [CrossRef]
- Jones, P.D.; Jonsson, T.; Wheeler, D. Extension to the North Atlantic oscillation using early instrumental pressure observations from Gibraltar and south-west Iceland. Int. J. Climatol. 1997, 17, 1433–1450. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. WIREs Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Johnson, S.C. Hierarchical clustering schemes. Psychometrika 1967, 32, 241–254. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Gouhier, T.C.; Grinsted, A.; Simko, V. R Package Biwavelet: Conduct Univariate and Bivariate Wavelet Analyses. 2018. Available online: https://github.com/tgouhier/biwavelet (accessed on 1 October 2022).
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso: A retrospective. J. R. Stat. Soc. Ser. B 2011, 73, 273–282. [Google Scholar] [CrossRef]
- Friedman, J.H.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ishwaran, H. The effect of splitting on random forests. Mach. Learn. 2014, 99, 75–118. [Google Scholar] [CrossRef] [PubMed]
- Liaw, A.; Hoffman, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Cook, K.H.; Vizy, E.K.; Launer, Z.S.; Patricola, C.M. Springtime Intensification of the Great Plains Low-Level Jet and Midwest Precipitation in GCM Simulations of the Twenty-First Century. J. Clim. 2008, 21, 6321–6340. [Google Scholar] [CrossRef]
- Tang, Y.; Winkler, J.; Zhong, S.; Bian, X.; Doubler, D.; Yu, L.; Walters, C. Future changes in the climatology of the Great Plains low-level jet derived from fine resolution multi-model simulations. Sci. Rep. 2017, 7, 5029. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amonkar, Y.; Doss-Gollin, J.; Lall, U. Compound Climate Risk: Diagnosing Clustered Regional Flooding at Inter-Annual and Longer Time Scales. Hydrology 2023, 10, 67. https://doi.org/10.3390/hydrology10030067
Amonkar Y, Doss-Gollin J, Lall U. Compound Climate Risk: Diagnosing Clustered Regional Flooding at Inter-Annual and Longer Time Scales. Hydrology. 2023; 10(3):67. https://doi.org/10.3390/hydrology10030067
Chicago/Turabian StyleAmonkar, Yash, James Doss-Gollin, and Upmanu Lall. 2023. "Compound Climate Risk: Diagnosing Clustered Regional Flooding at Inter-Annual and Longer Time Scales" Hydrology 10, no. 3: 67. https://doi.org/10.3390/hydrology10030067
APA StyleAmonkar, Y., Doss-Gollin, J., & Lall, U. (2023). Compound Climate Risk: Diagnosing Clustered Regional Flooding at Inter-Annual and Longer Time Scales. Hydrology, 10(3), 67. https://doi.org/10.3390/hydrology10030067






