Thermally Enhanced Spreading of Miscible Plumes in Porous Media
Abstract
1. Introduction
2. Materials and Methods
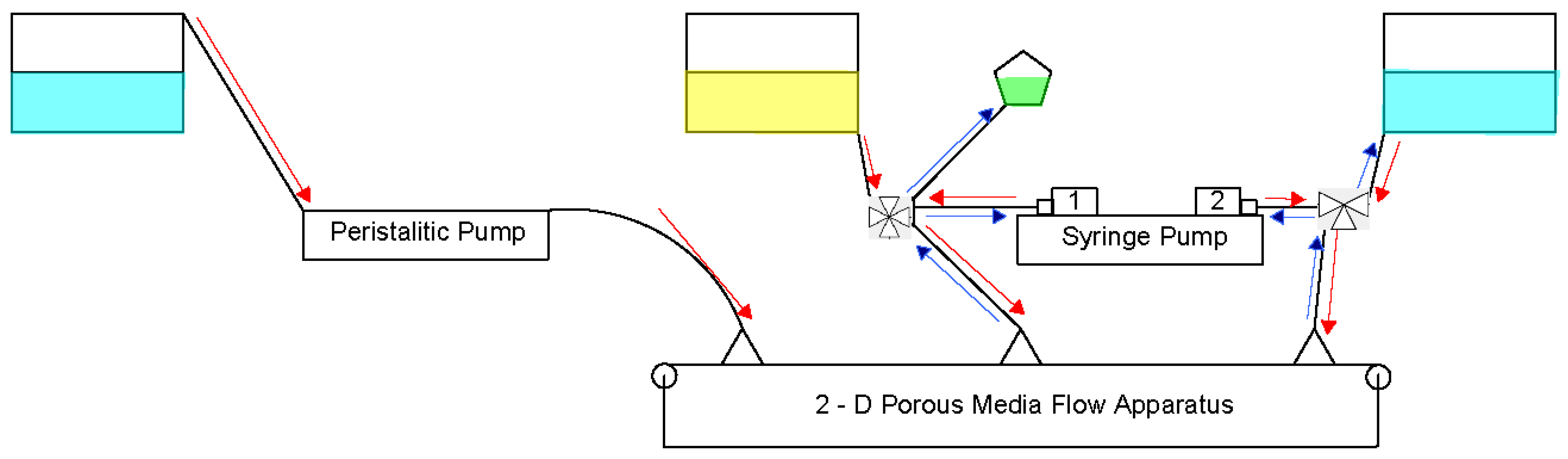
2.1. Apparatus
2.2. Experiments
2.3. Analysis
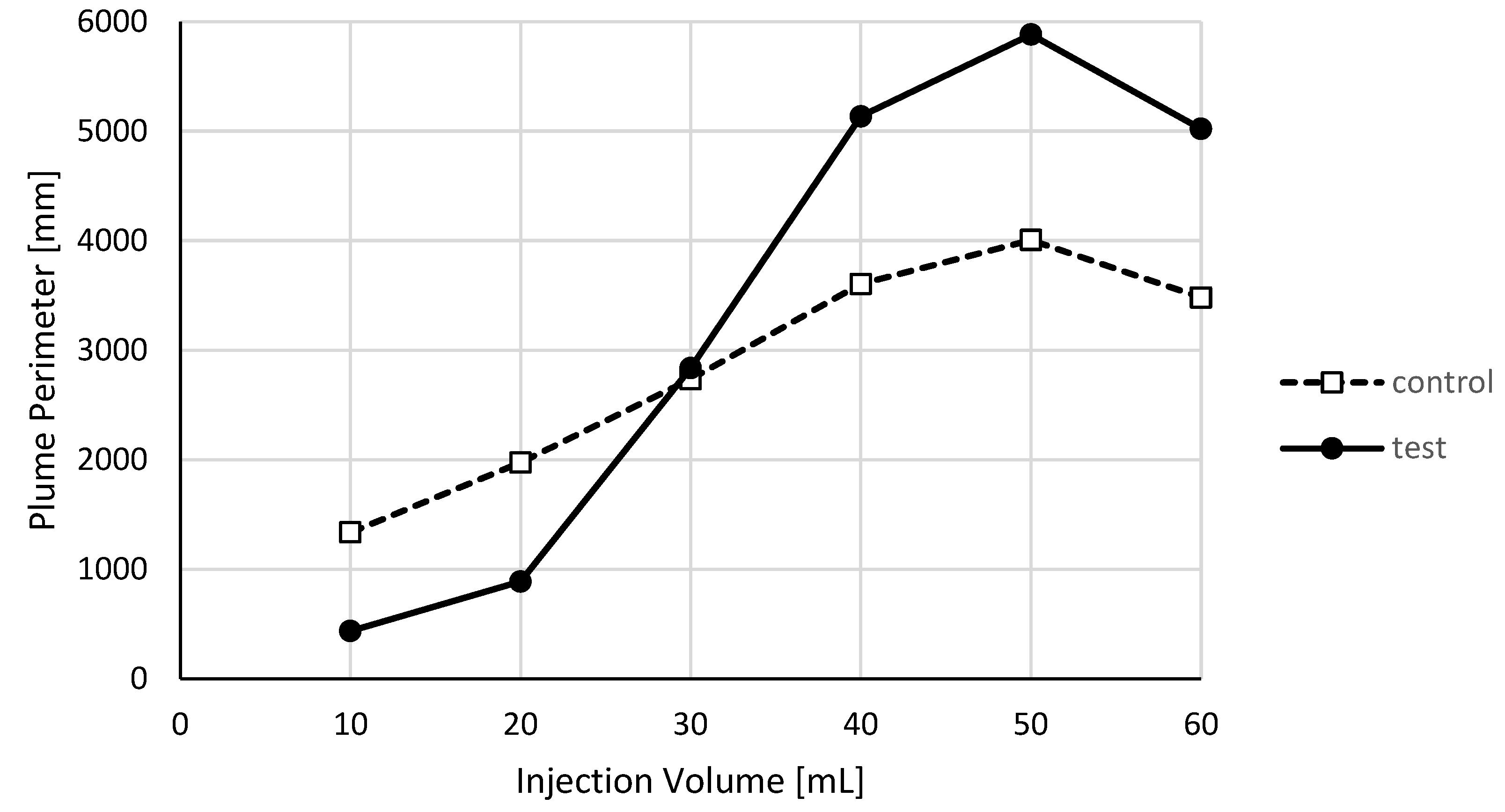
3. Results
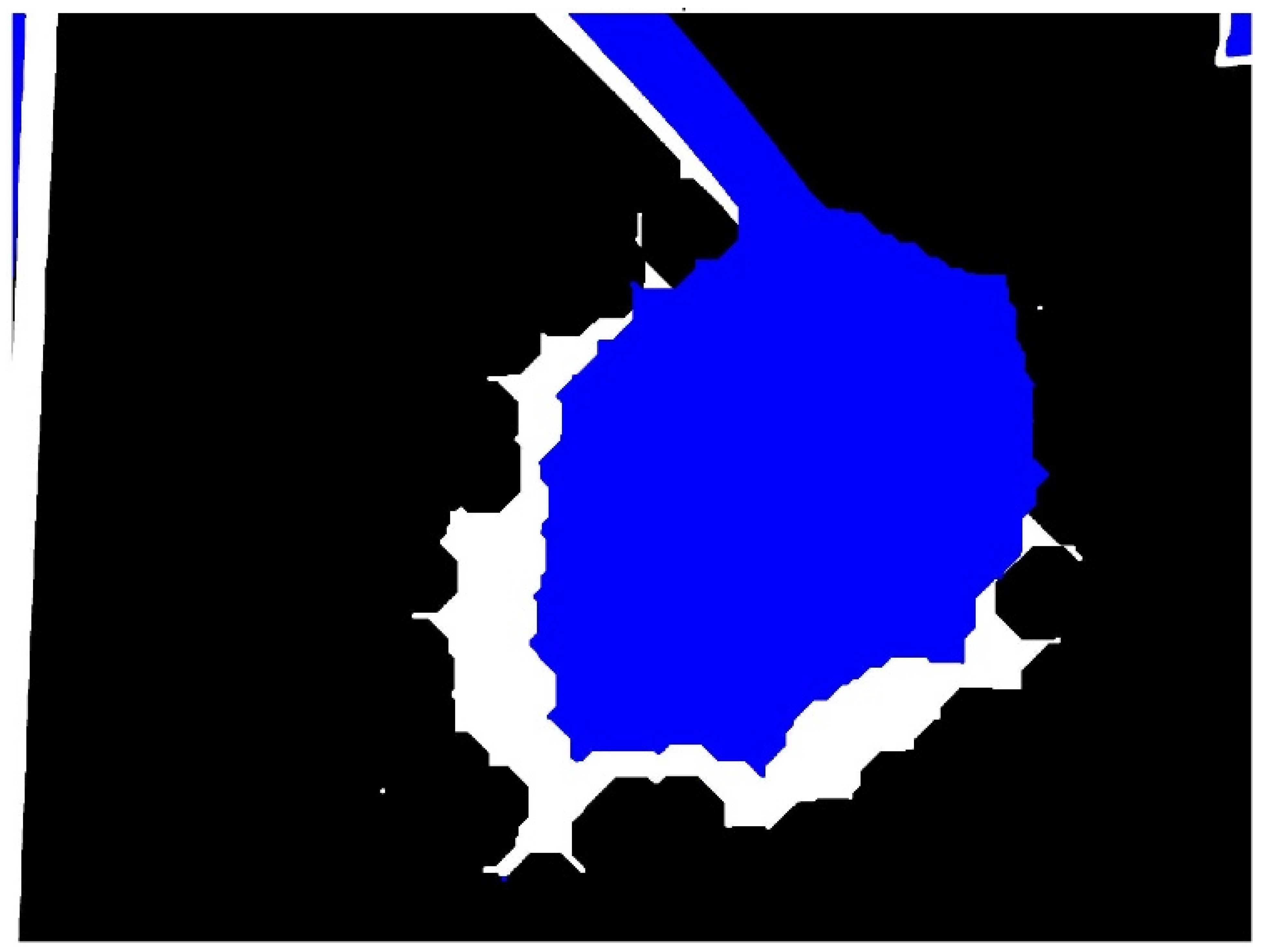
3.1. Binary Image Analysis
3.2. Morphological Image Analysis
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cirpka, O.A. Effects of sorption on transverse mixing in transient flows. J. Contam. Hydrol. 2005, 78, 207–229. [Google Scholar] [CrossRef]
- Sposito, G. Chaotic solute advection by unsteady groundwater flow. Water Resour. Res. 2006, 42, W06D03. [Google Scholar] [CrossRef]
- Bagtzoglou, A.C.; Oates, P.M. Chaotic advection and enhanced groundwater remediation. J. Mater. Civ. Eng. 2007, 19, 75–82. [Google Scholar] [CrossRef]
- Mays, D.C.; Neupauer, R.M. Plume spreading in groundwater by stretching and folding. Water Resour. Res. 2012, 48, W07501. [Google Scholar] [CrossRef]
- Zhang, P.F.; DeVries, S.L.; Dathe, A.; Bagtzoglou, A.C. Enhanced mixing and plume containment in porous media under time-dependent oscillatory flow. Environ. Sci. Technol. 2009, 43, 6283–6288. [Google Scholar] [CrossRef]
- Sather, L.J.; Roth, E.J.; Neupauer, R.M.; Crimaldi, J.P.; Mays, D.C. Experiments and simulations on plume spreading by engineered injection and extraction in refractive index matched porous media. Water Resour. Res. 2023, 59, e2022WR032943. [Google Scholar] [CrossRef]
- Lester, D.; Metcalfe, G.; Trefry, M.G.; Ord, A.; Hobbs, B.; Rudman, M. Lagrangian topology of a periodically reoriented potential flows Symmetry, optimization, and mixing. Phys. Rev. E 2009, 80, 036298. [Google Scholar] [CrossRef]
- Cho, M.S.; Solano, F.; Thomson, N.R.; Trefry, M.G.; Lester, D.R.; Metcalfe, G. Field trials of chaotic advection to enhance reagent delivery. Ground Water Monit. Remediat. 2019, 39, 23–39. [Google Scholar] [CrossRef]
- Videbæk, T.E.; Nagel, S.R. Diffusion-driven transition between two regimes of viscous fingering. Phys. Rev. Fluids 2019, 4, 033902. [Google Scholar] [CrossRef]
- Flowers, T.C.; Hunt, J.R. Viscous and gravitational contributions to mixing during vertical brine transport in water-saturated porous media. Water Resour. Res. 2007, 43, W01407. [Google Scholar] [CrossRef]
- Saffman, P.C. Viscous fingering in Hele-Shaw cells. J. Fluid Mech. 1986, 173, 73–94. [Google Scholar] [CrossRef]
- Chen, J.-D. Radial viscous fingering patterns in Hele-Shaw cells. Exp. Fluids 1987, 5, 363–371. [Google Scholar] [CrossRef]
- Homsy, G.M. Viscous fingering in porous media. Annu. Rev. Fluid Mech. 1987, 19, 271–311. [Google Scholar] [CrossRef]
- Saghir, M.Z.; Chaalal, O.; Islam, M.R. Numerical and experimental modeling of viscous fingering during liquid–liquid miscible displacement. J. Pet. Sci. Eng. 2000, 26, 253–262. [Google Scholar] [CrossRef]
- Jha, B.; Cueto-Felgueroso, L.; Juanes, R. Fluid mixing from viscous fingering. Phys. Rev. Lett. 2011, 106, 194502. [Google Scholar] [CrossRef]
- Sandnes, B.; Flekkøy, E.G.; Knudsen, H.A.; Måløy, K.J.; See, H. Patterns and flow in frictional fluid dynamics. Nat. Commun. 2011, 2, 288. [Google Scholar] [CrossRef]
- Afshari, S.; Hejazi, S.H.; Kantzas, A. Role of medium heterogeneity and viscosity contrast in miscible flow regimes and mixing zone growth: A computational pore-scale approach. Phys. Rev. Fluids 2018, 3, 054501. [Google Scholar] [CrossRef]
- Kaslusky, S.F.; Udell, K.S. Co-Injection of air and steam for the prevention of the downward migration of DNAPLs during steam enhanced extraction: An experimental evaluation of optimum injection ratio predictions. J. Contam. Hydrol. 2005, 77, 325–347. [Google Scholar] [CrossRef]
- Kosegi, J.M.; Minsker, B.S.; Dougherty, D.E. Feasibility study of thermal in situ bioremediation. J. Environ. Eng. 2000, 126, 601–610. [Google Scholar] [CrossRef]
- Payne, F.C.; Quinnan, J.A.; Potter, S.T. Remediation Hydraulics; CRC Press: New York, NY, USA, 2008. [Google Scholar]
- Jackson, S.J.; Power, H.; Giddings, D. Immiscible thermo-viscous fingering in Hele-Shaw cells. Comput. Fluids 2017, 156, 621–641. [Google Scholar] [CrossRef]
- Islam, M.N.; Azaiez, J. Thermo-viscous fingering in quarter five-spot miscible displacements. Eur. J. Mech. B/Fluids 2011, 30, 107–119. [Google Scholar] [CrossRef]
- Tigera, R.G. Temperature Dependent Viscosity Driven Mixing in a Quasi-2D Porous Media Apparatus. Master’s Thesis, Department of Civil Engineering, University of Colorado Denver, Denver, CO, USA, 2020. [Google Scholar]
- Dullien, F.A.L. Porous Media: Fluid Transport and Pore Structure, 2nd ed.; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Repplier, F.N.; Rell, M.M.; Columbia, R.K. MS-21 Groundwater Temperatures Map of Colorado. In Colorado Geological Survey; Department of Natural Resources: Denver, CO, USA, 1981; Available online: https://coloradogeologicalsurvey.org/publications/groundwater-temperatures-map-colorado (accessed on 30 September 2022).
- Sharqawy, M.H.; Lienhard, V.J.H.; Zubair, S.M. The thermophysical properties of seawater: A review of existing correlations and data. Desalination Water Treat. 2010, 16, 354–380. [Google Scholar] [CrossRef]
- Dahal, U.; Adhikari, N.P. Molecular dynamics study of diffusion of heavy water in normal water at different temperatures. J. Mol. Liq. 2012, 167, 34–39. [Google Scholar] [CrossRef]
- MathWorks; Matlab 9.7.0.1319299 (R2019b) Update 5; MathWorks: Natick, MA, USA, 2020.
- Sharma, V.; Nand, S.; Pramanik, S.; Chen, C.-Y.; Mishra, M. Control of radial miscible viscous fingering. J. Fluid Mech. 2020, 884, A16. [Google Scholar] [CrossRef]
- An, B.; Solorzano, D.; Yuan, Q. Viscous fingering dynamics and flow regimes of miscible displacements in a sealed Hele-Shaw cell. Energies 2022, 15, 5798. [Google Scholar] [CrossRef]




| Experiment | Discharge [mL/min] | Péclet Number | Figure |
|---|---|---|---|
| 1 | 60 | 320 | S1 |
| 2 | 30 | 160 | S2 |
| 3 | 15 | 80 | S3 |
| 4 | 7.5 | 40 | S4 |
| Image Analysis Method * | ||
|---|---|---|
| Binary | Morphological | |
| control | 6610 ± 150 | 6540 ± 202 |
| test | 6108 ± 654 | 6025 ± 728 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tigera, R.G.; Benson, W.L.; Mays, D.C. Thermally Enhanced Spreading of Miscible Plumes in Porous Media. Hydrology 2023, 10, 98. https://doi.org/10.3390/hydrology10040098
Tigera RG, Benson WL, Mays DC. Thermally Enhanced Spreading of Miscible Plumes in Porous Media. Hydrology. 2023; 10(4):98. https://doi.org/10.3390/hydrology10040098
Chicago/Turabian StyleTigera, Ryan G., Whitney L. Benson, and David C. Mays. 2023. "Thermally Enhanced Spreading of Miscible Plumes in Porous Media" Hydrology 10, no. 4: 98. https://doi.org/10.3390/hydrology10040098
APA StyleTigera, R. G., Benson, W. L., & Mays, D. C. (2023). Thermally Enhanced Spreading of Miscible Plumes in Porous Media. Hydrology, 10(4), 98. https://doi.org/10.3390/hydrology10040098







