The Combined Power of Double Mass Curves and Bias Correction for the Maximisation of the Accuracy of an Ensemble Satellite-Based Precipitation Estimate Product
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Description
2.1.1. Study Area
2.1.2. Gauge Rainfall Data
2.1.3. Satellite-Based Precipitation Estimate (SPE) Products
- (1)
- The Tropical Rainfall Measuring Mission (TRMM) was launched in November 1997 through a collaboration between the National Aeronautics and Space Administration (NASA) and the Japan Aerospace Exploration Agency (JAXA). TRMM is a low-earth-orbit satellite equipped with Precipitation Radar (PR), TRMM Microwave Imager (TMI), Visible and Infrared Sensor (VIRS), lightning imaging sensor (LIS), and the Earth’s Radiant Energy System (CERES) [49]. The TRMM Multi-satellite Precipitation Analysis (TMPA) products are the combination of infrared (IR) data from geostationary satellites and microwave (MW) data from multiple satellites. The TRMM-3B42 V7 3-hourly precipitation products cover the tropical and subtropical regions with a spatial resolution at 0.25 × 0.25 grid scale. There are four steps in creating the products. Step 1, the passive microwave field of view from different sources is calibrated and combined using algorithms such as sensor-specific versions of the Goddard Profiling Algorithm (GPROF). Step 2, the IR precipitation estimates are computed using the histogram matching of monthly MW precipitation estimates. Step 3, the MW and IR precipitation estimates are merged, with IR estimates being utilised to fill in the gap where MW estimates are missing. Rain gauge data are finally utilised to rescale and calibrate the merged precipitation estimates. TRMM-3B42RT product is originally evaluated to provide the near-real-time data and is then bias-corrected using monthly gauge rainfall data from the Global Precipitation Climatology Centre (GPCC) to generate the post-real-time data, TRMM-3B42 product [50,51,52]. The datasets of these two products were downloaded from NASA’s Goddard Space Flight Center website (https://disc2.gesdisc.eosdis.nasa.gov/data/, accessed on 1 April 2020) and utilised in this study.
- (2)
- Climate Hazards Group Infrared Precipitation (CHIRPS) and Climate Hazards Group Infrared Precipitation with stations (CHIRPS) were developed by the University of California Santa Barbara’s Climate Hazards Group to support the United States Agency for International Development Famine Early Warning Systems Network (FEWS NET) [26]. Four steps are involved in producing CHIRPS dataset. Firstly, Infrared Precipitation (IRP) pentad rainfall estimates are first generated using local regressions between TRMM 3B42V7 precipitation analysis pentads and cold cloud duration with a uniform threshold of 235 K. Secondly, the temporal component of IRP pentadal is converted to percentage anomalies and multiplied by the spatial component CHPClim pendatal to produce the Climate Hazards Group IR Precipitation (CHIRP)—the unbiased gridded estimate. The adjusted IRP is then combined with gauged rainfall data from Global Telecommunications System (GTS) and Conagua (Mexico) to create a rapid preliminary version (CHIRPS-PL) (2-day latency). Finally, a later final version (CHIRPS) is delivered within the third week of the following month by using extra gauged rainfall observations, mainly from the USA, Central America, South America, and sub-Saharan Africa [53,54,55,56]. CHIRPS-PL and CHIRPS were employed in this study and were downloaded from https://data.chc.ucsb.edu/products, accessed on 15 April 2020.
- (3)
- The National Oceanic and Atmospheric Administration (NOAA) Climate Prediction Centre MORPHing method (CMORPH) generates precipitation data by merging passive microwave-based precipitation estimates from multiple low-earth-orbit (LEO) satellites and the infrared data from multiple geostationary satellites [57]. CMORPH uses thermal IR temperatures to create the cloud systems advection vectors (CSAVs) to fill the gaps where temporal and spatial observations of MW-based rain rates are not available. The CSAVs are later applied to propagate MW-based rain rates in forward and backward directions between two successive MW overpasses using linear interpolation to morph the shape and intensity of the propagated rainfall pattern to produce CMORPH-RAW [27,58]. The CMORPH-CRT is produced by adjusting the CMORPH-RAW against the CPC unified daily gauge-based analysis over land and the pentad Global Precipitation Climatology Centre (GPCC) over the ocean using the probability density function bias correction procedure [59]. The CMORPH–CRT is additionally combined with the gauge analysis using the optimal interpolation technique to generate the CMORPH–BLD product [7]. CMORPH-BLD are available at https://ftp.cpc.ncep.noaa.gov/precip/CMORPH_V1.0/BLD/0.25deg-DLY_EOD/GLB/2015/201501/, accessed on 30 April 2020.
2.2. Methods
2.2.1. Validation of Gauged Rainfall Data Using the DMC Procedure
2.2.2. Effect of the Validity of Gauged Rainfall Data on Their Correlation with SPE
2.2.3. Usefulness of DMC
2.2.4. Pixel-Based Comparison of SPE Products
2.2.5. Bias Correction Procedure for SPE Products
- (1)
- Linear bias correction (LBC)
- (2)
- Bias correction using regression analysis (RABC)
- (3)
- Bias correction using distribution transformation (DTBC)
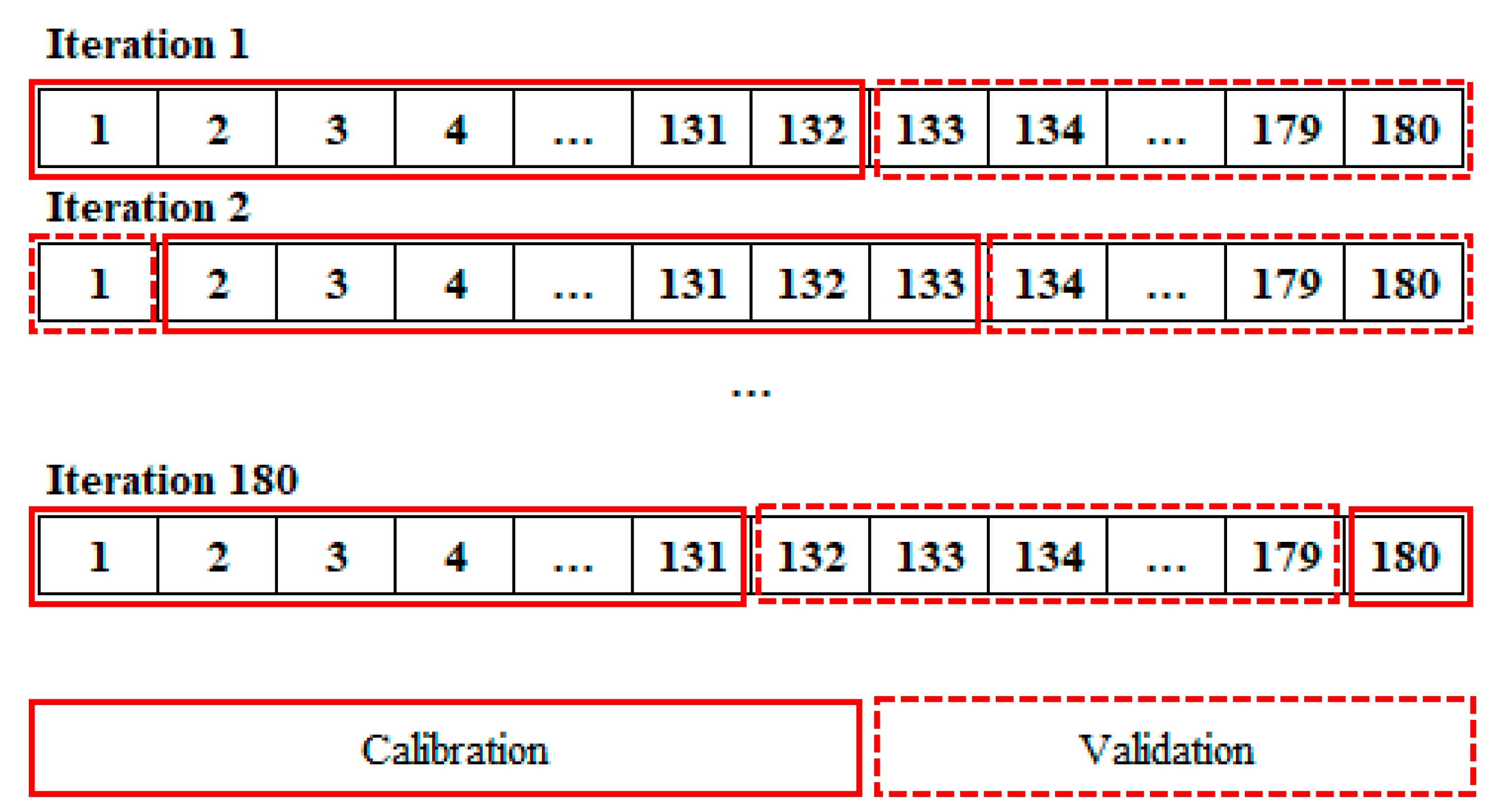
2.2.6. Cross-Validation of Bias Correction Procedures
3. Results and Discussion
3.1. Effect of Validity of Gauged Rainfall Data on Their Correlation with SPE Products
3.2. Usefulness of DMC
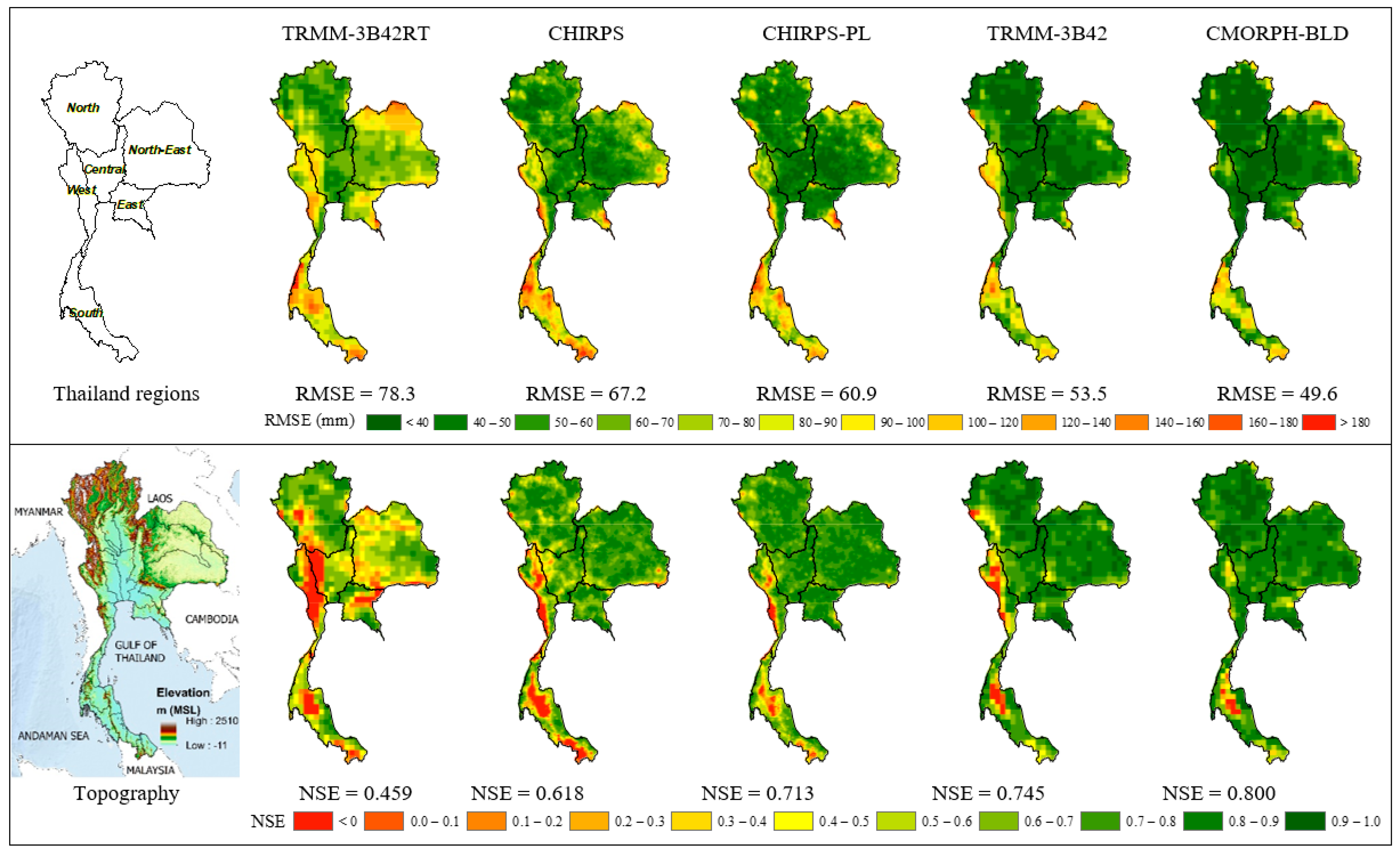
3.3. Pixel Based Comparison of SPE Products
3.4. Bias Correction of SPE Products
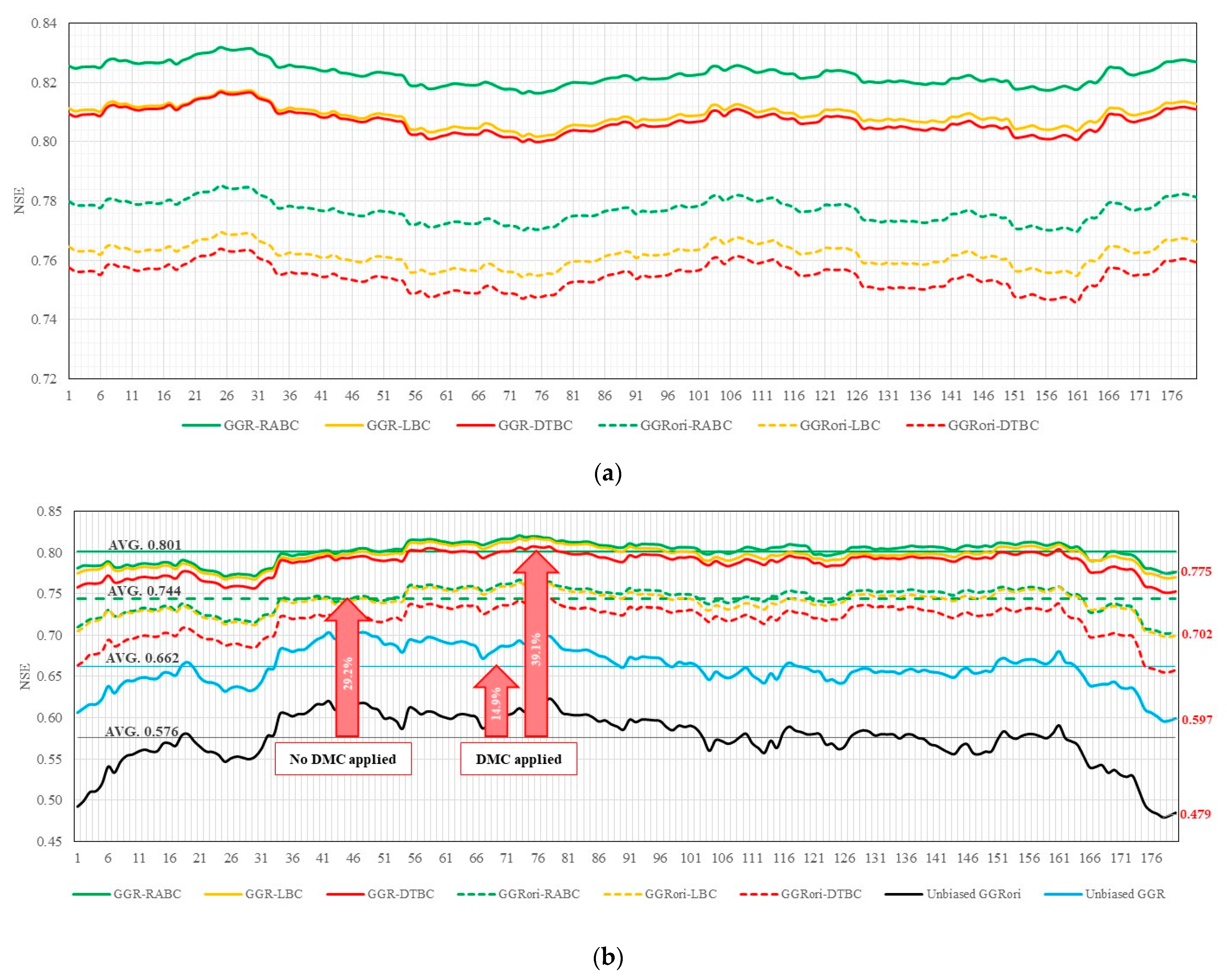
3.5. Ensemble Bias-Corrected SPE Products
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chappell, A.; Renzullo, L.J.; Raupach, T.H.; Haylock, M. Evaluating geostatistical methods of blending satellite and gauge data to estimate near real-time daily rainfall for Australia. J. Hydrol. 2013, 493, 105–114. [Google Scholar] [CrossRef]
- Taesombat, W.; Sriwongsitanon, N. Areal rainfall estimation using spatial interpolation techniques. Sci. Asia 2009, 35, 268–275. [Google Scholar] [CrossRef]
- Yoo, C. On the sampling errors from raingauges and microwave attenuation measurements. Stoch. Environ. Res. Risk Assess. 2000, 14, 69–77. [Google Scholar] [CrossRef]
- Dutton, M.; Jenkins, T.; Strangeways, I. A Heated Aerodynamic Universal Precipitation Gauge; World Meteorological Organization: Geneva, Switzerland, 2008; pp. 27–29. [Google Scholar]
- Ren, Z.; Li, M. Errors and correction of precipitation measurements in China. Adv. Atmos. Sci. 2007, 24, 449–458. [Google Scholar] [CrossRef]
- Sevruk, B. Adjustment of tipping-bucket precipitation gauge measurements. Atmos. Res. 1996, 42, 237–246. [Google Scholar] [CrossRef]
- Xie, P.; Xiong, A.Y. A conceptual model for constructing high-resolution gauge-satellite merged precipitation analyses. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Boushaki, F.I.; Hsu, K.-L.; Sorooshian, S.; Park, G.-H.; Mahani, S.; Shi, W. Bias adjustment of satellite precipitation estimation using ground-based measurement: A case study evaluation over the southwestern United States. J. Hydrometeorol. 2009, 10, 1231–1242. [Google Scholar] [CrossRef]
- Li, M.; Shao, Q. An improved statistical approach to merge satellite rainfall estimates and raingauge data. J. Hydrol. 2010, 385, 51–64. [Google Scholar] [CrossRef]
- Conti, F.L.; Hsu, K.-L.; Noto, L.V.; Sorooshian, S. Evaluation and comparison of satellite precipitation estimates with reference to a local area in the Mediterranean Sea. Atmos. Res. 2014, 138, 189–204. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, D.; Li, Z.; Mishra, A.K.; Wang, Y.; Yang, H. Multi-scale evaluation of six high-resolution satellite monthly rainfall estimates over a humid region in China with dense rain gauges. Int. J. Remote Sens. 2014, 35, 1272–1294. [Google Scholar] [CrossRef]
- Jiang, S.H.; Ren, L.L.; Yong, B.; Yang, X.L.; Shi, L. Evaluation of high-resolution satellite precipitation products with surface rain gauge observations from Laohahe Basin in northern China. Water Sci. Eng. 2010, 3, 405–417. [Google Scholar]
- Khan, S.I.; Hong, Y.; Gourley, J.J.; Khattak, M.U.K.; Yong, B.; Vergara, H.J. Evaluation of three high-resolution satellite precipitation estimates: Potential for monsoon monitoring over Pakistan. Adv. Space Res. 2014, 54, 670–684. [Google Scholar] [CrossRef]
- Awange, J.L.; Forootan, E. An evaluation of high-resolution gridded precipitation products over Bhutan (1998–2012). Int. J. Climatol. 2016, 36, 1067–1087. [Google Scholar]
- Liu, J.; Duan, Z.; Jiang, J.; Zhu, A. Evaluation of three satellite precipitation products TRMM 3B42, CMORPH, and PERSIANN over a subtropical watershed in China. Adv. Meteorol. 2015, 2015, 151239. [Google Scholar] [CrossRef]
- Mondal, A.; Lakshmi, V.; Hashemi, H. Intercomparison of trend analysis of multisatellite monthly precipitation products and gauge measurements for river basins of India. J. Hydrol. 2018, 565, 779–790. [Google Scholar] [CrossRef]
- Tan, M.L.; Ibrahim, A.L.; Duan, Z.; Cracknell, A.P.; Chaplot, V. Evaluation of six high-resolution satellite and ground-based precipitation products over Malaysia. Remote Sens. 2015, 7, 1504–1528. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Wang, Y.; Xie, P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.; Gao, B.; Jiao, Y.; Hong, Y.; Xu, T. Multiscale hydrologic applications of the latest satellite precipitation products in the Yangtze River Basin using a distributed hydrologic model. J. Hydrometeorol. 2015, 16, 407–426. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Gourley, J.J.; Huffman, G.J.; Tian, Y.; Cao, Q.; Yong, B.; Kirstetter, P.E.; Hu, J.; Hardy, J. Evaluation of the successive V6 and V7 TRMM multisatellite precipitation analysis over the Continental United States. Water Resour. Res. 2013, 49, 8174–8186. [Google Scholar] [CrossRef]
- Chen, Y.; Ebert, E.E.; Walsh, K.J.E.; Davidson, N.E. Evaluation of TRMM 3B42 precipitation estimates of tropical cyclone rainfall using PACRAIN data. J. Geophys. Res. Atmos. 2013, 118, 2184–2196. [Google Scholar] [CrossRef]
- Kirstetter, P.-E.; Hong, Y.; Gourley, J.J.; Schwaller, M.; Petersen, W.; Zhang, J. Comparison of TRMM 2A25 products, version 6 and version 7, with NOAA/NSSL ground radar–based National Mosaic QPE. J. Hydrometeorol. 2013, 14, 661–669. [Google Scholar] [CrossRef]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the Version-6 and Version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extremes? J. Hydrol. 2014, 508, 77–87. [Google Scholar]
- Xue, X.; Hong, Y.; Limaye, A.S.; Gourley, J.J.; Huffman, G.J.; Khan, S.I.; Dorji, C.; Chen, S. Statistical and hydrological evaluation of TRMM-based Multi-satellite Precipitation Analysis over the Wangchu Basin of Bhutan: Are the latest satellite precipitation products 3B42V7 ready for use in ungauged basins? J. Hydrol. 2013, 499, 91–99. [Google Scholar] [CrossRef]
- Zulkafli, Z.; Buytaert, W.; Onof, C.; Manz, B.; Tarnavsky, E.; Lavado, W.; Guyot, J.-L. A comparative performance analysis of TRMM 3B42 (TMPA) versions 6 and 7 for hydrological applications over Andean–Amazon river basins. J. Hydrol. 2014, 15, 581–592. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Duan, Z.; Liu, J.; Tuo, Y.; Chiogna, G.; Disse, M. Evaluation of eight high spatial resolution gridded precipitation products in Adige Basin (Italy) at multiple temporal and spatial scales. Sci. Total Environ. 2016, 573, 1536–1553. [Google Scholar] [CrossRef]
- Poortinga, A.; Bastiaanssen, W.; Simons, G.; Saah, D.; Senay, G.; Fenn, M.; Bean, B.; Kadyszewski, J. A self-calibrating runoff and streamflow remote sensing model for ungauged basins using open-access earth observation data. Remote Sens. 2017, 9, 86. [Google Scholar] [CrossRef]
- Simons, G.; Bastiaanssen, W.; Ngo, L.A.; Hain, C.R.; Anderson, M.; Senay, G. Integrating global satellite-derived data products as a pre-analysis for hydrological modelling studies: A case study for the Red River Basin. Remote Sens. 2016, 8, 279. [Google Scholar] [CrossRef]
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901–present. Earth Syst. Sci. Data 2013, 5, 71–99. [Google Scholar] [CrossRef]
- Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef]
- Habib, E.; Haile, A.T.; Sazib, N.; Zhang, Y.; Rientjes, T. Effect of Bias Correction of Satellite-Rainfall Estimates on Runoff Simulations at the Source of the Upper Blue Nile. Remote Sens. 2014, 6, 6688–6708. [Google Scholar] [CrossRef]
- Tesfagiorgis, K.; Mahani, S.E.; Krakauer, N.Y.; Khanbilvardi, R. Bias correction of satellite rainfall estimates using a radar-gauge product – a case study in Oklahoma (USA). Hydrol. Earth Syst. Sci. 2011, 15, 2631–2647. [Google Scholar] [CrossRef]
- Bouwer, L.M.; Aerts, J.C.; Van de Coterlet, G.M.; Van de Giesen, N.; Gieske, A.; Mannaerts, C. Evaluating Downscaling Methods for Preparing Global Circulation Model (GCM) Data for Hydrological Impact Modeling. Climate Change in Contrasting River Basins; CAB International Publishing: London, UK, 2004. [Google Scholar]
- Phoeurn, C.; Ly, S. Assessment of satellite rainfall estimates as a pre-analysis for water environment analytical tools: A case study for Tonle Sap Lake in Cambodia. Eng. J. 2018, 22, 229–241. [Google Scholar] [CrossRef]
- Cheema, M.J.M.; Bastiaanssen, W.G.M. Local calibration of remotely sensed rainfall from the TRMM satellite for different periods and spatial scales in the Indus Basin. Int. J. Remote Sens. 2012, 33, 2603–2627. [Google Scholar] [CrossRef]
- Shrestha, M.S. Bias-Adjustment of Satellite-Based Rainfall Estimates over the Central Himalayas of Nepal for Flood Prediction; Kyoto University: Kyoto, Japan, 2011. [Google Scholar]
- Yin, Z.-Y.; Zhang, X.; Liu, X.; Colella, M.; Chen, X. An assessment of the biases of satellite rainfall estimates over the Tibetan Plateau and correction methods based on topographic analysis. J. Hydrol. 2008, 9, 301–326. [Google Scholar] [CrossRef]
- Searcy, J.K.; Hardison, C.H. Double-Mass Curves; US Government Printing Office: Washington, DC, USA, 1960.
- Elgamal, A.; Reggiani, P.; Jonoski, A. Impact analysis of satellite rainfall products on flow simulations in the Magdalena River Basin, Colombia. J. Hydrol. Reg. Stud. 2017, 9, 85–103. [Google Scholar] [CrossRef]
- Gumindoga, W.; Rientjes, T.H.M.; Haile, A.T.; Makurira, H.; Reggiani, P. Bias correction schemes for CMORPH satellite rainfall estimates in the Zambezi River Basin. Hydrol. Earth Syst. Sci. Discuss. 2016, 33, 1–36. [Google Scholar]
- RØHr, P.C.; Killingtveit, Å. Rainfall distribution on the slopes of Mt Kilimanjaro. Hydrol. Sci. J. 2003, 48, 65–77. [Google Scholar] [CrossRef]
- Gao, P.; Geissen, V.; Ritsema, C.J.; Mu, X.M.; Wang, F. Impact of climate change and anthropogenic activities on stream flow and sediment discharge in the Wei River basin, China. Hydrol. Earth Syst. Sci. 2013, 17, 961. [Google Scholar] [CrossRef]
- Gao, P.; Mu, X.M.; Wang, F.; Li, R. Changes in streamflow and sediment discharge and the response to human activities in the middle reaches of the Yellow River. Hydrol. Earth Syst. Sci. 2011, 15, 1. [Google Scholar] [CrossRef]
- Hindall, S.M. Temporal trends in fluvial-sediment discharge in Ohio, 1950–1987. J. Soil Water Conserv. 1991, 46, 311–313. [Google Scholar]
- Yang, S.-l.; Zhao, Q.-y.; Belkin, I.M. Temporal variation in the sediment load of the Yangtze River and the influences of human activities. J. Hydrol. 2002, 263, 56–71. [Google Scholar] [CrossRef]
- Rutledge, A.T. Use of Double-Mass Curves to Determine Drawdown in a Long-Term Aquifer Test in North-Central Volusia County, Florida; US Department of the Interior, Geological Survey: Reston, Virginia, 1985; Volume 84.
- Alansi, A.W.; Amin, M.S.M.; Abdul Halim, G.; Shafri, H.Z.M.; Thamer, A.M.; Waleed, A.R.M.; Aimrun, W.; Ezrin, M.H. The effect of development and land use change on rainfall-runoff and runoff-sediment relationships under humid tropical condition: Case study of Bernam watershed Malaysia. Eur. J. Sci. Res. 2009, 31, 88–105. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kim, K.; Park, J.; Baik, J.; Choi, M. Evaluation of topographical and seasonal feature using GPM IMERG and TRMM 3B42 over Far-East Asia. Atmos. Res. 2017, 187, 95–105. [Google Scholar] [CrossRef]
- Satgé, F.; Xavier, A.; Pillco Zolá, R.; Hussain, Y.; Timouk, F.; Garnier, J.; Bonnet, M.-P. Comparative assessments of the latest GPM mission’s spatially enhanced satellite rainfall products over the main Bolivian watersheds. Remote Sens. 2017, 9, 369. [Google Scholar] [CrossRef]
- Yang, X.; Lu, Y.; Tan, M.L.; Li, X.; Wang, G.; He, R. Nine-Year systematic evaluation of the GPM and TRMM precipitation products in the Shuaishui river basin in East-Central China. Remote Sens. 2020, 12, 1042. [Google Scholar] [CrossRef]
- Bai, L.; Shi, C.; Li, L.; Yang, Y.; Wu, J. Accuracy of CHIRPS satellite-rainfall products over mainland China. Remote Sens. 2018, 10, 362. [Google Scholar] [CrossRef]
- Belay, A.S.; Fenta, A.A.; Yenehun, A.; Nigate, F.; Tilahun, S.A.; Moges, M.M.; Dessie, M.; Adgo, E.; Nyssen, J.; Chen, M. Evaluation and application of multi-source satellite rainfall product CHIRPS to assess spatio-temporal rainfall variability on data-sparse western margins of Ethiopian highlands. Remote Sens. 2019, 11, 2688. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Saeidizand, R.; Sabetghadam, S.; Tarnavsky, E.; Pierleoni, A. Evaluation of CHIRPS rainfall estimates over Iran. Q. J. R. Meteorol. Soc. 2018, 144, 282–291. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Haile, A.T.; Habib, E.; Rientjes, T. Evaluation of the climate prediction center (CPC) morphing technique (CMORPH) rainfall product on hourly time scales over the source of the Blue Nile River. Hydrol. Process. 2013, 27, 1829–1839. [Google Scholar] [CrossRef]
- Xie, P.; Joyce, R.; Wu, S. A 15-year high-resolution gauge-satellite merged analysis of precipitation. In Proceedings of the 27th Conference on Hydrology B, Raleigh, NC, USA, 26–27 August 2013. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Al-Dousari, A.; Ramdan, A.; Al Ghadban, A. Site-specific precipitation estimate from TRMM data using bilinear weighted interpolation technique: An example from Kuwait. J. Arid. Environ. 2008, 72, 1320–1328. [Google Scholar]
- Omotosho, T.V.; Oluwafemi, C.O. One-minute rain rate distribution in Nigeria derived from TRMM satellite data. J. Atmos. Sol. -Terr. Phys. 2009, 71, 625–633. [Google Scholar] [CrossRef]
- Kotu, V.; Deshpande, B. Data science: Concepts and Practice; Morgan Kaufmann: Burlington, MA, USA, 2018. [Google Scholar]




| SPE Product | Gauged Observation | Temporal Resolution | Spatial Resolution | Temporal Coverage | Spatial Coverage | Latency | Data Source |
|---|---|---|---|---|---|---|---|
| TRMM-3B42 V7 | GPCC | 3 h | 0.25 × 0.25° | 1998–2019 | 50° S–50° N | 2 months | https://disc2.gesdisc.eosdis.nasa.gov/data/TRMM_L3/TRMM_3B42_Daily.7/2015/01/ Accessed on 1 April 2020 |
| TRMM-3B42RT V7 | - | 3 h | 0.25 × 0.25° | 1998–2019 | 50° S–50° N | 8 h | https://disc2.gesdisc.eosdis.nasa.gov/data/TRMM_RT/TRMM_3B42RT_Daily.7/2015/01/ Accessed on 1 April 2020 |
| CHIRPS-PL V2.0 | GTS and Conagua | 2 days | 0.05 × 0.05° | 1981–2015 | 50° S–50° N | 1 week | https://data.chc.ucsb.edu/products/CHIRPS-2.0/prelim/global_monthly/tifs/ Accessed on 15 April 2020 |
| CHIRPS V2.0 | GPCC, GTS, and Conagua | 1 day | 0.05 × 0.05° | 1981– present | 50° S–50° N | 3 weeks | https://data.chc.ucsb.edu/products/CHIRPS-2.0/global_monthly/tifs/ Accessed on 15 April 2020 |
| CMORPH-BLD V1.0 | CPC unified daily gauge analysis, GPCC | 1 day | 0.25 × 0.25° | 1998– present | 60° S–60° N | 2 months | https://ftp.cpc.ncep.noaa.gov/precip/CMORPH_V1.0/BLD/0.25deg-DLY_EOD/GLB/2015/201501/ Accessed on 30 April 2020 |
| NSE Threshold | N | Discarded Data (%) | Double Mass Curve | TRMM-3B42 | TRMM-3B43RT | CHIRPS | CHIRPS-PL | CMORPH-BLD | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NSE (Original) | NSE (After) | NSE (Original) | NSE (After) | NSE (Original) | NSE (After) | NSE (Original) | NSE (After) | NSE (Original) | NSE (After) | NSE (Original) | NSE (After) | |||
| Original | 1779 | 0.00 | 0.758 | - | 0.575 | - | 0.354 | - | 0.512 | - | 0.608 | - | 0.612 | - |
| 0.60 | 1778 | 0.51 | 0.758 | 0.783 | 0.575 | 0.603 | 0.355 | 0.421 | 0.513 | 0.565 | 0.608 | 0.624 | 0.612 | 0.640 |
| 0.65 | 1776 | 0.85 | 0.758 | 0.790 | 0.576 | 0.604 | 0.355 | 0.421 | 0.513 | 0.566 | 0.608 | 0.628 | 0.613 | 0.643 |
| 0.70 | 1774 | 1.38 | 0.758 | 0.801 | 0.576 | 0.610 | 0.356 | 0.425 | 0.514 | 0.569 | 0.609 | 0.630 | 0.613 | 0.647 |
| 0.75 | 1764 | 2.39 | 0.759 | 0.817 | 0.581 | 0.616 | 0.361 | 0.427 | 0.519 | 0.569 | 0.612 | 0.636 | 0.618 | 0.652 |
| 0.80 | 1755 | 4.11 | 0.760 | 0.839 | 0.584 | 0.621 | 0.364 | 0.431 | 0.521 | 0.580 | 0.612 | 0.642 | 0.619 | 0.662 |
| 0.81 | 1752 | 4.96 | 0.761 | 0.845 | 0.584 | 0.621 | 0.364 | 0.429 | 0.522 | 0.579 | 0.613 | 0.644 | 0.620 | 0.662 |
| 0.82 | 1751 | 5.51 | 0.761 | 0.851 | 0.585 | 0.620 | 0.364 | 0.432 | 0.522 | 0.577 | 0.613 | 0.645 | 0.620 | 0.665 |
| 0.83 | 1746 | 6.21 | 0.761 | 0.857 | 0.586 | 0.622 | 0.365 | 0.433 | 0.523 | 0.577 | 0.613 | 0.648 | 0.621 | 0.662 |
| 0.84 | 1743 | 6.95 | 0.761 | 0.863 | 0.586 | 0.625 | 0.365 | 0.432 | 0.524 | 0.578 | 0.614 | 0.651 | 0.622 | 0.663 |
| 0.85 | 1733 | 7.29 | 0.761 | 0.869 | 0.587 | 0.624 | 0.366 | 0.430 | 0.525 | 0.576 | 0.615 | 0.653 | 0.623 | 0.664 |
| 0.90 | 1699 | 13.76 | 0.761 | 0.909 | 0.590 | 0.617 | 0.371 | 0.417 | 0.529 | 0.577 | 0.616 | 0.663 | 0.626 | 0.668 |
| 0.95 | 1605 | 27.21 | 0.763 | 0.953 | 0.597 | 0.616 | 0.378 | 0.412 | 0.539 | 0.572 | 0.619 | 0.666 | 0.632 | 0.673 |
| 1 | 432 | 80.74 | 0.777 | 1.000 | 0.557 | 0.479 | 0.326 | 0.482 | 0.477 | 0.451 | 0.578 | 0.467 | 0.591 | 0.538 |
| Region | Code | Basin | Number of Station | DMC | Random Removal | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Discard (%) | Density (km2/St.) | Reducing RMSE (mm) | St. | Remove (%) | Density (km2/St.) | Increasing RMSE (mm) | ||||
| North | 06 | Ping | 101 | 4.9 | 331.7 | 10.8 | 11 | 10.9 | 367.0 | 10.6 |
| 02N | Khong | 22 | 2.7 | 477.8 | 13.7 | 3 | 13.6 | 528.1 | 12.9 | |
| 08 | Yom | 49 | 5.9 | 479.0 | 16.1 | 16 | 32.7 | 684.2 | 16.9 | |
| 07 | Wang | 21 | 4.0 | 539.7 | 11.3 | 5 | 23.8 | 674.6 | 10.7 | |
| 09 | Nan | 63 | 4.5 | 545.4 | 10.8 | 13 | 20.6 | 671.3 | 10.6 | |
| 03 | Kok | 14 | 5.8 | 561.5 | 14.6 | 3 | 21.4 | 663.6 | 12.0 | |
| 01 | Salawin | 13 | 5.0 | 1592.2 | 23.0 | 4 | 30.8 | 2122.9 | 24.8 | |
| Central | 10 | Chao Phraya | 254 | 4.9 | 78.9 | 10.1 | 47 | 18.5 | 96.0 | 10.1 |
| 12 | Pasak | 120 | 10.4 | 129.1 | 28.1 | 93 | 77.5 | 538.7 | 28.2 | |
| 13 | Tha Chin | 77 | 5.5 | 173.0 | 4.4 | 10 | 13.0 | 195.5 | 4.5 | |
| 11 | Sakae Krang | 18 | 3.8 | 297.4 | 10.8 | 5 | 27.8 | 388.9 | 9.6 | |
| North-East | 04 | Chi | 163 | 5.7 | 299.6 | 19.5 | 70 | 42.9 | 517.2 | 19.6 |
| 05 | Mun | 190 | 5.1 | 370.2 | 15.6 | 59 | 31.1 | 530.4 | 15.5 | |
| 02NE | Khong | 123 | 3.6 | 383.4 | 20.1 | 38 | 30.9 | 548.3 | 20.6 | |
| East | 16 | Bang Pakong | 51 | 7.2 | 209.8 | 12.4 | 15 | 29.4 | 289.2 | 12.9 |
| 18 | East Coast Gulf | 46 | 8.3 | 284.6 | 22.0 | 11 | 23.9 | 363.7 | 20.9 | |
| 15 | Phachinburi | 27 | 5.8 | 372.0 | 20.7 | 10 | 37.0 | 568.9 | 21.6 | |
| 17 | Tonle sap | 8 | 13.8 | 583.7 | 35.0 | 6 | 75.0 | 2043.0 | 37.2 | |
| West | 19 | Phetchaburi | 35 | 4.4 | 178.9 | 3.4 | 5 | 14.3 | 201.9 | 4.0 |
| 20 | Prachuapkhiri- Khan Coast | 23 | 8.6 | 310.1 | 5.5 | 5 | 21.7 | 375.4 | 6.1 | |
| 14 | Mae Klong | 65 | 5.8 | 471.6 | 19.8 | 19 | 29.2 | 656.1 | 19.8 | |
| South | 23 | Thale Sap Songkhla | 59 | 8.7 | 146.2 | 8.4 | 9 | 15.3 | 169.6 | 8.4 |
| 21 | Peninsula-East Coast | 97 | 14.3 | 255.6 | 19.5 | 20 | 20.6 | 314.1 | 19.2 | |
| 25 | Peninsula-West Coast | 72 | 13.5 | 260.8 | 26.1 | 25 | 34.7 | 391.2 | 26.9 | |
| 24 | Pattani | 10 | 27.0 | 365.5 | 25.3 | 6 | 60.0 | 731.0 | 25.8 | |
| 22 | Tapi | 22 | 24.7 | 589.6 | 16.4 | 6 | 27.3 | 753.4 | 15.7 | |
| Summation/Average | 1743 | 6.95 | 395.7 | 16.3 | 514 | 30.2 | 591.7 | 16.3 | ||
| Region | Indicator | TRMM-3B42RT | CHIRPS | CHIRPS-PL | TRMM-3B42 | CMORPH-BLD |
|---|---|---|---|---|---|---|
| Central | RMSE (mm) | 67.2 | 52.3 | 44.3 | 39.4 | 37.7 |
| NSE | 0.393 | 0.655 | 0.760 | 0.797 | 0.817 | |
| North | RMSE (mm) | 61.3 | 54.6 | 51.5 | 43.3 | 39.7 |
| NSE | 0.621 | 0.720 | 0.761 | 0.795 | 0.852 | |
| West | RMSE (mm) | 90.8 | 83.6 | 70.0 | 75.0 | 47.8 |
| NSE | −0.028 | 0.151 | 0.435 | 0.366 | 0.749 | |
| North-East | RMSE (mm) | 80.6 | 60.6 | 56.1 | 49.6 | 49.8 |
| NSE | 0.525 | 0.746 | 0.790 | 0.824 | 0.829 | |
| East | RMSE (mm) | 79.2 | 63.1 | 60.4 | 48.8 | 50.2 |
| NSE | 0.488 | 0.736 | 0.780 | 0.820 | 0.806 | |
| South | RMSE (mm) | 108.7 | 112.5 | 99.3 | 84.0 | 80.0 |
| NSE | 0.304 | 0.299 | 0.525 | 0.603 | 0.634 | |
| Thailand | RMSE (mm) | 78.3 | 67.2 | 60.9 | 53.5 | 49.6 |
| NSE | 0.459 | 0.618 | 0.713 | 0.745 | 0.800 |
| SPE Product | Rainfall Dataset | BC Method | Bias Correction (BC) | NSE Improvements (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Raw (GGRori) | DMC-Corrected (GGR) | Calibration | Validation | Provided by BC to: | Overall (DMC + BC) | |||||
| GGRori | GGR | GGRori | GGR | GGRori | GGR | |||||
| CMORPH-BLD | 0.710 | 0.792 (11.5%) | RABC | 0.812 | 0.862 | 0.782 | 0.843 | 10.1 | 6.5 | 18.7 |
| LBC | 0.802 | 0.854 | 0.783 | 0.842 | 10.2 | 6.4 | 18.6 | |||
| DTBC | 0.797 | 0.853 | 0.764 | 0.836 | 7.6 | 5.7 | 17.7 | |||
| TRMM- 3B42 | 0.639 | 0.728 (13.9%) | RABC | 0.811 | 0.859 | 0.780 | 0.839 | 22.1 | 15.2 | 31.3 |
| LBC | 0.800 | 0.850 | 0.783 | 0.841 | 22.5 | 15.4 | 31.6 | |||
| DTBC | 0.796 | 0.850 | 0.764 | 0.835 | 19.6 | 14.6 | 30.7 | |||
| CHIRPS | 0.525 | 0.622 (18.5%) | RABC | 0.768 | 0.815 | 0.736 | 0.793 | 40.2 | 27.6 | 51.2 |
| LBC | 0.754 | 0.802 | 0.734 | 0.790 | 39.9 | 27 | 50.5 | |||
| DTBC | 0.744 | 0.798 | 0.706 | 0.777 | 34.6 | 24.9 | 48 | |||
| CHIRPS-PL | 0.667 | 0.740 (10.9%) | RABC | 0.762 | 0.809 | 0.729 | 0.787 | 9.4 | 6.4 | 18 |
| LBC | 0.742 | 0.790 | 0.719 | 0.776 | 7.8 | 4.9 | 16.3 | |||
| DTBC | 0.737 | 0.791 | 0.698 | 0.770 | 4.7 | 4.1 | 15.4 | |||
| TRMM- 3B42RT | 0.337 | 0.430 (27.6%) | RABC | 0.728 | 0.767 | 0.690 | 0.740 | 104.7 | 72.3 | 119.6 |
| LBC | 0.707 | 0.747 | 0.681 | 0.729 | 102 | 69.7 | 116.3 | |||
| DTBC | 0.696 | 0.741 | 0.654 | 0.716 | 93.8 | 66.6 | 112.5 | |||
| Average | 0.576 | 0.662 (14.9%) | RABC | 0.776 | 0.822 | 0.744 | 0.801 | 29.2 | 20.9 | 39.1 |
| LBC | 0.761 | 0.808 | 0.740 | 0.796 | 28.5 | 20.1 | 38.2 | |||
| DTBC | 0.754 | 0.807 | 0.717 | 0.787 | 24.6 | 18.8 | 36.7 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sriwongsitanon, N.; Kaprom, C.; Tantisuvanichkul, K.; Prasertthonggorn, N.; Suiadee, W.; Bastiaanssen, W.G.M.; Williams, J.A. The Combined Power of Double Mass Curves and Bias Correction for the Maximisation of the Accuracy of an Ensemble Satellite-Based Precipitation Estimate Product. Hydrology 2023, 10, 154. https://doi.org/10.3390/hydrology10070154
Sriwongsitanon N, Kaprom C, Tantisuvanichkul K, Prasertthonggorn N, Suiadee W, Bastiaanssen WGM, Williams JA. The Combined Power of Double Mass Curves and Bias Correction for the Maximisation of the Accuracy of an Ensemble Satellite-Based Precipitation Estimate Product. Hydrology. 2023; 10(7):154. https://doi.org/10.3390/hydrology10070154
Chicago/Turabian StyleSriwongsitanon, Nutchanart, Chanphit Kaprom, Kamonpat Tantisuvanichkul, Nattakorn Prasertthonggorn, Watchara Suiadee, Wim G. M. Bastiaanssen, and James Alexander Williams. 2023. "The Combined Power of Double Mass Curves and Bias Correction for the Maximisation of the Accuracy of an Ensemble Satellite-Based Precipitation Estimate Product" Hydrology 10, no. 7: 154. https://doi.org/10.3390/hydrology10070154
APA StyleSriwongsitanon, N., Kaprom, C., Tantisuvanichkul, K., Prasertthonggorn, N., Suiadee, W., Bastiaanssen, W. G. M., & Williams, J. A. (2023). The Combined Power of Double Mass Curves and Bias Correction for the Maximisation of the Accuracy of an Ensemble Satellite-Based Precipitation Estimate Product. Hydrology, 10(7), 154. https://doi.org/10.3390/hydrology10070154






