A Review on Storage Process Models for Improving Water Quality Modeling in Rivers

Abstract

Water quality is intricately linked to the global water crisis since the availability of safe, clean water is essential for sustaining life and ensuring the well-being of communities worldwide. Pollutants such as industrial chemicals, agricultural runoff, and untreated sewage frequently enter rivers via surface runoff or direct discharges. This study provides an overview of the key mechanisms governing contaminant transport in rivers, with special attention to storage and hyporheic processes. The storage process conceptualizes a ubiquitous reactive boundary between the main channel (mobile zone) and its surrounding slower-flow areas (immobile zone). Research from the last five decades demonstrates the crucial role of storage and hyporheic zones in influencing solute residence time, nutrient cycling, and pollutant degradation. A review of solute transport models highlights significant advancements, including models like the transient storage model (TSM) and multirate mass transport (MRMT) model, which effectively capture complex storage zone dynamics and residence time distributions. However, more widely used models like the classical advection–dispersion equation (ADE) cannot hyporheic exchange, limiting their application in environments with significant storage contributions. Despite these advancements, challenges remain in accurately quantifying the relative contributions of storage zones to solute transport and degradation, especially in smaller streams dominated by hyporheic exchange. Future research should integrate detailed field observations with advanced numerical models to address these gaps and improve water quality predictions across diverse river systems.

1. Introduction

Contaminant transport in rivers worsens water scarcity by reducing the availability of clean and safe water. As pollutants accumulate, water treatment becomes more challenging and costly. This, in turn, increases the pressure on limited water resources and contributes to the overall water crisis [1]. Streams are exposed to contaminants from both point and nonpoint sources due to increasing climate and land use changes. Pollutants degrade surface water and groundwater quality, threatening the ecological functions of streams [2,3]. Streams were once seen mainly as drainage routes. However, continuous water exchange among main flow, sediments, riparian zones, floodplain areas, and groundwater has been known to occur [4]. Tracer tests highlight the relative influences of various factors on the fate of solutes and pollutants [5].

Contaminants spread vertically, laterally, and longitudinally, interacting with slower-flowing waters around a river. This interaction slows the movement of suspended and dissolved matter, providing more opportunities for geochemical and biological processing [6]. Specialists managing or studying rivers must evaluate the relative significance of important processes influencing pollution transport, including advection, dispersion, transient storage, and chemical (or biochemical) reactions [7,8]. Advection refers to the bulk movement of pollutants in a stream by the average flow velocity, from the source to downstream areas [9]. The dispersion mechanism, driven by velocity profile gradients, affects the spatial pattern of the pollution plume [10]. Storage processes represent the influence of slower in-stream and near-stream areas like lateral pools, woody debris, hyporheic zones, eddies, boulders, riparian vegetation, and stagnant zones [11].

Dead or stagnant zones form near concave banks and behind dunes, separated from the main streamflow. They are considered in the calculation of the mean stream cross-section but reduce the effective flow area [12,13]. Hyporheic exchange is a spatiotemporally variable interface between the surface and groundwater, which increases solute residence time in streams, allowing for their adsorption and storage [14,15]. Storage zones are shown in Figure 1. This illustration highlights the major storage processes, including hyporheic exchange, lateral cavity formation, and dead zones. Hyporheic zones represent the regions of subsurface water flow that interact with stream water, enhancing solute retention and residence time. Lateral cavities and dead zones along the stream bank slow water movement and act as transient storage areas, facilitating further biogeochemical reactions and pollutant transformation before the solutes re-enter the main flow. Advection–dispersion occurs mainly in the riffle section, while stagnant zones facilitate mass exchange with the main flow. Storage processes lead to skewness and tail in natural streams’ observed solute breakthrough curves (BTCs) [16].

In-stream storage zones play a critical role in regulating hydro-biogeochemical processes. For instance, hyporheic zones promote nutrient cycling by facilitating interactions between microbial communities and organic matter within sediments. These interactions support microbial respiration and denitrification, directly affecting nitrogen and carbon fluxes. Lateral cavities and dead zones serve as active sites for biogeochemical reactions, where extended residence times enable a further transformation of pollutants through microbial degradation, nitrification, and phosphorus adsorption. Together, these processes contribute to enhanced water quality as solutes undergo various physical, chemical, and biological modifications before returning to the main channel [17,18].

Determining the relationship among stream-related processes, especially storage mechanisms, and physical stream conditions to understand ecological functioning has been the focus of recent research [19] while also considering nutrient cycling [20], hydrological characteristics [21], and geomorphological settings [22]. As a result, researchers have developed various models with different mathematical and physical concepts to represent the impacts of stream-related processes on solute transport in river systems [23]. The classic advection–dispersion equation (ADE) is a widely used model to simulate the fate and transport of conservative pollution. New models have been developed by adding additional equations, terms, and parameters [24,25].

Objectives:

The current review aims to conduct the following:

• Summarize the key physical and chemical processes influencing solute transport in rivers, with particular attention to storage mechanisms and hyporheic exchange.
• Review and compare the current mathematical models used to simulate solute transport, highlighting how they incorporate storage processes.
• Identify gaps in existing research, particularly in the role of storage processes in ecosystem functions, and propose future directions for enhancing water quality modeling.

Over the past few decades, a major focus of hydrologic research has been on gaining a better understanding of the fundamental physical drivers of solute transport, with a particular emphasis on storage and hyporheic zones [26]. The present study provides an overview of the current understanding of solute transport processes in rivers. Findings of more than 150 journal papers were synthesized from previous studies to summarize the key aspect of the storage process. “Storage Zone”, “Hyporheic Zone”, and “Solute Transport” are the main keywords used to find articles in databases. This study illustrates the critical importance of solute transport processes considering storage zones and their role in ecosystem functions. It highlights significant knowledge gaps regarding existing physical processes.

2. Advection–Dispersion Equation

A fundamental model used to quantify solute transport is the advection–dispersion equation. Since the 1970s, the classical advection–dispersion equation has been the standard model for channel solute transport [27]. It was initially presented to describe transport in pipelines [28,29]. The classical advection–dispersion equation for solute concentration is as follows.

$${\displaystyle \frac{\partial C}{\partial t}}=-U{\displaystyle \frac{\partial C}{\partial x}}+D{\displaystyle \frac{{\partial }^{2}C}{\partial x^2}}$$

(1)

where t is time [T], x is the distance [L], C is the solute concentration in the stream [ML⁻³], D is the longitudinal dispersion coefficient [L²T⁻¹], and U is the cross-sectional mean flow velocity [LT⁻¹]. The ADE was the initial model applied to study the mixing of solutes in rivers without incorporating solute residence in storage and hyporheic zones [30]. The dispersion coefficient results primarily from transverse and vertical velocity gradients, whereas turbulent diffusion and molecular diffusion are typically negligible [31]. The longitudinal dispersion coefficient in natural streams can vary significantly based on flow conditions, river discharge, and hydrodynamic factors. The coefficient can range from approximately 10⁻¹ m²/s to 10³ m²/s, with larger values observed in rivers with higher discharges and complex channel structures [32,33]. In contrast, turbulent diffusion and molecular diffusion have lower values, on the order of 10⁻² and 10⁻⁹ m²/s, respectively [34,35]. Based on the hydraulic conditions, turbulent diffusion may vary in the range of [10⁻³–1] m²/s [35].

In streams, the influence of vertical velocity gradients on longitudinal dispersion is negligible relative to that of transverse velocity gradients. Tracer tests are an important technique for measuring physical transport and processes. Their most basic application is to inject an instantaneous or constant-rate injection of a conservative (non-reactive) tracer compound at an upstream point and monitor its breakthrough over time at downstream stations [36]. Estimating the longitudinal dispersion coefficient in rivers using the related relationships or models derived from tracer studies is one of the most reliable approaches for practical applications [37,38,39]. While estimating the longitudinal dispersion coefficient through tracer studies provides valid values for the specific conditions during experimentation [40], this approach has limitations. Many researchers have related the coefficient to hydrodynamic and geomorphological parameters, developing empirical formulas [41]. However, these relationships calculate dispersion using average flow conditions and can generate very different coefficient values between formulas [42]. Overall, these empirical relationships are only accurate within their validated range, often failing outside of it. Methodologies used to assess formulas include a comparison of indices and benchmarks, parametric analysis, evaluating the extent of validity, moment and fitting methods, and sensitivity and uncertainty analysis [43]. In summary, while tracer studies provide localized dispersion values, empirical formulas relate to averaged conditions and have limited validity ranges. Multiple methods help evaluate formula accuracy.

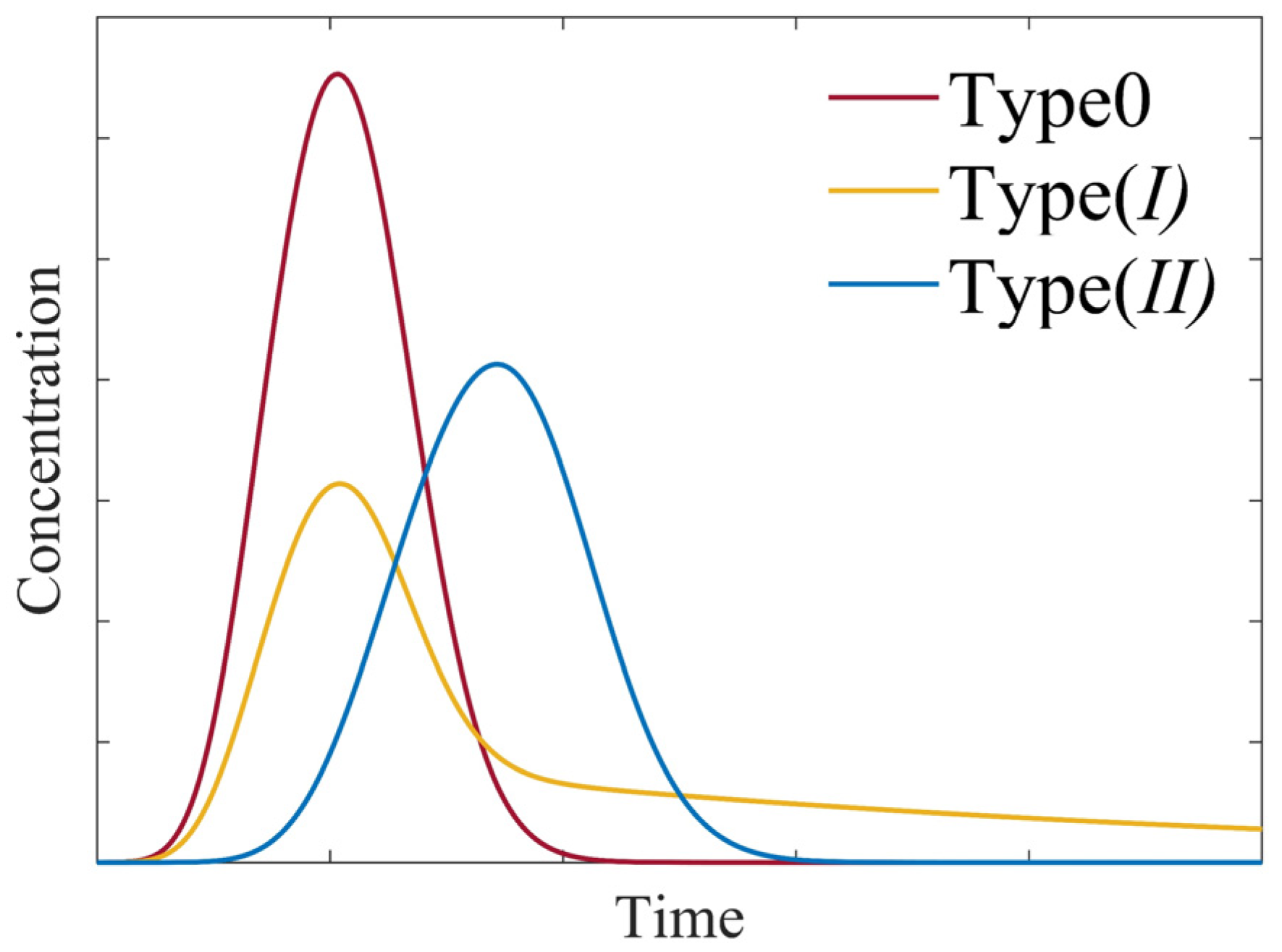
3. Solute Breakthrough Curves and Storage Process

Tracer experiments are generally based on two specific injection functions: instantaneous or constant-rate injection. First, instantaneous injection is a mechanism in which a relatively large mass of solute is instantaneously released (usually in a time scale of seconds) into the river to label a single parcel of its flow [44,45]. Constant-rate injection is a mechanism in which a solute load is continuously introduced to the river at a constant rate for a known duration, labeling many parcels of its flow passing the injection point [46,47]. Tracer tests provide valuable insights into solute transport processes, helping to clearly identify their behavior [48]. The plotted tracer concentration as a function of time at a particular station is known as the breakthrough curve (BTC). Tracer breakthrough curves offer insights into hydrodynamic processes and stream characteristics [5].

Recently, researchers have sought to isolate the impacts of different contributions to obtain information on solute transport mechanisms [49]. Analyzing the shape and moments of breakthrough curves formed by conservative tracers enables the modeling of the effects of various mechanisms on solute transport. Conservative tracers, fluorescent dyes like rhodamine WT, in rivers refer to substances transported by the flow of water without undergoing any significant chemical, biological, or physical changes such as reactions, decay, adsorption, or degradation [50].

Early river studies found that the advection–dispersion equation did not fully depict observed tracer concentration–time curves, which often displayed skewed, low-concentration tails following the main tracer peak. This tailing was attributed to river storage zones [51,52]. However, the hydrology community had not considered the storage process concept until Bencala and Walters (1983) made the connection based on Uvas Creek experiments [53]. In summary, recent work uses breakthrough curve analysis to isolate storage zone impacts, building on early findings that skewed tails represent storage processes not captured by advection–dispersion models.

The main parameter used to evaluate the key role of storage and hyporheic processes in streams is the Damkohler number (Da) calculated from field data. The Damkohler number represents the relative exchange rate between storage zones and the main channel. It is calculated as the ratio between the time required for downstream tracer transport over a given reach length and the mean tracer residence time within storage zones [54,55].

$$DaI=\alpha {\displaystyle \frac{L}{U}}(1+{\displaystyle \frac{A}{A_S}})=\beta (1+{\displaystyle \frac{1}{\eta }})$$

(2)

A is the cross-sectional area of the stream channel [L²], As is the cross-sectional area of the storage zone [L²], α is the stream storage exchange coefficient [T⁻¹], and L is the stream length [L]. In the Damkohler number, the storage parameters η and β are formed. η is known as the spatial scale of the storage process, which is the relative size of the storage zone to the main stream. β determines the residence time of solutes in the storage zone by defining the exchange rate, which is the temporal scale of the storage process [56]. When the Damkohler number is much greater than one, the exchange rate among the storage, hyporheic zones, and the main channel is very quick, and it could be assumed that these two parts are in balance, and the storage process cannot be separated from the dispersion process. This condition is observed in slow-moving streams with rapid exchange. If the Damkohler number is much lower than one, the exchange between the main channel and the storage zone is very low and negligible. In such a stream, storage is not among the important processes in solute transport. In high-velocity and low exchange rates, rivers occur, resulting in long time scales of hyporheic and storage exchange [57].

Depending on the spatiotemporal scale of the storage process, various solute breakthrough curves with different forms are produced. Figure 2 depicts the sensitivity of the shape of the solute breakthrough curve to the value of β and η. Type0 is observed when β or η is zero. In this case, the form of the solute breakthrough curves is similar to the output of the classic advection–dispersion equation and follows a normal distribution [58]. The model produces type (I) for low to moderate Damkohler numbers. Such a shape of the BTC is observed due to the slow exchange of solutes between the main channel and the transient storage zone. The shape of the breakthrough curves follows a positively skewed normal distribution, with a shorter peak and longer tail compared to Type0 [59]. For high values of Damkohler numbers, Type (II) would be more probable. A symmetric normal distribution with a shorter peak and more delay is observed compared to the classic advection–dispersion equation. Type (II) illustrates a quick exchange between the main flow and the storage zones.

Under different geomorphological conditions in rivers, various residence time distributions (RTDs) form, illustrating distinct breakthrough curve shapes [60]. RTDs represent the time that water molecules or solutes spend in a specific segment of a river before exiting, crucial for understanding solute transport and ecological dynamics. Figure 3 illustrates the RTDs observed in natural streams.

RTDs observed in natural streams and rivers take several forms such as a power-law, exponential, log-normal, and upward distributions [61]. Each RTD type indicates specific hydrological processes, geomorphological features, and the role of transient storage zones:

• Power-law RTDs are commonly found in small alluvial streams, where there is a wide range of travel times due to complex flow paths and interactions with sediment and vegetation [62,63,64]. These streams often contain numerous transient storage zones, such as hyporheic exchange, eddies, and backwater regions, resulting in long solute retention times and extended tails in breakthrough curves.
• Exponential RTDs are frequently observed in stream reaches characterized by bedrock or significant pools that act as in-channel storage zones. This distribution indicates a relatively uniform flow path, where water is stored and released at a more consistent rate [65,66,67]. Streams dominated by such storage zones typically exhibit rapid solute turnover without prolonged tailing.
• Log-normal RTDs typically occur in larger or moderately sized rivers, reflecting the influence of multiple storage mechanisms. These include varying flow velocities, channel complexity, and a mix of surface and subsurface storage, resulting in intermediate solute retention times [68]. The log-normal distribution suggests a greater variety of retention times compared to more uniform flow systems.
• Upward RTDs have been documented in small flows, where water may experience prolonged residence times because of localized storage effects or slow-moving stream sections [69]. This distribution is often seen in low-gradient systems where backwaters, floodplains, or riparian vegetation flow slowly.

Although these geomorphological features strongly influence RTD types, the specific processes governing RTD formation are still not fully understood [70]. Factors such as sediment transport, vegetation interactions, channel morphology, and hydrodynamic conditions contribute to the complexity of RTD formation. Table 1 summarizes the five distinct types of storage model RTDs, including their characteristics and implications for solute transport. Field observations show varied RTD types linked to river geomorphology, but more research is needed to understand their formation mechanisms. Exploring these RTDs provide valuable insights into how rivers retain and transport solutes, crucial for improving water quality models and predicting pollutant fate.

Figure 3 illustrates breakthrough curves for various RTDs observed in natural streams. Each curve represents a distinct RTD type: upward (RTD+U, RTD0U), exponential (RTD0E), power-law (RTD-P), and log-normal (RTD-L). These distributions highlight the variation in solute retention and release, with each type reflecting distinct storage mechanisms and geomorphological influences.

Figure 2. Different solute breakthrough curves in streams.

Figure 2. Different solute breakthrough curves in streams.

Figure 3. Various residence time distributions in natural streams [71].

Figure 3. Various residence time distributions in natural streams [71].

Table 1. RTD properties.

RTD Type	Late Portion Shape	Stream Condition	Reference
RTD+U	Upward	some small streams	[69]
RTD0U	Upward	small streams
RTD0E	Exponential	reaches with bedrock and/or significant pools (in-channel storage zones), small streams	[72]
RTD-P	Power-law	small alluvial streams, moderate-sized rivers	[73]
RTD-L	Log-normal	moderate- to large-size rivers	[74]

Table 1. RTD properties.

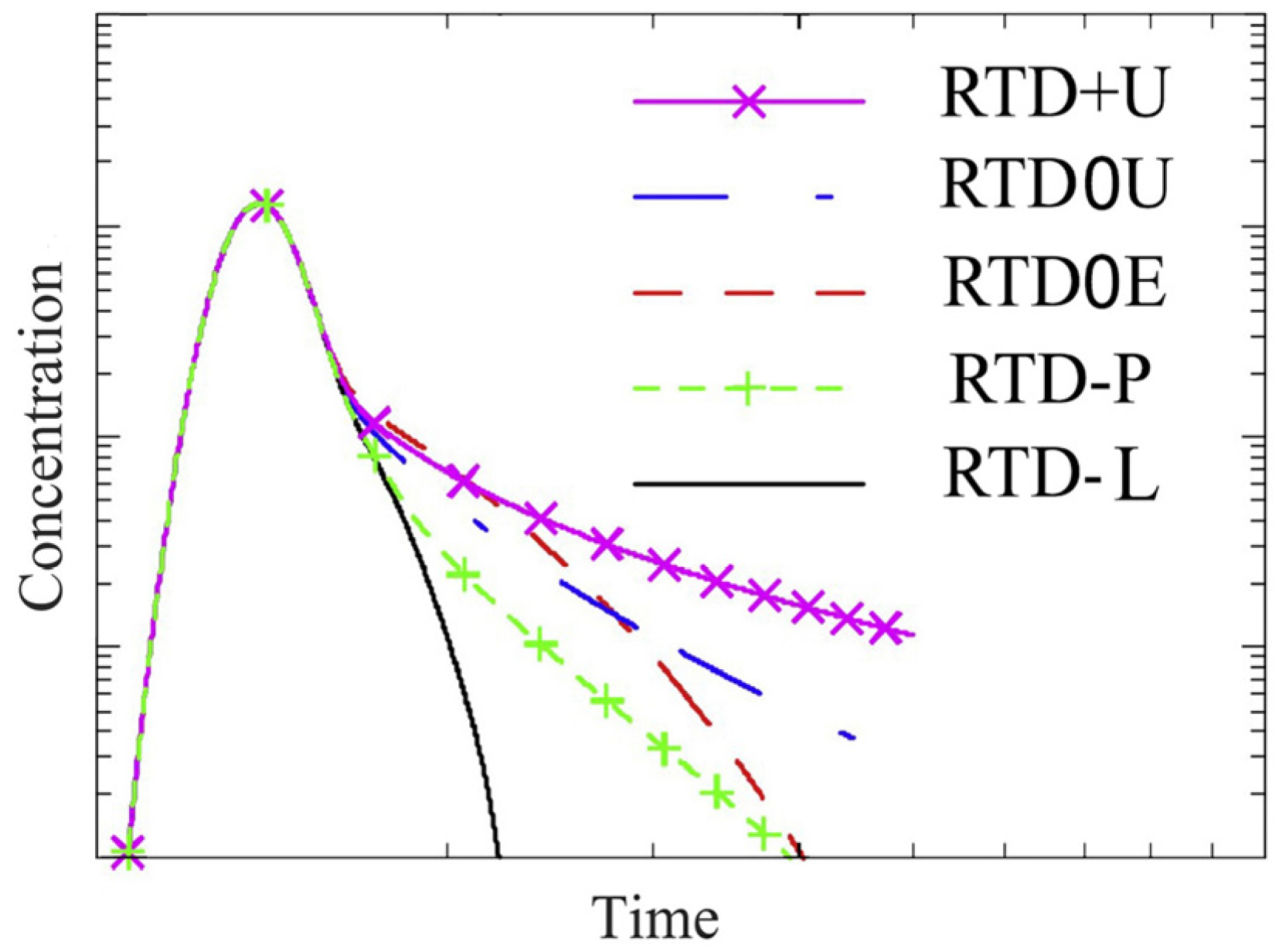
RTD Type	Late Portion Shape	Stream Condition	Reference
RTD+U	Upward	some small streams	[69]
RTD0U	Upward	small streams
RTD0E	Exponential	reaches with bedrock and/or significant pools (in-channel storage zones), small streams	[72]
RTD-P	Power-law	small alluvial streams, moderate-sized rivers	[73]
RTD-L	Log-normal	moderate- to large-size rivers	[74]

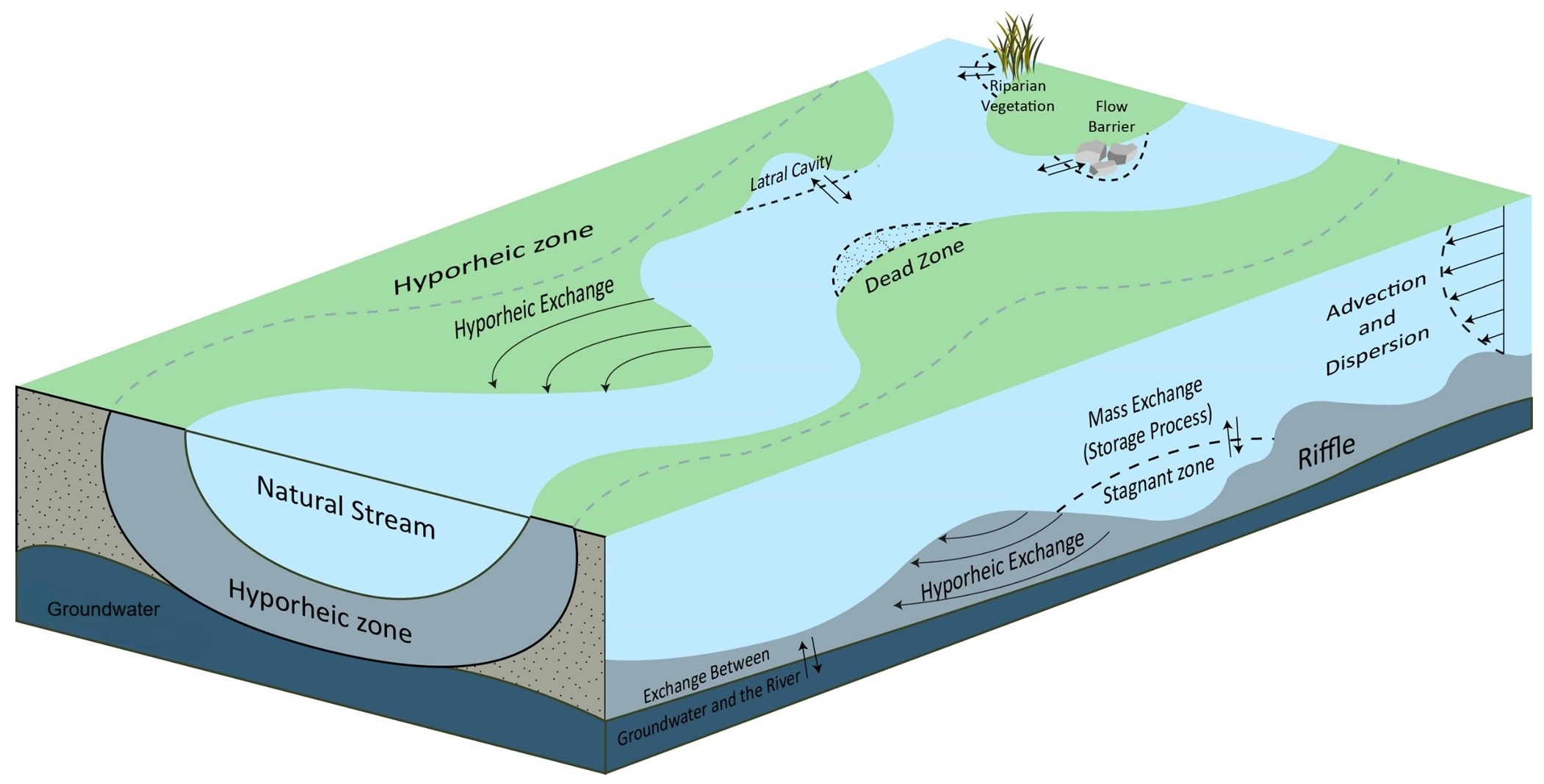
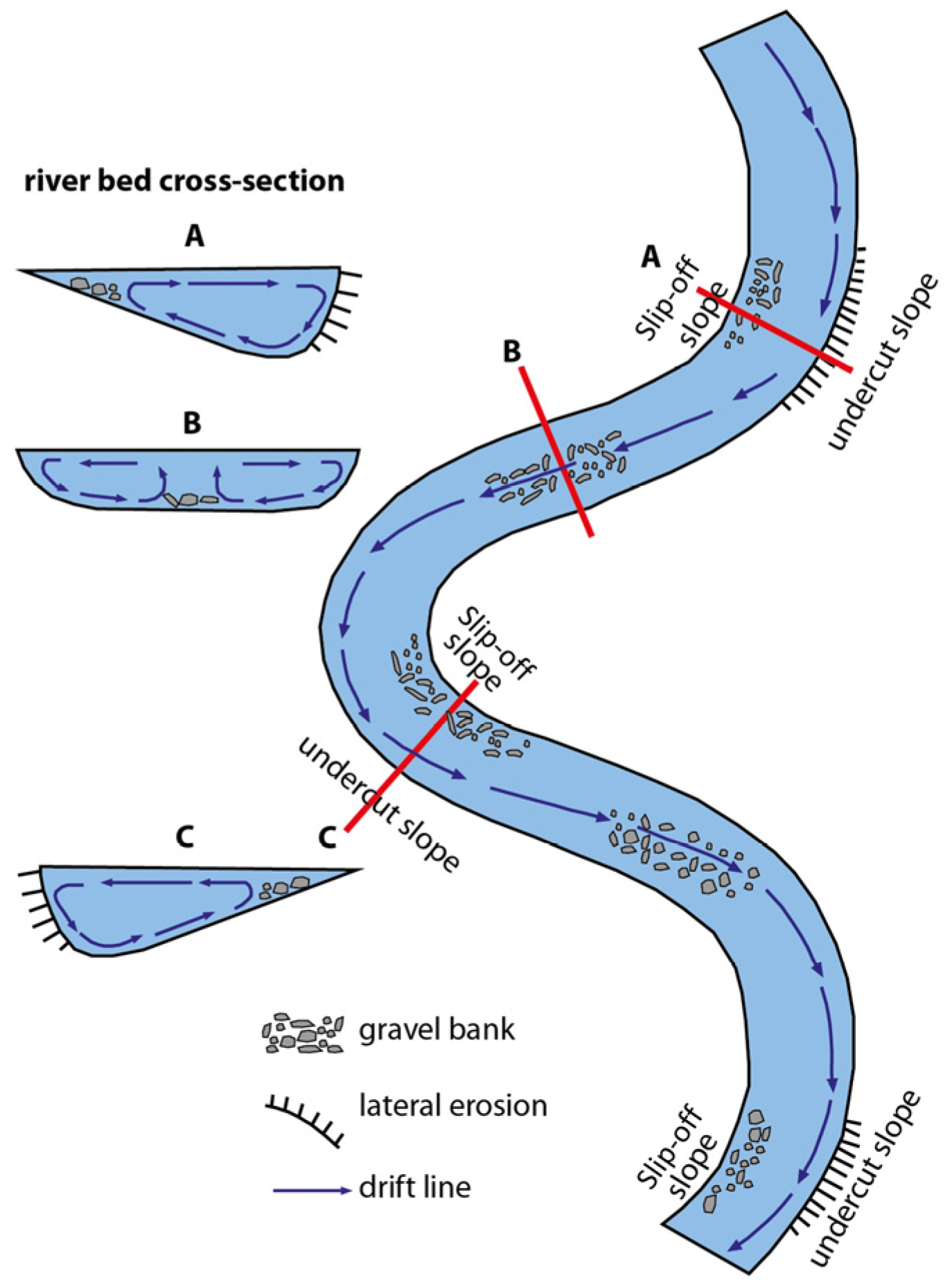
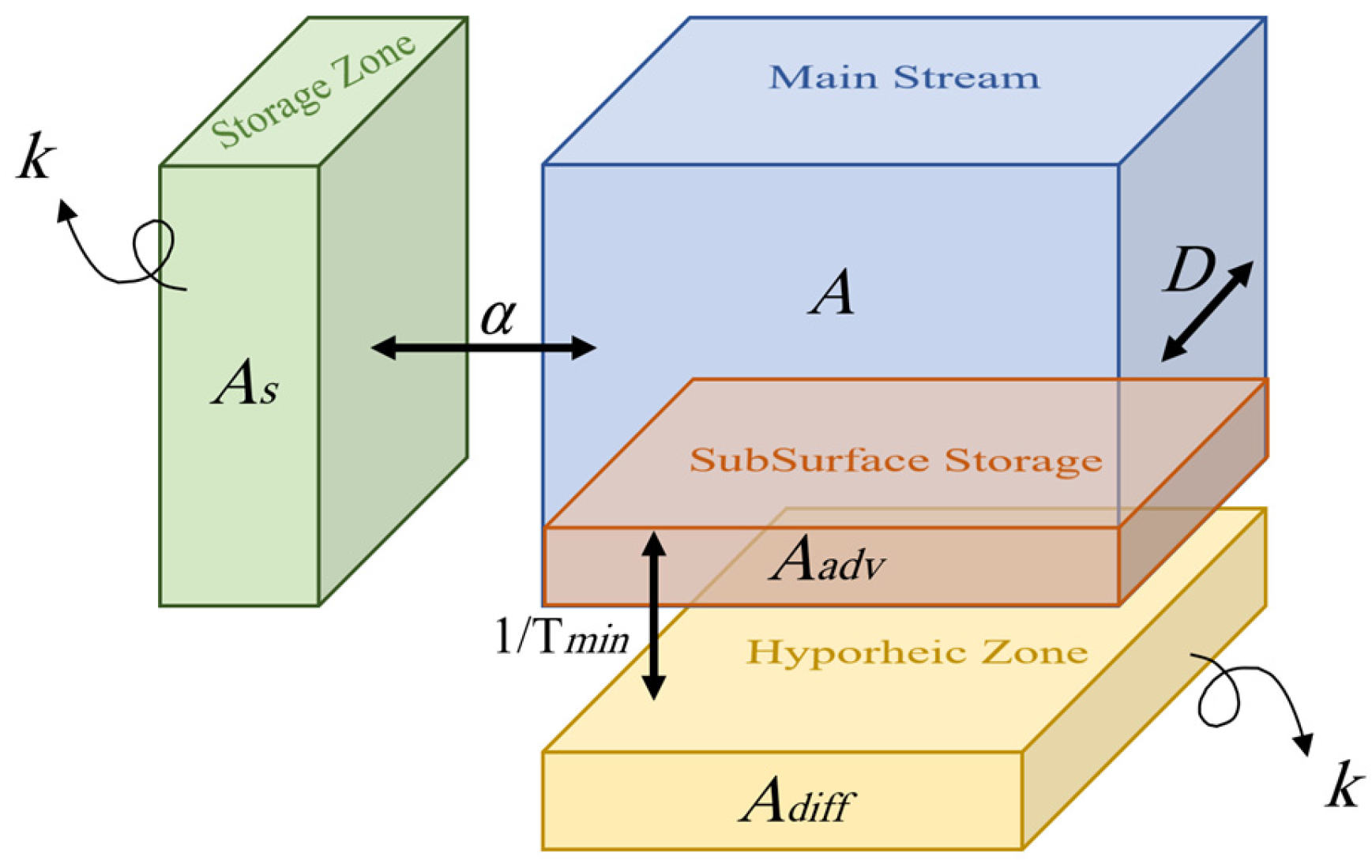
4. Mechanisms of Storage and Hyporheic Zones

Exchanges between storage zones and surface water occur across rivers, from upper to lower courses. Despite the diversity of environments, from mountain streams to wetlands and tidal rivers, common processes govern transient storage across these settings [75]. This section examines the key fundamental mechanisms underlying stream storage and hyporheic interactions. While conditions vary widely, similar core processes drive transient storage exchange across all river courses and habitats.

The exchange of water and solutes between a stream, its bed, and banks is driven by energy gradients at the riparian interface [76]. Hydrologists use hydraulic head measurements to characterize water energy [77,78]. The total hydraulic head has both static and dynamic components [79]. The hydrostatic head is the sum of hydrostatic pressure and elevation heads. The hydrodynamic head consists of velocity and non-hydrostatic pressure heads, arising from flow around bed roughness and momentum transfer, which represent flow field effects [80,81]. In hydrostatic conditions, the hydraulic head equals water depth [82]. Transient storage flow under hydrostatic conditions is also influenced by surface water depth and slope variations, which affect subsurface head gradients. This flow typically has the greatest impact on spatial scales shaped by larger topographic features in the riparian zone, such as bars, riffles, cascades, and meandering rivers [83,84]. Conversely, transient storage flow under hydrodynamic conditions tends to have its most pronounced effects at smaller scales of variability in stream velocity as it moves over submerged bedforms, influencing the transfer of momentum between surface water and the streambed [85]. Key factors such as bed slope, boulder size, dunes, cascades, riffles, vegetation patches, concave banks, or woody debris lying horizontally on the streambed are all crucial to hydrostatic and hydrodynamic conditions. For instance, in streams that are relatively steep, shallow, and slow-moving, the topography of pools and riffles, along with the meandering channel shape, is a primary factor driving the storage process [55], [57]. Surface water typically enters storage zones where the stream slope increases, such as around large boulders, gravel point bars, or within pool and riffle sequences. The transient storage flow then re-enters the stream close to the upstream ends of gentler sloped channels [75,77,86,87].

Other less frequently studied, yet significant, mechanisms influencing storage flow in streams include biological processes that facilitate transport across the streambed interface and flow turbulence [88,89]. Wave oscillations and currents drive flow inside permeable beds, serving as the primary mechanism for storage and hyporheic exchange in estuaries and shallow lake regions [90,91]. Tides also induce regular interactions between the surface and subsurface along coastal river banks [92]. Although transient storage flow is typically laminar, surface water turbulence can penetrate coarse sediments beneath fast-flowing rivers [93]. Biological processes, such as creating beaver dams, can pool water and drive its movement through bed sediment [94,95]. Salmon redds, which improve egg survival [96], also impact storage. Transpiration by riparian vegetation enlarges and decreases storage flow paths daily [97]. Additionally, feeding and burrowing by benthic organisms promote flow through the streambed interface, a process known as bioirrigation, and alter sediment structures, a process called bioturbation [98]. The growth and decay of aquatic plant roots generate preferential flow through sediment macropores [99]. Aquatic vegetation increases storage, aids river restoration, adds flow resistance, and affects pollutant transport [100,101]. Buoyancy forces from solute and temperature gradients drive storage exchange, likely dominating in deeper, calmer waters [102,103]. As a result, storage exchange occurs almost everywhere, except in rare cases of still waters with low-permeability sediments and minimal bioturbation, where dispersion tends to dominate subsurface transport [104].

5. Mathematical Models for In-Stream Pollutant Transport

The understanding of physical, chemical, and biological processes has deepened over the past few decades; these theoretical concepts have been integrated into mathematical models to predict the fate of solutes in river corridors [105]. Different mathematical models have been formulated to simulate solute transport in rivers coupled with storage and hyporheic exchange. These models have different mathematical formulations, physical concepts, numbers of equations and parameters, and RTD shapes [106,107].

5.1. Fractional Advection–Dispersion Equations

The fractional advection–dispersion equation (FRADE) extends the classical ADE by incorporating fractional-order derivatives of the Caputo type to model non-Fickian transport processes [108]. Fractional derivatives introduce non-local effects and memory that account for the complex heterogeneity of natural porous media. Specifically, the FRADE contains fractional spatial and/or temporal derivatives of the solute concentration, enhancing capabilities to represent subdiffusion, skewed plumes, early arrival, and heavy tailing not captured by the ADE [109,110].

$${\displaystyle \frac{{\partial }^{\gamma }C}{\partial t^{\gamma }}}=-U{\displaystyle \frac{\partial C}{\partial x}}+D{\displaystyle \frac{{\partial }^{\alpha }C}{\partial x^{\alpha }}}$$

(3)

where γ is the fractional coefficient of temporal derivatives, and α is the fractional coefficient of spatial derivatives. The ADE is a specific case of the S-FRADE with α = 2, whereas the FRADE generalizes this for α in the range of 1 to 2. The S-FRADE results are required when movement statistics do not satisfy the central limit theorem’s assumptions [111]. The T-FRADE captures the effects of episodic or discontinuous movement, which precisely mirrors the influence of the distribution of residence time with power-law in the fixed domain. The parameter γ is constrained to a range of 0 to 1, reflecting subdiffusive transport [112].

5.2. Transient Storage Model

The transient storage model (TSM) was the first model proposed to describe storage exchange and has been widely used for many years. This model focuses on the main channel part of the stream, where dispersion and advection dominate [113,114]. However, the storage zone is a well-mixed area where solutes could be temporarily stored and released back into the streamflow. The mass exchange between the storage zones and the main channel can be represented as a first-order mass transfer process [115]. The transient storage model’s coupled equations are as follows:

$$\begin{array}{l}{\displaystyle \frac{\partial C}{\partial t}}=-{\displaystyle \frac{Q}{A}}{\displaystyle \frac{\partial C}{\partial x}}+{\displaystyle \frac{1}{A}}{\displaystyle \frac{\partial }{\partial x}}(AD{\displaystyle \frac{\partial C}{\partial x}})+{\displaystyle \frac{q_{Lin}}{A}}(C_{Lin}-C)+\alpha (C_s-C)\\ {\displaystyle \frac{\partial C_s}{\partial t}}=-\alpha {\displaystyle \frac{A}{A_S}}(C_s-C)\end{array}$$

(4)

where C_Lin is the solute concentration in the lateral inflow [ML⁻³], C_s is the solute concentration in the storage zone [ML⁻³], Q is the volumetric flow rate [L³T⁻¹], and q_Lin is the lateral inflow [L²T⁻¹]. If α = 0, then there is no exchange, and the equations reduce to the ADE.

5.3. Modified Advection–Dispersion Equation

Singh (2002) claimed that the TSM does not reflect the physics of the dead zone [116]. Accordingly, the Modified Advection-Dispersion Equation (MADE) was developed. The MADE has fewer parameters than the transient storage model and fractional advection–dispersion equation and is easier to apply. It requires less computational effort but yields good results [12,117]. This model is as follows:

$$D{\displaystyle \frac{{\partial }^{2}C}{\partial x^2}}-U{\displaystyle \frac{\partial C}{\partial x}}=(1-\eta +k){\displaystyle \frac{\partial C}{\partial t}}$$

(5)

where k is the parameter that accounts for solute adsorption [–], and η is the average stagnant zone expressed as the fraction of the average cross-sectional [–]. This method is suggested for the simultaneous estimation of the dispersion coefficient, apparent (effective) velocity, and effective injected mass of the tracer from solute breakthrough curves observed at the downstream section. Equation (5) assumes linear equations for the treatment of dead zones and adsorption of the following forms:

$$c_{\eta }=\eta C$$

(6a)

$$c_k=kC$$

(6b)

where c_η is the concentration released from the stagnant zones [ML⁻³], and c_k is the adsorbed concentration [ML⁻³]. The stagnant zones in the streamflow tend to increase the apparent flow velocity, which is accountable for solute dispersion. At the same time, the adsorption of solute on soil particles or in dead zones reduces the apparent flow velocity in the stream.

$$U_a={\displaystyle \frac{U}{1-\eta +k}}$$

(7a)

$$D_a={\displaystyle \frac{D}{1-\eta +k}}$$

(7b)

where D_a is the apparent dispersion coefficient [L²T⁻¹], and U_a is the apparent flow velocity [LT⁻¹]. The impact of the in-stream storage zone is shown in Figure 4.

5.4. Multirate Mass Transfer Model

The first model used to indicate wide ranges of residence distribution time in rivers was the multirate mass transfer (MRMT) model. In the MRMT model, the mobile zone represents the primary flow and is modeled by the ADE, with an added source-sink term accounting for mass exchange with immobile areas [118,119].

$${\displaystyle \frac{\partial C}{\partial t}}+U{\displaystyle \frac{\partial C}{\partial x}}-D{\displaystyle \frac{{\partial }^{2}C}{\partial x^2}}=\mathrm{\Gamma }(x,t)$$

(8a)

$$\mathrm{\Gamma }(x,t)={\displaystyle \frac{\partial C}{\partial t}}\ast g(t)={\displaystyle \underset{0}{\overset{t}{\int }}\frac{\partial C(t-\tau )}{\partial \tau }}g(\tau )d\tau$$

(8b)

where τ is the lag time [T⁻¹], Γ is the rate of loss or gain of concentration [ML⁻³T⁻¹] to or from the immobile domain (loss early and gain at the late time), the asterisk sign denotes the convolution product, and g(t) is the memory function [T⁻¹]. The model has an adaptable residence time distribution that enables a much better match to tracer data compared to previously suggested models. The density function can take various forms based on a specific residence time distribution [120,121,122]. Among the possible formulations for g(t), it may be defined with a distribution of exponential residence times:

$$g(t)=\omega e^{-\omega t}$$

(9)

where ω is the first-order mass transfer rate coefficient [T⁻¹], equivalent to αA/A_S, and a power-law distribution was proposed as an effective model for storage exchange. In this case, the memory function is an integral function that represents the cumulative effect of exponential distributions weighted by a power-law function [62,118,122]. For the power-law RTD, g*(t) is as follows:

$$g*(t)={\displaystyle \frac{(k-2)}{({\omega }_{\max }^{k-2}-{\omega }_{\min }^{k-2})}}{\displaystyle {\int }_{{\omega }_{\min }}^{{\omega }_{\max }}{\omega }^{k-2}}{e}^{-\omega t}d\omega$$

(10)

where k is the power-law coefficient, which is given by the slope of the delayed concentration tail.

5.5. Averaging Advective Storage Path Model

The initial study that explicitly linked in-stream transport with residence time distributions predicted by physically based models was conducted by Wörman [68]. This study introduced the Advective Storage Path (ASP) model as a specific instance of the MRMT model, applicable when advective processes primarily govern storage exchange. Mixing in storage zones involves both advective and diffusive processes [30]. Solute transport in a stream can be coupled with storage exchange flux through a mass balance:

$${\displaystyle \frac{\partial c_{im}}{\partial t}}+{\displaystyle \frac{\partial W{c}_{im}}{\partial \eta }}=0$$

(11)

In Equation (11), η represents a coordinate along storage streamlines, W represents the advection velocity of the subsurface, and c_im is the immobile zone concentration. The concentration at a point η = L in the storage zone is then given by the following:

$$c_{im}(L,x,t)=c_m\left(x,t-{\displaystyle \underset{0}{\overset{L}{\int }}\frac{1}{W(\eta )}\mathrm{d}\eta }\right)$$

(12)

Using this framework, the net solute mass flux in the dissolved phase in the stream water could be found by integrating over the distribution of transport pathways:

$$\mathrm{\Gamma }(t)={\displaystyle \frac{1}{2}}\left(C(x,t){\displaystyle \frac{P}{A}}W-C(x,t-T)*f(T){\displaystyle \frac{P}{A}}W\right)$$

(13)

where P is the wetted perimeter, A is the cross-sectional area of the stream, and f(T) is the probability density function for residence time in the storage zone. The equal bed zone assumption is based on the mass continuity principle through the immobile area under the condition of a fixed exchange velocity, which is valid for hyporheic exchange in rivers where there is no net gain or loss of discharge in the downstream direction [123].

5.6. River Solute Transport Model

Another method for addressing the various spatiotemporal scales influencing storage and hyporheic exchange separates individual processes and physical domains affecting mass transport in surface flow. The solute transport in rivers (STIR) model integrates individual process solutions into a comprehensive probabilistic framework through a multi-compartment convolution method [124]. This assumes mass enters and exits storage and hyporheic zones only from the main flow, based on a particular trapping probability and residence time distribution. Individual trapping events are independent of prior storage history [125]. The overall residence time distribution in a river of length $x$ is as follows:

$$r(t;x)={\displaystyle {\int }_0^t{r}_w(t-\tau ;x)r_S}(\left.\tau \right|t-\tau )\mathrm{d}\tau$$

(14)

In Equation (14), r_W represents the residence distribution time relative to storage-free surface flow, and r_S represents the overall residence distribution time in the domains, which is, in turn, a convolution of the distributions in the individual domains:

$$r_S(\left.t\right|t_w)=r_{S_1}(\left.t\right|t_w)*r_{S_2}(\left.t\right|t_w)*\mathrm{\dots }*r_{S_N}(\left.t\right|t_w)$$

(15)

where t_w denotes the time spent in surface flow, and r_Si reflects the residence time distribution in the ith domain. The breakthrough curves in Equation (15) are influenced by the probability of mass trapping within a storage zone and the duration of time spent there. φ_i(t) is the probability density function for the time spent in the ith storage domain during any exchange. The RTD for n exchange events in the ith storage domain is the n-fold self-convolution of φ_i(t). Once the process is identified and its characteristics are established, the process- and domain-specific φ_i(t) can be included in the model.

$$p_i(\left.n\right|t_w)={\displaystyle \frac{{({\alpha }_i{t}_w)}^n}{n!}}{e}^{{\alpha }_i{t}_w}$$

(16)

The probability p_i(n|t_w) of a mass to be exchanged n times in the ith storage zone, under the assumption of independence of individual exchange events, can be modeled with a Poisson distribution based on a trapping rate α_i. The RTD for each storage zone convolved in Equation (15) is written as the sum of the residence distribution times for a given number of entries in the ith storage domain:

$$r_{S_i}(\left.t\right|t_w)={\displaystyle {\sum }_{n=0}^{\infty }{p}_i(\left.n\right|t_w})r_{\left.S_i\right|n}(t)$$

(17)

A feature of the model is that Equation (14) can be reformulated into a more convenient form using Laplace transforms, and also, the resulting RTD is the same as that found in the storage-free case but with a frequency alter, which is a function of the compartment-specific transport rates α_i and RTDs ϕ_i(t).

5.7. Continuous-Time Random Walk Model

The modeling frameworks discussed highlight the importance of accounting for the various spatiotemporal scales of storage exchange from different views. The Continuous-Time Random Walk (CTRW) method generally describes motion as a random walk with a continuous travel time distribution [126]. Random walks suitably represent transport in fluid flow due to underlying thermally driven molecular motion and sufficiently depict large-scale mixing like turbulence and dispersion [127].

$${\displaystyle \frac{\partial C(x,t)}{\partial t}}={\displaystyle \underset{0}{\overset{t}{\int }}M(t-\tau )\left[-U_{\psi }\frac{\partial C(x,\tau )}{\partial x}+K_{\psi }\frac{{\partial }^{2}C(x,\tau )}{\partial x^2}\right]}d\tau$$

(18)

where M is a memory function; K_Ψ and U_Ψ are the time-invariant dispersion and velocity coefficients. The model provides a particular method for determining random walk results based on the mathematical construction. The continuous-time description distinguishes this from other random walk types solved for motion events or discrete intervals. The model characterizes motion as discrete jumps, described by the space-time probability density function Ψ(x,t), which results in a probabilistic evolution of the concentration profile based on the underlying motion statistics [128,129].

5.8. The Variable Residence Time Model

The Variable Residence Time (VART) model was developed for simulating solute transport in uniform flow [71]. Unlike STIR, ASP, CTRW, and MRMT, this model allows for the generation of different types of solute RTDs observed in streams while no user-specified RTD functions are required. This major advantage of VART has resulted in a more complex structure and a larger number of parameters compared to other prevalent one-dimensional solute transport models. The VART model has been proposed based on a double-layer conceptual model simulated storage and hyporheic zone in streams. The upper layer is the advection-dominated immobile zone which includes in-stream and shallow hyporheic zones. The lower layer is a diffusion-dominated immobile zone deeper in the bed and farther under the banks [61,130,131]. The model is as follows.

$$\begin{array}{l}{\displaystyle \frac{\partial C}{\partial t}}+U{\displaystyle \frac{\partial C}{\partial x}}=K_S{\displaystyle \frac{{\partial }^{2}C}{\partial x^2}}+{\displaystyle \frac{A_{adv}+A_{dif}}{A}}{\displaystyle \frac{1}{T_V}}(\lambda C_S-C)+{\displaystyle \frac{q_L}{A}}(C_L-C)\\ {\displaystyle \frac{\partial C_S}{\partial t}}={\displaystyle \frac{1}{T_V}}(C-C_S)+{\displaystyle \frac{q_h}{A_{adv}+A_{dif}}}(C_h-C_S)\end{array}$$

(19a)

$$T_V=\left\{\begin{array}{c}\begin{array}{ccc}{T}_{\min }& for& t\le T_{\min }\end{array}\\ \begin{array}{ccc}t& for& t\ge T_{\min }\end{array}\end{array}\right.$$

(19b)

$$t_S=\left\{\begin{array}{l}\begin{array}{ccc}\begin{array}{cc}\begin{array}{cc}0& \end{array}& \end{array}& for& t\le T_{\min }\end{array}\\ \begin{array}{ccc}t-T_{\min }& for& t\ge T_{\min }\end{array}\end{array}\right.$$

(19c)

$$A_{dif}=4\pi t_S{D}_S$$

(19d)

where K_s is the Fickian dispersion coefficient excluding the transient storage effect [L²], A_adv is the area of the advection-dominated storage zone [L²], A_dif is the area of the effective diffusion-dominated storage zone [L²], C_h is the solute concentration in the hyporheic inflow [ML⁻³], D_s is the channel width-modified effective diffusion coefficient [L²T⁻¹], q_h is the hyporheic flow gain/loss rate per unit channel length [L²T⁻¹], T_V is the actual varying residence time of the solute in storage zones [T], T_min is the minimum mean residence time [T], t_s is the time since solute release from the storage zone to the stream [T], and λ represents the subsurface hyporheic exchange induced [–]. A conceptual framework is shown in Figure 5. A comparison of the solute transport models discussed above is presented in

Table 2. Comparison of various solute transport models.

Models	Type of Storage Process	Parameters	Application	Pros	Cons	Sources
Classical Advection–Dispersion Equation (ADE)	None	(U, D)	The asymptotic result is continuous movement with mixing and a narrow velocity distribution.	Simple to implement; widely used for conservative solute transport.	It does not account for transient storage or hyporheic exchange, leading to inaccurate predictions in complex systems with significant storage zones.	[132]
Modified Advection–Dispersion Equation (MADE)	Only Type(II) of Breakthrough Curve	(Ua, Da)	A modified asymptotic result relative to advection–dispersion equation.	Improves the ADE by including breakthrough curve modifications for better accuracy in systems with storage zones.	Limited to specific types of storage, lacking flexibility in representing diverse hyporheic processes.	[117]
Fractional Advection–Dispersion Equation (FRADE)	Heavy-Tailed Power-Law Residence Time Distribution	(U, D, γ, α)	The long-term outcome of movement that is irregular in both time and space, characterized by significant shifts or extended periods of inactivity compared to the scale of measurement.	Captures heavy-tailed RTDs and provides better accuracy for systems with power-law distributions.	Complex to parameterize; may not perform well in systems with uniform or exponential RTDs.	[133]
Transient Storage Model (TSM)	Finite Volume, Well-Mixed Storage Zones	(U, D, A/As, α)	Fickian in-stream transport combined with first-order mass transfer in well-mixed stationary zones (similar to asymptotic Brownian motion).	Well suited for systems with mixed storage zones; models hyporheic exchange effectively.	Limited flexibility in handling complex RTD shapes (e.g., power-law distributions).	[65]
Multirate Mass Transport (MRMT)	Any Residence Time Distribution/Memory Function	Controlled by Memory Function	Fickian in-stream transport with storage times modeled by a memory function.	Capable of modeling a variety of RTDs, including those controlled by memory functions; handles hyporheic exchange well.	Computationally intensive due to the complexity of representing multiple rates of transport.	[120]
Advective Storage Path (ASP)	Any Residence Time Distribution/Memory Function	Controlled by Memory Function	The residence time distribution characterizes Fickian in-stream transport with storage times.	Can model detailed residence time distributions based on memory functions.	Requires detailed calibration data, limiting its application in field studies without sufficient data.	[68]
Continuous-Time Random Walk (CTRW)	Any Residence Time Distribution/Memory Function	Controlled by Memory Function	Brownian in-stream transport is characterized by a jump length distribution combined with a storage process modeled by a memory function.	Excellent for modeling Brownian transport and complex RTDs; flexible in capturing storage processes.	It is challenging to calibrate and difficult to apply to systems without clear RTD information.	[126]
Solute Transport in Rivers (STIR)	Any Residence Time Distribution/Memory Function	Controlled by Memory Function	Fickian in-stream transport combined with a storage process characterized by a specific RTD.	It combines flexibility in RTD representation with storage processes and is well suited for diverse stream conditions.	The complexity in defining RTD functions makes it harder to implement without extensive data.	[124]
Variable Residence Time Model (VART)	Any Residence Time Distribution without a Memory Function	(U, Ks, Tmin, A/As + Ds)	Fickian in-stream transport without any user-specified RTD functions.	Allows for user-defined RTDs and the flexible modeling of transient storage.	Requires significant user input and customization, which can be a barrier for broader applications.	[71]

.

6. Future Directions and Challenges

Although there has been extensive research on storage and hyporheic zones in rivers over the past several decades, major knowledge gaps remain that must be addressed to advance the understanding of storage processes and dynamics. Further studies are needed to address these critical gaps and enhance the incorporation of storage zones into pollutant transport models for rivers. Additional research in this area will be necessary to provide new insights into storage zone functioning and its influence on contaminant fate and transport. A summary of these gaps is as follows:

6.1. Incorporating System Complexity

Understanding coupled physical, geochemical, and biological mechanisms in storage and hyporheic zones remains limited as most studies have focused on specific processes. Interdisciplinary research is needed to investigate multiple hypotheses regarding storage and hyporheic zone functioning. Simplifications are common in storage zone research due to system complexity; however, avoiding systematic biases is essential. For example, most flume studies use stagnant bedforms even though bed movement impacts hyporheic exchange [134,135]. Representations of storage zones often lack empirical evidence on their spatiotemporal dynamics, such as diurnal variations in in-stream oxygen due to photosynthesis and respiration, which are rarely considered despite their potential impacts on riparian oxic zones. More holistic, interdisciplinary research is needed to advance our understanding of coupled storage processes.

6.2. Improving Scale Transferability

Most field studies of storage and hyporheic zones are restricted in scope, as they tend to be highly localized or lack adequate resolution to draw conclusions. Tracer tests are the primary technique for investigating storage processes; however, they only provide spatially averaged data [136]. Detailed sampling combined with tracer tests improves understanding, as in a few studies. Additionally, the temporal dynamics of storage zones are often overlooked because the methods are labor-intensive, resulting in one-time studies. However, comprehending the spatiotemporal and random variability is crucial crucial [137,138]. Thus, an improved sensing and modeling of storage processes are needed. In particular, the influence of temporal dynamics on ecological processes in the benthic and storage zones requires further evaluation. Temporal variations likely affect hydrologic exchange and streambed biota organization, so the boundary between benthic and storage zone communities may shift over time. Daily to seasonal variations could be studied by increasing sampling frequency or repeating seasonal protocols. Hydrostatic and hydrodynamic heads drive hyporheic flows that impact biogeochemistry and groundwater patterns, but their importance across scales remains uncertain [11].

6.3. Novel Research Methodologies

Research on the storage and hyporheic zone utilizes various approaches with tradeoffs. Field studies represent reality, but their complexity hinders understanding the process. Batch experiments offer an intermediate approach, providing some control while remaining closer to the reality. Flume studies are intermediate, allowing some control while remaining closer to reality. Modeling estimates unmeasurable variables based on data. Field measurements within storage zones using tracer studies improve the understanding of transport and residence times but have high logistical and economic costs, and implementing such data in models is challenging [57]. Each approach alone has limitations. Combining fieldwork, experiments, and modeling provides insights by offsetting individual shortcomings. Detailed storage process measurements from tracer studies, paired with suitable conceptual and numerical models, are required to interpret these measurements. Future research could further explore utilizing optimization models, which are extensively employed in various water quality modeling domains [139,140].

6.4. Standardization

Standardized methods and protocols across disciplines are needed to allow for a comparison of storage zone research from different sites. Simple, inexpensive, and easy-to-implement protocols would allow diverse researchers to apply them reliably. Metadata and system characterization standards would facilitate comparison. Method development and harmonization through collaborative projects are essential. Innovative techniques are needed to advance process understanding, such as tracing flow paths for targeted sampling. Most microbial activity measurements cannot resolve sub-daily fluctuations in storage zone conditions and effects on microbes [141]. Novel methods underway include dynamic pore water sampling, time-integrated passive sampling, and isotopic techniques, which will provide new insights into hyporheic processes.

6.5. Innovative Modeling Approaches

Current storage models typically couple separate groundwater and surface water models instead of using integrated approaches, though some fully coupled models exist. Since groundwater and surface water processes are now considered integrated, more comprehensive numerical models are needed to better resolve stream–aquifer interactions. Since these integrated approaches necessitate high spatial and temporal resolution, methods for upscaling must be developed. Commercial software now allows for the coupling of different physics processes across domains, which could reveal feedback in storage zone functioning [142]. The classical fate and transport modeling of in-stream pollutants often cannot capture storage and hyporheic processes and variability in conditions. Most models require more data on partitioning and degradation rates in situ, and relying on lab studies leads to uncertainty. Recent modeling showed that degradation is underestimated in small streams where the storage zone dominates [143]. Quantifying the storage zone’s relative contribution to in-stream compound removal requires assessing hyporheic reactivity and physical exchange, along with reach-scale removal. The hyporheic exchange length, and thus relative storage zone contribution, decreases with discharge [144].

Smart tracers represent a significant advancement in hydrological research, designed to provide more detailed information on water movement, interactions, and transformations within aquatic systems. Unlike traditional tracers that primarily measure flow paths or residence times, smart tracers can reveal biogeochemical processes, sediment–water interactions, and the dynamics of storage zones in rivers and streams.

• Reactive Tracers, such as Resazurin (Raz), undergo chemical transformations, converting to Resorufin (Rru) in the presence of microbial activity, allowing researchers to assess sediment–water interactions and biological activity in streams [145,146].
• Photosensitive Tracers change properties based on light exposure, enabling the differentiation between surface and hyporheic storage zones [147]. These tracers help quantify the impacts of various storage processes on solute transport [147].
• Isotopic Tracers use stable isotopes to provide distinct signatures for different water sources, such as groundwater or surface water, offering insights into flow paths and water source contributions [145,146].

The applications of smart tracers include quantifying surface versus hyporheic storage zone contributions, assessing biogeochemical processes like microbial activity and nutrient cycling, and improving the calibration of solute transport models in complex environments [57]. Despite their advantages, such as enhanced spatial and temporal resolution and the ability to integrate physical and biogeochemical processes, smart tracers present challenges regarding complex data interpretation and field implementation, which often require specialized equipment [142,146].

Smart tracers are essential tools for developing more accurate models of stream–aquifer interactions and improving water resource management strategies, as they provide a comprehensive understanding of hydrological dynamics and solute transport in riverine environments. The biogeochemical processes within storage zones, such as nutrient cycling and organic matter decomposition, are driven by microbial activities. These tracers allow for a better understanding of these biogeochemical mechanisms’ spatial and temporal variability, particularly microbial contributions to nutrient transformation and pollutant breakdown.

6.6. Integrating In-Stream Storage Zones in Watershed Models

Integrating in-stream storage zones, particularly hyporheic zones, into watershed models is essential for enhancing water quality predictions and understanding nutrient dynamics across large spatial scales. Hyporheic zones, as natural reactors, significantly influence the cycling of nitrogen, carbon, and other nutrients by extending residence times and providing environments conducive to biogeochemical transformations. However, traditional watershed models like SWAT often overlook the complex interactions within these storage zones, potentially leading to nutrient retention and underestimations of pollutant degradation [148].

Recent advancements, such as the SWAT-MRMT-R model, offer promising solutions by coupling SWAT with multirate mass transfer (MRMT) models and reactive transport mechanisms [148]. This combined framework allows for simulating biogeochemical processes in both the main river channel and its surrounding hyporheic zones, capturing the effects of transient storage zones with varied exchange rates and residence times. For example, this model has been applied successfully to study nitrate dynamics in the Columbia River, where hyporheic exchanges and biogeochemical gradients play a significant role in controlling surface water quality [148].

Applying such integrated models can enhance watershed management practices by allowing for targeted interventions. By simulating the mass transfer and reactive processes within hyporheic zones, these models provide a more comprehensive assessment of pollutant behavior, enabling the prediction of nutrient removal efficiency and the retention capacity of specific reaches. This approach is particularly valuable in watersheds affected by agricultural runoff and groundwater seepage, where nutrient inputs are spatially variable and driven by complex hydrological and chemical interactions [149,150], [151]. As a future direction, refining these integrated models to account for dynamic seasonal fluxes, spatial heterogeneity, and an improved characterization of exchange rates will be essential. Enhancing field-based measurements to parameterize hyporheic interactions at different scales can further bridge gaps between model predictions and observed data. Ultimately, this integrated modeling framework holds the potential to inform better watershed-scale management strategies aimed at improving water quality in large river networks.

6.7. Interdisciplinary Collaborations

Restoration techniques could improve storage flow residence times by targeting physical drivers and hydrogeological factors influencing storage flows. Nature-based solutions like coarse woody debris develop habitat structure and nutrient cycling. At the basin scale, reduced fine sediment delivery through improved land management can prevent streambed clogging and maintain conductivity and bedforms [152,153]. In-channel measures like channel narrowing, vegetation growth, and adding structures can increase velocities and scour fine sediments [154,155,156,157]. Many restoration practices improve coupling but do not control residence times, so water quality roots in alignment with reaction time scales. Restoration efficiency could be improved by targeting design variables like hydraulic gradients, conductivities, flow path geometries, and groundwater interactions to achieve specific biogeochemical outcomes [158,159]. Despite the potential to impact storage flows, evidence of improved water quality from restoration is limited, often because objectives are habitat-focused, diffuse pollution remains, and monitoring is inadequate. Research should aim to integrate storage flow goals into restoration practices. Frameworks exist to prioritize locations for storage flow restoration. As restoration addresses habitat degradation and biodiversity, targeting hyporheic communities is logical for holistic functioning. Engineered storage zones could treat stormwater, wastewater, and agricultural flows, but more research on efficiency and integration with existing management is needed.

Interventions that alter storage zone characteristics, like increasing the residence time, can influence hydro-biogeochemical processes. Specifically, these adjustments encourage nutrient uptake, microbial respiration, and pollutant breakdown. Restoration efforts that target biogeochemical outcomes, such as enhancing microbial habitat within hyporheic zones, could lead to more substantial improvements in water quality quality [18,160].

7. Conclusions

This review highlights the critical role of storage processes and hyporheic exchange in influencing solute transport in river systems. Through the synthesis of more than 150 journal articles, we identified key physical and chemical mechanisms, including advection, dispersion, and the complex dynamics within storage zones such as lateral cavities, dead zones, and hyporheic zones, which significantly affect the residence time and fate of solutes. These processes are essential for understanding pollutant transport and ecosystem functions, such as nutrient cycling and biogeochemical transformations.

Comparing solute transport models reveals significant advancements in how these models incorporate storage processes. For example, the transient storage model (TSM) and multirate mass transport (MRMT) model provide detailed representations of storage zones and effectively simulate complex residence time distributions. However, models such as the classical advection–dispersion equation (ADE) lack the ability to capture hyporheic exchange and transient storage, limiting their application in environments with significant storage contributions. Newer models, such as the Continuous-Time Random Walk (CTRW) and Variable Residence Time Model (VART), offer promising flexibility but are often complex to parameterize, making field-scale applications challenging.

Despite these advancements, significant gaps remain in understanding the relative contributions of storage zones, particularly the role of hyporheic exchange in solute removal and degradation. Quantifying these contributions is crucial for improving model accuracy, especially in systems dominated by transient storage. The use of smart tracers has emerged as an innovative approach to quantify surface versus hyporheic storage contributions more accurately and assess biogeochemical processes in situ, offering valuable data for model calibration.

Future research should address these gaps by integrating detailed field studies with advanced numerical models. Additionally, efforts to develop methods for scaling results across river networks will be critical for improving water quality predictions. By synthesizing data from diverse river systems and identifying common parameters that control transport and exchange processes, we can enhance the accuracy of solute transport models and make meaningful contributions to global water resource management.