Statistical Model Development for Estimating Soil Hydraulic Conductivity Through On-Site Investigations
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Grain Size Analysis and Porosity Determination
2.3. Estimation of Hydraulic Conductivity Using Laboratory Method and Empirical Relationships
- Hazen [36]
- 2.
- Slichter [37]
- 3.
- Terzaghi [38]
- 4.
- 5.
- Harleman [42]
- 6.
- Beyer [43]
- 7.
- USBR [44]
- 8.
- Alyamani & Sen [45]
- 9.
- Chapius [46]
2.4. Statistical Model Development
3. Results and Discussion
3.1. Sieve Analysis and Hydrometer Analysis
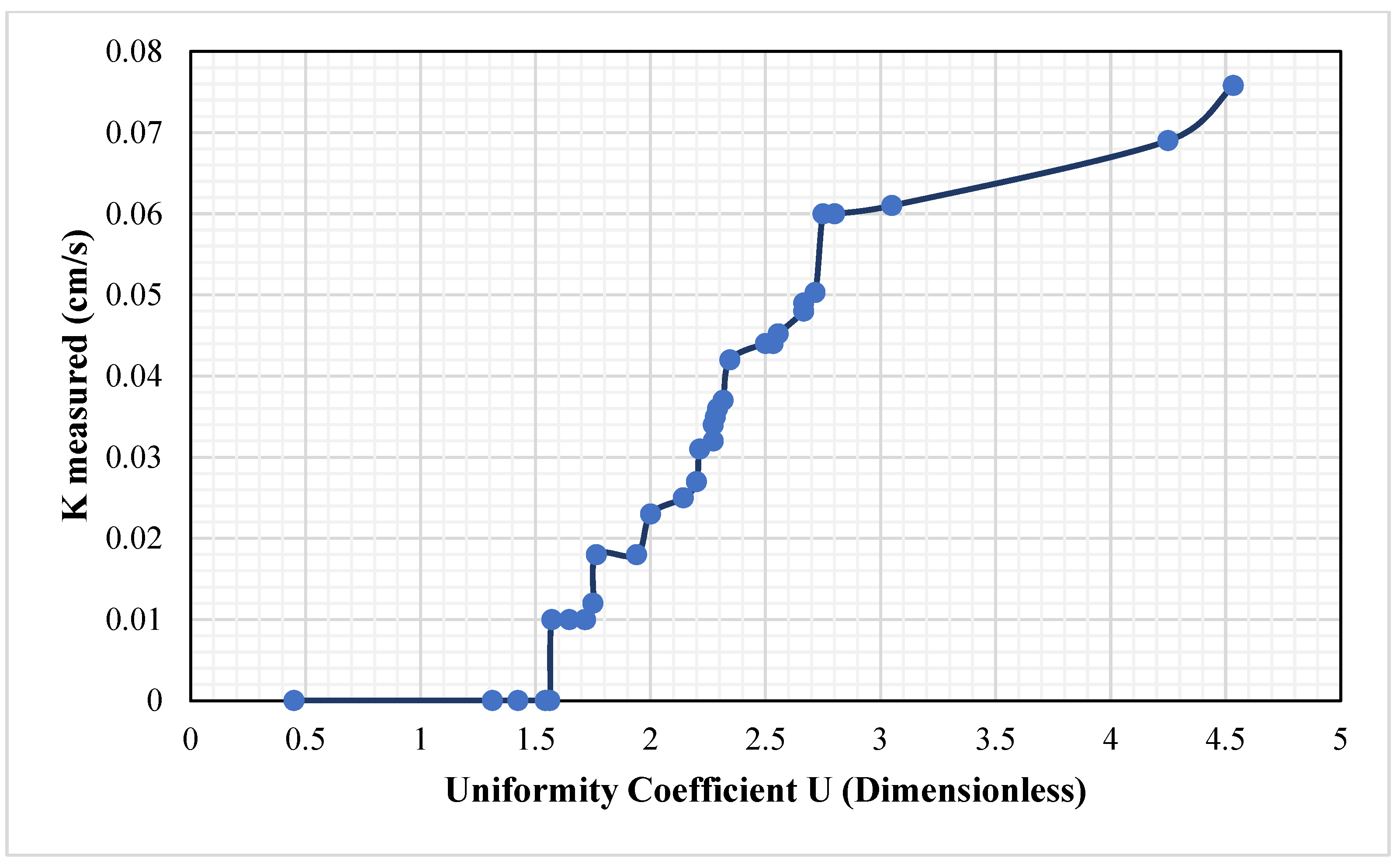
3.2. Relationship of Hydraulic Conductivity with Grain Size, Coefficient of Uniformity, and Porosity
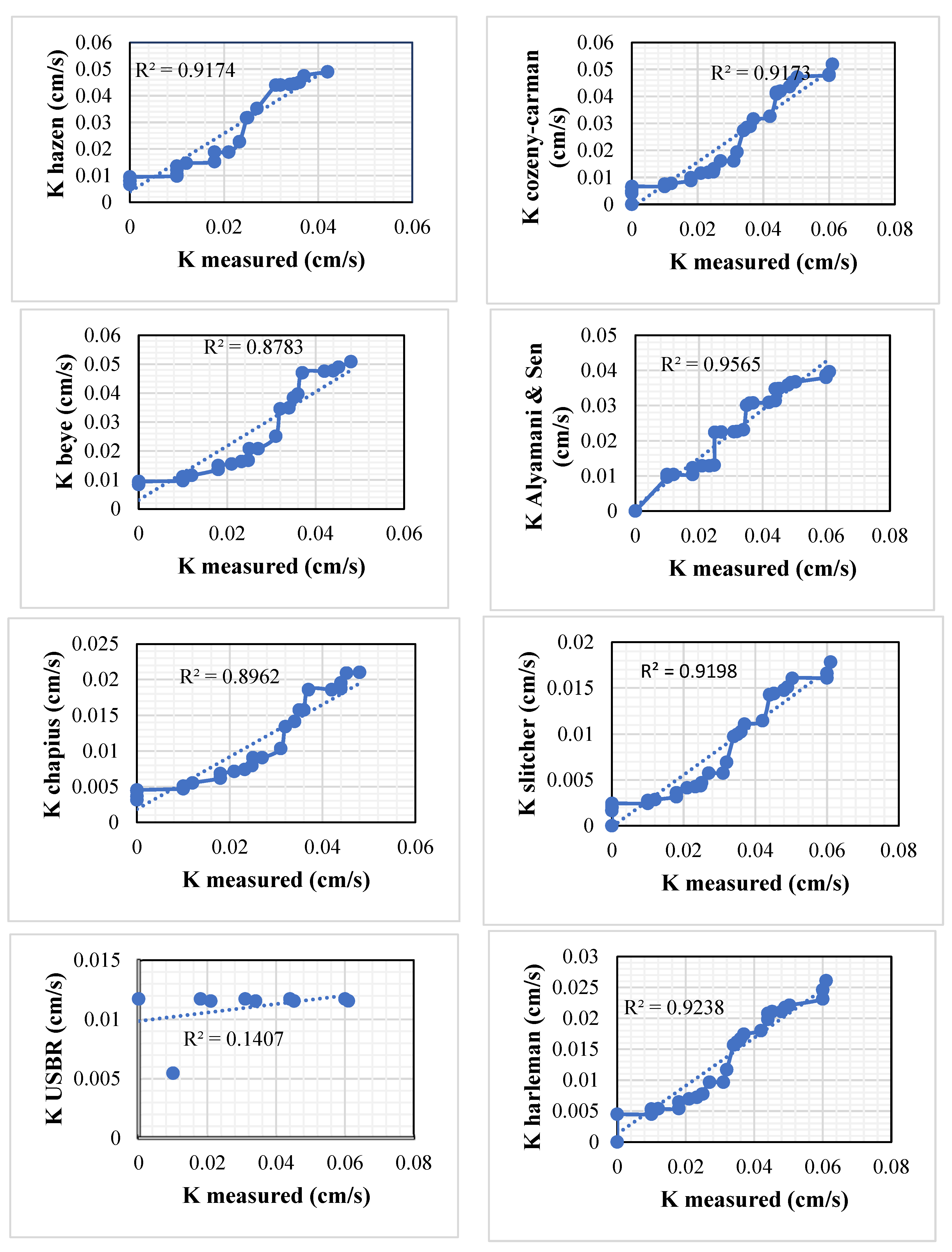
3.3. Estimation of Hydraulic Conductivity Using Empirical Relationship
3.4. Comparison of Measured and Empirical Hydraulic Conductivity
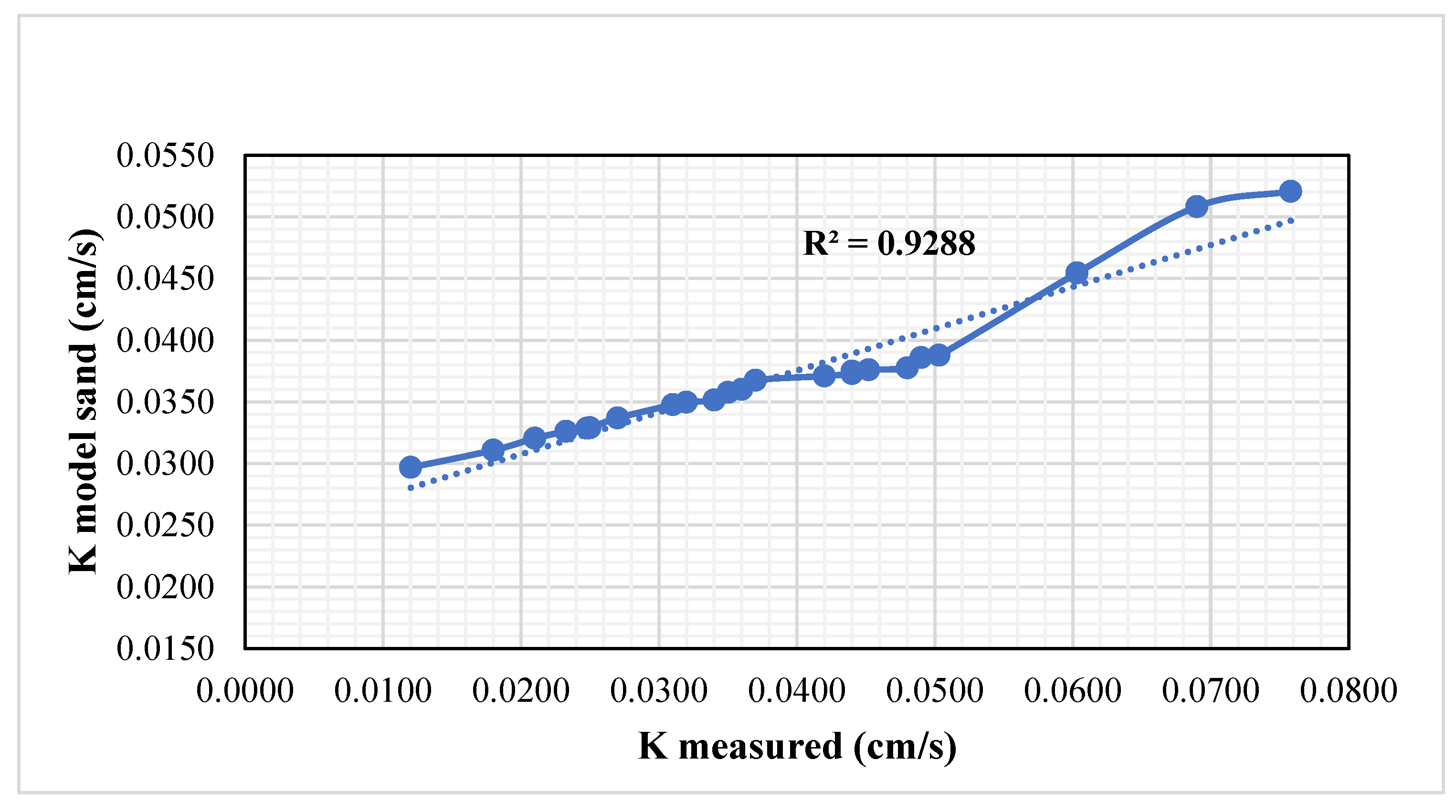
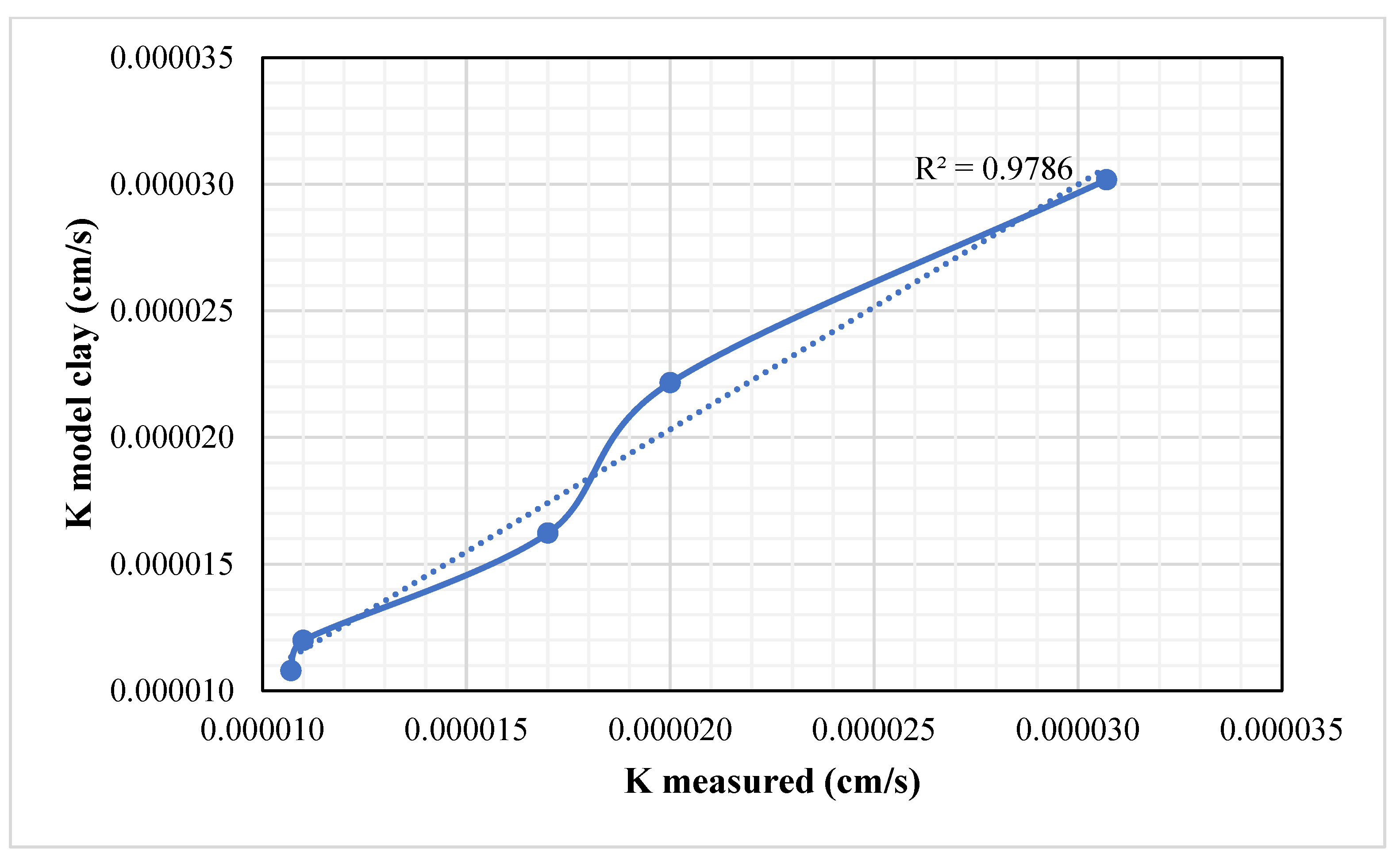
3.5. Development of Statistical Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
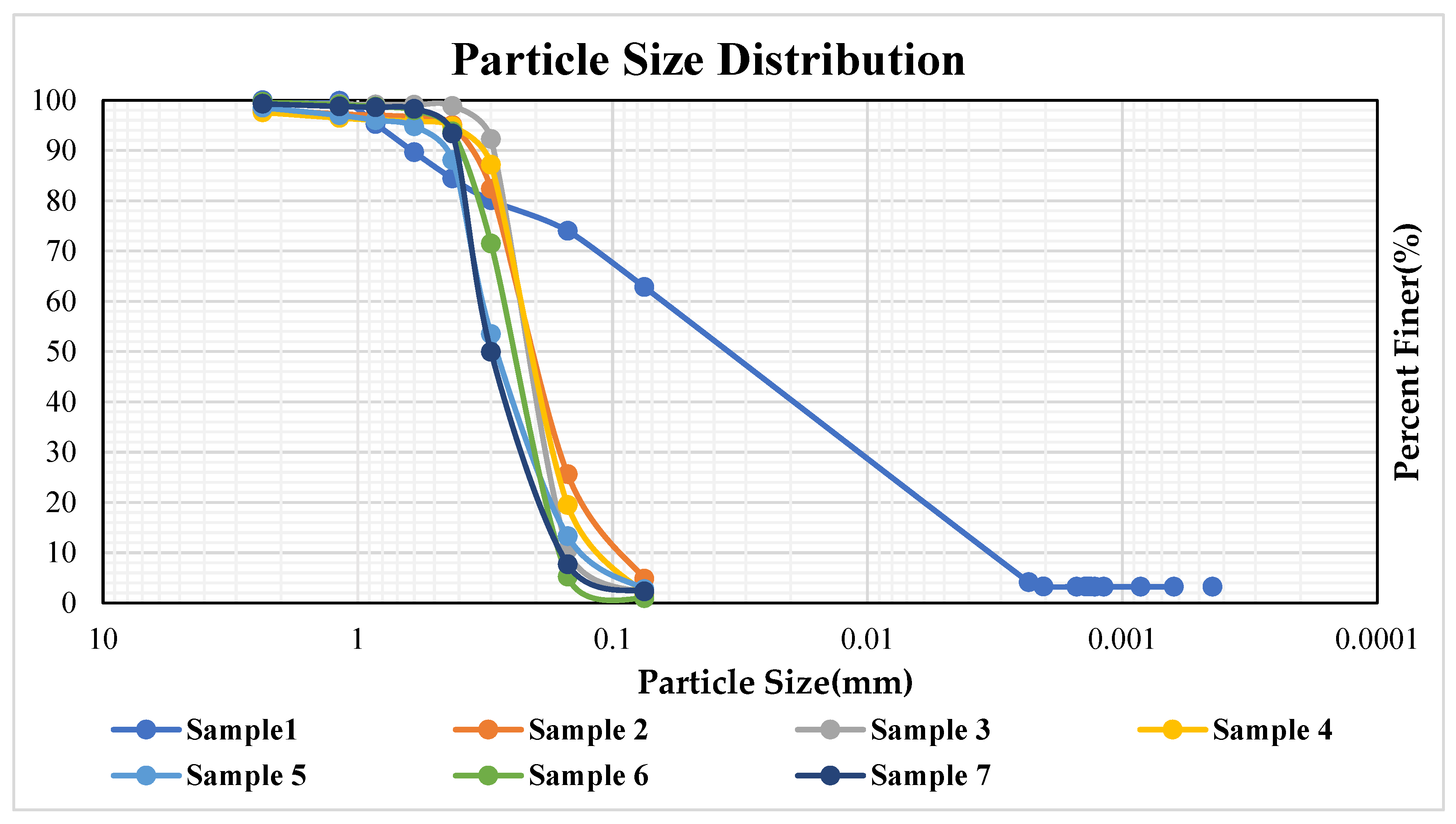


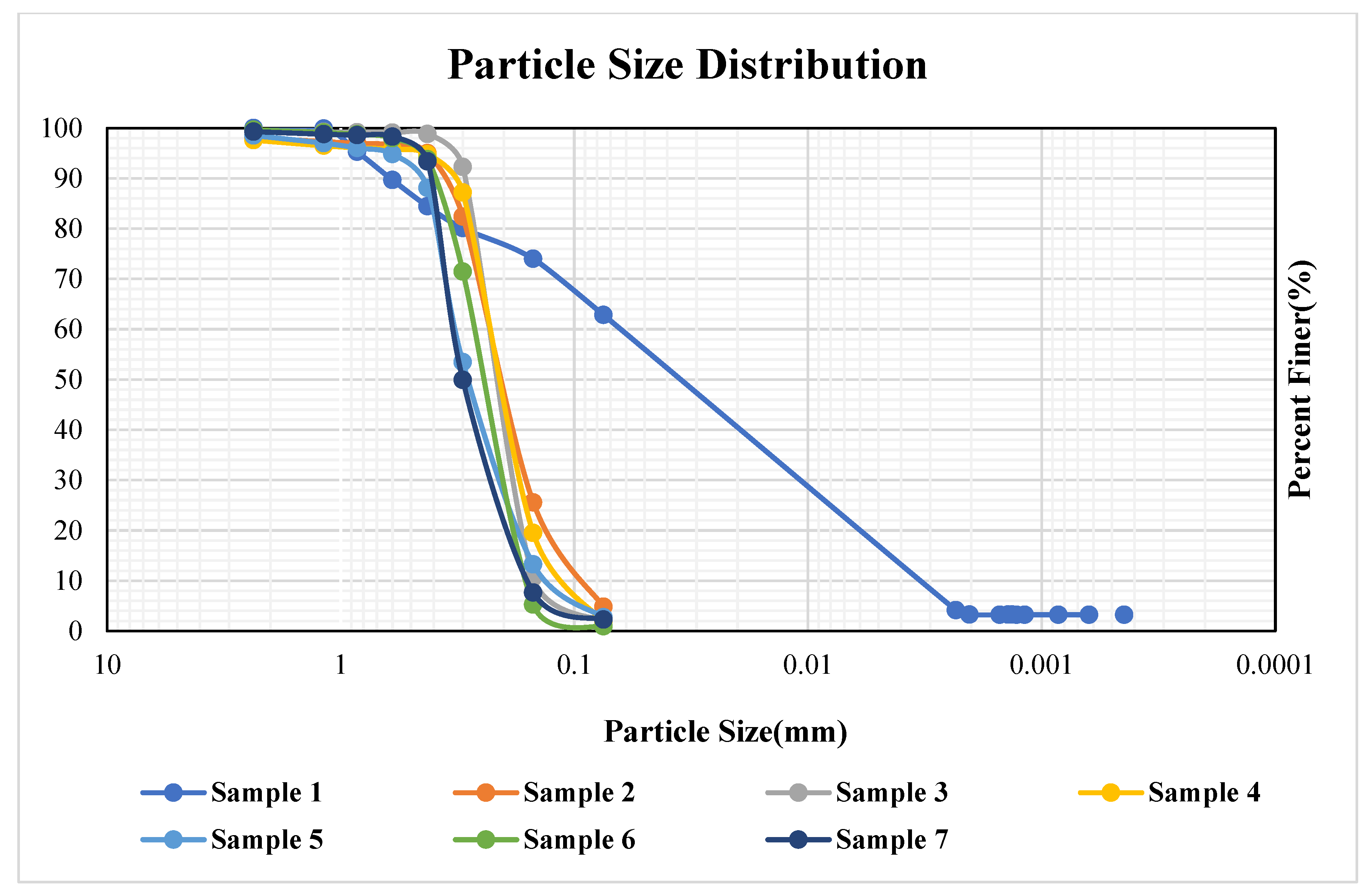
| Sample | %Silt | %Clay | %Sand | Classification |
|---|---|---|---|---|
| 1 | 48 | 10 | 42 | Silt Loam |
| 2 | 13 | 2 | 85 | Loamy Sand |
| 3 | 11 | 1 | 89 | Sand |
| 4 | 7 | 0.5 | 92.5 | Sand |
| 5 | 20 | 2 | 78 | Loamy Sand |
| 6 | 19 | 2 | 79 | Sand |
| 7 | 7 | 0.5 | 92.5 | Sand |
| Sample | %Silt | %Clay | %Sand | Classification |
|---|---|---|---|---|
| 1 | 61 | 10 | 29 | Silt Loam |
| 2 | 5 | 1 | 84 | Sand |
| 3 | 6 | 0.5 | 93.5 | Sand |
| 4 | 0.5 | 7 | 92.5 | Sand |
| 5 | 12 | 1 | 87 | Sand |
| 6 | 5 | 0.2 | 94.8 | Sand |
| 7 | 4 | 1 | 85 | Sand |
| Sample | %Silt | %Clay | %Sand | Classification |
|---|---|---|---|---|
| 1 | 60 | 10 | 30 | Silt Loam |
| 2 | 17 | 3 | 80 | Loamy Sand |
| 3 | 11 | 1 | 89 | Sand |
| 4 | 35 | 7 | 58 | Sandy Loam |
| 5 | 10 | 2 | 88 | Sand |
| 6 | 8 | 2 | 90 | Sand |
| 7 | 5 | 2 | 93 | Sand |
| Sample | %Silt | %Clay | %Sand | Classification |
|---|---|---|---|---|
| 1 | 52 | 9 | 39 | Silt Loam |
| 2 | 21 | 5 | 74 | Loamy Sand |
| 3 | 10 | 2 | 88 | Sand |
| 4 | 8 | 1 | 91 | Sand |
| 5 | 19 | 3 | 88 | Loamy Sand |
| 6 | 22 | 4 | 74 | Loamy Sand |
| 7 | 6 | 1.5 | 92.5 | Sand |
| Location 2 | Location 3 | Location 4 | Location 5 | |
|---|---|---|---|---|
| Sample 1 | 0.0000107 | 0.0000113 | 0.0000185 | 0.000025 |
| Sample 2 | 0.044 | 0.031 | 0.032 | 0.069 |
| Sample 3 | 0.018 | 0.037 | 0.034 | 0.036 |
| Sample 4 | 0.025 | 0.018 | 0.027 | 0.045 |
| Sample 5 | 0.055 | 0.058 | 0.053 | 0.06 |
| Sample 6 | 0.012 | 0.042 | 0.021 | 0.048 |
| Sample 7 | 0.035 | 0.049 | 0.044 | 0.06 |
References
- Chandel, A.; Shankar, V. Evaluation of empirical relationships to estimate the hydraulic conductivity of borehole soil samples. Hydraul. Eng. 2021, 28, 368–377. [Google Scholar] [CrossRef]
- Albano, R.; Lacava, T.; Mazzariello, A.; Manfreda, S.; Adamowski, J.; Sole, A. How Can Seasonality Influence the Performance of Recent Microwave Satellite Soil Moisture Products? Remote Sens. 2024, 16, 3044. [Google Scholar] [CrossRef]
- Albano, R.; Manfreda, S.; Celano, G. MY SIRR: Minimalist agro-hYdrological model for Sustainable IRRigation management—Soil moisture and crop dynamics. SoftwareX 2017, 6, 107–117. [Google Scholar] [CrossRef]
- Mazzariello, A.; Albano, R.; Lacava, T.; Manfreda, S.; Sole, A. Intercomparison of recent microwave satellite soil moisture products on European ecoregions. J. Hydrol. 2023, 626, 130311. [Google Scholar] [CrossRef]
- Říha, J.; Petrula, L.; Hala, M.; Alhasan, Z. Assessment of empirical formulae for determining the hydraulic conductivity of glass beads. J. Hydrol. Hydromech. 2018, 66, 337–347. [Google Scholar] [CrossRef]
- Rosas, J.; Lopez, O.; Missimer, T.M.; Coulibaly, K.M.; Dehwah, A.H.; Sesler, K.; Lujan, L.R.; Mantilla, D. Determination of hydraulic conductivity from grain-size distribution for different depositional environments. Groundwater 2014, 52, 399–413. [Google Scholar] [CrossRef]
- Goodarzi, M.R.; Vazirian, M.; Niazkar, M. Hydraulic Conductivity Estimation: Comparison of Empirical Formulas Based on New Laboratory Experiments. Water 2024, 16, 1854. [Google Scholar] [CrossRef]
- Hong, B.; Li, X.; Wang, L.; Li, L.; Xue, Q.; Meng, J. Using the effective void ratio and specific surface area in the Kozeny–Carman equation to predict the hydraulic conductivity of loess. Water 2019, 12, 24. [Google Scholar] [CrossRef]
- Chandel, A.; Shankar, V.; Alam, M.A. Experimental investigations for assessing the influence of fly ash on the flowthrough porousmedia in Darcy regime. Water Sci. Technol. 2021, 83, 1028–1038. [Google Scholar] [CrossRef]
- Cheng, C.; Chen, X. Evaluation of methods for determination of hydraulic properties in an aquifer–aquitard system hydrologically connected to a river. Hydrogeol. J. 2007, 15, 669–678. [Google Scholar] [CrossRef]
- Odong, J. Evaluation of empirical formulae for determination of hydraulic conductivity based on grain-size analysis. J. Am. Sci. 2007, 3, 54–60. [Google Scholar]
- Song, J.; Chen, X.; Cheng, C.; Wang, D.; Lackey, S.; Xu, Z. Feasibility of grain-size analysis methods for determination of vertical hydraulic conductivity of streambeds. J. Hydrol. 2009, 375, 428–437. [Google Scholar] [CrossRef]
- Ishaku, J.M.; Gadzama, E.W.; Kaigama, U. Evaluation of empirical formulae for the determination of hydraulic conductivity based on grain-size analysis. J. Geol. Min. Res. 2011, 3, 105–113. [Google Scholar]
- Pliakas, F.; Petalas, C. Determination of Hydraulic Conductivity of Unconsolidated River Alluvium from Permeameter Tests, Empirical Formulas and Statistical Parameters Effect Analysis. Water Resour. Manag. 2011, 25, 2877–2899. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, S.R.; Kim, Y.T.; Go, G.H. Estimation of saturated hydraulic conductivity of Korean weathered granite soils using a regression analysis. Geomech. Eng. 2015, 9, 101–113. [Google Scholar] [CrossRef]
- Naeej, M.; Naeej, M.R.; Salehi, J.; Rahimi, R. Hydraulic conductivity prediction based on grain-size distribution using M5 model tree. Geomech. Geoengin. 2017, 12, 107–114. [Google Scholar] [CrossRef]
- Obianyo, J.I. Investigation of Empirical Models for Hydraulic Conductivity from Grain-size Distribution 1 1 Obianyo J.I. and 1 Eboh. FUPRE J. Sci. Ind. Res. 2020, 4, 60–70. [Google Scholar]
- Muhammad, S.; Ehsan, M.I.; Khalid, P. Optimizing exploration of quality groundwater through geophysical investigations in district Pakpattan, Punjab, Pakistan. Arab. J. Geosci. 2022, 15, 721. [Google Scholar] [CrossRef]
- Bhutta, M.N.; Smedema, L.K. One hundred years of waterlogging and salinity control in the Indus valley, Pakistan: A historical review. Irrig. Drain. J. Int. Comm. Irrig. Drain. 2007, 56, S81–S90. [Google Scholar] [CrossRef]
- Sikandar, P.; Bakhsh, A.; Arshad, M.; Rana, T. The use of vertical electrical sounding resistivity method for the location of low salinity groundwater for irrigation in Chaj and Rachna Doabs. Environ. Earth Sci. 2010, 60, 1113–1129. [Google Scholar] [CrossRef]
- Hasan, M.; Shang, Y.; Akhter, G.; Jin, W. Delineation of contaminated aquifers using integrated geophysical methods in Northeast Punjab, Pakistan. Environ. Monit. Assess. 2020, 192, 12. [Google Scholar] [CrossRef] [PubMed]
- Zakir-Hassan, G.; Hassan, F.R.; Punthakey, J.; Shabir, G. Challenges for groundwater-irrigated agriculture and management opportunities in Punjab province of Pakistan. Int. J. Agric. Nutr. 2022, 4, 61–73. [Google Scholar] [CrossRef]
- Qureshi, A.S. Challenges and opportunities of groundwater management in Pakistan. In Groundwater of South Asia; Springer: Berlin/Heidelberg, Germany, 2018; pp. 735–757. [Google Scholar]
- Watto, M.A.; Mugera, A.W. Groundwater depletion in the Indus Plains of Pakistan: Imperatives, repercussions and management issues. Int. J. River Basin Manag. 2016, 14, 447–458. [Google Scholar] [CrossRef]
- Razzaq, A.; Liu, H.; Xiao, M.; Mehmood, K.; Shahzad, M.A.; Zhou, Y. Analyzing past and future trends in Pakistan’s groundwater irrigation development: Implications for environmental sustainability and food security. Environ. Sci. Pollut. Res. 2023, 30, 35413–35429. [Google Scholar] [CrossRef]
- Ashiq, M.M.; Rehman, H.U.; Khan, N.M. Impact of large diameter recharge wells for reducing groundwater depletion rates in an urban area of Lahore, Pakistan. Environ. Earth Sci. 2020, 79, 403. [Google Scholar] [CrossRef]
- Qureshi, A.S. Improving food security and livelihood resilience through groundwater management in Pakistan. Glob. Adv. Res. J. Agric. Sci. 2015, 4, 687–710. [Google Scholar]
- Iqbal, J.; Su, C.; Rashid, A.; Yang, N.; Baloch, M.Y.; Talpur, S.A.; Ullah, Z.; Rahman, G.; Rahman, N.U.; Sajjad, M.M. Hydrogeochemical assessment of groundwater and suitability analysis for domestic and agricultural utility in southern Punjab, Pakistan. Water 2021, 13, 3589. [Google Scholar] [CrossRef]
- Lytton, B.S.L.; Ali, A.; Garthwaite, B.; Punthakey, J.F. Groundwater in Pakistan’s Indus Basin: Present and Future Prospects. 2021. Available online: https://documents.worldbank.org/en/publication/documents-reports/documentdetail/501941611237298661/groundwater-in-pakistan-s-indus-basin-present-and-future-prospects (accessed on 20 December 2024).
- Qureshi, A.S. Groundwater governance in pakistan: From colossal development to neglected management. Water 2020, 12, 3017. [Google Scholar] [CrossRef]
- Carter, M.R.; Gregorich, E.G. Soil Sampling and Methods of Analysis; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- KR, A.D. Soil Mechanics and Foundation Engineering, 6th ed.; Standard Publishers Distributors: Delhi, India, 2006; pp. 14–22. [Google Scholar]
- ASTM D7928; Soil Hydrometer Testing: Sedimentation Method Techniques & Equipment. ASTM: West Conshohocken, PA, USA, 2007.
- ASTM D2434-19; Standard Test Method for Permeability of Granular Soils (Constant Head). ASTM: West Conshohocken, PA, USA, 2009.
- Rushton, K.R. Groundwater Hydrology: Conceptual and Computational Models; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Hazen, A. Some physical properties of sand gravel with special reference to their use in filtration. In State Sanitation: A Review of the Work of the Massachusetts State Board of Health Volume II; Harvard University Press: Cambridge, MA, USA; London, UK, 1917; pp. 232–248. [Google Scholar]
- Slichter, C.S. Theoretical Investigation of the Motion of Ground Waters; U.S. Department of the Interior, Geological Survey, Water Resources Division, Ground Water Branch: Olivette, MO, USA, 1899; pp. 295–384. [Google Scholar]
- Terzaghi, K. Principles of soil mechanics III—Determination of Permeability of Clay. Eng. News-Rec. 1925, 95, 19–27. [Google Scholar]
- Carman, P.C. Flow of Gases Through Porous Media; Academic Press Inc.: New York, NY, USA, 1956. [Google Scholar]
- Carman, P.C. Fluid flow through granular beds. Trans. Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Kozeny, J. Via capillary conduit the water in the ground. R. Acad. Sci. Vienna Proc. Cl. I 1927, 136, 271–306. [Google Scholar]
- Harleman, D.R.F.; Mehlhorn, P.F.; Rumer, R.R., Jr. Dispersion-permeability correlation in porous media. J. Hydraul. Div. 1963, 89, 67–85. [Google Scholar] [CrossRef]
- Beyer, W. On the determination of hydraulic conductivity of gravels and sands from grain-size distributions. Wasserwirtsch.-Wassertech. 1964, 14, 165–169. [Google Scholar]
- Cudworth, A.G. Flood Hydrology Manual: A Water Resources Technical Publication; U.S. Department of the Interior, Bureau of Reclamation: Denver, CO, USA, 1989. [Google Scholar]
- Alyamani, M.S.; Şen, Z. Determination of hydraulic conductivity from complete grain-size distribution curves. Groundwater 1993, 31, 551–555. [Google Scholar] [CrossRef]
- Chapuis, R.P.; Dallaire, V.; Marcotte, D.; Chouteau, M.; Acevedo, N.; Gagnon, F. Evaluating the hydraulic conductivity at three different scales within an unconfined sand aquifer at Lachenaie, Quebec. Can. Geotech. J. 2005, 42, 1212–1220. [Google Scholar] [CrossRef]
- Sepahvand, A.; Singh, B.; Sihag, P.; Samani, A.N.; Ahmadi, H.; Nia, S.F. Assessment of the various soft computing techniques to predict sodium absorption ratio (SAR). ISH J. Hydraul. Eng. 2021, 27, 124–135. [Google Scholar] [CrossRef]
- Sihag, P.; Singh, V.P.; Angelaki, A.; Kumar, V.; Sepahvand, A.; Golia, E. Modelling of infiltration using artificial intelligence techniques in semi-arid Iran. Hydrol. Sci. J. 2019, 64, 1647–1658. [Google Scholar] [CrossRef]

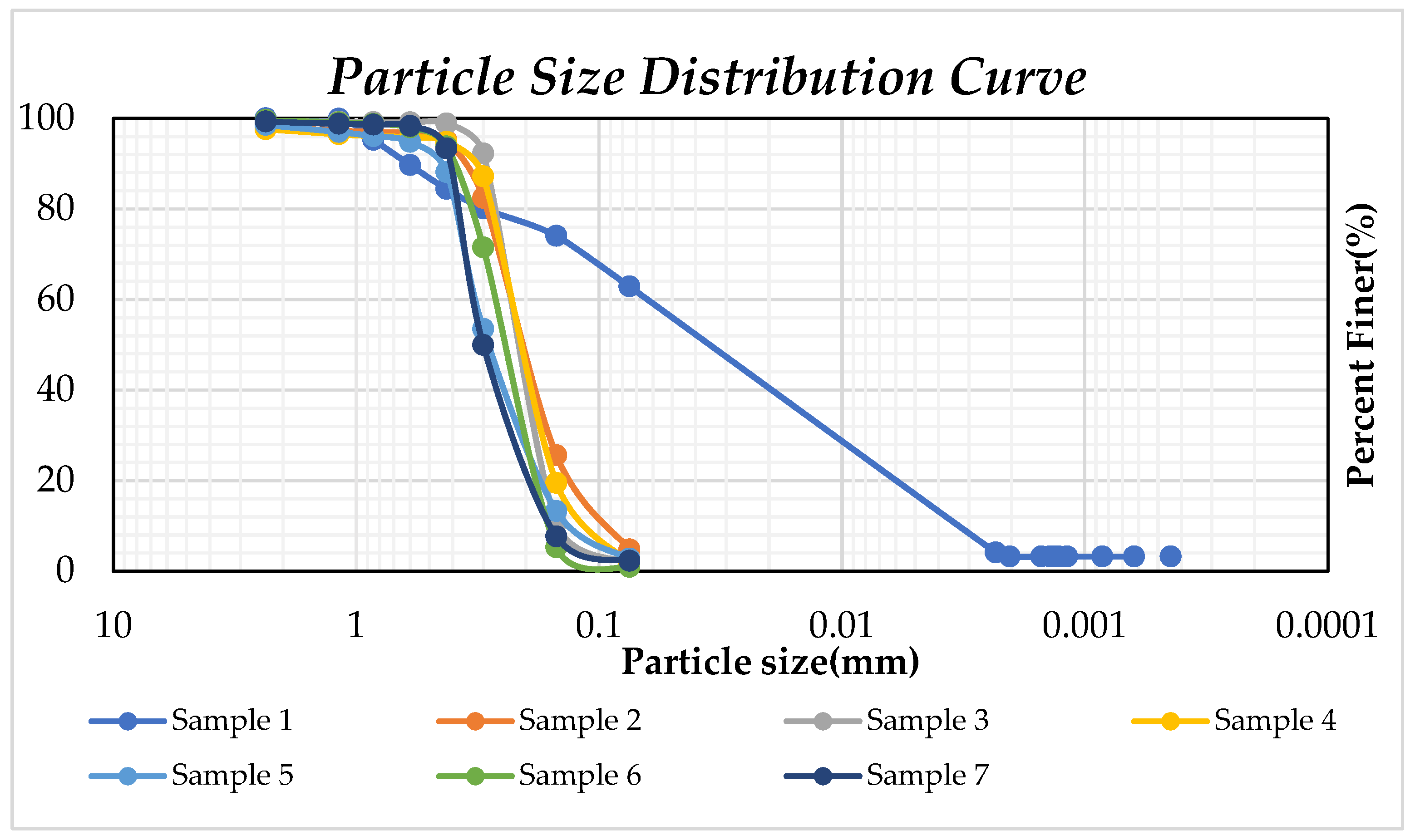
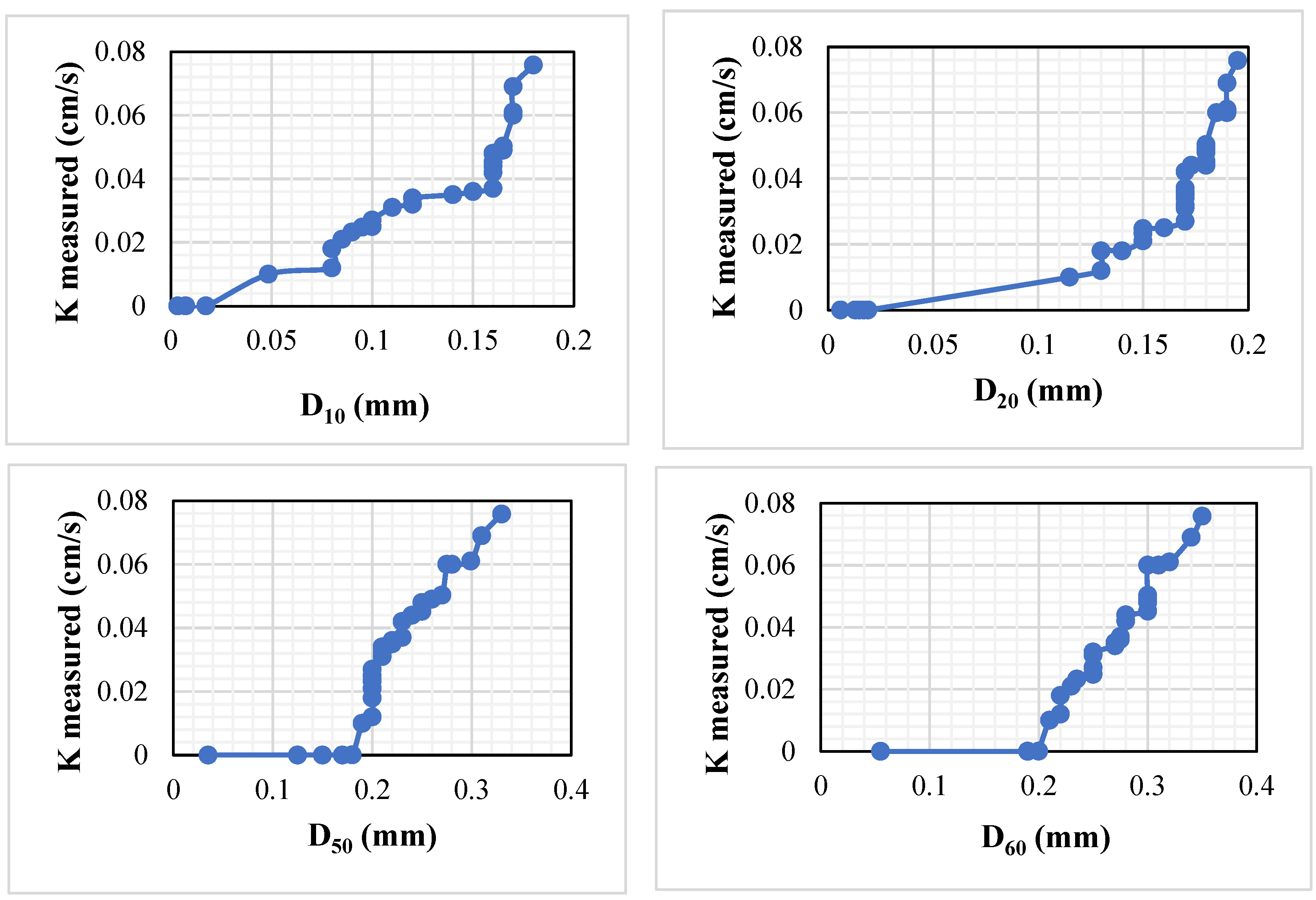

| Researcher | Area of Study | Techniques | Conclusion |
|---|---|---|---|
| J. Odong [11] | China | Empirical relationship | Kozeny Carman was the best estimator |
| A Chandel [1] | India | Empirical relationships, lab methods, and regression analysis | Developed model was the best estimator |
| J. Song [12] | Nebraska and Elkhorn River | Falling-head permeameter test | Changed C values computed stream bed Kv |
| J. M. Ishaku [13] | Nigeria | Empirical equations | Terzaghi and K-C formulas were the best estimators |
| F. Pliakas [14] | Greece | Lab method, empirical relationship | Loudon formula was most accurate |
| J. Rosas [6] | Four depositional environments at global locations | Lab test and the empirical relationship | Empirical hydraulic conductivity does not correlate with measured values |
| S. Yoon [15] | South Korea | Regression analysis | Regression model showed R2 = 0.92 |
| M. Naeej [16] | Iran | Lab method and model tree method | Model tree formula provided accurate results |
| J. Michael [17] | Nigeria | Seven empirical models and constant head method | Kozeny model was the best estimator |
| Sample | %Silt | %Clay | %Sand | Classification |
|---|---|---|---|---|
| 1 | 55 | 8 | 37 | Silt Loam |
| 2 | 20 | 6 | 74 | Sandy Loam |
| 3 | 8 | 2.6 | 89.4 | Sand |
| 4 | 15 | 5 | 80 | Loamy Sand |
| 5 | 10 | 3 | 87 | Sand |
| 6 | 4.3 | 1 | 94.7 | Sand |
| 7 | 6.6 | 1 | 92.4 | Sand |
| Hazen (cm/s) | Slitcher (cm/s) | Terzaghi (cm/s) | K-C (cm/s) | Harleman (cm/s) | Beyer (cm/s) | USBR (cm/s) | A&S (cm/s) | Chapius (cm/s) |
|---|---|---|---|---|---|---|---|---|
| - | 0.00000141 | - | 0.00000303 | 0.000014 | - | - | 0.0000117 | - |
| - | 0.0043 | - | 0.0119 | 0.0072 | 0.0155 | - | 0.0103 | 0.0071 |
| 0.0474 | 0.0160 | - | 0.0478 | 0.0218 | 0.0508 | - | 0.0380 | 0.0212 |
| 0.0153 | 0.0047 | - | 0.0132 | 0.0078 | 0.0168 | - | 0.0129 | 0.0795 |
| 0.0317 | 0.0097 | - | 0.0274 | 0.0162 | 0.0349 | 0.01173 | 0.0227 | 0.0134 |
| 0.0490 | 0.0161 | - | 0.0471 | 0.0232 | 0.0527 | - | 0.0347 | 0.0210 |
| 0.04503 | 0.0143 | - | 0.0409 | 0.0221 | 0.0490 | 0.01156 | 0.0309 | 0.0185 |
| K (lab) | Hazen | Slitcher | K-C | Harleman | Beyer | USBR | A&S | Chapius |
|---|---|---|---|---|---|---|---|---|
| 0.0000307 | - | 0.00000141 | 0.00000303 | 0.000014 | - | - | 0.0000117 | - |
| 0.02327 | - | 0.0043 | 0.0119 | 0.0072 | 0.0155 | - | 0.0103 | 0.0071 |
| 0.0503 | 0.0474 | 0.0160 | 0.0478 | 0.0218 | 0.0508 | - | 0.0380 | 0.0212 |
| 0.0248 | 0.0153 | 0.0047 | 0.0132 | 0.0078 | 0.0168 | - | 0.0129 | 0.0795 |
| 0.0452 | 0.0317 | 0.0097 | 0.0274 | 0.0162 | 0.0349 | 0.01173 | 0.0227 | 0.0134 |
| 0.0610 | 0.0490 | 0.0161 | 0.0471 | 0.0232 | 0.0527 | - | 0.0347 | 0.0210 |
| 0.0758 | 0.04503 | 0.0143 | 0.0409 | 0.0221 | 0.0490 | 0.01156 | 0.0309 | 0.0185 |
| K Measured | U | Porosity (n) | D50 | |
|---|---|---|---|---|
| K measured | 1 | |||
| U | 0.015033 | 1 | ||
| Porosity (n) | 0.045516 | −0.9386189 | 1 | |
| D50 | −0.19974 | 0.31038783 | −0.19459 | 1 |
| U | Porosity (n) | D50 | K Measured | |
|---|---|---|---|---|
| U | 1 | |||
| Porosity (n) | 0.763178093 | 1 | ||
| D50 | 0.862107974 | 0.448747 | 1 | |
| K measured | 0.805867619 | 0.974282 | 0.5111618 | th1 |
| Statistical Parameter | RMSE (cm/s) | MAE (cm/s) | Cc (Dimensionless) |
|---|---|---|---|
| Hazen | 0.007 | 0.006 | 0.917 |
| Kozeny–Carman | 0.008 | 0.007 | 0.917 |
| Slitcher | 0.025 | 0.021 | 0.45 |
| Alyamani and Sen | 0.01 | 0.007 | 0.956 |
| Harleman et al. | 0.019 | 0.017 | 0.924 |
| Beyer | 0.006 | 0.05 | 0.889 |
| USBR | 0.01 | 0.009 | 0.423 |
| Chapius et al. | 0.017 | 0.014 | 0.906 |
| Developed model | 0.013 | 0.0011 | 0.927 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waleed, M.; Inam, M.A.; Albano, R.; Samad, A.; Farid, H.U.; Shoaib, M.; Ali, M.U. Statistical Model Development for Estimating Soil Hydraulic Conductivity Through On-Site Investigations. Hydrology 2025, 12, 55. https://doi.org/10.3390/hydrology12030055
Waleed M, Inam MA, Albano R, Samad A, Farid HU, Shoaib M, Ali MU. Statistical Model Development for Estimating Soil Hydraulic Conductivity Through On-Site Investigations. Hydrology. 2025; 12(3):55. https://doi.org/10.3390/hydrology12030055
Chicago/Turabian StyleWaleed, Muhammad, Muhammad Azhar Inam, Raffaele Albano, Abdul Samad, Hafiz Umar Farid, Muhammad Shoaib, and Muhammad Usman Ali. 2025. "Statistical Model Development for Estimating Soil Hydraulic Conductivity Through On-Site Investigations" Hydrology 12, no. 3: 55. https://doi.org/10.3390/hydrology12030055
APA StyleWaleed, M., Inam, M. A., Albano, R., Samad, A., Farid, H. U., Shoaib, M., & Ali, M. U. (2025). Statistical Model Development for Estimating Soil Hydraulic Conductivity Through On-Site Investigations. Hydrology, 12(3), 55. https://doi.org/10.3390/hydrology12030055









