Towards a Classification of Tunisian Dams for Enhanced Water Scarcity Governance: Parametric or Non-Parametric Approaches?
Abstract
1. Introduction
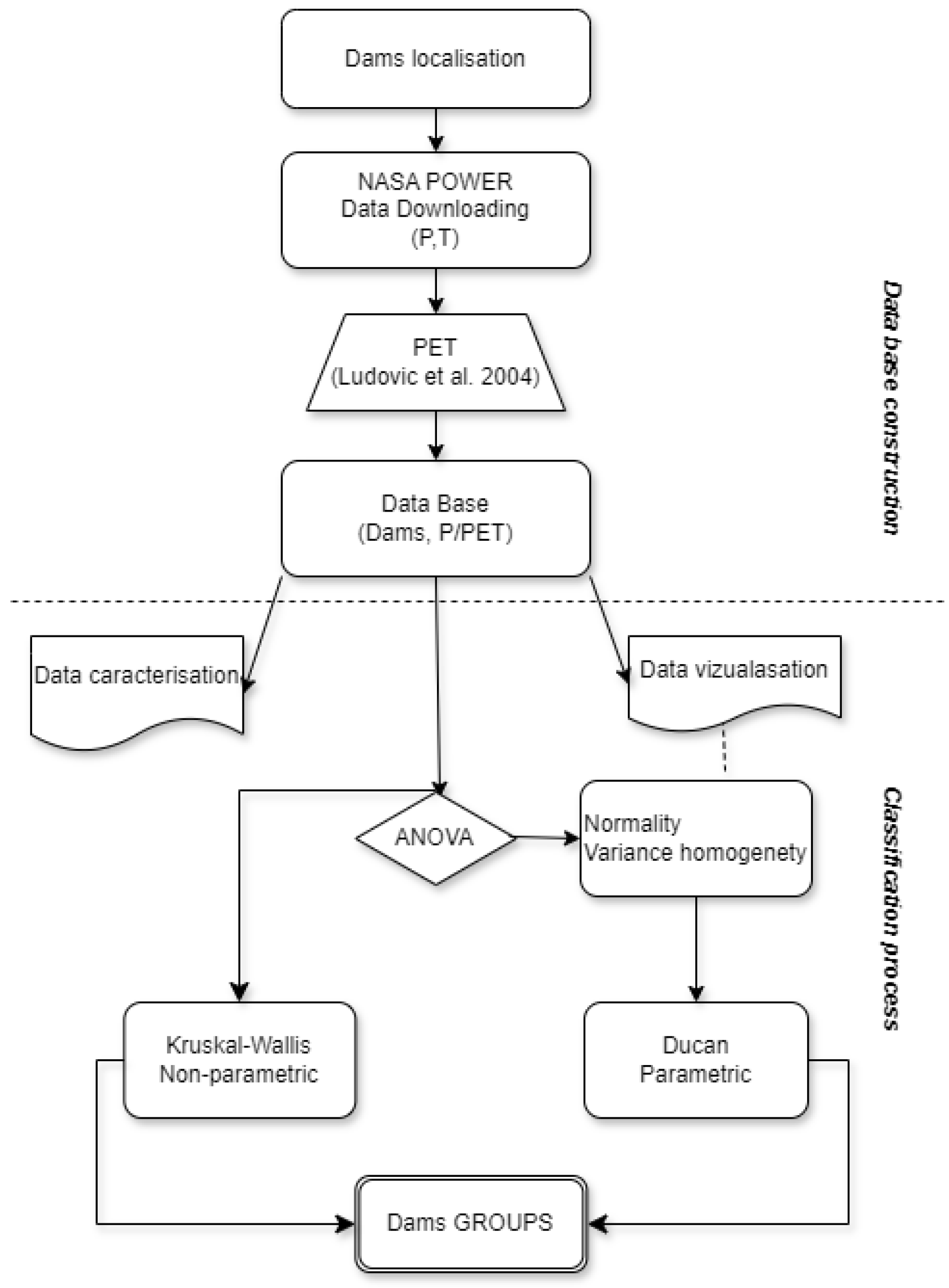
2. Material and Methods
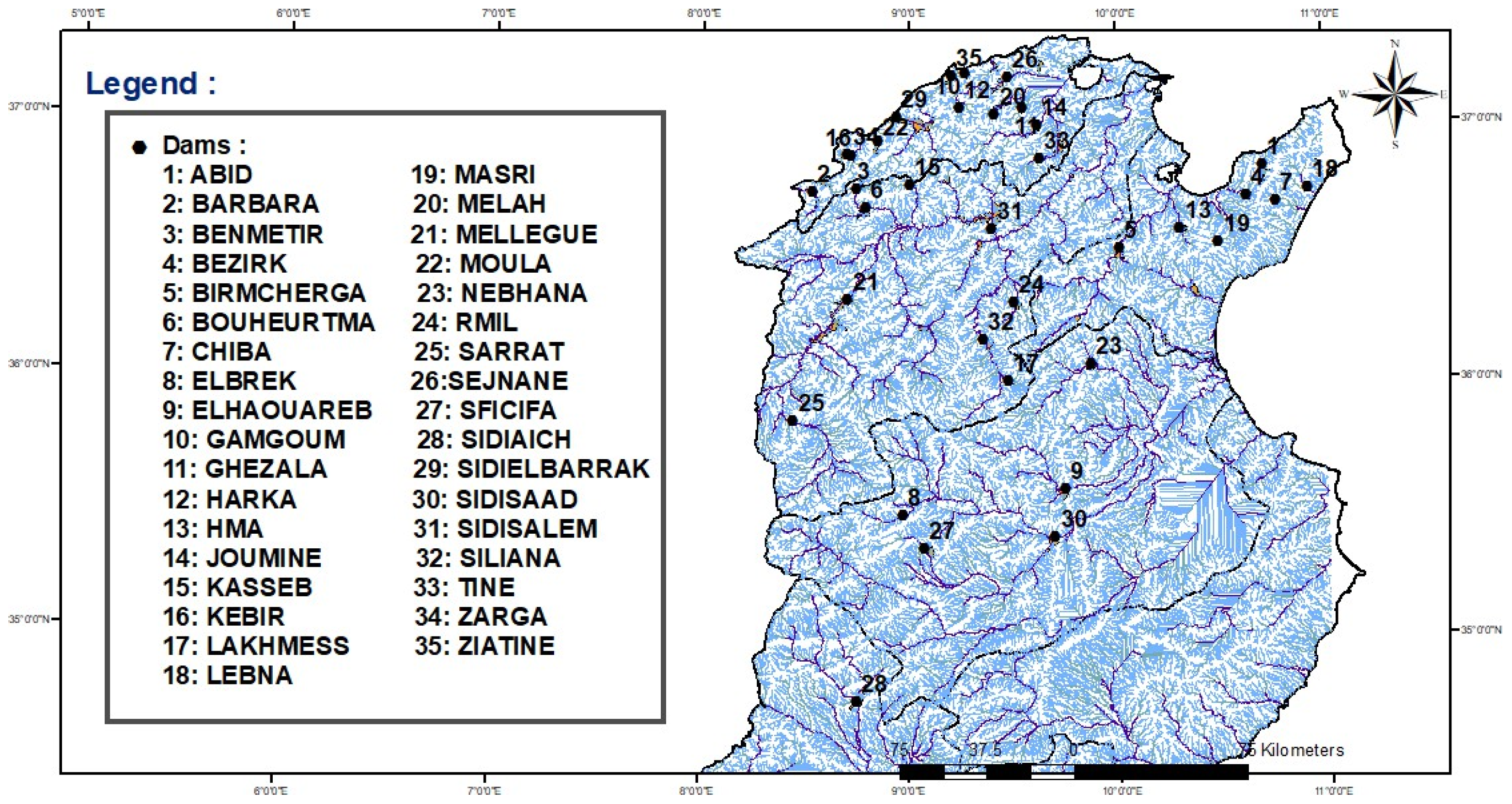
2.1. Database Construction
2.2. Method
3. Results and Discussion
3.1. The Main Descriptive Statistics of the Data
3.2. Normality Assumptions
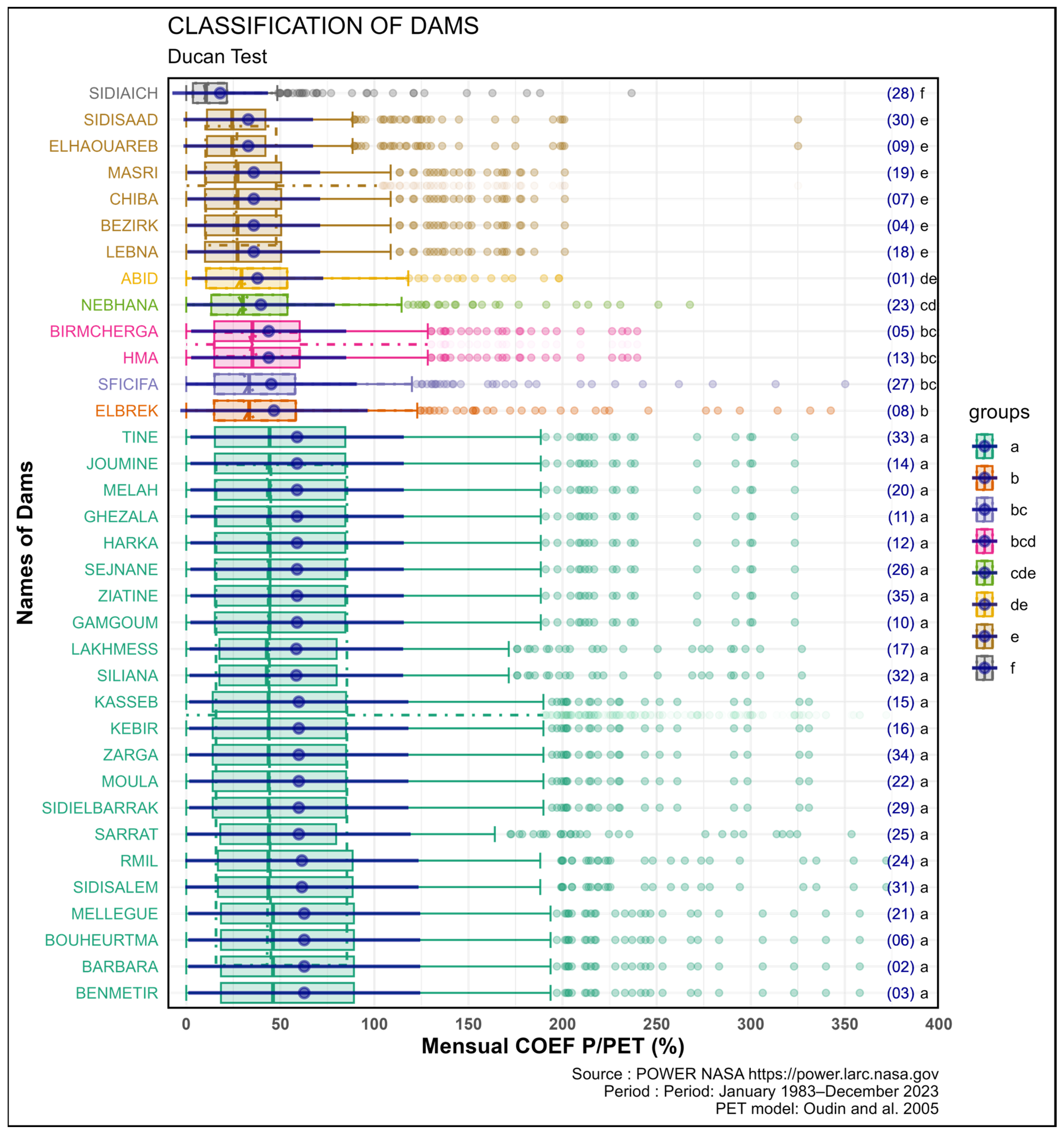
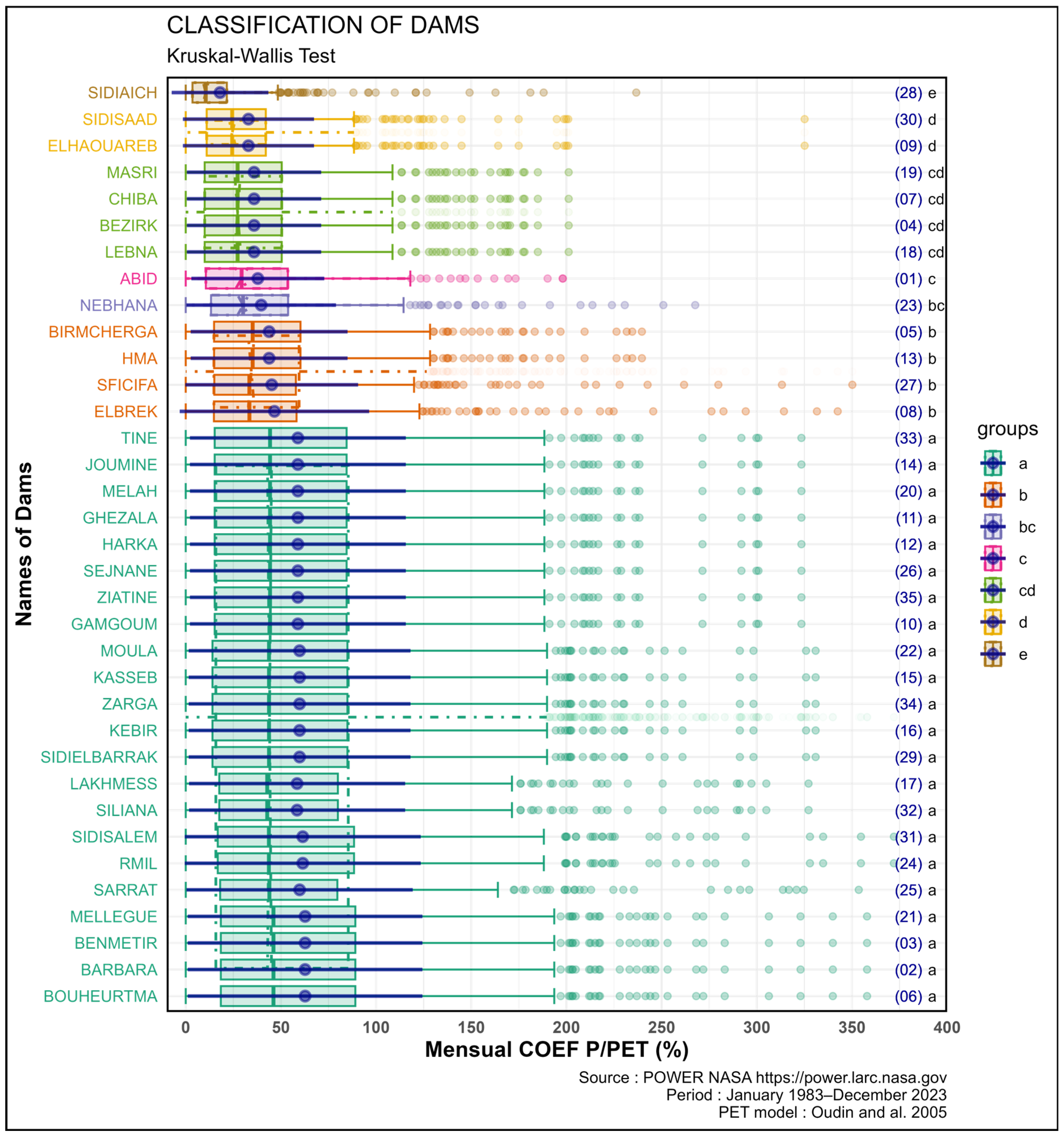
3.3. Classification Test
- Class 1 corresponds to group a of both the Kruskal–Wallis and Duncan’s tests. This class includes the dams {(03), (02), (09), (06), (21), (31), (24), (25), (29), (22), (34), (16), (15), (32), (17), (10), (35), (26), (12), (11), (20), (14), (33)}. These dams are located in the extreme northern watershed and the Medjerda watershed, which together form the “water tower” of Tunisia. They should be considered as a single hydraulic basin, as this basin serves as the primary source for potential water transfers. Furthermore, when updating the agricultural map, it is essential to avoid adopting crops that could be cultivated locally (within the hydraulic basin), and instead produce them elsewhere using transferred water resources.
- Class 2: This class includes the dams {(08), (27), (13), (05)}. They are located along the Tunisian Ridge, a natural barrier separating semi-arid regions from sub-humid regions.
- Class 3: This class comprises the dams {(01), (18), (04), (07), (19), (09), (30)}. This group of dams is located in the areas adjacent the Tunisian Ridge. These regions are agriculturally intensive, with significant pressure on water resources, often requiring careful allocation between drinking water and irrigation needs.
- Class 4: Dams treated as unique systems. Two systems are identified: {(23)} and {(28)}.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ben Boubaker, H.; Benzarti, Z.; Hénia, L. Tunisia’s water resources: Climate constraints and human pressure. In Eau et Environnement: Tunisie et Milieux Méditerranéens; Arnould, P., Hotyat, M., Eds.; Sociétés, Espaces, Temps; ENS Éditions: Lyon, France, 2003; pp. 37–52. ISBN 978-2-84788-422-7. [Google Scholar]
- Cherif, A. Tunisia’s water issue in north-eastern regions: The need, local resources, and inter-regional transfers. In Eau et Environnement: Tunisie et Milieux Méditerranéens; Arnould, P., Hotyat, M., Eds.; Sociétés, Espaces, Temps; ENS Éditions: Lyon, France, 2003; pp. 53–61. ISBN 978-2-84788-422-7. [Google Scholar]
- FAO. Country Profile—Tunisia; Food and Agriculture Organization of the United Nations: Rome, Italy, 2015; p. 20. [Google Scholar]
- Falkenmark, M.; Naturvetenskapliga, F. The Massive Water Scarcity Now Threatening Africa—Why Isn’t It Being Addressed? Ambio 1989, 18, 112–118. [Google Scholar]
- Caretta, M.A.; Mukherji, A.; Arfanuzzaman, M.; Betts, R.A.; Gelfan, A.; Hirabayashi, Y.; Lissner, T.K.; Liu, J.; Lopez Gunn, E.; Morgan, R.; et al. Water. In Climate Change 2022: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Pörtner, H.-O., Roberts, D.C., Tignor, M., Poloczanska, E.S., Mintenbeck, K., Alegría, A., Craig, M., Langsdorf, S., Löschke, S., Möller, V., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022; pp. 551–712. [Google Scholar]
- Tramblay, Y.; Koutroulis, A.; Samaniego, L.; Vicente-Serrano, S.M.; Volaire, F.; Boone, A.; Le Page, M.; Llasat, M.C.; Albergel, C.; Burak, S.; et al. Challenges for Drought Assessment in the Mediterranean Region under Future Climate Scenarios. Earth-Sci. Rev. 2020, 210, 103348. [Google Scholar] [CrossRef]
- Tramblay, Y.; Llasat, M.C.; Randin, C.; Coppola, E. Climate Change Impacts on Water Resources in the Mediterranean. Reg. Environ. Change 2020, 20, 83. [Google Scholar] [CrossRef]
- Treguer, D.; Verner, D.; Redwood, J.; Christensen, J.; McDonnell, R.; Elbert, C.; Konishi, Y.; Belghazi, S. Climate Variability, Drought, and Drought Management in Morocco’s Agricultural Sector; World Bank: Washington, DC, USA, 2018. [Google Scholar]
- Horchani, A. Water in Tunisia: A National Perspective 2007. In Agricultural Water Management: Proceedings of a Workshop in Tunisia; The National Academies Press: Washington, DC, USA, 2007. [Google Scholar]
- Ministry of Agriculture, Water Resources and Fisheries, Bureau of Planning and Water Balance. Development of the Vision and Strategy for the Water Sector in Tunisia by 2050; STUDI International: Tunis, Republic of Tunisia; KfW: Frankfurt, Germany; GIZ: Tunis, Republic of Tunisia; African Development Bank: Abidjan, Côte d’Ivoire, 2022. Available online: http://www.onagri.nat.tn/uploads/secteur-eau/1.pdf (accessed on 15 September 2024).
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 978-0-12-815823-4. [Google Scholar]
- Smida, H.; Abdellaoui, C.; Zairi, M.; Dhia, H.B. Mapping of Areas Vulnerable to Agricultural Pollution Using the DRASTIC Method Coupled with a Geographic Information System (GIS): Case of the Chaffar Aquifer (Southeastern Tunisia). Sci. Chang. Planétaires/Sécheresse 2010, 21, 131–146. [Google Scholar]
- Anis, Z.; Wissem, G.; Vali, G.; Smida, H.; Essghaier, G.M. GIS-Based Landslide Susceptibility Mapping Using Bivariate Statistical Methods in North-Western Tunisia. Open Geosci. 2019, 11, 708–726. [Google Scholar] [CrossRef]
- Trabelsi, R.; Zaïri, M.; Smida, H.; Dhia, H.B. Coastal Aquifer Salinization: Case of the Northern Sahel Aquifer of Sfax, Tunisia. Comptes Rendus Geosci. 2005, 337, 515–524. [Google Scholar] [CrossRef]
- Fisher, R.A. The Correlation between Relatives on the Supposition of Mendelian Inheritance. Earth Environ. Sci. Trans. R. Soc. Edinb. 1919, 52, 399–433. [Google Scholar] [CrossRef]
- Fisher, R.A. Studies in Crop Variation. I. An Examination of the Yield of Dressed Grain from Broadbalk. J. Agric. Sci. 1921, 11, 107–135. [Google Scholar] [CrossRef]
- Scheffé, H. The Analysis of Variance; John Wiley & Sons: Hoboken, NJ, USA, 1956; ISBN 978-0-471-34505-3. [Google Scholar]
- Eisenhart, C. The Assumptions Underlying the Analysis of Variance. Biometrics 1947, 3, 1–21. [Google Scholar] [CrossRef]
- Lix, L.M.; Keselman, J.C.; Keselman, H.J. Consequences of Assumption Violations Revisited: A Quantitative Review of Alternatives to the One-Way Analysis of Variance “F” Test. Rev. Educ. Res. 1996, 66, 579–619. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, J.; Peng, A.; Liu, G.; Zhang, R. Quantifying the Contribution of Uncertainty Sources of Artificial Neural Network Models Using ANOVA for Reservoir Power Generation. Hydrol. Res. 2022, 53, 1455–1467. [Google Scholar] [CrossRef]
- Mashauri, F.; Mbuluyo, M.; Nkongolo, N. Influence Des Paramètres Hydro-Morphométriques Sur l’écoulement Des Eaux Des Sous-Bassins Versants de La Tshopo, République Démocratique Du Congo. RIG 2023, 32, 79–98. [Google Scholar] [CrossRef]
- Massuel, S.; Séguis, L.; Niel, H.; Cappelaere, B.; Delclaux, F.; Peugeot, C. Typology of watersheds in advance of hydrological modelling of a Sahelian region. In Proceedings of the International Conference “Hydrology of the Mediterranean and Semiarid Regions”, Montperllier, France, 1–4 April 2003; IASH Publication: Wallingford, UK, 2003. [Google Scholar]
- Mohammed, A. Application of Anova Statistical Tool for Water Quality Management of Kainji Reservoir. UJET 2017, 3, 9–25. [Google Scholar]
- Oudin, L. Search for a Relevant Potential Evapotranspiration Model as Input to a Global Rainfall-Runoff Model. Ph.D. Thesis, ENGREF (AgroParisTech), Paris, France, 2004. [Google Scholar]
- NASA POWER|Prediction of Worldwide Energy Resources. Available online: https://power.larc.nasa.gov/ (accessed on 15 April 2025).
- Suarez, M.J.; da Silva, A.; Dee, D.; Bloom, S.; Bosilovich, M.; Pawson, S.; Schubert, S.; Wu, M.-L.; Sienkiewicz, M.; Stajner, I. Documentation and Validation of the Goddard Earth Observing System (GEOS) Data Assimilation System, Version 4; 2005. Available online: https://ntrs.nasa.gov/citations/20050175690 (accessed on 15 September 2024).
- Reichle, R.H.; Draper, C.S.; Liu, Q.; Girotto, M.; Mahanama, S.P.P.; Koster, R.D.; Lannoy, G.J.M.D. Assessment of MERRA-2 Land Surface Hydrology Estimates. J. Clim. 2017, 30, 2937–2960. [Google Scholar] [CrossRef]
- Reichle, R.H.; Liu, Q.; Koster, R.D.; Draper, C.S.; Mahanama, S.P.P.; Partyka, G.S. Land Surface Precipitation in MERRA-2. J. Clim. 2017, 30, 1643–1664. [Google Scholar] [CrossRef]
- Abubakar, I.M.; Idi, B.Y. Statistical Analysis of NASA POWER Meteorological Data for the Assessment of Climate Variability in Adamawa State. Environ. Technol. Sci. J. 2024, 15, 119–129. [Google Scholar] [CrossRef]
- Oderinde, F.O.; Ayelokun, O.; Oderinde, F.O.; Aiyelokun, O. Decadal and Trend Analysis of Potential Evapotranspiration in Oluyole, LGA, Oyo State Nigeria. J. Meteorol. Clim. Sci. 2021, 19, 1–9. [Google Scholar]
- Mouelhi, S.; Madani, K.; Lebdi, F. A Structural Overview through GR(s) Models Characteristics for Better Yearly Runoff Simulation. Open J. Mod. Hydrol. 2013, 3, 179–187. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which Potential Evapotranspiration Input for a Lumped Rainfall–Runoff Model? Part 2—Towards a Simple and Efficient Potential Evapotranspiration Model for Rainfall–Runoff Modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Feir-Walsh, B.J.; Toothaker, L.E. An Empirical Comparison of the ANOVA F-Test, Normal Scores Test and Kruskal-Wallis Test under Violation of Assumptions. Educ. Psychol. Meas. 1974, 34, 789–799. [Google Scholar] [CrossRef]
- Norman, G. Likert Scales, Levels of Measurement and the “Laws” of Statistics. Adv. Health Sci. Educ. Theory Pract. 2010, 15, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Blanca, M.J.; Alarcón, R.; Arnau, J.; Bono, R.; Bendayan, R. Non-Normal Data: Is ANOVA Still a Valid Option? Psicothema 2017, 29, 552–557. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, M.D.; Dumontier, M.; Aalbersberg, I.J.; Appleton, G.; Axton, M.; Baak, A.; Blomberg, N.; Boiten, J.-W.; da Silva Santos, L.B.; Bourne, P.E.; et al. The FAIR Guiding Principles for Scientific Data Management and Stewardship. Sci. Data 2016, 3, 160018. [Google Scholar] [CrossRef] [PubMed]
- RStudio Team. RStudio: Integrated Development Environment for R; RStudio, PBC: Boston, MA, USA, 2024. [Google Scholar]
- de Mendiburu, F.; Yaseen, M. Agricolae: Statistical Procedures for Agricultural Research; 2020. Available online: https://cran.r-project.org/web/packages/agricolae/index.html (accessed on 15 September 2024).
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016; ISBN 978-3-319-24277-4. [Google Scholar]
- Iannone, R.; Cheng, J.; Schloerke, B.; Hughes, E.; Lauer, A.; Seo, J.; Brevoort, K.; Roy, O. Gt: Easily Create Presentation-Ready Display Tables; 2025. Available online: https://gt.rstudio.com (accessed on 15 September 2024).
- QGIS Development Team. QGIS Geographic Information System; QGIS Association. Available online: https://www.qgis.org (accessed on 15 September 2024).
- Quarto Development Team. Quarto: Open-Source Scientific and Technical Publishing System; Posit Software, PBC: Boston, MA, USA, 2024. [Google Scholar]
- Mouelhi, S.; Saida, N.; Sihem, J.; Mohamed, S.; Mouelhi, S.; Nemri, S.; Jebari, S.; Slimani, M. Using the Markov Chain for the Generation of Monthly Rainfall Series in a Semi-Arid Zone. Open J. Mod. Hydrol. 2016, 6, 51–65. [Google Scholar] [CrossRef]


| NAMES OF DAMS | P | PET | COEF = P/PET | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Mean | SD | Max | Min | Mean | SD | Max | Min | Mean | SD | Max | |
| ABID | 0 | 38 | 33 | 200 | 68 | 110 | 23 | 157 | 0 | 38 | 35 | 198 |
| BARBARA | 0 | 52 | 42 | 258 | 49 | 102 | 30 | 165 | 0 | 63 | 63 | 407 |
| BENMETIR | 0 | 52 | 42 | 258 | 49 | 102 | 30 | 165 | 0 | 63 | 63 | 407 |
| BEZIRK | 0 | 35 | 33 | 198 | 64 | 109 | 26 | 161 | 0 | 36 | 35 | 201 |
| BIRMCHERGA | 0 | 40 | 33 | 170 | 55 | 107 | 30 | 169 | 0 | 44 | 41 | 240 |
| BOUHEURTMA | 0 | 52 | 42 | 258 | 49 | 102 | 30 | 165 | 0 | 63 | 63 | 407 |
| CHIBA | 0 | 35 | 33 | 198 | 64 | 109 | 26 | 161 | 0 | 36 | 35 | 201 |
| ELBREK | 0 | 36 | 32 | 273 | 37 | 93 | 33 | 160 | 0 | 48 | 54 | 528 |
| ELHAOUAREB | 0 | 32 | 29 | 231 | 56 | 110 | 32 | 174 | 0 | 33 | 34 | 325 |
| GAMGOUM | 0 | 52 | 42 | 221 | 58 | 105 | 27 | 163 | 0 | 59 | 57 | 323 |
| GHEZALA | 0 | 52 | 42 | 221 | 58 | 105 | 27 | 163 | 0 | 59 | 57 | 323 |
| HARKA | 0 | 52 | 42 | 221 | 58 | 105 | 27 | 163 | 0 | 59 | 57 | 323 |
| HMA | 0 | 40 | 33 | 170 | 55 | 107 | 30 | 169 | 0 | 44 | 41 | 240 |
| JOUMINE | 0 | 52 | 42 | 221 | 58 | 105 | 27 | 163 | 0 | 59 | 57 | 323 |
| KASSEB | 0 | 54 | 46 | 230 | 62 | 106 | 24 | 158 | 0 | 60 | 58 | 331 |
| KEBIR | 0 | 54 | 46 | 230 | 62 | 106 | 24 | 158 | 0 | 60 | 58 | 331 |
| LAKHMESS | 0 | 46 | 37 | 233 | 43 | 97 | 31 | 162 | 0 | 59 | 59 | 410 |
| LEBNA | 0 | 35 | 33 | 198 | 64 | 109 | 26 | 161 | 0 | 36 | 35 | 201 |
| MASRI | 0 | 35 | 33 | 198 | 64 | 109 | 26 | 161 | 0 | 36 | 35 | 201 |
| MELAH | 0 | 52 | 42 | 221 | 58 | 105 | 27 | 163 | 0 | 59 | 57 | 323 |
| MELLEGUE | 0 | 52 | 42 | 258 | 49 | 102 | 30 | 165 | 0 | 63 | 63 | 407 |
| MOULA | 0 | 54 | 46 | 230 | 62 | 106 | 24 | 158 | 0 | 60 | 58 | 331 |
| NEBHANA | 0 | 37 | 31 | 189 | 54 | 107 | 30 | 170 | 0 | 40 | 39 | 268 |
| RMIL | 0 | 50 | 41 | 237 | 50 | 102 | 30 | 165 | 0 | 61 | 62 | 372 |
| SARRAT | 0 | 47 | 37 | 235 | 41 | 97 | 32 | 162 | 0 | 61 | 62 | 426 |
| SEJNANE | 0 | 52 | 42 | 221 | 58 | 105 | 27 | 163 | 0 | 59 | 57 | 323 |
| SFICIFA | 0 | 38 | 31 | 213 | 45 | 101 | 32 | 167 | 0 | 45 | 45 | 350 |
| SIDIAICH | 0 | 16 | 18 | 152 | 51 | 108 | 35 | 173 | 0 | 18 | 25 | 237 |
| SIDIELBARRAK | 0 | 54 | 46 | 230 | 62 | 106 | 24 | 158 | 0 | 60 | 58 | 331 |
| SIDISAAD | 0 | 32 | 29 | 231 | 56 | 110 | 32 | 174 | 0 | 33 | 34 | 325 |
| SIDISALEM | 0 | 50 | 41 | 237 | 50 | 102 | 30 | 165 | 0 | 61 | 62 | 372 |
| SILIANA | 0 | 46 | 37 | 233 | 43 | 97 | 31 | 162 | 0 | 59 | 59 | 410 |
| TINE | 0 | 52 | 42 | 221 | 58 | 105 | 27 | 163 | 0 | 59 | 57 | 323 |
| ZARGA | 0 | 54 | 46 | 230 | 62 | 106 | 24 | 158 | 0 | 60 | 58 | 331 |
| ZIATINE | 0 | 52 | 42 | 221 | 58 | 105 | 27 | 163 | 0 | 59 | 57 | 323 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mouelhi, S.; Kanzari, S.; Ben Mariem, S.; Zemni, N. Towards a Classification of Tunisian Dams for Enhanced Water Scarcity Governance: Parametric or Non-Parametric Approaches? Hydrology 2025, 12, 96. https://doi.org/10.3390/hydrology12040096
Mouelhi S, Kanzari S, Ben Mariem S, Zemni N. Towards a Classification of Tunisian Dams for Enhanced Water Scarcity Governance: Parametric or Non-Parametric Approaches? Hydrology. 2025; 12(4):96. https://doi.org/10.3390/hydrology12040096
Chicago/Turabian StyleMouelhi, Safouane, Sabri Kanzari, Sana Ben Mariem, and Nesrine Zemni. 2025. "Towards a Classification of Tunisian Dams for Enhanced Water Scarcity Governance: Parametric or Non-Parametric Approaches?" Hydrology 12, no. 4: 96. https://doi.org/10.3390/hydrology12040096
APA StyleMouelhi, S., Kanzari, S., Ben Mariem, S., & Zemni, N. (2025). Towards a Classification of Tunisian Dams for Enhanced Water Scarcity Governance: Parametric or Non-Parametric Approaches? Hydrology, 12(4), 96. https://doi.org/10.3390/hydrology12040096





