Model-Based Attribution of High-Resolution Streamflow Trends in Two Alpine Basins of Western Austria
Abstract
:1. Introduction
2. Study Site and Data
3. Methods
3.1. Hydrological Model Setup
3.2. Calibration and Validation Scheme
- (1)
- As recommended in Krause et al. [44], we derived several statistical measures to compare the simulated with the observed hydrograph, which included the Nash-Sutcliffe efficiency (NSE, [45]), the modified index of agreement (MD, [46]) and the coefficient of determination (R2). As the model efficiency is often overestimated by the standard Nash-Sutcliffe efficiency in time series with strong seasonality, the benchmark Nash-Sutcliffe coefficient based on a calendar-day model (NSEbench, [47]) was also computed.
- (2)
- To consider glacier growth and shrinkage within the calibration process, we derived the following two measures calculated from simulated and observed extents of the Vernagt glacier: First, the “probability of detection” (POD) is the percentage of grid cells that were detected correctly (both in simulated and observed grids). Next, the “false alarm rate” (FAR) indicates the percentage of grid cells in the simulated glacier grid that were not found in the observed one [48]. Finally, the absolute simulated and observed glacier areas were compared.
- (3)
- As the glacier extents only gave information about the conditions at the beginning and end of the calibration period, we then used seasonal mass balances of the Vernagt glacier to calibrate the model. Thus, the temporal dynamic of ice melt and accumulation was also accounted for.
- (4)
- After this, discrepancies in the total simulated water budget were considered by comparing simulated average annual streamflow and average seasonal mass balances to the observed ones.
- (5)
- Most important for the goal of the present study was to fit the simulated trends to the observed trends during calibration. This was conducted for trends in annual streamflow, trends in glacier mass balances and, lastly, for highly resolved trends. This last point, the agreement of the simulated high-resolution trends with the observed trends, was the basis for the trend attribution attempt in the present analysis.
3.3. Trend Detection
3.4. Trend Attribution
4. Results
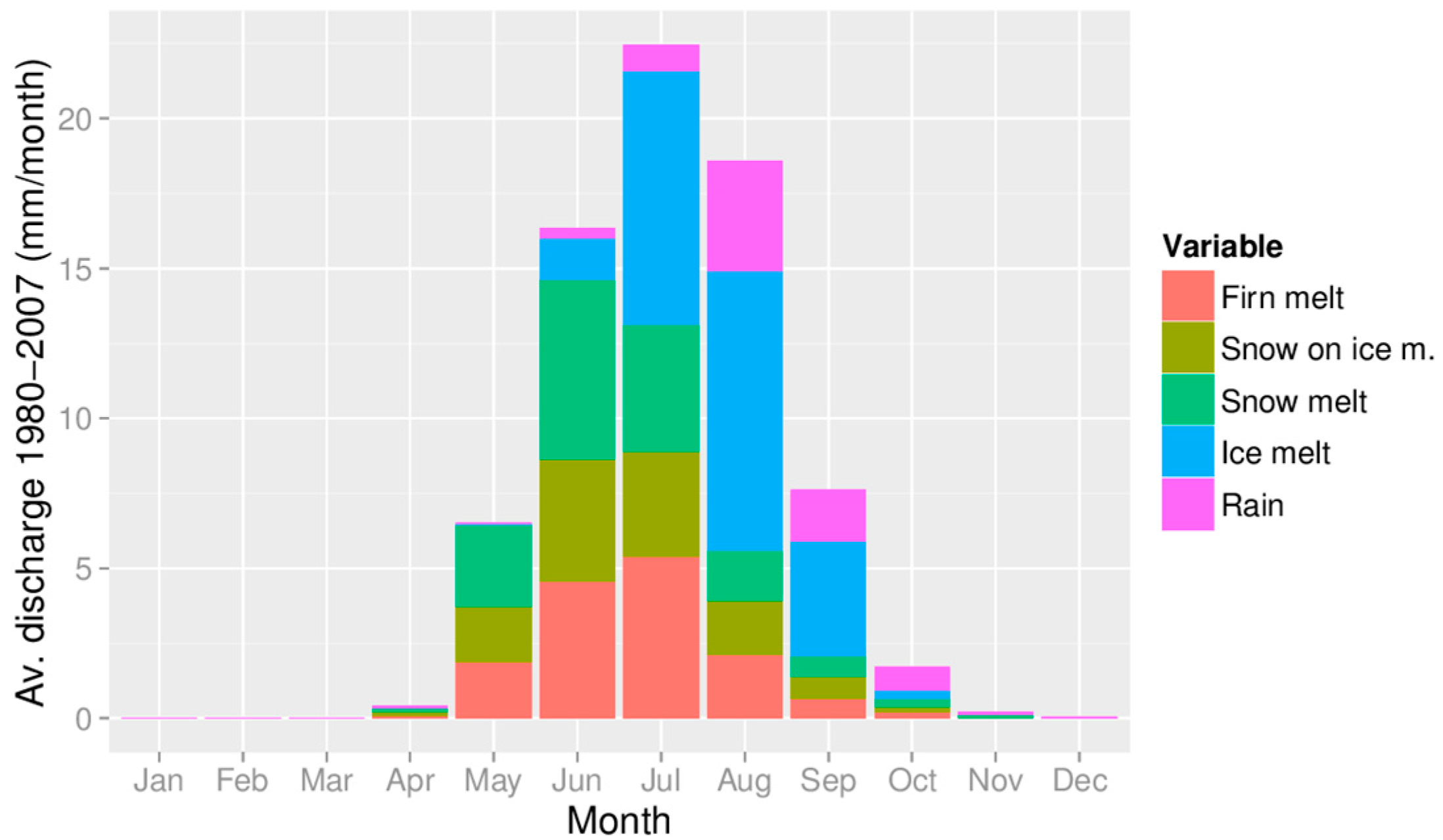
4.1. Calibration and Validation Results
4.2. Attribution of Streamflow Trends
5. Discussion
5.1. Overall Model Skill
5.2. Modelling Streamflow Trends
5.3. Model-Based Trend Attribution
5.4. The Role of Evapotranspiration
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix

References
- Braun, L.N.; Escher-Vetter, H.; Siebers, M.; Weber, M. Water balance of the highly glaciated Vernagt basin, Ötztal Alps. In Proceedings of the “Alpine Space—Man And Environment” Conference, Innsbruck, Austria, 28–29 September 2006.
- Viviroli, D.; Archer, D.R.; Buytaert, W.; Fowler, H.J.; Greenwood, G.B.; Hamlet, A.F.; Huang, Y.; Koboltschnig, G.; Litaor, M.I.; López-Moreno, J.I.; et al. Climate change and mountain water resources: Overview and recommendations for research, management and policy. Hydrol. Earth Syst. Sci. 2011, 15, 471–504. [Google Scholar] [CrossRef] [Green Version]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Pellicciotti, F.; Bauder, A.; Parola, M. Effect of glaciers on streamflow trends in the Swiss Alps. Water Resour. Res. 2010. [Google Scholar] [CrossRef]
- Molnar, P.; Burlando, P.; Pellicciotti, F. Streamflow Trends in Mountainous Regions, Encyclopedia of Snow, Ice and Glaciers; Springer: Berlin, Germany, 2011; pp. 1084–1089. [Google Scholar]
- Cramer, W.; Yohe, G.W.; Auffhammer, M.; Huggel, C.; Molau, U.; Dias, M.A.F.D.; Solow, A.; Stone, D.A.; Tibig, L. Detection and attribution of observed impacts. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects; Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 979–1037. [Google Scholar]
- Merz, B.; Vorogushyn, S.; Uhlemann, S.; Delgado, J.; Hundecha, Y. HESS Opinions “More efforts and scientific rigour are needed to attribute trends in flood time series”. Hydrol. Earth Syst. Sci. 2012, 16, 1379–1387. [Google Scholar] [CrossRef]
- Delgado, J.M.; Apel, H.; Merz, B. Flood trends and variability in the Mekong river. Hydrol. Earth Syst. Sci. 2010, 14, 407–418. [Google Scholar] [CrossRef]
- Kormann, C.; Francke, T.; Renner, M.; Bronstert, A. Attribution of high resolution streamflow trends in Western Austria—An approach based on climate and discharge station data. Hydrol. Earth Syst. Sci. 2015, 19, 1225–1245. [Google Scholar] [CrossRef]
- Blöschl, G.; Ardoin-Bardin, S.; Bonell, M.; Dorninger, M.; Goodrich, D.; Gutknecht, D.; Matamoros, D.; Merz, B.; Shand, P.; Szolgay, J. At what scales do climate variability and land cover change impact on flooding and low flows? Invited Commentary. Hydrol. Process. 2007, 21, 1241–1247. [Google Scholar] [CrossRef]
- Mote, P.W.; Hamlet, A.F.; Clark, M.P.; Lettenmaier, D.P. Declining mountain snowpack in Western North America. Bull. Am. Meteorol. Soc. 2005, 86, 1–39. [Google Scholar] [CrossRef]
- Hodgkins, G.A.; Dudley, R.W. Changes in the timing of winter—spring streamflows in eastern North America, 1913–2002. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Knowles, N.; Dettinger, M.D.; Cayan, D.R. Trends in snowfall versus rainfall in the Western United States. J. Clim. 2006, 19, 4545–4559. [Google Scholar] [CrossRef]
- Kormann, C.; Francke, T.; Bronstert, A. Detection of regional climate change effects on alpine hydrology by daily resolution trend analysis in Tyrol, Austria. J. Water Clim. Chang. 2015, 6, 124–143. [Google Scholar] [CrossRef]
- Douville, H.; Ribes, A.; Decharme, B.; Alkama, R.; Sheffield, J. Anthropogenic influence on multidecadal changes in reconstructed global evapotranspiration. Nat. Clim. Chang. 2013, 3, 59–62. [Google Scholar] [CrossRef]
- Stewart, I.; Cayan, D.; Dettinger, M. Changes toward earlier streamflow timing across western North America. J. Clim. 2005, 18, 1136–1155. [Google Scholar] [CrossRef]
- Birsan, M.V.; Molnar, P.; Pfaundler, M.; Burlando, P. Streamflow trends in Switzerland. J. Hydrol. 2005, 314, 312–329. [Google Scholar] [CrossRef]
- Stahl, K.; Moore, R.D. Influence of watershed glacier coverage on summer streamflow in British Columbia, Canada. Water Resour. Res. 2006. [Google Scholar] [CrossRef]
- Hidalgo, H.G.; Das, T.; Dettinger, M.D.; Cayan, D.R.; Pierce, D.W.; Barnett, T.P.; Bala, G.; Mirin, A.; Wood, A.W.; Bonfils, C.; et al. Detection and Attribution of Streamflow Timing Changes to Climate Change in the Western United States. J. Clim. 2009, 22, 3838–3855. [Google Scholar] [CrossRef]
- Hamlet, A.F.; Mote, P.W.; Clark, M.P.; Lettenmaier, D.P. Twentieth-century trends in runoff, evapotranspiration, and soil moisture in the western United States. J. Clim. 2007, 20, 1468–1486. [Google Scholar] [CrossRef]
- Maurer, E.P.; Stewart, I.T.; Bonfils, C.; Duffy, P.B.; Cayan, D. Detection, attribution, and sensitivity of trends toward earlier streamflow in the Sierra Nevada. J. Geophys. Res. Atmos. 2007, 112, 1984–2012. [Google Scholar] [CrossRef]
- Duethmann, D.; Bolch, T.; Farinotti, D.; Kriegel, D.; Vorogushyn, S.; Merz, B.; Pieczonka, T.; Jiang, T.; Su, B.; Güntner, A. Attribution of streamflow trends in snow and glacier melt dominated catchments of the Tarim River, Central Asia. Water Resour. Res. 2015, 51, 1944–7973. [Google Scholar] [CrossRef]
- Déry, S.J.; Stahl, K.; Moore, R.D.; Whitfield, P.H.; Menounos, B.; Burford, J.E. Detection of runoff timing changes in pluvial, nival, and glacial rivers of western Canada. Water Resour. Res. 2009. [Google Scholar] [CrossRef]
- Kim, J.-S.; Jain, S. High-resolution streamflow trend analysis applicable to annual decision calendars: A western United States case study. Clim. Chang. 2010, 102, 699–707. [Google Scholar] [CrossRef]
- Patzelt, G. Das Ötztal—Topographische Kennzeichnung. In Glaziale und Periglaziale Lebensräume im Raum Obergurgl; Koch, E.M., Erschbamer, B., Eds.; Innsbruck University Press: Innsbruck, Austria, 2010; pp. 9–11. [Google Scholar]
- Braun, L.; Weber, M.; Mauser, W.; Prasch, M. Hydrometeorological Monitoring of Vernagtferner as an Essential Basis for Snow and Glacier Modelling in the GLOWA-Danube Project. The Application of Observations and Models for Assessing Water Resources and Risks in Mountain Areas, with the Related Uncertainties; Société Hydrotechnique de France (SHF): Paris, France, 2011; pp. 207–221. [Google Scholar]
- Mayr, E.; Hagg, W.; Mayer, C.; Braun, L. Calibrating a spatially distributed conceptual hydrological model using runoff, annual mass balance and winter mass balance. J. Hydrol. 2013, 478, 40–49. [Google Scholar] [CrossRef]
- Austrian Federal Ministry of Agriculture, Forestry, Environment and Water Management (BMLFUW). Hydrologischer Atlas Österreichs; BMLFUW: Vienna, Austria, 2007.
- Kuhn, M.; Lambrecht, A.; Abermann, J. Austrian Glacier Inventory 1998. Available online: http://doi.pangaea.de/10.1594/PANGAEA.809196 (accessed on 16 February 2015).
- Abermann, J.; Seiser, B.; Meran, I.; Stocker-Waldhuber, M.; Goller, M.; Fischer, A. The Third Glacier Inventory of North Tyrol, Austria, for 2006. Available online: http://doi.pangaea.de/10.1594/PANGAEA.806960 (accessed on 16 February 2015).
- Zemp, M.; Nussbaumer, S.U.; Naegeli, K.; Gärtner-Roer, I.; Paul, F.; Hoelzle, M.; Haeberli, W. WGMS Glacier Mass Balance Bulletin No. 12 (2010–2011); ICSU(WDS)/IUGG(IACS)/UNEP/UNESCO/WMO, World Glacier Monitoring Service: Zurich, Switzerland, 2013; p. 106. [Google Scholar]
- Stahl, K.; Moore, R.D.; Shea, J.M.; Hutchinson, D.; Cannon, A.J. Coupled modelling of glacier and streamflow response to future climate scenarios. Water Resour. Res. 2008. [Google Scholar] [CrossRef]
- Schaefli, B.; Huss, M. Integrating point glacier mass balance observations into hydrologic model identification. Hydrol. Earth Syst. Sci. 2011, 15, 1227–1241. [Google Scholar] [CrossRef]
- Graeff, T.; Zehe, E.; Blume, T.; Francke, T.; Schröder, B. Predicting event response in a nested catchment with generalized linear models and a distributed watershed model. Hydrol. Process. 2012, 26, 3749–3769. [Google Scholar] [CrossRef]
- Jasper, K.; Calanca, P.; Gyalistras, D.; Fuhrer, J. Differential impacts of climate change on the hydrology of two alpine river basins. Clim. Res. 2004, 26, 113–129. [Google Scholar] [CrossRef]
- Schulla, J. Model Description WaSiM (Water Balance Simulation Model). Available online: http://www.wasim.ch/downloads/doku/wasim/wasim_2013_en.pdf (accessed on 30 July 2015).
- Chen, J.; Ohmura, A. Estimation of Alpine Glacier Water Resources and Their Change Since the 1870s; IAHS Publ.: Wallingford, UK, 1990; pp. 127–135. [Google Scholar]
- Bahr, D.B.; Meier, M.F.; Peckham, S.D. The physical basis of glacier volume-area scaling. J. Geophys. Res. 1997, 102, 20–355. [Google Scholar] [CrossRef]
- Anderson, E.A. National Weather Service River Forecast System—Snow Accumulation and Ablation Model; Tech. Mem., NWS-HYDRO-17; National Oceanographic and Atmospheric Administration (NOAA), U.S. Department of Commerce: Washington, DC, UK, 1973; p. 217.
- Hock, R. Modeling of Glacier Melt and Discharge. Ph.D. Thesis, Verlag Geographisches Institut ETH Zürich, Zürich, Netherlands, 1998; p. 140. [Google Scholar]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Niehoff, D.; Fritsch, U.; Bronstert, A. Land-use impacts on storm-runoff generation: Scenarios of land-use change and simulation of hydrological response in a meso-scale catchment in SW-Germany. J. Hydrol. 2000, 267, 80–93. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models (1), a discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M. HydroGOF: Goodness-of-Fit Functions for Comparison of Simulated and Observed Hydrological Time Series. R Package Version 0.3–8. 2014. Available online: http://www.rforge.net/hydroGOF/ (accessed on 20 January 2015).
- Schaefli, B.; Gupta, H. Do Nash values have value? Hydrol. Process. 2007, 21, 2075–2080. [Google Scholar] [CrossRef]
- Murphy, A.; Winkler, R. A general framework for forecast verification. Mon. Weather Rev. 1986, 119, 1330–1338. [Google Scholar] [CrossRef]
- Tolson, B.A; Shoemaker, C.A. Dynamically dimensioned search algorithm for computationally efficient watershed model calibration. Water Resour. Res. 2007. [Google Scholar] [CrossRef]
- Francke, T. Particle Swarm Optimization and Dynamically Dimensioned Search, Optionally Using Parallel Computing Based on Rmpi. R Package Version 0.9–989. 2014. Available online: https://www.rforge.net/doc/packages/ppso/00Index.html (accessed on 20 February 2015).
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; Elsevier Science: Amsterdam, the Netherlands, 1992. [Google Scholar]
- Stahl, K.; Tallaksen, L.M.; Hannaford, J.; van Lanen, H.A.J. Filling the white space on maps of European runoff trends: Estimates from a multi-model ensemble. Hydrol. Earth Syst. Sci. 2012, 16, 2035–2047. [Google Scholar] [CrossRef] [Green Version]
- Morin, E. To know what we cannot know: Global mapping of minimal detectable absolute trends in annual precipitation. Water Resour. Res. 2011. [Google Scholar] [CrossRef]
- Bronstert, A.; Kolokotronis, V.; Schwandt, D.; Straub, H. Comparison and Evaluation of regional climate scenarios for hydrological impact analysis: General scheme and application example. Int. J. Clim. 2007, 27, 1579–1594. [Google Scholar] [CrossRef]
- Strasser, U.; Bernhardt, M.; Weber, M.; Liston, G.E.; Mauser, W. Is snow sublimation important in the alpine water balance? Cryosphere 2008, 2, 53–66. [Google Scholar] [CrossRef]
- Schimon, W.; Schöner, W.; Böhm, R.; Haslinger, K.; Blöschl, G.; Merz, R.; Blaschke, A.P.; Viglione, A.; Parajka, J.; Kroiß, H.; et al. Anpassungsstrategien an den Klimawandel für Österreichs Wasserwirtschaft; Bundesministerium für Land und Forstwirtschaft, Umwelt und Wasserwirtschaft: Vienna, Austria, 2011. [Google Scholar]
- Radić, V.; Hock, R.; Oerlemans, J. Volume–area scaling vs. flowline modelling in glacier volume projections. Ann. Glaciol. 2007, 46, 234–240. [Google Scholar] [CrossRef]
- DeWalle, D.R.; Henderson, Z.; Rango, A. Spatial and temporal variations in snowmelt degree-day factors computed from SNOTEL data in the Upper Rio Grande basin. In Proceedings of the Western Snow Conference, Granby, CO, USA, 20 May 2002; p. 73.
- Bormann, K.J.; Evans, J.P.; McCabe, M.F. Constraining snowmelt in a temperature-index model using simulated snow densities. J. Hydrol. 2014, 517, 652–667. [Google Scholar] [CrossRef]
- Blumer, F. Altitudinal Dependence of Precipitation in the Alps. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 1994. [Google Scholar]
- Jost, G.; Moore, R.D.; Menounos, B.; Wheate, R. Quantifying the contribution of glacier runoff to streamflow in the upper Columbia River Basin, Canada. Hydrol. Earth Syst. Sci. 2012, 16, 849–860. [Google Scholar] [CrossRef] [Green Version]
- Schaefli, B.; Hingray, B.; Niggli, M.; Musy, A. A conceptual glacio-hydrological model for high mountainous catchments. Hydrol. Earth Syst. Sci. 2005, 9, 95–109. [Google Scholar] [CrossRef]
- Konz, M.; Seibert, J. On the value of glacier mass balances for hydrological model calibration. J. Hydrol. 2010, 385, 238–246. [Google Scholar] [CrossRef] [Green Version]
- Fountain, A.G. Effect of snow and firn hydrology on the physical and chemical characteristics of glacial runoff. Hydrol. Process. 1996, 10, 509–521. [Google Scholar] [CrossRef]
- Kramer, R.J.; Bounoua, L.; Zhang, P.; Wolfe, R.E.; Huntington, T.G.; Imhoff, M.L.; Thome, K.; Noyce, G.L. Evapotranspiration trends over the eastern United States during the 20th century. Hydrology 2015, 2, 93–111. [Google Scholar] [CrossRef]
- Alaoui, A.; Willimann, E.; Jasper, K.; Felder, G.; Herger, F.; Magnusson, J.; Weingartner, R. Modelling the effects of land use and climate changes on hydrology in the Ursern valley, Switzerland. Hydrol. Process. 2014, 28, 3602–3614. [Google Scholar] [CrossRef]
- Tecklenburg, C.; Francke, T.; Kormann, C.; Bronstert, A. Modeling of water balance response to an extreme future scenario in the Ötztal catchment, Austria. Adv. Geosci. 2012, 32, 63–68. [Google Scholar] [CrossRef]










| Gauging Station | Brunau | Vernagtbach |
|---|---|---|
| Gauged river | Ötztaler Ache | Vernagtbach |
| Minimum altitude (m a.s.l.) | 706 | 2640 |
| Mean altitude (m a.s.l.) | 2230 | 3127 |
| Maximum altitude (m a.s.l.) | 3768 | 3535 |
| Catchment area (km2) | 847 | 11 |
| Coniferous forest | 17% | 0% |
| Rock | 27% | 29% |
| Meadows/alpine pastures | 41% | 1% |
| Glacier | 13% | 69% |
| Parameter | Value |
|---|---|
| Lapse rates | |
| Temperature gradient (°C/m) | −0.006 |
| Precipitation gradient (mm/m) | 0.0024 |
| Ice model | |
| Degree-day-factor for ice (mm/°C/d) | 7.9 |
| Degree-day-factor for firn (mm/°C/d) | 7.2 |
| Degree-day-factor for snow on ice (mm/°C/d) | 4.8 |
| V-A-scaling (m) | 29.8 |
| V-A-exponent ( ) | 1.36 |
| Snow model | |
| Temperature limit for rain (°C) | 1.5 |
| Temperature limit for snow melt (°C) | 0.9 |
| Degree-day-factor for snow (mm/°C/d) | 2.4 |
| Transition zone for rain-snow (°C) | 0.9 |
| Soil model | |
| Recession parameter (m) | 0.04 |
| Correction factor for transmissivities ( ) | 0.002 |
| Calibration Period | Validation Periods | ||
|---|---|---|---|
| Vernagtbach | 1980–2007 | 1975–1979 | 2008–2012 |
| Nash-Sutcliffe efficiency * | 0.82 | 0.74 | 0.81 |
| R2 * | 0.82 | 0.83 | 0.82 |
| Index of agreement, mod. * | 0.85 | 0.83 | 0.84 |
| NS bench efficiency * | 0.46 | 0.68 | 0.52 |
| Mean annual Q obs (mm) * | 1959 | 1179 | 2381 |
| Mean annual Q sim (mm) * | 1937 | 1419 | 2221 |
| Mean summer MB obs (mm) | −1484 | −750 | −1751 |
| Mean summer MB sim (mm) | −1654 | −908 | −1950 |
| Mean winter MB obs (mm) | 934 | 931 | 833 |
| Mean winter MB sim (mm) | 979 | 973 | 893 |
| Brunau | |||
| Nash-Sutcliffe efficiency | 0.91 | 0.91 | 0.87 |
| R2 | 0.91 | 0.92 | 0.89 |
| Index of agreement, mod. | 0.89 | 0.88 | 0.88 |
| NS bench efficiency | 0.77 | 0.76 | 0.62 |
| Mean annual Q obs (mm) * | 1090 | 1011 | 1079 |
| Mean annual Q sim (mm) * | 1064 | 891 | 866 |
| 1997 | 2007 | |
|---|---|---|
| POD | 0.93 | 0.9 |
| FAR | 0.02 | 0.04 |
| Observed Extent (km2) | 8.8 | 8.3 |
| Simulated Extent (km2) | 8.8 | 8 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kormann, C.; Bronstert, A.; Francke, T.; Recknagel, T.; Graeff, T. Model-Based Attribution of High-Resolution Streamflow Trends in Two Alpine Basins of Western Austria. Hydrology 2016, 3, 7. https://doi.org/10.3390/hydrology3010007
Kormann C, Bronstert A, Francke T, Recknagel T, Graeff T. Model-Based Attribution of High-Resolution Streamflow Trends in Two Alpine Basins of Western Austria. Hydrology. 2016; 3(1):7. https://doi.org/10.3390/hydrology3010007
Chicago/Turabian StyleKormann, Christoph, Axel Bronstert, Till Francke, Thomas Recknagel, and Thomas Graeff. 2016. "Model-Based Attribution of High-Resolution Streamflow Trends in Two Alpine Basins of Western Austria" Hydrology 3, no. 1: 7. https://doi.org/10.3390/hydrology3010007
APA StyleKormann, C., Bronstert, A., Francke, T., Recknagel, T., & Graeff, T. (2016). Model-Based Attribution of High-Resolution Streamflow Trends in Two Alpine Basins of Western Austria. Hydrology, 3(1), 7. https://doi.org/10.3390/hydrology3010007







