Hydrostats: A Python Package for Characterizing Errors between Observed and Predicted Time Series
Abstract
:1. Introduction
2. Hydrostats Python Package
2.1. Background
2.2. Development Methods and Approach
2.3. Hydrostats Use
2.4. Pre-Processing (hydrostats.data)
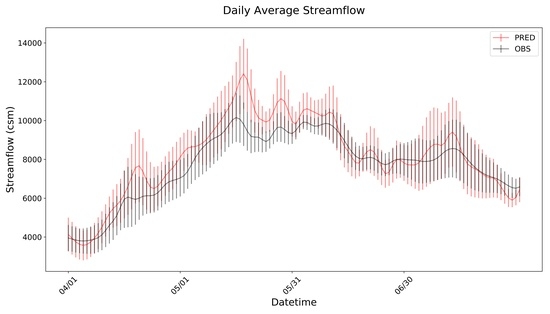
2.5. Visualization (hydrostats.visualization)
2.6. Error Metrics (hydrostats.metrics)
2.7. Forecast Error Metrics
2.8. Code Optimization
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Snow, A.D.; Christensen, S.D.; Swain, N.R.; Nelson, E.J.; Ames, D.P.; Jones, N.L.; Ding, D.; Noman, N.S.; David, C.H.; Pappenberger, F. A high-resolution national-scale hydrologic forecast system from a global ensemble land surface model. JAWRA J. Am. Water Resour. Assoc. 2016, 52, 950–964. [Google Scholar] [CrossRef]
- Swain, N.R.; Christensen, S.D.; Snow, A.D.; Dolder, H.; Espinoza-Dávalos, G.; Goharian, E.; Jones, N.L.; Nelson, E.J.; Ames, D.P.; Burian, S.J. A new open source platform for lowering the barrier for environmental web app development. Environ. Model. Softw. 2016, 85, 11–26. [Google Scholar] [CrossRef] [Green Version]
- Reich, N.G.; Lessler, J.; Sakrejda, K.; Lauer, S.A.; Iamsirithaworn, S.; Cummings, D.A. Case study in evaluating time series prediction models using the relative mean absolute error. Am. Stat. 2016, 70, 285–292. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krause, P.; Boyle, D.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Roberts, W. Hydrostats-Python Package. Available online: https://pypi.org/project/hydrostats/ (accessed on 30 September 2018).
- Roberts, W. Hydrostats Source Code—Github. Available online: https://github.com/BYU-Hydroinformatics/hydrostats/ (accessed on 30 September 2018).
- McKinney, W. Python for Data Analysis: Data Wrangling with Pandas, Numpy, and Ipython; O’Reilly Media, Inc.: Boston, MA, USA, 2012. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2d graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Roberts, W. Hydroerr—Hydrologic Error Metrics, Python Library. Available online: https://pypi.org/project/HydroErr/ (accessed on 30 September 2018).
- Roberts, W. HydroErr Documentation—Github. Available online: https://byu-hydroinformatics.github.io/HydroErr/ (accessed on 30 September 2018).
- Roberts, W. HydroErr Source Code—Github. Available online: https://github.com/BYU-Hydroinformatics/HydroErr (accessed on 30 September 2018).
- Roberts, W. Hydrostats Documentation—Github. Available online: https://byu-hydroinformatics.github.io/Hydrostats/ (accessed on 30 September 2018).
- Roberts, W. A python package for computing error metrics for observed and predicted time series. In 9th International Congress on Environmental Modeling & Software; International Environmental Modeling & Software Society: Fort Collins, CO, USA, 2018. [Google Scholar]
- Kluyver, T.; Ragan-Kelley, B.; Pérez, F.; Granger, B.E.; Bussonnier, M.; Frederic, J.; Kelley, K.; Hamrick, J.B.; Grout, J.; Corlay, S. Jupyter Notebooks—A publishing Format for Reproducible Computational Workflows; ELPUB: Amsterdam, Netherlands, 2016; pp. 87–90. [Google Scholar]
- Oliphant, T.E. A Guide to Numpy; Trelgol Publishing: Provo, UT, USA, 2006; Volume 1. [Google Scholar]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools for Python. Available online: http://www.scipy.org/ (accessed on 30 September 2018).
- Lam, S.K.; Pitrou, A.; Seibert, S. Numba: A llvm-based python jit compiler. In Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, Austin, TX, USA, 15–20 November 2015; ACM: Austin, TX, USA, 2015; p. 7. [Google Scholar]
- Gazoni, E.; Clark, C. Openpyxl—A Python Library to Read/Write Excel 2010 xlsx/xlsm Files. Available online: https://openpyxl.readthedocs.io/en/stable/ (accessed on 30 September 2018).
- McKinney, W. Data structures for statistical computing in python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28–30 June 2010; pp. 51–56. [Google Scholar]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424, 264–277. [Google Scholar] [CrossRef]
- Murphy, A.H.; Epstein, E.S. Skill scores and correlation coefficients in model verification. Mon. Weather Rev. 1989, 117, 572–582. [Google Scholar] [CrossRef]
- Robila, S.A.; Gershman, A. Spectral matching accuracy in processing hyperspectral data. In Proceedings of the International Symposium on Signals, Circuits and Systems, 2005, ISSCS 2005, Iasi, Romania, 14–15 July 2005; pp. 163–166. [Google Scholar]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Ferro, C.A.; Richardson, D.S.; Weigel, A.P. On the effect of ensemble size on the discrete and continuous ranked probability scores. Meteorol. Appl. 2008, 15, 19–24. [Google Scholar] [CrossRef] [Green Version]
- DeLong, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 1988, 837–845. [Google Scholar] [CrossRef]
- Sun, X.; Xu, W. Fast implementation of delong’s algorithm for comparing the areas under correlated receiver operating characteristic curves. IEEE Signal Process. Lett. 2014, 21, 1389–1393. [Google Scholar] [CrossRef]
- Walt, S.v.d.; Colbert, S.C.; Varoquaux, G. The numpy array: A structure for efficient numerical computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- Mielke, P.W.; Berry, K.J. Permutation Methods: A Distance Function Approach; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (mae) over the root mean square error (rmse) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roberts, W.; Williams, G.P.; Jackson, E.; Nelson, E.J.; Ames, D.P. Hydrostats: A Python Package for Characterizing Errors between Observed and Predicted Time Series. Hydrology 2018, 5, 66. https://doi.org/10.3390/hydrology5040066
Roberts W, Williams GP, Jackson E, Nelson EJ, Ames DP. Hydrostats: A Python Package for Characterizing Errors between Observed and Predicted Time Series. Hydrology. 2018; 5(4):66. https://doi.org/10.3390/hydrology5040066
Chicago/Turabian StyleRoberts, Wade, Gustavious P. Williams, Elise Jackson, E. James Nelson, and Daniel P. Ames. 2018. "Hydrostats: A Python Package for Characterizing Errors between Observed and Predicted Time Series" Hydrology 5, no. 4: 66. https://doi.org/10.3390/hydrology5040066
APA StyleRoberts, W., Williams, G. P., Jackson, E., Nelson, E. J., & Ames, D. P. (2018). Hydrostats: A Python Package for Characterizing Errors between Observed and Predicted Time Series. Hydrology, 5(4), 66. https://doi.org/10.3390/hydrology5040066