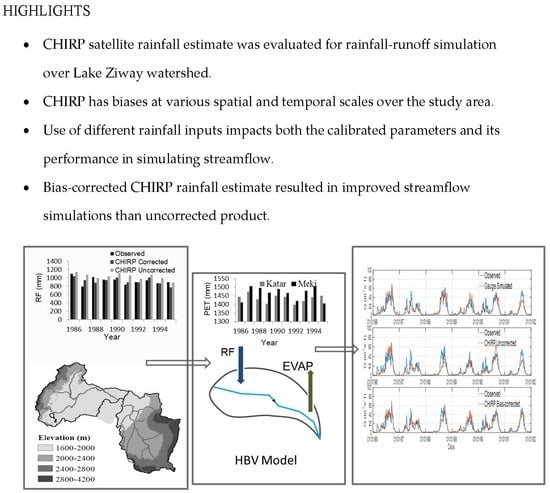
Evaluation and Bias Correction of CHIRP Rainfall Estimate for Rainfall-Runoff Simulation over Lake Ziway Watershed, Ethiopia
Abstract
:1. Introduction
2. Study Area and Datasets
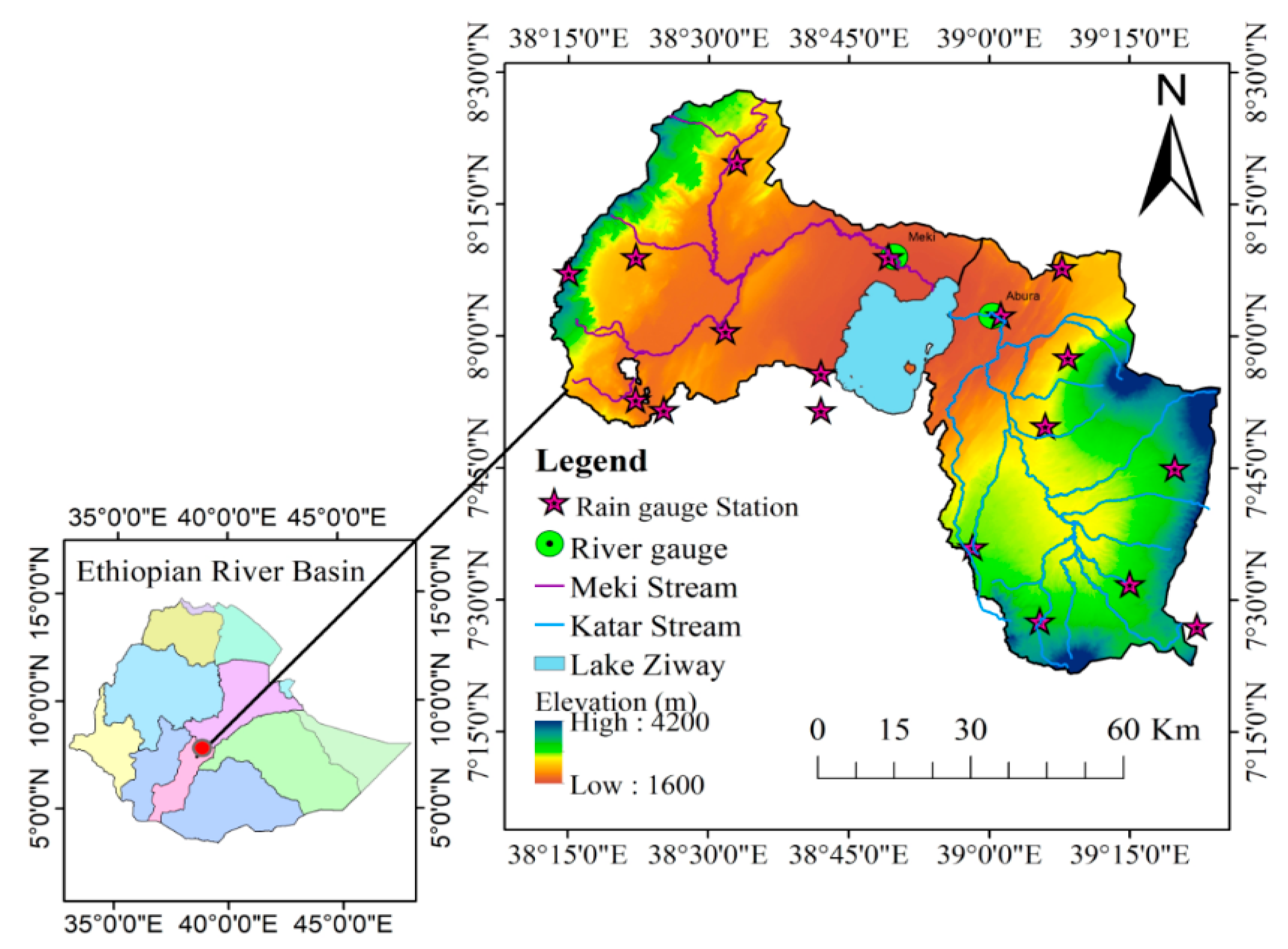
2.1. Study Area
2.2. Rain Gauge Data
2.3. Satellite Rainfall Data
3. Methods
3.1. Evaluation of CHIRP Satellite Rainfall
3.2. CHIRP Satellite Bias Correction
3.3. HBV Hydrological Model
Model Calibration and Evaluation
4. Results and Discussion
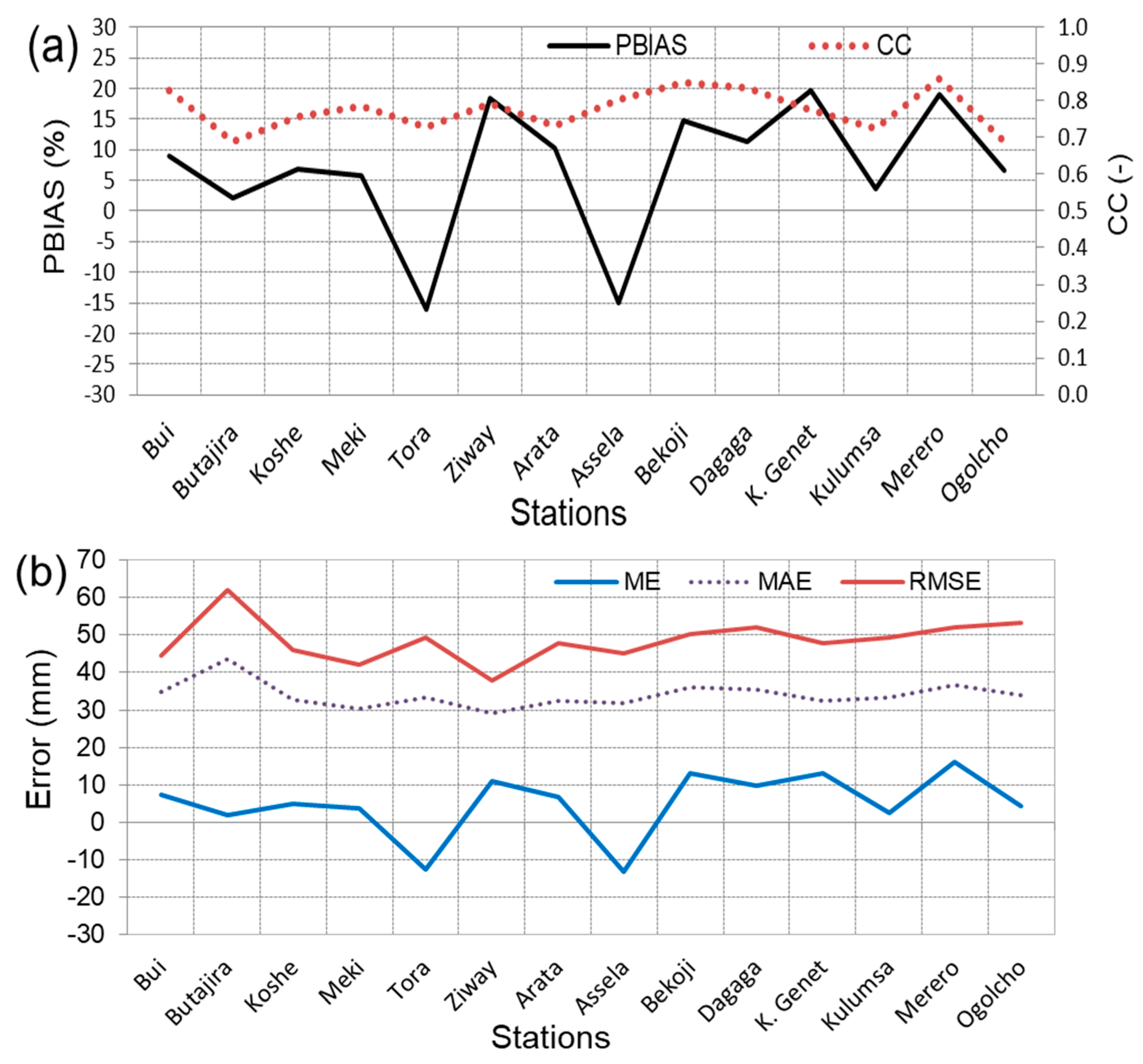
4.1. Evaluation of CHIRP Data at Multiple Spatiotemporal Scales
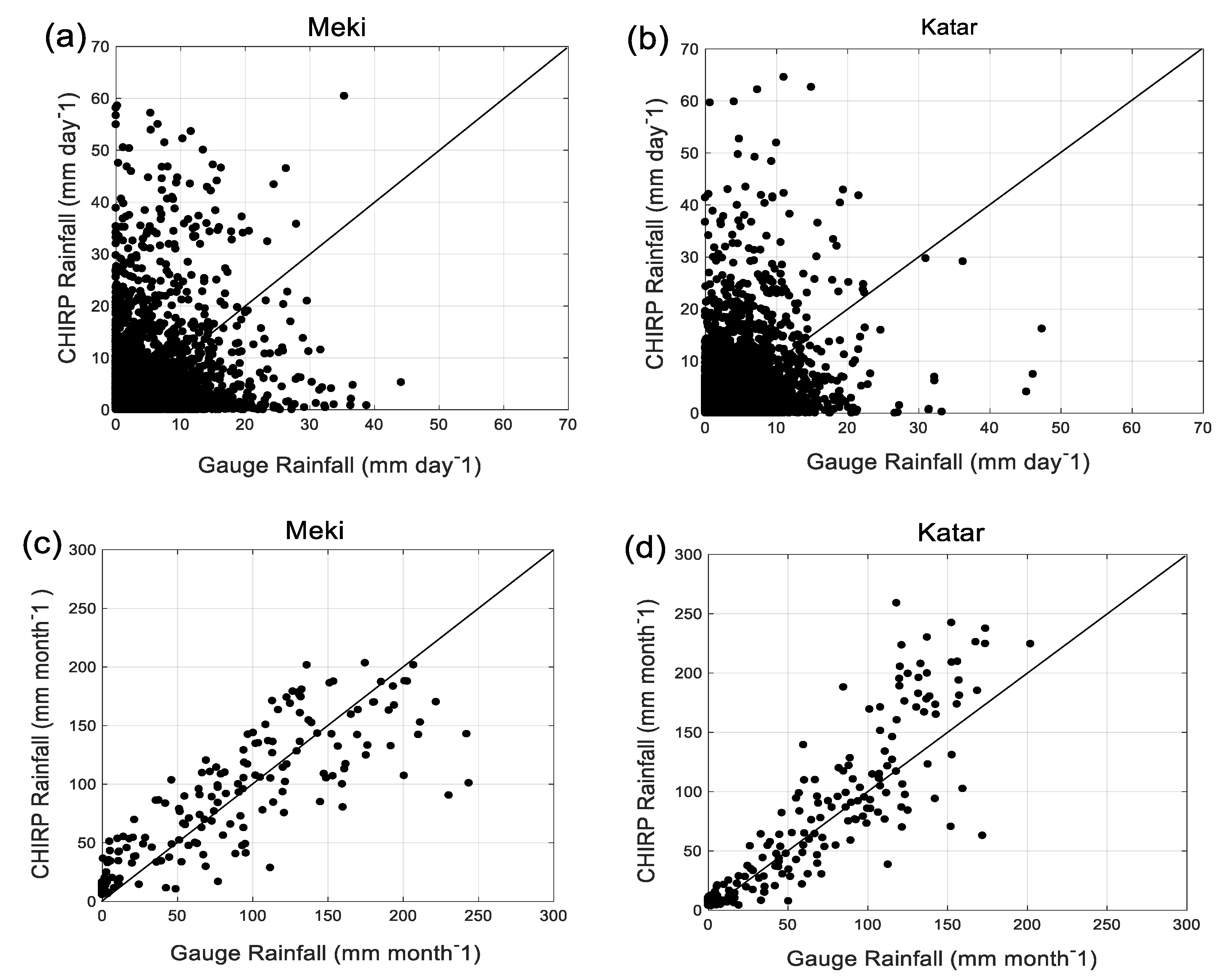
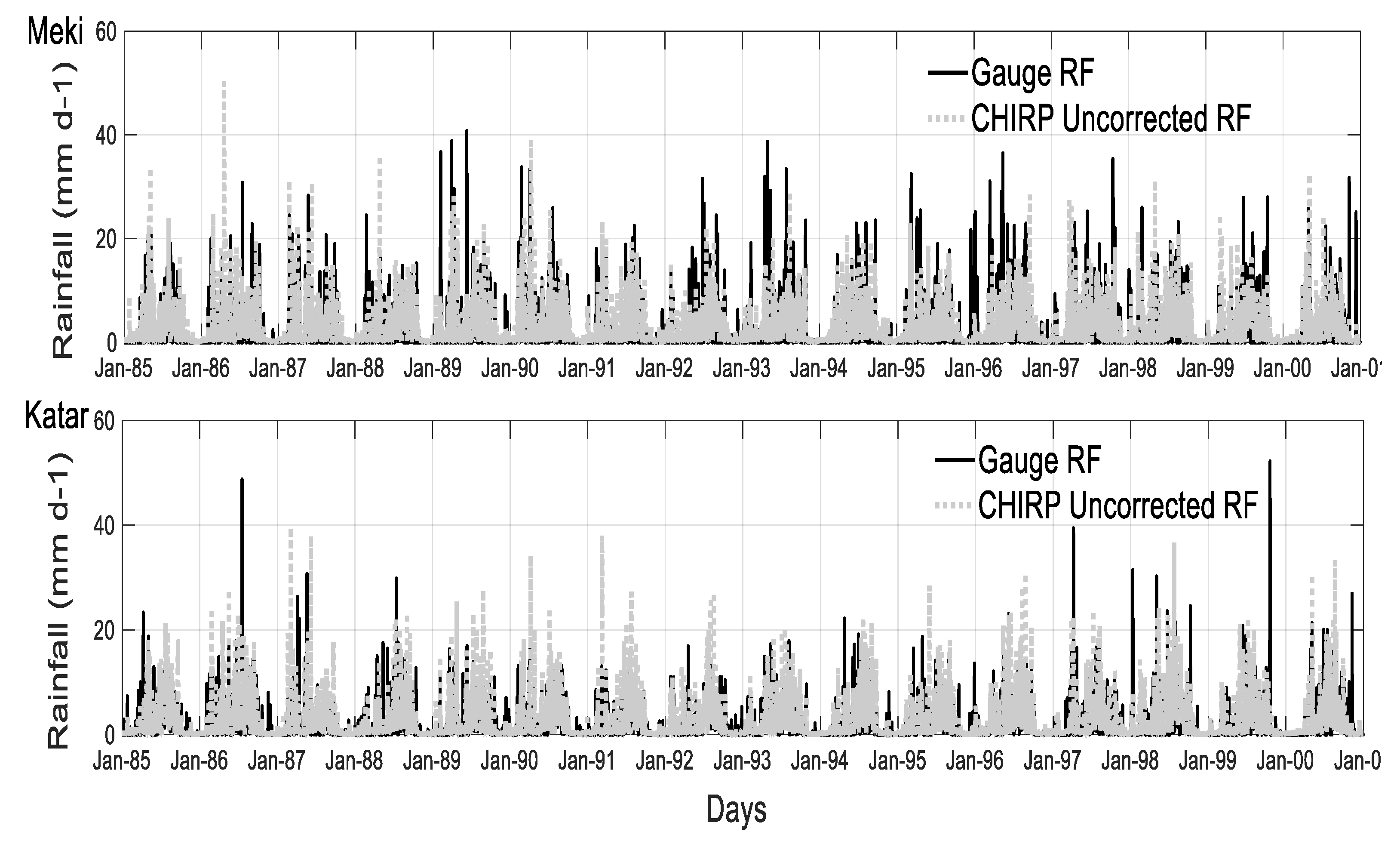
4.1.1. Point-Scale Daily Rainfall Comparison
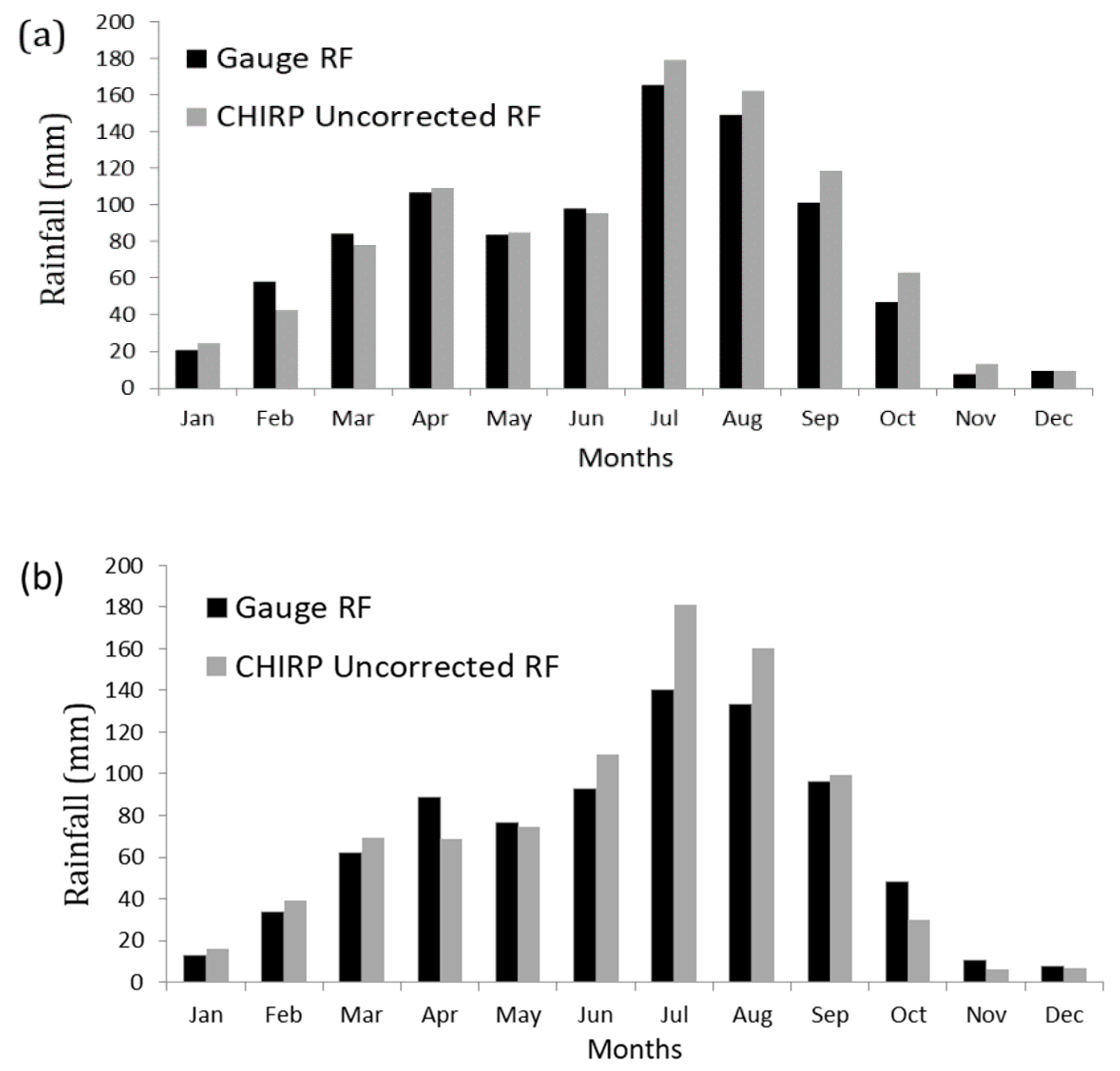
4.1.2. Point-Scale Monthly Rainfall Comparison
4.1.3. Catchment-Scale Rainfall Comparison
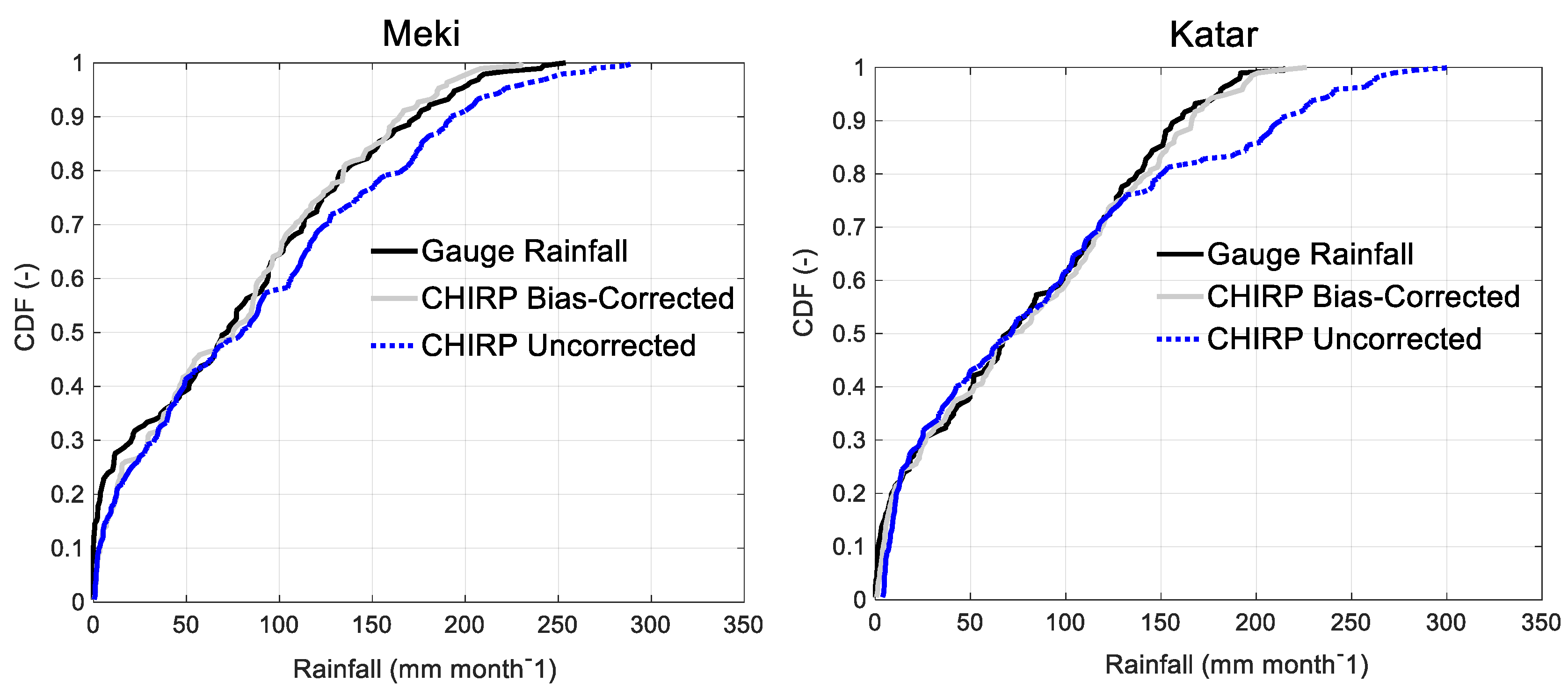
4.2. CHIRP Satellite Bias Correction
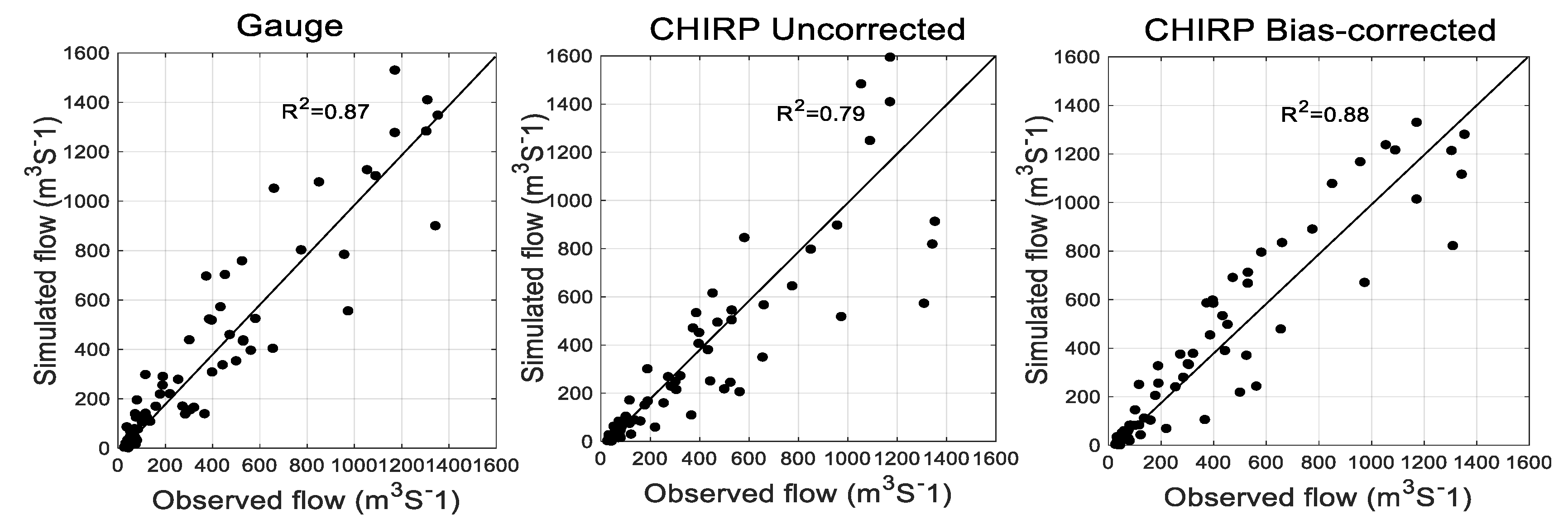
4.3. Model Calibration and Evaluation
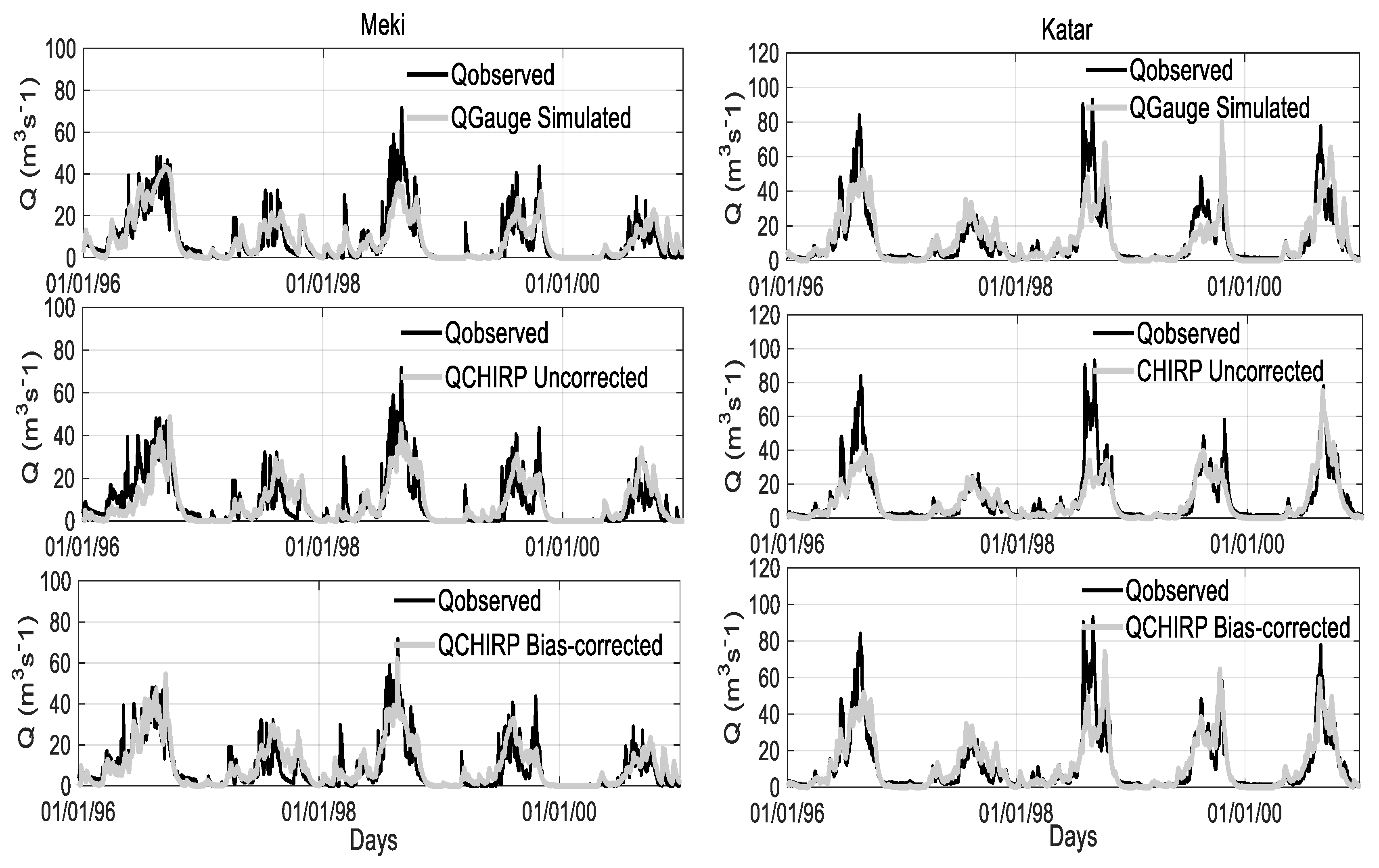
4.4. Evaluating the Value of Bias Correction on Streamflow
5. Conclusions
- The results showed that the CHIRP satellite rainfall had biases at various spatial and temporal scales over Lake Ziway watershed. CHIRP had PBIAS ranging from −16 to 20% and lower correlation at a daily time step with the rain gauge data. Overall, CHIRP performance better improved at monthly and areal catchment scales.
- We found comparable calibrated model parameters and model performances for the gauge and the bias-corrected CHIRP satellite rainfalls in simulating daily streamflow of the two catchments. However, calibrated model parameters significantly changed when the uncorrected CHIRP rainfall input served as model input. Changes up to 55% and 63% were obtained for water balance and routing controlling parameters, respectively, as compared to the gauge-based simulations. Hence, this study shows that common optimized parameter values could not be achieved for different rainfall inputs over the study area.
- The simulated streamflow better captured the observed hydrographs when using the bias-corrected CHIRP satellite rainfall input compared to the uncorrected CHIRP satellite. We note that biases in satellite rainfall inputs were translated to simulated streamflow through the HBV hydrological model. The application of non-linear bias correction effectively reduced the rainfall bias and revealed improved streamflow simulation compared to the uncorrected product.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fuka, D.R.; Walter, M.T.; MacAlister, C.; Degaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the Climate Forecast System Reanalysis as weather input data for watershed models. Hydrol. Process. 2014, 28, 5613–5623. [Google Scholar] [CrossRef]
- Gebremichael, M.; Bitew, M.M.; Hirpa, F.A.; Tesfay, G.N. Accuracy of satellite rainfall estimates in the Blue Nile Basin: Lowland plain versus Highland Mountain. Water Resour. Res. 2014, 50, 8775–8790. [Google Scholar] [CrossRef]
- Dinku, T. Validation of the CHIRPS Satellite Rainfall Estimate. In Seasonal Prediction of Hydro-Climatic Extremes in the Greater Horn of Africa, Proceedings of the 7th International Precipitation Working Group (IPWG) Workshop, Tsukuba, Japan, 17–21 November 2014; Columbia University: New York, NY, USA, 2014. [Google Scholar]
- Katsanos, D.; Retalis, A.; Michaelides, S. Validation of a high-resolution precipitation database (CHIRPS) over Cyprus for a 30-year period. Atmos. Res. 2016, 169, 459–464. [Google Scholar] [CrossRef]
- Habib, E.; Haile, A.T.; Sazib, N.; Zhang, Y.; Rientjes, T. Effect of bias correction of satellite-rainfall estimates on runoff simulations at the source of the Upper Blue Nile. Remote Sens. 2014, 6, 6688–6708. [Google Scholar] [CrossRef]
- Yong, B.; Ren, L.-L.; Hong, Y.; Wang, J.-H.; Gourley, J.J.; Jiang, S.-H.; Chen, X.; Wang, W. Hydrologic evaluation of Multisatellite Precipitation Analysis standard precipitation products in basins beyond its inclined latitude band: A case study in Laohahe basin, China. Water Resour. Res. 2010, 46, W07542. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; WahWin, K.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Assessment of GPM and TRMM multi-satellite precipitation products in streamflow simulations in a data-sparse mountainous watershed in Myanmar. Remote Sens. 2017, 9, 302. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Kidd, C.; Levizzani, V.; Marzano, F.S. A maximum entropy approach to satellite quantitative precipitation estimation (QPE). Int. J. Remote Sens. 2004, 25, 4629–4639. [Google Scholar] [CrossRef]
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Arkin, P.; Chang, A.; Ferraro, R.; Gruber, A.; Janowiak, J.; McNab, A.; Rudolf, B.; Schneider, U. The global precipitation climatology project (GPCP) combined precipitation dataset. Bull. Am. Meteorol. Soc. 1997, 78, 5–20. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Funk, C.; Verdin, A.; Michaelsen, J.; Peterson, P.; Pedreros, D.; Husak, G. A global satellite-assisted precipitation climatology. Earth Syst. Sci. Data 2015, 7, 275–287. [Google Scholar] [CrossRef] [Green Version]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern of Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Haile, A.T.; Habib, E.; Rientjes, T. Evaluation of the Climate Prediction Center (CPC) morphing technique (CMORPH) rainfall product on hourly time scales over the source of the Blue Nile River. Hydrol. Process. 2013, 27, 1829–1839. [Google Scholar] [CrossRef]
- Bhatti, H.; Rientjes, T.; Haile, A.; Habib, E.; Verhoef, W. Evaluation of bias correction method for satellite-based rainfall data. Sensors 2016, 16, 884. [Google Scholar] [CrossRef] [PubMed]
- Vernimmen, R.R.; Hooijer, A.; Aldrian, E.; Van Dijk, A.I. Evaluation and bias correction of satellite rainfall data for drought monitoring in Indonesia. Hydrol. Earth Syst. Sci. 2012, 16, 133–146. [Google Scholar] [CrossRef] [Green Version]
- Berg, P.; Feldmann, H.; Panitz, H.-J. Bias correction of high resolution regional climate model data. J. Hydrol. 2012, 448, 80–92. [Google Scholar] [CrossRef]
- Haerter, J.O.; Eggert, B.; Moseley, C.; Piani, C.; Berg, P. Statistical precipitation bias correction of gridded model data using point measurements. Geophys. Res. Lett. 2015, 42, 1919–1929. [Google Scholar] [CrossRef] [Green Version]
- Xue, X.; Hong, Y.; Limaye, A.S.; Gourley, J.J.; Huffman, G.J.; Khan, S.I.; Dorji, C.; Chen, S. Statistical and hydrological evaluation of TRMM-based Multi-satellite Precipitation Analysis over the Wangchu Basin of Bhutan: Are the latest satellite precipitation products 3B42V7 ready for use in ungauged basins? J. Hydrol. 2013, 499, 91–99. [Google Scholar] [CrossRef]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the Version-6 and Version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extremes? J. Hydrol. 2014, 508, 77–87. [Google Scholar]
- Zeweldi, D.A.; Gebremichael, M.; Downer, C.W. On CMORPH rainfall for streamflow simulation in a small, Hortonian watershed. J. Hydrometeorol. 2011, 12, 456–466. [Google Scholar] [CrossRef]
- Artan, G.; Gadain, H.; Smith, J.L.; Asante, K.; Bandaragoda, C.J.; Verdin, J.P. Adequacy of satellite derived rainfall data for stream flow modeling. Nat. Hazards 2007, 43, 167–185. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Ayana, E.K.; Maathuis, B.H.P.; MacAlister, C.; Philpot, W.D.; Leyton, J.M.O.; Steenhuis, T.S. Performance of bias corrected MPEG rainfall estimate for rainfall-runoff simulation in the upper Blue Nile Basin, Ethiopia. J. Hydrol. 2018, 556, 1182–1191. [Google Scholar] [CrossRef]
- Lakew, H.B.; Moges, S.A.; Asfaw, D.H. Hydrological Evaluation of Satellite and Reanalysis Precipitation Products in the Upper Blue Nile Basin: A Case Study of Gilgel Abbay. Hydrology 2017, 4, 39. [Google Scholar] [CrossRef]
- Ayehu, G.T.; Tadesse, T.; Gessesse, B.; Dinku, T. Validation of new satellite rainfall products over the Upper Blue Nile Basin, Ethiopia. Atmos. Meas. Tech. 2018, 11, 1921–1936. [Google Scholar] [CrossRef] [Green Version]
- Awange, J.L.; Forootan, E. An evaluation of high-resolution gridded precipitation products over Bhutan (1998–2012). Int. J. Climatol. 2016, 36, 1067–1087. [Google Scholar]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pederos, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A Quasi-Global Precipitation Time Series for Drought Monitoring; U.S. Geological Survey Data Series 832; U.S. Department of the Interior: Reston, VA, USA, 2014; pp. 1–12.
- Bitew, M.M.; Gebremichael, M.; Ghebremichael, L.T.; Bayissa, Y.A. Evaluation of High-Resolution Satellite Rainfall Products through Streamflow Simulation in a Hydrological Modeling of a Small Mountainous Watershed in Ethiopia. J. Hydrometeorol. 2012, 13, 338–350. [Google Scholar] [CrossRef]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias correction of daily precipitation simulated by a regional climate model: A comparison of methods. Int. J. Climatol. 2013, 33, 1367–1381. [Google Scholar] [CrossRef]
- Wörner, V.; Kreye, P.; Meon, G. Effects of Bias-Correcting Climate Model Data on the Projection of Future Changes in High Flows. Hydrology 2019, 6, 46. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Collick, A.S.; Tilahun, S.A.; Langan, S.; Rientjes, T.H.; Steenhuis, T.S. Comparing TRMM 3B42, CFSR and ground-based rainfall estimates as input for hydrological models, in data scarce regions: The Upper Blue Nile Basin, Ethiopia. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 2081–2112. [Google Scholar] [CrossRef]
- Rientjes, T.H.M.; Perera, B.U.J.; Haile, A.T.; Reggiani, P.; Muthuwatta, L.P. Regionalisation for lake level simulation—The case of Lake Tana in the Upper Blue Nile, Ethiopia. Hydrol. Earth Syst. Sci. 2011, 15, 1167–1183. [Google Scholar] [CrossRef]
- Abdo, K.S.; Fiseha, B.M.; Rientjes, T.H.; Gieske, A.S.; Haile, A.T. Assessment of climate change impacts on the hydrology of Gilgel Abay catchment in Lake Tana basin, Ethiopia. Hydrol. Process. 2009, 23, 3661–3669. [Google Scholar] [CrossRef]
- Wale, A.; Rientjes, T.H.M.; Gieske, A.S.M.; Getachew, H.A. Ungauged catchment contributions to Lake Tana’s water balance. Hydrol. Process. 2009, 23, 3682–3693. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Paper; United Nations Food and Agriculture Organization (FAO): Rome, Italy, 1998; p. 300. [Google Scholar]
- Johansson, B. IHMS Integrated Hydrological Modeling System Manual Version 6.3; Swedish Meteorological and Hydrological institute: Stockholm, Sweden, 2013; p. 144.
- Lindström, G.; Johansson, B.; Persson, M.; Gardelin, M.; Bergström, S. Development and test of the distributed HBV-96 hydrological model. J. Hydrol. 1997, 201, 272–288. [Google Scholar] [CrossRef]
- Gumindoga, W.; Rientjes, T.H.; Haile, A.T.; Makurira, H.; Reggiani, P. Performance of bias correction schemes for CMORPH rainfall estimates in the Zambezi River Basin. Hydrol. Earth Syst. Sci. Discuss. 2019, 23, 2915–2938. [Google Scholar] [CrossRef]
- Saber, M.; Yilmaz, K. Bias Correction of Satellite-Based Rainfall Estimates for Modeling Flash Floods in Semi-Arid regions: Application to Karpuz River, Turkey. Nat. Hazards Earth Syst. Sci. Discuss. 2016, 1–35. [Google Scholar] [CrossRef]
- Saber, M.; Yilmaz, K. Evaluation and Bias Correction of Satellite-Based Rainfall Estimates for Modeling Flash Floods over the Mediterranean region: Application to Karpuz River Basin, Turkey. Water 2018, 10, 657. [Google Scholar] [CrossRef]



| S. No | Statistical Measures | Equation | Unit | Best Fit |
|---|---|---|---|---|
| 1 | Pearson correlation coefficient (CC) | - | 1 | |
| 2 | Percentage relative bias (PBIAS) | % | 0 | |
| 3 | Mean error (ME) | mm | 0 | |
| 4 | Mean absolute error (MAE) | mm | 0 | |
| 5 | Root mean squared error (RMSE) | mm | 0 | |
| 6 | Probability of detection (POD) | - | 1 | |
| 7 | False alarm ratio (FAR) | - | 0 | |
| 8 | Critical success index (CSI) | - | 1 |
| Parameter | Description | Unit | Value Range | Initial Value |
|---|---|---|---|---|
| FC | Field capacity at maximum soil moisture storage | mm | 100–1500 | 200 |
| BETA | The exponent in drainage from the soil layer | - | 1–4 | 2.0 |
| LP | The limit for the potential evapotranspiration | - | 0.1–1 | 0.9 |
| K4 | The recession coefficient for the lower zone | d−1 | 0.001–0.1 | 0.01 |
| Khq | The recession coefficient for the upper zone | d−1 | 0.005–0.5 | 0.1 |
| Alfa | The coefficient for non-linearity of flow | - | 0–1.5 | 0.6 |
| CFLUX | The maximum capillary flow from the upper zone | mm | 0–2 | 1.0 |
| PERC | Percolation capacity from upper to the lower zone | mm d−1 | 0.01–6 | 0.5 |
| Statistical Measures | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Catchment | Stations | CC (-) | PBIAS (%) | ME (mm d−1) | MAE (mm d−1) | RMSE (mm d−1) | POD (-) | FAR (-) | CSI (-) |
| Bui | 0.29 | 8.99 | 0.25 | 3.50 | 6.88 | 0.69 | 0.56 | 0.36 | |
| Butajira | 0.23 | 2.05 | 0.06 | 3.98 | 7.97 | 0.57 | 0.55 | 0.39 | |
| Meki | Koshe | 0.22 | 6.87 | 0.16 | 3.38 | 7.32 | 0.56 | 0.67 | 0.30 |
| Meki | 0.22 | 5.76 | 0.12 | 3.04 | 6.71 | 0.66 | 0.66 | 0.29 | |
| Tora | 0.17 | −15.99 | −0.41 | 3.46 | 7.52 | 0.62 | 0.65 | 0.29 | |
| Ziway | 0.20 | 18.46 | 0.36 | 3.09 | 6.49 | 0.69 | 0.68 | 0.28 | |
| Arata | 0.17 | 10.29 | 0.23 | 3.27 | 7.19 | 0.56 | 0.60 | 0.31 | |
| Assela | 0.26 | −14.96 | −0.43 | 3.34 | 6.70 | 0.69 | 0.46 | 0.43 | |
| Bekoji | 0.32 | 14.64 | 0.43 | 3.47 | 6.76 | 0.51 | 0.34 | 0.49 | |
| Katar | Dagaga | 0.28 | 11.23 | 0.32 | 3.48 | 6.81 | 0.67 | 0.36 | 0.49 |
| K.Genet | 0.23 | 19.64 | 0.44 | 3.08 | 6.35 | 0.68 | 0.51 | 0.40 | |
| Kulumsa | 0.21 | 3.67 | 0.08 | 3.20 | 6.81 | 0.56 | 0.52 | 0.35 | |
| Merero | 0.40 | 18.96 | 0.53 | 2.90 | 5.43 | 0.59 | 0.26 | 0.48 | |
| Ogolcho | 0.18 | 6.51 | 0.14 | 3.14 | 6.97 | 0.67 | 0.63 | 0.32 | |
| Statistical Measures | ||||||||
|---|---|---|---|---|---|---|---|---|
| Catchment | CC (-) | PBIAS (%) | ME (mm d−1) | MAE (mm d−1) | RMSE (mm d−1) | POD (-) | FAR (-) | CSI (-) |
| Meki | 0.37 | 3.8 | 0.1 | 1.0 | 4.9 | 0.62 | 0.39 | 0.45 |
| Katar | 0.40 | −2.0 | 0.3 | 1.1 | 4.1 | 0.70 | 0.25 | 0.50 |
| Statistical Measures | ||||||||
|---|---|---|---|---|---|---|---|---|
| Catchment | CC (-) | PBIAS (%) | ME (mm d−1) | MAE (mm d−1) | RMSE (mm d−1) | POD (-) | FAR (-) | CSI (-) |
| Meki | 0.56 | −0.7 | 0.1 | 0.8 | 4.0 | 0.76 | 0.28 | 0.57 |
| Katar | 0.64 | 0.3 | 0.1 | 0.8 | 3.5 | 0.82 | 0.19 | 0.64 |
| Parameters | Gauge Rainfall | CHIRP Uncorrected Rainfall | CHIRP Bias-Corrected Rainfall |
|---|---|---|---|
| FC | 850 | 960 | 860 |
| BETA | 1.94 | 1.95 | 1.96 |
| LP | 0.5 | 0.5 | 0.5 |
| K4 | 0.07 | 0.1 | 0.1 |
| Khq | 0.02 | 0.2 | 0.1 |
| Alfa | 1.05 | 1.2 | 0.8 |
| CFLUX | 0.01 | 0.2 | 0.01 |
| PERC | 1.5 | 4.5 | 1.15 |
| Calibration NSE (-) | 0.67 | 0.65 | 0.71 |
| RVE (%) | −1.63 | −13.5 | −1.47 |
| Validation NSE (-) | 0.70 | 0.64 | 0.64 |
| RVE (%) | 1.27 | −4.96 | 3.84 |
| Parameters | Gauge Rainfall | CHIRP Uncorrected | CHIRP Bias-Corrected Rainfall |
|---|---|---|---|
| FC | 860 | 930 | 820 |
| BETA | 2.98 | 2.95 | 3.05 |
| LP | 0.7 | 0.6 | 0.7 |
| K4 | 0.1 | 0.08 | 0.1 |
| Khq | 0.08 | 0.2 | 0.12 |
| Alfa | 1.15 | 1.2 | 1.1 |
| CFLUX | 0.002 | 0.015 | 0.005 |
| PERC | 2.15 | 3.5 | 2.75 |
| Calibration NSE (-) | 0.78 | 0.70 | 0.80 |
| RVE (%) | −0.80 | −13.4 | −1.28 |
| Validation NSE (-) | 0.70 | 0.67 | 0.74 |
| RVE (%) | 1.96 | −16.8 | 3.04 |
| Catchment | Performance Measure | CHIRP Uncorrected | CHIRP Bias-Corrected |
|---|---|---|---|
| Meki | BIAS | 0.82 | 0.96 |
| RVE | 17 | 5.0 | |
| Katar | BIAS | 0.84 | 0.90 |
| RVE | 11 | 3.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goshime, D.W.; Absi, R.; Ledésert, B. Evaluation and Bias Correction of CHIRP Rainfall Estimate for Rainfall-Runoff Simulation over Lake Ziway Watershed, Ethiopia. Hydrology 2019, 6, 68. https://doi.org/10.3390/hydrology6030068
Goshime DW, Absi R, Ledésert B. Evaluation and Bias Correction of CHIRP Rainfall Estimate for Rainfall-Runoff Simulation over Lake Ziway Watershed, Ethiopia. Hydrology. 2019; 6(3):68. https://doi.org/10.3390/hydrology6030068
Chicago/Turabian StyleGoshime, Demelash Wondimagegnehu, Rafik Absi, and Béatrice Ledésert. 2019. "Evaluation and Bias Correction of CHIRP Rainfall Estimate for Rainfall-Runoff Simulation over Lake Ziway Watershed, Ethiopia" Hydrology 6, no. 3: 68. https://doi.org/10.3390/hydrology6030068
APA StyleGoshime, D. W., Absi, R., & Ledésert, B. (2019). Evaluation and Bias Correction of CHIRP Rainfall Estimate for Rainfall-Runoff Simulation over Lake Ziway Watershed, Ethiopia. Hydrology, 6(3), 68. https://doi.org/10.3390/hydrology6030068