GEO-CWB: GIS-Based Algorithms for Parametrising the Responses of Catchment Dynamic Water Balance Regarding Climate and Land Use Changes
Abstract
1. Introduction
2. Materials and Methods
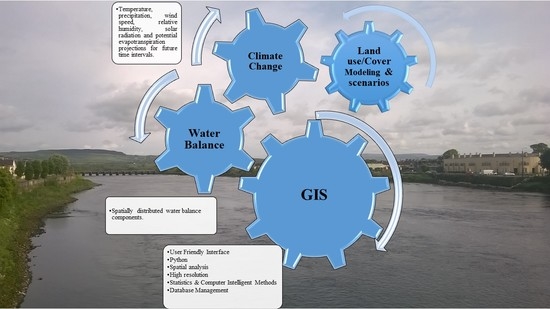
2.1. The Conceptualisation of GEO-CWB Framework
2.2. GEO-CWB: The Physical Base and Algorithm Design
- Land cover: Vegetation area fraction, bare area fraction, impervious area fraction, open water area fraction, rooting depth, leaf area index, minimal stomatal resistance, interception percentage, and vegetation height.
- Precipitation.
- Potential evapotranspiration.
- Wind speed.
- Temperature.
- Groundwater level.
- Soil texture: Porosity, wilting point, field capacity, residual water content, a soil empirical parameter for Evapotranspiration (ET) calculation, plant available water, tension saturated height, and soil evaporation depth.
- Slope.
- Topography: Digital Elevation Model DEM raster.
- Average porosity (as a single value) or average porosity raster.
- Runoff coefficients: this table contains the runoff coefficients for each single combination of soil, slope, and land use types.
- GEO-CWB does not take into account the bedrock geologies of the catchment, so at the moment, it is not possible to get the absolute groundwater recharge value because the data is not available for the Shannon catchment [34]. GEO-CWB instead uses the recharge caps applied to different geological aquifers, which are available for Ireland. So, the aquifer can only accept up to a maximum amount of water. Anything more than this leads to an increase in the subsurface flow/runoff via shallow subsoil pathways [35,36]. These kinds of caps and levels have lots of variabilities and uncertainties in addition to the fact that they are not mapped or available for the Shannon catchment at both temporal and spatial scales. GEO-CWB calculates the subsurface water component which includes both the subsurface flow and the groundwater recharge. The model separates the two main components, subsurface flow and groundwater recharge, once the spatially distributed data for the recharge caps are available.
- The actual evapotranspiration, soil evaporation, and transpiration components for the catchment are calculated based on pre-calculated potential evapotranspiration maps. As the actual evapotranspiration is the summation of some calculated sub-fractions of Potential Evapotranspiration (PET) as illustrated in the GEO-CWB equations illustrated in the next sections. Depending on which fraction of each cell is being modelled, the evapotranspiration could be equal to PET (open water fraction) or fraction of it (bare soil or impervious surface fractions) or just equal to the simulated transpiration (vegetated fraction).
- GEO-CWB calculates evapotranspiration and interception components individually, which means that the total water loss from precipitation in the catchment is the summation of the two components. A summary of the GEO-CWB assumptions and limitations is provided in Table 1.
2.2.1. GEO-CWB Calculation Stages
2.2.2. GEO-CWB-Stage (1)—Dynamical Water Balance
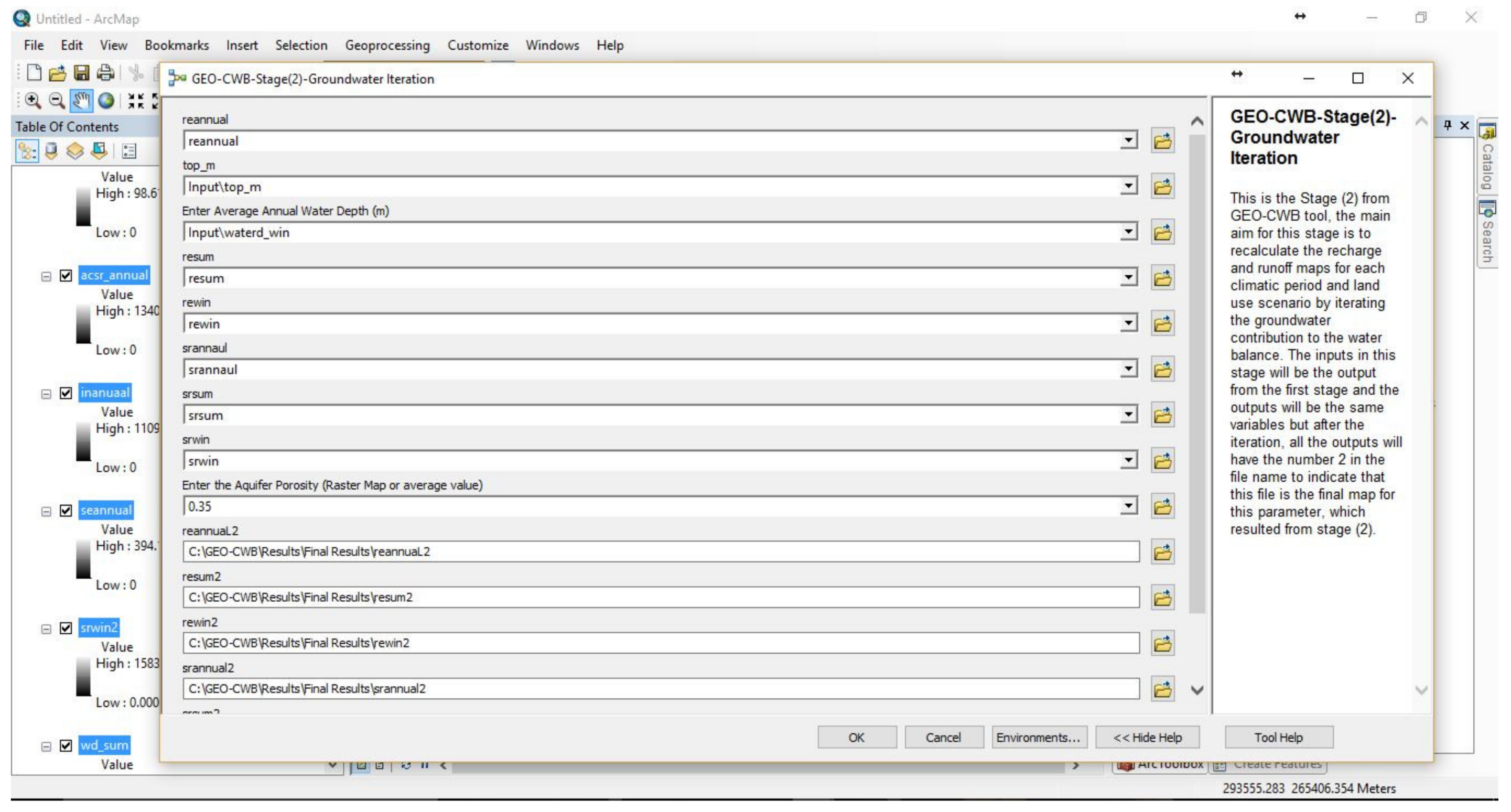
2.2.3. GEO-CWB-Stage (2)—Surface Runoff Iteration (Calibration Process)
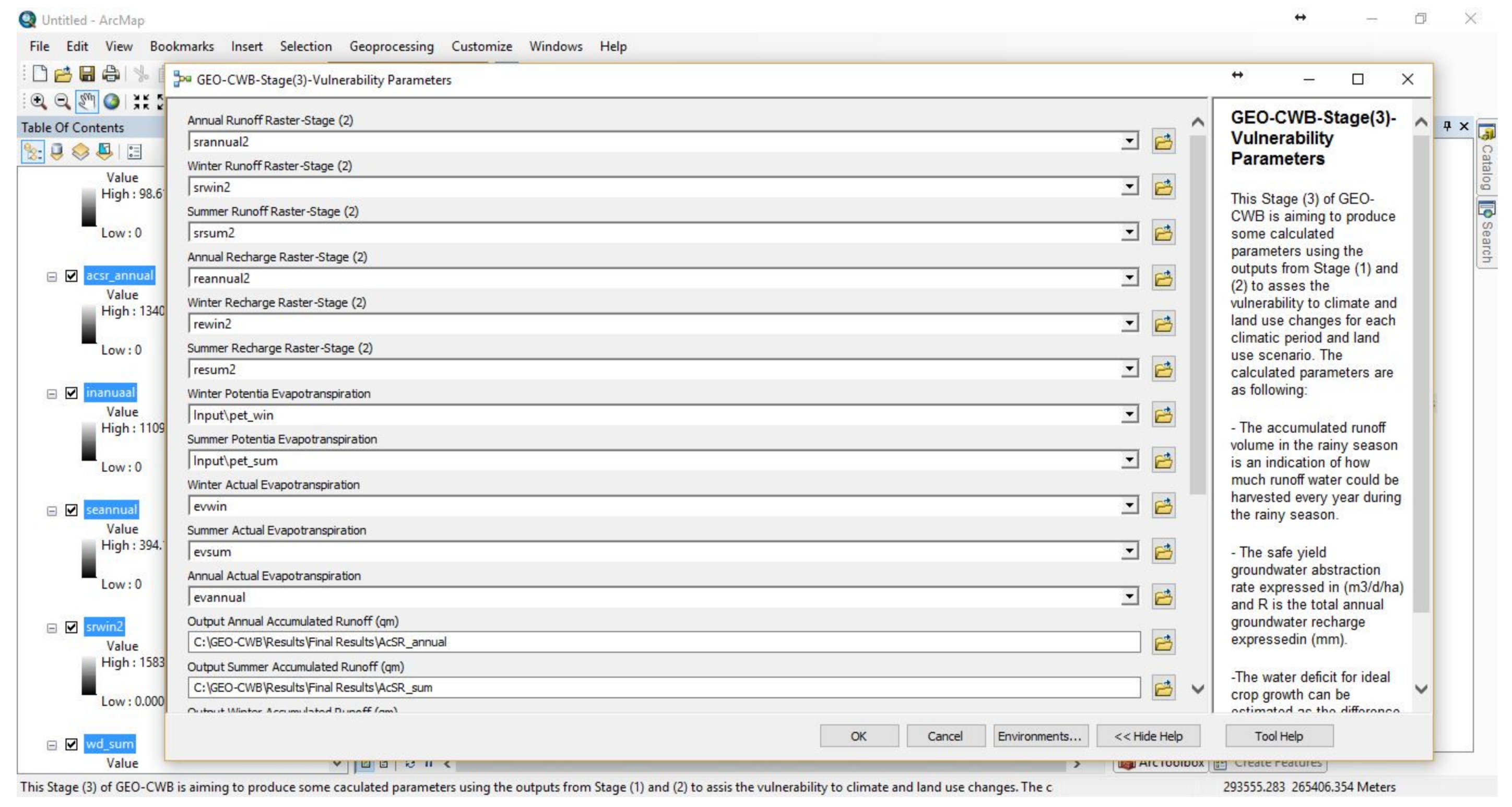
2.2.4. GEO-CWB-Stage (3)—Climate and Land Use Vulnerability Parameters
- The accumulated runoff volume in the rainy season was an indication of how much runoff water could be harvested every year during the rainy season.
- The safe yield groundwater abstraction rate expressed in (m3/d/ha). GEO-CWB produced groundwater safe yield maps, which estimated how much groundwater can be pumped sustainably without depleting the groundwater resources. Safe yield is usually expressed as a percentage of the groundwater recharge. Several authors from the least conservative 100% to a reasonably conservative 10% have suggested different values [39,40,41]. In general, sustainable yield should be considerably less than the groundwater recharge to sustain both the quantity and quality of streams, springs, wetlands, and groundwater dependent ecosystems [39,40,41]. Based on the different studies reviewed, GEO-CWB adapted the 25% as a sustainable groundwater yield percentage from the calculated subsurface water component. This was a simplistic formula for a country such as Ireland which has such differences in geology and aquifer types, so the results for Shannon were just a good indication for the decision makers.
- The water deficit for ideal crop growth (WD) can be estimated as the difference between the crop water requirement and the actual evapotranspiration that was feasible only by rainfall. The crop water requirement can be defined as the amount of water needed to meet the water loss through evapotranspiration for optimal crop growth, which can be estimated as a crop coefficient time’s reference evapotranspiration of well-watered grass [42,43]. Crop coefficients vary between 0.70 and 1.15 depending on crop type and growing stage. The crop coefficient can be assumed to be one and reference evaporation to equal PET, which allows an estimation of how much water was needed for supplementary irrigation for optimal crop growth [44,45]. This calculation can be made on an annual basis, but it was more interesting to do this separately for the summer season, and the winter season, GEO-CWB used Equation (42) in Appendix B, where WD was the water deficit, PET was the potential evapotranspiration, ET was the actual evapotranspiration, and Dn was the number of days in the season.
2.2.5. GEO-CWB-Stage (4)-Statistics Tables
- The frequency
- The summation of all the cells
- The mean of all cells
- The minimum value
- The maximum value
- The range
- The standard deviation
- The count of the cell numbers
2.2.6. GEO-CWB Integration with GIS
2.3. GEO-CWB Application: Climate and Land Use Changes Effects on the Shannon River Catchment
2.4. Data Setup and Study Area
- Land cover scenarios simulated by [32].
- Precipitation simulated by [49].
- Potential evapotranspiration simulated by [46].
- Wind speed simulated by [49].
- Temperature simulated by [49].
- Groundwater level obtained from Geological Survey Ireland (GSI).
- Soil texture obtained from GSI.
- Slope obtained from NASA’s Shuttle Radar Topography Mission (SRTM).
- Topography (DEM raster) obtained from NASA’s SRTM.
- Average porosity derived from data collected by GSI.
- River flow and levels data which were obtained from Irish Environmental Protection Agency (EPA), Office of Public Works (OPW), and Electricity Supply Board (ESB).
3. Results and Discussion
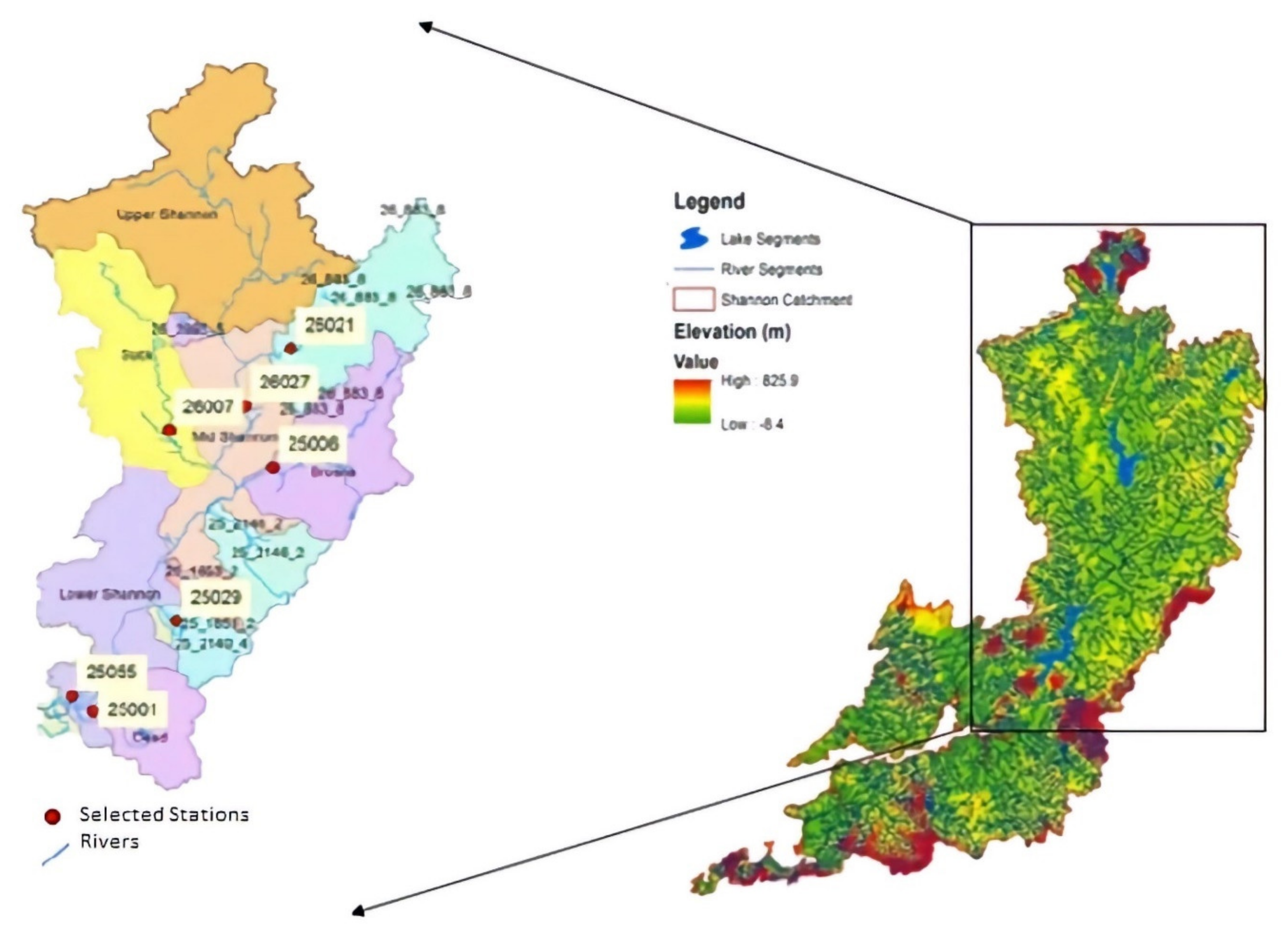
3.1. GEO-CWB Validation
3.2. Water Balance Simulated Parameters Results and Discussions
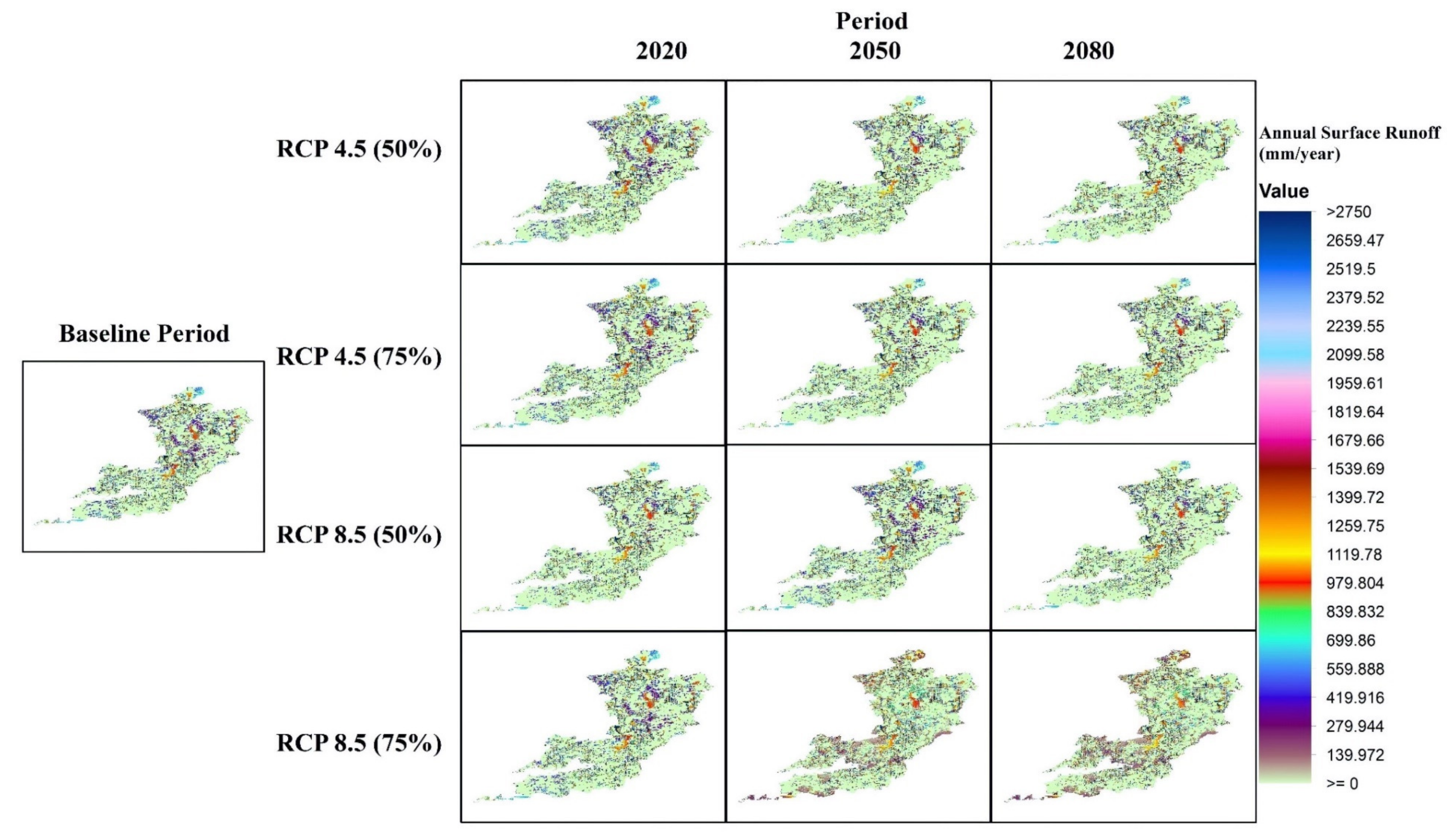
3.2.1. Surface Runoff
3.2.2. Subsurface Water Component
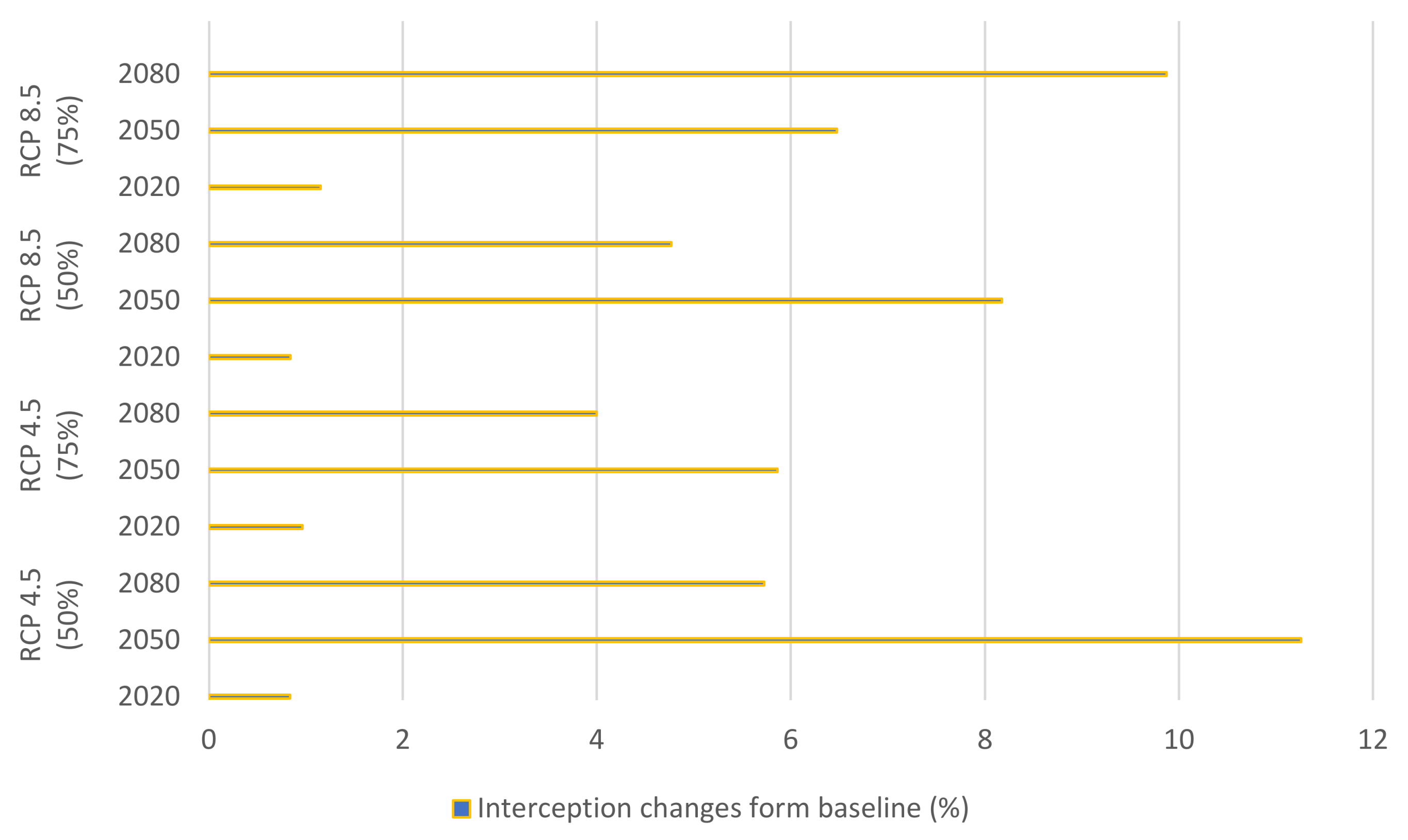
3.2.3. Rainfall Interception
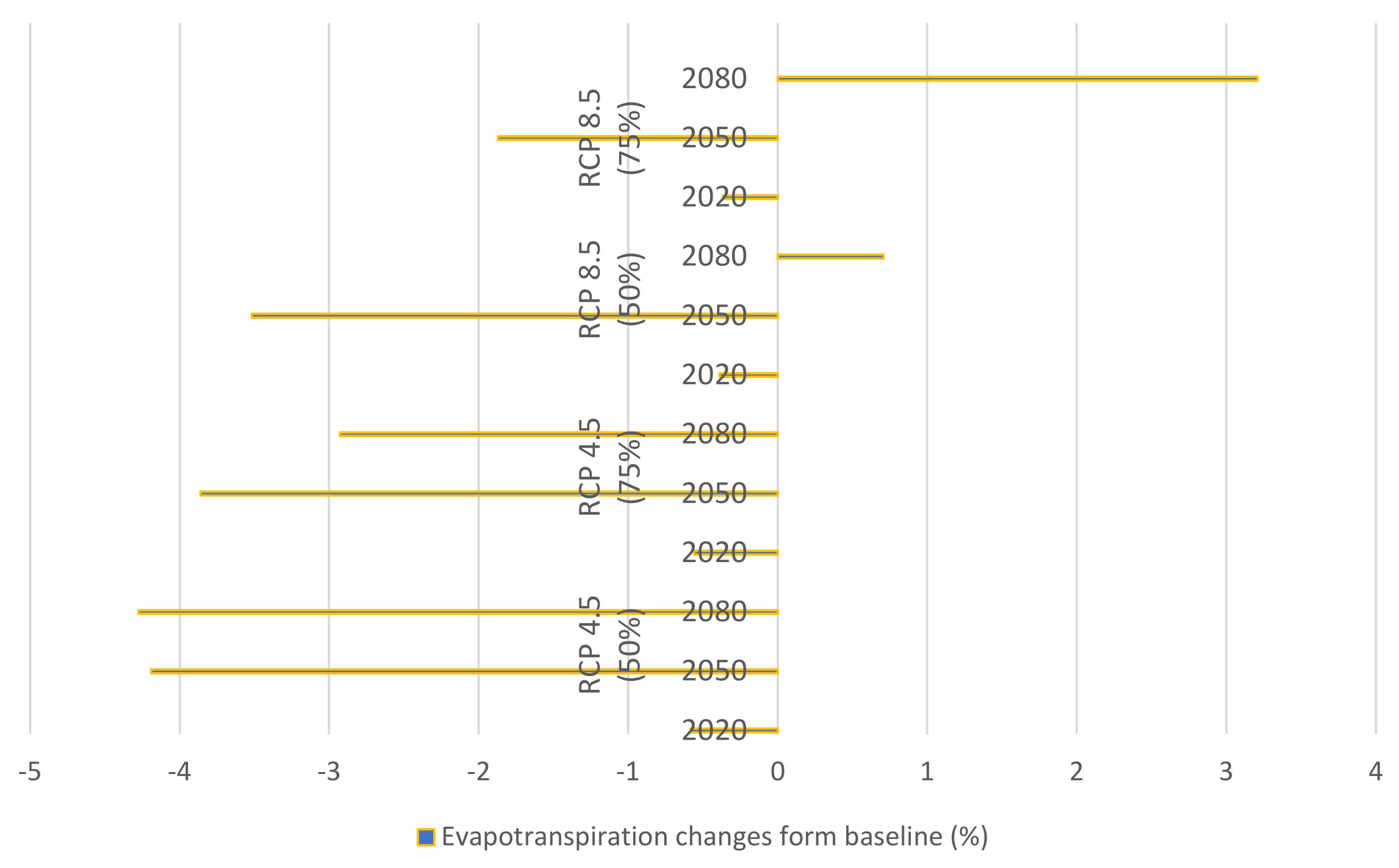
3.2.4. Evapotranspiration
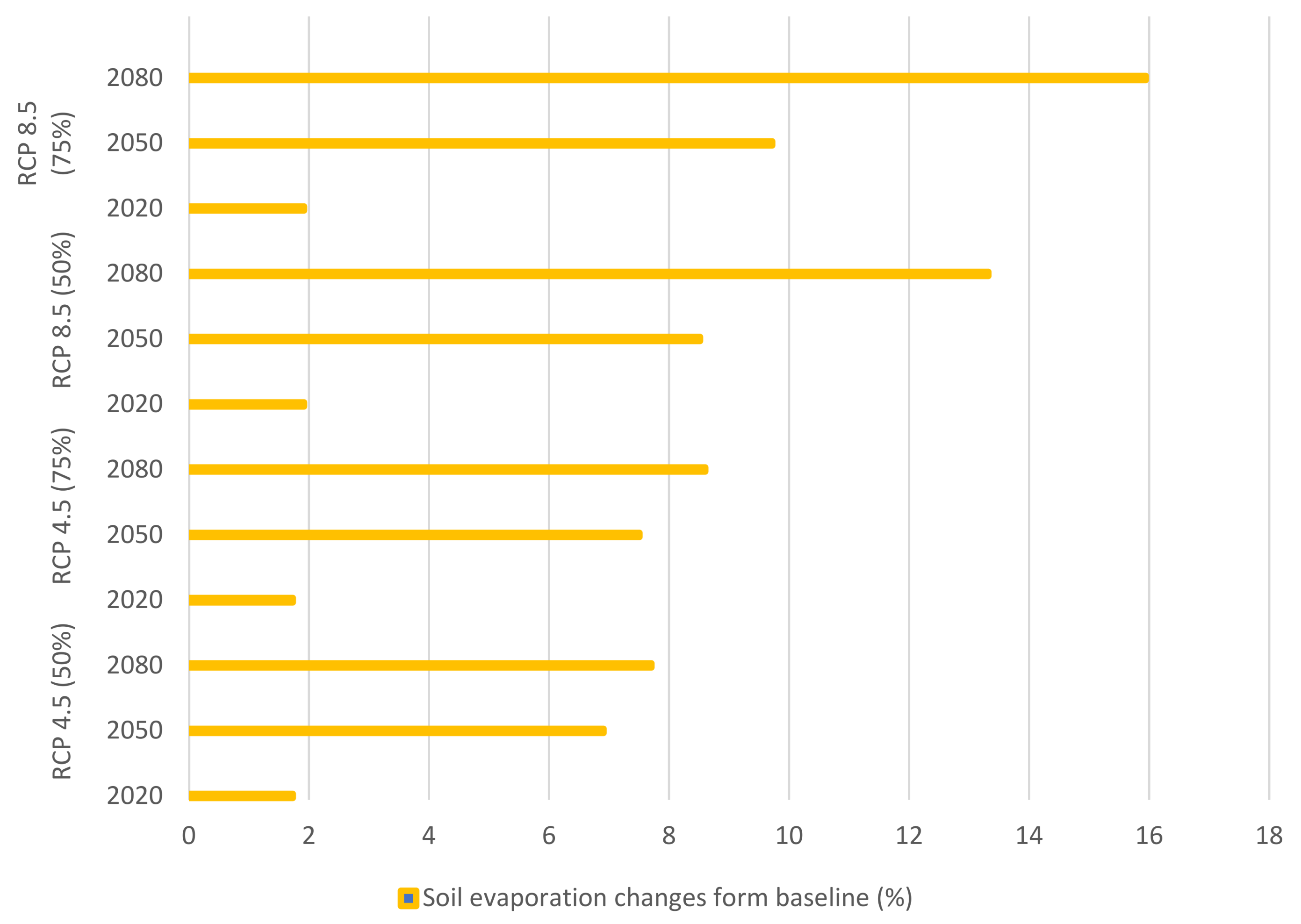
3.2.5. Soil Evaporation
3.2.6. Transpiration
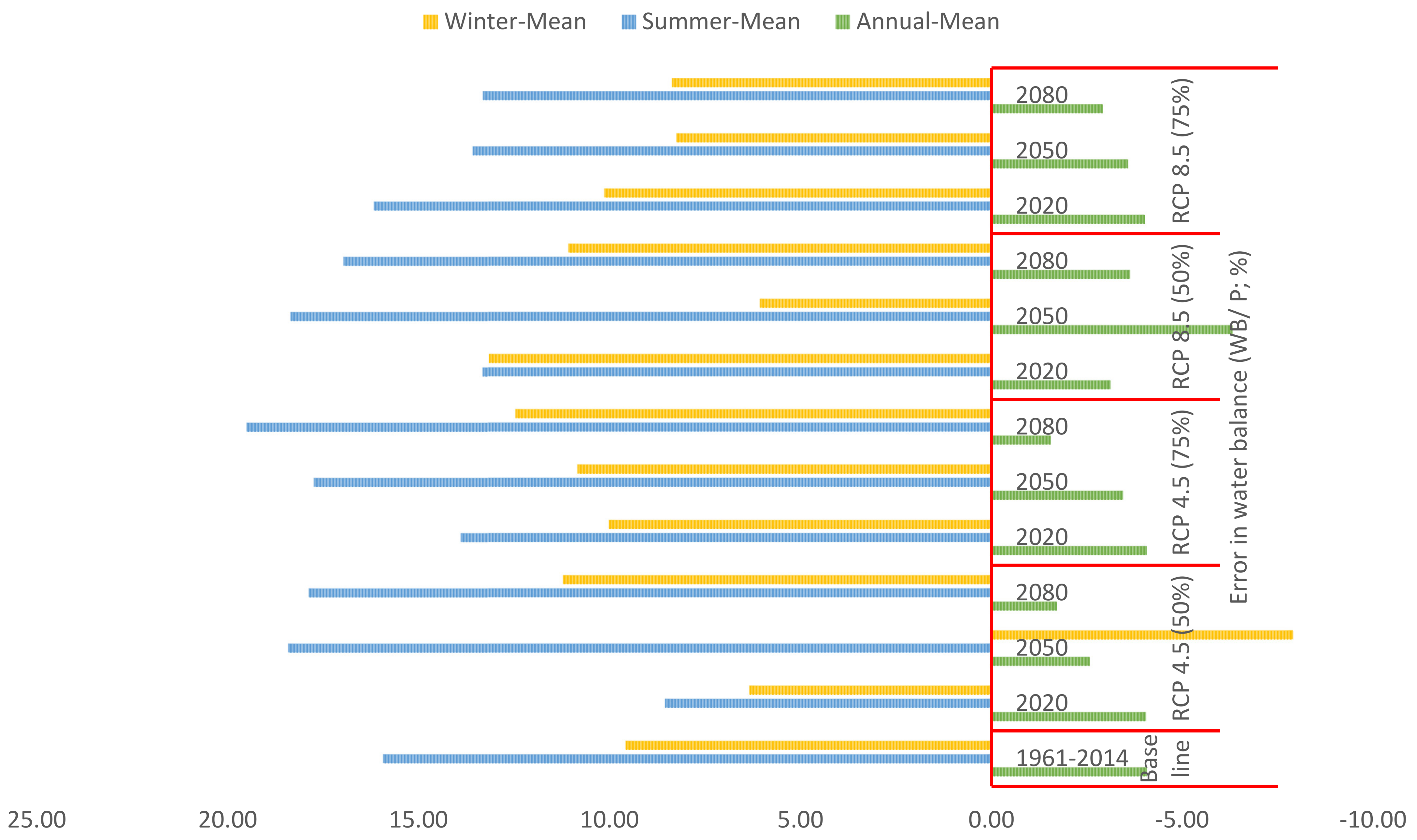
3.2.7. Error in Water Balance/Change in Storage
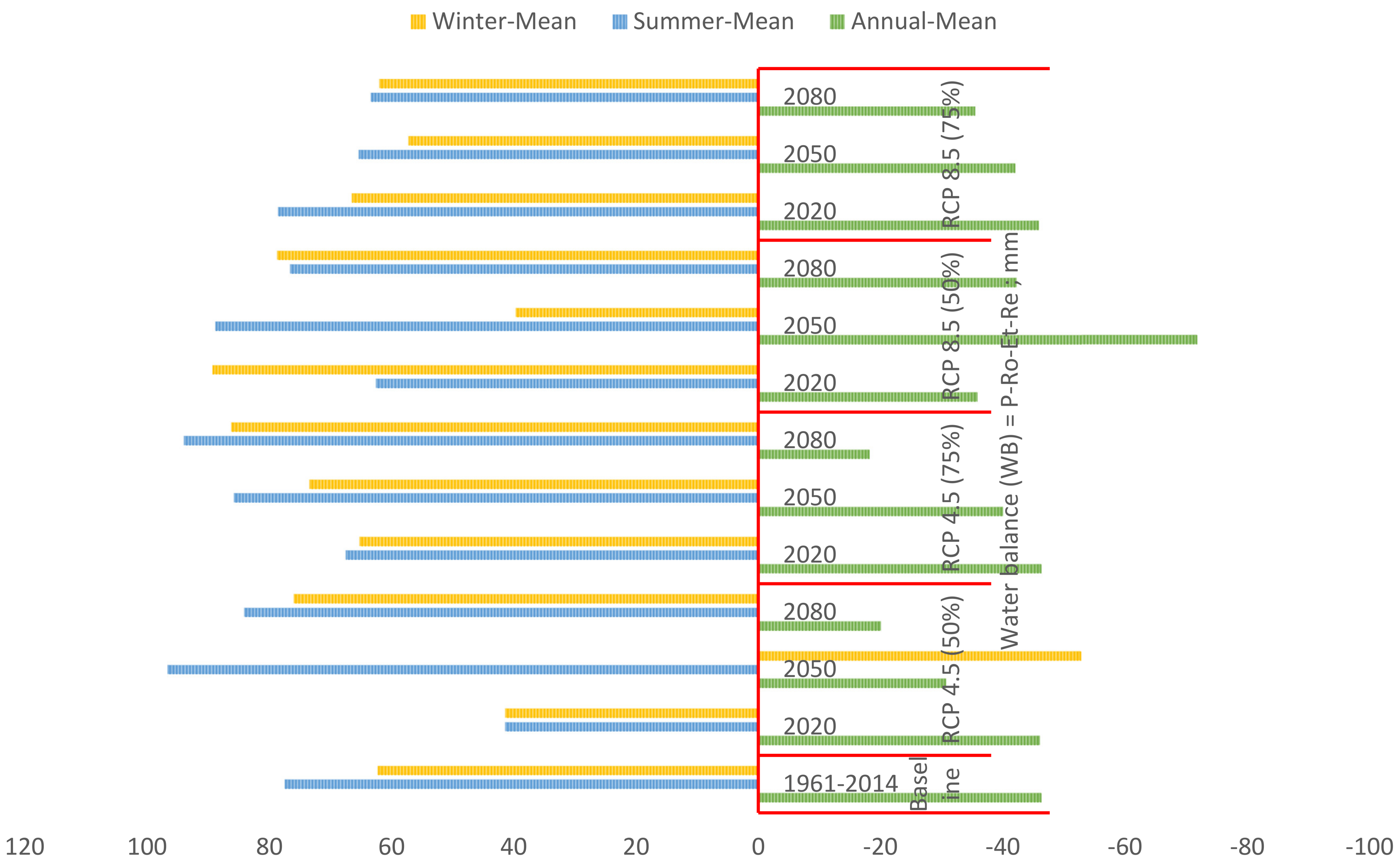
3.2.8. Simulated and Projected Water Balance for Shannon Catchment
3.2.9. Vulnerability Parameters Results
Accumulated Surface Runoff Volume
The Safe Yield Groundwater Abstraction
The Water Deficit for Ideal Crop
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. GEO-CWB Cell-by-Cell Calculations Flow Chart

Appendix B. GEO-CWB Main Equations
| Fv: | Vegetated fraction |
| Fow: | Open water |
| Fbs: | bare soil fraction |
| Fis: | Impervious surface fraction |
| P: | Precipitation |
| I: | Interception |
| Sv: | Surface runoff in the vegetated fraction |
| Tv: | Transpiration |
| Trv: | Reference transpiration |
| Eo: | Seasonal potential evapotranspiration |
| Sr: | Potential surface runoff |
| C: | Vegetation coefficient |
| T: | Temperature |
| H: | Vegetation height |
| hw: | Wind measuring height |
| U: | Wind speed (Km/hr) |
| Gwd: | Groundwater depth |
| Rd: | Rood depth |
| ht: | Tension saturated height |
| PWA: | Plant available water content |
| a: | Calibrated soil texture factor [59] |
| Eps: | Penman evaporation for wet soil |
| So: | Runoff of open water fraction |
| Ro: | subsurface water of open water fraction |
| Pet: | Potential evapotranspiration |
| Rcell: | The cell subsurface water component |
Appendix C. GEO-CWB User Interfaces


Appendix D. GEO-CWB Spatially Distributed Mapped Results
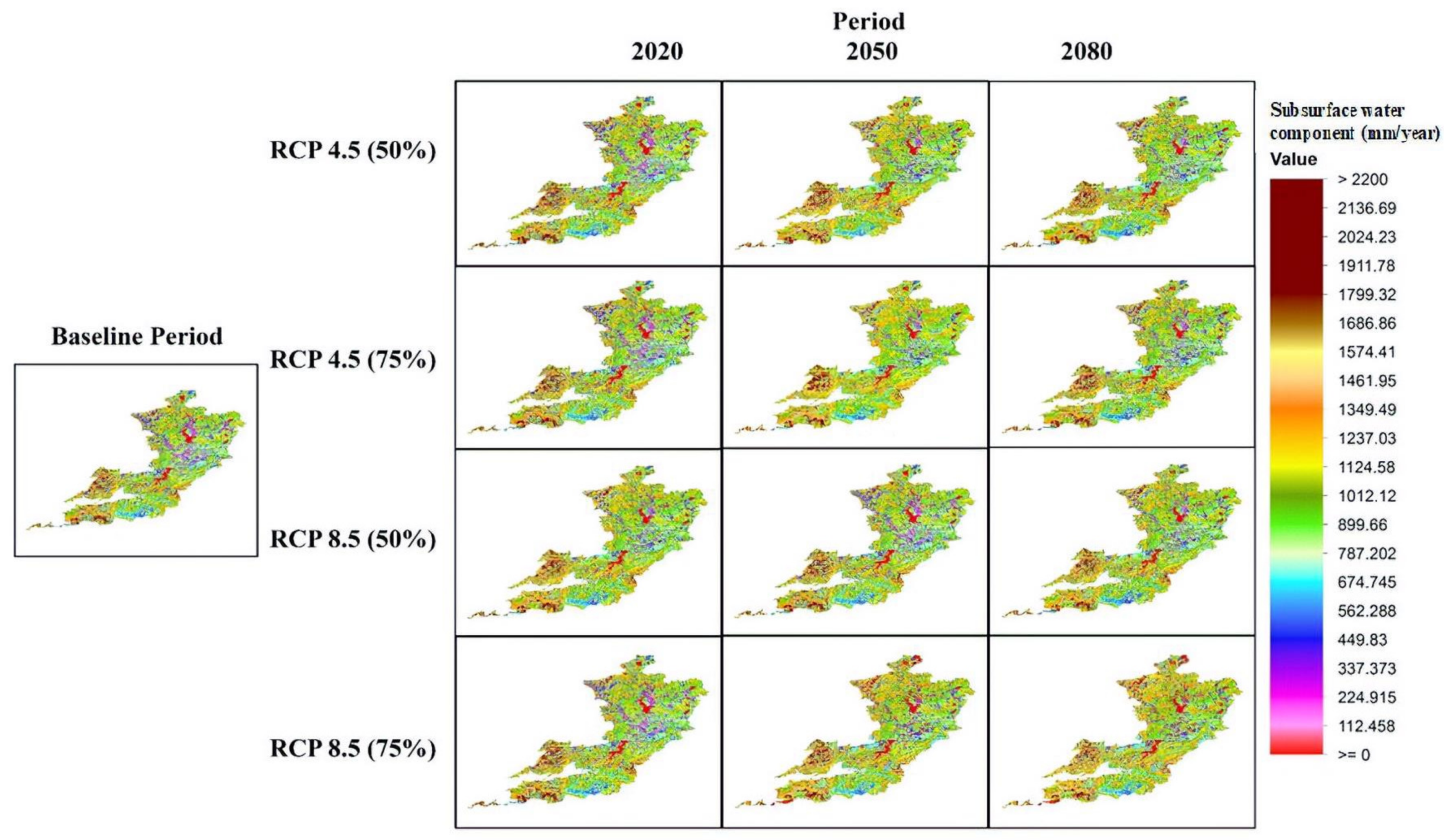
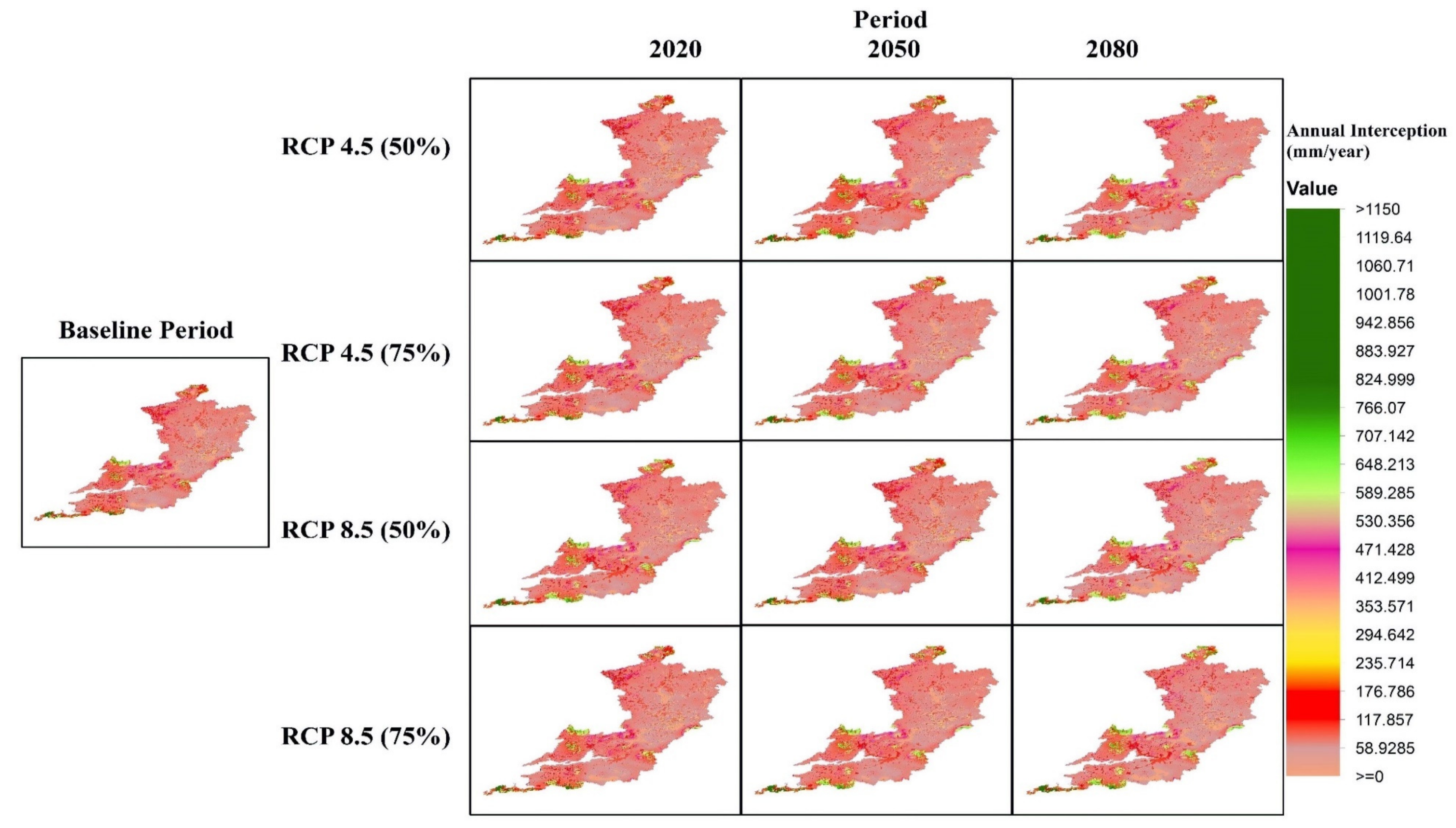
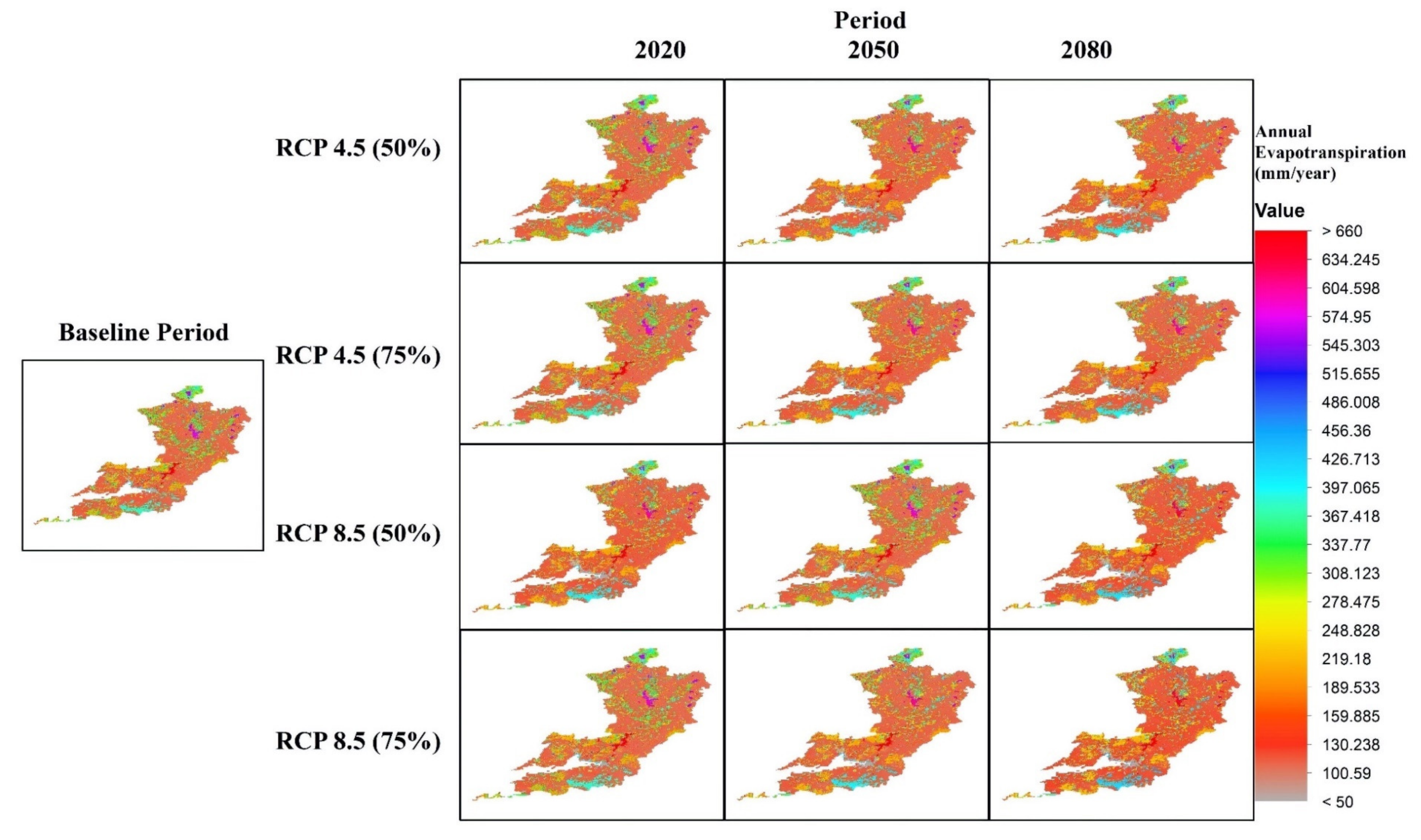
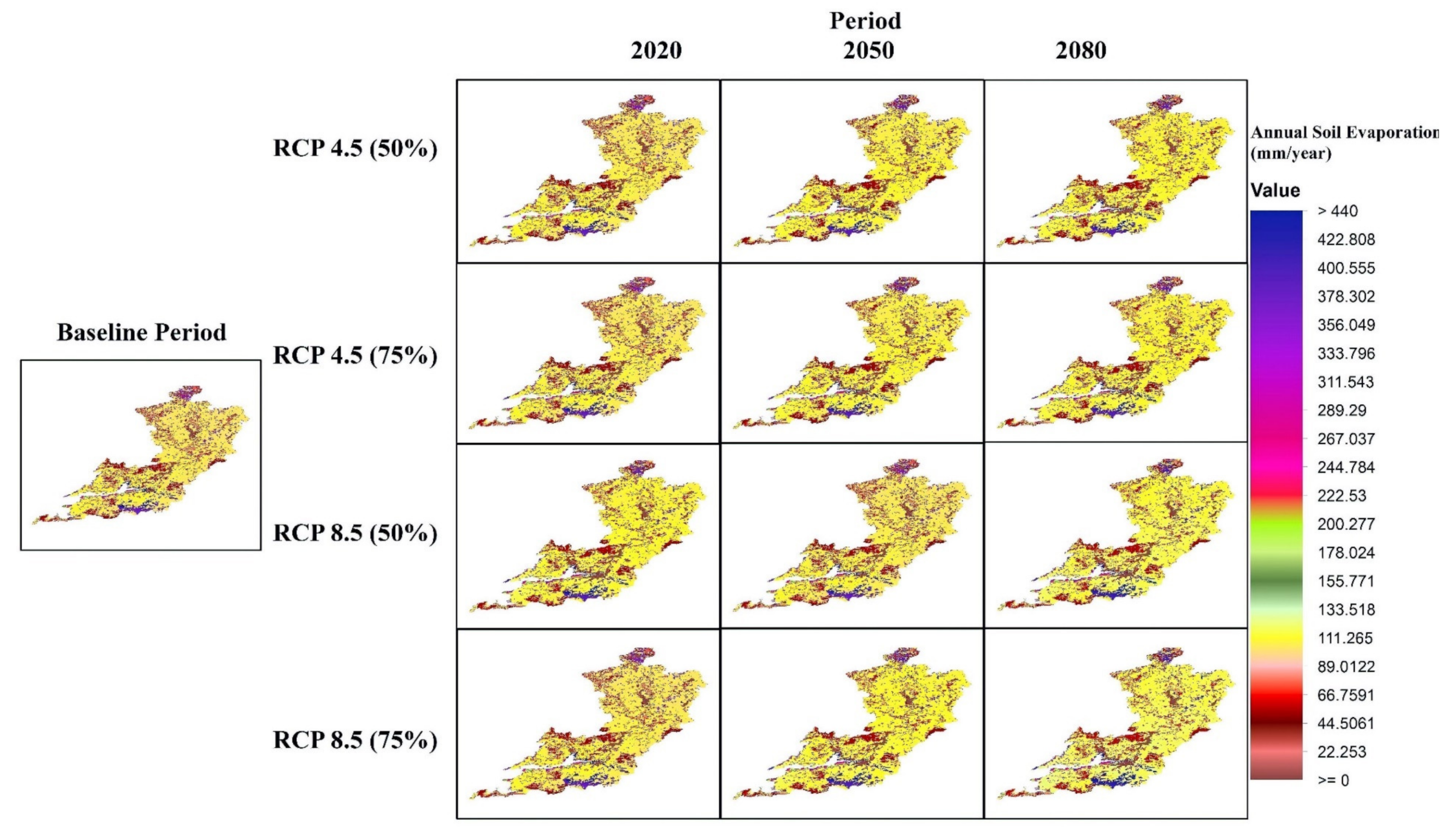

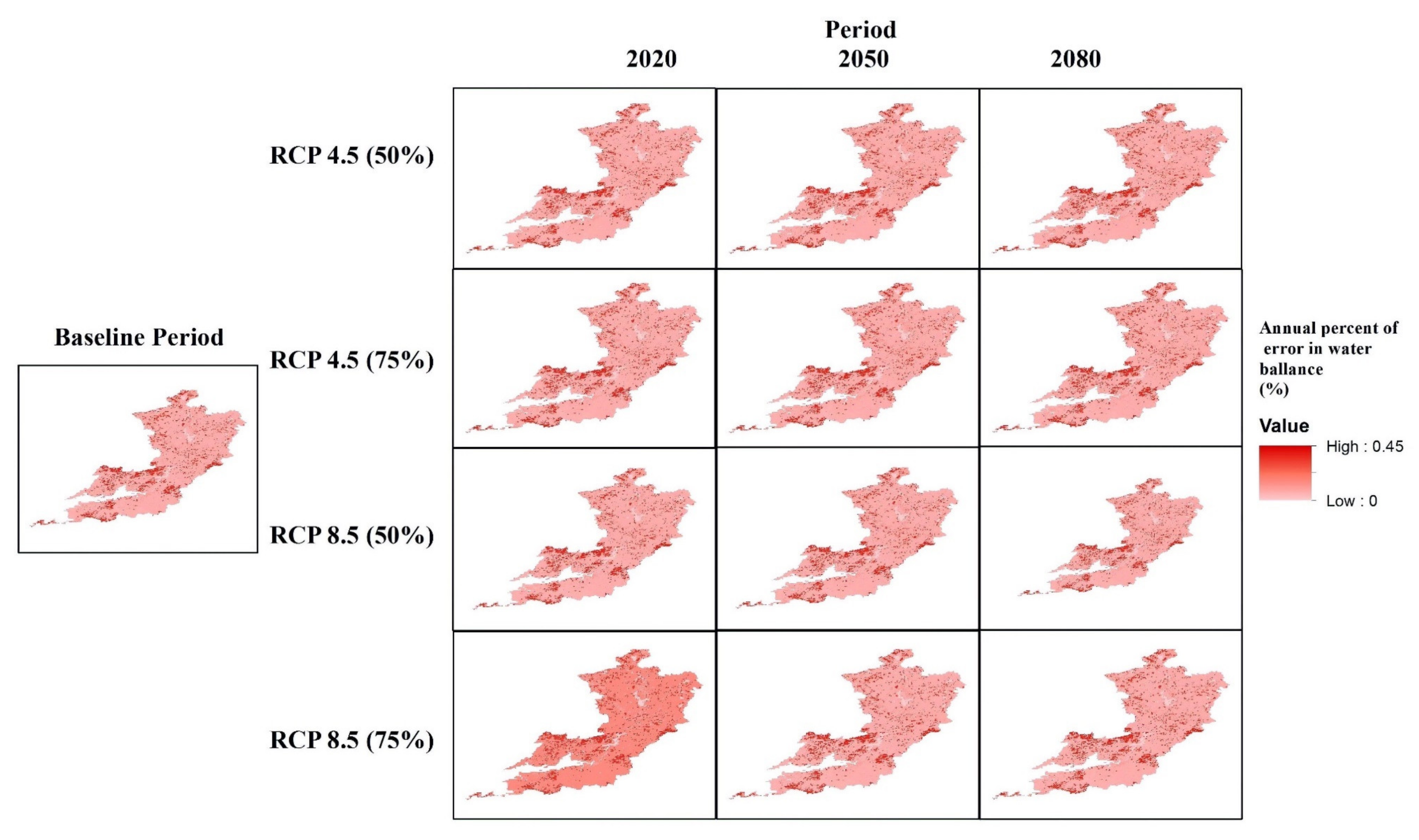
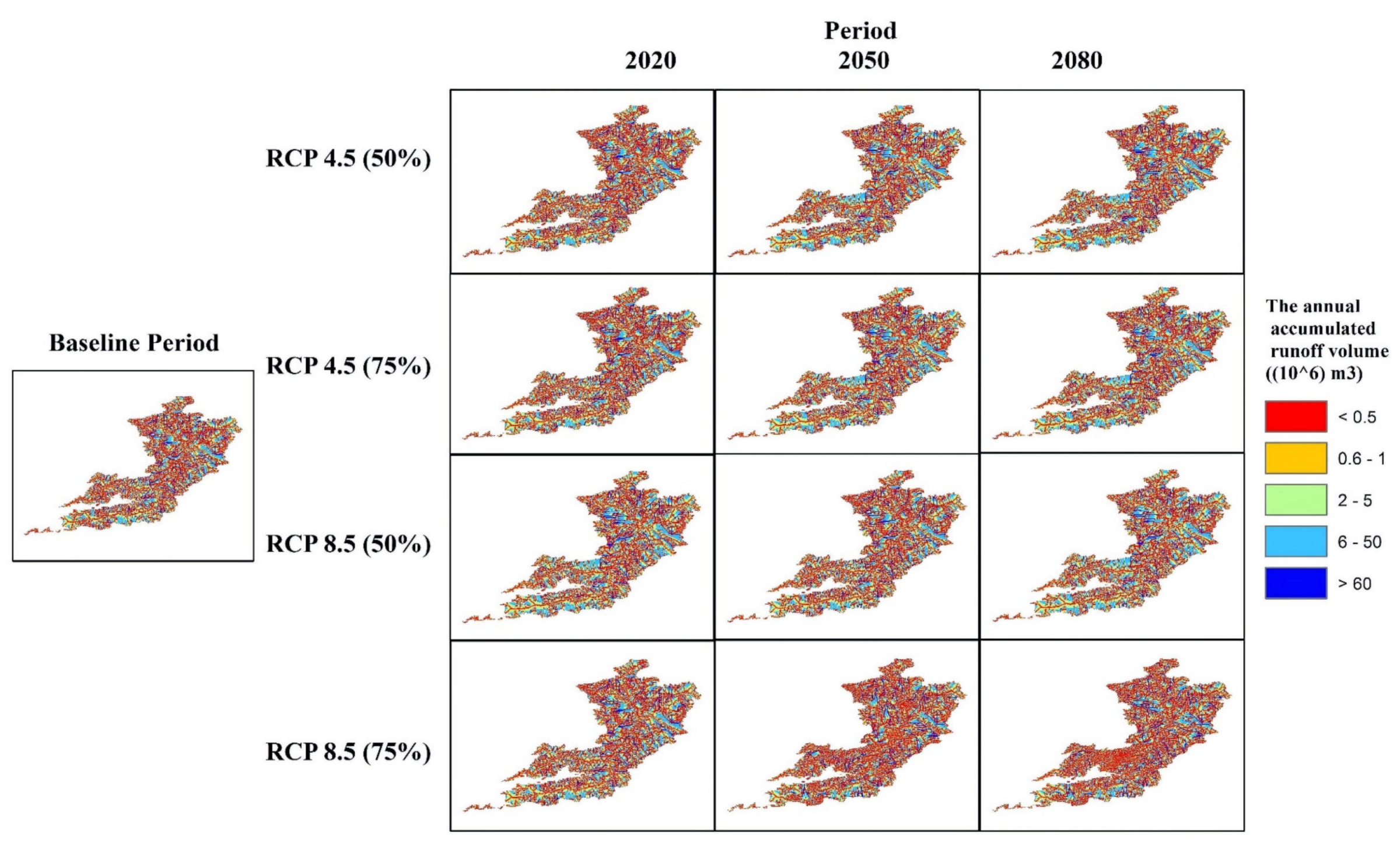

| Scenario | Period | Component | Annual-Mean | Annual-SD | Summer-Mean | Summer-SD | Winter-Mean | Winter-SD |
|---|---|---|---|---|---|---|---|---|
| Baseline Period | 1961–2014 | Runoff (Ro) mm | 271.30 | 496.61 | 34.05 | 99.44 | 47.73 | 139.91 |
| Evapotranspiration (Et) mm | 166.37 | 107.21 | 126.57 | 81.69 | 39.81 | 25.57 | ||
| Interception (In) mm | 125.59 | 142.46 | 82.09 | 47.16 | 43.49 | 97.57 | ||
| Transpiration (Tr) mm | 30.63 | 55.28 | 23.57 | 42.48 | 7.06 | 12.90 | ||
| Soil evaporation (Se) mm | 102.29 | 70.58 | 77.57 | 53.48 | 24.72 | 17.10 | ||
| Subsurface water component (Re) mm | 744.90 | 292.95 | 248.14 | 116.48 | 500.27 | 180.84 | ||
| Precipitation (P) mm | 1136.27 | 224.02 | 486.22 | 83.58 | 650.04 | 143.10 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −46.30 | − | 77.46 | − | 62.23 | − | ||
| Error in water balance (WB/P; %) | −4.07 | − | 15.93 | − | 9.57 | − | ||
| RCP 4.5 (50%) | 2020 | Runoff (Ro) mm | 267.25 | 497.17 | 31.10 | 95.72 | 44.02 | 135.86 |
| Evapotranspiration (Et) mm | 165.40 | 106.65 | 130.38 | 84.19 | 35.03 | 22.52 | ||
| Interception (In) mm | 126.64 | 144.18 | 82.49 | 47.63 | 44.14 | 99.66 | ||
| Transpiration (Tr) mm | 30.25 | 55.49 | 24.05 | 44.08 | 6.21 | 11.51 | ||
| Soil evaporation (Se) mm | 104.06 | 71.11 | 81.81 | 55.85 | 22.24 | 15.27 | ||
| Subsurface water component (Re) mm | 751.09 | 291.00 | 281.44 | 118.93 | 532.92 | 180.11 | ||
| Precipitation (P) mm | 1137.67 | 223.67 | 484.31 | 83.02 | 653.37 | 143.43 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −46.07 | − | 41.39 | − | 41.40 | − | ||
| Error in water balance (WB/P; %) | −4.05 | − | 8.55 | − | 6.34 | − | ||
| 2050 | Runoff (Ro) mm | 252.44 | 502.26 | 21.46 | 85.47 | 28.97 | 115.74 | |
| Evapotranspiration (Et) mm | 159.40 | 100.55 | 125.46 | 79.40 | 159.40 | 100.55 | ||
| Interception (In) mm | 139.73 | 159.42 | 92.65 | 54.54 | 47.07 | 107.60 | ||
| Transpiration (Tr) mm | 30.13 | 58.04 | 23.99 | 46.56 | 6.15 | 11.95 | ||
| Soil evaporation (Se) mm | 109.36 | 71.99 | 86.04 | 56.56 | 23.32 | 11.43 | ||
| Subsurface water component (Re) mm | 812.41 | 292.70 | 281.44 | 118.93 | 532.92 | 180.11 | ||
| Precipitation (P) mm | 1193.54 | 239.25 | 525.06 | 96.41 | 668.48 | 144.61 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −30.71 | − | 96.70 | − | −52.81 | − | ||
| Error in water balance (WB/P; %) | −2.57 | − | 18.42 | − | −7.90 | − | ||
| 2080 | Runoff (Ro) mm | 255.15 | 505.23 | 17.87 | 74.50 | 27.04 | 112.85 | |
| Evapotranspiration (Et) mm | 159.26 | 100.00 | 125.50 | 78.85 | 33.97 | 21.24 | ||
| Interception (In) mm | 132.78 | 157.02 | 83.50 | 48.72 | 49.27 | 110.69 | ||
| Transpiration (Tr) mm | 30.23 | 58.10 | 23.99 | 46.20 | 6.22 | 12.10 | ||
| Soil evaporation (Se) mm | 110.17 | 72.58 | 86.64 | 57.00 | 23.53 | 15.59 | ||
| Subsurface water component (Re) mm | 780.54 | 275.63 | 242.86 | 102.99 | 540.57 | 179.85 | ||
| Precipitation (P) mm | 1174.86 | 221.16 | 470.30 | 78.75 | 677.55 | 145.37 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −20.09 | − | 84.07 | − | 75.97 | − | ||
| Error in water balance (WB/P; %) | −1.71 | − | 17.88 | − | 11.21 | − | ||
| RCP 4.5 (75%) | 2020 | Runoff (Ro) mm | 267.54 | 497.54 | 31.19 | 95.97 | 42.94 | 135.64 |
| Evapotranspiration (Et) mm | 165.44 | 106.67 | 130.41 | 84.21 | 35.03 | 22.52 | ||
| Interception (In) mm | 126.80 | 144.06 | 82.75 | 47.80 | 44.05 | 99.38 | ||
| Transpiration (Tr) mm | 30.59 | 58.16 | 24.25 | 46.11 | 6.37 | 12.19 | ||
| Soil evaporation (Se) mm | 104.06 | 71.11 | 81.81 | 55.85 | 22.24 | 15.27 | ||
| Subsurface water component (Re) mm | 750.40 | 290.99 | 256.58 | 114.34 | 508.22 | 180.39 | ||
| Precipitation (P) mm | 1137.08 | 223.94 | 485.67 | 83.51 | 651.41 | 143.17 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −46.30 | − | 67.49 | − | 65.22 | − | ||
| Error in water balance (WB/P; %) | −4.07 | − | 13.90 | − | 10.01 | − | ||
| 2050 | Runoff (Ro) mm | 251.07 | 499.78 | 19.78 | 78.93 | 29.27 | 116.93 | |
| Evapotranspiration (Et) mm | 159.95 | 100.95 | 126.10 | 79.58 | 33.86 | 21.35 | ||
| Interception (In) mm | 132.95 | 159.13 | 85.24 | 49.60 | 47.71 | 109.03 | ||
| Transpiration (Tr) mm | 30.29 | 55.55 | 24.08 | 44.13 | 6.21 | 11.52 | ||
| Soil evaporation (Se) mm | 109.97 | 72.42 | 86.51 | 56.90 | 23.47 | 15.53 | ||
| Subsurface water component (Re) mm | 789.54 | 283.24 | 251.52 | 107.93 | 540.83 | 181.64 | ||
| Precipitation (P) mm | 1160.53 | 226.42 | 483.15 | 83.18 | 677.38 | 145.71 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −40.03 | − | 85.75 | − | 73.42 | − | ||
| Error in water balance (WB/P; %) | −3.45 | − | 17.75 | − | 10.84 | − | ||
| 2080 | Runoff (Ro) mm | 250.23 | 498.52 | 19.25 | 76.90 | 29.25 | 116.94 | |
| Evapotranspiration (Et) mm | 161.50 | 101.86 | 127.29 | 80.36 | 34.22 | 21.59 | ||
| Interception (In) mm | 130.61 | 154.59 | 82.79 | 47.82 | 47.80 | 109.21 | ||
| Transpiration (Tr) mm | 29.98 | 57.80 | 23.80 | 45.89 | 6.19 | 12.03 | ||
| Soil evaporation (Se) mm | 111.09 | 73.13 | 87.39 | 57.45 | 23.70 | 15.68 | ||
| Subsurface water component (Re) mm | 779.81 | 280.36 | 241.13 | 104.39 | 542.03 | 182.13 | ||
| Precipitation (P) mm | 1173.33 | 229.49 | 481.63 | 82.99 | 691.69 | 149.02 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −18.21 | − | 93.96 | − | 86.19 | − | ||
| Error in water balance (WB/P; %) | −1.55 | − | 19.51 | − | 12.46 | − | ||
| RCP 8.5 (50%) | 2020 | Runoff (Ro) mm | 267.31 | 497.26 | 31.07 | 95.61 | 44.06 | 135.97 |
| Evapotranspiration (Et) mm | 165.72 | 106.85 | 130.63 | 84.35 | 35.09 | 22.56 | ||
| Interception (In) mm | 126.65 | 144.23 | 82.44 | 47.57 | 44.20 | 99.79 | ||
| Transpiration (Tr) mm | 30.91 | 58.72 | 24.50 | 46.54 | 6.44 | 12.39 | ||
| Soil evaporation (Se) mm | 104.25 | 71.25 | 81.97 | 55.96 | 22.28 | 15.30 | ||
| Subsurface water component (Re) mm | 751.22 | 291.01 | 245.23 | 113.83 | 510.43 | 180.86 | ||
| Precipitation (P) mm | 1148.40 | 221.01 | 469.49 | 78.51 | 678.90 | 145.49 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −35.85 | − | 62.56 | − | 89.32 | − | ||
| Error in water balance (WB/P; %) | −3.12 | − | 13.33 | − | 13.16 | − | ||
| 2050 | Runoff (Ro) mm | 248.62 | 500.57 | 18.18 | 75.77 | 27.54 | 114.95 | |
| Evapotranspiration (Et) mm | 160.52 | 100.77 | 126.44 | 79.42 | 34.09 | 21.43 | ||
| Interception (In) mm | 135.86 | 160.86 | 85.55 | 50.26 | 50.30 | 113.05 | ||
| Transpiration (Tr) mm | 30.14 | 58.13 | 23.88 | 46.08 | 6.28 | 12.19 | ||
| Soil evaporation (Se) mm | 111.00 | 73.17 | 87.26 | 57.44 | 23.74 | 15.73 | ||
| Subsurface water component (Re) mm | 800.57 | 281.89 | 250.47 | 105.79 | 552.82 | 183.27 | ||
| Precipitation (P) mm | 1137.92 | 223.58 | 483.88 | 82.79 | 654.09 | 143.43 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −71.79 | − | 88.79 | − | 39.64 | − | ||
| Error in water balance (WB/P; %) | −6.31 | − | 18.35 | − | 6.06 | − | ||
| 2080 | Runoff (Ro) mm | 247.67 | 499.28 | 17.07 | 71.30 | 28.11 | 117.33 | |
| Evapotranspiration (Et) mm | 167.55 | 105.22 | 131.96 | 82.93 | 35.60 | 22.41 | ||
| Interception (In) mm | 131.58 | 159.44 | 80.06 | 46.32 | 51.52 | 115.49 | ||
| Transpiration (Tr) mm | 30.31 | 55.59 | 24.09 | 44.16 | 6.22 | 11.53 | ||
| Soil evaporation (Se) mm | 115.92 | 79.37 | 91.20 | 59.95 | 24.73 | 16.00 | ||
| Subsurface water component (Re) mm | 788.75 | 278.67 | 225.74 | 97.05 | 567.92 | 186.71 | ||
| Precipitation (P) mm | 1161.69 | 218.05 | 451.37 | 73.34 | 710.32 | 148.23 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −42.28 | − | 76.60 | − | 78.69 | − | ||
| Error in water balance (WB/P; %) | −3.64 | − | 16.97 | − | 11.08 | − | ||
| RCP 8.5 (75%) | 2020 | Runoff (Ro) mm | 267.80 | 497.98 | 30.04 | 95.22 | 42.46 | 135.14 |
| Evapotranspiration (Et) mm | 165.76 | 106.88 | 130.67 | 84.37 | 35.10 | 22.57 | ||
| Interception (In) mm | 127.04 | 144.75 | 82.71 | 47.79 | 44.33 | 100.08 | ||
| Transpiration (Tr) mm | 30.35 | 55.66 | 24.13 | 44.22 | 6.22 | 11.54 | ||
| Soil evaporation (Se) mm | 104.25 | 71.25 | 81.97 | 55.96 | 22.28 | 15.30 | ||
| Subsurface water component (Re) mm | 754.03 | 292.01 | 246.32 | 114.30 | 512.10 | 181.40 | ||
| Precipitation (P) mm | 1141.70 | 224.82 | 485.55 | 83.49 | 656.15 | 140.97 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −45.89 | − | 78.52 | − | 66.49 | − | ||
| Error in water balance (WB/P; %) | −4.02 | − | 16.17 | − | 10.13 | − | ||
| 2050 | Runoff (Ro) mm | 284.54 | 510.21 | 47.65 | 129.97 | 70.52 | 191.81 | |
| Evapotranspiration (Et) mm | 163.26 | 102.95 | 128.72 | 81.24 | 34.55 | 21.79 | ||
| Interception (In) mm | 133.72 | 158.41 | 84.90 | 49.37 | 48.82 | 111.56 | ||
| Transpiration (Tr) mm | 30.61 | 59.02 | 24.22 | 46.82 | 6.24 | 12.32 | ||
| Soil evaporation (Se) mm | 112.23 | 73.93 | 88.31 | 58.09 | 23.92 | 15.84 | ||
| Subsurface water component (Re) mm | 769.38 | 312.20 | 239.64 | 111.71 | 531.45 | 207.82 | ||
| Precipitation (P) mm | 1175.13 | 229.75 | 481.39 | 82.96 | 693.73 | 149.32 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −42.05 | − | 65.38 | − | 57.21 | − | ||
| Error in water balance (WB/P; %) | −3.58 | − | 13.58 | − | 8.25 | − | ||
| 2080 | Runoff (Ro) mm | 283.70 | 511.54 | 46.63 | 127.69 | 74.62 | 203.68 | |
| Evapotranspiration (Et) mm | 171.71 | 107.81 | 135.48 | 85.13 | 36.28 | 22.83 | ||
| Interception (In) mm | 137.99 | 167.35 | 84.46 | 49.56 | 53.78 | 120.66 | ||
| Transpiration (Tr) mm | 33.19 | 63.05 | 26.30 | 50.01 | 6.93 | 13.24 | ||
| Soil evaporation (Se) mm | 118.60 | 78.23 | 93.41 | 61.52 | 25.20 | 16.71 | ||
| Subsurface water component (Re) mm | 796.81 | 317.32 | 230.45 | 108.94 | 568.42 | 216.87 | ||
| Precipitation (P) mm | 1216.77 | 235.33 | 475.93 | 82.05 | 741.29 | 156.21 | ||
| Water balance (WB) = P-Ro-Et-Re; mm | −35.45 | − | 63.37 | − | 61.97 | − | ||
| Error in water balance (WB/P; %) | −2.91 | − | 13.31 | − | 8.36 | − |
References
- Zhang, L.; Potter, N.; Hickel, K.; Zhang, Y.; Shao, Q. Water balance modeling over variable time scales based on the Budyko framework–Model development and testing. J. Hydrol. 2008, 360, 117–131. [Google Scholar] [CrossRef]
- Van Dijk, A.I.; Gash, J.H.; van Gorsel, E.; Blanken, P.D.; Cescatti, A.; Emmel, C.; Gielen, B.; Harman, I.N.; Kiely, G.; Merbold, L. Rainfall interception and the coupled surface water and energy balance. Agric. For. Meteorol. 2015, 214, 402–415. [Google Scholar] [CrossRef]
- Tekleab, S.; Uhlenbrook, S.; Mohamed, Y.; Savenije, H.; Temesgen, M.; Wenninger, J. Water balance modeling of Upper Blue Nile catchments using a top-down approach. Hydrol. Earth Syst. Sci. 2011, 15, 2179. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, H.; Yang, D.; Jayawardena, A. Quantifying the effect of vegetation change on the regional water balance within the Budyko framework. Geophys. Res. Lett. 2016, 43, 1140–1148. [Google Scholar] [CrossRef]
- le Roux, B.; van der Laan, M.; Vahrmeijer, T.; Bristow, K.L.; Annandale, J.G. Establishing and testing a catchment water footprint framework to inform sustainable irrigation water use for an aquifer under stress. Sci. Total Environ. 2017, 599, 1119–1129. [Google Scholar] [CrossRef]
- Marhaento, H.; Booij, M.J.; Rientjes, T.; Hoekstra, A.Y. Attribution of changes in the water balance of a tropical catchment to land use change using the SWAT model. Hydrol. Process. 2017, 31, 2029–2040. [Google Scholar] [CrossRef]
- Pfister, L.; Martínez-Carreras, N.; Hissler, C.; Klaus, J.; Carrer, G.E.; Stewart, M.K.; McDonnell, J.J. Bedrock geology controls on catchment storage, mixing, and release: A comparative analysis of 16 nested catchments. Hydrol. Process. 2017, 31, 1828–1845. [Google Scholar] [CrossRef]
- Staudinger, M.; Stoelzle, M.; Seeger, S.; Seibert, J.; Weiler, M.; Stahl, K. Catchment water storage variation with elevation. Hydrol. Process. 2017, 31, 2000–2015. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Schwalm, C.R.; Huntingford, C.; Sitch, S.; Ahlström, A.; Arneth, A.; Camps-Valls, G.; Ciais, P.; Friedlingstein, P. Compensatory water effects link yearly global land CO2 sink changes to temperature. Nature 2017, 541, 516–520. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Tian, F.; Yang, Y.; Han, S.; Qiu, G. Quantifying the magnitude of the impact of climate change and human activity on runoff decline in Mian River Basin, China. Water Sci. Technol. 2010, 62, 783–791. [Google Scholar] [CrossRef]
- Yonghui, Y.; Fei, T. Abrupt change of runoff and its major driving factors in Haihe River Catchment. China. J. Hydrol. 2009, 374, 373–383. [Google Scholar]
- Junkermann, W.; Hacker, J.; Lyons, T.; Nair, U. Land use change suppresses precipitation. Atmos. Chem. Phys. 2009, 9, 6531–6539. [Google Scholar] [CrossRef]
- Gharbia, S.; Gill, L.; Johnston, P.; Pilla, F. GEO-CWB: A dynamic water balance tool for catchment water management. In Proceedings of the 5th International Multidisciplinary Conference on Hydrology and Ecology (HydroEco2015), Vienna, Austria, 13–16 April 2015. [Google Scholar]
- Gharbia, S.S.; Aish, A.; Pilla, F.; Gharbia, A.S. Potential Effects of Climate Change on Groundwater Recharge-a Case Study of the Gaza Strip, Palestine. In Proceedings of the XVth IWRA World Water Congress, Edinburgh, Scotland, 25–29 May 2015. [Google Scholar]
- Bonsch, M.; Humpenöder, F.; Popp, A.; Bodirsky, B.; Dietrich, J.P.; Rolinski, S.; Biewald, A.; Lotze-Campen, H.; Weindl, I.; Gerten, D. Trade-offs between land and water requirements for large-scale bioenergy production. Gcb Bioenergy 2016, 8, 11–24. [Google Scholar] [CrossRef]
- Wang, R.; Zimmerman, J. Hybrid analysis of blue water consumption and water scarcity implications at the global, national, and basin levels in an increasingly globalized world. Environ. Sci. Technol. 2016, 50, 5143–5153. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Kumar, R.; Flörke, M.; Yang, T.; Hundecha, Y.; Kraft, P.; Gao, C.; Gelfan, A.; Liersch, S.; Lobanova, A. Evaluation of an ensemble of regional hydrological models in 12 large-scale river basins worldwide. Clim. Chang. 2017, 141, 381–397. [Google Scholar] [CrossRef]
- Kauffeldt, A.; Wetterhall, F.; Pappenberger, F.; Salamon, P.; Thielen, J. Technical review of large-scale hydrological models for implementation in operational flood forecasting schemes on continental level. Environ. Model. Softw. 2016, 75, 68–76. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.; Dwarakish, G. A review on hydrological models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Sorooshian, S.; Duan, Q.; Gupta, V.K. Calibration of Rainfall-Runoff models: Application of global optimization to the Sacramento Soil Moisture Accounting Model. Water Resour. Res. 1993, 29, 1185–1194. [Google Scholar] [CrossRef]
- Pontes, P.R.M.; Fan, F.M.; Fleischmann, A.S.; de Paiva, R.C.D.; Buarque, D.C.; Siqueira, V.A.; Jardim, P.F.; Sorribas, M.V.; Collischonn, W. MGB-IPH model for hydrological and hydraulic simulation of large floodplain river systems coupled with open source GIS. Environ. Model. Softw. 2017, 94, 1–20. [Google Scholar] [CrossRef]
- Khan, A.; Ghoraba, S.; Arnold, J.G.; Luzio, M. Hydrological modeling of upper Indus Basin and assessment of deltaic ecology. Int. J. Mod. Eng. Res 2014, 4, 73–85. [Google Scholar]
- Rahmati, O.; Kornejady, A.; Samadi, M.; Nobre, A.D.; Melesse, A.M. Development of an automated GIS tool for reproducing the HAND terrain model. Environ. Model. Softw. 2018, 102, 1–12. [Google Scholar] [CrossRef]
- Sanzana, P.; Gironás, J.; Braud, I.; Branger, F.; Rodriguez, F.; Vargas, X.; Hitschfeld, N.; Muñoz, J.; Vicuña, S.; Mejía, A. A GIS-based urban and peri-urban landscape representation toolbox for hydrological distributed modeling. Environ. Model. Softw. 2017, 91, 168–185. [Google Scholar] [CrossRef]
- Akgun, A.; Erkan, O. Landslide susceptibility mapping by geographical information system-based multivariate statistical and deterministic models: In an artificial reservoir area at Northern Turkey. Arab. J. Geosci. 2016, 9, 165. [Google Scholar] [CrossRef]
- Müller, M.; Thompson, S. Comparing statistical and process-based flow duration curve models in ungauged basins and changing rain regimes. Earth Syst. Sci. 2016, 20, 669–683. [Google Scholar] [CrossRef]
- Daly, C.; Gibson, W.P.; Taylor, G.H.; Johnson, G.L.; Pasteris, P. A knowledge-based approach to the statistical mapping of climate. Clim. Res. 2002, 22, 99–113. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “Goodness-Of-Fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D. Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Ku, C.-A. Incorporating spatial regression model into cellular automata for simulating land use change. Appl. Geogr. 2016, 69, 1–9. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Liu, X.; Ai, B.; Li, S. Capturing the varying effects of driving forces over time for the simulation of urban growth by using survival analysis and cellular automata. Landsc. Urban Plan. 2016, 152, 59–71. [Google Scholar] [CrossRef]
- Gharbia, S.S.; Abd Alfatah, S.; Gill, L.; Johnston, P.; Pilla, F. Land use scenarios and projections simulation using an integrated GIS cellular automata algorithms. Modeling Earth Syst. Environ. 2016, 2, 151. [Google Scholar] [CrossRef]
- Liao, J.; Tang, L.; Shao, G.; Su, X.; Chen, D.; Xu, T. Incorporation of extended neighborhood mechanisms and its impact on urban land-use cellular automata simulations. Environ. Model. Softw. 2016, 75, 163–175. [Google Scholar] [CrossRef]
- Misstear, B.; Brown, L.; Daly, D. A methodology for making initial estimates of groundwater recharge from groundwater vulnerability mapping. Hydrogeol. J. 2009, 17, 275–285. [Google Scholar] [CrossRef]
- Mockler, E.; Bruen, M. Parameterizing dynamic water quality models in ungauged basins: Issues and solutions. Underst. Freshw. Qual. Probl. A Chang. World 2013, 361, 235–242. [Google Scholar]
- O’Brien, R.J.; Misstear, B.D.; Gill, L.W.; Deakin, J.L.; Flynn, R. Developing an integrated hydrograph separation and lumped modelling approach to quantifying hydrological pathways in Irish river catchments. J. Hydrol. 2013, 486, 259–270. [Google Scholar] [CrossRef][Green Version]
- Gharbia, S.S. An Integrated Water Resources, Climate and Land Use Changes Model for Shannon River Catchment; Trinity College Dublin: Dublin, Ireland, 2017. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar]
- Voudouris, K. Groundwater balance and safe yield of the coastal aquifer system in NEastern Korinthia, Greece. Appl. Geogr. 2006, 26, 291–311. [Google Scholar] [CrossRef]
- Kalf, F.R.; Woolley, D.R. Applicability and methodology of determining sustainable yield in groundwater systems. Hydrogeol. J. 2005, 13, 295–312. [Google Scholar] [CrossRef]
- Zhou, Y. A critical review of groundwater budget myth, safe yield and sustainability. J. Hydrol. 2009, 370, 207–213. [Google Scholar] [CrossRef]
- Vaux Jr, H.J.; Pruitt, W.O. Crop-water production functions. In Advances in Irrigation; Elsevier: Amsterdam, The Netherlands, 1983; Volume 2, pp. 61–97. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. Faorome 1998, 300, D05109. [Google Scholar]
- Zhang, Y.; Kendy, E.; Qiang, Y.; Changming, L.; Yanjun, S.; Hongyong, S. Effect of soil water deficit on evapotranspiration, crop yield, and water use efficiency in the North China Plain. Agric. Water Manag. 2004, 64, 107–122. [Google Scholar] [CrossRef]
- Kendy, E.; Gérard-Marchant, P.; Todd Walter, M.; Zhang, Y.; Liu, C.; Steenhuis, T.S. A soil-water-balance approach to quantify groundwater recharge from irrigated cropland in the North China Plain. Hydrol. Process. 2003, 17, 2011–2031. [Google Scholar] [CrossRef]
- Gharbia, S.S.; Smullen, T.; Gill, L.; Johnston, P.; Pilla, F. Spatially distributed potential evapotranspiration modeling and climate projections. Sci. Total Environ. 2018, 633, 571–592. [Google Scholar] [CrossRef] [PubMed]
- Gharbia, S.S.; Johnston, P.; Gill, L.; Pilla, F. Using GIS based algorithms for GCMs’ performance evaluation. In Proceedings of the 2016 18th Mediterranean Electrotechnical Conference (MELECON), Lemesos, Cyprus, 18–20 April 2016; pp. 1–6. [Google Scholar]
- Gharbia, S.S.; Gill, L.; Johnston, P.; Pilla, F. Trans-boundary European River’s Long-term Changes Analysis for Water Level and Streamflow Regime. In Proceedings of the 42nd IAH Congress (AQUA2015), Rome, Italy, 13–18 September 2015. [Google Scholar]
- Gharbia, S.S.; Gill, L.; Johnston, P.; Pilla, F. Multi-GCM ensembles performance for climate projection on a GIS platform. Modeling Earth Syst. Environ. 2016, 2, 102. [Google Scholar] [CrossRef]
- Misstear, B.; Brown, L.; Johnston, P. Estimation of groundwater recharge in a major sand and gravel aquifer in Ireland using multiple approaches. Hydrogeol. J. 2009, 17, 693–706. [Google Scholar] [CrossRef]
- Gebreyohannes, T.; De Smedt, F.; Walraevens, K.; Gebresilassie, S.; Hussien, A.; Hagos, M.; Amare, K.; Deckers, J.; Gebrehiwot, K. Application of a spatially distributed water balance model for assessing surface water and groundwater resources in the Geba basin, Tigray, Ethiopia. J. Hydrol. 2013, 499, 110–123. [Google Scholar] [CrossRef]
- Tóth, J. Gravitational Systems of Groundwater Flow: Theory, Evaluation, Utilization; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Haitjema, H.M.; Mitchell-Bruker, S. Are water tables a subdued replica of the topography? Ground Water 2005, 43, 781–786. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Misstear, B.; Brown, L.; Williams, N.H. Groundwater recharge to a fractured limestone aquifer overlain by glacial till in County Monaghan, Ireland. Q. J. Eng. Geol. Hydrogeol. 2008, 41, 465–476. [Google Scholar] [CrossRef]
- Fitzsimons, V.P.; Misstear, B.D. Estimating groundwater recharge through tills: A sensitivity analysis of soil moisture budgets and till properties in Ireland. Hydrogeol. J. 2006, 14, 548–561. [Google Scholar] [CrossRef]
- Misstear, B.D. Groundwater recharge assessment: A key component of river basin management. In Proceedings of the River Basin Management, Offaly, Ireland, 21 November 2000; pp. 52–59. [Google Scholar]
- Dunin, F.; O’Loughlin, E.; Reyenga, W. Interception loss from eucalypt forest: Lysimeter determination of hourly rates for long term evaluation. Hydrol. Process. 1988, 2, 315–329. [Google Scholar] [CrossRef]
- Vandewiele, G.; Xu, C.-Y.; Huybrechts, W. Regionalisation of physically-based water balance models in Belgium. Application to ungauged catchments. Water Resour. Manag. 1991, 5, 199–208. [Google Scholar] [CrossRef]






| Output Parameters | Assumptions/Limitations |
|---|---|
| Surface Runoff | It represents the direct surface runoff, and it does not include the subsurface runoff (subsurface flow via shallow subsoil pathways) |
| Subsurface water | This includes many components mainly subsurface flow via shallow pathways and the groundwater recharge component. |
| Interception | Based on the vegetation type interception fraction represents a constant percentage of the annual precipitation value, which is the main part of the total water loss in the catchment. |
| Evapotranspiration | Depending on which fraction of each cell is being modelled, the evapotranspiration could be equal to PET (open water fraction) or fraction of it (bare soil or impervious surface fractions) or just equal to the simulated transpiration (vegetated fraction). |
| Soil evaporation | Based on the soil type, soil evaporation is a fraction of the PET. |
| Transpiration | Based on the vegetation type, root depth, groundwater level, soil moisture, tension saturated height, temperature, and many other factors, transpiration is calculated for the vegetated fraction of each cell. |
| Hydrometric Stations | Simulated Average Daily Flow (m3/s) | Observed Average Daily Flow (m3/s) | Difference (m3/s) | Error % |
|---|---|---|---|---|
| Inny | 16.90 | 15.51 | 1.39 | 8.99 |
| Mid-Shannon | 15.31 | 17.76 | −2.45 | −13.78 |
| Suck | 22.91 | 20.57 | 2.34 | 11.37 |
| Brosna | 12.96 | 14.94 | −1.99 | −13.30 |
| Nenagh | 9.15 | 6.83 | 2.31 | 33.88 |
| Dead | 14.26 | 12.89 | 1.37 | 10.60 |
| Lower-Shannon | 152.30 | 153.96 | −1.66 | −1.08 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gharbia, S.S.; Gill, L.; Johnston, P.; Pilla, F. GEO-CWB: GIS-Based Algorithms for Parametrising the Responses of Catchment Dynamic Water Balance Regarding Climate and Land Use Changes. Hydrology 2020, 7, 39. https://doi.org/10.3390/hydrology7030039
Gharbia SS, Gill L, Johnston P, Pilla F. GEO-CWB: GIS-Based Algorithms for Parametrising the Responses of Catchment Dynamic Water Balance Regarding Climate and Land Use Changes. Hydrology. 2020; 7(3):39. https://doi.org/10.3390/hydrology7030039
Chicago/Turabian StyleGharbia, Salem S., Laurence Gill, Paul Johnston, and Francesco Pilla. 2020. "GEO-CWB: GIS-Based Algorithms for Parametrising the Responses of Catchment Dynamic Water Balance Regarding Climate and Land Use Changes" Hydrology 7, no. 3: 39. https://doi.org/10.3390/hydrology7030039
APA StyleGharbia, S. S., Gill, L., Johnston, P., & Pilla, F. (2020). GEO-CWB: GIS-Based Algorithms for Parametrising the Responses of Catchment Dynamic Water Balance Regarding Climate and Land Use Changes. Hydrology, 7(3), 39. https://doi.org/10.3390/hydrology7030039