Sensitivity of the Evapotranspiration Deficit Index to Its Parameters and Different Temporal Scales
Abstract
:1. Introduction
2. Materials and Methods
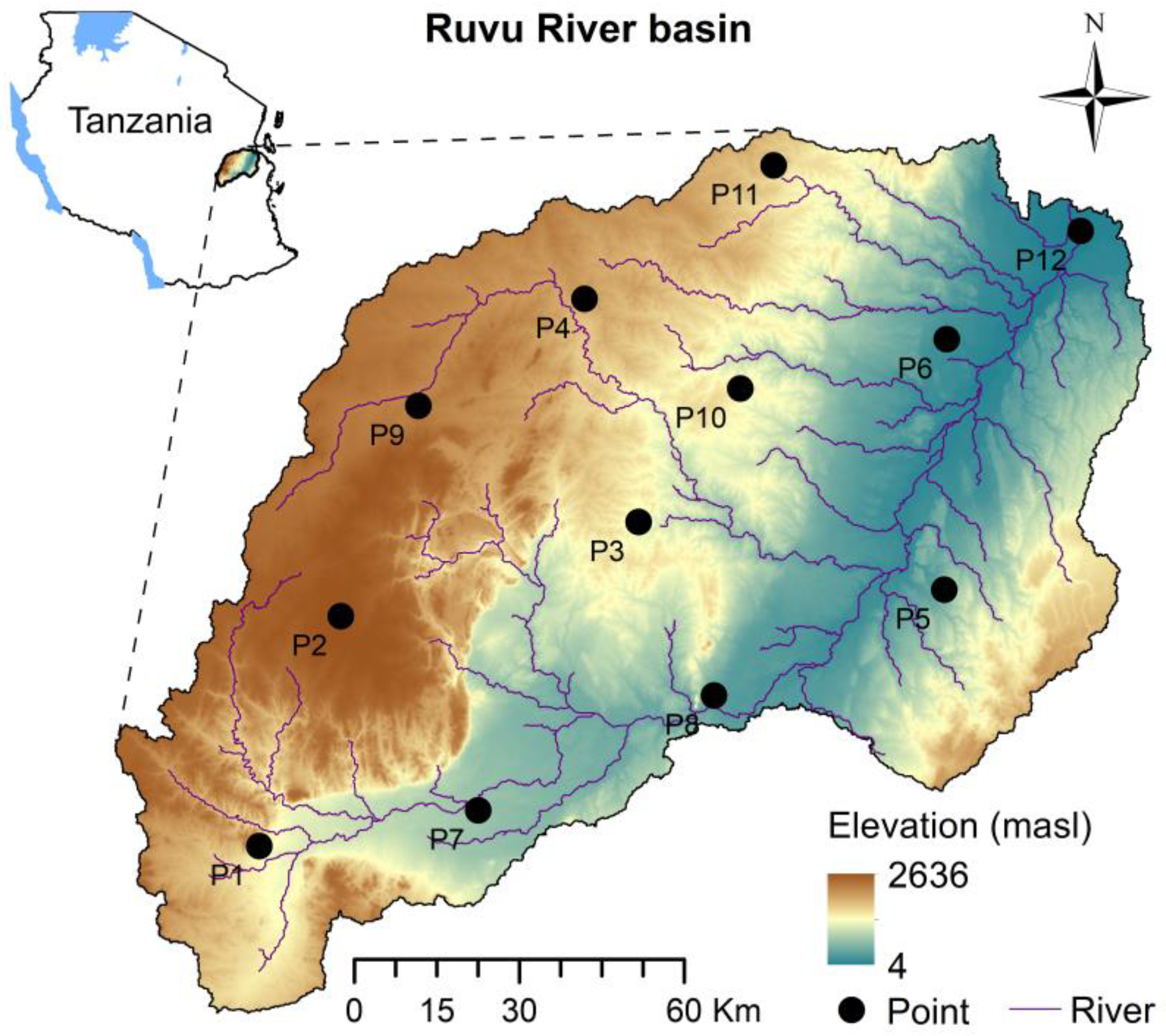
2.1. Case Study
2.2. Main Datasets Used
2.3. Evapotranspiration Deficit Index Approach
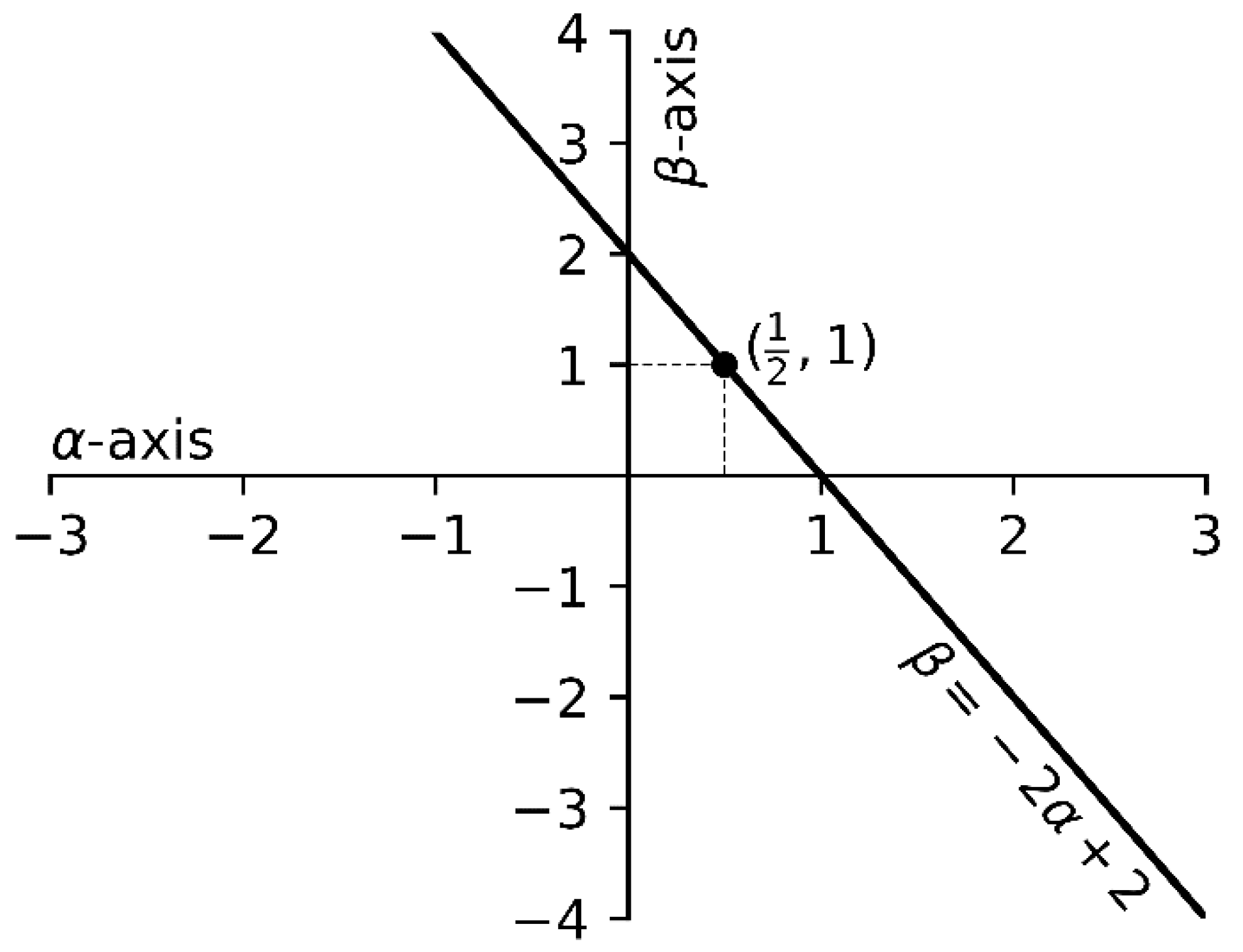
2.3.1. Parameter Sensitivity Test
2.3.2. Temporal Scale Sensitivity Test
3. Results and Discussion
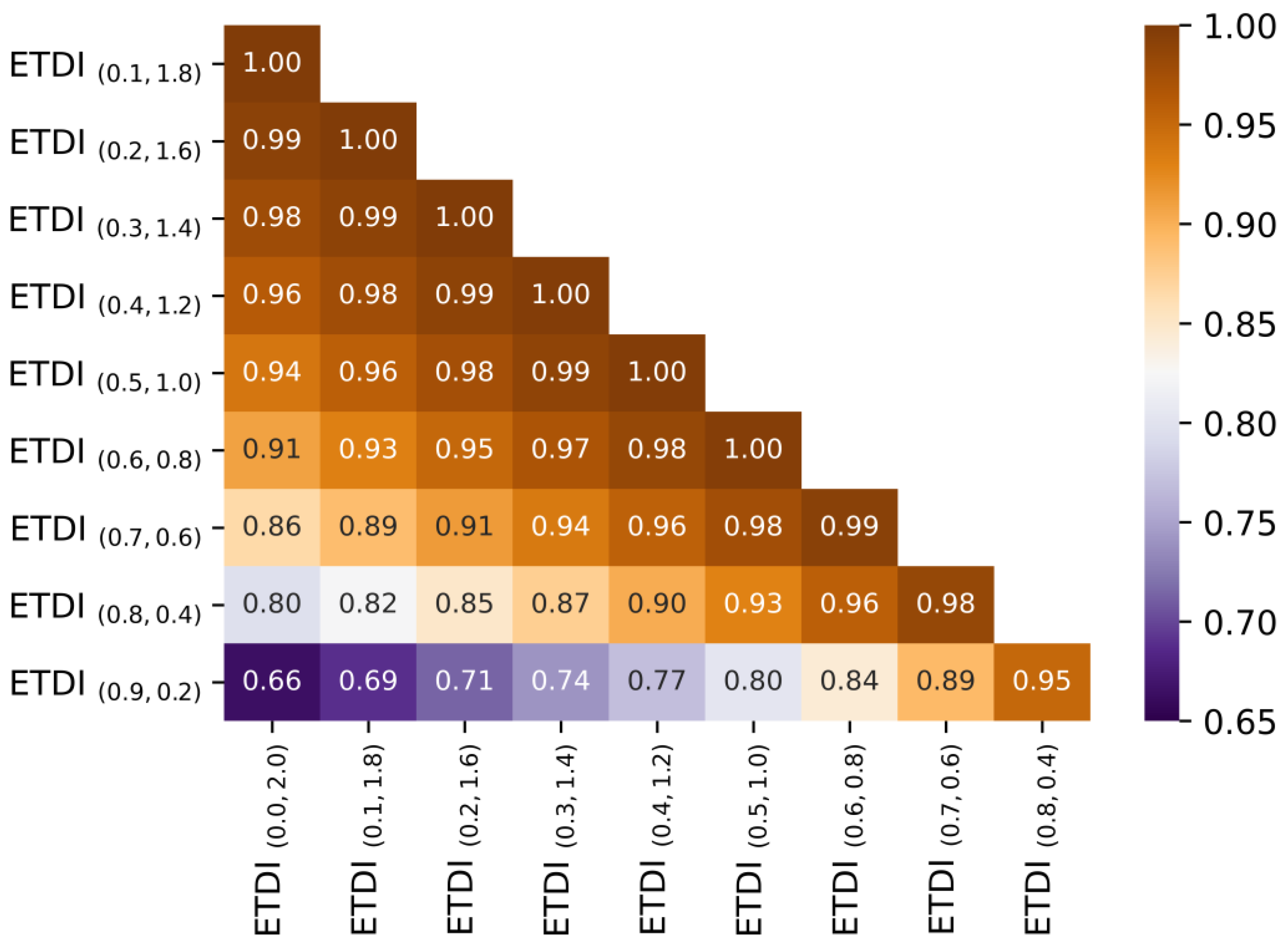
3.1. Parameter Sensitivity
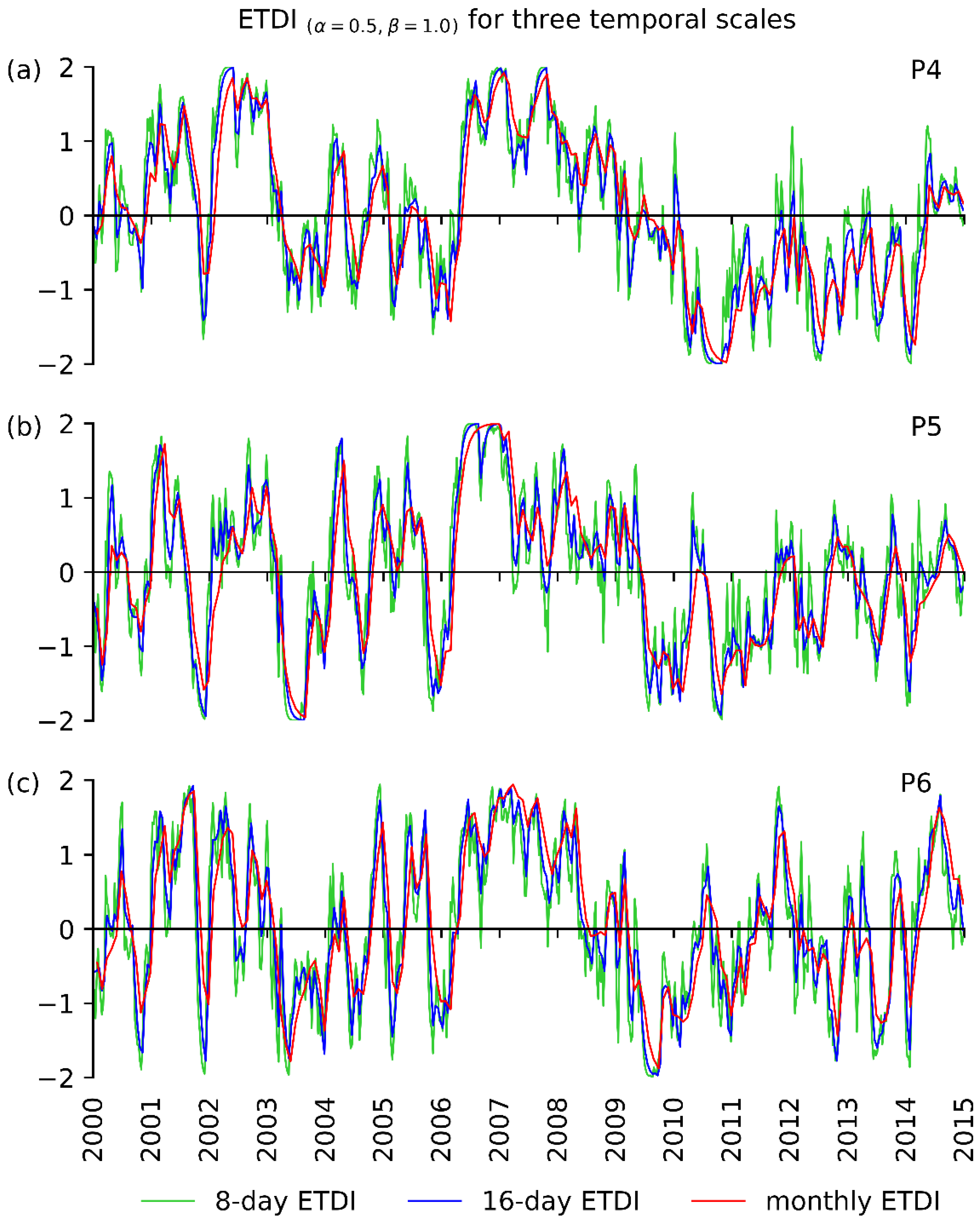
3.2. Temporal Scale Sensitivity
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ziolkowska, J. Socio-Economic Implications of Drought in the Agricultural Sector and the State Economy. Economies 2016, 4, 19. [Google Scholar] [CrossRef]
- Bayissa, Y.; Maskey, S.; Tadesse, T.; van Andel, S.; Moges, S.; van Griensven, A.; Solomatine, D. Comparison of the Performance of Six Drought Indices in Characterizing Historical Drought for the Upper Blue Nile Basin, Ethiopia. Geosciences 2018, 8, 81. [Google Scholar] [CrossRef] [Green Version]
- Kim, T.-W.; Jehanzaib, M. Drought Risk Analysis, Forecasting and Assessment under Climate Change. Water 2020, 12, 1862. [Google Scholar] [CrossRef]
- Liu, S.; Shi, H.; Niu, J.; Chen, J.; Kuang, X. Assessing Future Socioeconomic Drought Events under a Changing Climate over the Pearl River Basin in South China. J. Hydrol. Reg. Stud. 2020, 30, 100700. [Google Scholar] [CrossRef]
- Peng, J.; Dadson, S.; Hirpa, F.; Dyer, E.; Lees, T.; Miralles, D.G.; Vicente-Serrano, S.M.; Funk, C. A Pan-African High-Resolution Drought Index Dataset. Earth Syst. Sci. Data 2020, 12, 753–769. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A.; Herrero-Jiménez, C.M. Satellite Soil Moisture for Agricultural Drought Monitoring: Assessment of the SMOS Derived Soil Water Deficit Index. Remote Sens. Environ. 2016, 177, 277–286. [Google Scholar] [CrossRef]
- Das, P.K.; Das, R.; Das, D.K.; Midya, S.K.; Bandyopadhyay, S.; Raj, U. Quantification of Agricultural Drought over Indian Region: A Multivariate Phenology-Based Approach. Nat. Hazards 2020, 101, 255–274. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Drought Characterization from a Multivariate Perspective: A Review. J. Hydrol. 2015, 527, 668–678. [Google Scholar] [CrossRef]
- Touma, D.; Ashfaq, M.; Nayak, M.A.; Kao, S.-C.; Diffenbaugh, N.S. A Multi-Model and Multi-Index Evaluation of Drought Characteristics in the 21st Century. J. Hydrol. 2015, 526, 196–207. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A. A Soil Water Based Index as a Suitable Agricultural Drought Indicator. J. Hydrol. 2015, 522, 265–273. [Google Scholar] [CrossRef]
- Yang, H.; Wang, H.; Fu, G.; Yan, H.; Zhao, P.; Ma, M. A Modified Soil Water Deficit Index (MSWDI) for Agricultural Drought Monitoring: Case Study of Songnen Plain, China. Agric. Water Manag. 2017, 194, 125–138. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and Evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for Agricultural Drought Monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Šebenik, U.; Brilly, M.; Šraj, M. Drought Analysis Using the Standardized Precipitation Index (SPI). Acta Geogr. Slov. 2017, 57. [Google Scholar] [CrossRef] [Green Version]
- Shah, R.; Bharadiya, N.; Manekar, V. Drought Index Computation Using Standardized Precipitation Index (SPI) Method for Surat District, Gujarat. Aquat. Procedia 2015, 4, 1243–1249. [Google Scholar] [CrossRef]
- Pramudya, Y.; Onishi, T. Assessment of the Standardized Precipitation Index (SPI) in Tegal City, Central Java, Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2018, 129, 012019. [Google Scholar] [CrossRef]
- Li, J.Z.; Wang, Y.X.; Li, S.F.; Hu, R. A Nonstationary Standardized Precipitation Index Incorporating Climate Indices as Covariates. J. Geophys. Res. Atmos. 2015, 120, 12082–12095. [Google Scholar] [CrossRef] [Green Version]
- Trambauer, P.; Maskey, S.; Werner, M.; Pappenberger, F.; van Beek, L.P.H.; Uhlenbrook, S. Identification and Simulation of Space–Time Variability of Past Hydrological Drought Events in the Limpopo River Basin, Southern Africa. Hydrol. Earth Syst. Sci. 2014, 18, 2925–2942. [Google Scholar] [CrossRef] [Green Version]
- Jacobi, J.; Perrone, D.; Duncan, L.L.; Hornberger, G. A Tool for Calculating the Palmer Drought Indices. Water Resour. Res. 2013, 49, 6086–6089. [Google Scholar] [CrossRef]
- Sivakumar, M.V.K.; Motha, R.P.; Wilhite, D.A.; Wood, D.A. Agricultural Drought Indices. In Proceedings of the WMO/UNISDR Expert Group Meeting on Agricultural Drought Indices (AGM-11, WAOB-2011), Murcia, Spain, 2–4 June 2010; WMO/TD No. 1572. World Meteorological Organization: Geneva, Switzerland, 2011. [Google Scholar]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A Review of Drought Indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- Esfahanian, E.; Nejadhashemi, A.P.; Abouali, M.; Adhikari, U.; Zhang, Z.; Daneshvar, F.; Herman, M.R. Development and Evaluation of a Comprehensive Drought Index. J. Environ. Manag. 2017, 185, 31–43. [Google Scholar] [CrossRef] [Green Version]
- Wambura, F.J.; Dietrich, O. Analysis of Agricultural Drought Using Remotely Sensed Evapotranspiration in a Data-Scarce Catchment. Water 2020, 12, 998. [Google Scholar] [CrossRef] [Green Version]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. 2008. Available online: http://srtm.csi.cgiar.org (accessed on 28 October 2017).
- Kashaigili, J.J. Rapid Environmental Flow Assessment for the Ruvu River, A Consultancy Report submitted to iWASH. 2011. Available online: http://www.suaire.sua.ac.tz/bitstream/handle/123456789/1481/Kashaigili17.pdf (accessed on 28 October 2017).
- Hassan, I.H.; Mdemu, M.V.; Shemdoe, R.S.; Stordal, F. Drought Pattern along the Coastal Forest Zone of Tanzania. Atmos. Clim. Sci. 2014, 4, 369–384. [Google Scholar] [CrossRef] [Green Version]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS Global Terrestrial Evapotranspiration Algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Ntale, H.K.; Gan, T.Y. Drought Indices and Their Application to East Africa. Int. J. Climatol. 2003, 23, 1335–1357. [Google Scholar] [CrossRef]
- Sharafati, A.; Nabaei, S.; Shahid, S. Spatial Assessment of Meteorological Drought Features over Different Climate Regions in Iran. Int. J. Climatol. 2020, 40, 1864–1884. [Google Scholar] [CrossRef]
- Pei, Z.; Fang, S.; Wang, L.; Yang, W. Comparative Analysis of Drought Indicated by the SPI and SPEI at Various Timescales in Inner Mongolia, China. Water 2020, 12, 1925. [Google Scholar] [CrossRef]
- Raible, C.C.; Bärenbold, O.; Gómez-Navarro, J.J. Drought Indices Revisited—Improving and Testing of Drought Indices in a Simulation of the Last Two Millennia for Europe. Tellus A Dyn. Meteorol. Oceanogr. 2017, 69, 1287492. [Google Scholar] [CrossRef] [Green Version]
- Brito, S.S.B.; Cunha, A.P.M.A.; Cunningham, C.C.; Alvalá, R.C.; Marengo, J.A.; Carvalho, M.A. Frequency, Duration and Severity of Drought in the Semiarid Northeast Brazil Region. Int. J. Climatol. 2018, 38, 517–529. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Vogt, J.; Barbosa, P. European Drought Climatologies and Trends Based on a Multi-Indicator Approach. Glob. Planet. Chang. 2015, 127, 50–57. [Google Scholar] [CrossRef]
- Karl, T.R. The Sensitivity of the Palmer Drought Severity Index and Palmer’s Z-Index to Their Calibration Coefficients Including Potential Evapotranspiration. J. Clim. Appl. Meteorol. 1986, 25, 77–86. [Google Scholar] [CrossRef] [Green Version]
- Palmer, W.C. Meteorological Drought. In Research Paper No. 45; US Department of Commerce Weather Bureau: Washington, DC, USA, 1965; Volume 30. [Google Scholar]
- Ogunrinde, A.T.; Oguntunde, P.G.; Olasehinde, D.A.; Fasinmirin, J.T.; Akinwumiju, A.S. Drought Spatiotemporal Characterization Using Self-Calibrating Palmer Drought Severity Index in the Northern Region of Nigeria. Results Eng. 2020, 5, 100088. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S.; Hayes, M.J. A Self-Calibrating Palmer Drought Severity Index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Jain, V.K.; Pandey, R.P.; Jain, M.K.; Byun, H.-R. Comparison of Drought Indices for Appraisal of Drought Characteristics in the Ken River Basin. Weather Clim. Extrem. 2015, 8, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Byun, H.-R.; Wilhite, D.A. Objective Quantification of Drought Severity and Duration. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]



| Extreme | ETDIt−1 | WSAt | ETDIt at (α < 0, β > 2) | ETDIt at (0 ≤ α ≤ 1, 2 ≥ β ≥ 0) | ETDIt at (α > 1, β < 0) |
|---|---|---|---|---|---|
| Dry–Dry | −2 | −1 | −2 | −2 | −2 |
| Wet–Wet | +2 | +1 | +2 | +2 | +2 |
| Dry–Wet | −2 | +1 | >+2 | −2 to +2 | <−2 |
| Wet–Dry | +2 | −1 | <−2 | −2 to +2 | >+2 |
| Parameter | Events | Total Duration (Month) | Duration per Event (Month) |
|---|---|---|---|
| ETDI(0.0,2.0) | 11 | 42 | 4 |
| ETDI(0.1,1.8) | 10 | 38 | 4 |
| ETDI(0.2,1.6) | 8 | 39 | 5 |
| ETDI(0.3,1.4) | 8 | 41 | 5 |
| ETDI(0.4,1.2) | 10 | 47 | 5 |
| ETDI(0.5,1.0) | 10 | 51 | 5 |
| ETDI(0.6,0.8) | 10 | 51 | 5 |
| ETDI(0.7,0.6) | 9 | 50 | 6 |
| ETDI(0.8,0.4) | 9 | 54 | 6 |
| ETDI(0.9,0.2) | 4 | 40 | 10 |
| Point | Time Series | Events | Total Duration (Months) | Duration per Event (Months) |
|---|---|---|---|---|
| P1 | 8-day | 10 | 51 | 5 |
| 16-day | 9 | 29 | 3 | |
| 1-month | 8 | 17 | 2 | |
| P2 | 8-day | 7 | 33 | 5 |
| 16-day | 5 | 16 | 3 | |
| 1-month | 5 | 9 | 2 | |
| P3 | 8-day | 10 | 59 | 6 |
| 16-day | 9 | 31 | 3 | |
| 1-month | 8 | 16 | 2 | |
| P4 | 8-day | 7 | 51 | 7 |
| 16-day | 7 | 31 | 4 | |
| 1-month | 2 | 15 | 7 | |
| P5 | 8-day | 9 | 46 | 5 |
| 16-day | 10 | 29 | 3 | |
| 1-month | 9 | 15 | 2 | |
| P6 | 8-day | 11 | 54 | 5 |
| 16-day | 11 | 29 | 3 | |
| 1-month | 8 | 12 | 2 | |
| P7 | 8-day | 11 | 59 | 5 |
| 16-day | 9 | 30 | 3 | |
| 1-month | 7 | 13 | 2 | |
| P8 | 8-day | 9 | 59 | 7 |
| 16-day | 7 | 30 | 4 | |
| 1-month | 6 | 15 | 3 | |
| P9 | 8-day | 8 | 63 | 8 |
| 16-day | 8 | 30 | 4 | |
| 1-month | 5 | 14 | 3 | |
| P10 | 8-day | 9 | 54 | 6 |
| 16-day | 7 | 26 | 4 | |
| 1-month | 8 | 14 | 2 | |
| P11 | 8-day | 14 | 52 | 4 |
| 16-day | 12 | 30 | 3 | |
| 1-month | 7 | 17 | 2 | |
| P12 | 8-day | 15 | 54 | 4 |
| 16-day | 11 | 32 | 3 | |
| 1-month | 9 | 17 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wambura, F.J. Sensitivity of the Evapotranspiration Deficit Index to Its Parameters and Different Temporal Scales. Hydrology 2021, 8, 26. https://doi.org/10.3390/hydrology8010026
Wambura FJ. Sensitivity of the Evapotranspiration Deficit Index to Its Parameters and Different Temporal Scales. Hydrology. 2021; 8(1):26. https://doi.org/10.3390/hydrology8010026
Chicago/Turabian StyleWambura, Frank Joseph. 2021. "Sensitivity of the Evapotranspiration Deficit Index to Its Parameters and Different Temporal Scales" Hydrology 8, no. 1: 26. https://doi.org/10.3390/hydrology8010026
APA StyleWambura, F. J. (2021). Sensitivity of the Evapotranspiration Deficit Index to Its Parameters and Different Temporal Scales. Hydrology, 8(1), 26. https://doi.org/10.3390/hydrology8010026




