Improvements in Sub-Catchment Fractional Snowpack and Snowmelt Parameterizations and Hydrologic Modeling for Climate Change Assessments in the Western Himalayas
Abstract
:1. Introduction
2. Materials and Methods
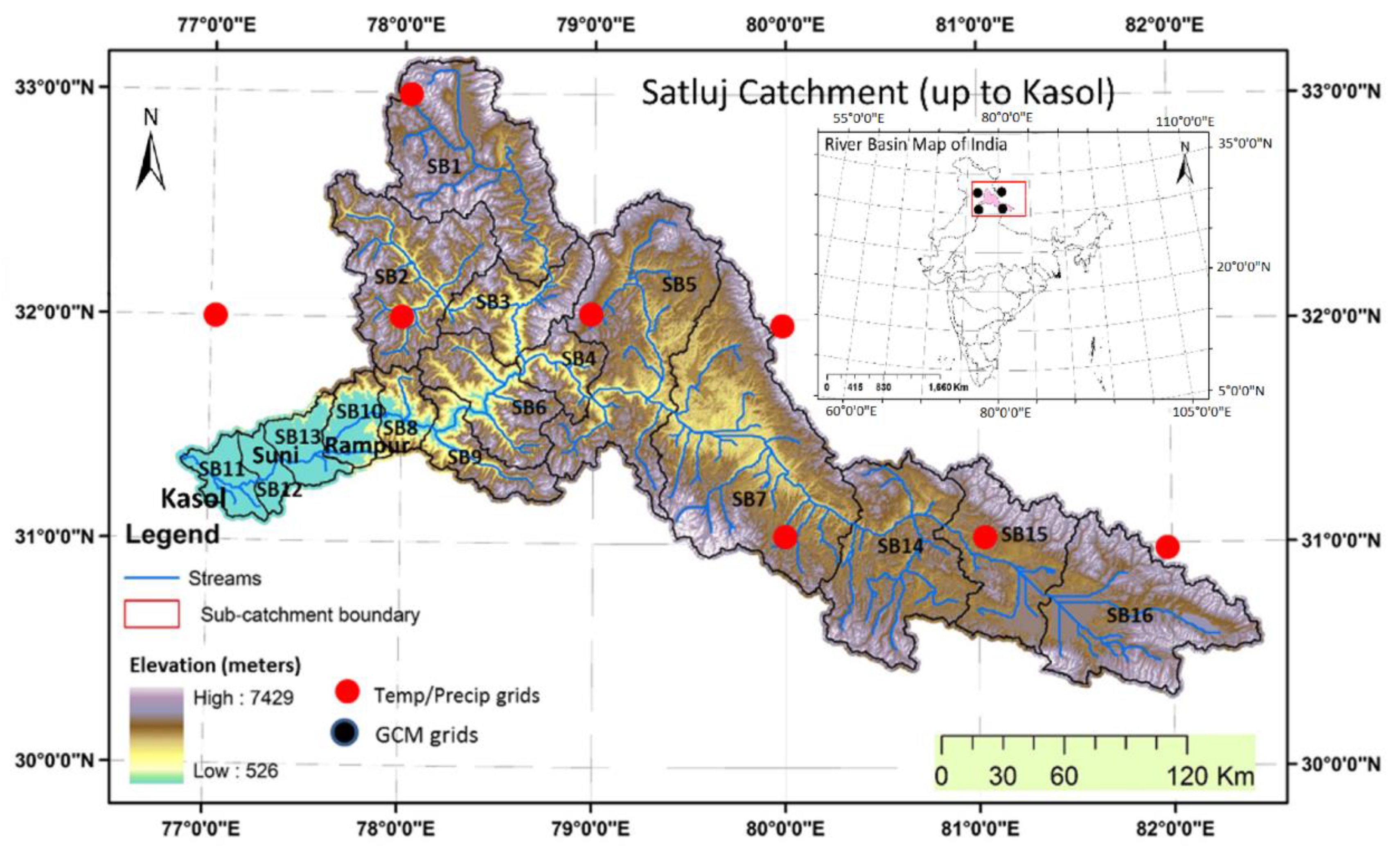
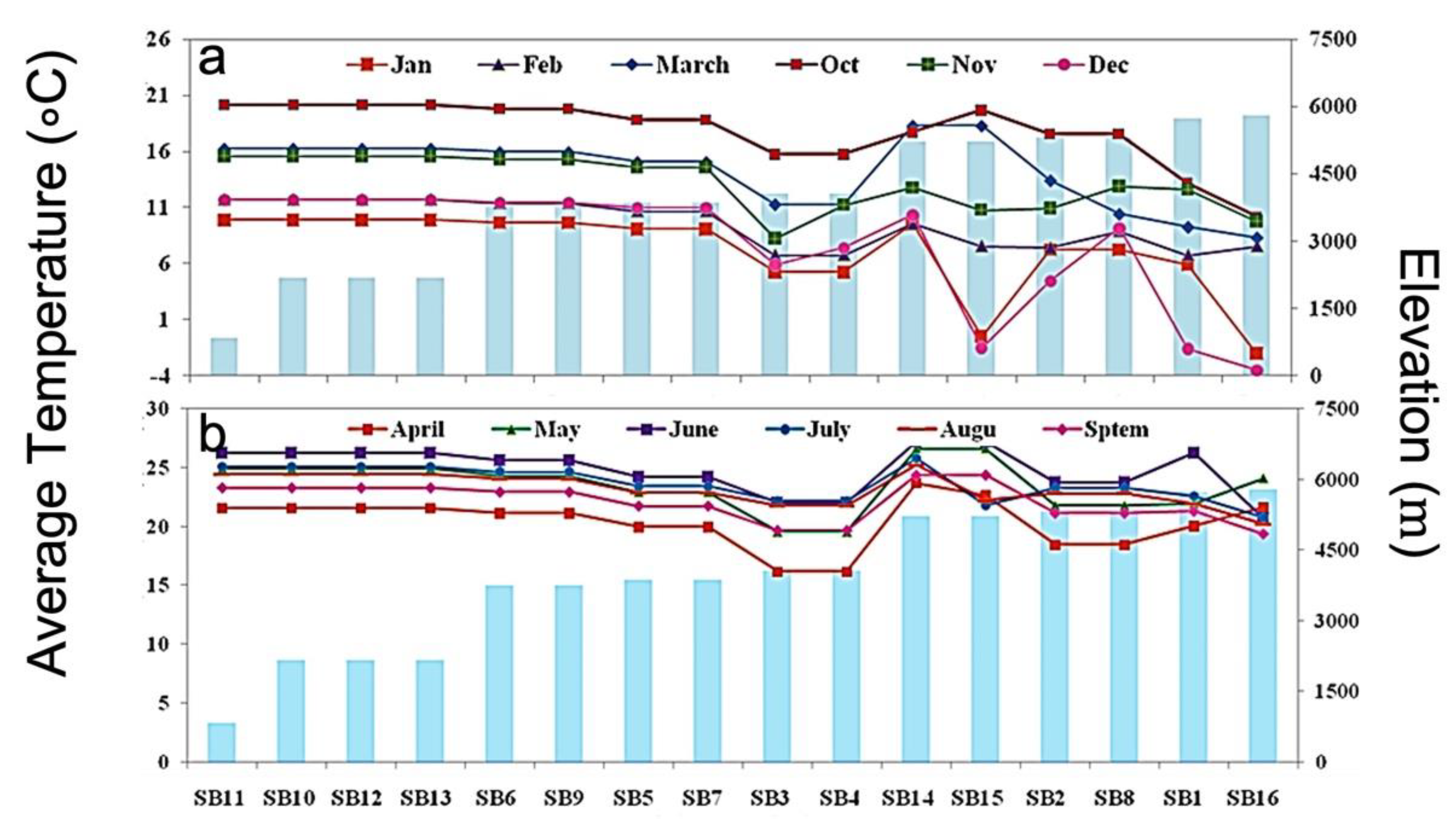
2.1. Study Area
2.2. Meteorological and Thematic Data
2.3. GCM Datasets and Projection Scenarios
2.4. Modeling Approach
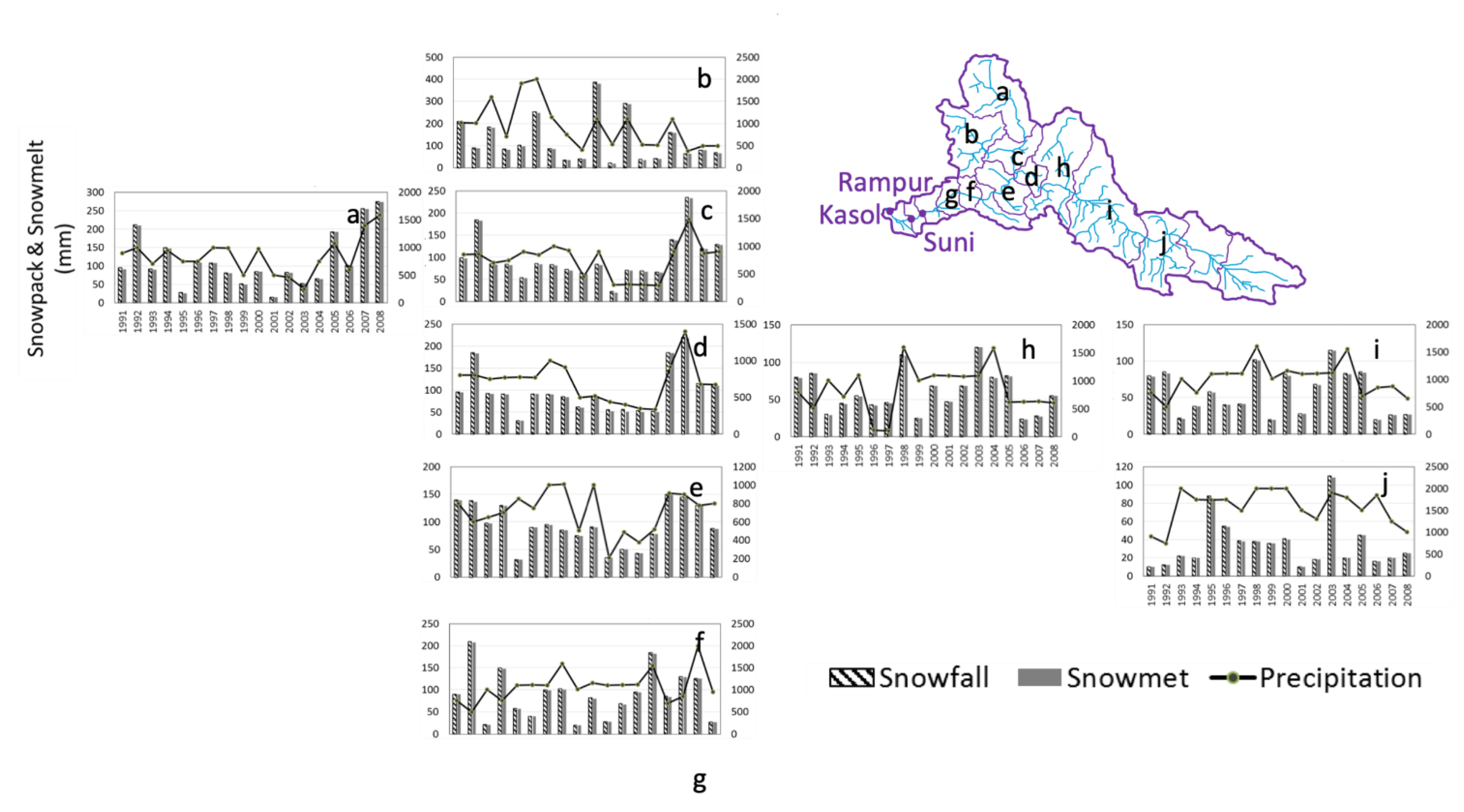
2.5. Elevation Band Approach for Snowpack and Snowmelt Measurement
2.5.1. TLR and PLR Computation and Their Adjustments at Each Elevation Band
2.5.2. Snow Accumulation
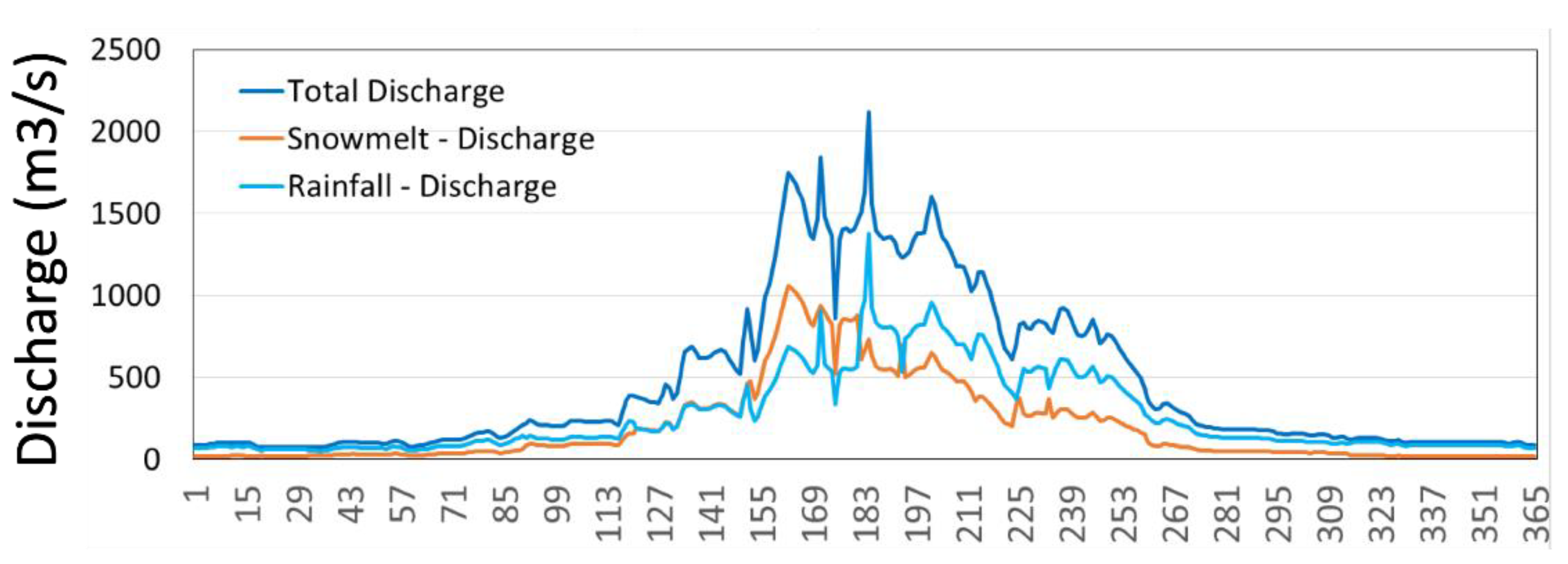
2.5.3. Snowmelt and Glacier Melt
2.6. Model Calibration and Validation
2.7. Parameter Uncertainty and Sensitivity Analysis
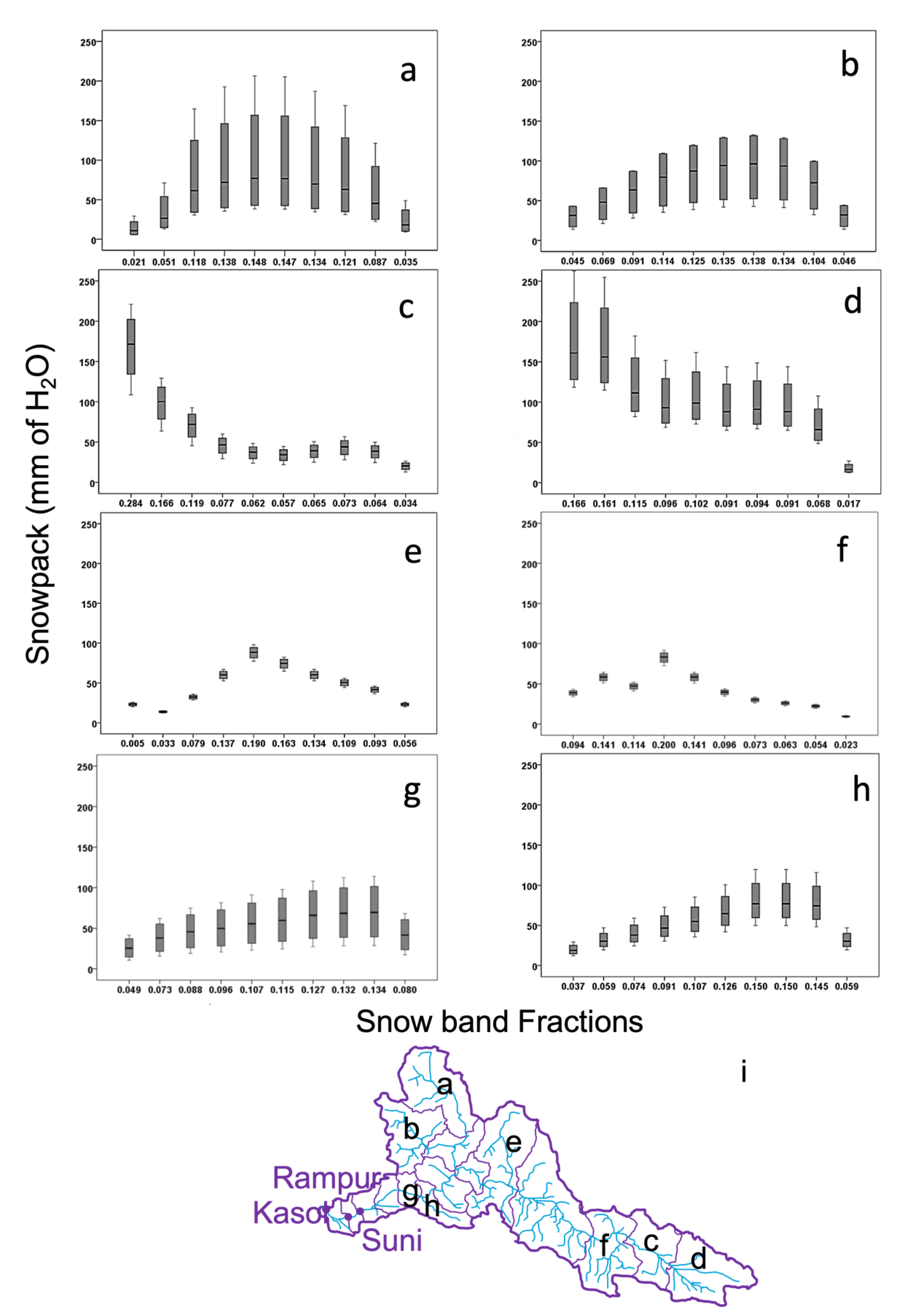
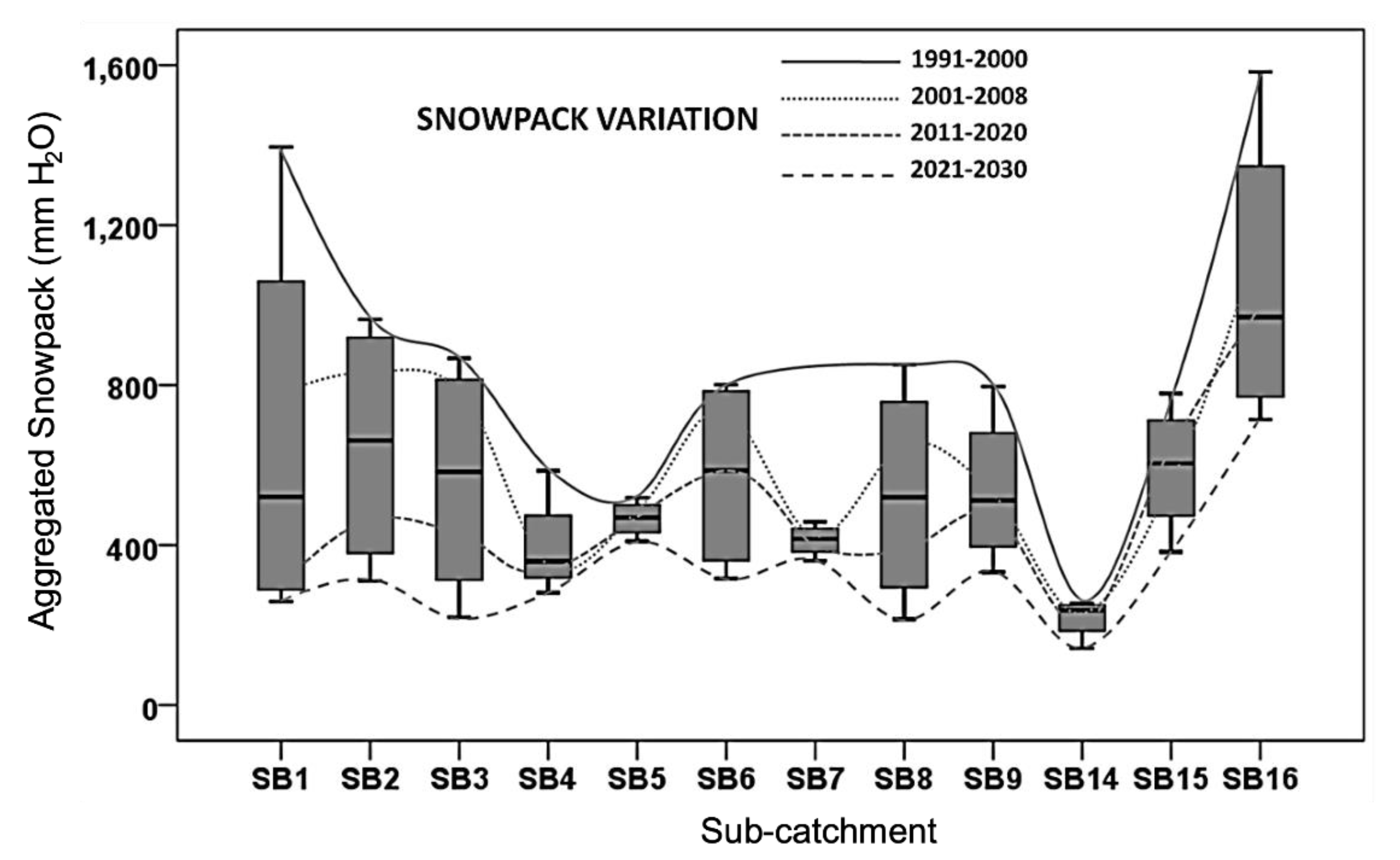
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bolch, T.; Kulkarni, A.; Kääb, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The state and fate of Himalayan glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef] [Green Version]
- Singh, V.; Jain, S.K.; Shukla, S. Glacier change and glacier runoff variation in the Himalayan Baspa River basin. J. Hydrol. 2021, 593, 125918. [Google Scholar] [CrossRef]
- Bhambri, R.; Bolch, T. Glacier mapping: A review with special reference to the Indian Himalayas. Prog. Phys. Geogr. 2009, 33, 672–704. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Ramanathan, V.; Washington, W.M. Observed high-altitude warming and snow cover retreat over Tibet and the Himalayas enhanced by black carbon aerosols. Atmos. Chem. Phys. 2016, 16, 1303–1315. [Google Scholar] [CrossRef] [Green Version]
- IPCC. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Climate Change 2013—The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschungm, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.; Umesh, K.H.; Kumar, N. Modelling and estimation of different components of streamflow for Gangotri Glacier basin, Himalayas. Hydrol. Sci. J. 2008, 53, 309–322. [Google Scholar] [CrossRef]
- Siemens, K.; Dibike, Y.; Shrestha, R.R.; Prowse, T. Runoff Projection from an Alpine Watershed in Western Canada: Application of a Snowmelt Runoff Model. Water 2021, 13, 1199. [Google Scholar] [CrossRef]
- Shukla, S.; Jain, S.K.; Kansal, M.L. Hydrological modelling of a snow/glacier-fed western Himalayan basin to simulate the current and future streamflows under changing climate scenarios. Sci. Total Environ. 2021, 795, 148871. [Google Scholar] [CrossRef]
- Jain, S.K.; Tyagi, J.; Singh, V. Simulation of runoff and sediment yield for a Himalayan watershed using SWAT. J. Water Resour. Protect. 2010, 2, 267–281. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, C.Y.; Hao, Z.; Zhang, L.; Ju, Q.; Lai, X. Variation of Melt Water and Rainfall Runoff and Their Impacts on Streamflow Changes during Recent Decades in Two Tibetan Plateau Basins. Water 2020, 12, 3112. [Google Scholar] [CrossRef]
- Munoz-Arriola, F.; Lettenmaier, D.P.; Zhu, C.; Avissar, R. Water resources sensitivity of the Rio Yaqui Basin, México to agriculture extensification under multi-scale climate conditions. Water Resour. Res. 2009, 45, W00A20. [Google Scholar] [CrossRef]
- Muñoz Arriola, F.; Salgado Rabadán, J.H.; Rocchiccioli, H.M.; Shukla, S.; Güitrón De los Reyes, A.; Sánchez, L.R. Surface Hydrology in the Grijalva River Basin: Calibration of the Variable Infiltration Capacity Model. Aqua-LAC 2011, 3, 68–79. [Google Scholar] [CrossRef]
- Frans, C.; Istanbulluoglu, E.; Vimal, M.; Munoz-Arriola, F.; Lettenmaier, D.P. On runoff trends in the Upper Mississippi River Basin: Influences of climate and land use. Geophys. Res. Lett. 2013, 40, 1104–1110. [Google Scholar] [CrossRef]
- Khan, M.; Munoz-Arriola, F.; Shaik, R.; Greer, P. Spatial heterogeneity of temporal shifts in extreme precipitation across India. J. Clim. Chang. 2019, 5, 19–31. [Google Scholar] [CrossRef]
- Singh, P.; Jain, S.K. Snow and glacier melt in the Satluj River at Bhakra Dam in the western Himalayan region. Hydrol. Sci. J. 2002, 47, 93–106. [Google Scholar] [CrossRef]
- Mote, P.W.; Hamlet, A.F.; Lettenmaier, D.P. Variability and trends in mountain snowpack in western North America. In Proceedings of the Western Snow Conference, Richmond, BC, Canada, 19–22 April 2004; pp. 15–22. [Google Scholar]
- Mote, P.W. Climate-driven variability and trends in mountain snowpack in western North America. J. Clim. 2006, 19, 6209–6220. [Google Scholar] [CrossRef]
- Frans, C.; Istanbulluoglu, E.; Lettenmaier, D.P.; Naz, B.; Clarke, G.; Condom, T.; Burns, P.; Nolin, A. Predicting glacio-hydrologic change in the headwaters of the Zongo River, Cordillera Real, Bolivia. Water Resour. Res. 2015, 51, 9029–9052. [Google Scholar] [CrossRef]
- Jain, S.K.; Goswami, A.; Saraf, A.K. Accuracy assessment of MODIS, NOAA and IRS data in snow cover mapping under Himalayan conditions. Int. J. Remote Sens. 2008, 29, 5863–5878. [Google Scholar] [CrossRef]
- Tiwari, S.; Kar, S.C.; Bhatla, R. Examination of snowmelt over Western Himalayas using remote sensing data. Theor. Appl. Climatol. 2016, 125, 227–239. [Google Scholar] [CrossRef]
- Singh, V.; Goyal, M.K. Analysis and trends of precipitation lapse rate and extreme indices over north Sikkim eastern Himalayas under CMIP5ESM-2M RCPs experiments. Atmos. Res. 2016, 167, 34–60. [Google Scholar] [CrossRef]
- Singh, V.; Goyal, M.K. Changes in climate extremes by the use of CMIP5 coupled climate models over eastern Himalayas. Environ. Earth Sci. 2016, 75, 1–27. [Google Scholar] [CrossRef]
- Gardner, A.S.; Sharp, M.J.; Koerner, R.M.; Labine, C.; Boon, S.; Marshall, S.J.; Lewis, D. Near-surface temperature lapse rates over Arctic glaciers and their implications for temperature downscaling. J. Clim. 2009, 22, 4281–4298. [Google Scholar] [CrossRef]
- Gascoin, S. Snowmelt and Snow Sublimation in the Indus Basin. Water 2021, 13, 2621. [Google Scholar] [CrossRef]
- Change, I.C.; Working Group I Contribution to the Fifth Assessment. Climate Change 2013: The Physical Science Basis. Report of the Intergovernmental Panel on Climate Change; IPCC: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Shrestha, B.; Babel, M.S.; Maskey, S.; van Griensven, A.; Uhlenbrook, S.; Green, A.; Akkharath, I. Impact of climate change on sediment yield in the Mekong River Catchment: A case study of the Nam Ou Catchment, Lao PDR. Hydrol. Earth Syst. Sci. 2013, 17, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Fontaine, T.A.; Cruickshank, T.S.; Arnold, J.G. Development of a snowfall-snowmelt routine for mountainous terrain for the soil water assessment tool (SWAT). J. Hydrol. 2002, 262, 209–223. [Google Scholar] [CrossRef]
- Goyal, M.K.; Sarma, A.K. Analysis of the change in temperature trends in Subansiri River basin for RCP scenarios using CMIP5 datasets. Theor. Appl Climatol. 2017, 129, 1175–1187. [Google Scholar]
- Narsimlu, B.; Gosain, A.K.; Chahar, B.R. Assessment of future climate change impacts on water resources of Upper Sind River Catchment, India, using SWAT Model. Water Resour. Manag. 2013, 27, 3647–3662. [Google Scholar] [CrossRef]
- Beniston, M. Is snow in the Alps receding or disappearing? Wiley Interdiscip. Rev. Clim. Chang. 2012, 3, 349–358. [Google Scholar] [CrossRef] [Green Version]
- Sridhar, V.; Nayak, A. Implications of climate-driven variability and trends for the hydrologic assessment of the Reynolds Creek Experimental Watershed Idaho. J. Hydrol. 2010, 385, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Singh, V.; Bankar, N.; Salunkhe, S.S.; Bera, A.K.; Sharma, J.R. Hydrological streamflow modeling on Tungabhadra catchment: Parameterization and uncertainty analysis using SWAT CUP. Curr. Sci. 2013, 104, 1187–1199. [Google Scholar]
- Ficklin, D.L.; Barnhart, B.L. SWAT hydrologic model parameter uncertainty and its implications for hydroclimatic projections in snowmelt-dependent watersheds. J. Hydrol. 2014, 27, R713–R715. [Google Scholar] [CrossRef] [Green Version]
- Amaranto, A.; Pianosi, F.; Solomatine, D.; Corzo-Perez, G.; Munoz-Arriola, F. Sensitivity Analysis of Hydroclimatic Controls of Data-driven Groundwater Forecast in Irrigated Croplands. J. Hydrol. 2020, 587, 124957. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, R.; Bhardwaj, A.; Sam, L.; Shekhar, M.; Singh, A.; Kumar, R.; Gupta, A. Changing climate and glacio-hydrology in Indian Himalayan Region: A review. Wiley Interdiscip. Rev. Clim. Chang. 2016, 7, 393–410. [Google Scholar] [CrossRef] [Green Version]
- Neupane, R.P.; Yao, J.; White, J.D. Estimating the effects of climate change on the intensification of monsoonal-driven stream discharge in a Himalayan watershed. Hydrol Process. 2013, 28, 6236–6250. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniri, J.R.; Williams, J.R. Soil Water Assessment Tool Theoretical Documentation Version 9; Technical Report No. 406 for Texas Water Resources Institute; Texas A & M University: College Station, TX, USA, 2011. [Google Scholar]
- GLCF. Shuttle Radar Topography Mission (SRTM) Technical Guide; University of Maryland: College Park, MD, USA, 2005; Available online: https://cgiarcsi.community/data/srtm-90m-digital-elevation-database-v4-1/ (accessed on 2 December 2021).
- FAO. The Digitized Soil Map of the World and Derived Soil Properties (Version 3.6); FAO Land and Water Digital Media Series 1; FAO: Rome, Italy, 2007. [Google Scholar]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Qiao, L.; Pan, Z.; Herrmann, R.; Hong, Y. Hydrological variability and uncertainty of lower Missouri River Catchment under changing climate. J. Am. Water Resour. Assoc. (JAWRA) 2013, 50, 246–260. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, P.; Seftigen, K.; Ou, T.; Giese, M.; Barthel, R. Hydroclimate changes over Sweden in the twentieth and twenty-first centuries: A millennium perspective. Geogr. Ann. Ser. A Phys. Geogr. 2021, 103, 103–131. [Google Scholar] [CrossRef]
- Apurv, T.; Mehrotra, R.; Sharma, A.; Goyal, M.K.; Dutta, S. Impact of climate change on floods in the Brahmaputra basin using CMIP5 decadal predictions. J. Hydrol. 2015, 527, 281–291. [Google Scholar] [CrossRef]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Snell, S.E.; Gopal, S.; Kaufmann, R.K. Spatial interpolation of surface air temperatures using artificial neural networks: Evaluating their use for downscaling GCMs. J. Clim. 2000, 13, 886–895. [Google Scholar] [CrossRef]
- Thornton, P.K.; Van de Steeg, J.; Notenbaert, A.; Herrero, M. The impacts of climate change on livestock and livestock systems in developing countries: A review of what we know and what we need to know. Agric. Syst. 2009, 101, 113–127. [Google Scholar] [CrossRef]
- Mahmood, R.; Babel, M.S. Evaluation of SDSM developed by annual and monthly sub-models for downscaling temperature and precipitation in the Jhelum Catchment, Pakistan and India. Theor. Appl. Climatol. 2012, 113, 27–44. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment—Part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Anderson, E.A. A Point Energy and Mass Balance Model of a Snow Cover; NOAA Technical Report NWS 19; NOAA: Silver Spring, MD, USA, 1976; p. 150. [Google Scholar]
- Jain, S.K.; Goswami, A.; Saraf, A.K. Determination of land surface temperature and its lapse rate in the Satluj River basin using NOAA data. Int. J. Remote Sens. 2008, 29, 3091–3103. [Google Scholar] [CrossRef]
- Grusson, Y.; Sun, X.; Gascoin, S.; Sauvage, S.; Raghavan, S.; Anctil, F.; Sáchez-Pérez, J.M. Assessing the capability of the SWAT model to simulate snow, snow melt and streamflow dynamics over an alpine watershed. J. Hydrol. 2015, 531, 574–588. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Yang, J.; Maximov, I.; Siber, R.; Bogner, K.; Mieleitner, J.; Zobrist, J.; Srinivasan, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, N. Impact assessment of climate change on the hydrological response of a snow and glacier melt runoff dominated Himalayan River. J. Hydrol. 1997, 193, 316–350. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Yang, H. Hydrological modelling of the Chaohe Catchment in China: Statistical model formulation and Bayesian inference. J. Hydrol. 2007, 340, 167–182. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Guo, H.; He, D. Combining the SWAT model with sequential uncertainty fitting algorithm for streamflow prediction and uncertainty analysis for the Lake Dianchi Catchment, China. Hydrol. Process. 2014, 28, 521–533. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT-CUP4: SWAT Calibration and Uncertainty Programs—A User Manual; Swiss Federal Institute of Aquatic Science and Technology (Eawag): Dübendorf, Switzerland, 2011. [Google Scholar]
- Tang, Q.; Vivoni, E.; Munoz-Arriola, F.; Lettenmaier, D.P. Predictability of evapotranspiration patterns using remotely-sensed vegetation dynamics during the North American monsoon. J. Hydrometeorol. 2012, 13, 103–121. [Google Scholar] [CrossRef]
- Amaranto, A.; Munoz-Arriola, F.; Corzo-Perez, G.; Solomatine, D. A Spatially enhanced data-driven multi-model to improve semi-seasonal groundwater forecasts in the High Plains aquifer, USA. Water Resour. Res. 2019, 55, 5941–5961. [Google Scholar] [CrossRef] [Green Version]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Johnston, R.; Smakhtin, V. Hydrological modeling of large river basins: How much is enough? Water Resour. Manag. 2014, 28, 2695–2730. [Google Scholar] [CrossRef] [Green Version]
- Pellicciotti, F.; Buergi, C.; Immerzeel, W.W.; Konz, M.; Shrestha, A.B. Challenges and uncertainties in hydrological modeling of remote Hindu Kush–Karakoram–Himalayan (HKH) basins: Suggestions for calibration strategies. Mt. Res. Dev. 2012, 32, 39–50. [Google Scholar] [CrossRef]
- Shukla, S.; Kansal, M.L.; Jain, S.K. Snow cover area variability assessment in the upper part of the Satluj river basin in India. Geocarto Int. 2017, 32, 1285–1306. [Google Scholar] [CrossRef]
- Sarzaeim, P.; Ou, W.; de Oliveira, L.A.; Munoz-Arriola, F. Flood-Risk Analytics for Climate-Resilient Agriculture Using Remote Sensing in the Northern High Plains. Geo-Extreme 2021, 2021, 234–244. [Google Scholar] [CrossRef]
- Wilson, A.; Cifelli, R.; Munoz-Arriola, F.; Giovannettone, J.; Vano, J.; Parzybok, T.; Dufour, A.; Jasperse, J.; Mahoney, K.; McCormick, B. Efforts to Build Infrastructure Resiliency to Future Hydroclimate Extremes. Geo-Extreme 2020, 2020, 222–233. [Google Scholar] [CrossRef]


| Model Simulation Details | |
|---|---|
| General details | Satluj catchment |
| Simulation period (years) | 16 |
| Warm up (years) | 2 |
| Hydrological response units (HRUs) | 358 |
| Sub-basins | 16 |
| Output time step | Daily, Monthly |
| Watershed area (km2) | 51,055 |
| Water Balance Ratios | |
| Streamflow/precipitation | 0.63 |
| Baseflow/total flow | 0.25 |
| Surface runoff/total flow | 0.45 |
| Percolation/precipitation | 0.26 |
| Deep recharge/precipitation | 0.01 |
| ET/precipitation | 0.36 |
| Water Balance Components (mm) | |
| ET | 382.0 |
| Precipitation | 1073.5 |
| Surface runoff | 304.8 |
| Lateral flow | 113.0 |
| Return Flow | 259.0 |
| Percolation to shallow aquifer | 283.4 |
| Revaporation from shallow aquifer | 10.2 |
| Recharge to deep aquifer | 14.2 |
| Calibration (1991–2000) | ||||||||
| Outlet Station | Daily | Monthly | ||||||
| p-Factor | r-Factor | R2 | NSE | p-Factor | r-Factor | R2 | NSE | |
| Rampur | 0.46 | 1.89 | 0.75 | 0.61 | 0.41 | 1.90 | 0.71 | 0.64 |
| Kasol | 0.57 | 1.50 | 0.76 | 0.63 | 0.57 | 1.57 | 0.78 | 0.67 |
| Suni | 0.52 | 1.60 | 0.72 | 0.59 | 0.49 | 1.43 | 0.73 | 0.60 |
| Validation (2001–2008) | ||||||||
| Outlet Station | Daily | Monthly | ||||||
| p-Factor | r-Factor | R2 | NSE | p-Factor | r-Factor | R2 | NSE | |
| Rampur | 0.43 | 1.89 | 0.62 | 0.54 | 0.45 | 1.92 | 0.65 | 0.55 |
| Kasol | 0.52 | 1.67 | 0.71 | 0.59 | 0.60 | 1.62 | 0.73 | 0.61 |
| Suni | 0.52 | 1.72 | 0.65 | 0.58 | 0.58 | 1.52 | 0.71 | 0.60 |
| Variables | SWAT | Jain et al., 2010 | Singh and Kumar, 1997 | Tiwari et al., 2016 | Singh and Jain, 2002 |
|---|---|---|---|---|---|
| Snowpack | 61% (Winter) | 65% (Winter) | 53% (summer)–64% (Winter) | 75% (Winter) | 59% (summer)–72% (Winter) |
| Snowmelt at Satluj | 58% (maximum) | 59% (maximum) | 64% (maximum) | 63% (maximum) | 59% (maximum) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, V.; Muñoz-Arriola, F. Improvements in Sub-Catchment Fractional Snowpack and Snowmelt Parameterizations and Hydrologic Modeling for Climate Change Assessments in the Western Himalayas. Hydrology 2021, 8, 179. https://doi.org/10.3390/hydrology8040179
Singh V, Muñoz-Arriola F. Improvements in Sub-Catchment Fractional Snowpack and Snowmelt Parameterizations and Hydrologic Modeling for Climate Change Assessments in the Western Himalayas. Hydrology. 2021; 8(4):179. https://doi.org/10.3390/hydrology8040179
Chicago/Turabian StyleSingh, Vishal, and Francisco Muñoz-Arriola. 2021. "Improvements in Sub-Catchment Fractional Snowpack and Snowmelt Parameterizations and Hydrologic Modeling for Climate Change Assessments in the Western Himalayas" Hydrology 8, no. 4: 179. https://doi.org/10.3390/hydrology8040179
APA StyleSingh, V., & Muñoz-Arriola, F. (2021). Improvements in Sub-Catchment Fractional Snowpack and Snowmelt Parameterizations and Hydrologic Modeling for Climate Change Assessments in the Western Himalayas. Hydrology, 8(4), 179. https://doi.org/10.3390/hydrology8040179






