Russian Rivers Streamflow Forecasting Using Hydrograph Extrapolation Method

Abstract

This paper presents a method of hydrograph extrapolation, intended for simple and efficient streamflow forecasting with up to 10 days lead time. The forecast of discharges or water levels is expressed by a linear formula depending on their values on the date of the forecast release and the five previous days. Such forecast techniques were developed for more than 2700 stream gauging stations across Russia. Forecast verification has shown that this method can be successfully applied to large rivers with a smooth shape of hydrographs, while for small mountain catchments, the accuracy of the method tends to be lower. The method has been implemented into real-time continuous operations in the Hydrometcentre of Russia. In the territory of Russia, 18 regions have been identified with a single dependency of the maximum lead time of good forecasts on the area and average slope of the catchment surface for different catchments of each region; the possibilities of forecasting river streamflow by the method of hydrograph extrapolation are approximately estimated. The proposed method can be considered as a first approximation while solving the problem of forecasting river flow in conditions of a lack of meteorological information or when it is necessary to quickly develop a forecasting system for a large number of catchments.

1. Introduction

Improving hydrological forecast accuracy and increasing lead times as well as expanding the scope of forecast application is necessary for improving the efficiency of water resources management, and the safety of the population and infrastructure from the frequent floods caused by intense snowmelt, rain floods and ice jams in the territory of Russia. An important role here is given to continuous issuing of short- and medium-term flood forecasts with lead times of up to 5 and 10 days, respectively [1,2,3].

There are a variety of models and methods applied in operational short and medium-term streamflow forecasting in the present time [3]. These methods more or less take into account the peculiarity of runoff formation in the catchment area and the movement of water within the river network. They are implemented as physical–mathematical and conceptual models or as statistical dependencies of the predicted value on the hydrological and meteorological characteristics known by the date of the forecast [1,2,4,5,6,7].

Statistical methods are a very widely used mathematical tool, used as the basis for many hydrological analyses and forecasting techniques. They are based on historical data and statistical analysis, including simple gauge-to-gauge relationships, as well as relationships of streamflow characteristics with additional meteorological variables. The strength of the statistical models is that they can be relatively easily developed and quite efficiently implemented in operational use [8,9], which makes them commonly used as a starting point while developing more sophisticated flood forecasting system [2].

The proposed forecasting method based on hydrograph extrapolation falls within the statistical methods category—it implies statistical analysis of historical data and rather simple development and implementation in hydrological short and medium term forecasting practice.

This method is characterized by a simple scheme for obtaining short-term and medium-term forecasts of discharges and water levels based on data from hydrological observations only. For large flat rivers with a smooth shape of hydrographs, it can give quite satisfactory results with significant savings in time and labor costs. The exceptional natural diversity of Russia makes it possible to assume the applicability of this method in other regions of the world in conditions when the relevance and necessity of forecasting river flow from a large number of catchments at the same time makes it difficult to use more complex and laborious methods based on modern hydrological and meteorological models.

The information support subsystem in automated mode provides an extensive hydrometeorological information base for real-time forecasting. It is based on the use of a modern database management system, which operates within the automated system for processing operational information of the Hydrometeorological Center of Russia [10]. The subsystem for making and issuing hydrological forecasts is based on the work of automated software tools that implement a variety of methods of hydrological forecasting and output updating.

For operational delivery of observed and forecasted products to users, the subsystem of preparation and delivery of information-analytical and forecast products to users is implemented. The subsystem is implemented based on WEB and GIS technologies, which allows integration and visualization in a single information environment (the Internet) of all output products. Interaction with users is carried out using a WEB application; the functionality of application is developed taking into account users’ requirements [11,12].

2. Materials and Methods

2.1. The Method

The smooth changes of average daily flow rates and water levels throughout the year, typical for fairly large rivers, provide the basis for the simplest version of flow forecasting by extrapolating the hydrograph. Such extrapolation can provide the forecast of the average daily water discharge with the lead-time $\Delta t$ days in the form of a generalized polynomial:

$$\widehat{Q}(t+\Delta t)=c_0(t)+c_1(t){\phi }_1(\Delta t)+\dots +c_k{\phi }_k(\Delta t)$$

(1)

where $\widehat{Q}(t+\Delta t)$ is the streamflow forecast, $c_0(t)$, $c_1(t)$, …, $c_k(t)$—coefficients described below; ${\phi }_1(\Delta t)$,…,${\phi }_k(\Delta t)$ are some predefined functions. For example, in the case of ${\phi }_1(\Delta t)=\Delta t$,…,${\phi }_k(\Delta t)={(\Delta t)}^k$, Formula (1) means the extrapolation of the hydrograph to $\Delta t$ days ahead by polynomials to the power of $k$. In particular, for a value of $k=1$, a linear extrapolation is performed, and for a value of $k=2$, a parabolic extrapolation is performed. Depending on the forecast date $t$, values $c_0(t)$, $c_1(t)$, …, $c_k(t)$ in the Formula (1) are determined based on the assumption that the sequence of observed discharges $Q(t)$, $Q(t-1)$, …, $Q(t-k)$ for the forecast date and for $k$ previous days are described by the same generalized polynomial. This assumption is expressed as a system of equations:

$$\left\{\begin{array}{l}Q(t-i)=c_0(t)+c(t){\phi }_1(-i)+\dots +c_k(t){\phi }_k(-i),\\ i=0,1,\dots ,k.\end{array}\right.$$

(2)

The solution of the system (2) leads to linear expression of the values $c_0(t)$, $c_1(t)$, …., $c_k(t)$ in terms of discharges $Q(t)$, $Q(t-1)$, …, $Q(t-k)$. After substituting these expressions into Formula (1), it takes the form:

$$\widehat{Q}(t+\Delta t)={\displaystyle \sum _{i=0}^k{a}_i(\Delta t)Q(t-i)}+b(\Delta t).\hspace{1em}{\displaystyle \sum _{i=0}^k{a}_i(\Delta t)Q(t-i)}$$

(3)

Thus, the extrapolation of the hydrograph using any polynomial of the Formula (1) leads to the fact that the forecast $\widehat{Q}(t+\Delta t)$ is expressed as a linear combination of the corresponding date of the forecast of water discharge $Q(t)$ and $k$ previous discharges $Q(t-1)$, …, $Q(t-k)$.

The values $\widehat{Q}(t+\Delta t)$ determined by Formula (3) can take extremely and unrealistic high and low values. Extremely high values $\widehat{Q}(t+\Delta t)$ can occur when predicting water discharges on a steep rise of streamflow during spring floods or rainfall induced floods. Extremely low and even negative values $\widehat{Q}(t+\Delta t)$ can occur when forecasting water discharges and water levels during a steep spring flood or rain flood recession period.

In order to avoid unrealistically low and high forecast values, the results of Formula (3) application shall be adjusted by replacing such extreme values $\widehat{Q}(t+\Delta t)$ with acceptable minimum $minQ$ or acceptable maximum $maxQ$ discharge values. The final scheme of water discharge forecast is expressed by the formula:

$$\tilde{Q}(t+\Delta t)=\left\{\begin{array}{ll}minQ& if \widehat{Q}(t+\Delta t)<minQ;\\ \widehat{Q}(t+\Delta t)& if minQ\le \widehat{Q}(t+\Delta t)\le maxQ;\\ maxQ& if \widehat{Q}(t+\Delta t)>maxQ.\end{array}\right.$$

(4)

The generalized extrapolation of the average daily water levels leads to a similar formula, which expresses the forecast of the water level $\widehat{H}(t+\Delta t)$ in the form of a linear combination of the average daily level known by the date of the forecast $H(t)$ and $k$ levels $H(t-1)$,…,$H(t-k)$ for the previous days:

$$\widehat{H}(t+\Delta t)={\displaystyle \sum _{i=0}^k{a}_i(\Delta t)H(t-i)}+b(\Delta t).$$

(5)

The results of applying Formula (5) are adjusted in the same way by replacing the extreme values $\widehat{H}(t+\Delta t)$ with an acceptable minimum $minH$ or maximum $maxH$ values of water level. The final forecast scheme of water level is expressed by the formula:

$$\tilde{H}(t+\Delta t)=\left\{\begin{array}{ll}minH& if \widehat{H}(t+\Delta t)<minH;\\ \widehat{H}(t+\Delta t)& if minH\le \widehat{H}(t+\Delta t)\le maxH;\\ maxH& if \widehat{H}(t+\Delta t)>maxH.\end{array}\right.$$

(6)

Limiting the permissible values of streamflow rates and water levels using Formulas (4) and (6) allows one to avoid unnecessarily low and high flow rates. However, in this case, there is a danger of underestimating the expected extreme characteristics of the river streamflow. In order to reduce the likelihood of such an underestimation, an estimate of a quantile corresponding to close to 100% of the annual probability of exceeding, for example, 99%, should be used as an acceptable minimum. An estimate of the quantile corresponding to a near 0% annual probability of exceeding, for example, 1%, should be used as an acceptable maximum.

This method is a variant of the Wiener filter, which is widely used in various branches of science [13,14]. The method can be also considered as a particular option of the forecast correction scheme which takes into account the autocorrelation of their errors [15].

It is not absolutely robust, since it requires a statistical assessment of the parameters of Formulas (3) and (4) or (5) and (6). However, when using a sufficient amount of data over a long period, the estimates of these parameters can be quite stable.

The method can be used for short- or medium-term forecasting of river runoff and water level during a certain phase of the water regime or throughout the year. It is not purely formal, since the water discharge and water levels taken into account in Formulas (3) and (5) for $k+1$ days indirectly characterize the flow of meltwater or rainwater, the replenishment or depletion of soil moisture and groundwater reserves, the change in riverbed and floodplain water reserves, and the transformation of a spring flood wave or rain flood during the previous period. The possibilities of using this method are confirmed by its sufficiently successful application for obtaining short-term forecasts of river runoff in the Kama river basin [16].

2.2. Implementation

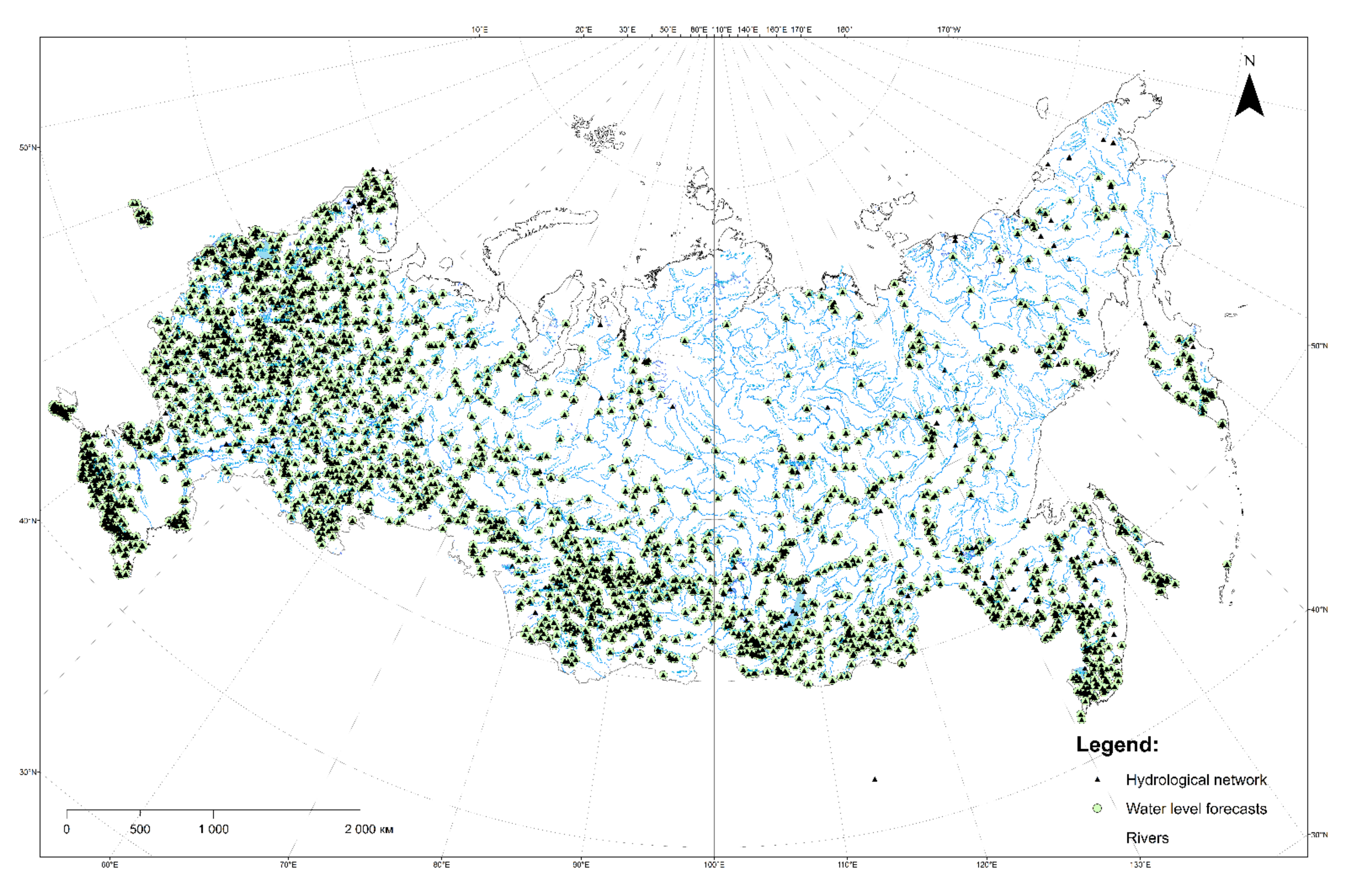
The hydrograph extrapolation method was used to predict the average daily discharge and water levels at stream gauging stations across Russia throughout the year. The method for daily water level forecasting was applied at 2776 gauges, for discharge forecasting—for 2098 stream gauging stations (Figure 1). In each case, a continuous time series of daily hydrological observations was used to develop the method for the period from 1 January 2010 to 31 December 2019.

For a given forecast lead time $\Delta t$ = 1, …, 10 the parameters $a_0(\Delta t)$, $a_1(\Delta t)$,…, $a_k(\Delta t)$ and $b(\Delta t)$ used in Formula (3) or (5) were estimated by the least square method. The minimum and maximum values of discharges and water levels included in Formulas (4) and (6) were determined from the long-term series of hydrological observations.

For each value of the lead-time $\Delta t$ from 1 to 10 days, the optimal number $k$ was selected for Formulas (3) and (5), at which the value of forecast root-mean-square error is minimal. The analysis showed that for all values of the forecast lead-time $\Delta t$ = 1, …, 10, the values of such optimal parameter $k$ did not exceed 5. On this basis, all forecasts of average daily discharges and water levels were determined according to the Formulas (3) and (5) using $k$ = 5.

As permissible minima and maxima of river runoff in Formulas (4) and (6), estimates of quantiles corresponding to the annual probability of exceeding 99% and 1% were used, obtained for the entire period of long-term observations available for each river section.

As an example,

Table 1. Parameters of Formulas (3) and (4) for daily streamflow forecasting at gauging station Serafimovich on the Don River.

Δt, Days	a0	a1	a2	a3	a4	a5	b	minQ, m3/s	maxQ, m3/s
1	1.435	−0.309	−0.082	0.053	−0.048	−0.054	2.21	148	5531
2	1.746	−0.522	−0.068	0.015	−0.065	−0.118	5.48	148	5531
3	1.981	−0.605	−0.129	0.02	−0.169	−0.117	9.41	148	5531
4	2.236	−0.740	−0.143	−0.068	−0.199	−0.116	13.84	148	5531
5	2.462	−0.829	−0.255	−0.099	−0.141	−0.178	18.90	148	5531
6	2.689	−1.007	−0.309	−0.048	−0.128	−0.249	24.57	148	5531
7	2.829	−1.126	−0.282	−0.046	−0.105	−0.335	30.87	148	5531
8	2.898	−1.136	−0.299	−0.044	−0.064	−0.435	37.65	148	5531
9	2.977	−1.168	−0.309	−0.025	−0.050	−0.52	44.75	148	5531
10	3.116	−1.208	−0.315	−0.037	−0.027	−0.658	60.09	148	5531

indicates values of parameters of Formulas (3) and (4) for generating forecasts of the average daily water discharges of the Don River near Serafimovich with a lead time $\Delta t$ = 1, …, 10 days.

In order to automate the procedure for generating forecasts and quality assessment for any set of gauging stations, a computer program was developed using Python programming language and set up in the Hydrometcenter of Russia. The computer program includes the following steps:

―

reading and processing data that can be stored in one or more files;

―

estimation of the parameters of the forecast scheme for each gauging station;

―

evaluation of various indicators of the received forecasts quality;

―

creating a separate directory for each gauge, where the parameters of the forecast generation scheme and its quality indicators are stored;

―

creating the result table with forecasts.

2.3. Forecasts Verification

The quality of short- and medium-term forecasts of average daily discharges and water levels was evaluated based on an independent data sample that was not taken into account when determining the parameters of the forecast formulas. For this purpose, the jackknife approach was applied [17,18]:

(1)

first year was excluded from the 10-year observation period;

(2)

data for the remaining 9 years were used to estimate the parameters of the forecast generation scheme;

(3)

resulting estimates were substituted into Formulas (3) and (4) or (5) and (6) to predict discharges or water levels during the excluded year;

(4)

for the excluded year (independent sample), a series of forecast errors for 365 or (for a leap year) 366 days was formed;

(5)

data for the excluded first year were returned and the next year excluded;

(6)

data for the second year were excluded on the next step of cross-validation;

(7)

after repeating the described procedure for all 10 years, an $N$-long series of forecast errors, obtained on an independent material, was formed ($N$ = 3652).

The check performed in this way showed that when using the data of daily observations for 10 years, the parameters of the formulas for obtaining the forecast are quite stable, since their estimates practically coincided for each of the 10 options for excluding data for one of 10 years.

If we denote the average value of the predicted value per day $t$ by $Y(t)$ and its forecast by $\tilde{Y}(t)$, then for the period from 1 January 2010 to 31 December 2019, the Nash–Sutcliffe model efficiency coefficient is determined by the formula:

$$NSE=1-\frac{{\displaystyle \sum _{i=1}^N[Y(t)}-\tilde{Y}(t){]}^2}{{\displaystyle \sum _{i=1}^N{[Y(t)-\overline{Y}]}^2}},$$

(7)

where $\overline{Y}$ is the arithmetic mean of the series $Y(1)$, …, $Y(N)$ of the actual values of the modeled characteristic [18]. This indicator does not exceed 1; moreover, the equality $NSE=1$ is achieved for an absolutely exact model that ensures the coincidence of the quantities $Y$ and $\tilde{Y}$. Equality $NSE=0$ means that modeling is as accurate as calculating a quantity $Y$ from its mean $\overline{Y}$. Negative $NSE$ values indicate completely unsatisfactory simulation results.

The paper [15] proposes the following classification of the quality of models: a model can be considered good if $NSE\ge 0.80$; satisfactory provided $0.36\le NSE<0.80$; unsatisfactory provided $NSE<0.36$.

For all river sections and flow characteristics, the average forecast error $Y(t)$−$\tilde{Y}(t)$ is zero, that is, the extrapolation of the hydrograph does not give systematic forecast errors.

For the forecast of the Don River daily streamflow near Serafimovich, lead times varying from 1 to 10 days, $NSE$ values are presented in

Table 2. NSE values for daily flow forecasts at major gauging stations.

Index	Gauge Name	River	NSE Values for Different Lead-Times, Days
			1	2	3	4	5	6	7	8	9	10
10,031	Bologor’e	Ob’	0.99	0.99	0.99	0.99	0.99	0.99	0.98	0.97	0.97	0.96
11,055	Ust’-Ishim	Irtysh	0.99	0.99	0.99	0.99	0.99	0.98	0.98	0.97	0.96	0.95
11,801	Salekhard	Ob’	0.99	0.99	0.99	0.98	0.98	0.97	0.96	0.95	0.94	0.93
9803	Igarka	Yenisey	0.99	0.99	0.98	0.96	0.94	0.91	0.89	0.86	0.82	0.78
3821	Kiusur	Lena	0.99	0.98	0.95	0.90	0.85	0.79	0.73	0.66	0.60	0.55
5033	Bogorodskoye	Amur	0.99	0.99	0.99	0.98	0.97	0.96	0.94	0.93	0.91	0.89
77,801	Verkhnee Lebyazhye	Volga	0.99	0.99	0.99	0.98	0.96	0.95	0.92	0.90	0.88	0.85
1801	Srednekolymsk	Kolyma	0.99	0.97	0.93	0.89	0.84	0.79	0.75	0.70	0.65	0.61
70,801	Ust’-Pinega	Northern Dvina	0.99	0.99	0.97	0.95	0.92	0.89	0.86	0.83	0.79	0.76

.

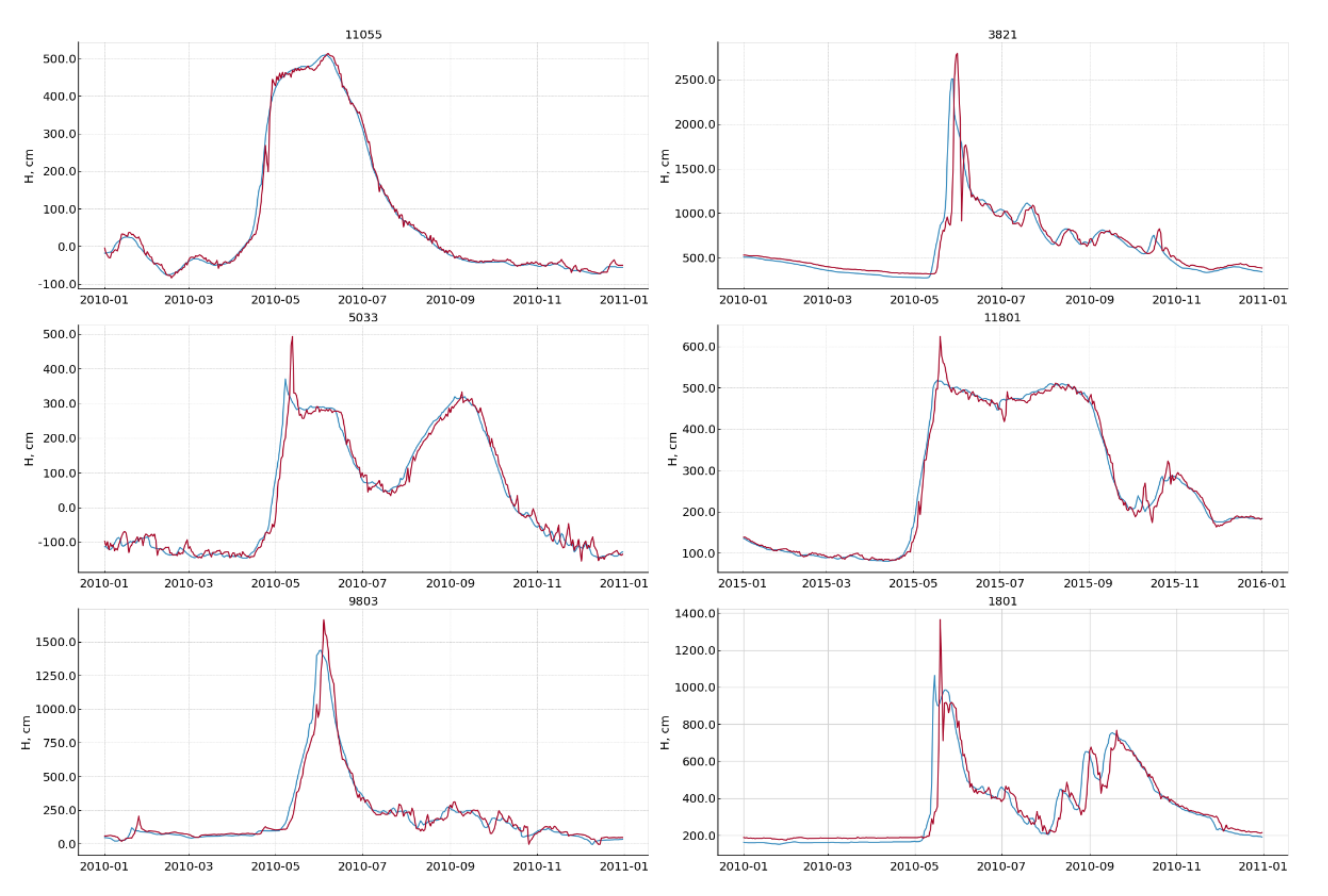
Figure 2 shows observed and forecasted hydrographs at major gauging stations in 2010–2011; streamflow forecast lead-time is 5 days.

3. Results

For the stream gauging stations across Russia, the results of streamflow and water level forecast verification make it possible to assess the performance of the used method of hydrograph extrapolation and the automated system of forecast preparation and issuance.

The number of gauging stations where satisfactory or good forecasts (NSE ≥0.36) of discharges Q, m³/s, and water level H, cm have been achieved using the technique is given in

Table 3. The number of gauging stations with satisfactory forecasts of various lead times.

Elements	Δt, Days
	1	2	3	4	5	6	7	8	9	10
Q, m3/s	2069	2015	1922	1810	1685	1565	1425	1276	1125	1008
H, cm	2775	2769	2755	2724	2692	2634	2558	2476	2360	2237

.

The data in this table show that with lead time $\Delta t$ = 1 day, satisfactory forecasts of water discharge can be obtained for 2069 gauging stations, satisfactory forecasts of water levels for 2775 stations; with lead time $\Delta t$ = 2 days, for 2015 and 2769 stations, respectively, etc. At the same time, the stations for which satisfactory forecasts were obtained with a longer lead time are also included in the number of stations with satisfactory forecasts with lead time $\Delta t$.

It is important that with maximum lead time for medium-term forecasts $\Delta t$ = 10 days, water discharges are forecasted satisfactorily for 1008 gauging stations and water levels for 2237 stations.

Table 4. The number of stream gauging stations with good forecasts of various lead times.

Elements	Δt, Days
	1	2	3	4	5	6	7	8	9	10
Q	1864	1442	1020	726	531	411	324	252	203	160
H	2707	2438	1971	1509	1177	908	733	600	513	426

shows the numbers of stream gauging stations where flow and water level forecasts were good for lead times from 1 to 10 days (efficiency coefficient not less than 0.8).

Information given in Table 3 and Table 4 demonstrates that in general, water levels are better forecasted than discharges using the technique. This is due to the significantly higher amplitude of fluctuations of discharge and thus, the less smooth change in time.

In addition, for every lead time, the number of gauging stations with satisfactory flow forecasts significantly exceeds the corresponding number with good forecasts.

Generally, the accuracy of the hydrograph extrapolation method turned out to be lower for rivers with a small catchment area and large watershed slope, in particular, for small mountain rivers. This is due to the fact that under such conditions, river runoff responds quickly (sometimes it takes a few hours) to snow melting or rainfall [2,7,18]. As a result, the water regime is determined by a series of short-term floods, outside of the winter low-water period, one can speak of a saw-tooth flow hydrograph, and it is difficult to predict this with sufficient accuracy even for the next day. For such rivers, it is necessary to use methods that are based on modeling the processes of river runoff. Due to this, an automated system for preparing and issuing short-term forecasts of small Russian rivers runoff is being developed in the present time; it is based on conceptual models of river runoff formation including the Hydrometcenter of the Russia model and the Swedish HBV model [8,19].

The change of average daily water discharge and levels is smooth, as in Figure 2, for rivers with big catchment area and small watershed slope; therefore, the hydrograph extrapolation method allows satisfactory and good forecasts to be made with a sufficiently long lead-time. This method gives good forecasts with lead time up to 10 days for such large Russian rivers as the Amur, Lena, Yenisey, Ob, Irtysh, Tobol, Kama, Don, Northern Dvina and Pechora.

The efficiency coefficient value is decreasing with an increase in the lead time of the forecast ∆t. This allows determining of the maximum lead time for good forecasts max(∆t) in such a way that forecasts with efficiency coefficient value not less than 0.8 can be obtained for all values ∆t not exceeding max(∆t).

For water discharges, the average value of maximum lead time of good forecasts is 3.3 days, and for water levels, 4.7 days. For satisfactory forecasts of water discharges and water levels, maximum lead times are 7.6 and 9.4 days, respectively.

One of the most important tasks of the operational hydrological forecasting system is the forecasts provision to end users (including hydrologists at regional offices, National Disaster Management Agency, Cities administrations and others) in a timely and effective manner. For this purpose, the system for monitoring and forecasting of floods and other adverse hydrological phenomena was developed based on the recent advances of GIS-WEB technologies [11,19]. Forecasts of water levels, automatically issued according to the abovementioned techniques, are sent to the delivery system in the form of web services. The user, in a real time mode, using a regular web interface, has access to forecasts of flows and water levels (Figure 3). During operation, the systems demonstrated the accuracy and reliability of forecasting, the efficiency of bringing the output products to the end users for making correct and timely decisions aimed at minimizing damage from the passage of floods.

The ability to extrapolate the hydrograph is characterized by the maximum lead time of good forecasts max(∆t) when NSE ≥ 0.80. Maximum lead time of good forecasts depends on not only the catchment area size and watershed slope but also on other natural (climate, relief, landscape) as well manmade conditions of river flow formation. Thus, defining the relation between maximum lead time max(∆t) and the catchment area and watershed slope is possible only for geographically homogeneous regions. For such areas, the smoothness of the hydrographs’ shape increases with an increase in the catchment area A and a decrease in its average slope I. Consequently, with an increase in A and a decrease in I, the maximum lead time of good forecasts max(∆t) should increase.

When identifying such regions, data on 1879 river gauges with natural river flow located throughout the entire territory of Russia were used. For each gauge, according to the data of daily observations, the maximum lead time of good forecasts max(∆t) was calculated using the hydrograph extrapolation method. The values of the watershed area A and its average slope I were obtained.

As a first approximation, the predictability indicator max(∆t) and the catchment area A and the average slope I dependence were analyzed. For this purpose, various types of the function f(A, I) were considered, for each of which the correlation coefficient r between f(A, I) and the max(∆t) was estimated. The variant of f(A, I) was chosen as the optimal one, where the coefficient r had the maximum value. The logarithm of the catchment area ln(A) turned out to be such an optimal variant. The maximum value of r appeared to be 0.50. The tightness of the max(∆t) and ln(A) dependence turned out to be insufficient for assessing the predictability of river flow in specific river sections using the values of A and I. In this regard, the search for closer dependences of the indicator max(∆t) on the optimal type of the function f(A, I) was considered for geographically homogeneous regions.

When identifying regions with a single dependence of the max(∆t) and the area A and the average slope I of the catchments, the goal was to achieve, at least, its relative geographical homogeneity. To achieve this goal, the information contained in the Big Geographical Atlas of Russia was taken into account [18]. The procedure for identifying each region included the following steps:

• identification of the “core” formed by catchments with fairly similar flow formation conditions and its regime;
• preliminary identification of the optimal type of the function f(A, I), which has the maximum correlation coefficient r with the index max(∆t);
• adding adjacent catchments if their data do not significantly reduce the value of r;
• refinement of the optimal type of the function f(A, I);
• discarding adjacent catchments if their data negatively influenced the relationship.

Thus, 18 regions were identified with a single dependence of the predictability indicator of river runoff max(∆t) on the function of morphometric characteristics of the catchment area f(A, I) corresponding to each region. These regions cover about 80% of the entire country and are shown in Figure 4.

Table 5. Characteristics of the selected regions.

№	Region of Russia	N	f(A, I)	r
1	North-West territories	71	ln(A)	0.76
2	Northern Dvina river basin	75	ln(A)	0.77
3	Pechora river basin	46	A	0.84
4	Kama river basin	129	(A/I)½	0.82
5	Oka river basin	66	(A/I)½	0.84
6	Don river basin	75	ln(A)	0.80
7	Kuban river basin	25	(A/I)½	0.77
8	Terek river basin	33	ln(A) + 1.3ln(I)	0.76
9	Tobol river basin	36	ln(A)	0.81
10	Irtysh river basin	78	ln(A/I)	0.80
11	Upper Ob’ river basin	162	(A/I)½	0.82
12	Lower Ob’ river basin	32	ln(A)	0.91
13	Yenisei river basin	80	(A/I)½	0.76
14	Lena river basin	88	ln(A/I)	0.75
15	North-East territories	63	ln(A) − 4ln(I)	0.79
16	Amur river basin	54	ln(A)	0.88
17	Far-East territories	43	A	0.75
18	Sakhalin island	25	(A/I)½	0.75

shows the name, number of river gauges N, optimal type of the function f(A, I) and the correlation coefficient r of the relationship with max(∆t) for each region.

As an example, Figure 5 shows the relationship between max(Δt) and ln(A) for the Lower part of the Ob river basin (Region 12 in Figure 4).

Judging by the point distribution, one can state that, for river catchment areas more than 300,000 km², forecast efficiency is good for lead times more than 5 days; for areas with 700,000 km² or more, lead times with good forecast efficiency may reach up to 10 days.

Similar and more detailed relationships for different regions of Russia allows assessing in advance the possibility of using the hydrograph extrapolation method in flow forecasting.

In Table 4, it is worth noting that application of f(A, I) = ln(A) + 1.3ln(I) as the optimal argument for the Terek river basin (mountainous basin in the south of European Russia) indicates that in this region, the maximum lead time is satisfactory. According to forecasts, max(∆t) increases with an increase in the average slope of the river basin surface. This unexpected result has a fairly simple explanation.

The rivers of the Terek basin have the highest values of slopes; the catchments are located mainly high in the mountains. Snow and glacier flow origin predominates here. It provides a smooth shape of the hydrograph in general. The rivers have the smallest slopes, the catchments of which are located mainly on the plain. For them, rain food pre-possesses. It provides the sharp outlines of individual floods and the sawtooth character of the hydrograph as a whole [20]. Thus, for the Terek river basin, the average slope of the river basin indirectly characterizes the location of the catchment area of the river and its flow origin, and this determines the features of the hydrograph shape and the possibility of its extrapolation.

The hydrograph extrapolation method was used to obtain a forecast of water discharge with a lead-time ∆t from 1 to 10 days. In this regard, the values of the indicator max(∆t), which determines the maximum lead-time of good forecasts, are also limited to 10 days. As a result, for many regions, the relationship of this indicator with the morphometric characteristics f(A, I) becomes nonlinear as it increases and the value of max(∆t) approaches 10. This leads to the fact that the correlation coefficient r, which characterizes the tightness of the statistical relationship and the degree of its linearity, underestimates the actual tightness of the relationship between max(∆t) and the argument f(A, I). If discharges are predicted with a lead time of more than 10 days, the nature of this dependence would be linear in the entire range of values and the correlation coefficients r would be greater.

For all selected regions, the relationship of the max(∆t) and morphometric characteristics f(A, I) turned out to be insufficiently close to allow determination of the maximum lead time of satisfactory forecasts at certain values of area A and the average slope I of a catchment. However, these relationships allow estimation of the extremely low value of f(A, I), which provides satisfactory forecasts with a sufficiently long lead time, and an extremely high value, in which satisfactory forecasts are possible only with a short lead time or are impossible at all (max(∆t) = 0).

Thus, identified regional dependencies allow estimating the threshold values of the area and average slope of the catchment, beyond which, satisfactory forecasts are possible with a sufficiently long lead time, or, conversely, only with a short lead time or are not possible at all.

4. Discussion

The authors are far from considering the proposed hydrograph extrapolation method as an alternative to other methods used in streamflow forecasting. In each specific case, the use of meteorological observations and forecasts, as well as taking into account the landscape structure of the catchment using a well-chosen model of the formation of river flow, will make it possible to obtain more accurate forecasts of discharges and water levels in comparison with the hydrograph extrapolation method. An example would be: a method for short-term forecasting of river runoff in the Kuban basin and the Black Sea coast of the Caucasus based on the model of formation of thaw-rain runoff of mountain rivers of the Hydrometeorological Center of Russia and the meteorological model COSMO–Ru [21]; a method for short-term forecasting of the Kama River tributaries based on the HBV hydrological model and the COSMO–Ru meteorological model [20].

The only but indisputable advantage of the hydrograph extrapolation method is its simplicity. For its implementation, only the data of hydrological observations and the standard statistical estimates of the parameters contained in the formulas for obtaining the forecast obtained on their basis are needed. As shown by the results of applying this method to predict the flow of hundreds of Russian rivers, it allows one quickly and with maximum savings in time and resources to obtain satisfactory and good short-term and medium-term forecasts of streamflow and water level.

Thus, the hydrograph extrapolation method can be considered as a first approximation while solving the problem of forecasting river flow in conditions of a lack of meteorological information or when it is necessary to quickly obtain forecasts for a large number of catchments. It seems that at the next stages, in order to obtain more accurate results, comprehensive work is required to develop and implement more complex and physically based methods.

5. Conclusions

The proposed method of hydrograph extrapolation makes it possible to obtain a scheme for forecasting of the streamflow and water level in a river section in the form of two simple formulas, the parameters of which are estimated from the data of hydrological observations. In order to implement this method in the Hydrometeorological Center of Russia, the automated system has been developed that allows continuous issuing of streamflow and water level forecasts with a lead time up to 10 days for 2776 river sections located practically throughout the country.

The verification of these forecasts based on the data of daily hydrological observations for the period from 2010 to 2019 showed that the proposed method allows obtaining of good and satisfactory results for fairly large rivers with a smooth shape of hydrographs. In particular, good forecasts of water levels with a lead time of ten days can be produced for more than 400 river sections. Limiting the permissible values of streamflow rates and water levels using the method may lead to underestimating the expected extreme characteristics of the river streamflow, which has been taken into account while using the method in operational forecasting. The maximum lead time of good forecasts, for which the Nash–Sutcliffe efficiency coefficient is not less than 0.8, is taken as an indicator of the possibilities for forecasting river runoff.

On the territory of Russia, 18 regions are identified, for each of which this indicator can be calculated depending on the area and average slope of the catchment surface. The values of these morphometric characteristics have been determined, at which good forecasts are possible with a sufficiently long lead time of 8–10 days, or, conversely, only with a short lead time of 1–2 days, or are not possible at all.