Comparison of Regionalisation Techniques for Peak Streamflow Estimation in Small Catchments in the Pilbara, Australia
Abstract
:1. Introduction
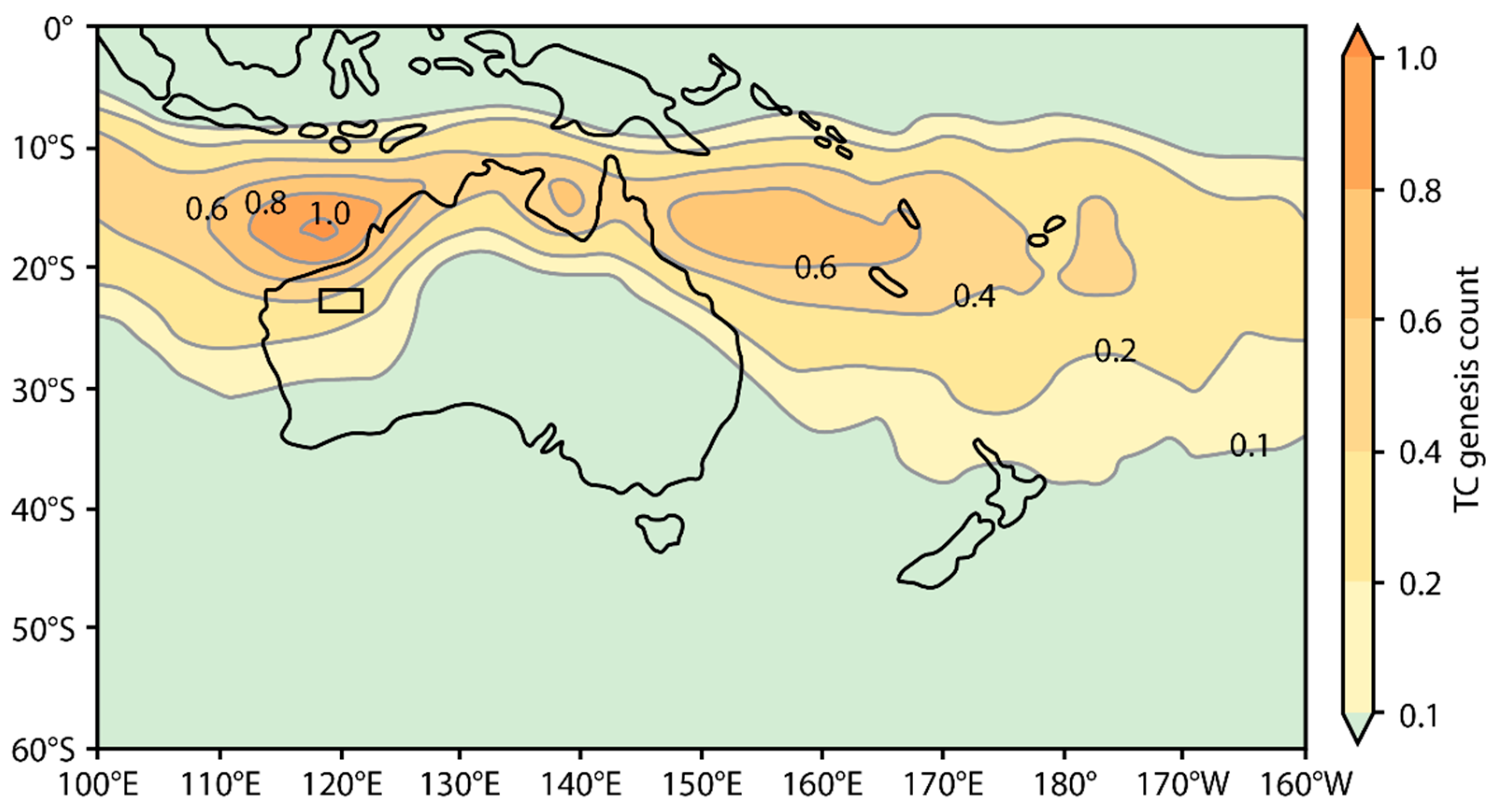
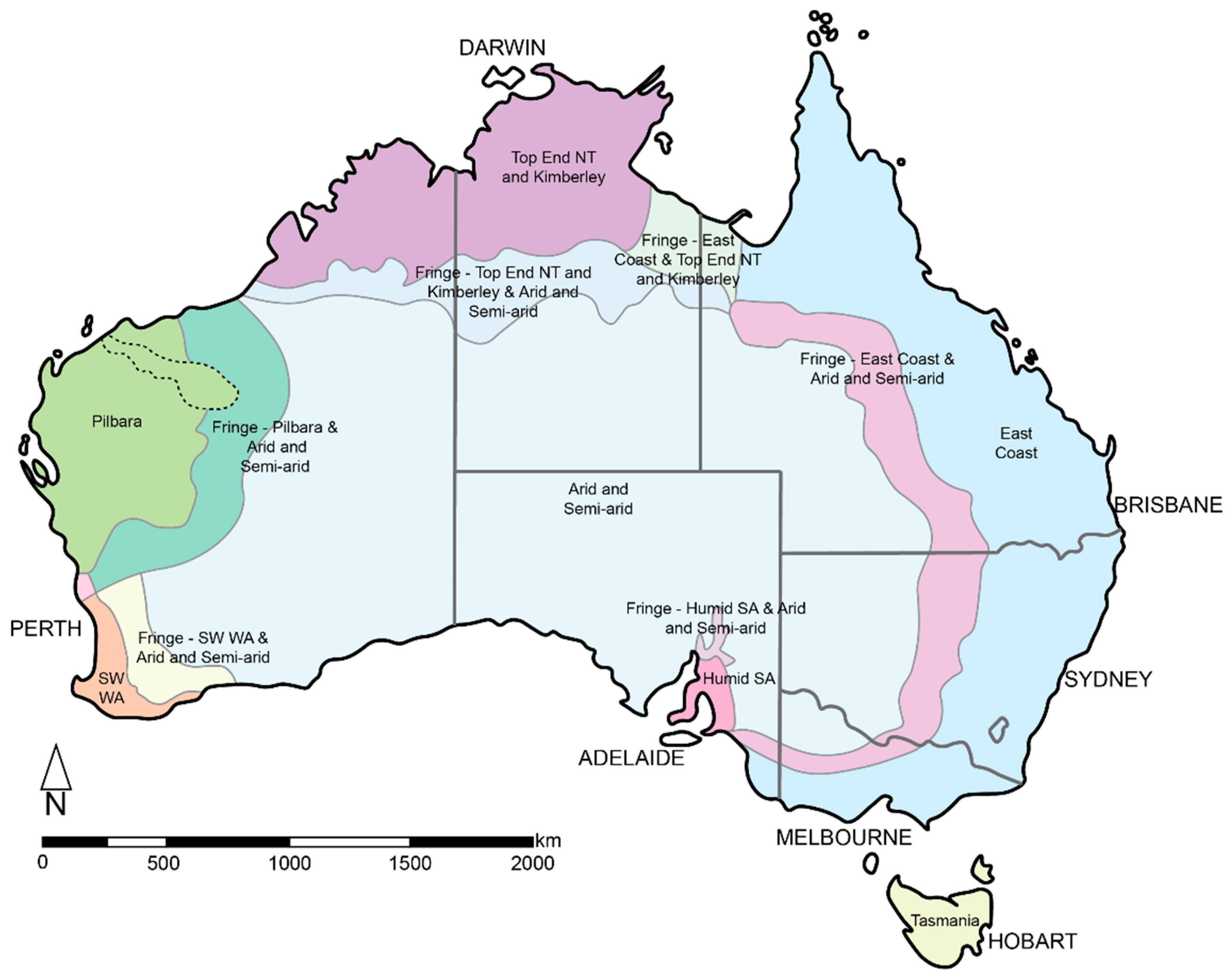
2. Study Area
3. Materials and Methods
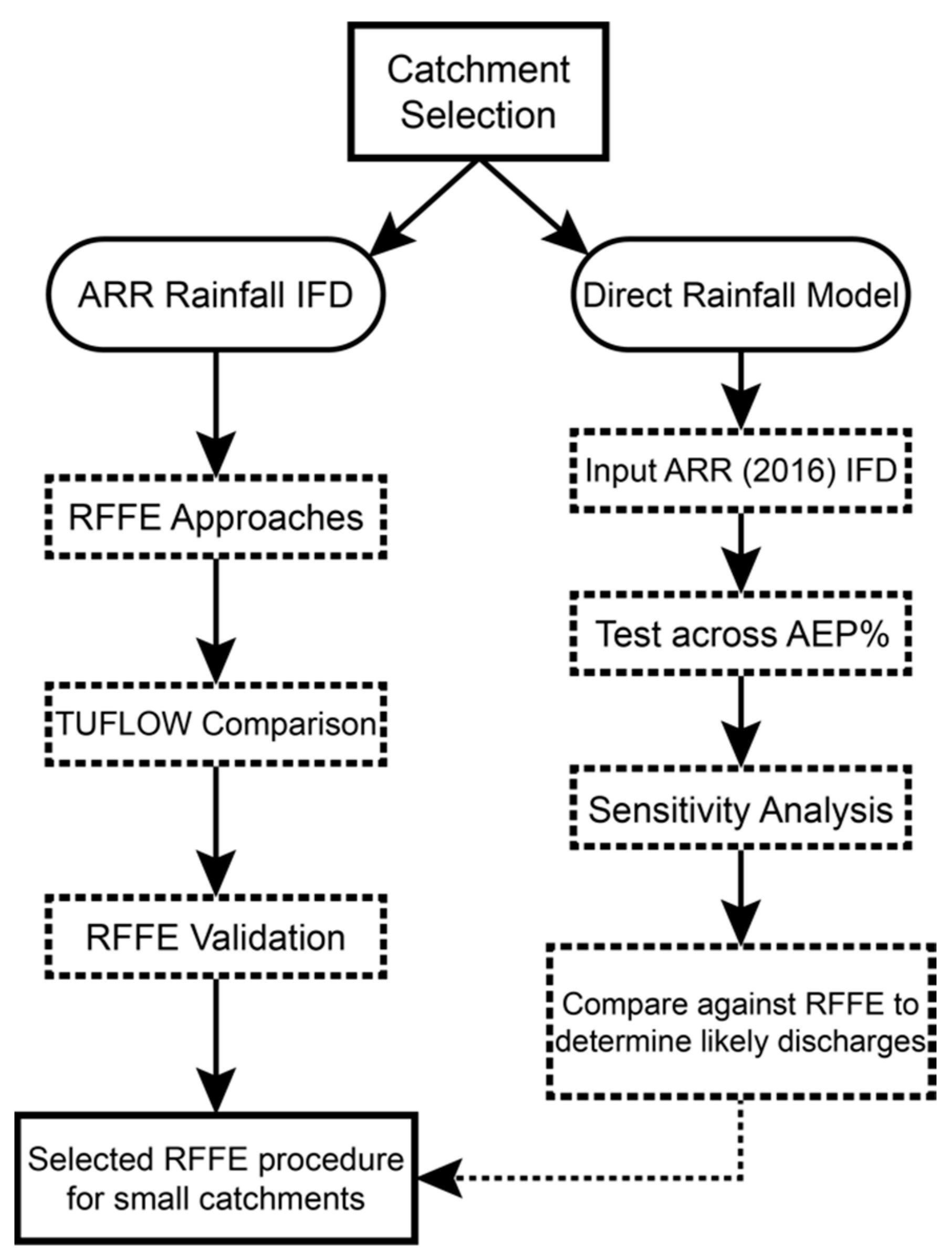
3.1. General Approach
3.2. Regionalisation Approaches
3.3. Regional Flood Frequency Estimation (RFFE)
3.3.1. Quartile Regression Technique
3.3.2. Parameter Regression Technique
3.3.3. Index Flood Method
3.4. Australian Rainfall and Runoff (ARR) RFFE
3.5. Direct Rainfall Modelling
3.5.1. Inputs
Catchment DEMs
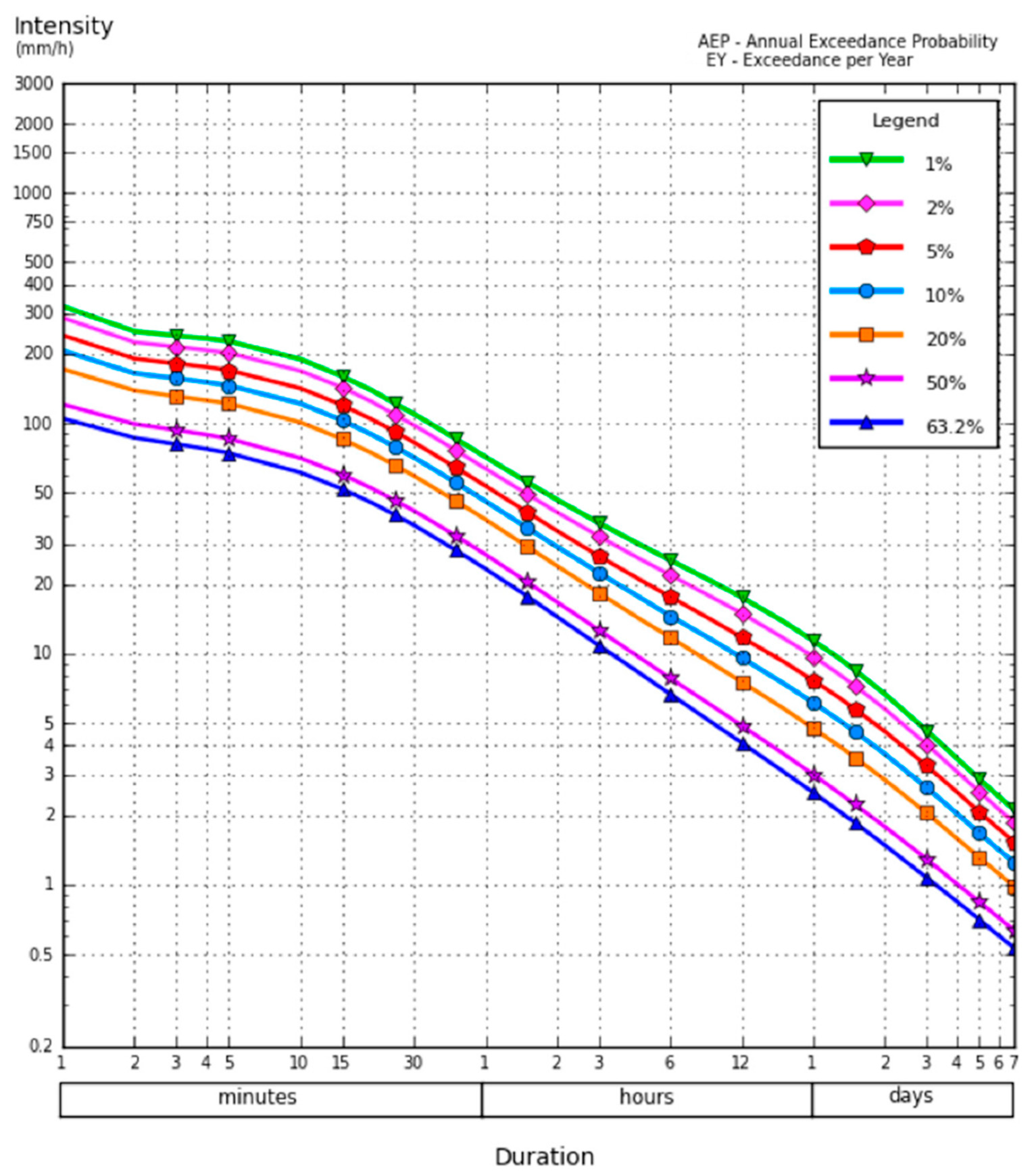
Rainfall
3.5.2. Roughness
3.5.3. Output
Discharge
3.6. Sensitivity Analysis
3.7. Procedure for Evaluating RFFE Approaches
4. Results
4.1. Estimates of Peak Discharge for RFFE Methods
4.2. Direct Rainfall Catchment Modelling
4.3. TUFLOW Sensitivity Analysis
5. Discussion
5.1. Direct Rainfall Model Performance
5.1.1. Sensitivity Analysis
5.1.2. Applicability of Direct Rainfall Modelling in Headwater Catchments
5.2. RFFE Evaluation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hailegeorgis, T.T.; Alfredsen, K. Regional flood frequency analysis and prediction in ungauged basins including estimation of major uncertainties for mid-Norway. J. Hydrol. Reg. Stud. 2017, 9, 104–126. [Google Scholar] [CrossRef]
- Rahman, A.; Haddad, K.; Zaman, M.; Ishak, E.; Kuczera, G.; Weinmann, E. Australian Rainfall and Runoff Revision Project 5: Regional Flood Methods: Stage 2 Report. P5/S2/015. 2012. Available online: http://www.arr.org.au/wp-content/uploads/2013/Projects/ARR_Project5_Stage2_Report_Final_.pdf (accessed on 24 August 2022).
- Feldman, A.D. Flood Hydrograph and Peak Flow Frequency Analysis; US Army Corps of Engineers: Davis, CA, USA, 1979.
- Canterford, R.P.; Pescod, N.R.; Pearce, N.H.; Turner, L.H.; Atkinson, R.J. Frequency analysis of Australian rainfall data as used for flood analysis and design. In Regional Flood Frequency Analysis: Proceedings of the International Symposium on Flood Frequency and Risk Analyses, Baton Rouge, LA, USA, 14–17 May 1987; Springer: Dordrecht, The Netherlands, 1987; pp. 293–302. [Google Scholar]
- Ladson, A.R.; Weinmann, E. Hydrology—An Australian Introduction. Australas. J. Water Resour. 2008, 12, 71–72. [Google Scholar] [CrossRef]
- Pilgrim, D.H.; Chapman, T.G.; Doran, D.G. Problems of rainfall-runoff modelling in arid and semi-arid regions. Hydrol. Sci. J. 1988, 33, 379400. [Google Scholar] [CrossRef]
- Chamber of Minerals and Energy of Western Australia (CME). Iron Ore. 2022. Available online: https://www.cmewa.com.au/about/wa-resources/iron-ore/ (accessed on 24 August 2022).
- Refsgaard, J.C.; Knudsen, J. Operational Validation and Intercomparison of Different Types of Hydrological Models. Water Resour. Res. 1996, 32, 2189–2202. [Google Scholar] [CrossRef]
- Flatley, A.; Markham, A. Establishing effective mine closure criteria for river diversion channels. J. Environ. Manag. 2021, 287, 112287. [Google Scholar] [CrossRef]
- Huxley, C.; Syme, B. TUFLOW GPU-best practice advice for hydrologic and hydraulic model simulations. In Proceedings of the 37th Hydrology & Water Resources Symposium, Queenstown, New Zealand, 28 November–2 December 2016; pp. 195–203. [Google Scholar]
- Ball, J.E.; Babister, M.K.; Nathan, R.; Weinmann, P.E.; Weeks, W.; Retallick, M.; Testoni, I. Australian Rainfall and Runoff—A Guide to Flood Estimation; Institution of Engineers: Barton, Australia, 2016. [Google Scholar]
- Caddis, B.M.; Jempson, M.A.; Ball, J.E.; Syme, W.J. Incorporating hydrology into 2D hydraulic models–the direct rainfall approach. In Proceedings of the 9th National Conference on Hydraulics in Water Engineering, Darwin, Australia, 23–26 September 2008. [Google Scholar]
- Hall, J. Direct rainfall flood modelling: The good, the bad and the ugly. Aust. J. Water Resour. 2015, 19, 74–85. [Google Scholar] [CrossRef]
- Taylor, H.; Kerr, T. Designing for Mining: Challenges of Hydrological Design in the Pilbara. Hydrol. Water Resour. Symp. 2014, 2014, 4452. [Google Scholar]
- Taylor, M.; Haddad, K.; Zaman, M.; Rahman, A. Regional flood modelling in Western Australia: Application of regression-based methods using ordinary least squares. In Proceedings of the 19th International Congress on Modelling and Simulation, Perth, Australia, 12–16 December 2011; pp. 3803–3810. [Google Scholar]
- Rahman, A.; Zaman, M.; Haddad, K.; Kuczera, G.; Weinmann, E.; Weeks, W.; Rajaratnam, L.; Kemp, D. Development of a new regional flood frequency analysis method for semi-arid and arid regions of Australia. In Proceedings of the 34th Hydrology and Water Resources Symposium Sydney, Sydney, Australia, 19–22 November 2012; pp. 1433–1440. [Google Scholar]
- Flavell, D. Design flood estimation in Western Australia. Australas. J. Water Resour. 2012, 16, 1–20. [Google Scholar] [CrossRef]
- Davies, J.R.; Yip, E. Pilbara Regional Flood Frequency Analysis. In Proceedings of the Hydrology and Water Resources Symposium, Perth, Australia, 24–27 February 2014; pp. 182–189. [Google Scholar]
- Oreskes, N.; Shrader-Frechette, K.; Belitz, K. Verification, validation, and confirmation of numerical models in the earth sciences. Science 1994, 263, 641–646. [Google Scholar] [CrossRef] [PubMed]
- Annis, A.; Nardi, F.; Volpi, E.; Fiori, A. Quantifying the relative impact of hydrological and hydraulic modelling parameterizations on uncertainty of inundation maps. Hydrol. Sci. J. 2020, 65, 507–523. [Google Scholar] [CrossRef]
- Ahmadisharaf, E.; Kalyanapu, A.J.; Bates, P.D. A probabilistic framework for floodplain mapping using hydrological modeling and unsteady hydraulic modeling. Hydrol. Sci. J. 2018, 63, 1759–1775. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Koutroulis, A.G.; Komma, J.; Tsanis, I.K.; Wagner, W.; Blöschl, G. Initial soil moisture effects on flash flood generation—A comparison between basins of contrasting hydro-climatic conditions. J. Hydrol. 2016, 541, 206–217. [Google Scholar] [CrossRef]
- David, A.; Schmalz, B. Flood hazard analysis in small catchments: Comparison of hydrological and hydrodynamic approaches by the use of direct rainfall. J. Flood Risk Manag. 2020, 13, e12639. [Google Scholar] [CrossRef]
- Viglione, A.; Blösch, G. On the role of storm duration in the mapping of rainfall to flood return periods. Hydrol. Earth Syst. Sci. 2009, 13, 205–216. [Google Scholar] [CrossRef]
- Ball, J.; Babister, M.; Nathan, R.; Weeks, W.; Weinmann, E.; Retallick, M.; Testoni, I. (Eds.) Australian Rainfall and Runoff: A Guide to Flood Estimation; Geoscience Australia: Canberra, Australia, 2019. [Google Scholar]
- Ruprecht, J. Arid Zone Hydrology: Pilbara region of Western Australia. In Proceedings of the 23rd Hydrology and Water Resources Symposium, Hobart, Australia, 21–24 May 1996; pp. 301–305. [Google Scholar]
- Broit, A.; Boytar, G. Development of a methodology for catchments exhibiting sheet flow characteristics in the Pilbara region. Hydrol. Water Resour. Symp. 2014, 2014, 953–961. [Google Scholar]
- BHP Billiton Iron Ore Pty Ltd. BHP Billiton Iron Ore Pilbara Expansion: Strategic Proposal, 650 Environmental Scoping Document. November 2013. Available online: https://www.bhp.com/-/media/bhp/regulatory-information-media/iron-ore/western-australia-iron-ore/0000/referral-and-environmental-scoping-document/160316_ironore_waio_pilbarastrategicassessment_state_environmentalscopingdocument.pdf (accessed on 24 August 2022).
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Sudmeyer, R. Climate in the Pilbara. Bulletin 4873, Department of Agriculture and Food, Western Australia, Perth. Available online: https://library.dpird.wa.gov.au/bulletins/220/ (accessed on 24 August 2022).
- Charles, S.P.; Fu, G.; Silberstein, R.P.; Mpelasoka, F.; McFarlane, D.; Hodgson, G.; Teng, J.; Gabrovsek, C.; Ali, R.; Barron, O.; et al. Hydroclimate of the Pilbara: Past, Present, and Future. A Report to the Government of Western Australia and Industry Partners from the CSIRO Pilbara Water Resource Assessment; CSIRO Land and Water: Clayton, Australia, 2015; pp. 1–140. [Google Scholar]
- Ruprecht, J.; Ivansecu, S. Surface Hydrology of the Pilbara Region: Summary Report. Surface Water Hydrology Report; Series no. 32; Water and Rivers Commission: Perth, Australia, 2000. [Google Scholar]
- Wark, B.; Thomas, L. Does your rating curve hold water: The consequence of rating 860 curve errors. In Proceedings of the ANCOLD, Canberra, Australia, 21–22 October 2014; pp. 1–11. [Google Scholar]
- Harvey, M.; Pearcey, M.; Price, K.; Devkota, B. Geomorphic, hydraulic and sediment transport modelling for mine related channel realignment—Case Study: Caves Creek, Pilbara, Western Australia. In Hydrology and Water Resources Symposium; Engineers Australia: Queensland, Australia, 2014; pp. 259–266. [Google Scholar]
- MWH. Ecohydrological Conceptualisation of the Fortescue Marsh Region; Project No. 83501069; MWH: Melbourne, Australia, 2015; pp. 1–178. [Google Scholar]
- Bureau of Meterology (Australia). Tropical Cyclone Climatology Maps. Product Code: IDCJCM0011. 2019. Available online: http://www.bom.gov.au/climate/maps/averages/tropical-cyclones/ (accessed on 24 August 2022).
- Haque, M.M.; Rahman, A.; Haddad, K.; Kuczera, G.; Weeks, W. Development of a regional flood frequency estimation model for Pilbara, Australia. In Proceedings of the 21st International Congress on Modelling and Simulation, Gold Coast, Australia, 29 November–4 December 2015; pp. 2172–2178. [Google Scholar]
- CSIRO; McFarlane, D.M. Pilbara Water Resource Assessment: Upper Fortescue Region; A Report to the Government of Western Australia and Industry Partners from the CSIRO Pilbara Water Resources Assessment; CSIRO Land and Water Flagship: Clayton, Australia, 2015.
- Doherty, R. Calibration of HEC-RAS models for rating curve development in semi-arid regions of Western Australia. In Proceedings of the AHA 2010 Conference, Perth, Australia, 5–9 July 2010; pp. 1–25. [Google Scholar]
- Kemp, D.; Hewa, G. An Investigation into the Efficacy of Australian Rainfall and Runoff 2016 Procedures in the Mount Lofty Ranges, South Australia; Australian Flow Management Group, University of South Australia: Adelaide, Australia, 2019. [Google Scholar]
- Coombes, P.J.; Colegate, M.; Buchanan, S. Use of direct rain as an investigation process and design of basins using ARR2016 methods. In Proceedings of the Stormwater 2018, Sydney, Australia, 8–12 October 2018. [Google Scholar]
- Schumann, G.; Bates, P.D.; Apel, H.; Aronica, G.T. Global flood hazard mapping, modeling, and forecasting: Challenges and perspectives In Global Flood Hazard: Applications in Modeling, Mapping, and Forecasting; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018; pp. 239–244. [Google Scholar]
- Merz, R.; Bloschl, G.; Parajka, J. Regionalisation methods in rainfall-runoff modelling using large catchment samples. In Large Sample Basin Experiments for Hydrological Model Parameterization: Results of the Model Parameter Experiment—MOPEX; IAHS Publication: Wallingford, UK, 2006; Volume 307, pp. 117–125. [Google Scholar]
- Razavi, T.; Coulibaly, P. Improving streamflow estimation in ungauged basins using a multi-modelling approach. Hydrol. Sci. J. 2016, 61, 2668–2679. [Google Scholar] [CrossRef]
- Wagener, T.; Wheater, H.S. Parameter estimation and regionalization for continuous rainfall-runoff models including uncertainty. J. Hydrol. 2006, 320, 132–154. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Pandey, G.R.; Nguyen, V.T.T. A comparative study of regression-based methods in regional flood frequency analysis. J. Hydrol. 1999, 225, 92–101. [Google Scholar] [CrossRef]
- Rijal, N.; Rahman, A. Design flood estimation in ungauged catchments: Quantile regression technique and Probabilistic Rational Method compared. In Proceedings of the Modsim05: International Congress on Modelling and Simulation: Advances and Applications for Management and Decision Making, Melbourne, Australia, 12–15 December 2005. [Google Scholar]
- Mishra, B.K.; Takara, K.; Yamashiki, Y.; Tachikawa, Y. An assessment of predictive accuracy for two regional flood frequency estimation methods. Annu. J. Hydraul. Eng. JSCE 2010, 54, 7–12. [Google Scholar]
- Austroads. Guide to Bridge Technology Part 8: Hydraulic Design of Waterway Structures. 2018, pp. 1–157. Available online: https://austroads.com.au/publications/bridges/agbt08-18/media/AGBT08-18_Guide_to_Bridge_Technology_Part_8_Hydraulic_Design_of_Waterway_Structures.pdf (accessed on 24 August 2022).
- Rahman, A.; Haddad, K.; Kuczera, G. Features of regional flood frequency estimation (RFFE) model in Australian Rainfall and Runoff. In Proceedings of the 21st International Congress on Modelling and 792 Simulation, Gold Coast, Australia, 29 November–4 December 2015; pp. 2207–2213. [Google Scholar]
- Rahman, A.; Haddad, K.; Kuczera, G.; Weinmann, E. Chapter 3. Regional Flood Methods. In ARR Australian Rainfall and Runoff; Geoscience Australia: Canberra, Australia, 2019. [Google Scholar]
- Rahman, A.; Haddad, K.; Haque, M.M.; Kuczera, G.; Weinmann, E. Australian Rainfall and Runoff, Project 5: Regional Flood Methods: Stage 3 Report; Geoscience Australia: Canberra, Australia, 2015; ISBN 978-0-85825-796 869-3. [Google Scholar]
- Farquharson, F.A.K.; Meigh, J.R.; Sutcliffe, J.V. Regional Flood Frequency Analysis in arid and semi-arid areas. J. Hydrol. 1992, 138, 487–501. [Google Scholar] [CrossRef]
- BMT. TUFLOW Classic/HPC User Manual. Build 2018-03-AD. 2018, pp. 1–443. Available online: https://www.tuflow.com/Download/TUFLOW/Releases/2018-03/TUFLOW%20Manual.2018-65703.pdf (accessed on 20 June 2021).
- Syme. TUFLOW HPC. TUFLOW UK Conference, Bristol. 2018, pp. 1–63. Available online: https://tuflow.com/media/4964/201804-tuflow-hpc-overview-tuflow-conference-uk.pdf (accessed on 24 August 2022).
- Engineers Australia. Australian Rainfall and Runoff Revision Project 15: Two Dimensional Modelling in Urban and Rural Floodplains. Stage 1 and 2 Draft Report; Geoscience Australia: Canberra, Australia, 2012. Available online: https://arr.ga.gov.au/__data/assets/pdf_file/0019/40573/ARR_Project15_TwoDimensional_Modelling_DraftReport.pdf (accessed on 24 August 2022).
- Gomi, T.; Sidle, R.C.; Richardson, J.S. Undersftanding processes and downstream linkages of headwater systems: Headwaters differ from downstream reaches by their close coupling to hillslope processes, more temporal and spatial variation, and their need for different means of protection from land use. BioScience 2002, 52, 905–916. [Google Scholar]
- Hirschmuller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 328–341. [Google Scholar] [CrossRef]
- Bureau of Meteorology (Australia). Design Rainfall System 2016. 2016. Available online: http://www.bom.gov.au/water/designRainfalls/revised-ifd/ (accessed on 10 July 2022).
- Podger, S.; Babister, M.; Ward, M. Determination of pre-burst rainfalls for Australian rainfall and runoff. In Proceedings of the Hydrology and Water Resources Symposium, Melbourne, Australia, 3–6 December 2018; pp. 649–660. [Google Scholar]
- RioTinto. Resource Development: Marillana Creek Regional Flow Balance and Catchment Hydrology; Appendix A9; Rio Tinto: London, UK, 2010; pp. 1–46. [Google Scholar]
- Foglia, L.; Hill, M.C.; Mehl, S.W.; Burlando, P. Sensitivity analysis, calibration, and testing of a distributed hydrological model using error-based weighting and one objective function. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Vaze, J.; Jordan, P.; Beecham, R.; Frost, A.; Summerell, G. Guidelines for Rainfall-Runoff Modelling: Towards Best Practice Model Application; eWater Cooperative Research Centre: Canberra, Australia, 2011; ISBN 978-1-921543-51-7. [Google Scholar]
- Department of Primary Industries and Regional Development. Typical Values for Manning’s Coefficient (n) for Bare Soil Waterways. 2018. Available online: https://www.agric.wa.gov.au/water-management/mannings-roughness-coefficient (accessed on 24 August 2022).
- Rogers, A.D.; Davies, J.R. ARR 2015 Unpacked—Implications for stormwater design in WA. In Proceedings of the IPWEA State Conference, Freemantle, Australia, 9–11 March 2016; pp. 1–12. [Google Scholar]

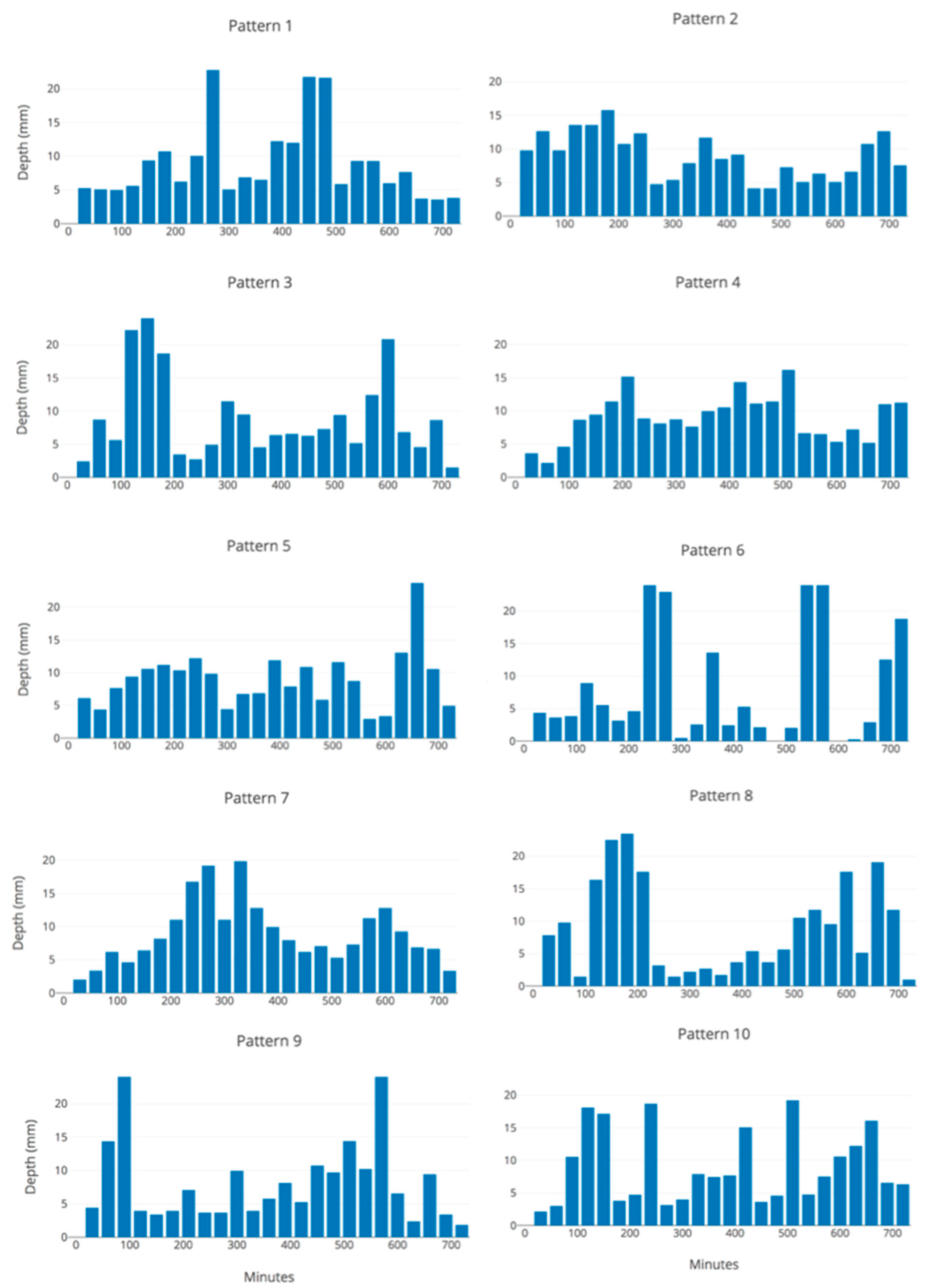

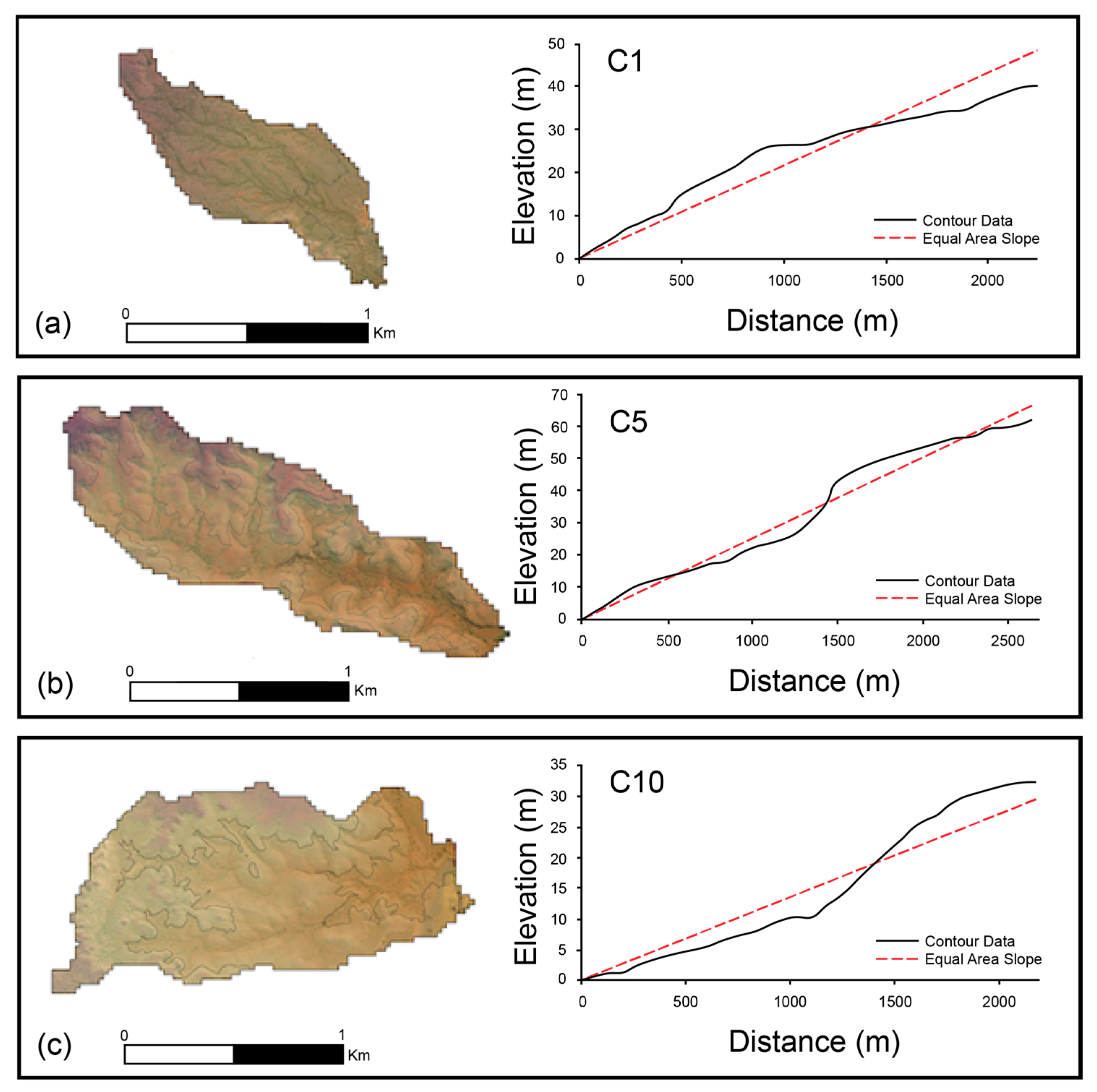
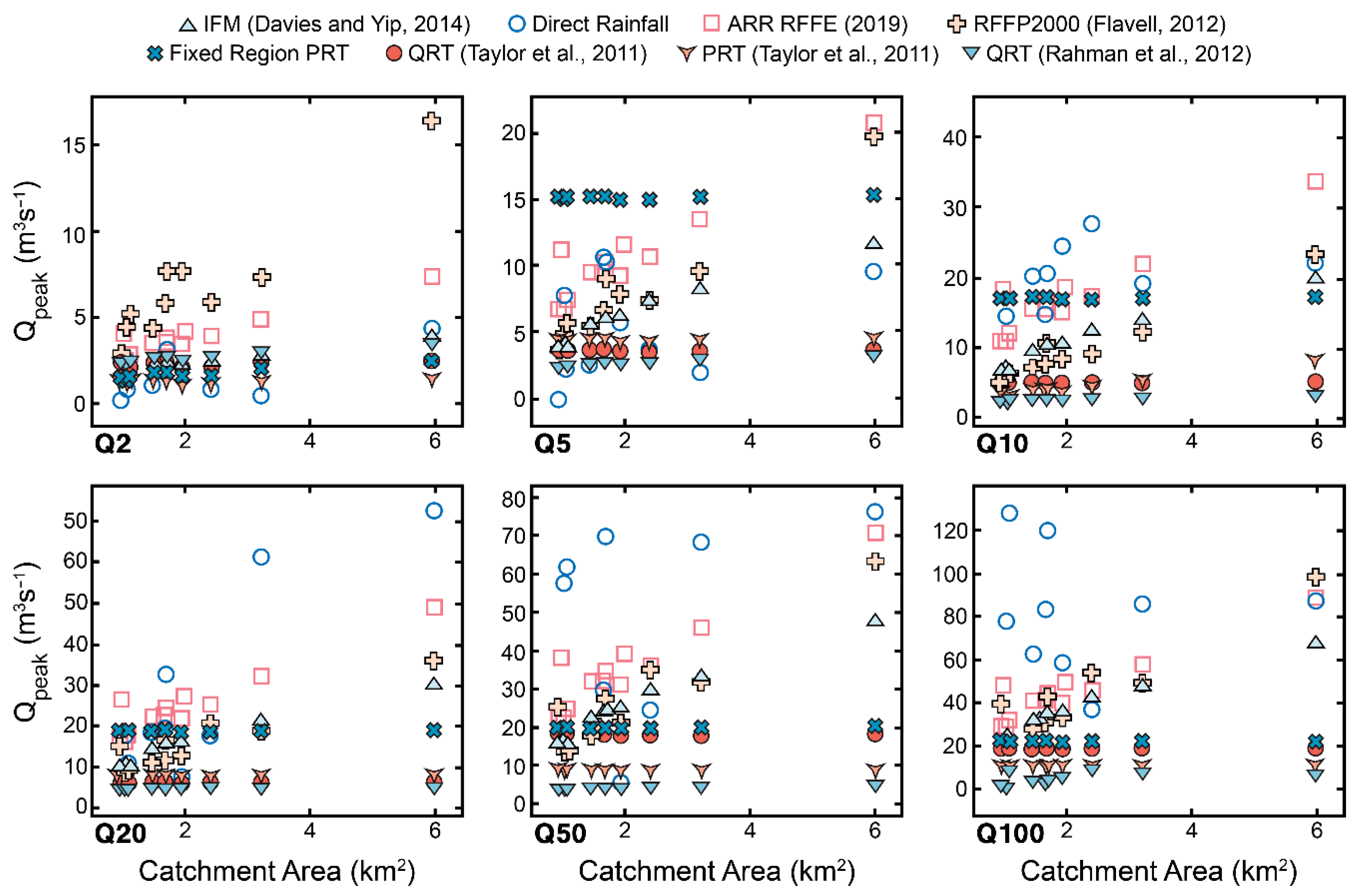

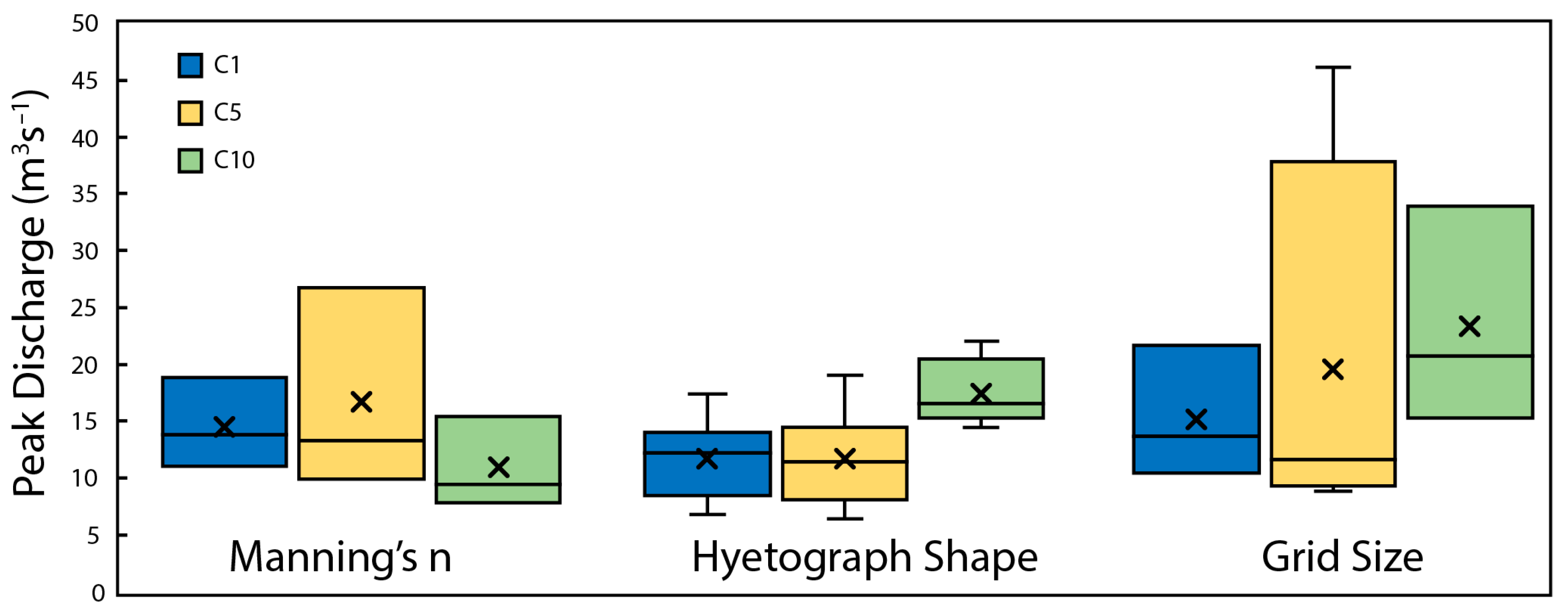
| Method | Equation |
|---|---|
| ARR (Australian Rainfall and Runoff Regional Flood Frequency Estimation Model) RFFE Model | Qx = Q10 × GFx with Q10 as: log10 = b0 + b1 log10 (area) + b2 log10(I6,50) Where b0, b1 and b2 are regression coefficients, estimated using OLS regression, area is the catchment area in km2 and I6,50 is the design rainfall intensity at catchment centroid for a 6 h duration and 50% AEP. The values of b0, b1 and b2 and the regional Growth Factors (GFx) are embedded into the RFFE Model 2015. |
| Index Flood Method (IFM) (Davies and Yip, 2014) [18] | For a small catchment area: Q5 = 7.32 × 10−8 A0.651 I1hr, 2 yrs5.251 Frequency Factors: 2ARI = 0.31, 5ARI = 1.0 10 ARI = 1.70, 20ARI = 2.58, 50ARI = 4.15, 100ARI = 5.82 |
| Parameter Regression Technique (PRT) (Taylor et al., 2011) [15] | M = −11.411 + 0.527 × ln(area) + 7.765 × ln(I12hr,2) S = C1:g = C2 where C1 and C2 are regional average M = 2.54 + 0.52[ln(area) − 4.71] + 8.08[ln(I12,2) − 1.47] |
| Fixed Region Parameter Regression Technique (PRT) (Rahman et al., 2012a) [2] | M = 2.54 + 0.52[ln(area) − 4.71] + 8.08[ln(I12hr,2) − 1.47] stdev = 1.45 + 0.10(zarea) + 0.07(zforest) (4.8.17) skew = −0.49 − 0.08(zarea) − 0.64(zsden) (4.8.18) |
| Quartile Regression Technique QRT (Taylor et al., 2011) [15] | ln(Q2) = −11.366 + 0.521 × ln(area) + 7.858 × ln(I12hr,2) ln(Q5) = −15.913 + 0.486 × ln(area) + 5.336 × ln(I1hr,2) ln(Q10) = −14.285 + 0.465 × ln(area) + 5.055 × ln(I1hr,2) ln(Q20) = −12.949 + 0.445 × ln(area) + 4.824 × ln(I1hr,2) ln(Q50) = −4.914 + 0.431 × ln(area) + 5.705 × ln(I12hr,2) ln(Q100) = −4.072 + 0.413 × ln(area) + 5.412 × ln(I12hr,2) |
| Quartile Regression Technique QRT (Rahman et al., 2012) [2] | ln(Q2) = 2.66 + 0.51(ln(area) − 4.71) + 8.08 [ln(I12,2) − 1.47] ln(Q5) = 3.90 + 0.48[ln(area) − 4.71] + 7.20 [ln(I12,2) − 1.47] ln(Q10) = 4.51 + 0.45[ln(area) − 4.71] + 6.74 [ln(I12,2) − 1.47] ln(Q20) = 5.01 + 0.44[ln(area) − 4.71] + 6.19 [ln(I12,2) − 1.47] ln(Q50) = 5.59 + 0.41[ln(area) − 4.71] + 5.66 [ln(I12,2) − 1.47] ln(Q100) = 5.87 + 0.39[ln(area) − 4.71] + 5.34 [ln(I12,1) − 1.47] |
| RFFP (Flavell, 2012) [17] | Q2 = 1.72 × 10−64(ASe0.5)0.8 LAT−12.17 LONG38.77 (L2/A)−1.05 Q5 = 7.47 × 10−46(ASe0.5)0.81 LAT−14.62 LONG31.40 (L2/A)−0.68 Q10 =2.36 × 10−34(ASe0.5)0.81 LAT−15.24 LONG26.28 (L2/A)−0.39 With the largest value from two Q20 equations being adopted for the Q20 value: Q20 = 1.98 × 10 − 23(ASe0.5)0.79 LAT−15.08LONG20.91 Q20 = Q10 = (13.21A0.61)/(8.74A0.60) Q50 = Q20 × frequency factor (Q50/Q20) Q100 = Q20 × frequency factor (Q100/Q20) A = catchment area (km2), Se = equivalent uniform slope (m/km) and L = mainstream length (km) |
| Catchment | Area (km2) | Latitude | Longitude | Se (m/km) | L (km) |
|---|---|---|---|---|---|
| 1 | 1.05 | −22.711924 | 118.955892 | 18.54 | 1.13 |
| 2 | 0.96 | −22.694436 | 119.001585 | 40.57 | 0.71 |
| 3 | 1.68 | −22.695323 | 119.045882 | 16.65 | 1.10 |
| 4 | 1.48 | −22.690506 | 119.087058 | 22.97 | 1.64 |
| 5 | 1.71 | −22.697491 | 119.084533 | 37.61 | 1.55 |
| 6 | 1.95 | −22.732084 | 118.965195 | 12.49 | 1.37 |
| 7 | 5.99 | −22.765762 | 119.159322 | 22.48 | 2.06 |
| 8 | 3.23 | −22.804315 | 119.161401 | 22.72 | 1.30 |
| 9 | 1.1 | −22.795682 | 119.109156 | 26.71 | 1.17 |
| 10 | 2.42 | −22.735894 | 118.980309 | 16.85 | 1.21 |
| Catchment | Area (km2) | 50AEP | 20AEP | 10AEP | 5AEP | 2AEP | 1AEP |
|---|---|---|---|---|---|---|---|
| 1 | 1.05 | 2.35 | 6.75 | 11.0 | 16.0 | 23.3 | 29.0 |
| 2 | 0.96 | 2.37 | 6.78 | 11.0 | 16.1 | 23.4 | 29.1 |
| 3 | 1.68 | 3.34 | 9.59 | 15.6 | 22.7 | 33.1 | 41.2 |
| 4 | 1.48 | 3.32 | 9.52 | 15.5 | 26.6 | 32.8 | 40.9 |
| 5 | 1.71 | 3.59 | 10.3 | 16.8 | 24.4 | 35.5 | 44.3 |
| 6 | 1.95 | 3.22 | 9.24 | 15.1 | 21.9 | 31.9 | 39.7 |
| 7 | 5.99 | 7.21 | 20.7 | 33.7 | 49.0 | 71.3 | 88.9 |
| 8 | 3.23 | 4.70 | 13.5 | 22.0 | 32.0 | 46.5 | 58.0 |
| 9 | 1.1 | 2.59 | 7.44 | 12.1 | 17.6 | 25.6 | 32.0 |
| 10 | 2.42 | 3.72 | 10.7 | 17.4 | 25.3 | 36.8 | 45.9 |
| Catchment | 2ARI | 5ARI | 10ARI | 20ARI | 50ARI | 100ARI |
|---|---|---|---|---|---|---|
| 1 | 0.51 | 7.75 | 16.56 | 17.58 | 58.10 | 77.79 |
| 3 | 2.24 | 10.63 | 12.45 | 19.39 | 30.37 | 83.30 |
| 4 | 0.80 | 2.68 | 3.50 | 18.41 | 21.22 | 62.69 |
| 5 | 2.88 | 10.11 | 27.40 | 32.56 | 70.25 | 120.11 |
| 6 | 1.38 | 5.75 | 7.32 | 7.50 | 6.32 | 58.53 |
| 7 | 4.16 | 9.60 | 52.0 | 72.66 | 76.73 | 87.60 |
| 8 | 0.20 | 1.95 | 52.29 | 61.26 | 68.82 | 85.86 |
| 9 | 2.20 | 2.37 | 9.78 | 10.97 | 62.24 | 128.20 |
| 10 | 0.64 | 3.72 | 10.7 | 17.4 | 25.3 | 36.80 |
| Catchment | Grid Size | Hyetograph | Manning’s n | Qpeak (m3 s−1) |
|---|---|---|---|---|
| 1 | 5 | 7 | 0.028 | 18.76 |
| 1 | 5 | 7 | 0.035 | 13.71 |
| 1 | 5 | 7 | 0.042 | 11.02 |
| 1 | 5 | 1 | 0.035 | 17.22 |
| 1 | 5 | 2 | 0.035 | 7.38 |
| 1 | 5 | 3 | 0.035 | 14.24 |
| 1 | 5 | 4 | 0.035 | 8.67 |
| 1 | 5 | 5 | 0.035 | 10.70 |
| 1 | 5 | 6 | 0.035 | 6.68 |
| 1 | 5 | 7 | 0.035 | 13.71 |
| 1 | 5 | 8 | 0.035 | 9.98 |
| 1 | 5 | 9 | 0.035 | 13.58 |
| 1 | 5 | 10 | 0.035 | 13.66 |
| 1 | 2 | 7 | 0.035 | 10.54 |
| 1 | 5 | 7 | 0.035 | 13.71 |
| 1 | 10 | 7 | 0.035 | 21.61 |
| 5 | 5 | 7 | 0.028 | 26.62 |
| 5 | 5 | 7 | 0.035 | 13.30 |
| 5 | 5 | 7 | 0.042 | 9.86 |
| 5 | 5 | 1 | 0.035 | 7.87 |
| 5 | 5 | 2 | 0.035 | 10.75 |
| 5 | 5 | 3 | 0.035 | 17.36 |
| 5 | 5 | 4 | 0.035 | 18.90 |
| 5 | 5 | 5 | 0.035 | 13.01 |
| 5 | 5 | 6 | 0.035 | 11.60 |
| 5 | 5 | 7 | 0.035 | 13.30 |
| 5 | 5 | 8 | 0.035 | 7.92 |
| 5 | 5 | 9 | 0.035 | 9.25 |
| 5 | 5 | 10 | 0.035 | 6.29 |
| 5 | 1 | 7 | 0.035 | 8.93 |
| 5 | 2 | 7 | 0.035 | 10.10 |
| 5 | 5 | 7 | 0.035 | 13.30 |
| 5 | 10 | 7 | 0.035 | 46.21 |
| 10 | 5 | 7 | 0.028 | 9.48 |
| 10 | 5 | 7 | 0.035 | 15.45 |
| 10 | 5 | 7 | 0.042 | 7.80 |
| 10 | 5 | 1 | 0.035 | 14.28 |
| 10 | 5 | 2 | 0.035 | 14.66 |
| 10 | 5 | 3 | 0.035 | 16.96 |
| 10 | 5 | 4 | 0.035 | 16.00 |
| 10 | 5 | 5 | 0.035 | 17.55 |
| 10 | 5 | 6 | 0.035 | 20.34 |
| 10 | 5 | 7 | 0.035 | 15.45 |
| 10 | 5 | 8 | 0.035 | 20.22 |
| 10 | 5 | 9 | 0.035 | 15.27 |
| 10 | 5 | 10 | 0.035 | 21.91 |
| 10 | 2 | 7 | 0.035 | 20.82 |
| 10 | 5 | 7 | 0.035 | 15.45 |
| 10 | 10 | 7 | 0.035 | 33.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flatley, A.; Rutherfurd, I. Comparison of Regionalisation Techniques for Peak Streamflow Estimation in Small Catchments in the Pilbara, Australia. Hydrology 2022, 9, 165. https://doi.org/10.3390/hydrology9100165
Flatley A, Rutherfurd I. Comparison of Regionalisation Techniques for Peak Streamflow Estimation in Small Catchments in the Pilbara, Australia. Hydrology. 2022; 9(10):165. https://doi.org/10.3390/hydrology9100165
Chicago/Turabian StyleFlatley, Alissa, and Ian Rutherfurd. 2022. "Comparison of Regionalisation Techniques for Peak Streamflow Estimation in Small Catchments in the Pilbara, Australia" Hydrology 9, no. 10: 165. https://doi.org/10.3390/hydrology9100165
APA StyleFlatley, A., & Rutherfurd, I. (2022). Comparison of Regionalisation Techniques for Peak Streamflow Estimation in Small Catchments in the Pilbara, Australia. Hydrology, 9(10), 165. https://doi.org/10.3390/hydrology9100165








