Experimental Investigation of the Effects of Porosity, Hydraulic Conductivity, Strength, and Flow Rate on Fluid Flow in Weakly Cemented Bio-Treated Sands
Abstract
:1. Introduction
2. Materials and Methods
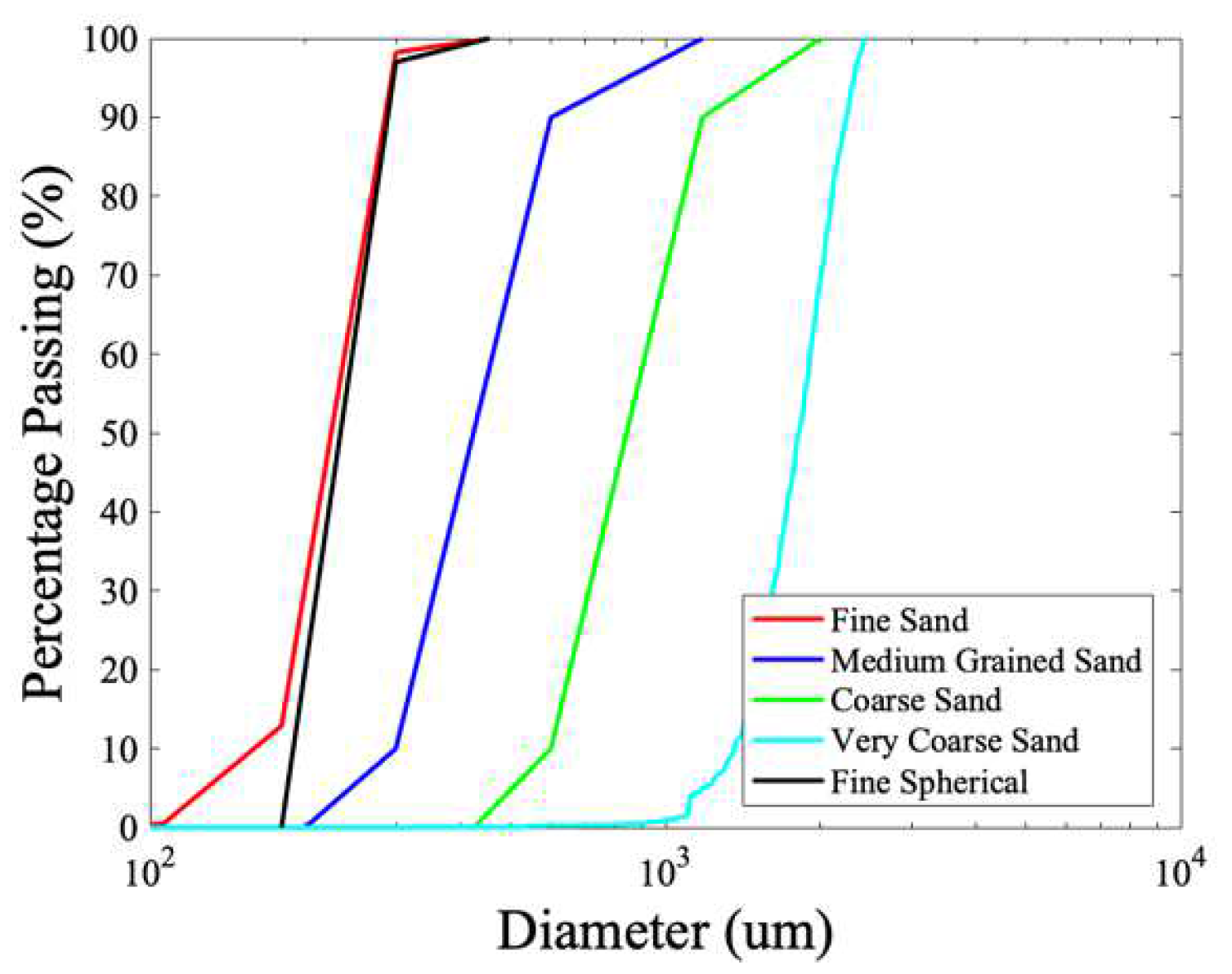
2.1. Base Materials
2.2. Assessment of Physical and Mechanical Properties of Bio-Cemented Sands
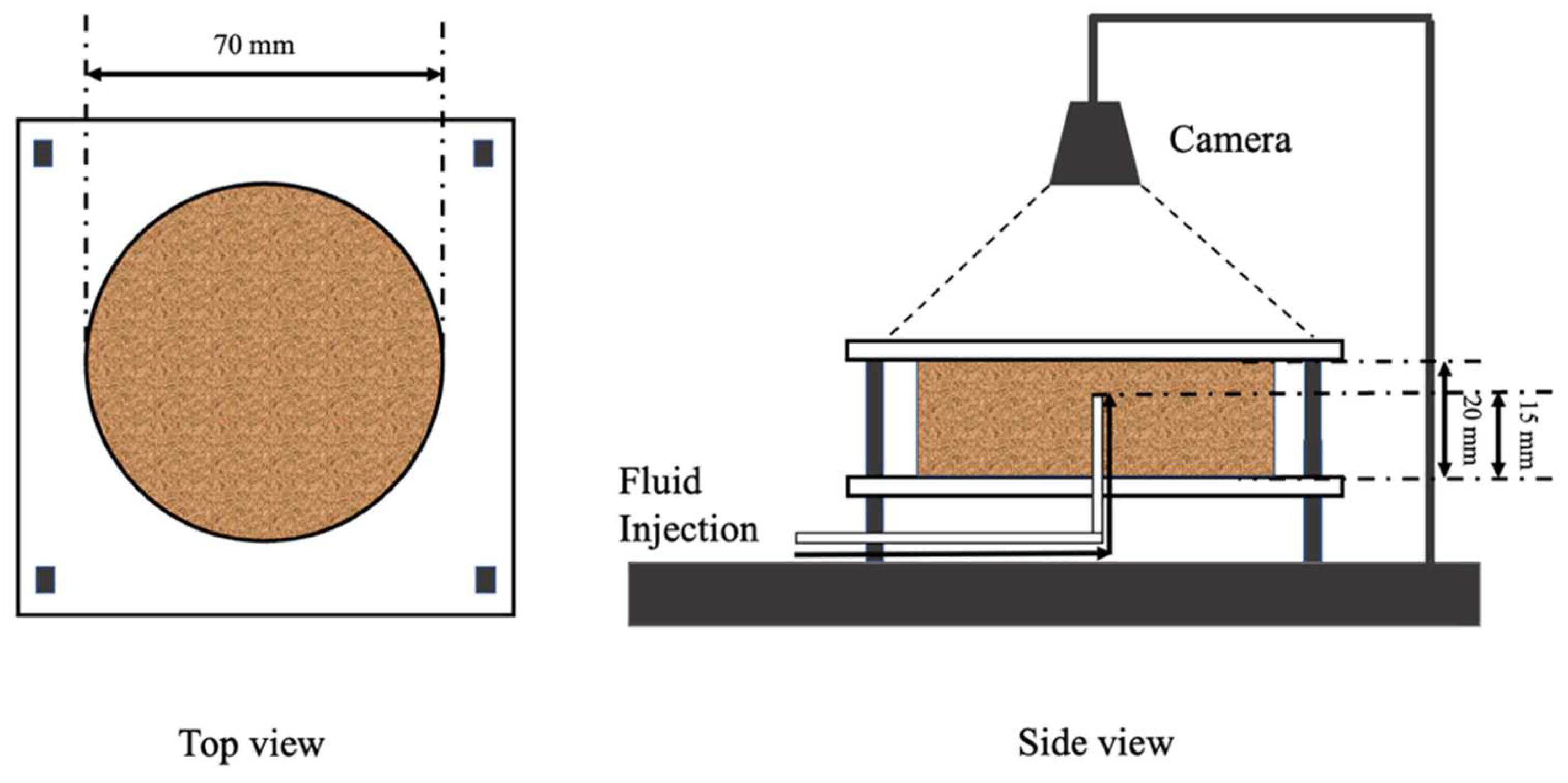
2.3. Experimental Setup of the Fluid Injection Experiments
2.4. Experimental Program
3. Results and Discussion
3.1. The Physical and Mechanical Properties of the Bio-Treated Specimens
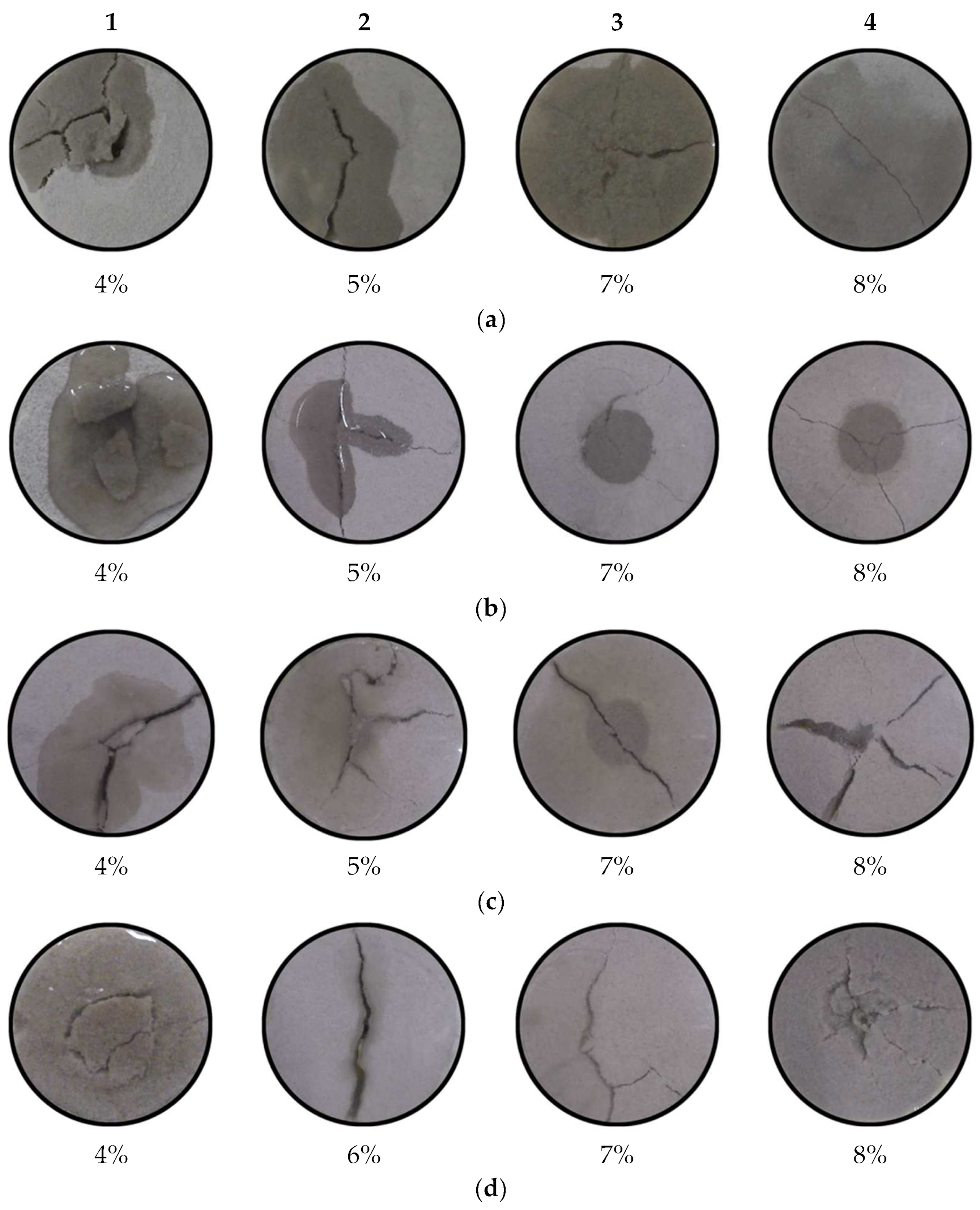
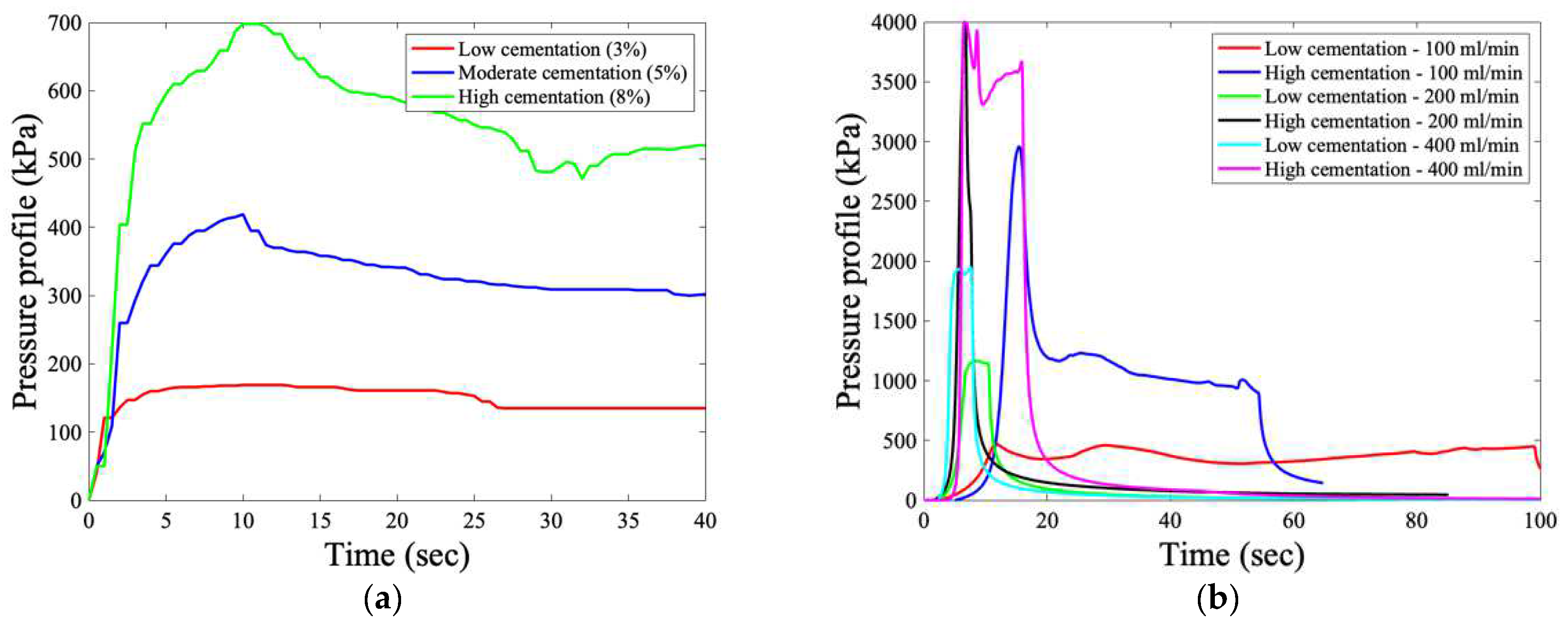
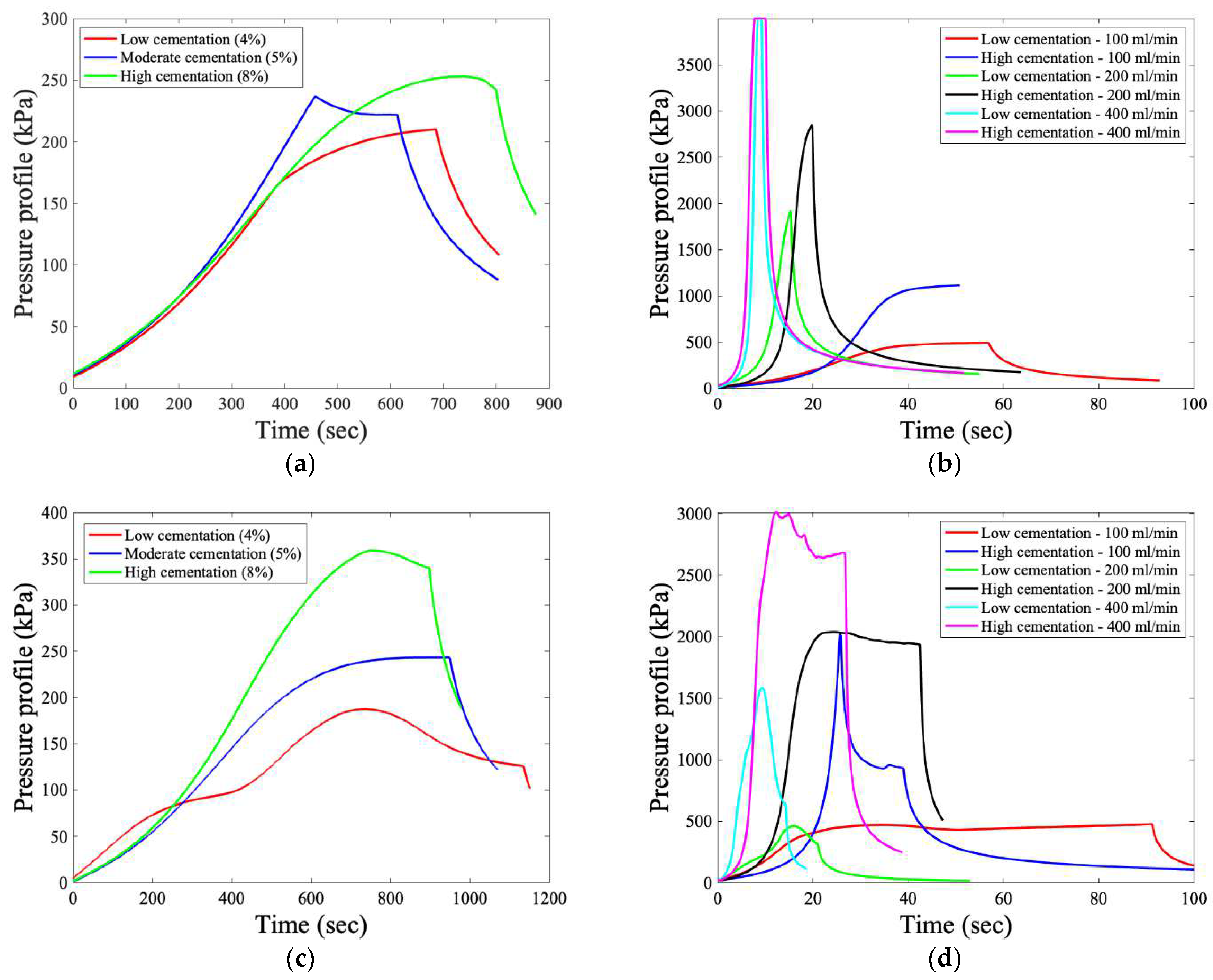
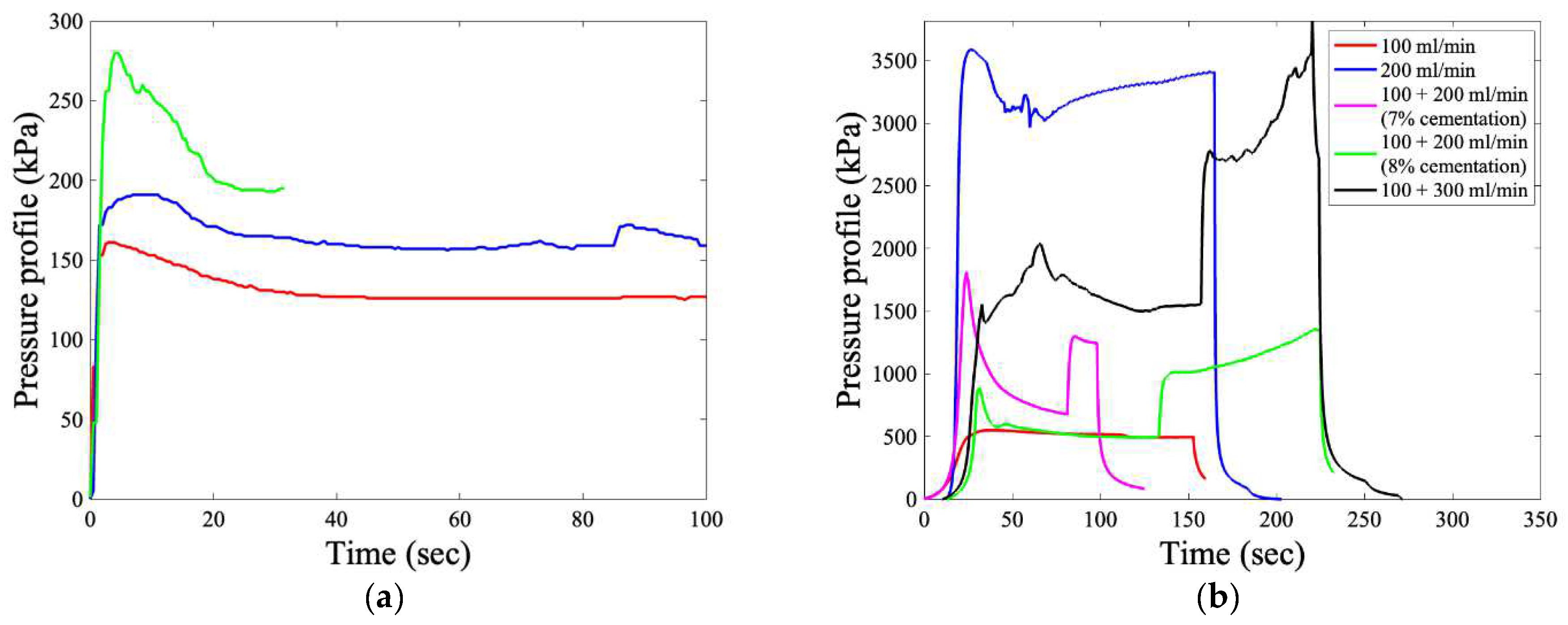
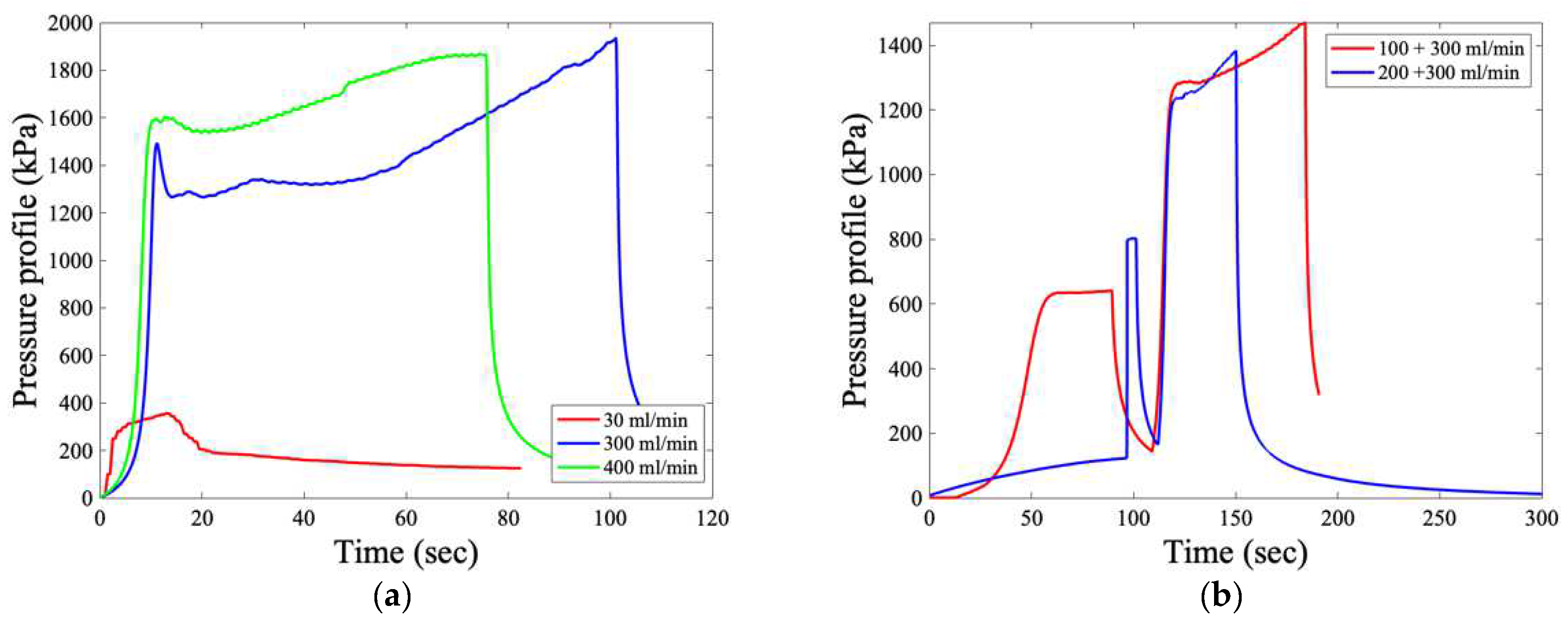
3.2. Fluid Injection Experiments
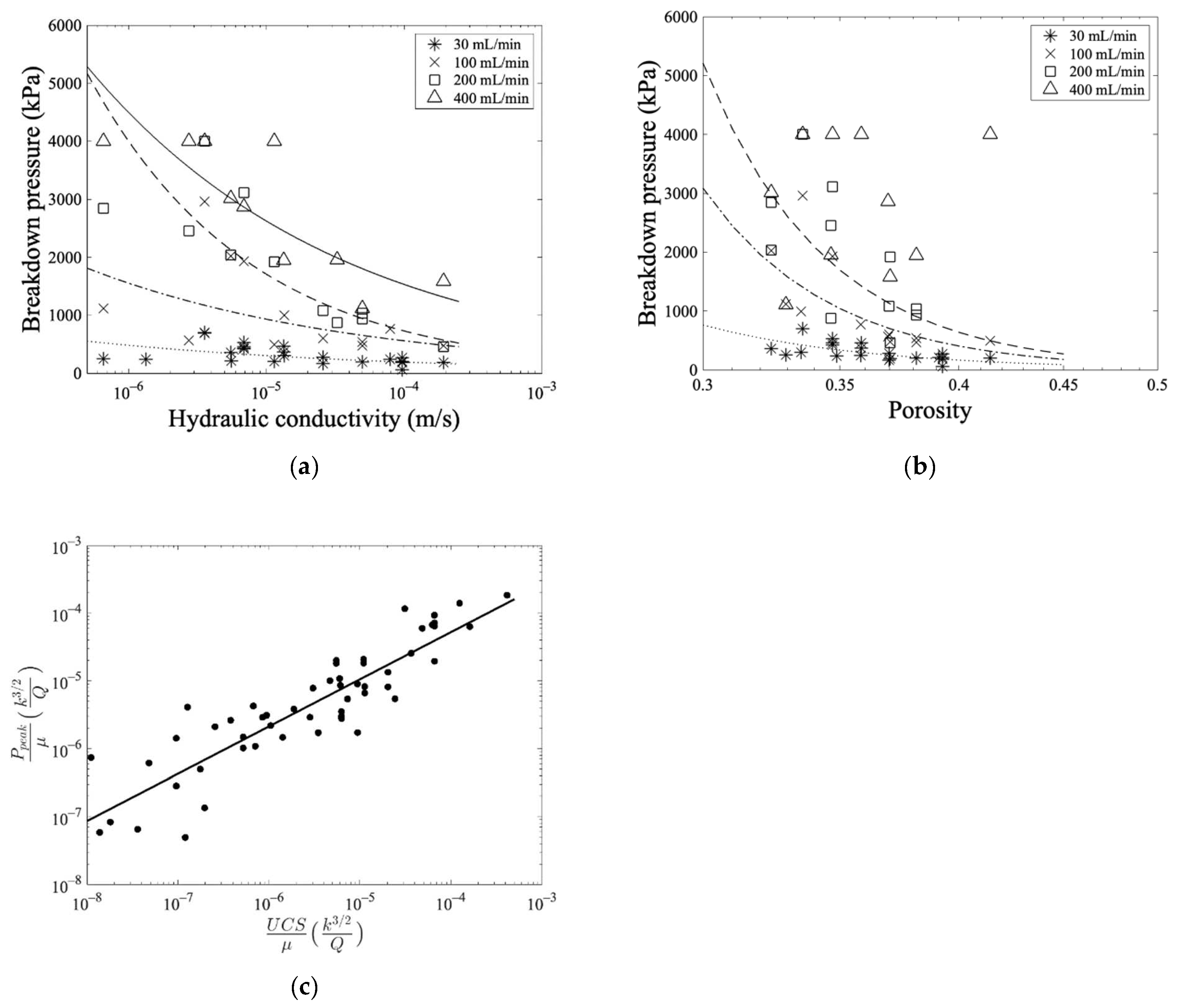
3.3. Correlation of the Peak Pressures with the Engineering Properties
3.4. Analysis of Peak Injection Pressures
3.5. Comparison of the Results Obtained in Weakly Cemented Media against Cohesionless Sands
3.6. Applicabilty of the Findings in the Field of Hydrology
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Gibson, M.T.; Campana, M.E.; Nazy, D. Estimating Aquifer Storage and Recovery (ASR) Regional and Local Suitability: A Case Study in Washington State, USA. Hydrology 2018, 5, 7. [Google Scholar] [CrossRef] [Green Version]
- de Rooij, G. Modeling fingered flow of water in soils owing to wetting front instability: A review. J. Hydrol. 2000, 231-232, 277–294. [Google Scholar] [CrossRef]
- Rezanezhad, F.; Vogel, H.-J.; Roth, K. Experimental study of fingered flow through initially dry sand. Hydrol. Earth Syst. Sci. Discuss 2006, 3, 2595–2620. Available online: www.hydrol-earth-syst-sci-discuss.net/3/2595/2006/ (accessed on 31 August 2022).
- Jerbi, C.; Fourno, A.; Noetinger, B.; Delay, F. A new estimation of equivalent matrix block sizes in fractured media with two-phase flow applications in dual porosity models. J. Hydrol. 2017, 548, 508–523. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wu, J.; Ye, S. Quantification of the fluid saturation of three phases of NAPL/Water/Gas in 2D porous media systems using a light transmission technique. J. Hydrol. 2020, 597, 125718. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Rezaei, N.; Zendehboudi, S.; Heagle, D. Fluid dynamic modeling of multiphase flow in heterogeneous porous media with matrix, fracture, and skin. J. Hydrol. 2019, 583, 124510. [Google Scholar] [CrossRef]
- Kaczmarek, M.; Marciniak, M.; Szczucińska, A. Experimental studies and modelling of the fluidization of sands. J. Hydrol. 2019, 579, 124205. [Google Scholar] [CrossRef]
- Schäfer, G.; Berez, A. Quantification of the hydraulic diffusivity of a bentonite-sand mixture using the water head decrease measured upon sudden flow interruption. Hydrol. Process. 2020, 34, 1934–1948. [Google Scholar] [CrossRef]
- Sharma, H.C.; Chauhan, H.S.; Ram, S. Hydraulics of a Well Pumped with Linearly Decreasing Discharge. J. Hydrol. 1985, 77, 281–291. [Google Scholar] [CrossRef]
- Ray, S. Modeling leakage pathways in subsurface formations: Fluid drainage through multiple fractures in porous media: Insights from Hele Shaw cell experiments. J. Hydrol. 2017, 547, 489–497. [Google Scholar] [CrossRef]
- Gago, P.A.; Raeini, A.Q.; King, P. A spatially resolved fluid-solid interaction model for dense granular packs/soft-sand. Adv. Water Resour. 2019, 136, 103454. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, Y.; Guo, W.; Li, Q. Experimental study of the characteristics of gas-injection barrier in two-dimensional porous media. J. Hydrol. 2020, 593, 125919. [Google Scholar] [CrossRef]
- Li, Z.; Wan, J.; Zhan, H.; Cheng, X.; Chang, W.; Huang, K. Particle size distribution on Forchheimer flow and transition of flow regimes in porous media. J. Hydrol. 2019, 574, 1–11. [Google Scholar] [CrossRef]
- Knorr, B.; Maloszewski, P.; Krämer, F.; Stumpp, C. Diffusive mass exchange of non-reactive substances in dual-porosity porous systems—Column experiments under saturated conditions. Hydrol. Process. 2015, 30, 914–926. [Google Scholar] [CrossRef]
- Wang, Y.; Almutairi, A.L.Z.; Bedrikovetsky, P.; Timms, W.A.; Privat, K.L.; Bhattacharyya, S.K.; Le-Hussain, F. In-situ fines migration and grains redistribution induced by mineral reactions—Implications for clogging during water injection in carbonate aquifers. J. Hydrol. 2022, 614, 128533. [Google Scholar] [CrossRef]
- Qiao, J.; Zeng, J.; Jiang, S.; Yang, G.; Zhang, Y.; Feng, X.; Feng, S. Investigation on the unsteady-state two-phase fluid transport in the nano-pore system of natural tight porous media. J. Hydrol. 2022, 607, 127516. [Google Scholar] [CrossRef]
- Lee, B.H.; Lee, S.K. Probing the water distribution in porous model sands with two immiscible fluids: A nuclear magnetic resonance micro-imaging study. J. Hydrol. 2017, 553, 637–650. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, Y.; Li, Y.; Zhou, X.; Wang, R. Modeling Fractures and Barriers as Interfaces for Porous Flow with Extended Finite-Element Method. J. Hydrol. Eng. 2018, 23, 1614. [Google Scholar] [CrossRef]
- Fang, H.; Zhu, J. New Approach for Simulating Groundwater Flow in Discrete Fracture Network. J. Hydrol. Eng. 2018, 23, 1665. [Google Scholar] [CrossRef]
- Konstantinou, C.; Kandasami, R.K.; Wilkes, C.; Biscontin, G. Fluid Injection Under Differential Confinement. Transp. Porous Media 2021, 139, 627–650. [Google Scholar] [CrossRef]
- Chang, H. Hydraulic Fracturing in Particulate Materials. PhD Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2004. [Google Scholar] [CrossRef]
- Khodaverdian, M.; Mcelfresh, P. Hydraulic Fracturing Stimulation in Poorly Consolidated Sand: Mechanisms and Consequences. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000; pp. 1–13. [Google Scholar]
- Wang, L.; Zheng, L.; Singh, K.; Wang, T.; Liu-Zeng, J.; Xu, S.; Chen, X. The effective pore volume of multiscale heterogenous fracture-porous media systems derived from the residence time of an inert tracer. J. Hydrol. 2022, 610, 127839. [Google Scholar] [CrossRef]
- Zhang, A.; Aral, M.M. Characterization of CO2 Injection into Deep Saline Aquifers Using Two-Phase Darcy-Forchheimer Flow. J. Hydrol. Eng. 2015, 20, 1097. [Google Scholar] [CrossRef]
- Sharma, P.K.; Joshi, N.; Srivastava, R.; Ojha, C.S.P. Reactive Transport in Fractured Permeable Porous Media. J. Hydrol. Eng. 2015, 20, 1096. [Google Scholar] [CrossRef]
- Kumar, G.S.; Sekhar, M. Spatial Moment Analysis for Transport of Nonreactive Solutes in Fracture-Matrix System. J. Hydrol. Eng. 2005, 10, 192–199. [Google Scholar] [CrossRef]
- Konstantinou, C. Hydraulic Fracturing of Artificially Generated Soft Sandstones. PhD Thesis, University of Cambridge, Cambridge, UK, 2021. [Google Scholar] [CrossRef]
- Konstantinou, C.; Biscontin, G.; Jiang, N.-J.; Soga, K. Application of microbially induced carbonate precipitation to form bio-cemented artificial sandstone. J. Rock Mech. Geotech. Eng. 2021, 13, 579–592. [Google Scholar] [CrossRef]
- Liu, Q.; Hu, R.; Hu, L.; Xing, Y.; Qiu, P.; Yang, H.; Fischer, S.; Ptak, T. Investigation of hydraulic properties in fractured aquifers using cross-well travel-time based thermal tracer tomography: Numerical and field experiments. J. Hydrol. 2022, 609, 127751. [Google Scholar] [CrossRef]
- Zhao, H.; Luo, N.; Illman, W.A. The importance of fracture geometry and matrix data on transient hydraulic tomography in fractured rocks: Analyses of synthetic and laboratory rock block experiments. J. Hydrol. 2021, 601, 126700. [Google Scholar] [CrossRef]
- Rubol, S.; Tonina, D.; Vincent, L.; Sohm, J.A.; Basham, W.; Budwig, R.; Savalia, P.; Kanso, E.; Capone, D.G.; Nealson, K.H. Seeing through porous media: An experimental study for unveiling interstitial flows. Hydrol. Process. 2018, 32, 402–407. [Google Scholar] [CrossRef]
- Wang, M.; Kulatilake, P.H.S.W. Understanding of hydraulic properties from configurations of stochastically distributed fracture networks. Hydrol. Process. 2007, 22, 1125–1135. [Google Scholar] [CrossRef]
- Chen, X.; Gosselin, D.C. Numerical simulation of radial gas flow: Effects of soil anisotropy, well placement and surface seal. J. Hydrol. Eng. 1998, 3, 52–61. [Google Scholar] [CrossRef]
- Huang, Y.; Yu, Z.; Zhou, Z. Simulating Groundwater Inflow in the Underground Tunnel with a Coupled Fracture-Matrix Model. J. Hydrol. Eng. 2013, 18, 1557–1561. [Google Scholar] [CrossRef]
- Kumar, G.S. Mathematical Modeling of Groundwater Flow and Solute Transport in Saturated Fractured Rock Using a Dual-Porosity Approach. J. Hydrol. Eng. 2014, 19, 986. [Google Scholar] [CrossRef]
- Lecampion, B.; Bunger, A.; Zhang, X. Numerical methods for hydraulic fracture propagation: A review of recent trends. J. Nat. Gas Sci. Eng. 2017, 49, 66–83. [Google Scholar] [CrossRef] [Green Version]
- Fomin, S.; Hashida, T.; Shimizu, A.; Matsuki, K.; Sakaguchi, K. Fractal concept in numerical simulation of hydraulic fracturing of the hot dry rock geothermal reservoir. Hydrol. Process. 2003, 17, 2975–2989. [Google Scholar] [CrossRef]
- Burbey, T.J.; Brandon, R.A. Characterization of a hydraulically induced crystalline-rock fracture. Hydrol. Process. 2016, 30, 3289–3302. [Google Scholar] [CrossRef]
- Hajjar, A.; Scholtès, L.; Oltéan, C.; Buès, M.A. Effects of the geometry of two-dimensional fractures on their hydraulic aperture and on the validity of the local cubic law. Hydrol. Process. 2018, 32, 2510–2525. [Google Scholar] [CrossRef]
- Papanastasiou, P. The Effective Fracture Toughness in Hydraulic Fracturing. Int. J. Fract. 1999, 96, 258–267. [Google Scholar] [CrossRef]
- Sarris, E.; Papanastasiou, P. The influence of pumping parameters in fluid-driven fractures in weak porous formations. Int. J. Numer Anal. Methods Geomech. 2015, 39, 635–654. [Google Scholar] [CrossRef]
- Papanastasiou, P.; Papamichos, E.; Atkinson, C. On the risk of hydraulic fracturing in CO2 geological storage. Int. J. Numer Anal. Methods Geomech. 2016, 40, 1472–1484. [Google Scholar] [CrossRef]
- Yin, Q.; Ma, G.; Jing, H.; Wang, H.; Su, H.; Wang, Y.; Liu, R. Hydraulic properties of 3D rough-walled fractures during shearing: An experimental study. J. Hydrol. 2017, 555, 169–184. [Google Scholar] [CrossRef]
- Konstantinou, C.; Biscontin, G.; Papanastasiou, P. Interpretation of Fluid Injection Experiments in Poorly Consolidated Sands. In Proceedings of the 56th U.S. Rock Mechanics/Geomechanics Symposium, Santa Fe, New Mexico, USA, 26–29 June 2022. [Google Scholar] [CrossRef]
- Cui, X.; Zheng, Z.; Zhang, H.; Zhang, C.; Li, X.; Zhu, P.; Chen, Z. Impact of water-rock interactions on indicators of hydraulic fracturing flowback fluids produced from the Jurassic shale of Qaidam Basin, NW China. J. Hydrol. 2020, 590, 125541. [Google Scholar] [CrossRef]
- Leven, C.; Sauter, M.; Teutsch, G.; Dietrich, P. Investigation of the effects of fractured porous media on hydraulic tests—An experimental study at laboratory scale using single well methods. J. Hydrol. 2004, 297, 95–108. [Google Scholar] [CrossRef]
- Hurt, R.S.; Wu, R.; Germanovich, L.; Chang, H.; Dyke, P.V. On Mechanics of Hydraulic Fracturing in Cohesionless Materials. In Proceedings of the AGU Fall Meeting, Eos Trans, San Francisco, CA, USA, 3–9 December 2005. [Google Scholar]
- de Pater, C.J.; Dong, Y. Fracture Containment in Soft Sands by Permeability or Strength Contrasts. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 19–21 January 2009; pp. 1–9. [Google Scholar]
- de Pater, C.J.; Dong, Y. Experimental Study of Hydraulic Fracturing in Sand as a Function of Stress and Fluid Rheology. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, College Station, TX, USA, 29–31 January 2007; pp. 1–10. [Google Scholar]
- Khodaverdian, M. Injectivity And Fracturing In Unconsolidated Sand Reservoirs: Waterflooding Case Study, Offshore Nigeria. In Proceedings of the 44th US Rock Mechanics Symposium and 5th U.S.-Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010; pp. 1–12. Available online: http://www.onepetro.org/mslib/servlet/onepetropreview?id=ARMA-10-139 (accessed on 13 September 2022).
- Germanovich, L.N.; Hurt, R.S.; Huang, H. Hydraulic Fracturing in Saturated Cohesionless Materials. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 9–14 December 2007. [Google Scholar]
- Chudnovsky, A.; Fan, J.; Shulkin, Y.; Shlyapobersky, J.; Schraufnagel, R. A New Hydraulic Fracture Tip Mechanism in a Statistically. In Proceedings of the 71st Annual Technical Conference and Exhibition (ATCE) of the Society of Petroleum Engineers, Denver, Colorado, 6–9 October 1996; pp. 1–12. [Google Scholar]
- Cao, C.; Xu, Z.; Chai, J.; Li, Y. Radial fluid flow regime in a single fracture under high hydraulic pressure during shear process. J. Hydrol. 2019, 579, 124142. [Google Scholar] [CrossRef]
- Bohloli, B.; de Pater, C. Experimental study on hydraulic fracturing of soft rocks: Influence of fluid rheology and confining stress. J. Pet. Sci. Eng. 2006, 53, 1–12. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, F.; Callahan, P.; Ayoub, J. Fluid injection experiments in two-dimensional porous media. Soc. Pet. Eng. J. vol. 2012, 17, 903–911. [Google Scholar] [CrossRef]
- Zhou, J.; Dong, Y.; de Pater, C.J.; Zitha, P.L.J. Experimental Study of the Impact of Shear Dilation and Fracture Behavior During Polymer Injection for Heavy Oil Recovery in Unconsolidated Reservoirs. In Proceedings of the Canadian Unconventional Resources & International Petroleum Conference, Calgary, AB, Canada, 19–21 October 2010; pp. 1–12. [Google Scholar]
- Dong, Y. Hydraulic Fracture Containment in Sand; Delft University of Technology: Delft, The Netherlands, 2010. [Google Scholar]
- Lei, G.; Liao, Q.; Patil, S. A new mechanistic model for conductivity of hydraulic fractures with proppants embedment and compaction. J. Hydrol. 2021, 601, 126606. [Google Scholar] [CrossRef]
- Rhett, D.W.; Teufel, L.W. Effect of Reservoir Stress Path on Compressibility and Permeability of Sandstones. In Proceedings of the SPE Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992; pp. 965–972. [Google Scholar] [CrossRef]
- Ren, S.; Gragg, S.; Zhang, Y.; Carr, B.J.; Yao, G. Borehole characterization of hydraulic properties and groundwater flow in a crystalline fractured aquifer of a headwater mountain watershed, Laramie Range, Wyoming. J. Hydrol. 2018, 561, 780–795. [Google Scholar] [CrossRef]
- Konstantinou, C.; Biscontin, G. Soil enhancement via microbially induced calcite precipitation. In Proceedings of the Tenth International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground, IS-Cambridge 2022, Cambridge, UK, 27–29 June 2022; pp. 765–772. [Google Scholar] [CrossRef]
- Konstantinou, C.; Biscontin, G.; Logothetis, F. Tensile Strength of Artificially Cemented Sandstone Generated via Microbially Induced Carbonate Precipitation. Materials 2021, 14, 4735. [Google Scholar] [CrossRef]
- ASTM. Compressive Strength and Elastic Moduli of Intact Rock Core Specimens under Varying States of Stress and Temperatures; ASTM International: West Conshohocken, PA, USA, 2004. [Google Scholar]
- Sharwood, W.J. The specific gravity of mixtures (discussion). Econ. Geol. 1912, 7, 588–590. [Google Scholar] [CrossRef]
- Gago, P.A.; Konstantinou, C.; Biscontin, G.; King, P. Stress inhomogeneity effect on fluid-induced fracture behavior into weakly consolidated granular systems. Phys. Rev. E 2020, 102, 040901. [Google Scholar] [CrossRef]
- Germanovich, L.N.; Hurt, R.; Ayoub, J.; Siebrits, E. Experimental Study of Hydraulic Fracturing in Unconsolidated Materials. In Proceedings of the SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 15–17 February 2012; pp. 1–15. [Google Scholar] [CrossRef]
- Konstantinou, C.; Stoianov, I. A comparative study of statistical and machine learning methods to infer causes of pipe breaks in water supply networks. Urban Water J. 2020, 17, 534–548. [Google Scholar] [CrossRef]
- Luo, J.; Kitanidis, P.K. Fluid residence times within a recirculation zone created by an extraction–injection well pair. J. Hydrol. 2004, 295, 149–162. [Google Scholar] [CrossRef]
- Suk, H.; Chen, J.-S.; Park, E.; Han, W.S.; Kihm, Y.H. Numerical evaluation of the performance of injection/extraction well pair operation strategies with temporally variable injection/pumping rates. J. Hydrol. 2021, 598, 126494. [Google Scholar] [CrossRef]
- Naets, I.; Ahkami, M.; Huang, P.-W.; Saar, M.O.; Kong, X.-Z. Shear induced fluid flow path evolution in rough-wall fractures: A particle image velocimetry examination. J. Hydrol. 2022, 610, 127793. [Google Scholar] [CrossRef]
- Abbasi, M.; Sharifi, M.; Kazemi, A. Fluid flow in fractured reservoirs: Estimation of fracture intensity distribution, capillary diffusion coefficient and shape factor from saturation data. J. Hydrol. 2019, 582, 124461. [Google Scholar] [CrossRef]
- Afzali, S.; Rezaei, N.; Zendehboudi, S.; Chatzis, I. Computational fluid dynamic simulation of multi-phase flow in fractured porous media during water-alternating-gas injection process. J. Hydrol. 2022, 610, 127852. [Google Scholar] [CrossRef]
- Tawara, Y.; Hosono, T.; Fukuoka, Y.; Yoshida, T.; Shimada, J. Quantitative assessment of the changes in regional water flow systems caused by the 2016 Kumamoto Earthquake using numerical modeling. J. Hydrol. 2020, 583, 124559. [Google Scholar] [CrossRef]
- Saha, G.; Quinn, M. Integrated Surface Water and Groundwater Analysis under the Effects of Climate Change, Hydraulic Fracturing and its Associated Activities: A Case Study from Northwestern Alberta, Canada. Hydrology 2020, 7, 70. [Google Scholar] [CrossRef]
- Suk, H.; Park, E. Numerical solution of the Kirchhoff-transformed Richards equation for simulating variably saturated flow in heterogeneous layered porous media. J. Hydrol. 2019, 579, 124213. [Google Scholar] [CrossRef]
- Wu, Y.-S.; Pan, L. Special relative permeability functions with analytical solutions for transient flow into unsaturated rock matrix. Water Resour. Res. 2003, 39, 1495. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Li, Y.; Zhao, G.; Chen, N.; Xu, Y. Experimental Investigation of Flow Characteristics in Porous Media at Low Reynolds Numbers (Re→0) under Different Constant Hydraulic Heads. Water 2019, 11, 2317. [Google Scholar] [CrossRef] [Green Version]
- Nelson, R.; Williams, G. Mathematical Treatment of Saturated Macroscopic Flow in Heterogeneous Porous Medium: Evaluating Darcy’s Law. Hydrology 2019, 7, 4. [Google Scholar] [CrossRef] [Green Version]
- Sabet, N.; Hassanzadeh, H.; Abedi, J. Dynamics of Viscous Fingering in Porous Media in the Presence of In Situ Formed Precipitates and Their Subsequent Deposition. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Q.; Wu, L.; Ritsema, C.; Dekker, L.; Feyen, J. Effects of soil water repellency on infiltration rate and flow instability. J. Hydrol. 2000, 231-232, 265–276. [Google Scholar] [CrossRef]





| Chemical Component | Concentration | |
|---|---|---|
| Bacterial solution (BS) | Yeast extract | 20 g/L |
| Ammonium sulphate | 10 g/L | |
| Tris buffer | 0.13 M | |
| Cementation solution (CS) | Calcium chloride | 0.25 M |
| Urea | 0.375 M | |
| Nutrient broth | 3 g/L |
| Type of Sand | Cementation Level Range | Flow Rate (mL/min) |
|---|---|---|
| Fine sand | 3, 4, 5, 6, 7, 8 | 30 |
| 4, 5, 7, 8 | 100 | |
| 4, 5, 7, 8 | 200 | |
| 4, 6, 7, 8 | 400 | |
| Glass beads | 4, 5, 7, 8 | 30 |
| 4, 6, 8 | 100 | |
| 4, 6, 8 | 200 | |
| 4, 6, 8 | 400 | |
| Medium-grained sand | 4, 5, 7, 8 | 30 |
| 4, 5, 7, 8 | 100 | |
| 4, 6, 8 | 200 | |
| 4, 6, 8 | 400 | |
| Coarse sand | 4, 5, 7, 9 | 30 |
| 7 | 100 | |
| 9 | 200 | |
| 7, 8 | 100 + 200 | |
| 9 | 100 + 300 | |
| Very coarse sand | 8 | 30 |
| 8 | 300 | |
| 5, 8, 10 | 400 | |
| 8 | 100 + 300 | |
| 8 | 200 + 300 |
| Type of Sand | Fit | R-Squared | |
|---|---|---|---|
| UCS = f(Cw) | Fine sand | UCS = 56.911exp(0.4018Cw) | 0.88 |
| Glass beads | UCS = 5.8203exp(0.5835Cw) | 0.98 | |
| Medium-grained sand | UCS = 91.073exp(0.3847Cw) | 0.96 | |
| Coarse sand | UCS = 29.925exp(0.4801Cw) | 0.97 | |
| Very coarse sand | UCS = 56.544exp(0.3568Cw) | 0.90 | |
| UCS = f(n) | Fine sand | UCS = 0.0888n−8.715 | 0.67 |
| Glass beads | UCS = 0.0077n−10.17 | 0.78 | |
| Medium-grained sand | UCS = 0.0045n−11.53 | 0.98 | |
| Coarse sand | UCS = 0.00078n−9.903 | 0.88 | |
| Very coarse sand | UCS = 0.0053n−9.526 | 0.84 | |
| HC = f(Cw) | Fine sand | HC = 0.0006exp(−0.66Cw) | 0.98 |
| Glass beads | HC = 0.0002exp(−0.715Cw) | 0.68 | |
| Medium-grained sand | HC = 0.0067exp(−0.887Cw) | 0.70 | |
| Coarse sand | HC = 0.0308exp(−0.883Cw) | 0.95 | |
| Very coarse sand | HC = 7 × 10−5exp(−0.312Cw) | 0.64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konstantinou, C.; Biscontin, G. Experimental Investigation of the Effects of Porosity, Hydraulic Conductivity, Strength, and Flow Rate on Fluid Flow in Weakly Cemented Bio-Treated Sands. Hydrology 2022, 9, 190. https://doi.org/10.3390/hydrology9110190
Konstantinou C, Biscontin G. Experimental Investigation of the Effects of Porosity, Hydraulic Conductivity, Strength, and Flow Rate on Fluid Flow in Weakly Cemented Bio-Treated Sands. Hydrology. 2022; 9(11):190. https://doi.org/10.3390/hydrology9110190
Chicago/Turabian StyleKonstantinou, Charalampos, and Giovanna Biscontin. 2022. "Experimental Investigation of the Effects of Porosity, Hydraulic Conductivity, Strength, and Flow Rate on Fluid Flow in Weakly Cemented Bio-Treated Sands" Hydrology 9, no. 11: 190. https://doi.org/10.3390/hydrology9110190
APA StyleKonstantinou, C., & Biscontin, G. (2022). Experimental Investigation of the Effects of Porosity, Hydraulic Conductivity, Strength, and Flow Rate on Fluid Flow in Weakly Cemented Bio-Treated Sands. Hydrology, 9(11), 190. https://doi.org/10.3390/hydrology9110190





