The Spatial Scale Dependence of The Hurst Coefficient in Global Annual Precipitation Data, and Its Role in Characterising Regional Precipitation Deficits within a Naturally Changing Climate
Abstract
:1. Introduction
2. Materials and Methods
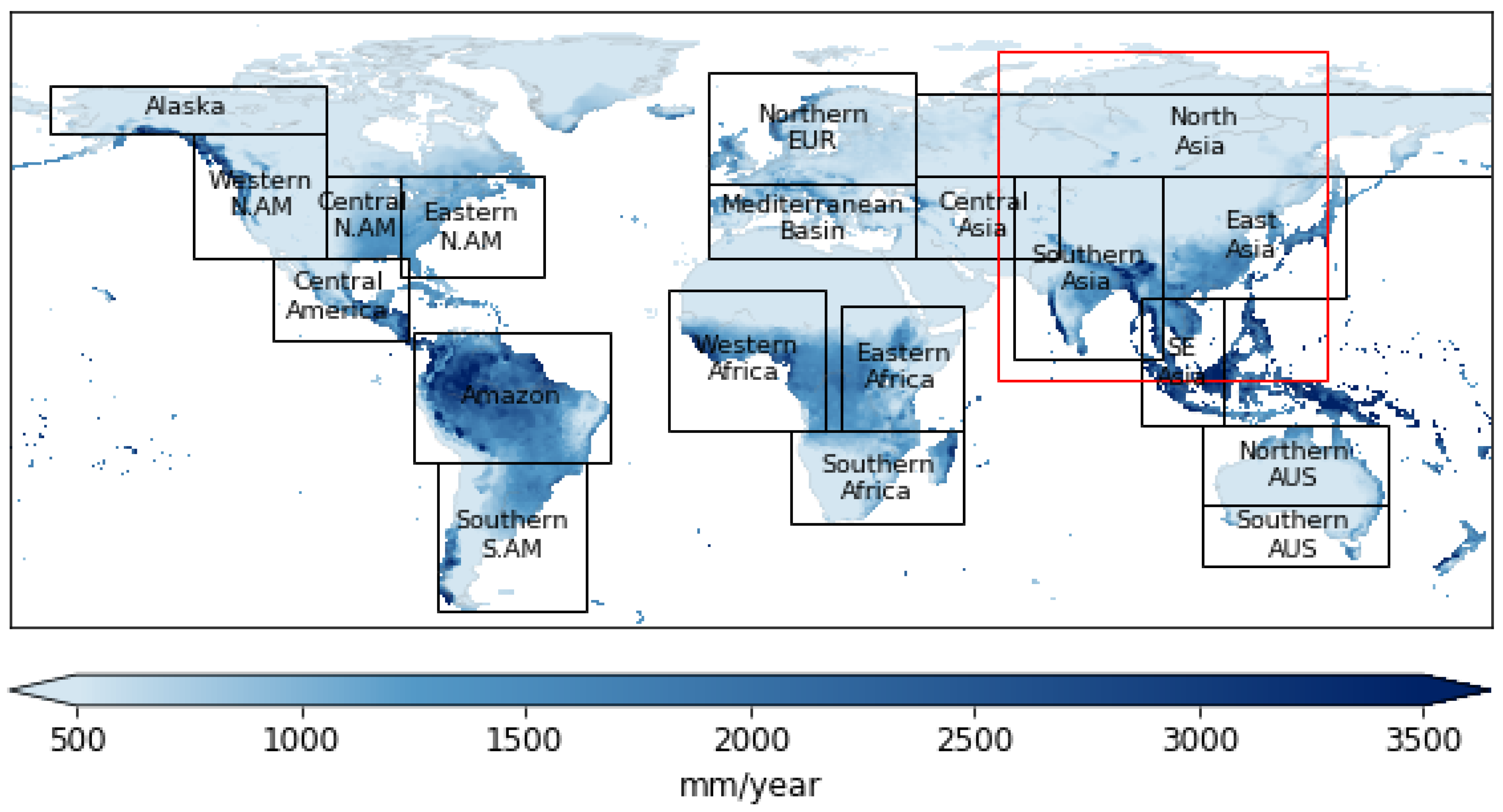
2.1. Data Sets
2.2. Estimation of the Hurst Coefficient H
2.3. Cumulative departure from the mean (CDM) plots
2.4. Spatial Scale Analysis of H for Average Regional Precipitation
2.5. Theoretical Explanation of the Increase in H with the Scale of Averaging
2.5.1. Introduction
2.5.2. Components with Equal Hurst Parameter
2.5.3. Components with Unequal Hurst Parameter
2.5.4. Generalization
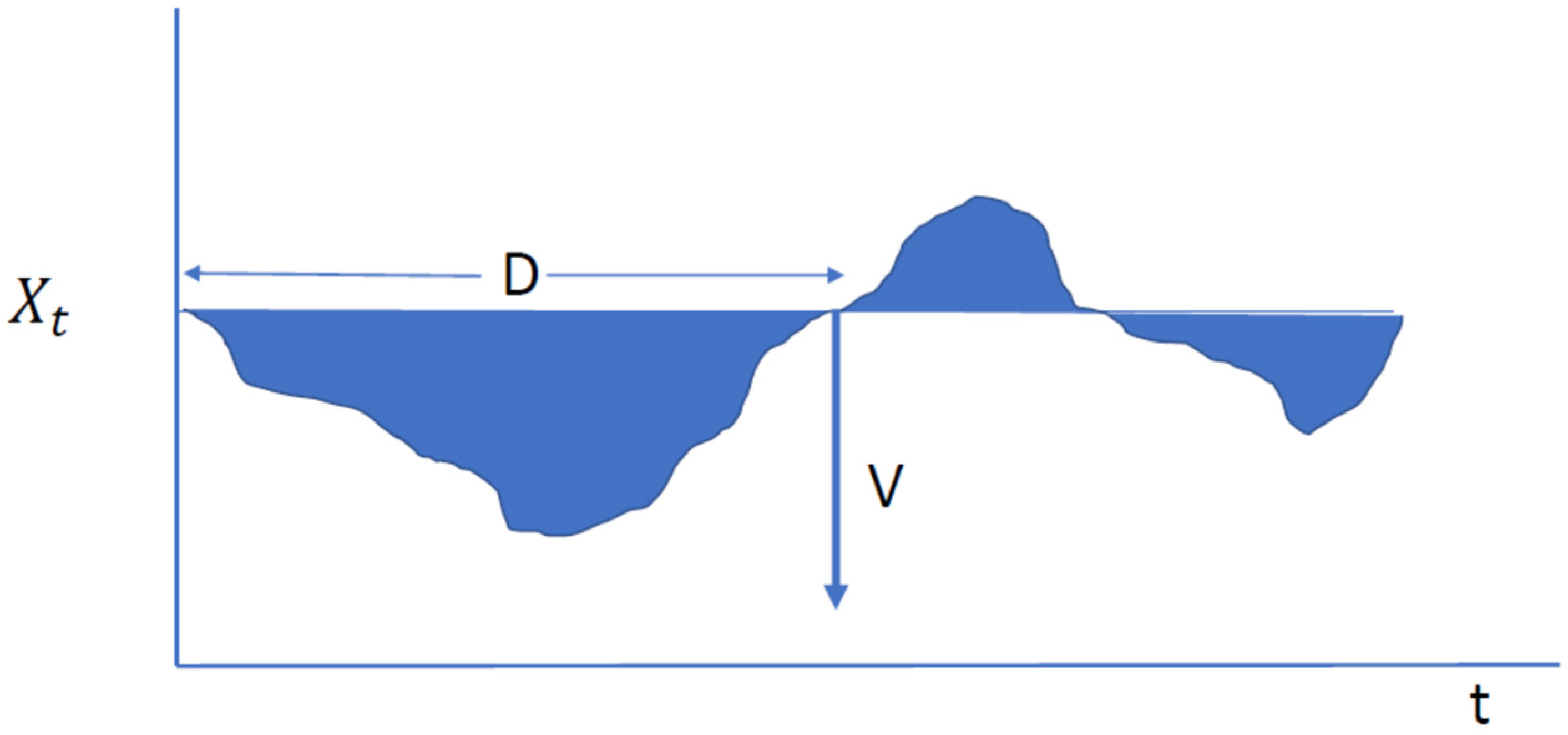
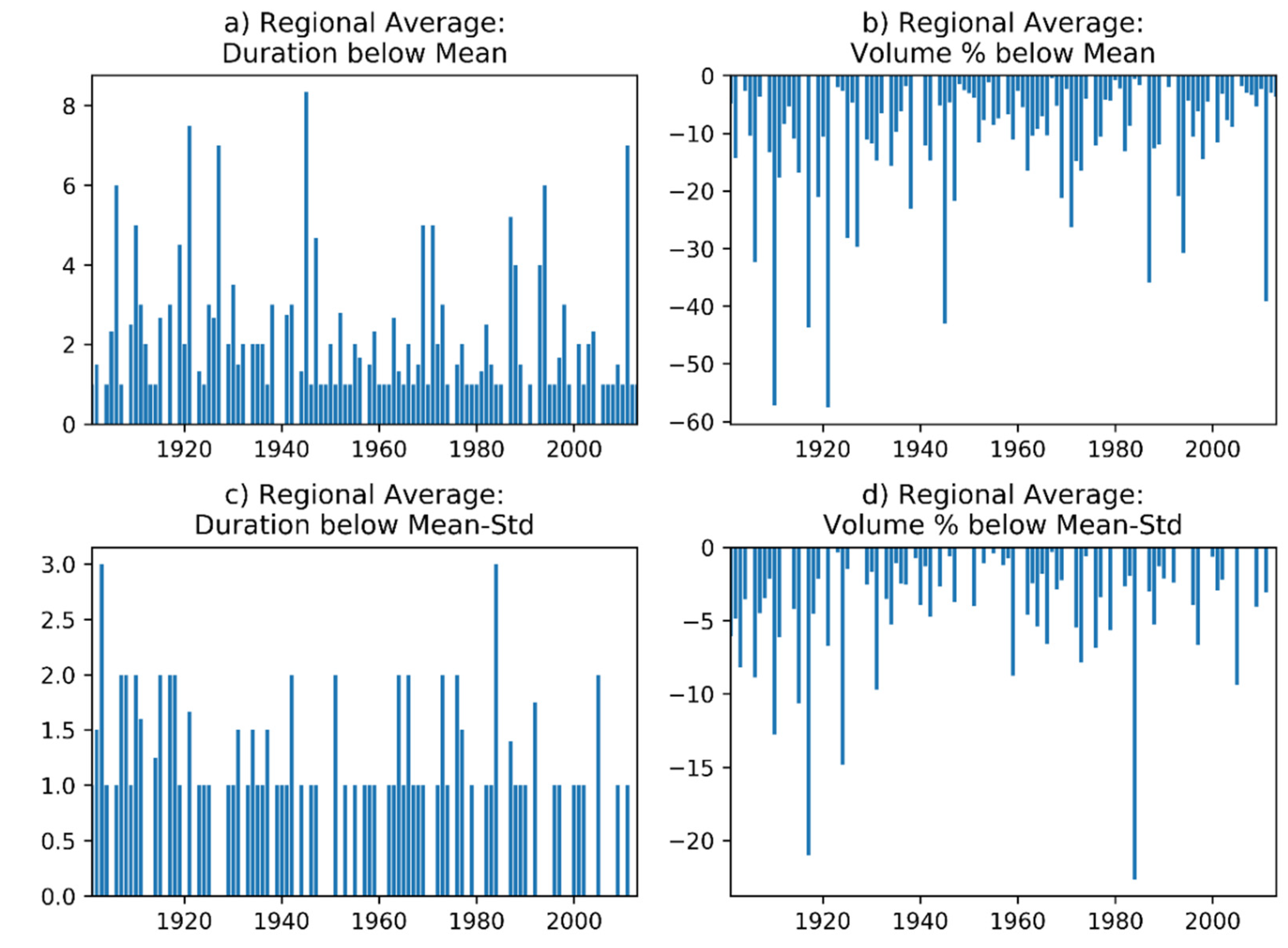
2.6. Crossing Properties of Regional Precipitation Deficits
3. Results
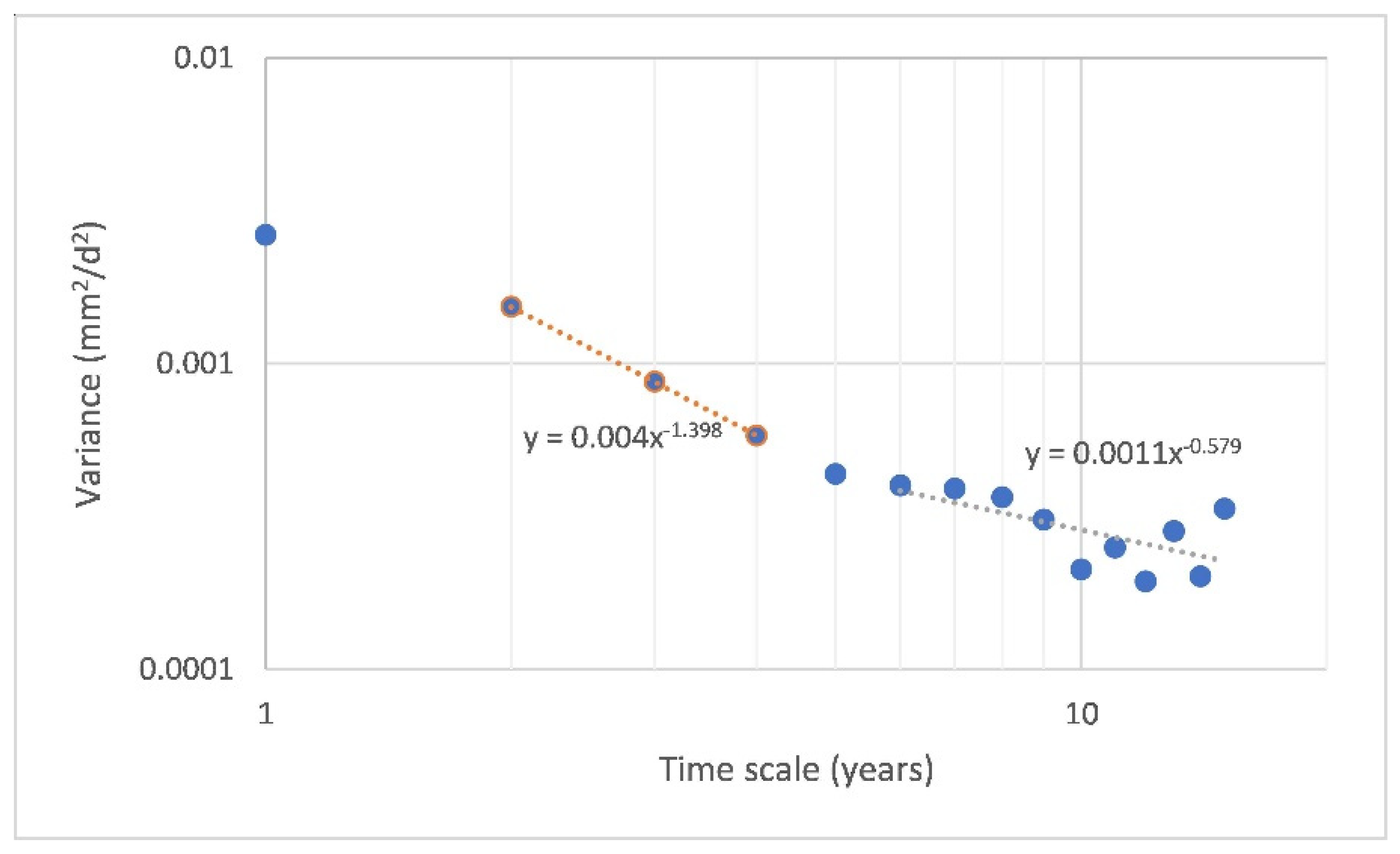
3.1. Monte Carlo Simulation of Theoretical Scale Dependence of H
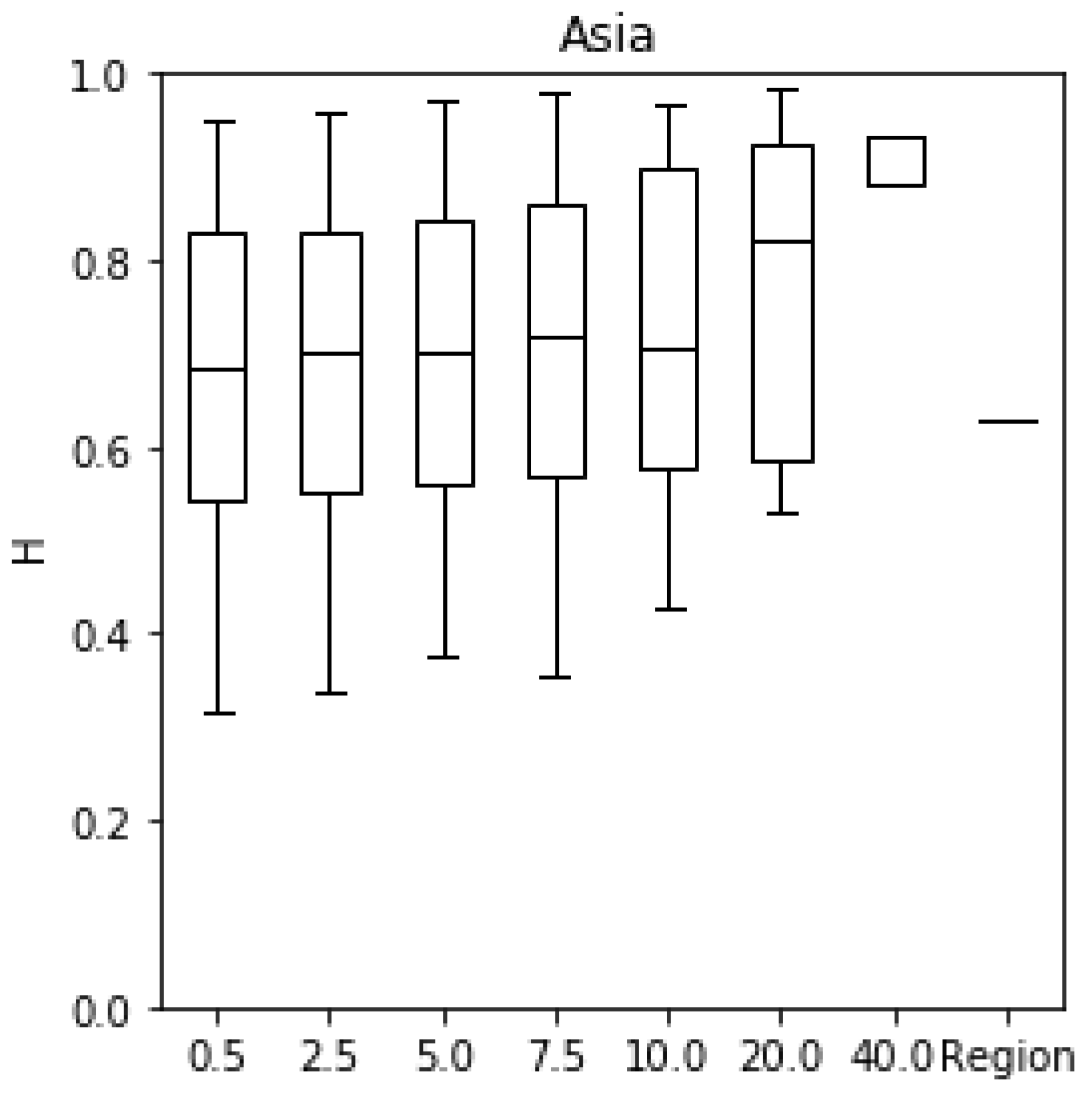
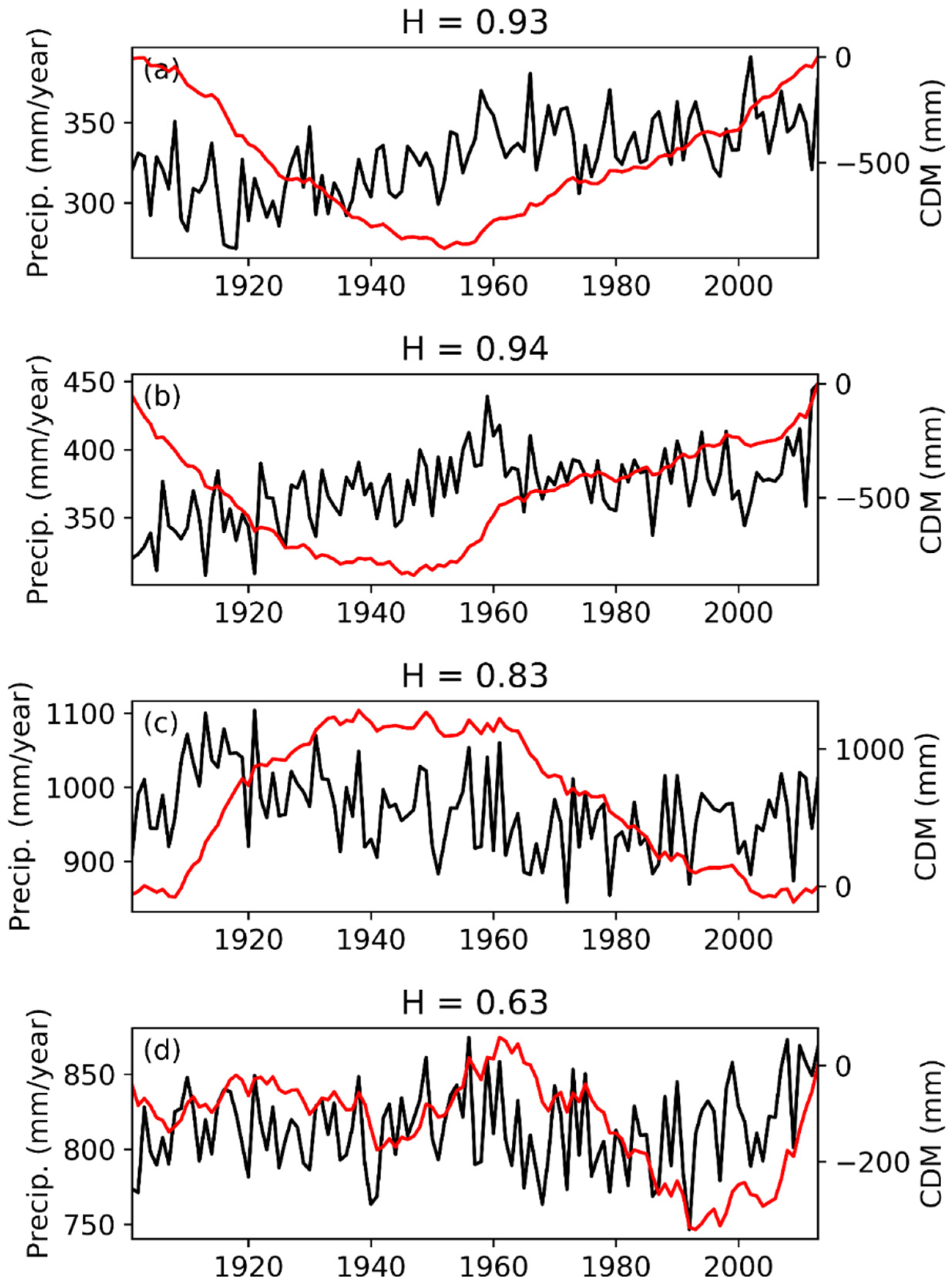
3.2. Spatial Scale Dependence of H for Average Annual Precipitation
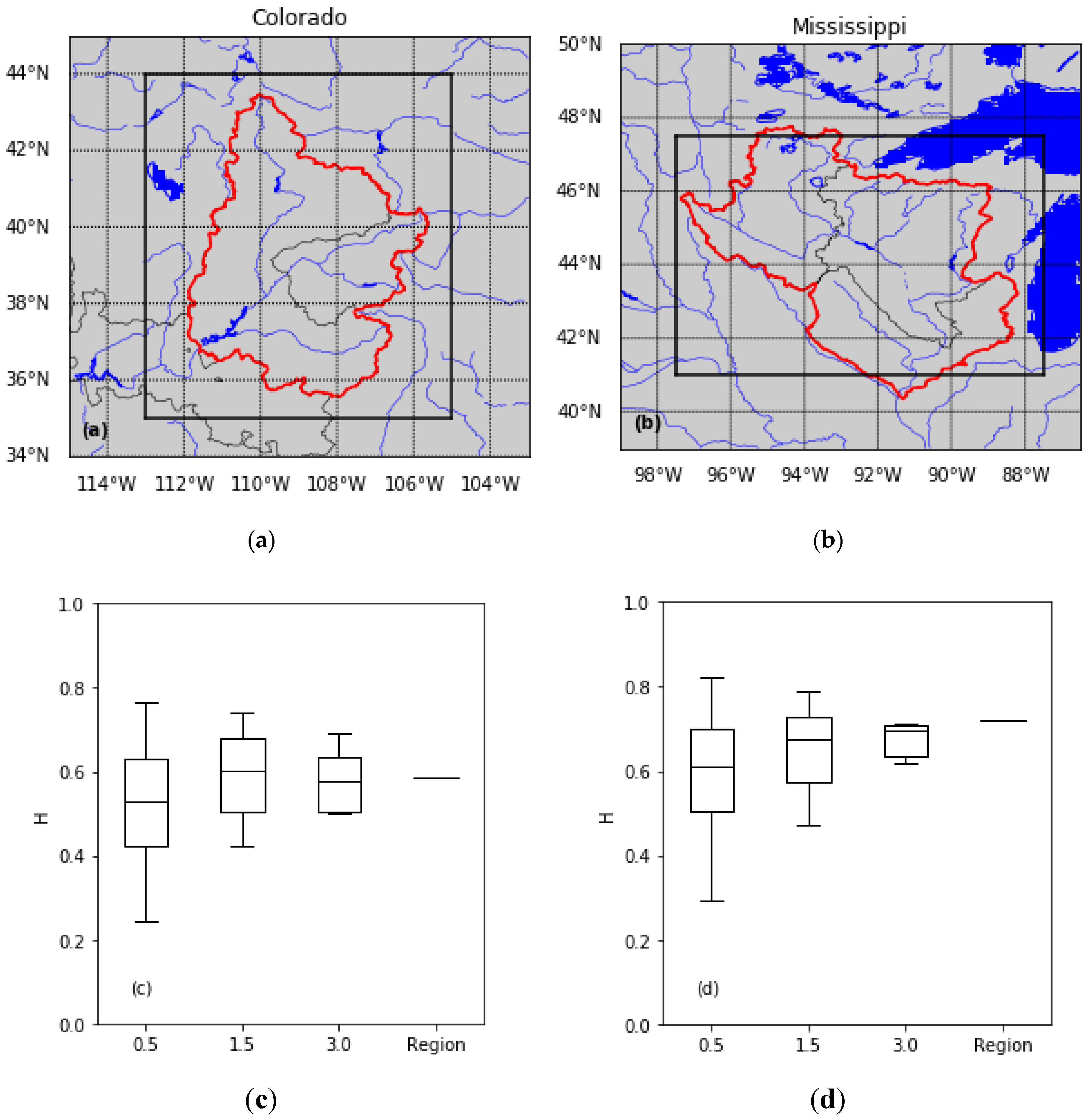
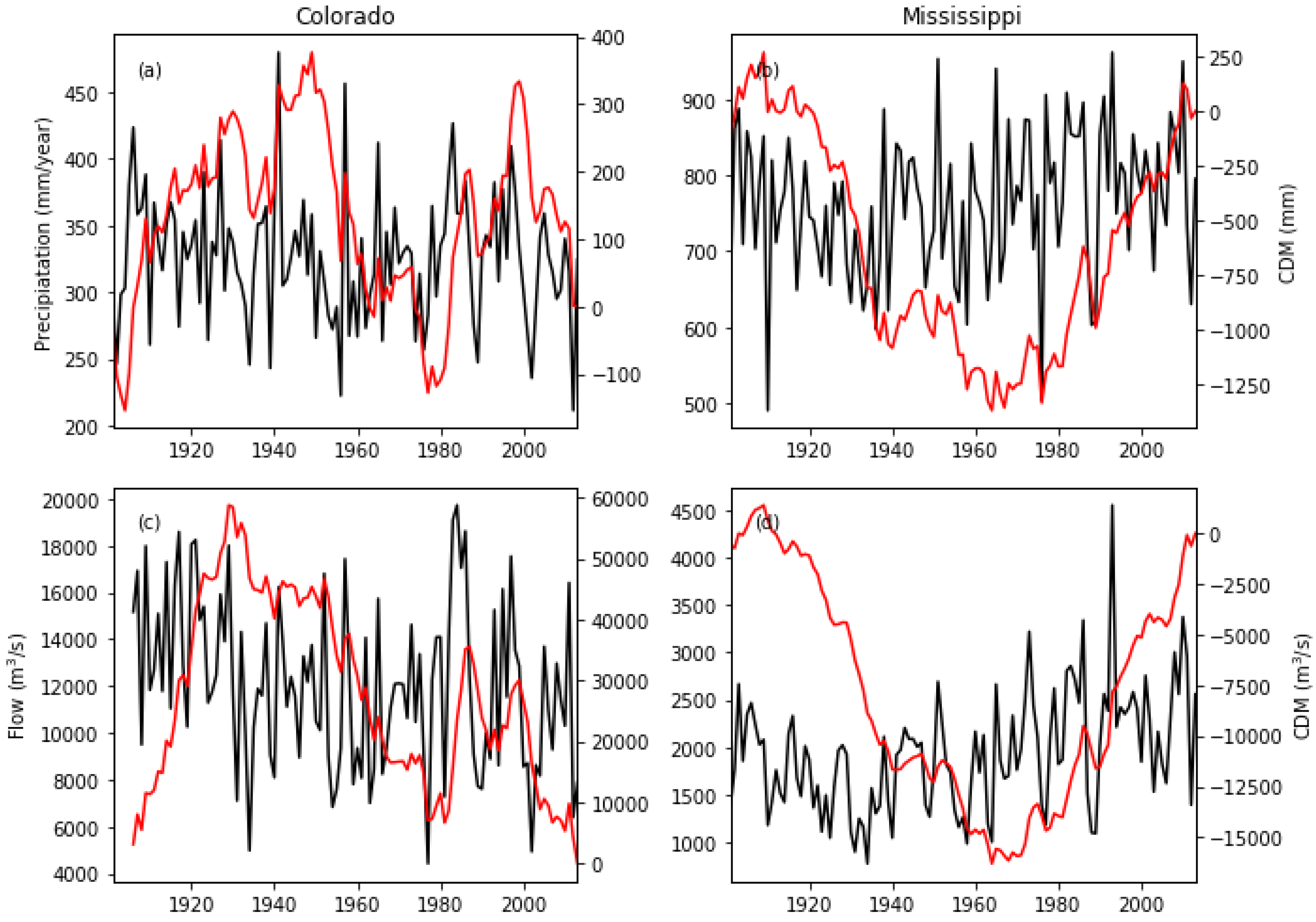
3.3. LTP in Catchment Boundary Box Precipitation and Rivers Flows
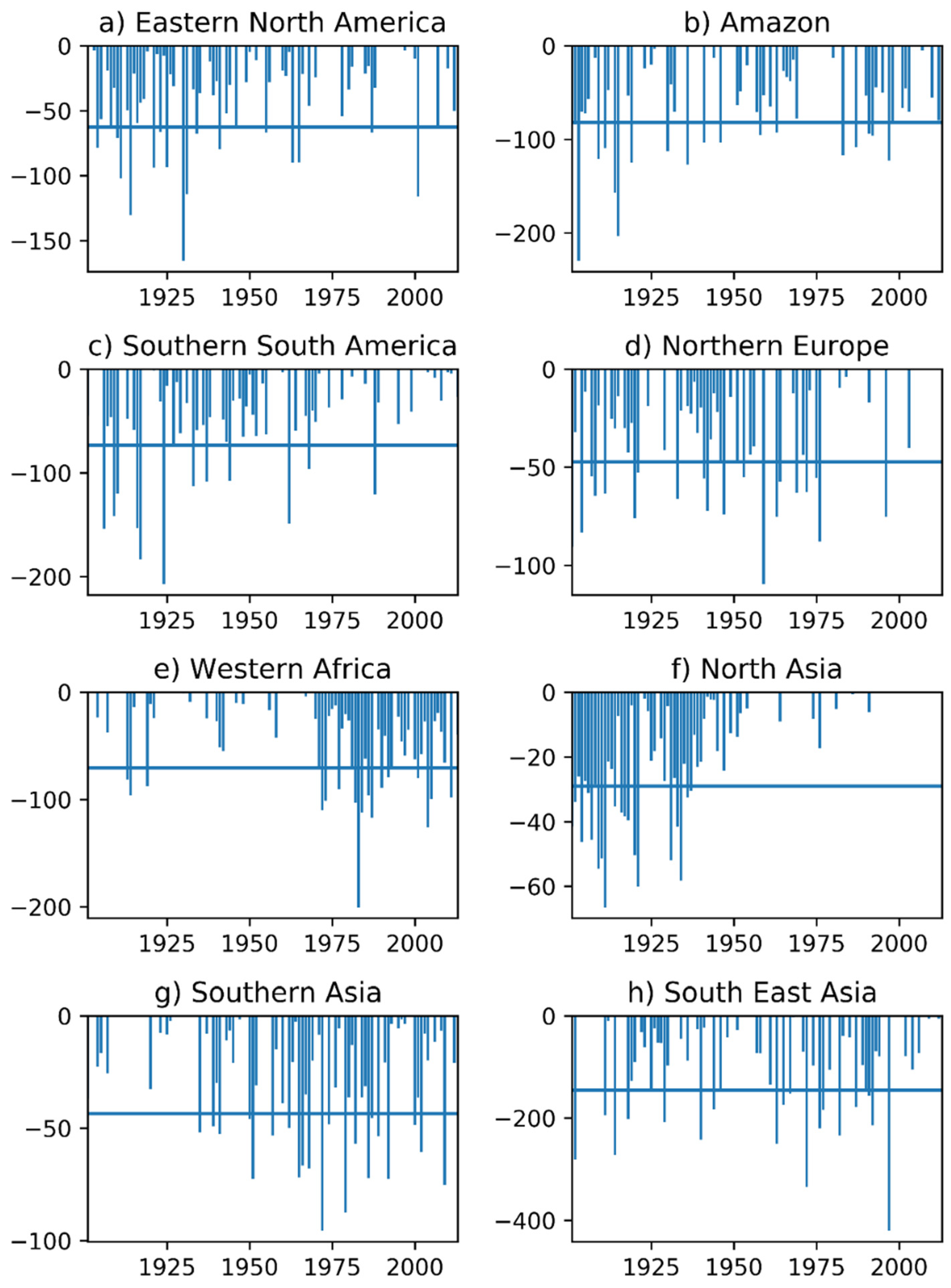
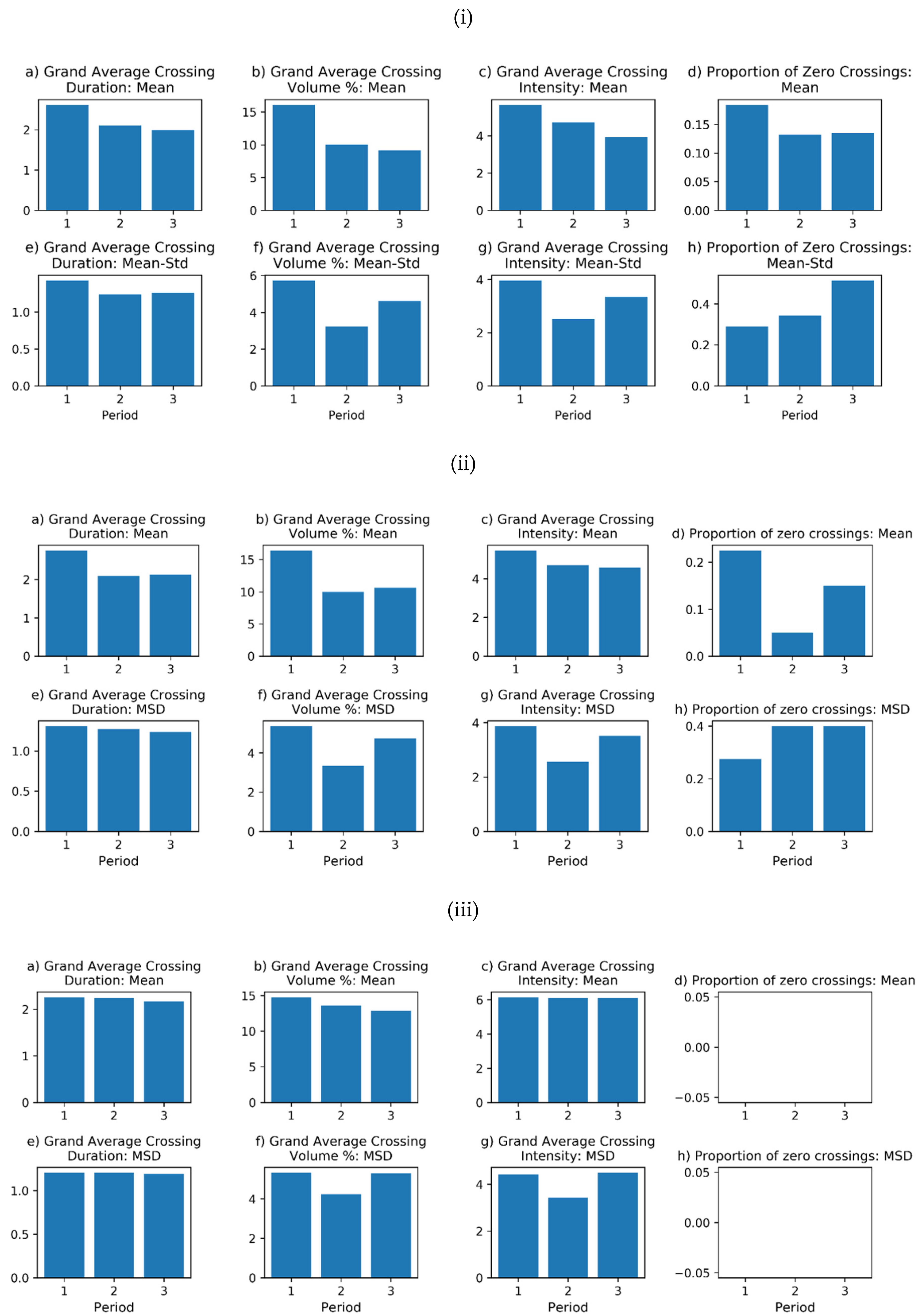
3.4. Analysis of the Crossing Properties of Precipitation Deficits
- Period 1: 1901–1938 (38 years)
- Period 2: 1939–1976 (38 years)
- Period 3: 1977–2013 (37 years)
4. Discussion
4.1. Spatial Scale Dependence of H For Annual Average Precipitation
- Western Russia, with an H of 0.93
- Eastern Russia, with an H of 0.94
- India and the Himalayas, with an H of 0.83.
4.2. Consistency of LTP in Annual Flows with Ltp in Basin Average Precipitation
4.3. Characteristics Of Precipitation Deficits For The Eight Ltp Regions
4.4. Precipitation Deficits, Droughts And Anthropogenic Climate Change
4.5. Implications For Policy Making And Risk Assessment In Sustainable Water Resources Planning And Management
5. Conclusions
- A theoretical result was derived for an HK stochastic process that explains how the Hurst coefficient can increase with the spatial scale of averaging, as observed for regional annual precipitation.
- Analysis of 11 climatic regions that exhibit weak LTP at the grid scale (H < 0.6) showed that five of the regions exhibit an increase in H with the scale of averaging, while the remainder do not.
- For a large region of Asia, an increase in H was observed up to the full regional scale of averaging, but a decrease was observed at the full regional scale, which was shown to be a consequence of contrasting modes of climatic oscillation for the subregions averaged. This result can be viewed as a statistical artefact in relation to theory, which would disappear as the sample size became very large.
- For the Colorado and Mississippi basins, LTP in annual river flows was shown to be attributable to LTP in basin average precipitation.
- For average precipitation at the regional scale, the Hurst coefficient H was shown to be a good descriptor of the crossing properties of precipitation deficits below the mean and the mean minus one standard deviation, both in terms of duration and volume.
- From a multi-decadal analysis of the crossing properties, no evidence was found to show that there has been any increase in precipitation deficits in recent decades that might be attributable to global warming.
- Precipitation deficits are a consequence of natural climatic variability/the level of LTP, so the Hurst coefficient and HK stochastic simulations conditioned on a historic data set should be used to test water resource system resilience and robustness, and not rely exclusively on GCM projections that do not reproduce the LTP in observational records.
- To facilitate the assessment of risk arising from LTP by water resources managers, a package for risk assessment and resilience and robustness testing should be developed and made available on the web in a form that will facilitate uptake.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hurst, H.E. Methods of using long-term storage in reservoirs. Proc. Inst. Civ. Eng. 1956, 5, 519–543. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Engineers 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wallis, J.R. Noah, Joseph, and Operational Hydrology. Water Resour. Res. 1968, 4, 909–918. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B.B.; Wallis, J.R. Computer Experiments With Fractional Gaussian Noises: Part 1, Averages and Variances. Water Resour. Res. 1969, 5, 228–241. [Google Scholar] [CrossRef]
- O’Connell, P.E. Stochastic modelling of long-term persistence in streamflow sequences; Imperial College: London, UK, 1974. [Google Scholar]
- O’Connell, P. A simple stochastic modelling of Hurst’s law. In Proceedings of the International Symposium on Mathematical Models in Hydrology, Warsaw, Poland, 26–31 July 1974; pp. 169–187. [Google Scholar]
- Boes, D.C.; Salas, J.D. Nonstationarity of the mean and the hurst Phenomenon. Water Resour. Res. 1978, 14, 135–143. [Google Scholar] [CrossRef]
- Hosking, J.R.M. Modeling persistence in hydrological time series using fractional differencing. Water Resour. Res. 1984, 20, 1898–1908. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Hurst-Kolmogorov Dynamics and Uncertainty. J. Am. Water Resour. Assoc. 2011, 47, 481–495. [Google Scholar] [CrossRef]
- O’Connell, P.E.; Koutsoyiannis, D.; Lins, H.F.; Markonis, Y.; Montanari, A.; Cohn, T. The scientific legacy of Harold Edwin Hurst (1880–1978). Hydrol. Sci. J. 2016, 61, 1571–1590. [Google Scholar] [CrossRef] [Green Version]
- Markonis, Y.; Koutsoyiannis, D. Climatic Variability Over Time Scales Spanning Nine Orders of Magnitude: Connecting Milankovitch Cycles with Hurst–Kolmogorov Dynamics. Surv. Geophys. 2013, 34, 181–207. [Google Scholar] [CrossRef]
- Iliopoulou, T.; Papalexiou, S.M.; Markonis, Y.; Koutsoyiannis, D. Revisiting long-range dependence in annual precipitation. J. Hydrol. 2018, 556, 891–900. [Google Scholar] [CrossRef]
- Bunde, A.; Büntgen, U.; Ludescher, J.; Luterbacher, J.; von Storch, H. Is there memory in precipitation? Nat. Clim. Change 2013, 3, 174–175. [Google Scholar] [CrossRef]
- Mudelsee, M. Long memory of rivers from spatial aggregation. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Potter, K.W. Annual precipitation in the northeast United States: Long memory, short memory, or no memory? Water Resour. Res. 1979, 15, 340–346. [Google Scholar] [CrossRef]
- O’Connell, E.; O’Donnell, G.; Koutsoyiannis, D. On the spatial scale dependence of long-term persistence in global annual precipitation data and the Hurst Phenomenon. Water Resour. Res. 2022; in review. [Google Scholar]
- Camuffo, D.; Bertolin, C.; Diodato, N.; Cocheo, C.; Barriendos, M.; Dominguez-Castro, F.; Garnier, E.; Alcoforado, M.J.; Nunes, M.F. Western Mediterranean precipitation over the last 300 years from instrumental observations. Clim. Change 2013, 117, 85–101. [Google Scholar] [CrossRef]
- Rowell, D.P.; Booth, B.B.B.; Nicholson, S.E.; Good, P. Reconciling Past and Future Rainfall Trends over East Africa. J. Clim. 2015, 28, 9768–9788. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Seneviratne, S.I. Anthropogenic climate change affects meteorological drought risk in Europe. Environ. Res. Lett. 2016, 11, 044005. [Google Scholar] [CrossRef]
- Cook, B.I.; Seager, R.; Williams, A.P.; Puma, M.J.; McDermid, S.; Kelley, M.; Nazarenko, L. Climate Change Amplification of Natural Drought Variability: The Historic Mid-Twentieth-Century North American Drought in a Warmer World. J. Clim. 2019, 32, 5417–5436. [Google Scholar] [CrossRef]
- Garreaud, R.D.; Boisier, J.P.; Rondanelli, R.; Montecinos, A.; Sepúlveda, H.H.; Veloso-Aguila, D. The Central Chile Mega Drought (2010–2018): A climate dynamics perspective. Int. J. Climatol. 2020, 40, 421–439. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Ziese, M. GPCC Full Data Monthly Product Version 7.0 at 0.5: Monthly Land-Surface Precipitation from Rain-Gauges built on GTS-based and Historic Data. 2015. Available online: https://opendata.dwd.de/climate_environment/GPCC/html/fulldata_v7_doi_download.html (accessed on 2 November 2022).
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, F.; Francisco, R. Uncertainties in regional climate change prediction: A regional analysis of ensemble simulations with the HADCM2 coupled AOGCM. Clim. Dyn. 2000, 16, 169–182. [Google Scholar] [CrossRef]
- Beran, J. Statistics for Long-Memory Processes; Routledge: London, UK, 1994. [Google Scholar]
- Koutsoyiannis, D. HESS Opinions "A random walk on water". Hydrol. Earth Syst. Sci. 2010, 14, 585–601. [Google Scholar] [CrossRef] [Green Version]
- Wuertz, D.; Setz, T.; Chalabi, Y. fArma: Rmetrics—Modelling ARMA Time Series Processes. R package, Version 3042.81. 2017. Available online: http://cran.nexr.com/web/packages/fArma/index.html (accessed on 2 November 2022).
- Tyralis, H.; Koutsoyiannis, D. Simultaneous estimation of the parameters of the Hurst–Kolmogorov stochastic process. Stoch. Environ. Res. Risk Assess. 2011, 25, 21–33. [Google Scholar] [CrossRef]
- Nordin, C.F.; Rosbjerg, D.M. Applications of crossing theory in hydrology. Int. Assoc. Sci. Hydrol. Bull. 1970, 15, 27–43. [Google Scholar] [CrossRef] [Green Version]
- Koutsoyiannis, D. Generic and parsimonious stochastic modelling for hydrology and beyond. Hydrol. Sci. J. 2016, 61, 225–244. [Google Scholar] [CrossRef] [Green Version]
- Milly, P.C.D.; Dunne, K.A. Colorado River flow dwindles as warming-driven loss of reflective snow energizes evaporation. Science 2020, 367, 1252–1255. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Zhang, X.; Adnan, M.; Badi, W.; Dereczynski, C.; Di Luca, A.; Ghosh, S.I.; Iskandar, J.; Kossin, S.; Lewis, F.; et al. Weather and Climate Extreme Events in a Changing Climate. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Section 11.6.1.1; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2021. [Google Scholar]
- Stephens, G.L.; Hakuba, M.Z.; Kato, S.; Gettelman, A.; Dufresne, J.-L.; Andrews, T.; Cole, J.N.S.; Willen, U.; Mauritsen, T. The changing nature of Earth’s reflected sunlight. Proc. R. Soc. A Math. Phys. Eng. Sci. 2022, 478, 20220053. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Revisiting the global hydrological cycle: Is it intensifying? Hydrol. Earth Syst. Sci. 2020, 24, 3899–3932. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Onof, C.; Christofides, A.; Kundzewicz, Z.W. Revisiting causality using stochastics: 1. Theory. Proc. R. Soc. A Math. Phys. Eng. Sci. 2022, 478, 20210835. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Onof, C.; Christofidis, A.; Kundzewicz, Z.W. Revisiting causality using stochastics: 2. Applications. Proc. R. Soc. A Math. Phys. Eng. Sci. 2022, 478, 20210836. [Google Scholar] [CrossRef]
- Johnson, F.; Westra, S.; Sharma, A.; Pitman, A.J. An Assessment of GCM Skill in Simulating Persistence across Multiple Time Scales. J. Clim. 2011, 24, 3609–3623. [Google Scholar] [CrossRef]
- Rocheta, E.; Sugiyanto, M.; Johnson, F.; Evans, J.; Sharma, A. How well do general circulation models represent low-frequency rainfall variability? Water Resour. Res. 2014, 50, 2108–2123. [Google Scholar] [CrossRef]
- Moon, H.; Gudmundsson, L.; Seneviratne, S.I. Drought Persistence Errors in Global Climate Models. J. Geophys. Res: Atmos. 2018, 123, 3483–3496. [Google Scholar] [CrossRef] [PubMed]
- Anagnostopoulos, G.G.; Koutsoyiannis, D.; Christofides, A.; Efstratiadis, A.; Mamassis, N. A comparison of local and aggregated climate model outputs with observed data. Hydrol. Sci. J. 2010, 55, 1094–1110. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Efstratiadis, A.; Mamassis, N.; Christofides, A. On the credibility of climate predictions. Hydrol. Sci. J. 2008, 53, 671–684. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Climate Extrapolations in Hydrology: The Expanded Bluecat Methodology. Hydrology 2022, 9, 86. [Google Scholar] [CrossRef]
- Cohn, T.A.; Lins, H.F. Nature’s style: Naturally trendy. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Clarke, R.T. On the (mis)use of statistical methods in hydro-climatological research. Hydrol. Sci. J. 2010, 55, 139–144. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G.; Lombardo, F. Untenable nonstationarity: An assessment of the fitness for purpose of trend tests in hydrology. Adv. Water Resour. 2018, 111, 132–155. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Climate change, the Hurst phenomenon, and hydrological statistics. Hydrol. Sci. J. 2003, 48, 3–24. [Google Scholar] [CrossRef]
- Merz, B.; Vorogushyn, S.; Uhlemann, S.; Delgado, J.; Hundecha, Y. HESS Opinions "More efforts and scientific rigour are needed to attribute trends in flood time series". Hydrol. Earth Syst. Sci. 2012, 16, 1379–1387. [Google Scholar] [CrossRef]
- Harrigan, S.; Murphy, C.; Hall, J.; Wilby, R.L.; Sweeney, J. Attribution of detected changes in streamflow using multiple working hypotheses. Hydrol. Earth Syst. Sci. 2014, 18, 1935–1952. [Google Scholar] [CrossRef] [Green Version]
- Mallucci, S.; Majone, B.; Bellin, A. Detection and attribution of hydrological changes in a large Alpine river basin. J. Hydrol. 2019, 575, 1214–1229. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Efstratiadis, A.; Georgakakos, K.P. Uncertainty Assessment of Future Hydroclimatic Predictions: A Comparison of Probabilistic and Scenario-Based Approaches. J. Hydrometeorol. 2007, 8, 261–281. [Google Scholar] [CrossRef]
- Kyte, E.A.; Quartly, G.D.; Srokosz, M.A.; Tsimplis, M.N. Interannual variations in precipitation: The effect of the North Atlantic and Southern oscillations as seen in a satellite precipitation data set and in models. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Reggiani, P.; Todini, E.; Boyko, O.; Buizza, R. Assessing uncertainty for decision-making in climate adaptation and risk mitigation. Int. J. Climatol. 2021, 41, 2891–2912. [Google Scholar] [CrossRef]
- O’Connell, E. Towards Adaptation of Water Resource Systems to Climatic and Socio-Economic Change. Water Resour. Manag. 2017, 31, 2965–2984. [Google Scholar] [CrossRef] [Green Version]
- 2030 Water Resources Group. Charting our Water Future; McKinsey and Company: New York, NJ, USA, 2009. Available online: https://www.mckinsey.com›chartingourwaterfuturepdf (accessed on 29 June 2022).
- WRG2030. Available online: https://2030wrg.org/ (accessed on 29 June 2022).
- Brown, C.; Wilby, R.L. An alternate approach to assessing climate risks. EOS Trans. Am. Geophys. Union 2012, 93, 401–402. [Google Scholar] [CrossRef]
- Maass, A.; Hufschmidt, M.M.; Dorfman, R.; Thomas Jr, H.A.; Marglin, S.A.; Fair, G.M. Design of Water-Resource Systems; Harvard University Press: Cambridge, MA, USA, 2013. [Google Scholar]



| Region | H (Grid) | H (Region) |
|---|---|---|
| Alaska | 0.65 | 0.66 |
| Central North America | 0.50 | 0.63 |
| Western North America | 0.56 | 0.68 |
| Central America | 0.59 | 0.63 |
| Mediterranean Basin | 0.60 | 0.65 |
| East Africa | 0.63 | 0.61 |
| Southern Africa | 0.53 | 0.63 |
| Central Asia | 0.62 | 0.58 |
| East Asia | 0.58 | 0.52 |
| Northern Australia | 0.55 | 0.57 |
| Southern Australia | 0.44 | 0.37 |
| Mean | 0.57 | 0.59 |
| Colorado | Mississippi | |||
|---|---|---|---|---|
| P | Q | P | Q | |
| H | 0.59 | 0.69 | 0.72 | 0.84 |
| Region | Dates | D | SV | I | Dates | D | SV | I |
|---|---|---|---|---|---|---|---|---|
| Mean | Mean-StDev | |||||||
| Eastern North America | 1907-11 1913-19 1921-27 | 5 7 7 | 26.5 32.4 29.7 | 5.3 4.6 4.2 | 1910-11 1914 1921 1923 1925 | 2 1 1 1 1 | 4.3 6.1 2.8 0.4 2.8 | 2.2 6.1 2.8 0.4 2.8 |
| Amazon | 1901-06 1965-69 | 6 5 | 32.3 10.4 | 5.4 2.1 | 1901-03 | 3 | 8.2 | 2.7 |
| Southern South America | 1906-10 1947-52 1967-71 | 5 6 5 | 57.2 27.0 26.2 | 11.4 4.5 5.2 | 1906 1909-10 1968 | 1 2 1 | 8.9 12.8 2.5 | 8.9 6.4 2.5 |
| Northern Europe | 1917-21 1936-47 | 5 12 | 32.2 58.9 | 6.4 4.9 | 1920-21 1941-42 1947 | 2 2 1 | 4.8 4.7 3.7 | 2.4 2.4 3.7 |
| Western Africa | 1970-87 1988-93 2000-11 | 18 5 12 | 142.3 34.8 77.5 | 7.9 7.0 6.5 | 1972-73 1977 1982-84 1986-87 1990 1992 2001 2004-05 2011 | 2 1 3 2 1 1 1 2 1 | 7.8 2.2 22.7 8.0 2.1 1.0 1.1 9.4 3.1 | 3.9 2.2 7.6 4.0 2.1 1.0 1.1 4.7 3.1 |
| North Asia | 1901-21 1928-45 | 21 18 | 184.4 95.7 | 8.8 5.3 | 1901-02 1904 1906-7 1909-11 1914 1916-18 1920-21 1931 1933-34 1936-37 | 2 1 2 3 1 3 2 1 2 2 | 4.2 4.1 4.5 20.5 1.5 6.8 12.5 5.5 10.0 1.2 | 2.1 4.1 2.3 6.8 1.5 2.2 6.3 5.5 5.0 0.6 |
| Southern Asia | 1962-69 2000-04 | 8 5 | 42.8 22.2 | 5.4 4.4 | 1962 1965-66 1968 2000 2002 | 1 2 1 1 1 | 0.8 6.6 3.1 6.3 2.2 | 0.8 3.3 3.1 6.3 2.2 |
| Southeast Asia | 1925-30 1989-94 | 6 6 | 23.4 30.7 | 3.9 5.1 | 1925 1929 1990-92 | 1 1 3 | 0.1 2.5 3.4 | 0.1 2.5 1.1 |
| Mean | MSD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Region | Mean | StDev | CV | H | ||||||
| Eastern North America | 1081 | 62.5 | 0.058 | 0.83 | 2.50 | 10.68 | 4.13 | 1.14 | 3.16 | 2.51 |
| Amazon | 1846 | 81.7 | 0.044 | 0.72 | 2.00 | 7.72 | 3.77 | 1.27 | 2.64 | 1.88 |
| Southern South America | 904 | 73.4 | 0.081 | 0.78 | 1.97 | 12.44 | 5.29 | 1.20 | 8.56 | 6.87 |
| Northern Europe | 711 | 47.3 | 0.066 | 0.81 | 2.17 | 12.94 | 6.18 | 1.33 | 4.21 | 3.37 |
| Western Africa | 903 | 70.3 | 0.078 | 0.91 | 3.28 | 19.25 | 3.71 | 1.55 | 5.76 | 3.05 |
| North Asia | 417 | 29 | 0.069 | 0.99 | 4.23 | 24.42 | 3.16 | 1.90 | 7.08 | 3.64 |
| Southern Asia | 781 | 43.5 | 0.056 | 0.85 | 2.22 | 9.44 | 3.90 | 1.17 | 2.73 | 2.32 |
| Southeast Asia | 2486 | 144.9 | 0.058 | 0.78 | 1.77 | 8.44 | 5.12 | 1.17 | 3.35 | 3.10 |
| (i) For the 8 LTP regions and the 1900–2013 data set. | ||||
| Period | Average Crossing Duration Mean | Average Crossing Volume % Mean | Average Crossing Intensity Mean | Proportion Zero Crossing Mean |
| 1 | 2.613 | 16.081 | 5.663 | 0.184 |
| 2 | 2.103 | 10.029 | 4.734 | 0.132 |
| 3 | 1.985 | 9.159 | 3.941 | 0.135 |
| Period | Average Crossing Duration MSD | Average Crossing Volume % MSD | Average Crossing Intensity MSD | Proportion Zero Crossing MSD |
| 1 | 1.427 | 5.739 | 3.969 | 0.289 |
| 2 | 1.240 | 3.231 | 2.524 | 0.342 |
| 3 | 1.258 | 4.618 | 3.347 | 0.514 |
| (ii) For the 8 LTP regions and the extended 1900–2020 data set | ||||
| Period | Average Crossing Duration Mean | Average Crossing Volume % Mean | Average Crossing Intensity Mean | Proportion Zero Crossing Mean |
| 1 | 2.753 | 16.414 | 5.443 | 0.225 |
| 2 | 2.098 | 10.001 | 4.688 | 0.050 |
| 3 | 2.127 | 10.638 | 4.559 | 0.150 |
| Period | Average Crossing Duration MSD | Average Crossing Volume % MSD | Average Crossing Intensity MSD | Proportion Zero Crossing MSD |
| 1 | 1.311 | 5.365 | 3.877 | 0.275 |
| 2 | 1.271 | 3.344 | 2.569 | 0.400 |
| 3 | 1.240 | 4.732 | 3.520 | 0.400 |
| (iii) For all 19 regions and the extended 1900–2020 data set. | ||||
| Period | Average Crossing Duration Mean | Average Crossing Volume % Mean | Average Crossing Intensity Mean | Proportion Zero Crossing Mean |
| 1 | 2.257 | 14.770 | 6.147 | 0 |
| 2 | 2.239 | 13.622 | 6.111 | 0 |
| 3 | 2.165 | 12.844 | 6.108 | 0 |
| Period | Average Crossing Duration MSD | Average Crossing Volume % MSD | Average Crossing Intensity MSD | Proportion Zero Crossing MSD |
| 1 | 1.207 | 5.332 | 4.420 | 0 |
| 2 | 1.207 | 4.230 | 3.428 | 0 |
| 3 | 1.192 | 5.307 | 4.492 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
O’Connell, E.; O’Donnell, G.; Koutsoyiannis, D. The Spatial Scale Dependence of The Hurst Coefficient in Global Annual Precipitation Data, and Its Role in Characterising Regional Precipitation Deficits within a Naturally Changing Climate. Hydrology 2022, 9, 199. https://doi.org/10.3390/hydrology9110199
O’Connell E, O’Donnell G, Koutsoyiannis D. The Spatial Scale Dependence of The Hurst Coefficient in Global Annual Precipitation Data, and Its Role in Characterising Regional Precipitation Deficits within a Naturally Changing Climate. Hydrology. 2022; 9(11):199. https://doi.org/10.3390/hydrology9110199
Chicago/Turabian StyleO’Connell, Enda, Greg O’Donnell, and Demetris Koutsoyiannis. 2022. "The Spatial Scale Dependence of The Hurst Coefficient in Global Annual Precipitation Data, and Its Role in Characterising Regional Precipitation Deficits within a Naturally Changing Climate" Hydrology 9, no. 11: 199. https://doi.org/10.3390/hydrology9110199
APA StyleO’Connell, E., O’Donnell, G., & Koutsoyiannis, D. (2022). The Spatial Scale Dependence of The Hurst Coefficient in Global Annual Precipitation Data, and Its Role in Characterising Regional Precipitation Deficits within a Naturally Changing Climate. Hydrology, 9(11), 199. https://doi.org/10.3390/hydrology9110199









