Daily Streamflow Forecasting in Mountainous Catchment Using XGBoost, LightGBM and CatBoost
Abstract
1. Introduction
1.1. Streamflow Forecasting
1.2. Data-Driven Models
1.3. Aim of the Present Study
2. Materials and Methods
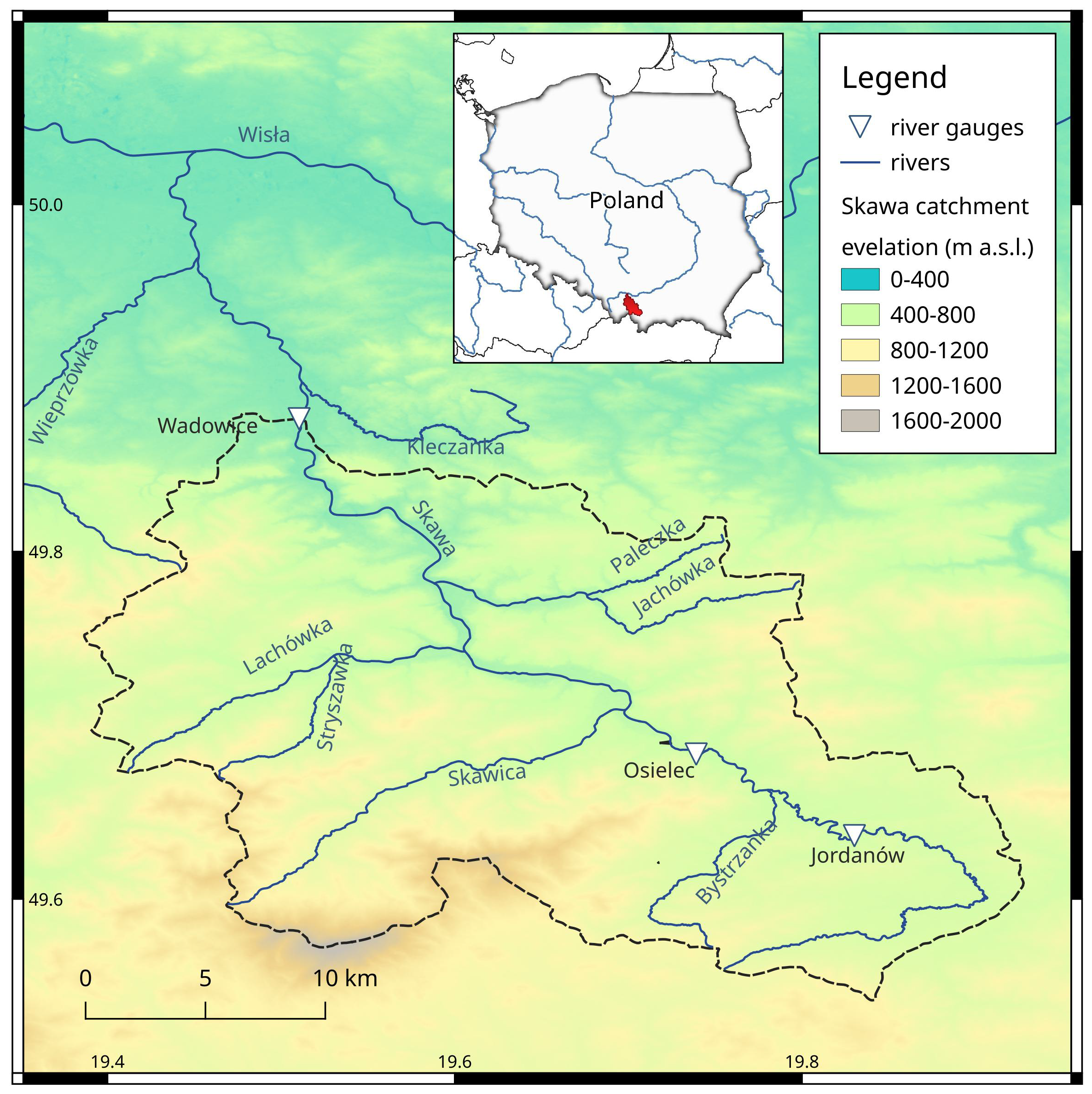
2.1. Study Area
2.2. Data
2.3. Baseline Models
2.3.1. Multiple Linear Regression (MLR)
2.3.2. Random Forest (RF)
2.4. Boosting Models
2.4.1. Extreme Gradient Boosting (XGBoost)
2.4.2. Light Gradient Boosting Machine (LGBoost)
2.4.3. Categorical Boosting (CatBoost)
2.5. Models Implementation
2.6. Evaluation Metrics
3. Results
4. Discussion
5. Conclusions
- 1.
- The gradient boosting algorithms used in models such as XGBoost, LightGBM and CatBoost are simple to implement, fast and robust. Compared to deep machine learning models (eg LSTM), they allow for easy interpretation of the significance of predictors.
- 2.
- The gradient boosting algorithms provide a good streamflow prediction in mountainous rivers. All tested models achieved Nash-Sutcliffe model efficiency (NSE) in the range of 0.85–0.89 and RMSE in the range of 6.8–7.8 ms.
- 3.
- In order to obtain an NSE above 0.8, the recommended period of training data should be not less than 12 years.
- 4.
- The XGBoost did not turn out to be the best model for the daily flow forecast, although it is the most used model. Assuming the use of models with their default parameters, the best results were obtained with CatBoost. By optimizing the hyperparameters, the best forecast results were obtained by LightGBM.
- 5.
- The differences between the model results are much smaller than the differences within the models themselves when suboptimal hyperparameters are used.
- 6.
- The predictions of the lowest streamflows are overestimated by all analyzed models.
Funding
Data Availability Statement
Conflicts of Interest
References
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef] [PubMed]
- Laimighofer, J.; Melcher, M.; Laaha, G. Low flow estimation beyond the mean–expectile loss and extreme gradient boosting for spatio-temporal low flow prediction in Austria. Hydrol. Earth Syst. Sci. Discuss. 2022, 26, 4553–4574. [Google Scholar] [CrossRef]
- Agana, N.A.; Homaifar, A. EMD-based predictive deep belief network for time series prediction: An application to drought forecasting. Hydrology 2018, 5, 18. [Google Scholar] [CrossRef]
- Sivapragasam, C.; Liong, S.Y. Flow categorization model for improving forecasting. Hydrol. Res. 2005, 36, 37–48. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Heddam, S.; Zounemat-Kermani, M.; Kisi, O.; Li, B. Least square support vector machine and multivariate adaptive regression splines for streamflow prediction in mountainous basin using hydro-meteorological data as inputs. J. Hydrol. 2020, 586, 124371. [Google Scholar] [CrossRef]
- Stoffel, M.; Wyżga, B.; Marston, R.A. Floods in mountain environments: A synthesis. Geomorphology 2016, 272, 1–9. [Google Scholar] [CrossRef]
- Abdul Kareem, B.; Zubaidi, S.L.; Ridha, H.M.; Al-Ansari, N.; Al-Bdairi, N.S.S. Applicability of ANN Model and CPSOCGSA Algorithm for Multi-Time Step Ahead River Streamflow Forecasting. Hydrology 2022, 9, 171. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Gauch, M.; Mai, J.; Gharari, S.; Lin, J. Data-driven vs. physically-based streamflow prediction models. In Proceedings of the 9th International Workshop on Climate Informatics, Paris, France, 2–4 October 2019. [Google Scholar]
- Xu, W.; Jiang, Y.; Zhang, X.; Li, Y.; Zhang, R.; Fu, G. Using long short-term memory networks for river flow prediction. Hydrol. Res. 2020, 51, 1358–1376. [Google Scholar] [CrossRef]
- Zealand, C.M.; Burn, D.H.; Simonovic, S.P. Short term streamflow forecasting using artificial neural networks. J. Hydrol. 1999, 214, 32–48. [Google Scholar] [CrossRef]
- Fleming, S.W.; Vesselinov, V.V.; Goodbody, A.G. Augmenting geophysical interpretation of data-driven operational water supply forecast modeling for a western US river using a hybrid machine learning approach. J. Hydrol. 2021, 597, 126327. [Google Scholar] [CrossRef]
- Başağaoğlu, H.; Chakraborty, D.; Lago, C.D.; Gutierrez, L.; Şahinli, M.A.; Giacomoni, M.; Furl, C.; Mirchi, A.; Moriasi, D.; Şengör, S.S. A Review on Interpretable and Explainable Artificial Intelligence in Hydroclimatic Applications. Water 2022, 14, 1230. [Google Scholar] [CrossRef]
- Jose, D.M.; Vincent, A.M.; Dwarakish, G.S. Improving multiple model ensemble predictions of daily precipitation and temperature through machine learning techniques. Sci. Rep. 2022, 12, 4678. [Google Scholar] [CrossRef]
- Cai, Y.; Zheng, W.; Zhang, X.; Zhangzhong, L.; Xue, X. Research on soil moisture prediction model based on deep learning. PLoS ONE 2019, 14, e0214508. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Batelaan, O.; Fadaee, M.; Hinkelmann, R. Ensemble machine learning paradigms in hydrology: A review. J. Hydrol. 2021, 598, 126266. [Google Scholar] [CrossRef]
- Choi, J.; Won, J.; Jang, S.; Kim, S. Learning Enhancement Method of Long Short-Term Memory Network and Its Applicability in Hydrological Time Series Prediction. Water 2022, 14, 2910. [Google Scholar] [CrossRef]
- Afshari, M. Using LSTM and XGBoost for Streamflow Prediction Based on Meteorological Time Series Data. Master’s Thesis, Utrecht University, Utrecht, The Netherlands, 2022. [Google Scholar]
- Liu, J.; Ren, K.; Ming, T.; Qu, J.; Guo, W.; Li, H. Investigating the effects of local weather, streamflow lag, and global climate information on 1-month-ahead streamflow forecasting by using XGBoost and SHAP: Two case studies involving the contiguous USA. Acta Geophys. 2022, 1–21. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Choubin, B.; Khalighi-Sigaroodi, S.; Malekian, A.; Kişi, Ö. Multiple linear regression, multi-layer perceptron network and adaptive neuro-fuzzy inference system for forecasting precipitation based on large-scale climate signals. Hydrol. Sci. J. 2016, 61, 1001–1009. [Google Scholar] [CrossRef]
- Abed, M.; Imteaz, M.A.; Ahmed, A.N.; Huang, Y.F. Modelling monthly pan evaporation utilising Random Forest and deep learning algorithms. Sci. Rep. 2022, 12, 13132. [Google Scholar] [CrossRef]
- Papacharalampous, G.A.; Tyralis, H. Evaluation of random forests and Prophet for daily streamflow forecasting. Adv. Geosci. 2018, 45, 201–208. [Google Scholar] [CrossRef]
- Bhusal, A.; Parajuli, U.; Regmi, S.; Kalra, A. Application of Machine Learning and Process-Based Models for Rainfall-Runoff Simulation in DuPage River Basin, Illinois. Hydrology 2022, 9, 117. [Google Scholar] [CrossRef]
- Graf, R.; Kolerski, T.; Zhu, S. Predicting Ice Phenomena in a River Using the Artificial Neural Network and Extreme Gradient Boosting. Resources 2022, 11, 12. [Google Scholar] [CrossRef]
- Weierbach, H.; Lima, A.R.; Willard, J.D.; Hendrix, V.C.; Christianson, D.S.; Lubich, M.; Varadharajan, C. Stream temperature predictions for river basin management in the Pacific Northwest and mid-Atlantic regions using machine learning. Water 2022, 14, 1032. [Google Scholar] [CrossRef]
- Gauch, M.; Mai, J.; Lin, J. The proper care and feeding of CAMELS: How limited training data affects streamflow prediction. Environ. Model. Softw. 2021, 135, 104926. [Google Scholar] [CrossRef]
- van den Munckhof, G. Forecasting River Discharge Using Machine Learning Methods. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2020. [Google Scholar]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. Super ensemble learning for daily streamflow forecasting: Large-scale demonstration and comparison with multiple machine learning algorithms. Neural Comput. Appl. 2021, 33, 3053–3068. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, USA, 3–8 December 2018; Volume 31. [Google Scholar]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H. Time series features for supporting hydrometeorological explorations and predictions in ungauged locations using large datasets. Water 2022, 14, 1657. [Google Scholar] [CrossRef]
- Bokwa, A.; Klimek, M.; Krzaklewski, P.; Kukułka, W. Drought Trends in the Polish Carpathian Mts. in the Years 1991–2020. Atmosphere 2021, 12, 1259. [Google Scholar] [CrossRef]
- Baran-Gurgul, K. The Risk of Extreme Streamflow Drought in the Polish Carpathians—A Two-Dimensional Approach. Int. J. Environ. Res. Public Health 2022, 19, 14095. [Google Scholar] [CrossRef]
- Kędra, M. Altered precipitation characteristics in two Polish Carpathian basins, with implications for water resources. Clim. Res. 2017, 72, 251–265. [Google Scholar] [CrossRef]
- Twardosz, R.; Cebulska, M.; Walanus, A. Anomalously heavy monthly and seasonal precipitation in the Polish Carpathian Mountains and their foreland during the years 1881–2010. Theor. Appl. Climatol. 2016, 126, 323–337. [Google Scholar] [CrossRef]
- Kholiavchuk, D.; Cebulska, M. The highest monthly precipitation in the area of the Ukrainian and the Polish Carpathian Mountains in the period from 1984 to 2013. Theor. Appl. Climatol. 2019, 138, 1615–1628. [Google Scholar] [CrossRef]
- Falarz, M.; Bednorz, E. Snow cover change. In Climate Change in Poland; Springer: Berlin/Heidelberg, Germany, 2021; pp. 375–390. [Google Scholar] [CrossRef]
- Wyżga, B. Impact of the channelization-induced incision of the Skawa and Wisłoka Rivers, southern Poland, on the conditions of overbank deposition. Regul. Rivers Res. Manag. Int. J. Devoted River Res. Manag. 2001, 17, 85–100. [Google Scholar] [CrossRef]
- Olive, D.J. Multiple Linear Regression; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Rao, H.; Shi, X.; Rodrigue, A.K.; Feng, J.; Xia, Y.; Elhoseny, M.; Yuan, X.; Gu, L. Feature selection based on artificial bee colony and gradient boosting decision tree. Appl. Soft Comput. 2019, 74, 634–642. [Google Scholar] [CrossRef]
- Gan, M.; Pan, S.; Chen, Y.; Cheng, C.; Pan, H.; Zhu, X. Application of the machine learning lightgbm model to the prediction of the water levels of the lower columbia river. J. Mar. Sci. Eng. 2021, 9, 496. [Google Scholar] [CrossRef]
- Cui, Z.; Qing, X.; Chai, H.; Yang, S.; Zhu, Y.; Wang, F. Real-time rainfall-runoff prediction using light gradient boosting machine coupled with singular spectrum analysis. J. Hydrol. 2021, 603, 127124. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J.; Liu, J. Streamflow forecasting using extreme gradient boosting model coupled with Gaussian mixture model. J. Hydrol. 2020, 586, 124901. [Google Scholar] [CrossRef]
- Forghanparast, F.; Mohammadi, G. Using Deep Learning Algorithms for Intermittent Streamflow Prediction in the Headwaters of the Colorado River, Texas. Water 2022, 14, 2972. [Google Scholar] [CrossRef]
- Meddage, D.; Ekanayake, I.; Herath, S.; Gobirahavan, R.; Muttil, N.; Rathnayake, U. Predicting Bulk Average Velocity with Rigid Vegetation in Open Channels Using Tree-Based Machine Learning: A Novel Approach Using Explainable Artificial Intelligence. Sensors 2022, 22, 4398. [Google Scholar] [CrossRef]
- Wang, S.; Peng, H.; Hu, Q.; Jiang, M. Analysis of runoff generation driving factors based on hydrological model and interpretable machine learning method. J. Hydrol. Reg. Stud. 2022, 42, 101139. [Google Scholar] [CrossRef]












| Predictor | Scenario 1 | Scenario 2 | Scenario 3 |
|---|---|---|---|
| Precipitation | X | X | |
| Precipitation lag1 | X | X | |
| Precipitation lag2 | X | X | |
| Runoff upstream (Osielec) | X | X | |
| Runoff upstream lag1 | X | X | |
| Runoff upstream lag2 | X | X | |
| Runoff lag1 (Wadowice) | X | ||
| Runoff lag2 | X |
| Model | Only Precipitation | Only Upstream Runoff | All Parameters | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NSE | RMSE | MAE | NSE | RMSE | MAE | NSE | RMSE | MAE | |
| MLR | 0.460 | 14.798 | 8.500 | 0.748 | 10.104 | 4.784 | 0.848 | 7.850 | 3.142 |
| RF | 0.533 | 13.765 | 8.385 | 0.773 | 9.595 | 4.073 | 0.848 | 7.841 | 2.606 |
| XGBoost | 0.467 | 14.692 | 8.364 | 0.777 | 9.506 | 3.958 | 0.839 | 8.082 | 2.633 |
| LGBoost | 0.524 | 13.888 | 8.224 | 0.759 | 9.885 | 3.960 | 0.876 | 7.077 | 2.508 |
| CatBoost | 0.436 | 15.120 | 8.343 | 0.739 | 10.274 | 4.041 | 0.886 | 6.800 | 2.400 |
| Model | NSE | RMSE | MAE | n_estimators | learning_rate |
|---|---|---|---|---|---|
| XGBoost | 0.850 | 7.798 | 2.598 | 500–10,000 | 0.1 |
| LGBoost | 0.886 | 6.785 | 2.696 | 200–10,000 | 0.5 |
| CatBoost | 0.878 | 7.024 | 2.462 | 1000–10,000 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szczepanek, R. Daily Streamflow Forecasting in Mountainous Catchment Using XGBoost, LightGBM and CatBoost. Hydrology 2022, 9, 226. https://doi.org/10.3390/hydrology9120226
Szczepanek R. Daily Streamflow Forecasting in Mountainous Catchment Using XGBoost, LightGBM and CatBoost. Hydrology. 2022; 9(12):226. https://doi.org/10.3390/hydrology9120226
Chicago/Turabian StyleSzczepanek, Robert. 2022. "Daily Streamflow Forecasting in Mountainous Catchment Using XGBoost, LightGBM and CatBoost" Hydrology 9, no. 12: 226. https://doi.org/10.3390/hydrology9120226
APA StyleSzczepanek, R. (2022). Daily Streamflow Forecasting in Mountainous Catchment Using XGBoost, LightGBM and CatBoost. Hydrology, 9(12), 226. https://doi.org/10.3390/hydrology9120226








