Remote Sensing of Sediment Discharge in Rivers Using Sentinel-2 Images and Machine-Learning Algorithms
Abstract
:1. Introduction
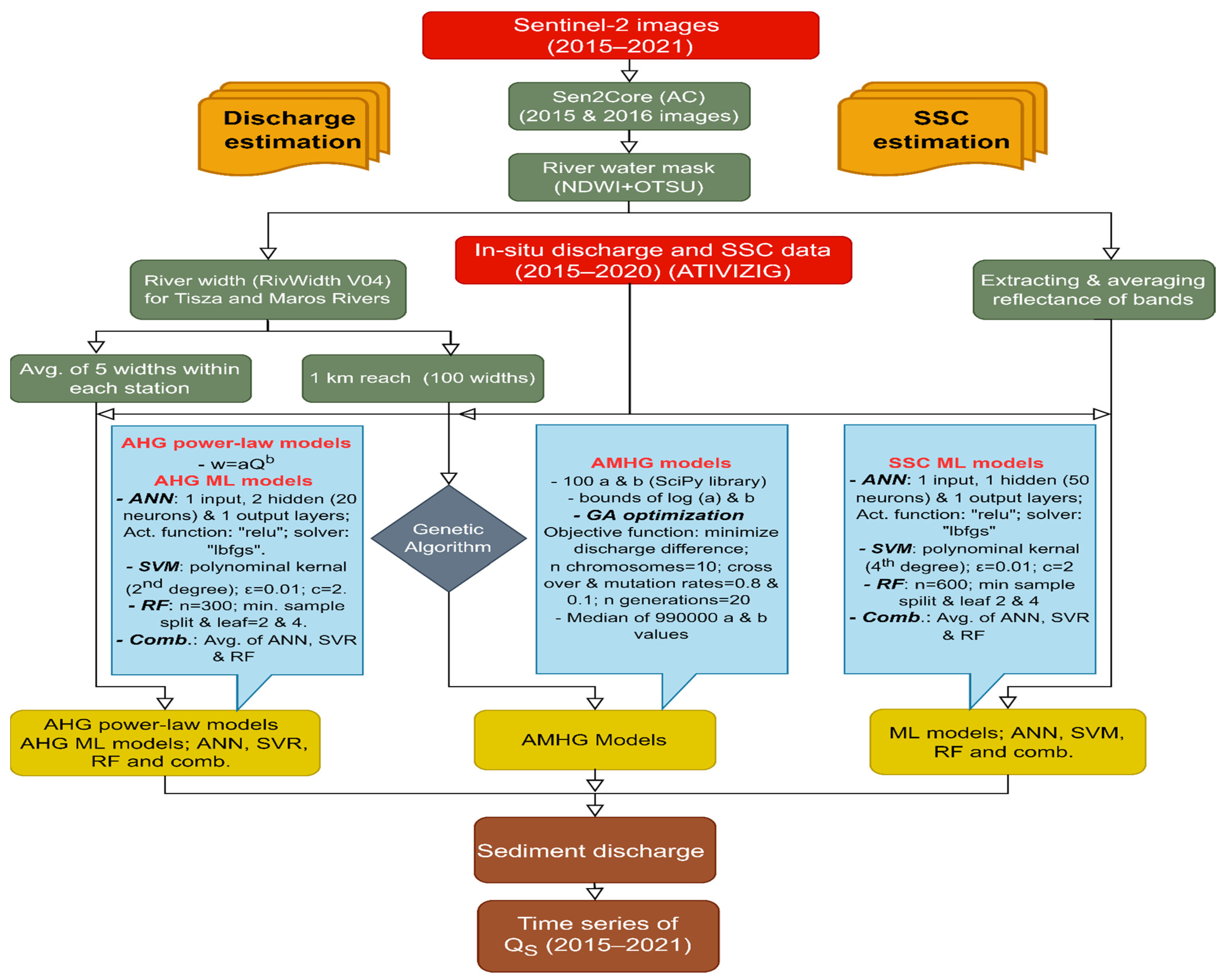
2. Materials and Methods
2.1. Study Area
2.2. In Situ Hydrological Data
2.3. Remote-Sensing Data
2.4. Pre-Processing of the Satellite Images
2.5. Water Discharge Estimation
2.5.1. At-a-Station Hydraulic Geometry (AHG), Power–Law, and Machine-Learning Models
2.5.2. At-Many-Stations Hydraulic Geometry (AMHG) Models
2.6. Suspended Sediment Estimation
2.7. Temporal Change of Suspended Sediment Discharge and Performance Evaluation
3. Results
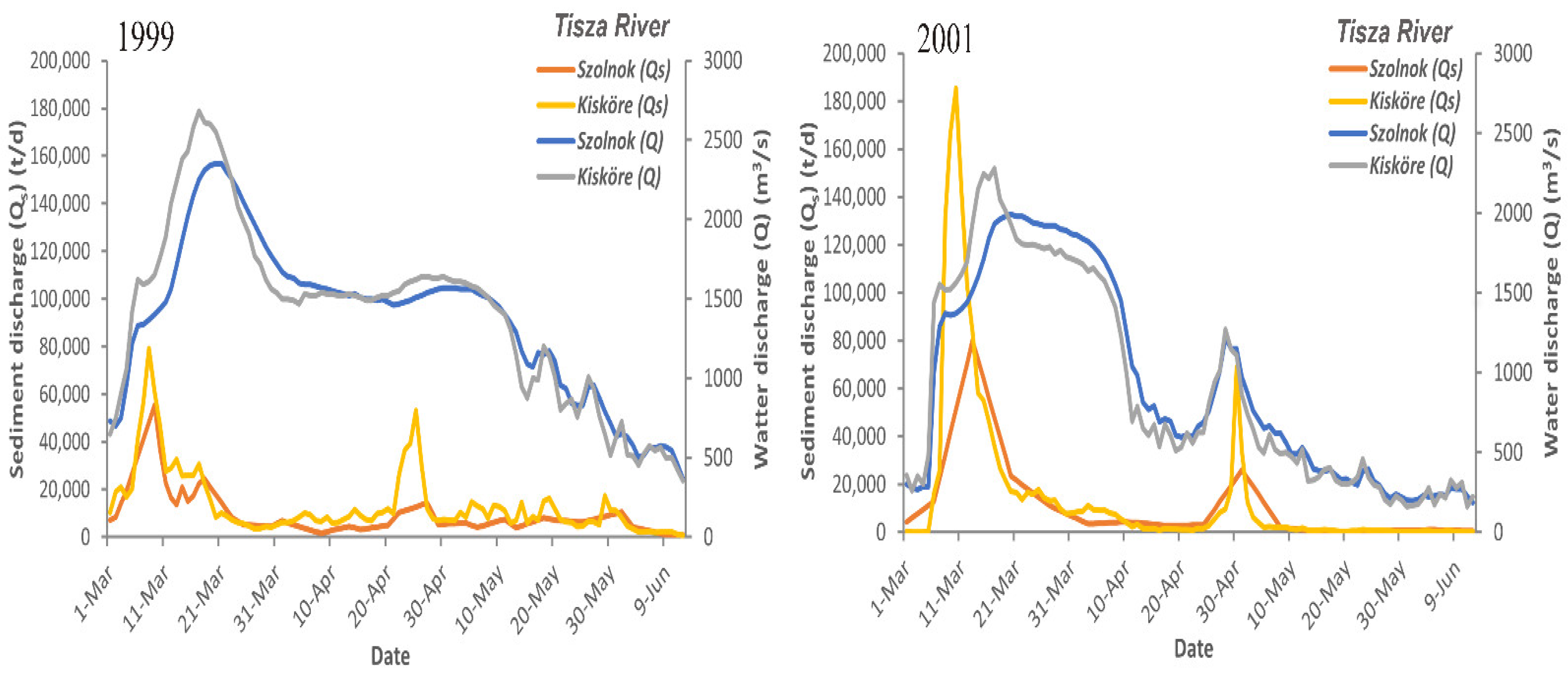
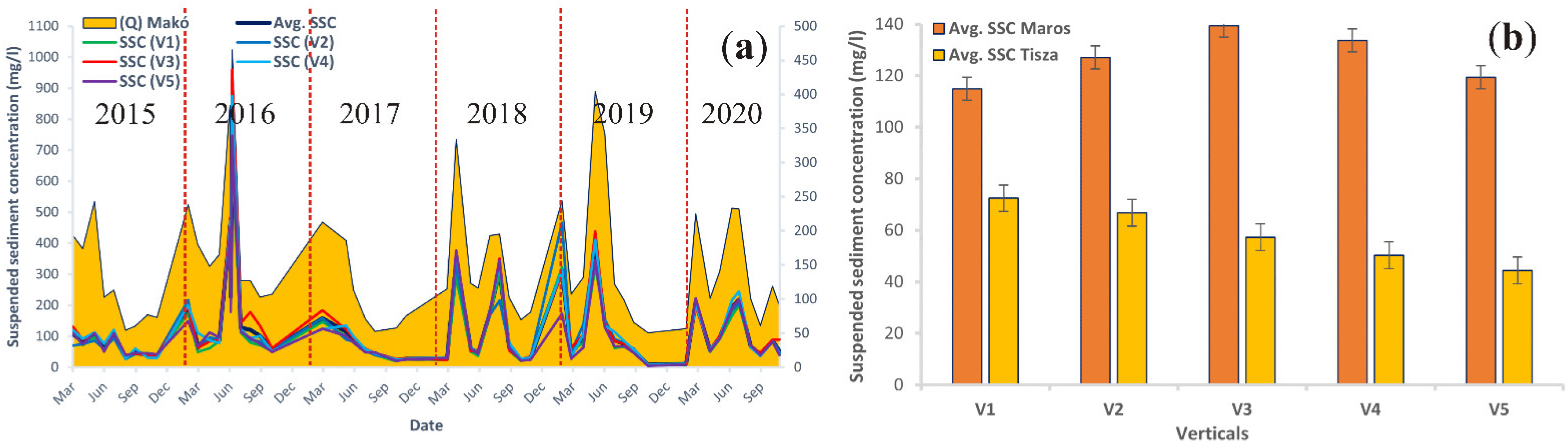
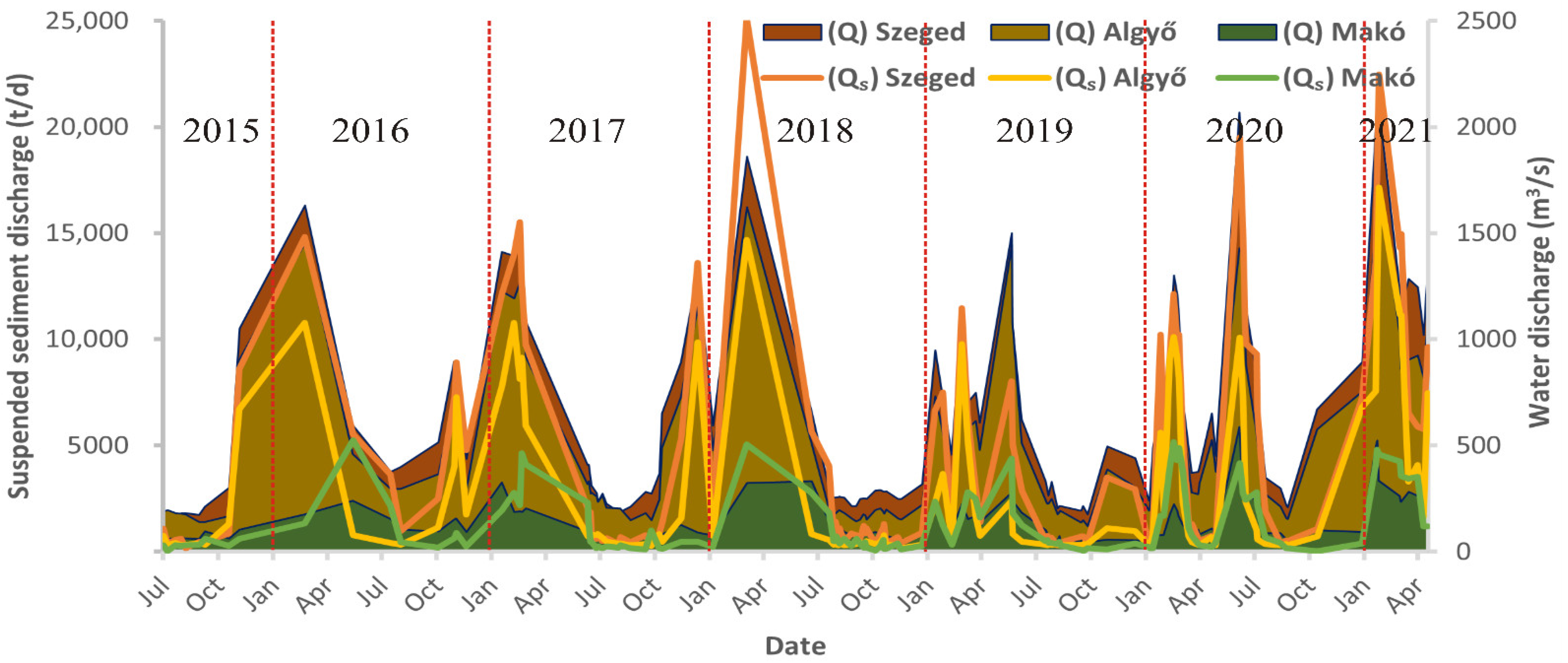
3.1. Temporal Change of Water Discharge and Suspended Sediment Concentration
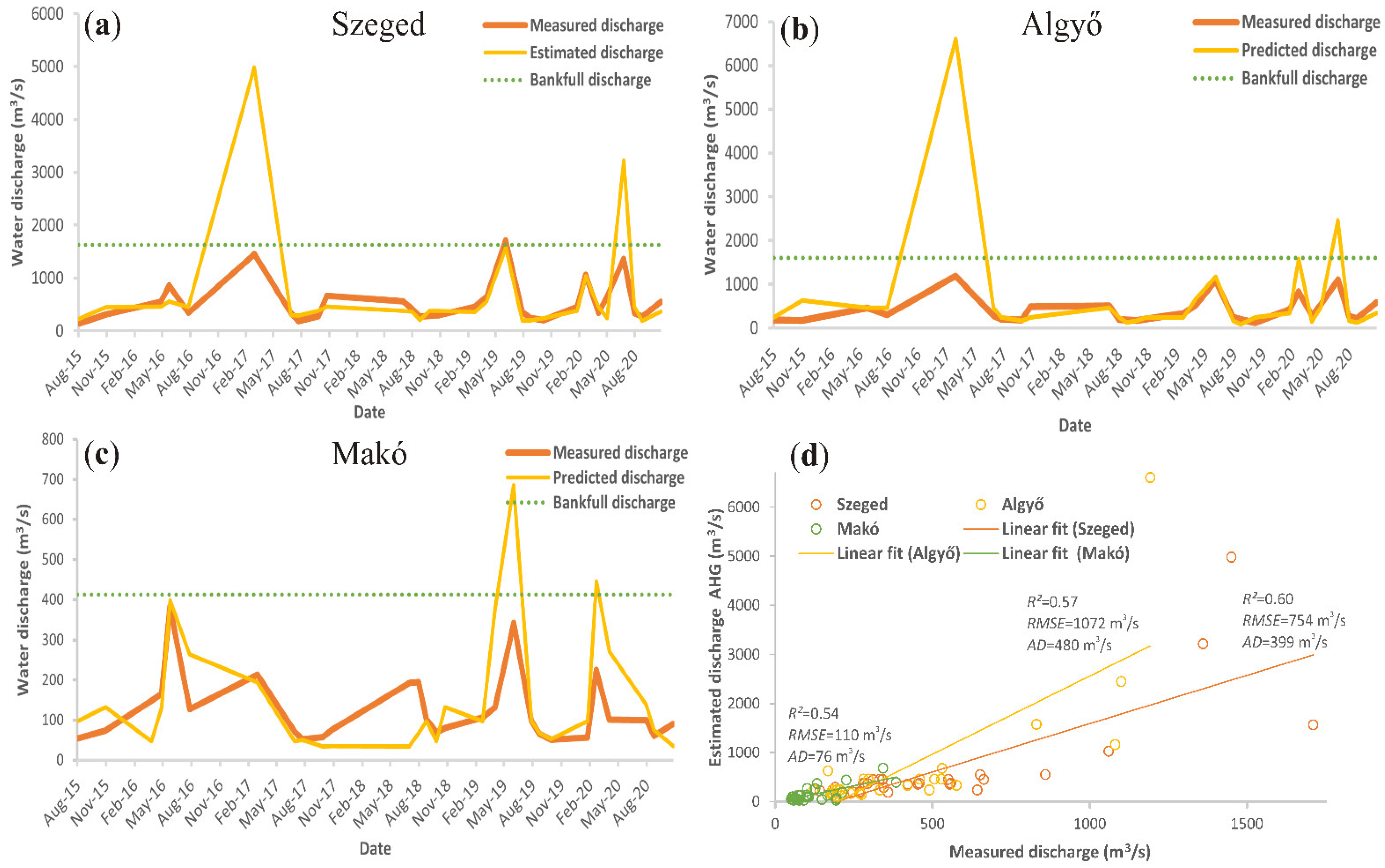
3.2. Estimating Water Discharge
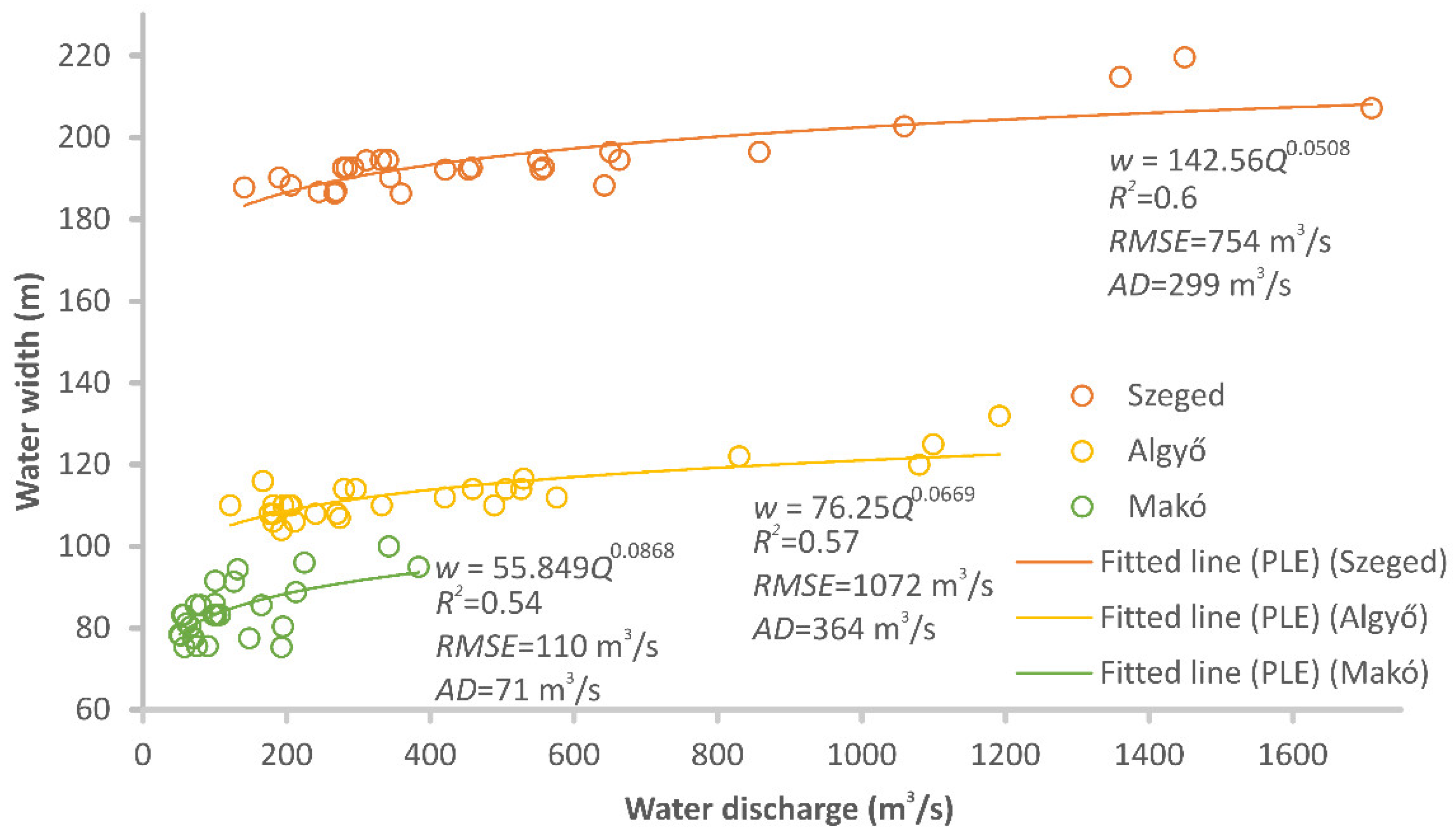
3.2.1. AHG Power–Law Models
3.2.2. AHG Machine-Learning Models
3.2.3. AMHG Models
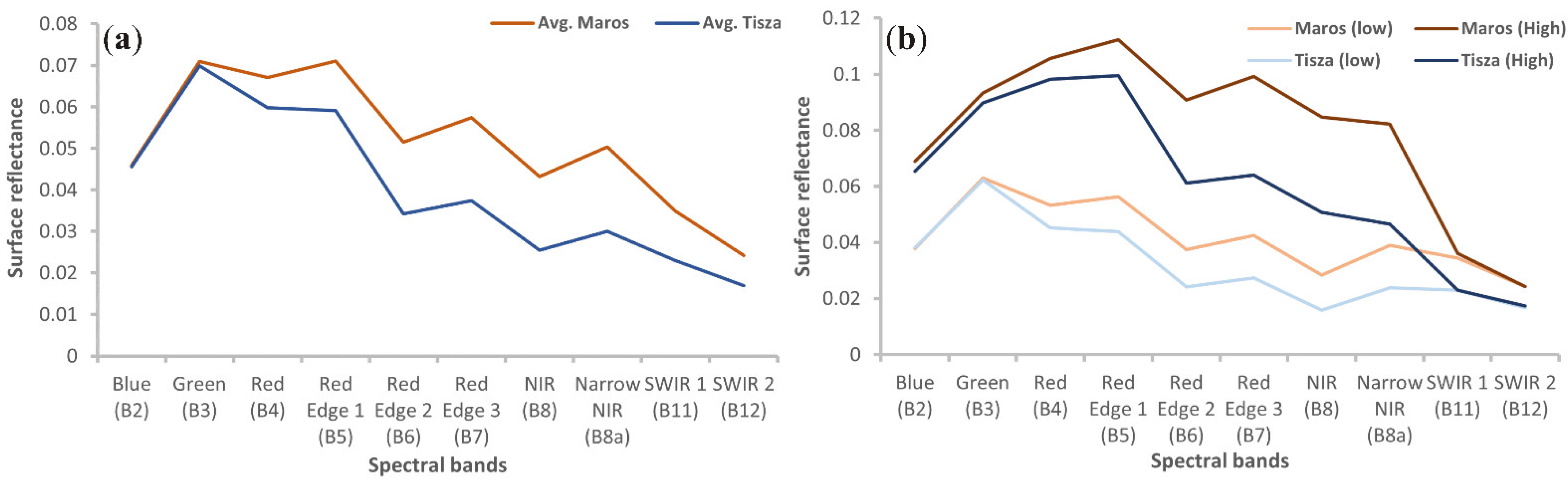
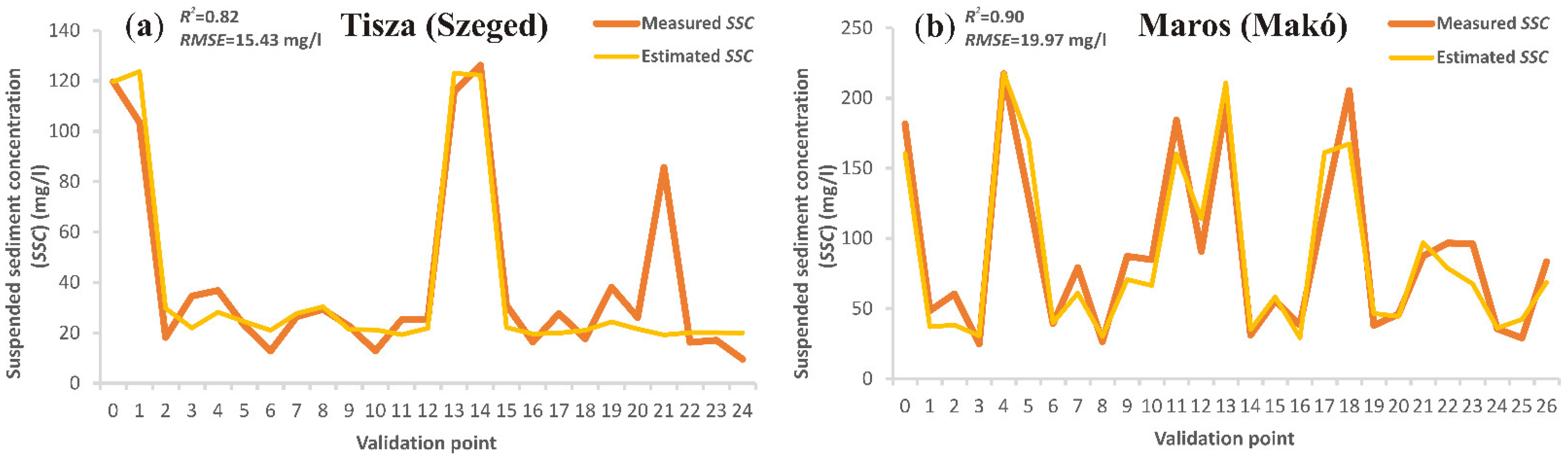
3.3. Estimating Suspended Sediment Concentration
3.4. Estimated Suspended Sediment Discharge of the Tisza and Maros Rivers Based on the Derived Models
4. Discussion
4.1. Suspended Sediment and Water Discharge Conditions in the Rivers Based on In Situ Measurements
4.2. Performance of the Water Discharge Models
4.3. Performance of the Suspended Sediment Models
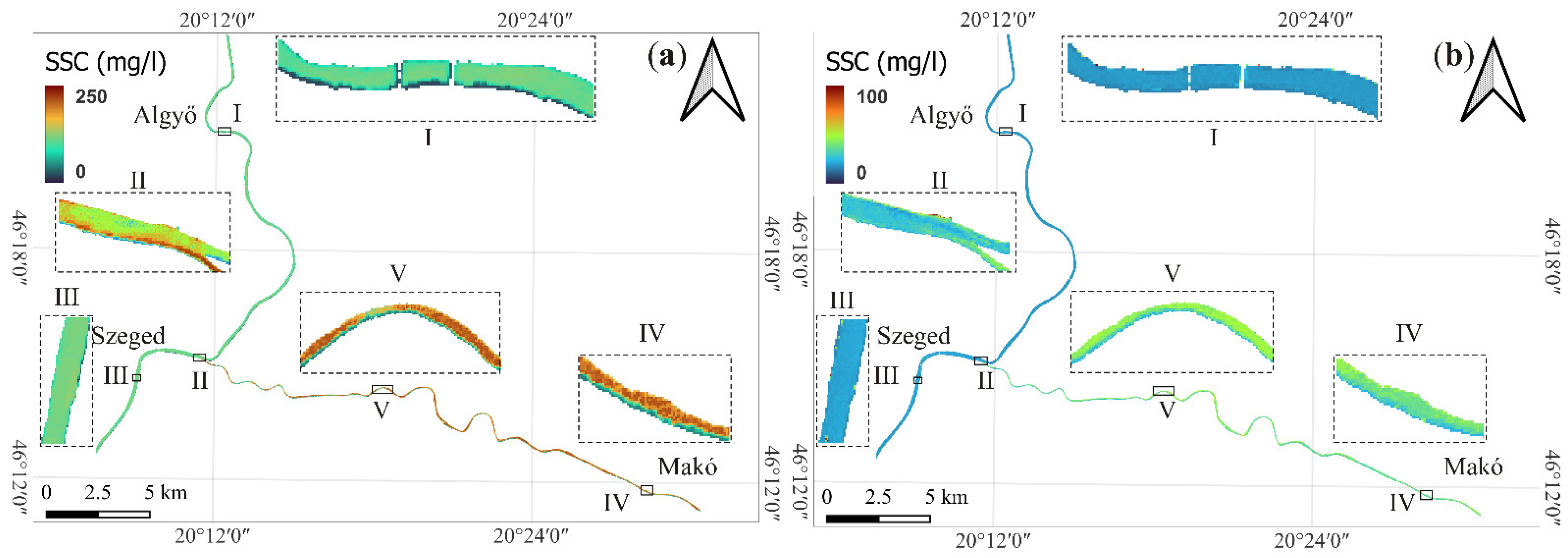
4.4. Suspended Sediment Concentration and Discharge Conditions of the Studied Rivers Based on Sentinel-2 Images
5. Conclusions
- The hydraulic geometry of the river channel in terms of the discharge–width relationship is very useful for estimating water discharge from space; however, the morphology of the selected reach (i.e., the shape of the cross-sectional profile) significantly affects the accuracy of the estimation.
- The automatic thresholding of the NDWI using the OTSU method was very useful, as it estimated the river width with an accuracy close to the pixel size. Thus, good channel width estimations could be obtained by applying this method on finer spatial resolution images, which would enhance the accuracy of water discharge estimations.
- Applied in a traditional way, the performance of the AMHG method outweighs the AHG power–law method, as was also reported in the former literature; however, our novel AHG machine-learning method performed as well as the AMHG method due to the capability of machine-learning algorithms for deriving complex regression models.
- Among the three tested algorithms for obtaining suspended sediment concentration based on Sentinel-2 images, the RF and ANN algorithms gave the best SSC estimations; thus, they are highly recommended for further studies. We also recommend combining algorithms to enhance the estimation accuracy significantly.
- The accuracy of the estimated Qs by this space-based alternative is limited by: (a) river width and the spatial resolution of the utilized images; (b) selected cross-section shape, as some shapes have more suitable hydraulic geometry than others; (c) bankfull discharge, as the models usually under- or overestimate the real discharge above this level due to losing the hydraulic geometry of the original cross-section; (d) shadow, sun glint, and surface wave in water pixels affecting the reflectance significantly, and consequently, the predicted SSC.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Curtis, W.F.; Culbertson, J.; Chase, E.B. Fluvial-Sediment Discharge to the Oceans from the Conterminous United States, 1st ed.; US Geological Survey: Reston, VA, USA, 1973; Volume 670, pp. 1–17. [Google Scholar]
- Flores, J.; Wu, J.; Stöckle, C.; Ewing, R.; Yang, X. Estimating river sediment discharge in the Upper Mississippi River using Landsat Imagery. Remote Sens. 2020, 12, 2370. [Google Scholar] [CrossRef]
- Mouyen, M.; Longuevergne, L.; Steer, P.; Crave, A.; Lemoine, J.-M.; Save, H.; Robin, C. Assessing modern river sediment discharge to the ocean using satellite gravimetry. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fryirs, K.; Brierley, G. Variability in sediment delivery and storage along river courses in Bega catchment, NSW, Australia: Implications for geomorphic river recovery. Geomorphology 2001, 38, 237–265. [Google Scholar] [CrossRef]
- Martinez, J.-M.; Guyot, J.-L.; Filizola, N.; Sondag, F. Increase in suspended sediment discharge of the Amazon River assessed by monitoring network and satellite data. Catena 2009, 79, 257–264. [Google Scholar] [CrossRef] [Green Version]
- Meade, R.H.; Moody, J.A. Causes for the decline of suspended-sediment discharge in the Mississippi River system, 1940–2007. Hydrol. Process. Int. J. 2010, 24, 35–49. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.; Piao, S.; Lü, Y.; Ciais, P.; Feng, X.; Wang, Y. Reduced sediment transport in the Yellow River due to anthropogenic changes. Nat. Geosci. 2016, 9, 38–41. [Google Scholar] [CrossRef]
- Walling, D. The changing sediment loads of the world’s rivers. Ann. Wars. Univ. Life Sci. SGGW Land Reclam. 2008, 39, 1–18. [Google Scholar] [CrossRef]
- Cook, S.; Chan, H.-L.; Abolfathi, S.; Bending, G.D.; Schäfer, H.; Pearson, J.M. Longitudinal dispersion of microplastics in aquatic flows using fluorometric techniques. Water Res. 2020, 170, 115337. [Google Scholar] [CrossRef]
- Milliman, J.D.; Giosan, L. River inputs. In Encyclopedia of Ocean Sciences, 3rd ed.; Cochran, J.K., Bokuniewicz, H.J., Yager, P.L., Eds.; Academic Press: Oxford, UK, 2019; Volume 1, pp. 100–107. [Google Scholar]
- Stonevičius, E.; Valiuškevičius, G.; Rimkus, E.; Kažys, J. Climate induced changes of Lithuanian rivers runoff in 1960–2009. Water Res. 2014, 41, 592–603. [Google Scholar] [CrossRef]
- Leopold, L.B.; Maddock, T. The Hydraulic Geometry of Stream Channels and Some Physiographic Implications, 1st ed.; US Government Printing Office: Washington, DC, USA, 1953; Volume 252, pp. 1–53. [Google Scholar]
- Gleason, C.J.; Durand, M.T. Remote Sensing of River Discharge: A Review and a Framing for the Discipline. Remote Sens. 2020, 12, 1107. [Google Scholar] [CrossRef] [Green Version]
- Kiss, T.; Fiala, K.; Sipos, G.; Szatmári, G. Long-term hydrological changes after various river regulation measures: Are we responsible for flow extremes? Hydrol. Res. 2019, 50, 417–430. [Google Scholar] [CrossRef] [Green Version]
- Zakwan, M. Spreadsheet-based modelling of hysteresis-affected curves. Appl. Water Sci. 2018, 8, 101. [Google Scholar] [CrossRef] [Green Version]
- Sipos, G.; Kiss, T.; Fiala, K. Morphological alterations due to channelization along the lower Tisza and Maros Rivers (Hungary). Geogr. Fiscica Din. Quat. 2007, 30, 239–247. [Google Scholar]
- Kiss, T.; Andrási, G. Hydro-morphological responses of the Drava river on various engineering works. Ekono. Ekohist. Čas. Gospod. Povij. Povij. Okoliš. 2017, 13, 14–24. [Google Scholar]
- Amissah, J.; Kiss, T.; Fiala, K. Morphological evolution of the lower Tisza River (Hungary) in the 20th century in response to human interventions. Water 2018, 10, 884. [Google Scholar] [CrossRef] [Green Version]
- Pavelsky, T.M. Using width-based rating curves from spatially discontinuous satellite imagery to monitor river discharge. Hydrol. Process. 2014, 28, 3035–3040. [Google Scholar] [CrossRef]
- Group, A.H.; Vörösmarty, C.; Askew, A.; Grabs, W.; Barry, R.; Birkett, C.; Döll, P.; Goodison, B.; Hall, A.; Jenne, R. Global water data: A newly endangered species. Eos Trans. Am. Geophys. Union 2001, 82, 54–58. [Google Scholar] [CrossRef]
- Mohsen, A.; Elshemy, M.; Zeidan, B.A. Change detection for Lake Burullus, Egypt using remote sensing and GIS approaches. Environ. Sci. Pollut. Res. 2018, 25, 30763–30771. [Google Scholar] [CrossRef]
- Stisen, S.; Jensen, K.H.; Sandholt, I.; Grimes, D.I.F. A remote sensing driven distributed hydrological model of the Senegal River basin. J. Hydrol. 2008, 354, 131–148. [Google Scholar] [CrossRef]
- Chen, J.; Wilson, C.; Chambers, D.; Nerem, R.; Tapley, B. Seasonal global water mass budget and mean sea level variations. Geophys. Res. Lett. 1998, 25, 3555–3558. [Google Scholar] [CrossRef] [Green Version]
- Hartanto, I.M.; van der Kwast, J.; Alexandridis, T.K.; Almeida, W.; Song, Y.; van Andel, S.J.; Solomatine, D.P. Data assimilation of satellite-based actual evapotranspiration in a distributed hydrological model of a controlled water system. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 123–135. [Google Scholar] [CrossRef]
- Li, Y.; Grimaldi, S.; Pauwels, V.R.N.; Walker, J.P. Hydrologic model calibration using remotely sensed soil moisture and discharge measurements: The impact on predictions at gauged and ungauged locations. J. Hydrol. 2018, 557, 897–909. [Google Scholar] [CrossRef]
- Laiolo, P.; Gabellani, S.; Campo, L.; Silvestro, F.; Delogu, F.; Rudari, R.; Pulvirenti, L.; Boni, G.; Fascetti, F.; Pierdicca, N.; et al. Impact of different satellite soil moisture products on the predictions of a continuous distributed hydrological model. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 131–145. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Lawrence Dingman, S.; Vorosmarty, C.J.; Bolster, C.H.; Congalton, R.G. Evaluating the potential for measuring river discharge from space. J. Hydrol. 2003, 278, 17–38. [Google Scholar] [CrossRef]
- Bates, P.; Horritt, M.; Smith, C.; Mason, D. Integrating remote sensing observations of flood hydrology and hydraulic modelling. Hydrol. Process. 1997, 11, 1777–1795. [Google Scholar] [CrossRef]
- Neal, J.; Schumann, G.; Bates, P.; Buytaert, W.; Matgen, P.; Pappenberger, F. A data assimilation approach to discharge estimation from space. Hydrol. Process. Int. J. 2009, 23, 3641–3649. [Google Scholar] [CrossRef]
- Temimi, M.; Lacava, T.; Lakhankar, T.; Tramutoli, V.; Ghedira, H.; Ata, R.; Khanbilvardi, R. A multi-temporal analysis of AMSR-E data for flood and discharge monitoring during the 2008 flood in Iowa. Hydrol. Process. 2011, 25, 2623–2634. [Google Scholar] [CrossRef] [Green Version]
- Gleason, C.J.; Smith, L.C. Toward global mapping of river discharge using satellite images and at-many-stations hydraulic geometry. Proc. Nat. Acad. Sci. USA 2014, 111, 4788–4791. [Google Scholar] [CrossRef] [Green Version]
- Mengen, D.; Ottinger, M.; Leinenkugel, P.; Ribbe, L. Modeling River Discharge Using Automated River Width Measurements Derived from Sentinel-1 Time Series. Remote Sens. 2020, 12, 3236. [Google Scholar] [CrossRef]
- Elmi, O.; Tourian, M.J.; Sneeuw, N. River discharge estimation using channel width from satellite imagery. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 727–730. [Google Scholar]
- Gleason, C.J.; Smith, L.C.; Lee, J. Retrieval of river discharge solely from satellite imagery and at-many-stations hydraulic geometry: Sensitivity to river form and optimization parameters. Water Resour. Res. 2014, 50, 9604–9619. [Google Scholar] [CrossRef]
- Durga Rao, K.H.V.; Shravya, A.; Dadhwal, V.K. A novel method of satellite based river discharge estimation using river hydraulic geometry through genetic algorithm technique. J. Hydrol. 2020, 589, 125361. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; O’Donnell, G.M.; Moore, P.; Kilsby, C.G.; Fowler, H.J.; Berry, P.A.M. Using satellite altimetry data to augment flow estimation techniques on the Mekong River. Hydrol. Process. 2010, 24, 3811–3825. [Google Scholar] [CrossRef]
- Michailovsky, C.I.; McEnnis, S.; Berry, P.A.M.; Smith, R.; Bauer-Gottwein, P. River monitoring from satellite radar altimetry in the Zambezi River basin. Hydrol. Earth Syst. Sci. 2012, 16, 2181–2192. [Google Scholar] [CrossRef] [Green Version]
- Durand, M.; Gleason, C.J.; Garambois, P.A.; Bjerklie, D.; Smith, L.C.; Roux, H.; Rodriguez, E.; Bates, P.D.; Pavelsky, T.M.; Monnier, J.; et al. An intercomparison of remote sensing river discharge estimation algorithms from measurements of river height, width, and slope. Water Resour. Res. 2016, 52, 4527–4549. [Google Scholar] [CrossRef] [Green Version]
- Kouraev, A.V.; Zakharova, E.A.; Samain, O.; Mognard, N.M.; Cazenave, A. Ob’ river discharge from TOPEX/Poseidon satellite altimetry (1992–2002). Remote Sens. Environ. 2004, 93, 238–245. [Google Scholar] [CrossRef] [Green Version]
- Perks, M.T. Suspended sediment sampling. In Geomorphological Techniques (Online Edition); Cook, S.J., Clarke, L.E., Nield, J.M., Eds.; British Society for Geomorphology: London, UK, 2014; pp. 1–7. [Google Scholar]
- Bogárdi, J.L. Fluvial sediment transport. In Advances in Hydroscience; Chow, V.T., Ed.; Elsevier: Amsterdam, The Netherlands, 1972; Volume 8, pp. 183–259. [Google Scholar]
- Bouchez, J.; Métivier, F.; Lupker, M.; Maurice, L.; Perez, M.; Gaillardet, J.; France-Lanord, C. Prediction of depth-integrated fluxes of suspended sediment in the Amazon River: Particle aggregation as a complicating factor. Hydrol. Process. 2011, 25, 778–794. [Google Scholar] [CrossRef]
- Shah-Fairbank Seema, C.; Julien Pierre, Y.; Baird Drew, C. Total Sediment Load from SEMEP Using Depth-Integrated Concentration Measurements. J. Hydraul. Eng. 2011, 137, 1606–1614. [Google Scholar] [CrossRef] [Green Version]
- Davis, B.E. A Guide to the Proper Selection and Use of Federally Approved Sediment and Water-Quality Samplers; US Department of the Interior, US Geological Survey: Washington, DC, USA, 2005; pp. 1–26. [Google Scholar]
- Pham, Q.V.; Ha, N.T.; Pahlevan, N.; Oanh, L.T.; Nguyen, T.B.; Nguyen, N.T. Using Landsat-8 Images for Quantifying Suspended Sediment Concentration in Red River (Northern Vietnam). Remote Sens. 2018, 10, 1841. [Google Scholar] [CrossRef] [Green Version]
- Mohsen, A.; Elshemy, M.; Zeidan, B. Water quality monitoring of Lake Burullus (Egypt) using Landsat satellite imageries. Environ. Sci. Pollut. Res. 2020, 28, 1–14. [Google Scholar] [CrossRef]
- Mohsen, A.; Kovács, F.; Mezősi, G.; Kiss, T. Sediment Transport Dynamism in the Confluence Area of Two Rivers Transporting Mainly Suspended Sediment Based on Sentinel-2 Satellite Images. Water 2021, 13, 3132. [Google Scholar] [CrossRef]
- Zhan, C.; Yu, J.; Wang, Q.; Li, Y.; Zhou, D.; Xing, Q.; Chu, X. Remote sensing retrieval of surface suspended sediment concentration in the Yellow River Estuary. Chin. Geogr. Sci. 2017, 27, 934–947. [Google Scholar] [CrossRef] [Green Version]
- Pereira, F.J.S.; Costa, C.A.G.; Foerster, S.; Brosinsky, A.; de Araújo, J.C. Estimation of suspended sediment concentration in an intermittent river using multi-temporal high-resolution satellite imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 153–161. [Google Scholar] [CrossRef]
- Marinho, R.R.; Harmel, T.; Martinez, J.-M.; Filizola Junior, N.P. Spatiotemporal Dynamics of Suspended Sediments in the Negro River, Amazon Basin, from In Situ and Sentinel-2 Remote Sensing Data. ISPRS Int. J. Geoinf. 2021, 10, 86. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Xu, J.; Zhang, Y.; Zhang, B. Comparison of different semi-empirical algorithms to estimate chlorophyll-a concentration in inland lake water. Environ. Monit. Assess. 2010, 170, 231–244. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Chen, S.; Qin, W.; Lu, T.; Li, J.; Cao, Y. A Semi-Empirical Chlorophyll-a Retrieval Algorithm Considering the Effects of Sun Glint, Bottom Reflectance, and Non-Algal Particles in the Optically Shallow Water Zones of Sanya Bay Using SPOT6 Data. Remote Sens. 2020, 12, 2765. [Google Scholar] [CrossRef]
- Ammenberg, P.; Flink, P.; Lindell, T.; Pierson, D.; Strombeck, N. Bio-optical modelling combined with remote sensing to assess water quality. Int. J. Remote Sens. 2002, 23, 1621–1638. [Google Scholar] [CrossRef]
- Manuel, A.; Blanco, A.C.; Tamondong, A.M.; Jalbuena, R.; Cabrera, O.; Gege, P. Optmization of bio-optical model parameters for turbid lake water quality estimation using Landsat 8 and wasi-2D. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 42, 67–72. [Google Scholar] [CrossRef] [Green Version]
- Silveira Kupssinskü, L.; Thomassim Guimarães, T.; Menezes de Souza, E.; Zanotta, D.C.; Roberto Veronez, M.; Gonzaga, L., Jr.; Mauad, F.F. A Method for Chlorophyll-a and Suspended Solids Prediction through Remote Sensing and Machine Learning. Sensors 2020, 20, 2125. [Google Scholar] [CrossRef] [Green Version]
- Peterson, K.T.; Sagan, V.; Sidike, P.; Cox, A.L.; Martinez, M. Suspended Sediment Concentration Estimation from Landsat Imagery along the Lower Missouri and Middle Mississippi Rivers Using an Extreme Learning Machine. Remote Sens. 2018, 10, 1503. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, I.; Shah, I. Suspended sediment concentration modeling using conventional and machine learning approaches in the Thames River, London Ontario. J. Water Manag. Model. 2018, 26, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Stumpf, R.P.; Goldschmidt, P.M. Remote sensing of suspended sediment discharge into the western Gulf of Maine during the April 1987 100-year flood. J. Coast. Res. 1992, 8, 218–225. [Google Scholar]
- Mangiarotti, S.; Martinez, J.M.; Bonnet, M.P.; Buarque, D.C.; Filizola, N.; Mazzega, P. Discharge and suspended sediment flux estimated along the mainstream of the Amazon and the Madeira Rivers (from in situ and MODIS Satellite Data). Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 341–355. [Google Scholar] [CrossRef] [Green Version]
- Gallay, M.; Martinez, J.-M.; Mora, A.; Castellano, B.; Yépez, S.; Cochonneau, G.; Alfonso, J.A.; Carrera, J.M.; López, J.L.; Laraque, A. Assessing Orinoco river sediment discharge trend using MODIS satellite images. J. S. Am. Earth Sci. 2019, 91, 320–331. [Google Scholar] [CrossRef]
- Lászlóffy, W. A Tisza: Vízi Munkálatok és Vízgazdálkodás a Tiszai Vízrendszerben; Akadémiai Kiadó: Budapest, Hungary, 1982; p. 609. [Google Scholar]
- Amissah, G.J. Channel Processes of a Large Alluvial River under Human Impacts. Ph.D. Thesis, University of Szeged, Szeged, Hungary, 2020. [Google Scholar]
- Sipos, G.; Kiss, T.; Oroszi, V. Geomorphological Process along the lowland sections of the maros/mures and Kôrôs/CRIS rivers. In Ecological Socio-Economic Relations in the Valleys of River KÔRÔS/Cris River Maros/Mures; Körmöczi, L., Ed.; Depatment of Ecology, University of Szeged: Szeged-Arad, Hungary, 2011; Volume 9, pp. 35–96. [Google Scholar]
- Kiss, T.; Oroszi, V.G.; Sipos, G.; Fiala, K.; Benyhe, B. Accelerated overbank accumulation after nineteenth century river regulation works: A case study on the Maros River, Hungary. Geomorphology 2011, 135, 191–202. [Google Scholar] [CrossRef]
- Boga, L.; Nováky, B. Magyarország Vizeinek Műszaki-Hidrológiai Jellemzése, Maros; Vízgazdálkodási Intézet: Budapest, Hungary, 1986; Volume 32, p. 80. (In Hungarian) [Google Scholar]
- Török, I. A Maros Alföldi Szakaszának Szabályozási Terve (0–51, 33 fkm); Regulation Plan of the Lowland Section of River Maros; ATIVIZIG: Szeged, Hungary, 1977. [Google Scholar]
- Lóczy, D.; Kis, É.; Schweitzer, F. Local flood hazards assessed from channel morphometry along the Tisza River in Hungary. Geomorphology 2009, 113, 200–209. [Google Scholar] [CrossRef]
- Bogárdi, J. Sediment. Transport in Alluvial Streams; Akademiai Kiado: Budapest, Hungary, 1974; p. 826. [Google Scholar]
- Csépes, E.; Bancsi, I.; Végvári, P.; Aranyné Rózsavári, A. Sediment transport study on the Middle Tisza (between Kisköre and Szolnok). MHT Szolnok (CD) 2003, 2, 1–10. (In Hungarian) [Google Scholar]
- Csépes, E.; Nagy, M.; Bancsi, I.; Végvári, P.; Kovács, P.; Szilágyi, E. The phases of water quality characteristics in the middle section of river Tisza in the light of the greatest flood of the century. Hidrol. Közlöny 2000, 80, 285–287. (In Hungarian) [Google Scholar]
- ESA. Available online: https://scihub.copernicus.eu/ (accessed on 6 June 2021).
- Revel, C.; Lonjou, V.; Marcq, S.; Desjardins, C.; Fougnie, B.; Coppolani-Delle Luche, C.; Guilleminot, N.; Lacamp, A.-S.; Lourme, E.; Miquel, C.; et al. Sentinel-2A and 2B absolute calibration monitoring. Eur. J. Remote Sens. 2019, 52, 122–137. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Atkinson, P.M. Spatio-temporal fusion for daily Sentinel-2 images. Remote Sens. Environ. 2018, 204, 31–42. [Google Scholar] [CrossRef] [Green Version]
- ESA. Available online: https://step.esa.int/main/download/snap-download/ (accessed on 20 June 2021).
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Pavelsky, T.M.; Smith, L.C. RivWidth: A Software Tool for the Calculation of River Widths From Remotely Sensed Imagery. IEEE Geosci. Remote Sens. Lett. 2008, 5, 70–73. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Youshen, X. A new neural network for solving linear and quadratic programming problems. IEEE Trans. Neural Netw. 1996, 7, 1544–1548. [Google Scholar] [CrossRef] [PubMed]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Sivanandam, S.; Deepa, S. Genetic algorithms. In Introduction to Genetic Algorithms; Sivanandam, S.N., Deepa, S.N., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 15–37. [Google Scholar]
- Porterfield, G. Computation of fluvial-sediment discharge. In Techniques of Water-Resources Investigations of the United States Geological Survey; US Government Printing Office: Washington, DC, USA, 1972; p. 66. [Google Scholar]
- Kiss, T.; Balogh, M.; Fiala, K.; Sipos, G. Morphology of fluvial levee series along a river under human influence, Maros River, Hungary. Geomorphology 2018, 303, 309–321. [Google Scholar] [CrossRef] [Green Version]
- Oeurng, C.; Sauvage, S.; Sánchez-Pérez, J.-M. Dynamics of suspended sediment transport and yield in a large agricultural catchment, southwest France. Earth Surf. Process. Landf. 2010, 35, 1289–1301. [Google Scholar] [CrossRef] [Green Version]
- Bača, P. Hysteresis effect in suspended sediment concentration in the Rybárik basin, Slovakia/Effet d’hystérèse dans la concentration des sédiments en suspension dans le bassin versant de Rybárik (Slovaquie). Hydrol. Sci. J. 2008, 53, 224–235. [Google Scholar] [CrossRef]
- Fang, H.Y.; Cai, Q.G.; Chen, H.; Li, Q.Y. Temporal changes in suspended sediment transport in a gullied loess basin: The lower Chabagou Creek on the Loess Plateau in China. Earth Surf. Process. Landf. 2008, 33, 1977–1992. [Google Scholar] [CrossRef]
- Klein, M. Anti clockwise hysteresis in suspended sediment concentration during individual storms: Holbeck catchment; Yorkshire, England. Catena 1984, 11, 251–257. [Google Scholar] [CrossRef]
- Hashiba, M.; Kai, T.; Yorozuya, A.; Motonaga, Y. Field observation of the river flood flow and suspended sediment distribution using ADCP. In Proceedings of the 9th International Symposium on Ultrasonic Doppler Methods for Fluid Mechanics and Fluid Engineering, Strasbourg, France, 27–29 August 2014; pp. 125–128. [Google Scholar]
- Jirka, G.H. Mixing and dispersion in rivers. In Proceedings of the Second International Conference on Fluvial Hyraulics, Napoli, Italy, 23–25 June 2004; pp. 13–27. [Google Scholar]
- Bzdok, D.; Altman, N.; Krzywinski, M. Statistics versus machine learning. Nat. Methods 2018, 15, 233–234. [Google Scholar] [CrossRef]
- Liu, H.; Li, Q.; Shi, T.; Hu, S.; Wu, G.; Zhou, Q. Application of Sentinel 2 MSI Images to Retrieve Suspended Particulate Matter Concentrations in Poyang Lake. Remote Sens. 2017, 9, 761. [Google Scholar] [CrossRef] [Green Version]
- Larson, M.D.; Simic Milas, A.; Vincent, R.K.; Evans, J.E. Landsat 8 monitoring of multi-depth suspended sediment concentrations in Lake Erie’s Maumee River using machine learning. Int. J. Remote Sens. 2021, 42, 4064–4086. [Google Scholar] [CrossRef]
- Premkumar, R.; Venkatachalapathy, R.; Visweswaran, S. Mapping of total suspended matter based on sentinel-2 data on the Hooghly River, India. Indian J. Ecol. 2021, 48, 159–165. [Google Scholar]
- Umar, M.; Rhoads, B.L.; Greenberg, J. Use of multispectral satellite remote sensing to assess mixing of suspended sediment downstream of large river confluences. J. Hydrol. 2018, 556, 325–338. [Google Scholar] [CrossRef]
- Larson, M.D.; Simic Milas, A.; Vincent, R.K.; Evans, J.E. Multi-depth suspended sediment estimation using high-resolution remote-sensing UAV in Maumee River, Ohio. Int. J. Remote Sens. 2018, 39, 5472–5489. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree Species Classification with Random Forest Using Very High Spatial Resolution 8-Band WorldView-2 Satellite Data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.K.; Roy, D.P. Using the 500 m MODIS land cover product to derive a consistent continental scale 30 m Landsat land cover classification. Remote Sens. Environ. 2017, 197, 15–34. [Google Scholar] [CrossRef]




| Station | AHG Machine-Learning | AHG Power–Law | AMHG | ||||
|---|---|---|---|---|---|---|---|
| Algorithm | R2 | RMSE (m3/s) | R2 | RMSE (m3/s) | R2 | RMSE (m3/s) | |
| Szeged | Support Vector Regression (SVR) | 0.65 | 131.97 | 0.6 | 754 | 0.67 | 268 |
| Random Forest (RF) | 0.71 | 154.12 | |||||
| Artificial Neural Network (ANN) | 0.76 | 119.94 | |||||
| Combined model | 0.83 | 99.9 | |||||
| Algyő | Support Vector Regression (SVR) | 0.72 | 98.92 | 0.57 | 1072 | 0.64 | 187 |
| Random Forest (RF) | 0.68 | 123.55 | |||||
| Artificial Neural Network (ANN) | 0.79 | 123.28 | |||||
| Combined model | 0.77 | 107.84 | |||||
| Makó | Support Vector Regression (SVR) | 0.85 | 33.65 | 0.54 | 110 | 0.55 | 62 |
| Random Forest (RF) | 0.81 | 25.37 | |||||
| Artificial Neural Network (ANN) | 0.85 | 30.98 | |||||
| Combined model | 0.88 | 25.93 | |||||
| Station | Algorithm | R2 | RMSE (mg/L) | RMSE/Mean Observed |
|---|---|---|---|---|
| Tisza River (Szeged) | Support Vector Regression (SVR) | 0.78 | 17.28 | 0.42 |
| Random Forest (RF) | 0.76 | 15.23 | 0.37 | |
| Artificial Neural Network (ANN) | 0.82 | 17.96 | 0.44 | |
| Combined model | 0.82 | 15.43 | 0.38 | |
| Maros River (Makó) | Support Vector Regression (SVR) | 0.78 | 24.9 | 0.28 |
| Random Forest (RF) | 0.90 | 19.97 | 0.22 | |
| Artificial Neural Network (ANN) | 0.85 | 22.72 | 0.25 | |
| Combined model | 0.88 | 19.75 | 0.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohsen, A.; Kovács, F.; Kiss, T. Remote Sensing of Sediment Discharge in Rivers Using Sentinel-2 Images and Machine-Learning Algorithms. Hydrology 2022, 9, 88. https://doi.org/10.3390/hydrology9050088
Mohsen A, Kovács F, Kiss T. Remote Sensing of Sediment Discharge in Rivers Using Sentinel-2 Images and Machine-Learning Algorithms. Hydrology. 2022; 9(5):88. https://doi.org/10.3390/hydrology9050088
Chicago/Turabian StyleMohsen, Ahmed, Ferenc Kovács, and Tímea Kiss. 2022. "Remote Sensing of Sediment Discharge in Rivers Using Sentinel-2 Images and Machine-Learning Algorithms" Hydrology 9, no. 5: 88. https://doi.org/10.3390/hydrology9050088
APA StyleMohsen, A., Kovács, F., & Kiss, T. (2022). Remote Sensing of Sediment Discharge in Rivers Using Sentinel-2 Images and Machine-Learning Algorithms. Hydrology, 9(5), 88. https://doi.org/10.3390/hydrology9050088






