Validation of the Finite Element Model versus Biomechanical Assessments of Dental Implants and Total Knee Replacements
Abstract
:1. Introduction
2. Materials and Methods
2.1. Part 1: Dental Implant
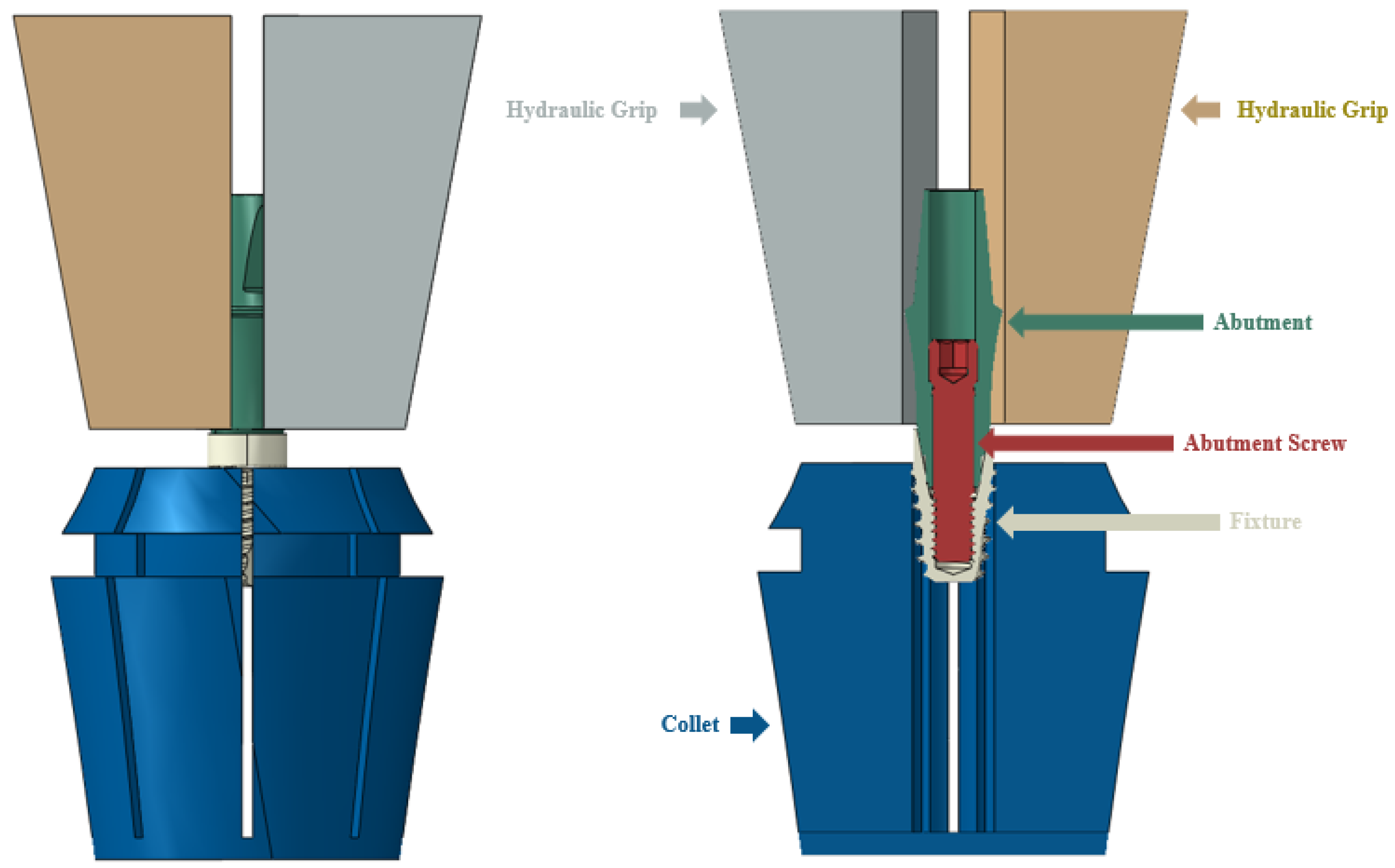
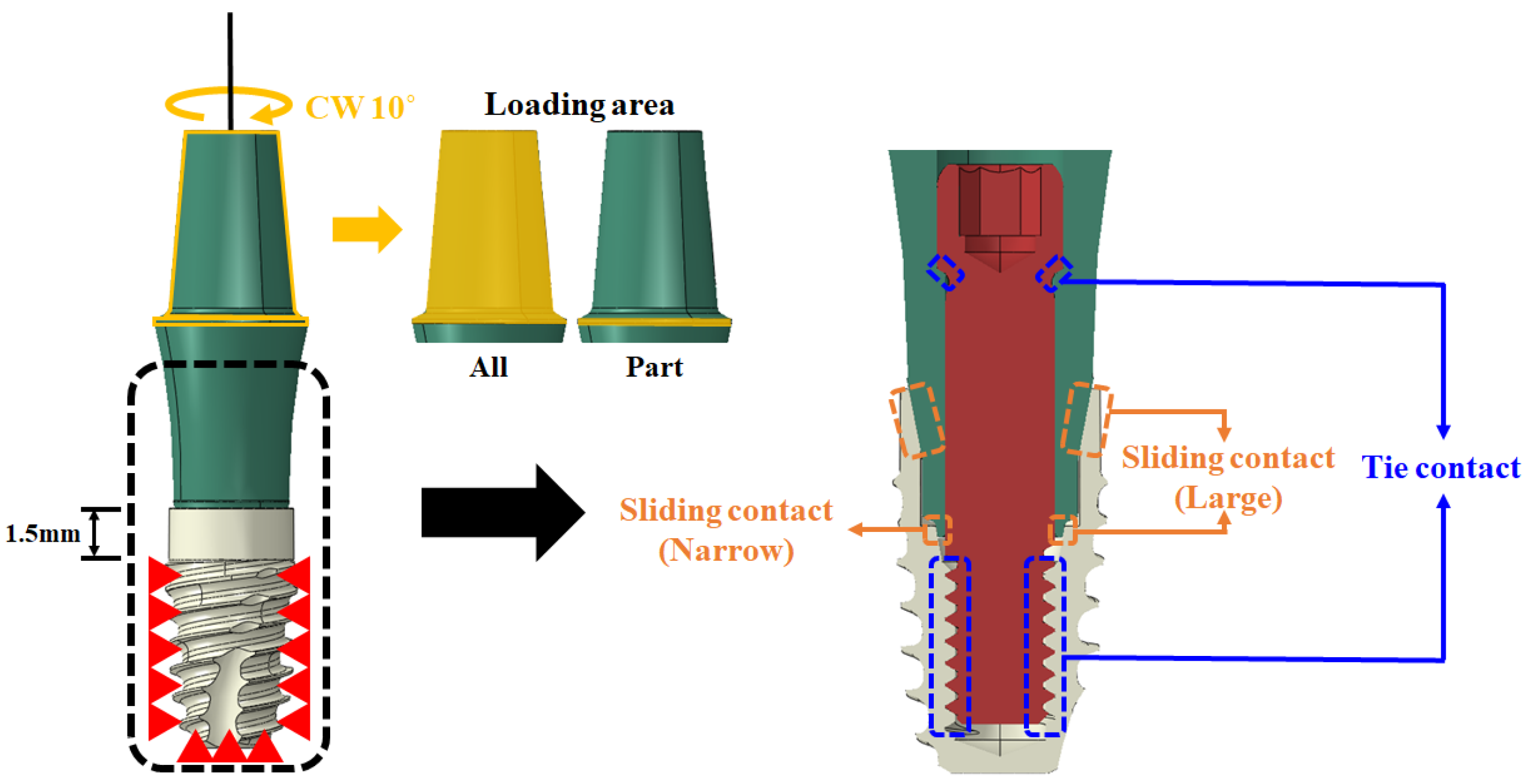
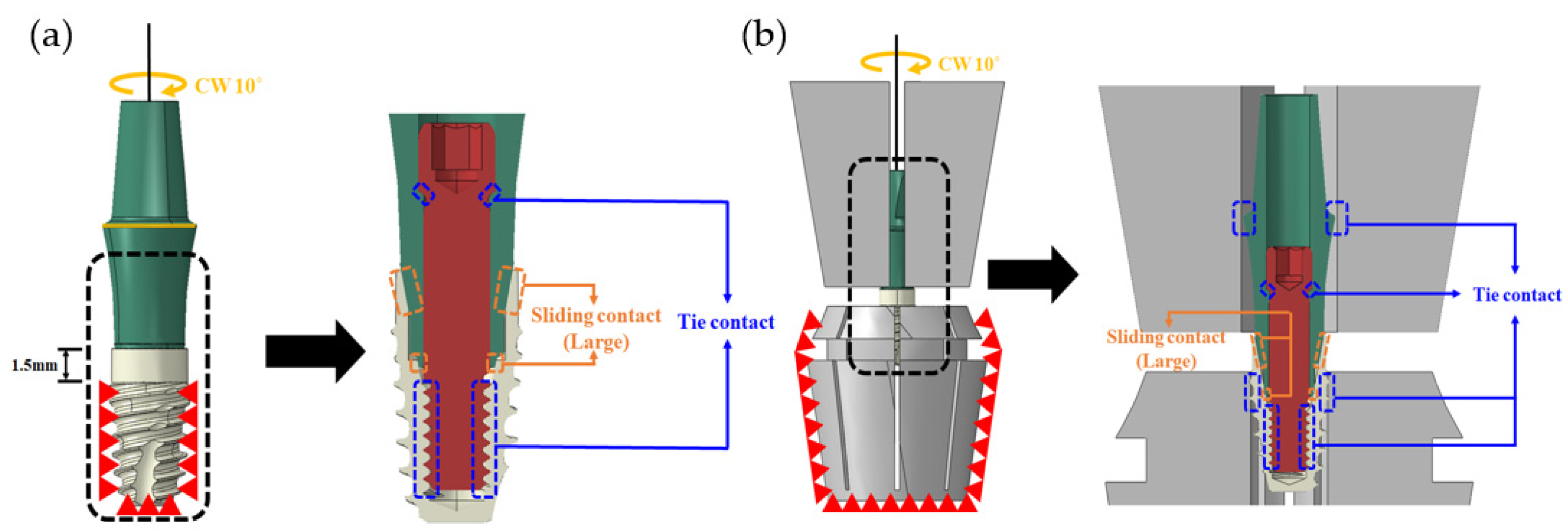
2.1.1. FE Model of Dental Implants
2.1.2. Simulation
2.1.3. Mechanical Test Method for FE Model Validation
2.2. Part 2: Total Knee Replacement (TKR)
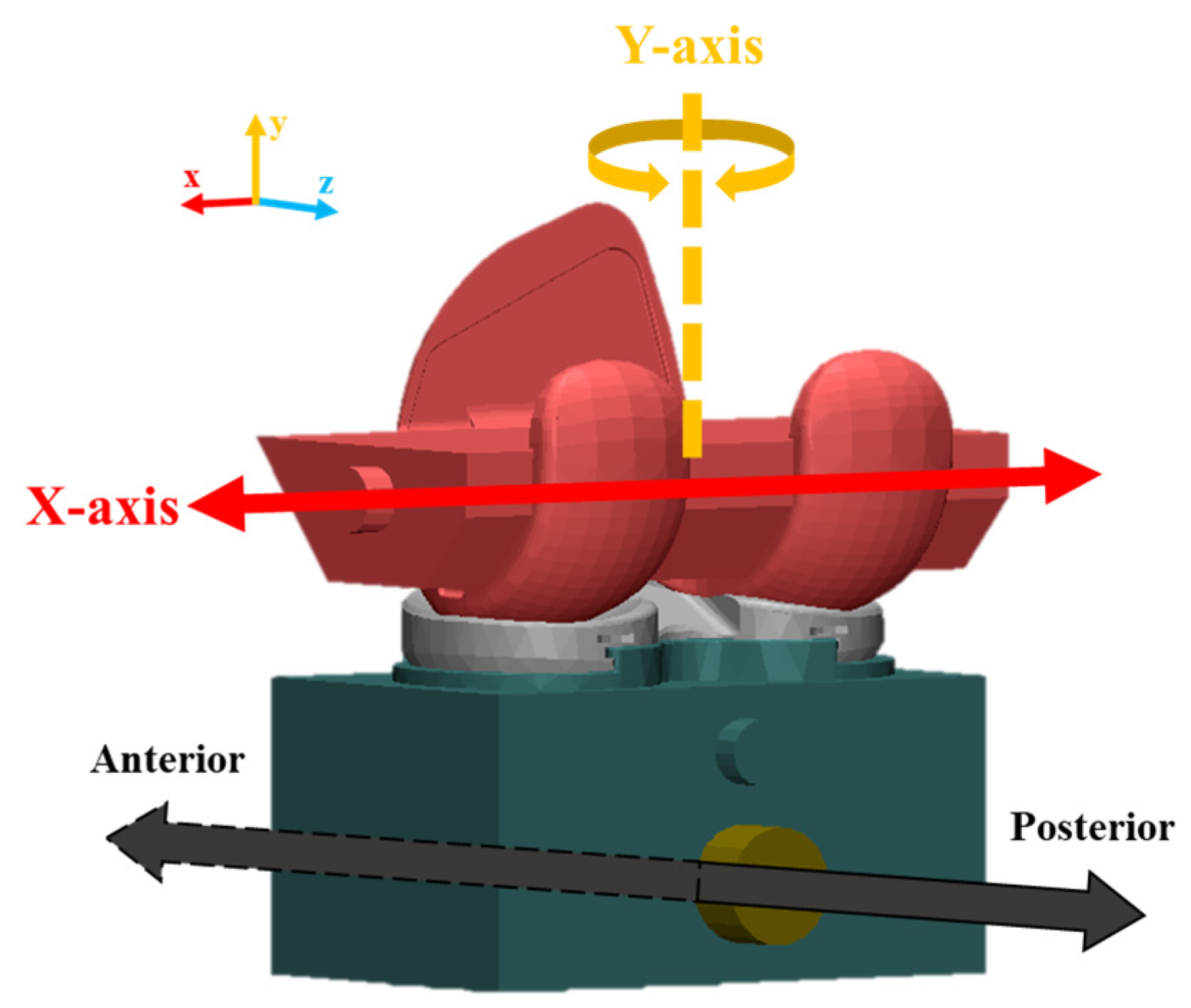
2.2.1. FE Model of TKR
2.2.2. Simulation
2.2.3. Mechanical Test for FE Model Validation
3. Results
3.1. Part 1: Dental Implant
3.1.1. Mechanical Test Results
3.1.2. Dental Implant Simulation
3.2. Part 2: Total Knee Replacement
3.2.1. Finite Element Modeling
3.2.2. Validation of the Finite Element Model
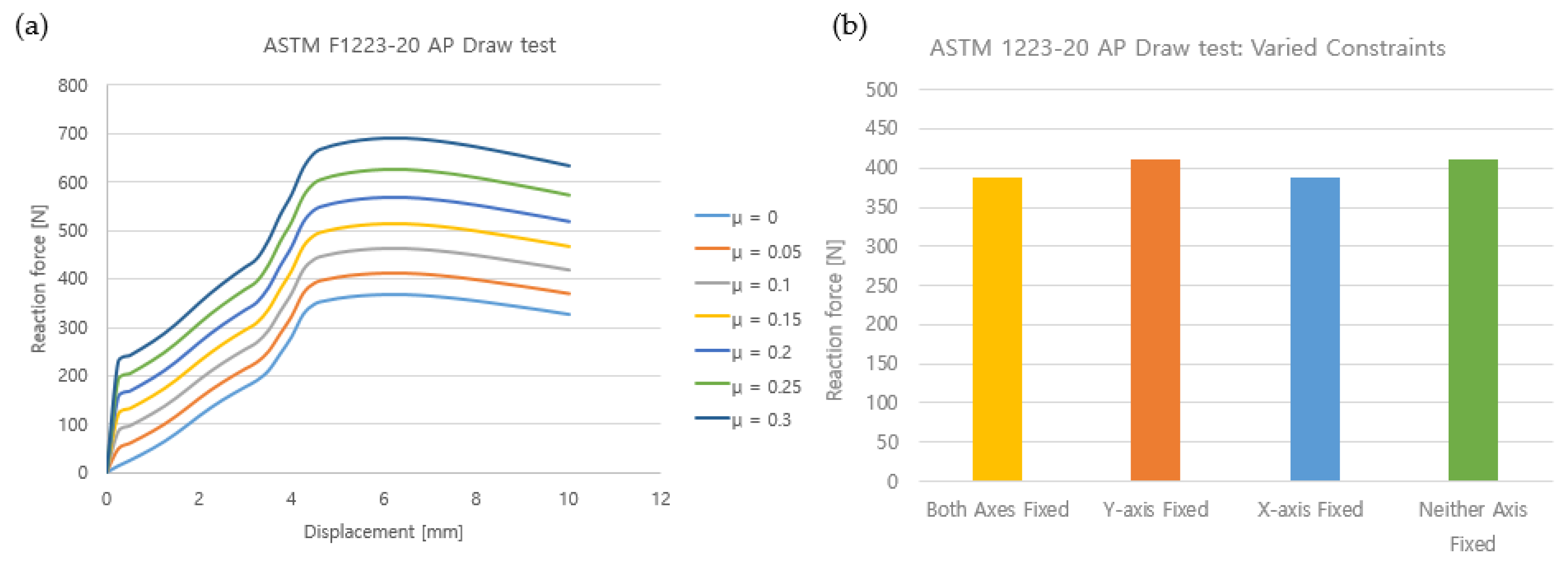
3.2.3. TKR Constraint Simulation
4. Discussion
4.1. Part 1: Dental Implants
4.2. Part 2: Total Knee Replacement (TKR)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fagan, M.J.; Julian, S.; Mohsen, A.M. Finite Element Analysis in Spine Research. Proc. Inst. Mech. Eng. Part H 2002, 216, 281–298. [Google Scholar] [CrossRef] [PubMed]
- Baumann, A.P.; Graf, T.; Peck, J.H.; Dmitriev, A.E.; Coughlan, D.; Lotz, J.C. Assessing the Use of Finite Element Analysis for Mechanical Performance Evaluation of Intervertebral Body Fusion Devices. JOR Spine 2021, 4, e1137. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Food and Drug Safety. Performance and Safety Evaluation Test Manual for Dental Implants; Ministry of Food and Drug Safety: Seoul, Republic of Korea, 2015; pp. 1–37.
- US Food and Drug Administration. Successes and Opportunities in Modeling & Simulation for FDA; US Food and Drug Administration: Silver Spring, MD, USA, 2022; pp. 1–29.
- ASME V&V 40; Assessing Credibility of Computational Modeling through Verification and Validation: Application to Medical Devices. The American Society of Mechanical Engineers: New York, NY, USA, 2018.
- ASTM F2996; Standard Practice for Finite Element Analysis (FEA) of Non-Modular Metallic Orthopaedic Hip Femoral Stems. ASTM International: West Conshohocken, PA, USA, 2020; Volume 13, pp. 1–11. [CrossRef]
- ASTM F3161; Standard Test Method for Finite Element Analysis (FEA) of Metallic Orthopaedic Total Knee Femoral Components under Closing Conditions. ASTM International: West Conshohocken, PA, USA, 2016; Volume 13, pp. 1–7. [CrossRef]
- Gomes, C.; Mesnard, M.; Ramos, A.A. Bone density and proximal support effects on dental implant stability–Finite element analysis and in vitro experiments. J. Stomatol. Oral Maxillofac. Surg. 2023, 124, 101512. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.L.; Lin, T.W.; Tsai, H.L.; Wu, Y.L.; Wu, A.Y.J. Biomechanical effects of bone atrophy, implant design, and vertical or tilted of posterior implant on all-on-four concept implantation: Finite element analysis. J. Med. Biol. Eng. 2022, 42, 488–497. [Google Scholar] [CrossRef]
- Sadighi, A.; Taghvaei, M.; Taheri, M.; Oeth, D.; Siegler, S.; Schaer, T.P.; Najafi, A.R. Numerical analysis of the mechanical response of novel swelling bone implants in polyurethane foams. J. Mech. Behav. Biomed. Mater. 2023, 143, 105871. [Google Scholar] [CrossRef]
- Baumann, A.P.; Hsieh, M.-T.; Dmitriev, A.E.; Lotz, J.C. The Relative Influence of Model Parameters on Finite Element Analysis Simulations of Intervertebral Body Fusion Device Static Compression Performance. Comput. Methods Biomech. Biomed. Eng. 2022, 26, 1742–1751. [Google Scholar] [CrossRef] [PubMed]
- ISO/TS 13498; Dentistry-Torsion Test of Implant Body/Connecting Part Joint of Endosseous Dental Implant Systems. ISO International Organization for Standardization: Geneve, Switzerland, 2011; Volume 1, pp. 1–7.
- ISO 14801; Dentistry-Implants Dynamic Loading Test for Endosseous Dental Imaplnts. ISO: Geneve, Swirzerland, 2016; Volume 3, pp. 1–6.
- ASTM F1223; Standard Test Method for Determination of Total Knee Replacement Constraint. ASTM International: West Conshohocken, PA, USA, 2020; Volume 13, pp. 1–9. [CrossRef]
- ASTM F2083; Standard Specification for Knee Replacement Prosthesis. ASTM International: West Conshohocken, PA, USA, 2021; Volume 13, pp. 1–10. [CrossRef]
- Musikul, T.; Kitkamthorn, U.; Mitsomwang, P.; Sindhupakorn, B.; Borrisutthekul, R. Influence of Axial Force and Characteristics of Axial Force Affecting on Total Knee Replacement Constraint Test. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1137, 012041. [Google Scholar] [CrossRef]
- Yan, L.; Jiang, A.; Qiu, T.; Jiang, F.; Xie, H. Dynamic constitutive models of Ti-6Al-4V based on isothermal ture stress-strain curves. J. Mater. Res. Technol. 2022, 19, 4733–4744. [Google Scholar] [CrossRef]
- Li, Q.; Xu, Y.B.; Bassim, M.N. Dynamic mechanical behavior of pure titanium. J. Mater. Process. Technol. 2004, 155, 1889–1892. [Google Scholar] [CrossRef]
- Tianye, L.; Peng, Y.; Jingli, X.; Qiushi, W.; GuangQuan, Z.; Wei, H. Finite element analysis of different internal fixation methods for the treatment of Pauwels type III femoral neck fracture. Biomed. Pharmacother. 2019, 112, 108658. [Google Scholar] [CrossRef]
- Ahmed, R.S.; Atiyah, K.A.; Abdulasahib, I.A. Control of vibration by using dynamic vibration absorber. IOP Conf. Ser. Mater. Sci. Eng. 2020, 881, 108658. [Google Scholar] [CrossRef]
- Saideepak, R. Inspection of CP Titanium Material and its Coefficient of Friction. Int. Res. J. Eng. Technol. 2021, 8, 318–326. [Google Scholar]
- de Ruiter, L.; Janssen, D.; Briscoe, A.; Verdonschot, N. A Preclinical Numerical Assessment of a Polyetheretherketone Femoral Component in Total Knee Arthroplasty during Gait. J. Exp. Orthop. 2017, 4, 3. [Google Scholar] [CrossRef] [PubMed]
- Cawley, D.T.; Kelly, N.; Simpkin, A.; Shannon, F.J.; McGarry, J.P. Full and Surface Tibial Cementation in Total Knee Arthroplasty: A Biomechanical Investigation of Stress Distribution and Remodeling in the Tibia. Clin. Biomech. 2012, 27, 390–397. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Food and Drug Safety. Medical Device Simulation Evaluation Using Computer Modeling; Ministry of Food and Drug Safety: Seoul, Republic of Korea, 2021; pp. 1–73.
- Cho, Y.J.; Kim, Y.H.; Jang, H.S.; Kang, T.J.; Lee, W.J. A Study of Multi-Surface Treatments on the Porous Ti Implant for the Enhancement of Bioactivity. Korean J. Mater. Res. 2008, 18, 229–234. [Google Scholar] [CrossRef]
- Ashtiani, R.E.; Alam, M.; Tavakolizadeh, S.; Abbasi, A. The Role of Biomaterials and Biocompatible Materials in Implant-Supported Dental Prosthesis. Evid.-Based Complement. Altern. Med. 2021, 2021, 3349433. [Google Scholar] [CrossRef]
- Steigenga, J.T.; Al-Shammari, K.F.; Nociti, F.H.; Misch, C.E.; Wang, H.L. Dental Implant Design and Its Relationship to Long-Term Implant Success. Implant Dent. 2003, 12, 306–317. [Google Scholar] [CrossRef]
- Skalak, R. Biomechanical considerations in osseointegrated prostheses. J. Prosthet. Dent. 1983, 49, 843–848. [Google Scholar] [CrossRef]
- Rieger, M.R.; Adams, W.K.; Kinzel, G.L. A finite element survey of eleven endosseous implants. J. Prosthet. Dent. 1990, 63, 457–465. [Google Scholar] [CrossRef]
- Holmgren, E.P.; Seckinger, R.J.; Kilgren, L.M.; Mante, F. Evaluating parameters of osseointegrated dental implants using finite element analysis-a two-dimensional comparative study examining the effects of implant diameter, implant shape, and load direction. J. Oral Implantol. 1998, 24, 80–88. [Google Scholar] [CrossRef]
- Brunski, J.B. Biomaterials and biomechanics in dental implant design. Int. J. Oral Maxillafoc. Implant. 1998, 3, 85–97. [Google Scholar]
- Seaton, P. Mechanics of tensile and shear stress generation in fixed partial denture retainers. J. Prosthet. Dent. 1994, 71, 237–244. [Google Scholar] [CrossRef] [PubMed]
- Kumararama, S.S.; Chowdhary, R. Selection of dental implants based on masticatory load of the patient: A novel approach. Indian J. Dent. Res. 2017, 28, 309–313. [Google Scholar] [CrossRef] [PubMed]
- Steinbrück, A.; Woiczinski, M.; Weber, P.; Müller, P.E.; Jansson, V.; Schröder, C. Posterior Cruciate Ligament Balancing in Total Knee Arthroplasty: A Numerical Study with a Dynamic Force-Controlled Knee Model. Biomed. Eng. Online 2014, 13, 19. [Google Scholar] [CrossRef]







| Model | Material | Young’s Modulus (MPa) | Poisson’s Rate | Reference |
|---|---|---|---|---|
| Abutment | Ti-6Al-4V alloy | Nonlinear | 0.35 | [17] |
| Abutment Screw | ||||
| Fixture | Titanium grade 4 | Nonlinear | 0.34 | [18] |
| Hydraulic Grip | Stainless steel | 207,000 | 0.3 | [19] |
| Collet | Spring steel | 210,000 | 0.3 | [20] |
| Components | Element Type | Number of Node | Number of Element | Element Size (mm) |
|---|---|---|---|---|
| Abutment (rigid, long) | Tetrahedral (C3D4) | 24,803 | 128,672 | 0.2 |
| Abutment (rigid, short) | 18,274 | 93,836 | ||
| Abutment (2-piece, long) | 17,601 | 80,544 | ||
| Abutment (2-piece, short) | 12,209 | 54,754 | ||
| Abutment (angled, 15°) | 18,041 | 88,784 | ||
| Abutment (angled, 25°) | 18,226 | 89,182 | ||
| Abutment screw | 9822 | 48,395 | ||
| Fixture | 20,379 | 95,225 | ||
| Hydraulic grip | 62,428 | 332,308 | 0.5 | |
| Collet | 39,194 | 191,212 |
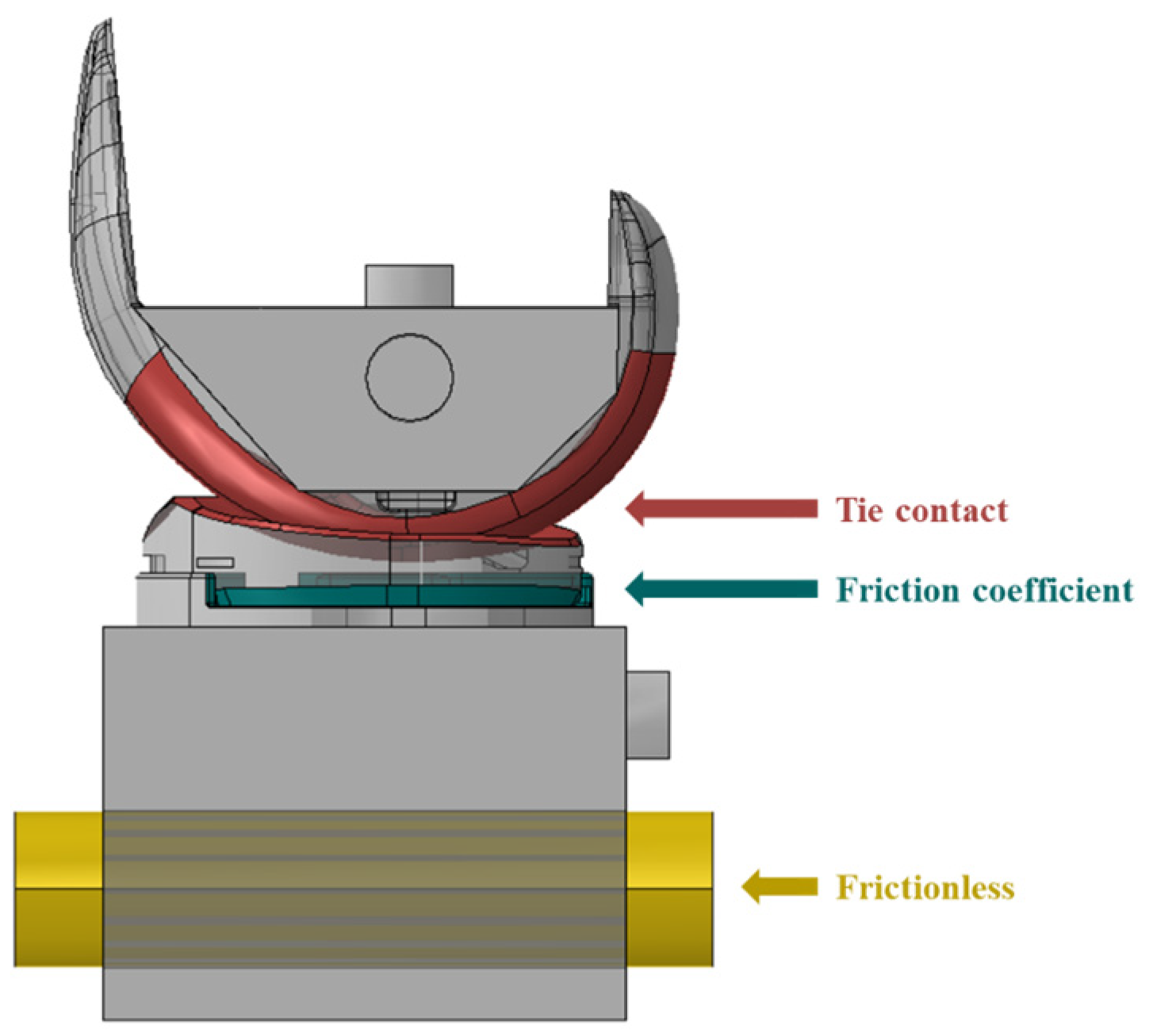
| Case | Abutment Loading Area | Sliding Contact | ||
|---|---|---|---|---|
| Area | Sliding Formulation | |||
| Finite Sliding | Small Sliding | |||
| Node to Surface | Surface to Surface | |||
| 1 | All | Fixed | O | |
| 2 | All | Fixed | O | |
| 3 | All | O | ||
| 4 | Part | O | ||
| 5 | Part | O | ||
| 6 | Part | O | ||
| Model | Material | Young’s Modulus (MPa) | Poisson’s Rate |
|---|---|---|---|
| Femoral Component | Co-Cr-Mo Ally | 21,000 | 0.33 |
| Baseplate | |||
| Jig | |||
| Rail | |||
| Insert | UHMWPE | 900 | 0.42 |
| Case | Boundary Condition | Elastic Modulus (MPa) | Friction Coefficient (μ) | |
|---|---|---|---|---|
| X-Axis (Medial–Lateral) | Y-Axis (Valgus–Varus) | |||
| 1 | Fixed | Fixed | 900 | 0~0.3 (0.05 units) |
| 2 | Fixed | 0.05 | ||
| 3 | Fixed | |||
| 4 | ||||
| 5 | ||||
| 6 | 855, 900, 945 | 0.15 | ||
| Components | Yield Angle (°) | Yield Torque (Nm) |
|---|---|---|
| Rigid type (Long) | 6.31 ± 0.25 | 0.81 ± 0.01 |
| Rigid type (Short) | 3.35 ± 0.60 | 0.61 ± 0.05 |
| 2-piece type (Long) | 6.02 ± 0.07 | 0.77 ± 0.03 |
| 2-piece type (Short) | 5.01 ± 0.09 | 0.92 ± 0.02 |
| Angled type (15°) | 5.02 ± 0.09 | 0.97 ± 0.02 |
| Angled type (25°) | 5.10 ± 0.26 | 0.95 ± 0.03 |
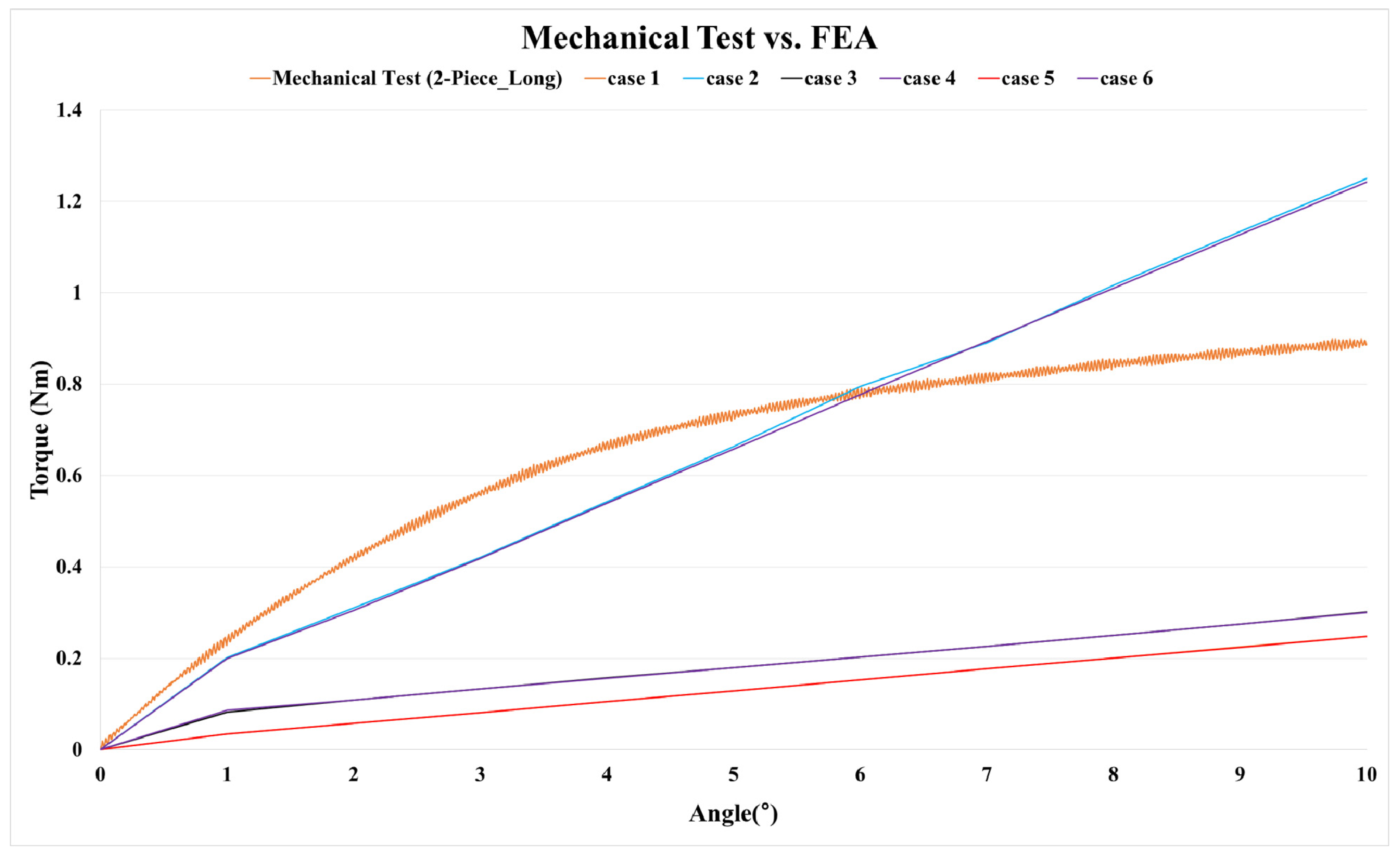
| Model | Results | Case | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 2-piece type (long) | FEA (Nm) | 0.15 | 0.80 | 0.20 | 0.78 | 0.15 | 0.20 |
| Mechanical test (Nm) | 0.77 | ||||||
| Error rate (%) | −80.5 | 3.9 | −74.0 | 1.3 | −80.5 | −74.0 | |
| Model (a) | |||||||
| Rigid (Long) | Rigid (Short) | 2-Piece (Long) | 2-Piece (Short) | Angled (15°) | Angled (25°) | ||
| Yield angle (°) | Experiment | 6.07~6.70 | 2.54~4.19 | 5.98~6.14 | 4.87~5.11 | 4.89~5.61 | 4.92~5.17 |
| Average | 6.31 | 3.35 | 6.02 | 5.01 | 5.10 | 5.02 | |
| FEA | 6 | 3 | 6 | 5 | 5 | 5 | |
| Error Rate (%) | −4.91 | −10.45 | −0.33 | −0.19 | −1.96 | −0.39 | |
| Yield Torque (Nm) | Experiment | 0.78~0.82 | 0.53~0.66 | 0.75~0.81 | 0.91~0.95 | 0.90~0.98 | 0.94~0.98 |
| Average | 0.80 | 0.61 | 0.77 | 0.92 | 0.95 | 0.97 | |
| FEA | 0.81 | 0.60 | 0.78 | 0.94 | 0.96 | 0.95 | |
| Error Rate (%) | 1.23 | 1.64 | 1.29 | 2.17 | 1.05 | −2.06 | |
| Model (b) | |||||||
| Rigid (Long) | Rigid (Short) | 2-Piece (Long) | 2-Piece (Short) | Angled (Long) | Angled (Short) | ||
| Yield angle (°) | Experiment | 6.07~6.70 | 2.54~4.19 | 5.98~6.14 | 4.87~5.11 | 4.89~5.61 | 4.92~5.17 |
| Average | 6.31 | 3.35 | 6.02 | 5.01 | 5.10 | 5.02 | |
| FEA | 6 | 3 | 6 | 5 | 5 | 5 | |
| Error Rate (%) | −4.91 | −10.45 | −0.33 | −0.19 | −1.96 | −0.39 | |
| Yield Torque (Nm) | Experiment | 0.78~0.82 | 0.53~0.66 | 0.76~0.80 | 0.91~0.95 | 0.90~0.98 | 0.94~0.98 |
| Average | 0.80 | 0.61 | 0.77 | 0.92 | 0.95 | 0.97 | |
| FEA | 0.47 | 0.75 | 0.40 | 0.64 | 0.61 | 0.76 | |
| Error Rate (%) | −41.25 | 22.95 | −48.05 | −30.43 | −35.79 | −21.65 | |
| Components | Element Type | Number of Nodes | Number of Elements | Element Size (mm) |
|---|---|---|---|---|
| Femoral Component + jig | Tetrahedral (C3D10) | 60,137 | 40,182 | 4 |
| Baseplate + jig | 40,542 | 25,971 | 2.5 | |
| Insert | 31,243 | 20,580 | 5 | |
| Rail | 686 | 357 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, K.-S.; Park, K.-M.; Ahn, J.-W.; Jo, M.-Y.; Oh, Y.-R.; Youn, J.-H.; Lee, J.-W.; Je, D.-Y.; Jung, T.-G. Validation of the Finite Element Model versus Biomechanical Assessments of Dental Implants and Total Knee Replacements. Bioengineering 2023, 10, 1365. https://doi.org/10.3390/bioengineering10121365
Kang K-S, Park K-M, Ahn J-W, Jo M-Y, Oh Y-R, Youn J-H, Lee J-W, Je D-Y, Jung T-G. Validation of the Finite Element Model versus Biomechanical Assessments of Dental Implants and Total Knee Replacements. Bioengineering. 2023; 10(12):1365. https://doi.org/10.3390/bioengineering10121365
Chicago/Turabian StyleKang, Kwan-Su, Kwang-Min Park, Jin-Woo Ahn, Min-Young Jo, Yu-Rim Oh, Jin-Ho Youn, Jeong-Woo Lee, Dong-Young Je, and Tae-Gon Jung. 2023. "Validation of the Finite Element Model versus Biomechanical Assessments of Dental Implants and Total Knee Replacements" Bioengineering 10, no. 12: 1365. https://doi.org/10.3390/bioengineering10121365
APA StyleKang, K.-S., Park, K.-M., Ahn, J.-W., Jo, M.-Y., Oh, Y.-R., Youn, J.-H., Lee, J.-W., Je, D.-Y., & Jung, T.-G. (2023). Validation of the Finite Element Model versus Biomechanical Assessments of Dental Implants and Total Knee Replacements. Bioengineering, 10(12), 1365. https://doi.org/10.3390/bioengineering10121365






