Multilayer In Vitro Human Skin Tissue Platforms for Quantitative Burn Injury Investigation
Abstract
:1. Introduction
2. Material and Methods
2.1. In Vitro Skin Platform Preparation
2.1.1. Cell Culture
2.1.2. Preparation of Collagen
2.1.3. Single-Layer Skin Platform Creation
2.1.4. Multilayer Skin Platform Creation
2.2. Platform Characterization
2.2.1. Cell Viability Testing
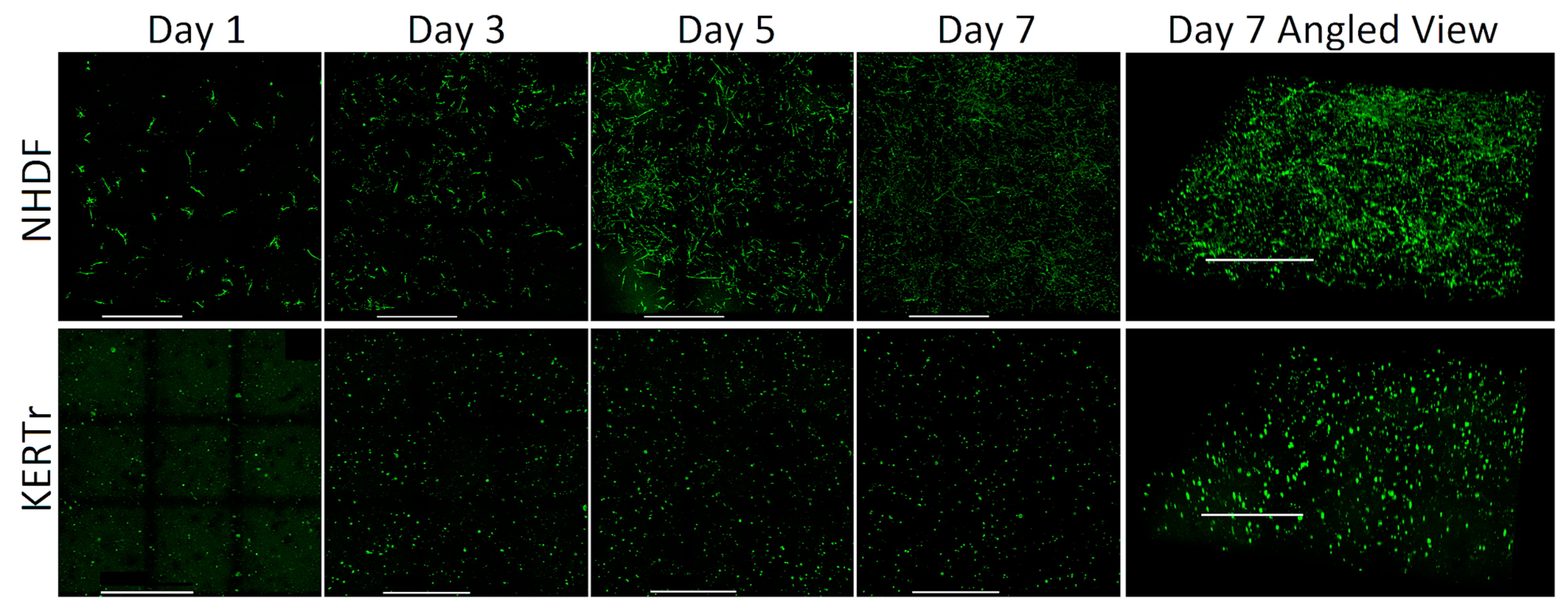
2.2.2. Spatial Distribution of Cells
2.2.3. Mechanical Testing
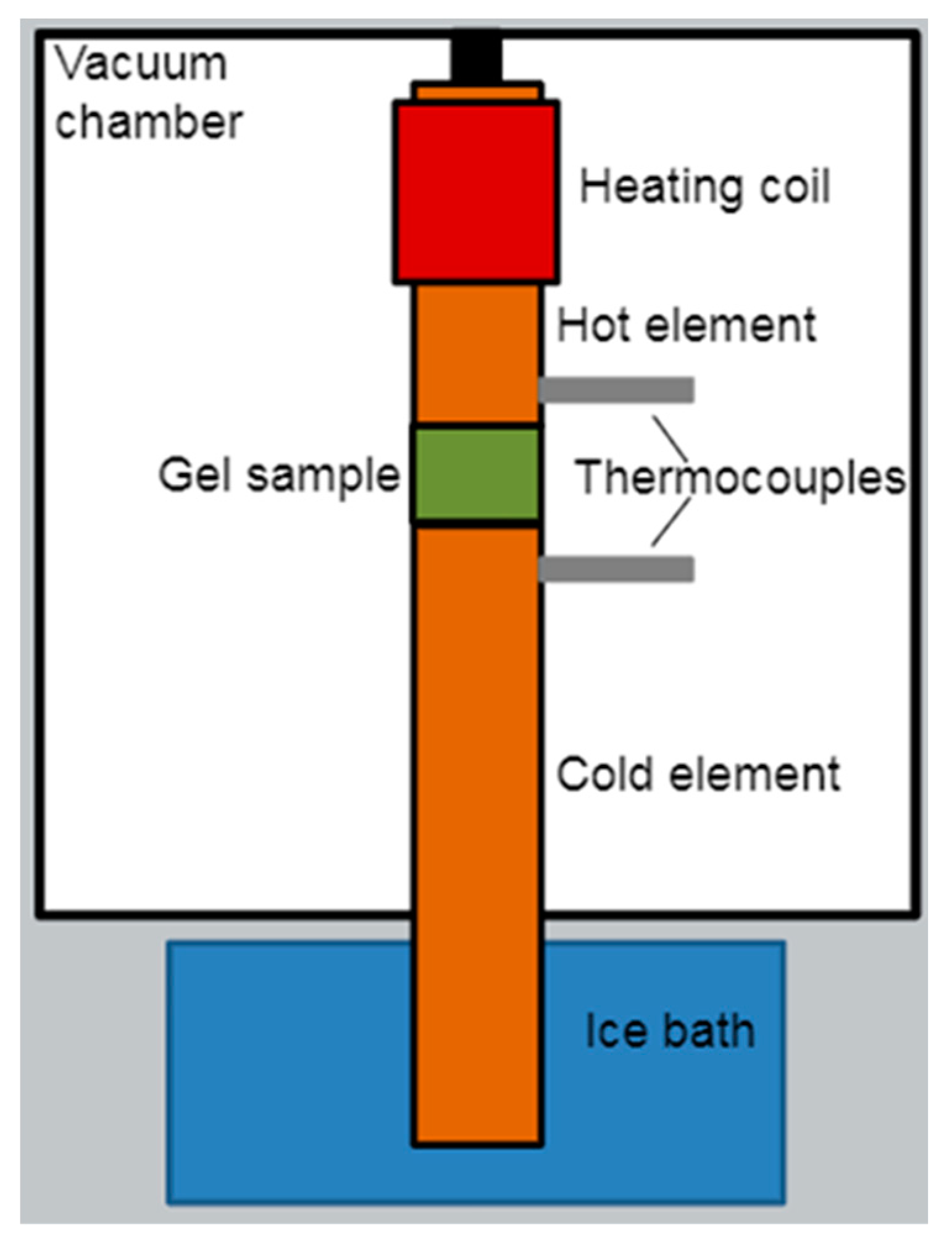
2.2.4. Specific Heat Capacity and Thermal Conductivity Characterization
2.2.5. Characterizing Thermal Collagen Degradation
2.3. Burn Testing
2.3.1. Contact Burn Testing
2.3.2. Cell Viability and Apoptosis in Burn Injury
2.3.3. Heat Shock Protein 70 Expression in Burn Injury
2.3.4. Burn Injury Evaluation
2.4. Computational Modeling of Temperature Profile
2.4.1. Calculating Temperature Distributions
2.4.2. Isoeffective Thermal Dose Calculations
2.4.3. Determining Arrhenius Coefficients for Contact Burns
2.4.4. Contact Burn Injury Thresholds and Predictions
3. Results
3.1. Characterization
3.1.1. Viability
3.1.2. Spatial Distribution of Cells
3.1.3. Mechanical Properties and Consistency Evaluation
3.1.4. Thermal Properties
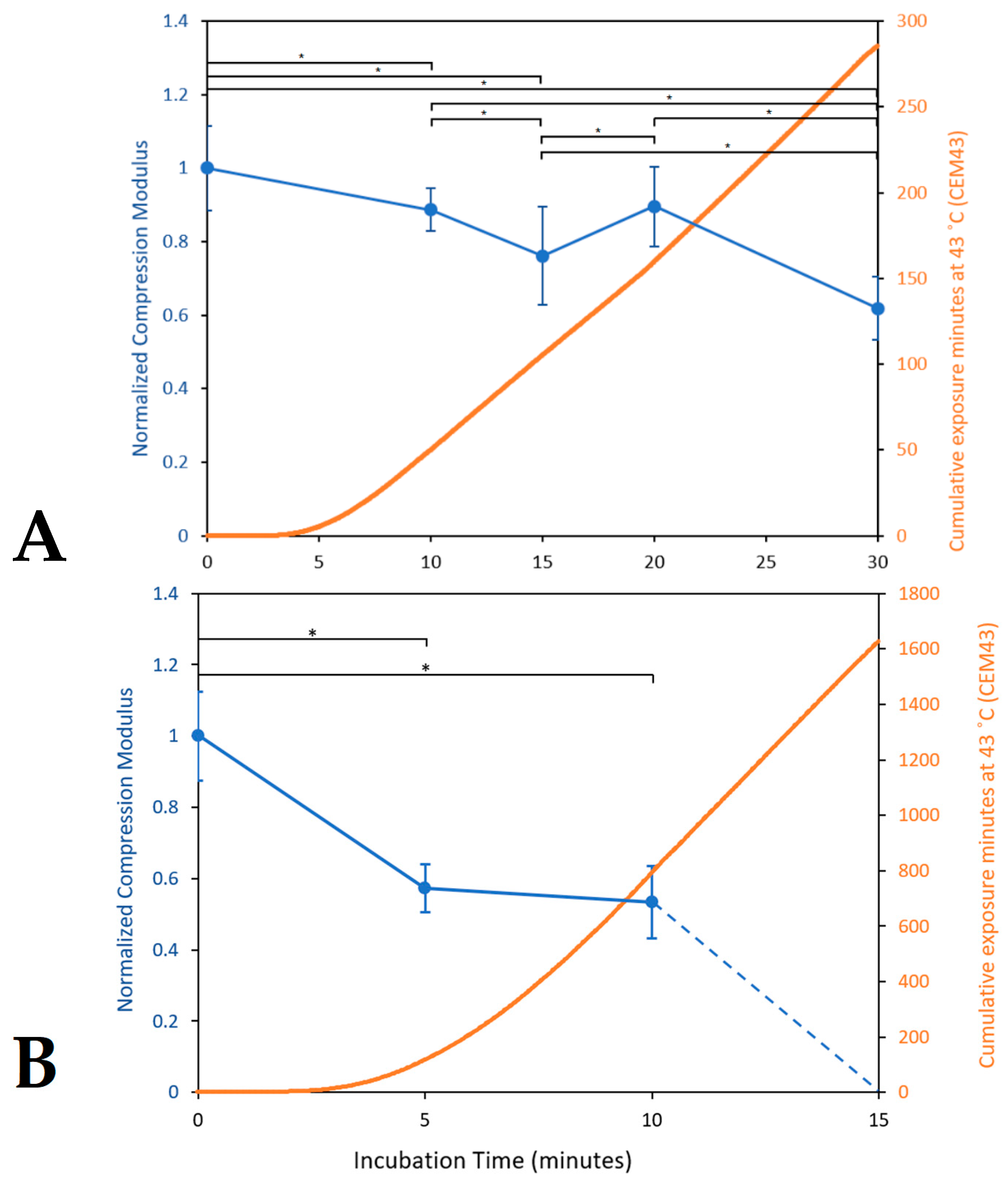
3.1.5. Characterizing Thermal Collagen Degradation
3.2. Burn Testing and Modeling
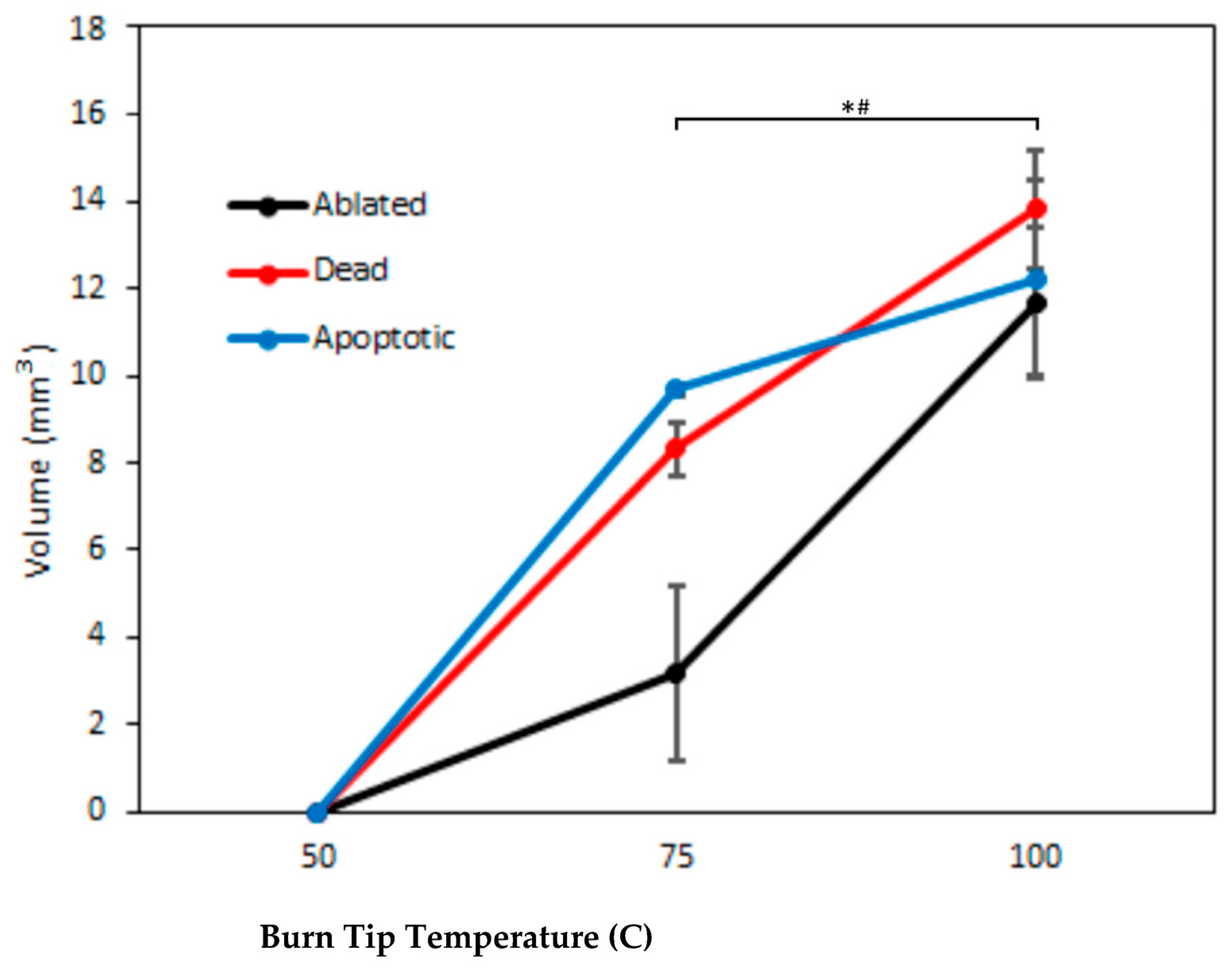
3.2.1. Contact Burn Testing Results
3.2.2. Contact Burn Modeling Results
4. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ryan, C.M.; Parry, I.; Richard, R. Functional outcomes following burn injury. J. Burn. Care Res. 2017, 38, e614–e617. [Google Scholar] [CrossRef] [PubMed]
- Kollias, S.; Stampolidis, N.; Kourakos, P.; Mantzari, E.; Koupidis, S.; Tsaousi, S.; Dimitrouli, A.; Atiyeh, B.; Castana, O. Abdominal compartment syndrome (ACS) in a severely burned patient. Ann. Burn. Fire Disasters 2015, 28, 5–8. [Google Scholar]
- Borrelli, M.J.; Thompson, L.L.; Cain, C.A.; Dewey, W.C. Time-temperature analysis of cell killing of BHK cells heated attemperatures in the range of 43.5 °C to 57.0 °C. Int. J. Radiat. Oncol. Biol. Phys. 1990, 19, 389–399. [Google Scholar] [CrossRef]
- Viglianti, B.L.; Dewhirst, M.W. Thresholds for thermal damage to normal tissues: An update. Int. J. Hyperth. 2013, 27, 320–343. [Google Scholar] [CrossRef]
- Martin, N.A.; Falder, S. ScienceDirect A review of the evidence for threshold of burn injury. Burns 2017, 43, 1624–1639. [Google Scholar] [CrossRef]
- He, X.; Bhowmick, S.; Bischof, J.C. Thermal Therapy in Urologic Systems: A Comparison of Arrhenius and Thermal Isoeffective Dose Models in Predicting Hyperthermic Injury. J. Biomech. Eng. 2009, 131, 074507. [Google Scholar] [CrossRef]
- Dewhirst, M.W.; Viglianti, B.L.; Lora-Michiels, M.; Hanson, M.; Hoopes, P.J. Basic Principles of Thermal Dosimetry and Thermal Thresholds for Tissue Damage From Hyperthermia. Int. J. Hyperth. 2003, 19, 267–294. [Google Scholar] [CrossRef]
- Rylander, M.N.; Feng, Y.; Zimmermann, K.; Kenneth, R.; Diller, K.R. Measurement and mathematical modeling of thermally induced injury and heat shock protein expression kinetics in normal and cancerous prostate cells. Int. J. Hyperth. 2010, 26, 748–764. [Google Scholar] [CrossRef]
- Hewitt, N.J.; Edwards, R.J.; Fritsche, E.; Goebel, C.; Aeby, P.; Scheel, J.; Reisinger, K.; Ouédraogo, G.; Duche, D.; Eilstein, J.; et al. Use of Human In Vitro Skin Models for Accurate and Ethical Risk Assessment: Metabolic Considerations. Toxicol. Sci. 2013, 133, 209–217. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhong, Y.; Subic, A.; Jazar, R.; Smith, J.; Gu, C. Prediction of tissue thermal damage. Technol. Health Care 2016, 24, S625–S629. [Google Scholar] [CrossRef] [Green Version]
- Van Rhoon, G.C.; Samaras, T. CEM43 °C thermal dose thresholds: A potential guide for magnetic resonance radiofrequency exposure levels? Eur. Radiol. 2013, 23, 2215–2227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wright, N.; Humphrey, J. Denaturation of collagen via heating: An irreversible rate process. Annu. Rev. Biomed. Eng. 2002, 4, 109–128. [Google Scholar] [CrossRef] [PubMed]
- Pearce, J.A.; Thomsen, S.L.M.D.; Vijverberg, H.; McMurray, T.J. Kinetics for Birefringence Changes in Thermally Coagulated Rat Skin Collagen; Proc. Society of Photo-Optical Instrumentation Engineers: Los Angeles, CA, USA; Bellingham, WA, USA, 1993; pp. 180–186. [Google Scholar]
- van Rhoon, G.C. Is CEM43 still a relevant thermal dose parameter for hyperthermia treatment monitoring? Int. J. Hyperth. 2016, 32, 50–62. [Google Scholar] [CrossRef]
- Pearce, J.A. Comparative analysis of mathematical models of cell death and thermal damage processes. Int. J. Hyperth. 2013, 29, 262–280. [Google Scholar] [CrossRef]
- Kashcooli, M.; Salimpour, M.R.; Shirani, E. Heat transfer analysis of skin during thermal therapy using thermal wave equation. J. Therm. Biol. 2017, 64, 7–18. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.B.; Wang, Z.K.; Tian, S.H.; Chen, X.F. Analysis and modelling of non-fourier heat behavior using the wavelet finite element method. Materials 2019, 12, 1337. [Google Scholar] [CrossRef] [Green Version]
- Chaudhari, A.A.; Vig, K.; Baganizi, D.R.; Sahu, R.; Dixit, S.; Dennis, V.; Singh, S.R.; Pillai, S.R.; Chaudhari, A.A.; Vig, K.; et al. Future Prospects for Scaffolding Methods and Biomaterials in Skin Tissue Engineering: A Review. Int. J. Mol. Sci. 2016, 17, 1974. [Google Scholar] [CrossRef]
- Ross, D.C.; Diller, K.R. An Experimental Investigation of Burn Injury in Living Tissue. ASME J. Heat Transf. 1976, 98, 292–296. [Google Scholar] [CrossRef]
- Henriques, F.C.; Moritz, A.R. Studies of Thermal Injury. I. The Conduction of Heat to and Through Skin and the Temperatures Attained Therein. A Theoretical and an Experimental Investigation. Am. J. Pathol. 1947, 23, 531–549. [Google Scholar]
- Weaver, J.A.; Stoll, A.M. Mathematical model of skin exposed to thermal radiation. Aerosp. Med. 1969, 40, 24–30. [Google Scholar] [CrossRef]
- Reijnders, C.M.A.; Van Lier, A.; Roffel, S.; Kramer, D.; Scheper, R.J.; Gibbs, S. Development of a Full-Thickness Human Skin Equivalent In Vitro Model Derived from TERT-Immortalized Keratinocytes and Fibroblasts. Tissue Eng. Part A 2015, 21, 2448–2459. [Google Scholar] [CrossRef] [Green Version]
- Vaughan, M.B.; Ramirez, R.D.; Brown, S.A.; Yang, J.C.; Wright, W.E.; Shay, J.W. A reproducible laser-wounded skin equivalent model to study the effects of aging in vitro. Rejuvenation Res. 2004, 7, 99–110. [Google Scholar] [CrossRef]
- Emanuelsson, P.; Kratz, G. Characterization of a new in vitro burn wound model. Burns 1997, 23, 32–36. [Google Scholar] [CrossRef] [PubMed]
- Auxenfans, C.; Fradette, J.; Lequeux, C.; Germain, L.; Kinikoglu, B.; Bechetoille, N.; Braye, F.; Auger, F.A.; Damour, O. Evolution of three dimensional skin equivalent models reconstructed in vitro by tissue engineering. Eur. J. Dermatol. 2009, 19, 107–113. [Google Scholar] [CrossRef]
- Middelkoop, E.; Van Den Bogaerdt, A.J.; Lamme, E.N.; Hoekstra, M.J. Porcine wound models for skin substitution and burn treatment. Biomaterials 2003, 25, 1559–1567. [Google Scholar] [CrossRef] [PubMed]
- Coolen, N.A.; Vlig, M.; Van Den Bogaerdt, A.J.; Middelkoop, E.; Ulrich, M.M.W. Development of an in vitro burn wound model. Wound Repair Regen. 2008, 16, 559–567. [Google Scholar] [CrossRef]
- Gallin, W.J.; Hepperle, B. Burn healing in organ cultures of embryonic chicken skin: A model system. Burns 1998, 24, 613–620. [Google Scholar] [CrossRef]
- Abdullahi, A.; Amini-Nik, S.; Jeschke, M.G. Animal models in burn research. NIH Public Access. Cell. Mol. Life Sci. 2009, 49, 1841–1850. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tepole, A.B.; Gart, M.; Gosain, A.K.; Kuhl, E. Characterization of living skin using multi-view stereo and isogeometric analysis. Acta Biomater. 2014, 10, 4822–4831. [Google Scholar] [CrossRef] [Green Version]
- Roy, D.C.; Tomblyn, S.; Isaac, K.M.; Kowalczewski, C.J.; Burmeister, D.M.; Burnett, L.R.; Christy, R.J. Ciprofloxacin-loaded keratin hydrogels reduce infection and support healing in a porcine partial-thickness thermal burn. Wound Repair Regen. 2016, 24, 657–668. [Google Scholar] [CrossRef]
- Koruda, M.; Gregg, R. Assessing Burn Wound Depth Using in Vitro Nuclear Magnetic Resonance (NMR). J. Surg. Res. 1986, 1, 475–481. [Google Scholar] [CrossRef]
- Hogg, P.; Rooney, P.; Leow-Dyke, S.; Brown, C.; Ingham, E.; Kearney, J.N. Development of a terminally sterilised decellularised dermis. Cell Tissue Bank. 2015, 16, 351–359. [Google Scholar] [CrossRef]
- Bailoo, J.D.; Reichlin, T.S.; Würbel, H. Refinement of experimental design and conduct in laboratory animal research. ILAR J. 2014, 55, 383–391. [Google Scholar] [CrossRef] [Green Version]
- Wiart, M.; Curiel, L.; Gelet, A.; Lyonnet, D.; Chapelon, J.Y.; Rouvière, O. Influence of perfusion on high-intensity focused ultrasound prostate ablation: A first-pass MRI study. Magn. Reson. Med. 2007, 58, 119–127. [Google Scholar] [CrossRef]
- Dewey, W.C.; Freeman, M.L.; Raaphorst, G.P.; Clark, E.P.; Wong, R.S.L.; Highfield, D.P.; Spiro, I.J.; Tomasovic, C.P.; Denman, D.L.; Coss, R.A. Cell Biology of Hyperthermia and Radiation; Radiation Biology in Cancer, Research; Meyn, R.E., Withers, H.R., Eds.; Raven Press: New York, NY, USA, 1980; pp. 589–621. [Google Scholar]
- Weinberg, W.A. The Biology of Cancer; Garland Science: New York, NY, USA, 2007. [Google Scholar]
- Matsuura, Y.; Noda, K.; Suzuki, S.; Kawai, K. Glucocorticoids suppress fibroblast apoptosis in an in vitro thermal injury model. Burns 2019, 45, 173–179. [Google Scholar] [CrossRef]
- Kamel, R.A.; Ong, J.F.; Junker, J.P.E. Tissue Engineering of Skin. J. Am. Coll. Surg. 2013, 217, 533–555. [Google Scholar] [CrossRef]
- Breetveld, M.; Richters, C.D.; Rustemeyer, T.; Scheper, R.J.; Gibbs, S. Comparison of wound closure after burn and cold injury in human skin equivalents. J. Investig. Dermatol. 2006, 126, 1918–1921. [Google Scholar] [CrossRef] [Green Version]
- Haisma, E.M.; de Breij, A.; Chan, H.; van Dissel, J.T.; Drijfhout, J.W.; Hiemstra, P.S.; El Ghalbzouri, A.; Nibbering, P.H. LL-37-derived peptides eradicate multidrug-resistant Staphylococcus aureus from thermally wounded human skin equivalents. Antimicrob. Agents Chemother. 2014, 58, 4411–4419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Torvi, D.A.; Dale, J.D. A Finite Element Model of Skin Subjected to a Flash Fire. J. Biomech. Eng. 1994, 116, 250–255. [Google Scholar] [CrossRef] [PubMed]
- Verhaart, R.F.; Rijnen, Z.; Fortunati, V.; Verduijn, G.M.; van Walsum, T.; Veenland, J.F.; Paulides, M.M. Temperature simulations in hyperthermia treatment planning of the head and neck region. Strahlenther. Onkol. 2014, 190, 1117–1124. [Google Scholar] [CrossRef] [PubMed]
- Zhai, L.; Li, J. Prediction methods of skin burn for performance evaluation of thermal protective clothing. Burns 2015, 41, 1385–1396. [Google Scholar] [CrossRef]
- Gibson, A.L.F.; Bennett, D.D.; Taylor, L.J. Improving the histologic characterization of burn depth. J. Cutan. Pathol. 2017, 44, 998–1004. [Google Scholar] [CrossRef] [PubMed]
- O’Connell-Rodwell, C.E.; Mackanos, M.A.; Simanovskii, D.; Cao, Y.-A.; Bachmann, M.H.; Schwettman, H.A.; Contag, C.H. In vivo analysis of heat-shock-protein-70 induction following pulsed laser irradiation in a transgenic reporter mouse. J. Biomed. Opt. 2008, 13, 030501. [Google Scholar] [CrossRef] [Green Version]
- Szot, C.S.; Buchanan, C.F.; Freeman, J.W.; Rylander, M.N. 3D in vitro bioengineered tumors based on collagen I hydrogels. Biomaterials 2011, 32, 7905–7912. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eaglstein, W.H.; Falanga, V. Tissue engineering and the development of Apligraf, a human skin equivalent. Cutis 1998, 62 (Suppl. S1), 1–8. [Google Scholar] [CrossRef] [PubMed]
- Helary, H.; Foucault-Bertaud, A.; Godeau, G.; Coulomb, B.; Giraud Guille, M.M. Fibroblast populated dense collagen matrices: Cell migration, cell density and metalloproteinases expression. Biomaterials 2005, 26, 1533–1543. [Google Scholar] [CrossRef]
- Antoine, E.E.; Vlachos, P.P.; Rylander, M.N. Review of Collagen I Hydrogels for Bioengineered Tissue Microenvironments: Characterization of Mechanics, Structure, and Transport. Tissue Eng. Part B Rev. 2014, 20, 683–696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castro, A.P.G.; Laity, P.; Shariatzadeh, M.; Wittkowske, C.; Holland, C.; Lacroix, D. Combined numerical and experimental biomechanical characterization of soft collagen hydrogel substrate. J. Mater. Sci. Mater. Med. 2016, 27, 79. [Google Scholar] [CrossRef] [Green Version]
- Antoine, E.E.; Vlachos, P.P.; Rylander, M.N. Tunable collagen I hydrogels for engineered physiological tissue micro-environments. PLoS ONE 2015, 10, e0122500. [Google Scholar] [CrossRef] [Green Version]
- Ní Annaidh, A.; Bruyère, K.; Destrade, M.; Gilchrist, M.D.; Otténio, M. Characterization of the anisotropic mechanical properties of excised human skin. J. Mech. Behav. Biomed. Mater. 2012, 5, 139–148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crichton, M.L.; Chen, X.; Huang, H.; Kendall, M.A.F. Elastic modulus and viscoelastic properties of full thickness skin characterised at micro scales. Biomaterials 2013, 34, 2087–2097. [Google Scholar] [CrossRef] [PubMed]
- Cameron, S.E.; D’Angelo, P.A.; Auerbach, M.A.; Ramsay, J.W. In vivo ultrasonic measures of skin layer thicknesses at various body locations and postures. In Proceedings of the SPIE 10580, Medical Imaging 2018: Ultrasonic Imaging and Tomography; SPIE: San Francisco, CA, USA, 2018; Volume 105801B. [Google Scholar] [CrossRef]
- Khaled, A.A.; Vafai, K. The role of porous media in modeling flow and heat transfer in biological tissues. Int. J. Heat Mass Transf. 2003, 46, 4989–5003. [Google Scholar] [CrossRef]
- Chen, S.S.; Wright, N.T.; Humphrey, J.D. Heat-induced changes in the mechanics of a collagenous tissue: Isothermal, isotonic shrinkage. J. Biomech. Eng. 1998, 120, 382–388. [Google Scholar] [CrossRef]
- Buettner, K. Effects of Extreme Heat and Cold on Human Skin. I. Analysis of Temperature Changes Caused by Different Kinds of Heat Application. J. Appl. Physiol. 1951, 3, 691–702. [Google Scholar] [CrossRef] [PubMed]
- Moussa, N.A.; McGrath, J.J.; Cravalho, E.G.; Asimacopoulos, P.J. Kinetics of thermal injury in cells. J. Biomech. Eng. 1977, 99, 155–159. [Google Scholar] [CrossRef]
- Agah, R. Quantitative Characterization of Arterial Tissue Thermal Damage. Master’s Thesis, Biomedical Engineering, The University of Texas at Austin, Austin, TX, USA, 1988. [Google Scholar]
- Dilier, K.R.; Hayes, L.J. A finite element model of burn injury in blood–perfused skin. J. Biomech. Eng. 1983, 105, 300–307. [Google Scholar] [CrossRef] [PubMed]
- Mallory, M.; Gogineni, E.; Jones, G.C.; Greer, L.; Simone, C.B. Therapeutic hyperthermia: The old, the new, and the upcoming. Crit. Rev. Oncol. Hematol. 2016, 97, 56–64. [Google Scholar] [CrossRef]
- Rylander, M.N.; Stafford, R.J.; Hazle, J.; Whitney, J.; Diller, K.R. Heat shock protein expression and temperature distribution in prostate tumours treated with laser irradiation and nanoshells. Int. J. Hyperth. 2011, 27, 791–801. [Google Scholar] [CrossRef]
- Prinsze, C.; Penning, L.C.; Dubbelman, T.M.A.R.; VanSteveninck, J. Interaction of Photodynamic Treatment and Either Hyperthermia or Ionizing Radiation and of Ionizing Radiation and Hyperthermia with Respect to Cell Killing of L929 Fibroblasts, Chinese Hamster Ovary Cells, and T24 Human Bladder Carcinoma Cells. Cancer Res. 1992, 52, 117–120. [Google Scholar]
- Raaphorst, G.P.; Azzam, E.I. Hyperthermia and thermal tolerance in normal and ataxia telangiectasia human cell strains. Cancer Res. 1983, 43, 2618–2621. [Google Scholar]
- Liang, X. Biomechanical Properties of In Vivo Human Skin From Dynamic Optical Coherence Elastography. IEEE Trans. Biomed. Eng. 2013, 57, 953–959. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sutradhar, A.; Miller, M.J. In vivo measurement of breast skin elasticity and breast skin thickness. Skin Res. Technol. 2013, 19, 191–199. [Google Scholar] [CrossRef] [PubMed]
- Cohen, M.L. Measurement of the thermal properties of human skin. A review. J. Investig. Dermatol. 1977, 69, 333–338. [Google Scholar] [CrossRef] [Green Version]
- Khatyr, F.; Imberdis, C.; Vescovo, P.; Varchon, D.; Lagarde, J.M. Model of the viscoelastic behaviour of skin in vivo and study of anisotropy. Skin Res. Technol. 2004, 10, 96–103. [Google Scholar] [CrossRef] [PubMed]
- Hensel, H.; Bender, F. Fortlanfende Bestimmang der Hautdurchblutung am Menschen mit einem elektrischen Wärmeleitmesser. Pfluegers Arch. Ges. Physiol. 1956, 263, 603–614. [Google Scholar] [CrossRef]
- Orgill, D.P.; Solari, M.G.; Barlow, M.S.; O’Connor, N.E. A finite-element model predicts thermal damage in cutaneous contact burns. J. Burn Care Rehabil. 1998, 19, 203–209. [Google Scholar] [CrossRef]
- Qin, Z.; Balasubramanian, S.K.; Wolkers, W.F.; Pearce, J.A.; Bischof, J.C. Correlated parameter fit of arrhenius model for thermal denaturation of proteins and cells. Ann. Biomed. Eng. 2014, 42, 2392–2404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sotoma, S.; Zhong, C.; Kah, J.C.Y.; Yamashita, H.; Plakhotnik, T.; Harada, Y.; Suzuki, M. In situ measurements of intracellular thermal conductivity using heater-thermometer hybrid diamond nanosensors. Sci. Adv. 2021, 7, eabd7888. [Google Scholar] [CrossRef]
- Rafieiolhosseini, N.; Ejtehadi, M.R. Thermal conductivity of the cell membrane in the presence of cholesterol and amyloid precursor protein. Phys. Rev. E 2020, 102, 042401. [Google Scholar] [CrossRef]
- Cubo, N.; Garcia, M.; Del Cañizo, J.F.; Velasco, D.; Jorcano, J.L. 3D bioprinting of functional human skin: Production and in vivo analysis. Biofabrication 2016, 9, 015006. [Google Scholar] [CrossRef] [Green Version]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brocklehurst, S.; Ghousifam, N.; Zuniga, K.; Stolley, D.; Rylander, M.N. Multilayer In Vitro Human Skin Tissue Platforms for Quantitative Burn Injury Investigation. Bioengineering 2023, 10, 265. https://doi.org/10.3390/bioengineering10020265
Brocklehurst S, Ghousifam N, Zuniga K, Stolley D, Rylander MN. Multilayer In Vitro Human Skin Tissue Platforms for Quantitative Burn Injury Investigation. Bioengineering. 2023; 10(2):265. https://doi.org/10.3390/bioengineering10020265
Chicago/Turabian StyleBrocklehurst, Sean, Neda Ghousifam, Kameel Zuniga, Danielle Stolley, and Marissa Nichole Rylander. 2023. "Multilayer In Vitro Human Skin Tissue Platforms for Quantitative Burn Injury Investigation" Bioengineering 10, no. 2: 265. https://doi.org/10.3390/bioengineering10020265
APA StyleBrocklehurst, S., Ghousifam, N., Zuniga, K., Stolley, D., & Rylander, M. N. (2023). Multilayer In Vitro Human Skin Tissue Platforms for Quantitative Burn Injury Investigation. Bioengineering, 10(2), 265. https://doi.org/10.3390/bioengineering10020265






