A Symmetry-Based Superposition Method for Planning and Surgical Outcome Assessment
Abstract
:1. Introduction
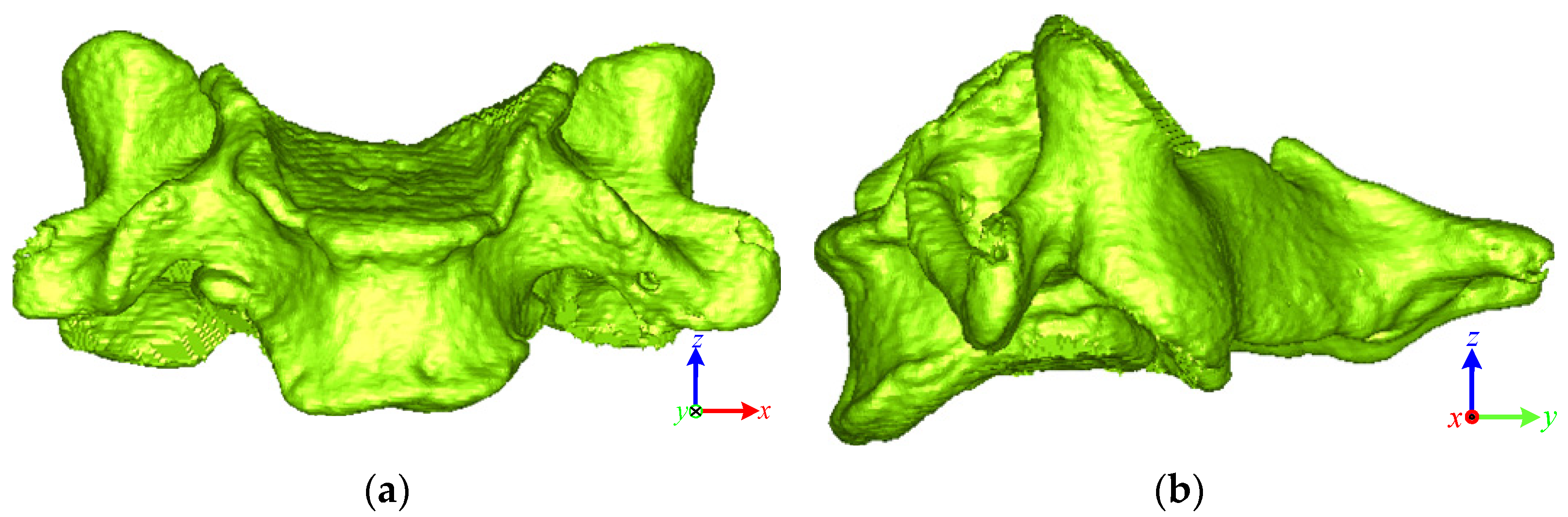
2. Materials and Methods
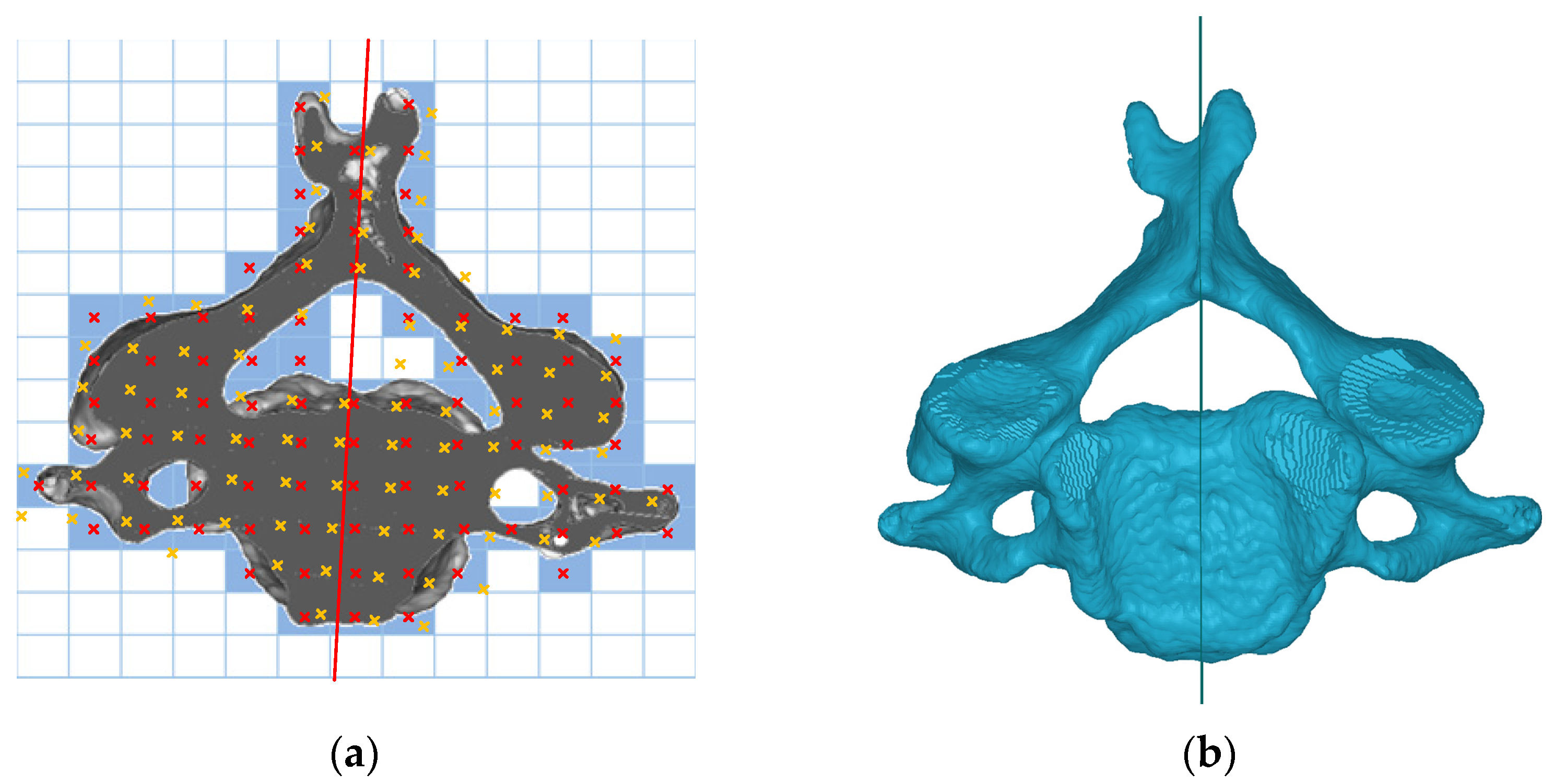
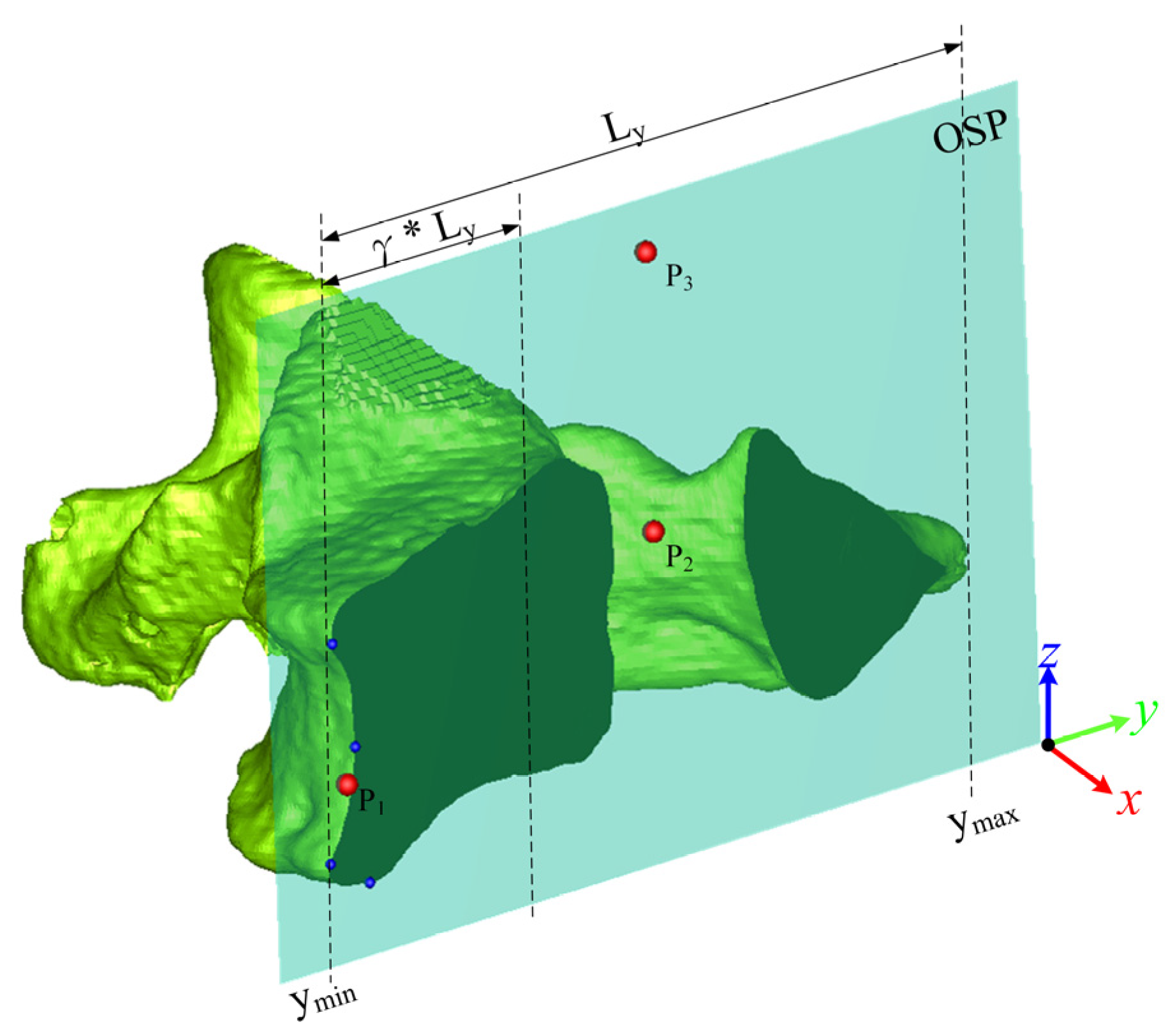
2.1. Optimal Symmetry Plane
2.2. OSP-Based Superposition Method
2.3. Clinical Evaluation
2.3.1. Stability Test
2.3.2. Comparison Test
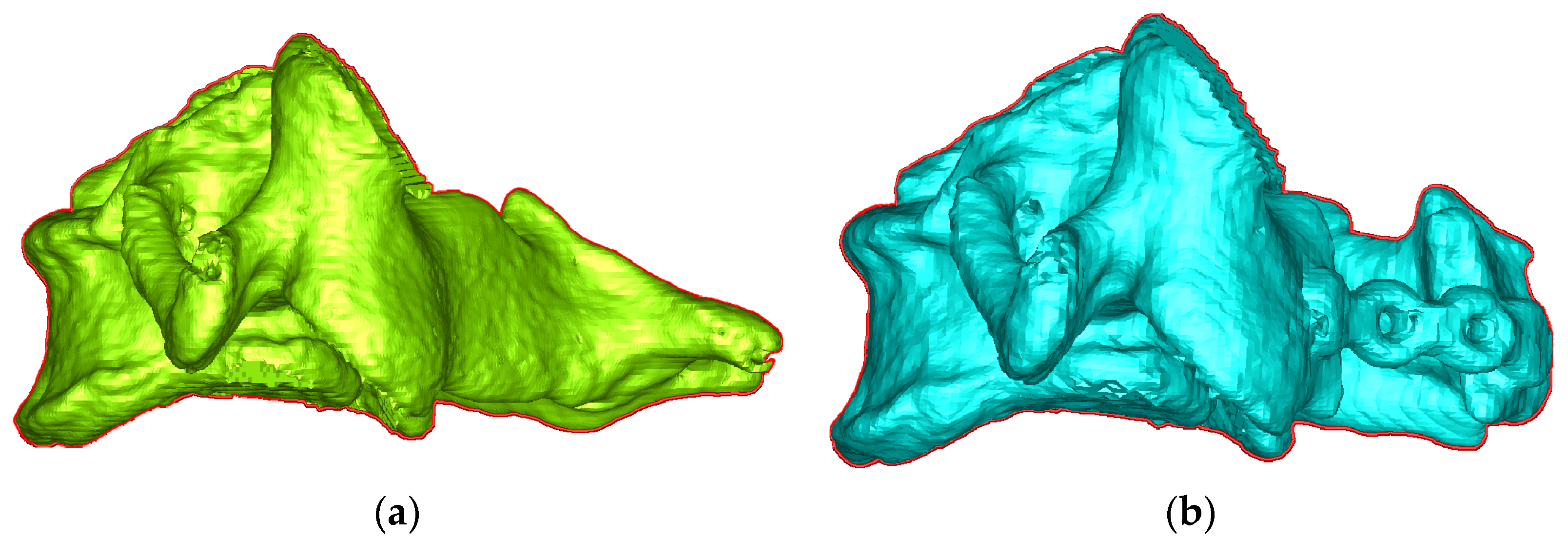
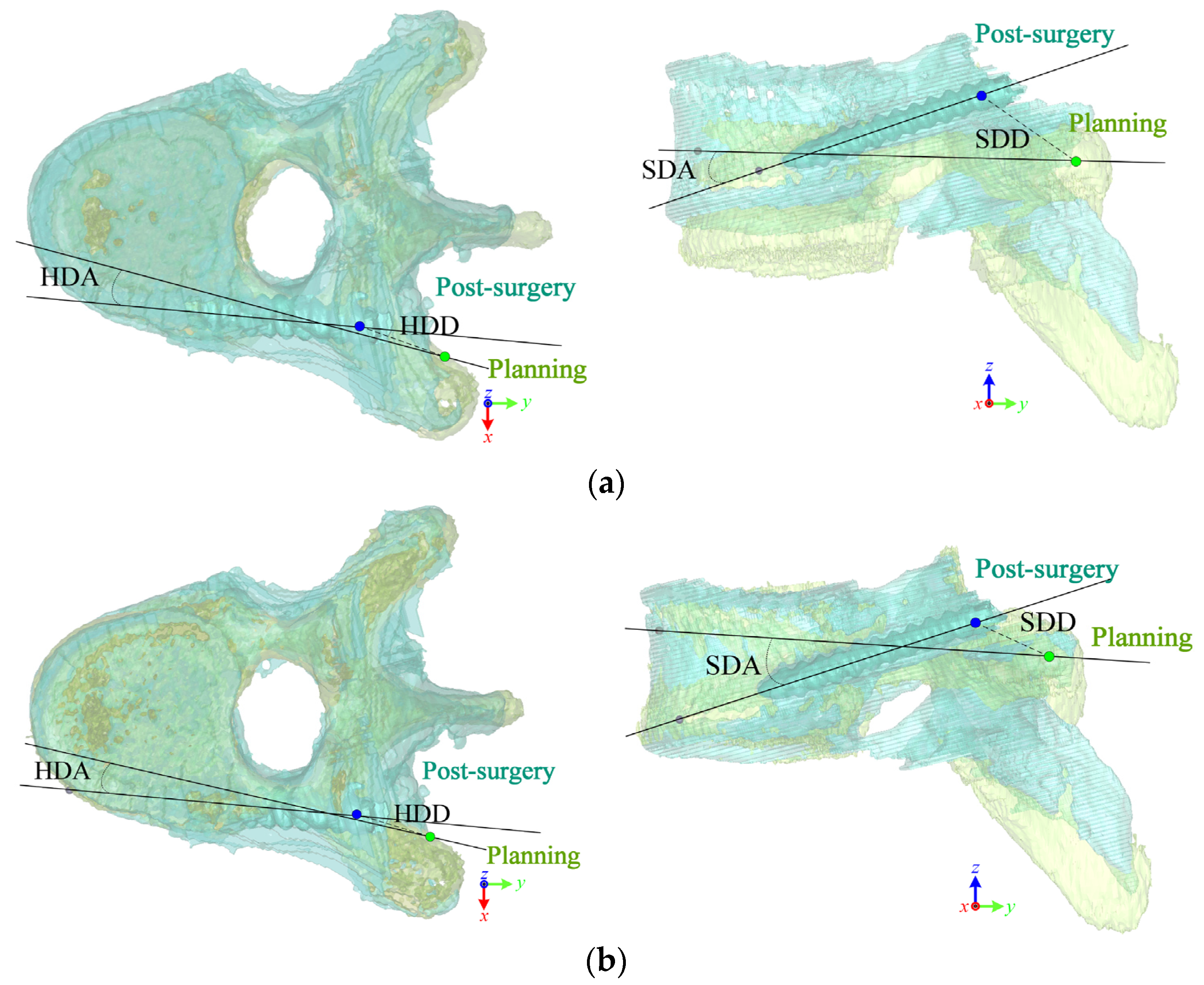
2.3.3. Case Study
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tempany, C.M.C.; Jayender, J.; Kapur, T.; Bueno, R.; Golby, A.; Agar, N.; Jolesz, F.A. Multimodal imaging for improved diagnosis and treatment of cancers. Cancer Am. Cancer Soc. 2015, 121, 817–827. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tandogan, R.N.; Kort, N.P.; Ercin, E.; van Rooij, F.; Nover, L.; Saffarini, M.; Hirschmann, M.T.; Becker, R.; Dejour, D.; Indelli, P.-F.; et al. Computer-assisted surgery and patient-specific instrumentation improve the accuracy of tibial baseplate rotation in total knee arthroplasty compared to conventional instrumentation: A systematic review and meta-analysis. Knee Surg. Sports Traumatol. Arthrosc. 2021, 30, 2654–2665. [Google Scholar] [CrossRef]
- Wu, H.H.; Su, I.-C.; Hsieh, C.-T.; Fang, J.-J.; Chang, C.-J. Accuracy and Safety of Using Customized Guiding Templates for Cervical Pedicle Screw Insertion in Severe Cervical Deformity, Fracture, and Subluxation: A Retrospective Study of 9 Cases. World Neurosurg. 2018, 116, e1144–e1152. [Google Scholar] [CrossRef]
- Nilsson, J.; Nysjö, F.; Nyström, I.; Kämpe, J.; Thor, A. Evaluation of in-house, haptic assisted surgical planning for virtual reduction of complex mandibular fractures. Int. J. Comput. Assist. Radiol. Surg. 2021, 16, 1059–1068. [Google Scholar] [CrossRef]
- Okada, T.; Iwasaki, Y.; Koyama, T.; Sugano, N.; Chen, Y.-W.; Yonenobu, K.; Sato, Y. Computer-Assisted Preoperative Planning for Reduction of Proximal Femoral Fracture Using 3-D-CT Data. IEEE Trans. Biomed. Eng. 2008, 56, 749–759. [Google Scholar] [CrossRef] [PubMed]
- Fürnstahl, P.; Székely, G.; Gerber, C.; Hodler, J.; Snedeker, J.; Harders, M. Computer assisted reconstruction of complex proximal humerus fractures for preoperative planning. Med. Image Anal. 2012, 16, 704–720. [Google Scholar] [CrossRef] [PubMed]
- Neal, M.L.; Kerckhoffs, R. Current progress in patient-specific modeling. Brief. Bioinform. 2010, 11, 111–126. [Google Scholar] [CrossRef] [Green Version]
- Sipari, S.; Iso-Mustajärvi, M.; Löppönen, H.; Dietz, A. The Insertion Results of a Mid-scala Electrode Assessed by MRI and CBCT Image Fusion. Otol. Neurotol. 2018, 39, e1019–e1025. [Google Scholar] [CrossRef]
- Cevidanes, L.H.S.; Bailey, L.J.; Tucker, G.R.; Styner, M.A.; Mol, A.; Phillips, C.L.; Proffit, W.R.; Turvey, T. Superimposition of 3D cone-beam CT models of orthognathic surgery patients. Dentomaxillofac. Radiol. 2005, 34, 369–375. [Google Scholar] [CrossRef] [Green Version]
- Tanioka, S.; Ishida, F.; Kuraishi, K.; Tanaka, K.; Shimosaka, S.; Suzuki, H.; Mizuno, M. A Novel Radiologic Assessment of Screw Loosening Focusing on Spatial Position Change of Screws Using an Iterative Closest Point Algorithm with Stereolithography Data: Technical Note. World Neurosurg. 2019, 124, 171–177. [Google Scholar] [CrossRef]
- Zeng, C.; Xing, W.; Wu, Z.; Huang, H.; Huang, W. A combination of three-dimensional printing and computer-assisted virtual surgical procedure for preoperative planning of acetabular fracture reduction. Injury 2016, 47, 2223–2227. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef] [Green Version]
- Chetverikov, D.; Stepanov, D.; Krsek, P. Robust Euclidean alignment of 3D point sets: The trimmed iterative closest point algorithm. Image Vis. Comput. 2005, 23, 299–309. [Google Scholar] [CrossRef]
- Du, S.; Zheng, N.; Ying, S.; Liu, J. Affine iterative closest point algorithm for point set registration. Pattern Recognit. Lett. 2010, 31, 791–799. [Google Scholar] [CrossRef]
- Nazem, F.; Ahmadian, A.; Seraj, N.D.; Giti, M. Two-stage point-based registration method between ultrasound and CT imaging of the liver based on ICP and unscented Kalman filter: A phantom study. Int. J. Comput. Assist. Radiol. Surg. 2014, 9, 39–48. [Google Scholar] [CrossRef]
- Memiş, A.; Varlı, S.; Bilgili, F. A novel approach for computerized quantitative image analysis of proximal femur bone shape deformities based on the hip joint symmetry. Artif. Intell. Med. 2021, 115, 102057. [Google Scholar] [CrossRef]
- Shrestha, L.; Alsadoon, A.; Prasad, P.W.C.; Alsallami, N.; Haddad, S. Augmented reality for dental implant surgery: Enhanced ICP. J. Supercomput. 2021, 77, 1152–1176. [Google Scholar] [CrossRef]
- Maharjan, N.; Alsadoon, A.; Prasad, P.W.C.; Abdullah, S.; Rashid, T.A. A novel visualization system of using augmented reality in knee replacement surgery: Enhanced bidirectional maximum correntropy algorithm. Int. J. Med. Robot. Comput. Assist. Surg. 2021, 17, e2223. [Google Scholar] [CrossRef] [PubMed]
- Paulano-Godino, F.; Jiménez-Delgado, J.J. Identification of fracture zones and its application in automatic bone fracture reduction. Comput. Meth. Prog. Biomed. 2017, 141, 93–104. [Google Scholar] [CrossRef]
- Tan, S.; Yao, J.; Flynn, J.A.; Yao, L.; Ward, M.M. Quantitative syndesmophyte measurement in ankylosing spondylitis using CT: Longitudinal validity and sensitivity to change over 2 years. Ann. Rheum. Dis. 2015, 74, 437–443. [Google Scholar] [CrossRef] [PubMed]
- Schlösser, T.P.; van Stralen, M.; Brink, R.C.; Chu, W.C.W.; Lam, T.-P.; Vincken, K.L.; Castelein, R.M.; Cheng, J.C.Y. Three-Dimensional Characterization of Torsion and Asymmetry of the Intervertebral Discs Versus Vertebral Bodies in Adolescent Idiopathic Scoliosis. Spine 2014, 39, E1159–E1166. [Google Scholar] [CrossRef]
- Vrtovec, T.; Vengust, R.; Likar, B.; Pernuš, F. Analysis of Four Manual and a Computerized Method for Measuring Axial Vertebral Rotation in Computed Tomography Images. Spine 2010, 35, E535–E541. [Google Scholar] [CrossRef]
- Kim, K.; Lee, S. Vertebrae localization in CT using both local and global symmetry features. Comput. Med. Imaging Graph. 2017, 58, 45–55. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, Y.-C.; Fang, J.-J. An Automatic Voxel-Based Method for Optimal Symmetry Plane Generation for the Maxillofacial Region in Severe Asymmetry Cases. J. Clin. Med. 2022, 11, 5689. [Google Scholar] [CrossRef]
- Lorensen, W.E.; Cline, H.E. Marching cubes: A high resolution 3D surface construction algorithm. ACM Siggraph Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Wang, M.-J.J.; Wu, W.-Y.; Huang, L.-K.; Wang, D.-M. Corner detection using bending value. Pattern Recognit. Lett. 1995, 16, 575–583. [Google Scholar] [CrossRef]
- Moore, F.R.; Langdon, G.G. A generalized firing squad problem. Inf. Control 1968, 12, 212–220. [Google Scholar] [CrossRef] [Green Version]
- Bentley, J.L. K-d trees for semidynamic point sets. In Proceedings of the Sixth Annual Symposium on Computational Geometry, Berkley, CA, USA, 7–9 June 1990; pp. 187–197. [Google Scholar]
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least-Squares Fitting of Two 3-D Point Sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 698–700. [Google Scholar] [CrossRef] [Green Version]
- Golub, G.H.; Reinsch, C. Singular value decomposition and least squares solutions. In Linear Algebra; Springer: Berlin/Heidelberg, Germany, 1971; pp. 134–151. [Google Scholar]
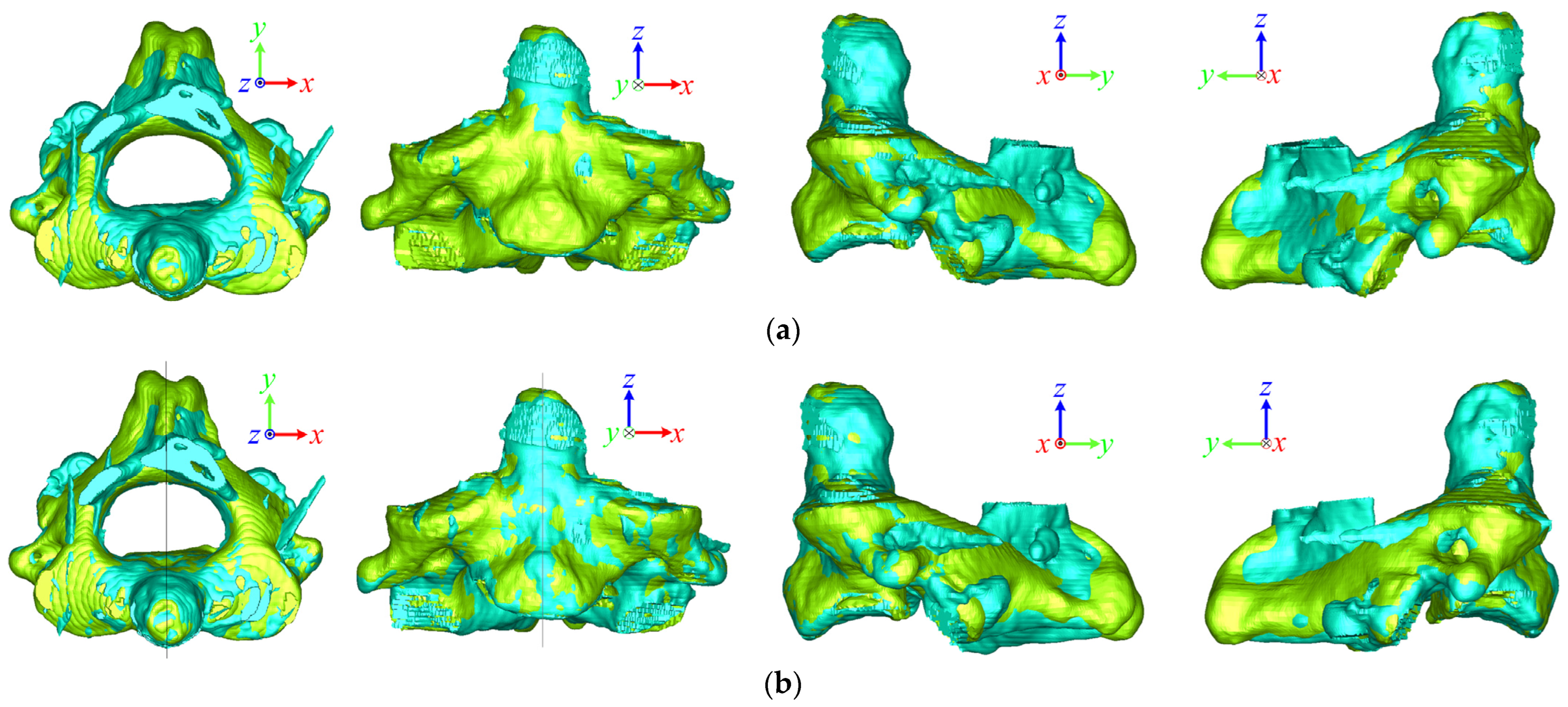
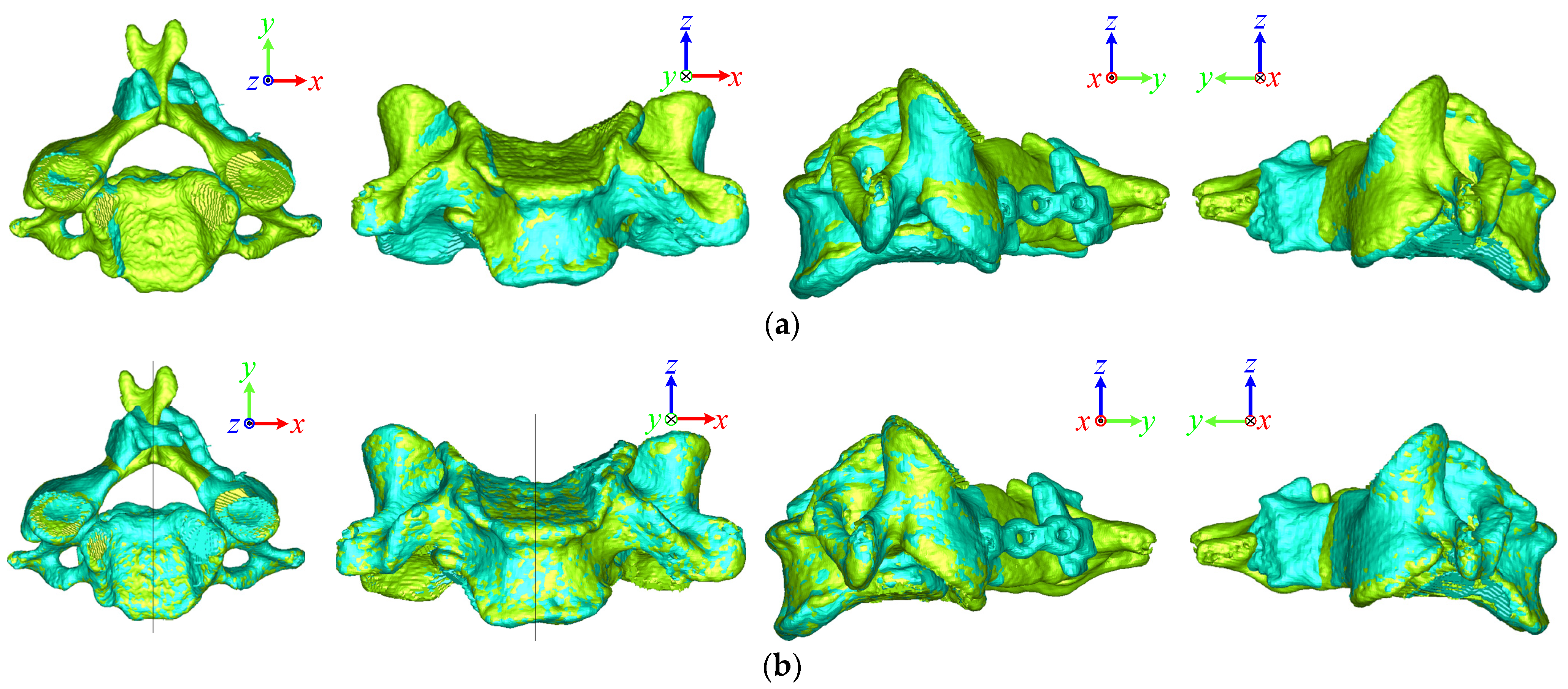
| Deviation Angle of Two OSPs | Superposition Deviation Btw Two Vertebral Bodies | |
|---|---|---|
| Same CT group | 0.43 ± 0.26° | 0.19 ± 0.03 mm |
| Different CT group | 0.45 ± 0.20° | 0.52 ± 0.22 mm |
| Statistical analysis (p-value) | 0.642 | <0.001 * |
| 23 vertebrae | 0.45 ± 0.23° | 0.37 ± 0.24 mm |
| ICP Algorithm | OSP-Based Contouring Method | |||||
|---|---|---|---|---|---|---|
| Vertebrae Deviation (mm) | Vertebral Body Deviation (mm) | Processing Time (s) | Vertebrae Deviation (mm) | Vertebral Body Deviation (mm) | Processing Time (s) | |
| Cervical | 1.14 ± 1.08 | 0.97 ± 0.80 | 25.07 ± 22.68 | 1.03 ± 1.46 | 0.58 ± 0.61 | 2.92 ± 1.82 |
| Thoracic | 1.02 ± 1.00 | 0.90 ± 0.74 | 36.99 ± 19.40 | 0.89 ± 1.09 | 0.63 ± 0.57 | 2.99 ± 1.48 |
| Lumbar | 0.98 ± 1.07 | 0.83 ± 0.75 | 48.13 ± 23.81 | 1.00 ± 1.19 | 0.81 ± 0.76 | 2.92 ± 1.84 |
| 55 vertebraeon average | 1.05 ± 1.04 | 0.91 ± 0.76 | 34.88 ± 23.18 | 0.96 ± 1.25 | 0.65 ± 0.62 | 2.96 ± 1.67 |
| Vertebral Deviation | Vertebral Body Deviation | Processing Time | |
|---|---|---|---|
| Cervical | 0.040 * | 0.001 * | <0.001 * |
| Thoracic | 0.061 | <0.001 * | <0.001 * |
| Lumbar | 0.283 | 0.397 | 0.003 * |
| 55 vertebrae | 0.020 * | <0.001 * | <0.001 * |
| Assessments | ICP Method | OSP-Based Contouring Method | Difference |
|---|---|---|---|
| DD | 7.44 mm | 2.50 mm | 4.94 mm |
| HDD | 3.65 mm | 2.19 mm | 1.46 mm |
| SDD | 6.53 mm | 1.69 mm | 4.84 mm |
| DA | 27.82° | 30.25° | −2.43° |
| HDA | 3.74° | 4.56° | −0.82° |
| SDA | 27.90° | 30.22° | −2.32° |
| Process time | 36 s | 1.10 s | 35 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsiao, Y.-C.; Fang, J.-J. A Symmetry-Based Superposition Method for Planning and Surgical Outcome Assessment. Bioengineering 2023, 10, 335. https://doi.org/10.3390/bioengineering10030335
Hsiao Y-C, Fang J-J. A Symmetry-Based Superposition Method for Planning and Surgical Outcome Assessment. Bioengineering. 2023; 10(3):335. https://doi.org/10.3390/bioengineering10030335
Chicago/Turabian StyleHsiao, Yu-Ching, and Jing-Jing Fang. 2023. "A Symmetry-Based Superposition Method for Planning and Surgical Outcome Assessment" Bioengineering 10, no. 3: 335. https://doi.org/10.3390/bioengineering10030335
APA StyleHsiao, Y. -C., & Fang, J. -J. (2023). A Symmetry-Based Superposition Method for Planning and Surgical Outcome Assessment. Bioengineering, 10(3), 335. https://doi.org/10.3390/bioengineering10030335






