MultiResUNet3+: A Full-Scale Connected Multi-Residual UNet Model to Denoise Electrooculogram and Electromyogram Artifacts from Corrupted Electroencephalogram Signals
Abstract
:1. Introduction
- The proposed MultiResUNet3+ can effectively denoise EOG, EMG, and concurrent EOG and EMG artifacts from corrupted EEG waveforms.
- We have created a diverse and representative semi-synthetic EEG dataset closely resembling real-world corrupted EEG signals. The proposed 1D-segmentation model was trained and evaluated using 5-fold cross-validation, which ensured the reliability and robustness of the proposed model.
- We used five well-established performance metrics to comprehensively assess and compare the denoising performance of each of the five 1D-segmentation models.
- Our developed model may be used for denoising multi-channel, actual EEG data as the model was trained with diverse artifactual data.
2. Materials and Methods
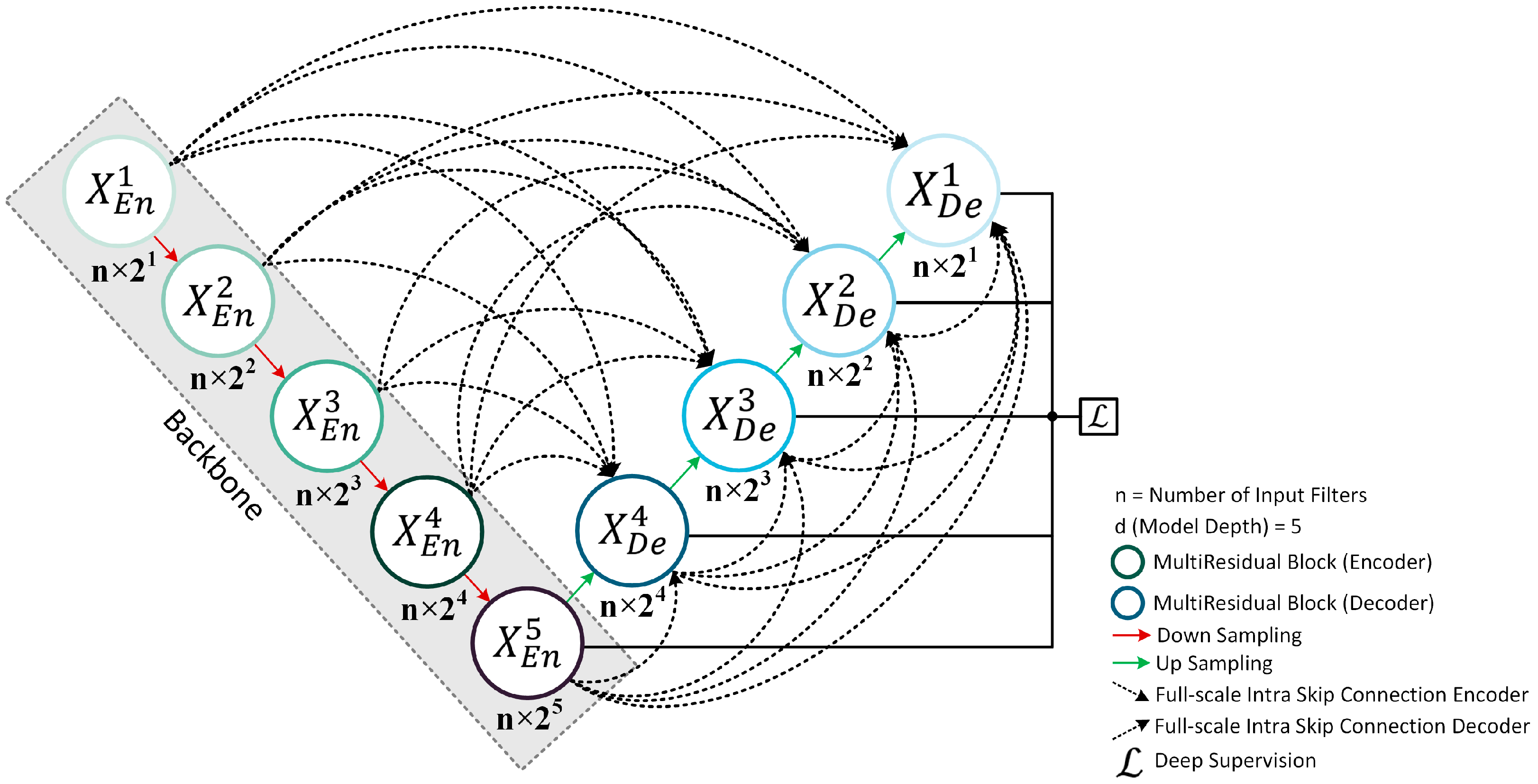
2.1. Proposed Novel MultiResUNet3+ Model Description
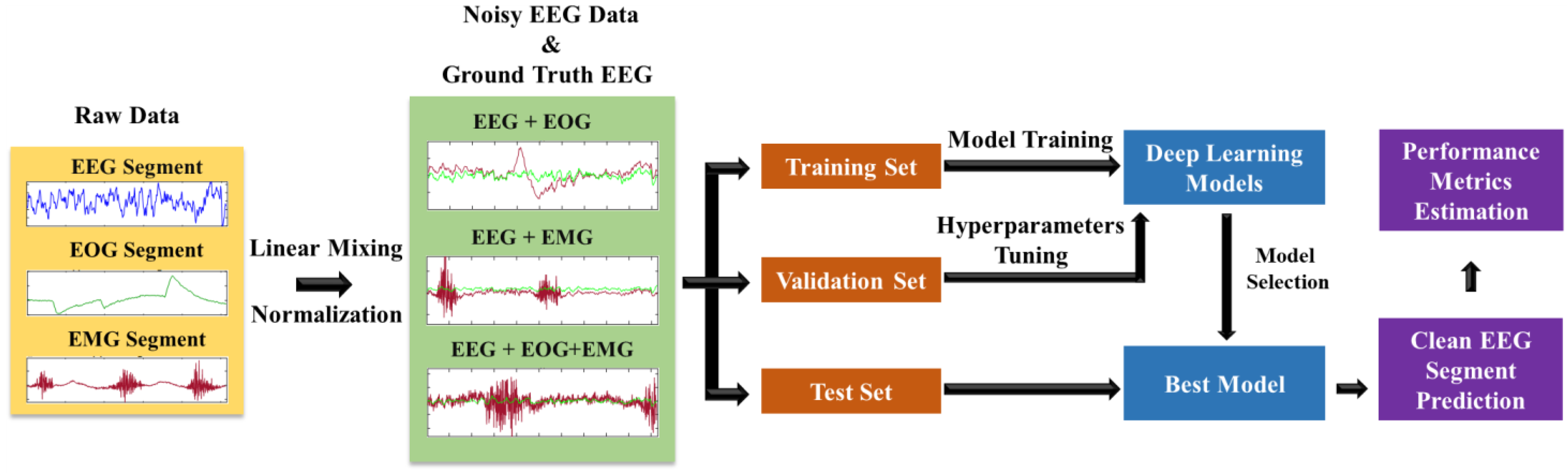
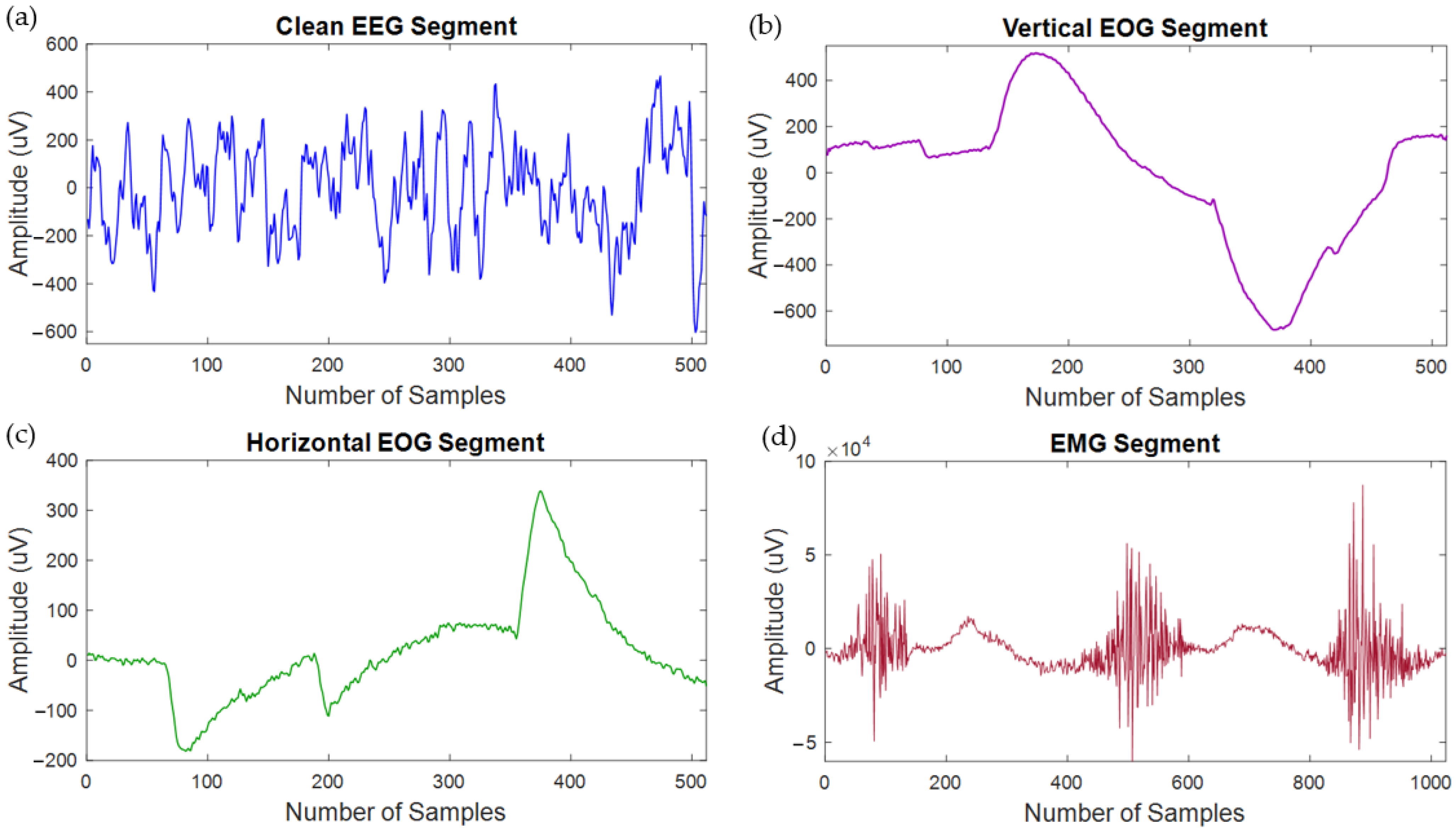
2.2. Dataset Description
2.3. Semi-Synthetic Electroencephalogram Segment Generation and Normalization
3. Experimental Setup
3.1. Experiment A
3.2. Experiment B
3.3. Performance Evaluation Metrics
4. Results
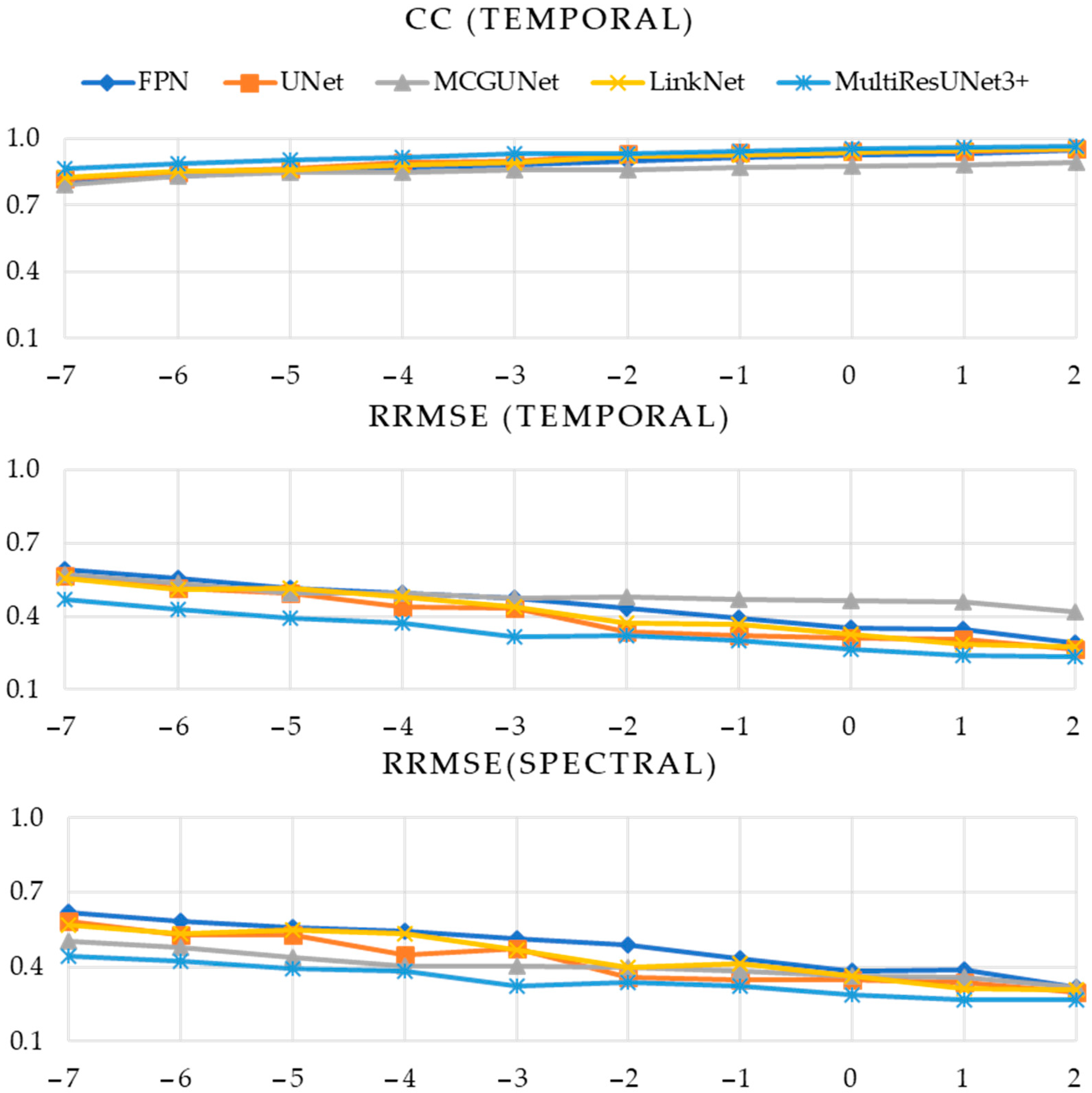
4.1. Experiment A Outcomes
4.2. Experiment B Outcomes
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wolpaw, J.R.; McFarland, D.J.; Neat, G.W.; Forneris, C.A. An EEG-based brain-computer interface for cursor control. Electroencephalogr. Clin. Neurophysiol. 1991, 78, 252–259. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Guo, Y.; Yang, P.; Chen, W.; Lo, B. Epilepsy seizure prediction on EEG using common spatial pattern and convolutional neural network. IEEE J. Biomed. Health Inform. 2019, 24, 465–474. [Google Scholar] [CrossRef]
- Ullah, I.; Hussain, M.; Aboalsamh, H. An automated system for epilepsy detection using EEG brain signals based on deep learning approach. Expert Syst. Appl. 2018, 107, 61–71. [Google Scholar] [CrossRef]
- Mammone, N.; De Salvo, S.; Bonanno, L.; Ieracitano, C.; Marino, S.; Marra, A.; Bramanti, A.; Morabito, F.C. Brain network analysis of compressive sensed high-density EEG signals in AD and MCI subjects. IEEE Trans. Industr. Inform. 2018, 15, 527–536. [Google Scholar] [CrossRef]
- Yang, S.; Bornot, J.M.S.; Wong-Lin, K.; Prasad, G. M/EEG-based bio-markers to predict the MCI and Alzheimer’s disease: A review from the ML perspective. IEEE Trans. Biomed. Eng. 2019, 66, 2924–2935. [Google Scholar] [CrossRef] [PubMed]
- Tripathy, R.; Acharya, U.R. Use of features from RR-time series and EEG signals for automated classification of sleep stages in deep neural network framework. Biocybern. Biomed. Eng. 2018, 38, 890–902. [Google Scholar] [CrossRef]
- Antonenko, P.; Paas, F.; Grabner, R.; Van Gog, T. Using electroencephalography to measure cognitive load. Educ. Psychol. Rev. 2010, 22, 425–438. [Google Scholar] [CrossRef]
- Gupta, V.; Chopda, M.D.; Pachori, R.B. Cross-subject emotion recognition using flexible analytic wavelet transform from EEG signals. IEEE Sens. J. 2018, 19, 2266–2274. [Google Scholar] [CrossRef]
- Xing, X.; Wang, Y.; Pei, W.; Guo, X.; Liu, Z.; Wang, F.; Ming, G.; Zhao, H.; Gui, Q.; Chen, H. A high-speed SSVEP-based BCI using dry EEG electrodes. Sci. Rep. 2018, 8, 14708. [Google Scholar] [CrossRef]
- Rahman, A.; Chowdhury, M.E.; Khandakar, A.; Tahir, A.M.; Ibtehaz, N.; Hossain, M.S.; Kiranyaz, S.; Malik, J.; Monawwar, H.; Kadir, M.A. Robust biometric system using session invariant multimodal EEG and keystroke dynamics by the ensemble of self-ONNs. Comput. Biol. Med. 2022, 142, 105238. [Google Scholar] [CrossRef]
- Flexer, A.; Bauer, H.; Pripfl, J.; Dorffner, G. Using ICA for removal of ocular artifacts in EEG recorded from blind subjects. Neural Netw. 2005, 18, 998–1005. [Google Scholar] [CrossRef] [PubMed]
- McMenamin, B.W.; Shackman, A.J.; Maxwell, J.S.; Bachhuber, D.R.; Koppenhaver, A.M.; Greischar, L.L.; Davidson, R.J. Validation of ICA-based myogenic artifact correction for scalp and source-localized EEG. NeuroImage 2010, 49, 2416–2432. [Google Scholar] [CrossRef] [PubMed]
- Jorge, J.; Bouloc, C.; Bréchet, L.; Michel, C.M.; Gruetter, R. Investigating the variability of cardiac pulse artifacts across heartbeats in simultaneous EEG-fMRI recordings: A 7T study. NeuroImage 2019, 191, 21–35. [Google Scholar] [CrossRef] [PubMed]
- Marino, M.; Liu, Q.; Del Castello, M.; Corsi, C.; Wenderoth, N.; Mantini, D. Heart–Brain interactions in the MR environment: Characterization of the ballistocardiogram in EEG signals collected during simultaneous fMRI. Brain Topogr. 2018, 31, 337–345. [Google Scholar] [CrossRef]
- Jiang, X.; Bian, G.-B.; Tian, Z. Removal of artifacts from EEG signals: A review. Sensors 2019, 19, 987. [Google Scholar] [CrossRef]
- Hossain, M.S.; Reaz, M.B.I.; Chowdhury, M.E.; Ali, S.H.; Bakar, A.A.A.; Kiranyaz, S.; Khandakar, A.; Alhatou, M.; Habib, R. Motion Artifacts Correction from EEG and fNIRS Signals using Novel Multiresolution Analysis. IEEE Access 2022, 10, 29760–29777. [Google Scholar] [CrossRef]
- Hossain, M.S.; Chowdhury, M.E.; Reaz, M.B.I.; Ali, S.H.M.; Bakar, A.A.A.; Kiranyaz, S.; Khandakar, A.; Alhatou, M.; Habib, R.; Hossain, M.M. Motion Artifacts Correction from Single-Channel EEG and fNIRS Signals Using Novel Wavelet Packet Decomposition in Combination with Canonical Correlation Analysis. Sensors 2022, 22, 3169. [Google Scholar] [CrossRef]
- Somers, B.; Francart, T.; Bertrand, A. A generic EEG artifact removal algorithm based on the multi-channel Wiener filter. J. Neural Eng. 2018, 15, 036007. [Google Scholar] [CrossRef]
- Shahabi, H.; Moghimi, S.; Zamiri-Jafarian, H. EEG eye blink artifact removal by EOG modeling and Kalman filter. In Proceedings of the 5th International Conference on Biomedical Engineering and Informatics, Chongqing, China, 16–18 October 2012; pp. 496–500. [Google Scholar]
- Correa, A.G.; Laciar, E.; Patiño, H.; Valentinuzzi, M. Artifact removal from EEG signals using adaptive filters in cascade. J. Phys. Conf. Ser. 2007, 90, 012081. [Google Scholar] [CrossRef]
- Gao, C.; Ma, L.; Li, H. An ICA/HHT hybrid approach for automatic ocular artifact correction. Intern. J. Pattern Recognit. Artif. Intell. 2015, 29, 1558001. [Google Scholar] [CrossRef]
- Mert, A.; Akan, A. Hilbert-Huang transform based hierarchical clustering for EEG denoising. In Proceedings of the 21st European Signal Processing Conference (EUSIPCO 2013), Marrakech, Morocco, 9–13 September 2013; pp. 1–5. [Google Scholar]
- Wang, G.; Teng, C.; Li, K.; Zhang, Z.; Yan, X. The removal of EOG artifacts from EEG signals using independent component analysis and multivariate empirical mode decomposition. IEEE J. Biomed. Health Inform. 2015, 20, 1301–1308. [Google Scholar] [CrossRef] [PubMed]
- Marino, M.; Liu, Q.; Koudelka, V.; Porcaro, C.; Hlinka, J.; Wenderoth, N.; Mantini, D. Adaptive optimal basis set for BCG artifact removal in simultaneous EEG-fMRI. Sci. Rep. 2018, 8, 8902. [Google Scholar] [CrossRef] [PubMed]
- Nam, H.; Yim, T.G.; Han, S.K.; Oh, J.B.; Lee, S.K. Independent component analysis of ictal EEG in medial temporal lobe epilepsy. Epilepsia 2002, 43, 160–164. [Google Scholar] [CrossRef] [PubMed]
- Urrestarazu, E.; Iriarte, J.; Alegre, M.; Valencia, M.; Viteri, C.; Artieda, J. Independent component analysis removing artifacts in ictal recordings. Epilepsia 2004, 45, 1071–1078. [Google Scholar] [CrossRef]
- De Clercq, W.; Vergult, A.; Vanrumste, B.; Van Paesschen, W.; Van Huffel, S. Canonical correlation analysis applied to remove muscle artifacts from the electroencephalogram. IEEE Trans. Biomed. Eng. 2006, 53, 2583–2587. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, D.; Zhi, L. Method of removing noise from EEG signals based on HHT method. In Proceedings of the First International Conference on Information Science and Engineering, Nanjing, China, 26–28 December 2009; pp. 596–599. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Chen, X.; Xu, X.; Liu, A.; McKeown, M.J.; Wang, Z.J. The use of multivariate EMD and CCA for denoising muscle artifacts from few-channel EEG recordings. IEEE Trans. Instrum. Meas. 2017, 67, 359–370. [Google Scholar] [CrossRef]
- Zeng, K.; Chen, D.; Ouyang, G.; Wang, L.; Liu, X.; Li, X. An EEMD-ICA approach to enhancing artifact rejection for noisy multivariate neural data. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 24, 630–638. [Google Scholar] [CrossRef]
- Chen, X.; Chen, Q.; Zhang, Y.; Wang, Z.J. A novel EEMD-CCA approach to removing muscle artifacts for pervasive EEG. IEEE Sens. J. 2018, 19, 8420–8431. [Google Scholar] [CrossRef]
- Sweeney, K.T.; McLoone, S.F.; Ward, T.E. The use of ensemble empirical mode decomposition with canonical correlation analysis as a novel artifact removal technique. IEEE Trans. Biomed. Eng. 2012, 60, 97–105. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems 25; Curran Associates, Inc.: Red Hook, NY, USA, 2012. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1306.3781. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems 30; Curran Associates, Inc.: Red Hook, NY, USA, 2017. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Advances in Neural Information Processing Systems 27; Curran Associates, Inc.: Red Hook, NY, USA, 2014. [Google Scholar]
- Sakhavi, S.; Guan, C.; Yan, S. Parallel convolutional-linear neural network for motor imagery classification. In Proceedings of the 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 2736–2740. [Google Scholar]
- Tabar, Y.R.; Halici, U. A novel deep learning approach for classification of EEG motor imagery signals. J. Neural Eng. 2016, 14, 016003. [Google Scholar] [CrossRef]
- Tang, Z.; Li, C.; Sun, S.J.O. Single-trial EEG classification of motor imagery using deep convolutional neural networks. Optik 2017, 130, 11–18. [Google Scholar] [CrossRef]
- Luo, T.-j.; Fan, Y.; Chen, L.; Guo, G.; Zhou, C. EEG signal reconstruction using a generative adversarial network with Wasserstein distance and temporal-spatial-frequency loss. Front. Neuroinform. 2020, 14, 15. [Google Scholar] [CrossRef] [PubMed]
- Corley, I.A.; Huang, Y. Deep EEG super-resolution: Upsampling EEG spatial resolution with generative adversarial networks. In Proceedings of the IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Las Vegas, NV, USA, 4–7 March 2018; pp. 100–103. [Google Scholar]
- Hartmann, K.G.; Schirrmeister, R.T.; Ball, T. EEG-GAN: Generative adversarial networks for electroencephalographic (EEG) brain signals. arXiv 2018, arXiv:1806.01875. [Google Scholar]
- Fahimi, F.; Dosen, S.; Ang, K.K.; Mrachacz-Kersting, N.; Guan, C. Generative adversarial networks-based data augmentation for brain-computer interface. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4039–4051. [Google Scholar] [CrossRef]
- Yang, B.; Duan, K.; Fan, C.; Hu, C.; Wang, J. Automatic ocular artifacts removal in EEG using deep learning. Biomed. Signal Process. Control. 2018, 43, 148–158. [Google Scholar] [CrossRef]
- Leite, N.M.N.; Pereira, E.T.; Gurjao, E.C.; Veloso, L.R. Deep convolutional autoencoder for EEG noise filtering. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Madrid, Spain, 3–6 December 2018; pp. 2605–2612. [Google Scholar]
- Sun, W.; Su, Y.; Wu, X.; Wu, X. A novel end-to-end 1D-ResCNN model to remove the artifacts from EEG signals. Neurocomputing 2020, 404, 108–121. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, M.; Wei, C.; Mantini, D.; Li, Z.; Liu, Q. EEGdenoiseNet: A benchmark dataset for deep learning solutions of EEG denoising. J. Neural Eng. 2021, 18, 056057. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, C.; Zhao, M.; Liu, Q.; Wu, H. A novel convolutional neural network model to remove muscle artifacts from EEG. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 1265–1269. [Google Scholar]
- Sawangjai, P.; Trakulruangroj, M.; Boonnag, C.; Piriyajitakonkij, M.; Tripathy, R.K.; Sudhawiyangkul, T.; Wilaiprasitporn, T. EEGANet: Removal of ocular artifact from the EEG signal using generative adversarial networks. IEEE J. Biomed. Health Inform. 2021, 26, 4913–4924. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Li, C.; Lou, K.; Wei, C.; Liu, Q. Embedding decomposition for artifacts removal in EEG signals. J. Neural Eng. 2022, 19, 026052. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.-Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Asadi-Aghbolaghi, M.; Azad, R.; Fathy, M.; Escalera, S.J. Multi-level context gating of embedded collective knowledge for medical image segmentation. arXiv 2020, arXiv:2003.05056. [Google Scholar]
- Chaurasia, A.; Culurciello, E. Linknet: Exploiting encoder representations for efficient semantic segmentation. In Proceedings of the 2017 IEEE Visual Communications and Image Processing (VCIP), St. Petersburg, FL, USA, 10–13 December 2017; pp. 1–4. [Google Scholar]
- Ibtehaz, N.; Rahman, M.S. MultiResUNet: Rethinking the U-Net architecture for multimodal biomedical image segmentation. Neural Netw. 2020, 121, 74–87. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Lin, L.; Tong, R.; Hu, H.; Zhang, Q.; Iwamoto, Y.; Han, X.; Chen, Y.-W.; Wu, J. Unet 3+: A full-scale connected unet for medical image segmentation. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1055–1059. [Google Scholar]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Granada, Spain, 20 September 2018; pp. 3–11. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. Proc. AAAI Conf. Artif. Intell. 2017, 31, 4278–4284. [Google Scholar] [CrossRef]
- Chen, X.; Peng, H.; Yu, F.; Wang, K. Independent vector analysis applied to remove muscle artifacts in EEG data. IEEE Trans. Instrum. Meas. 2017, 66, 1770–1779. [Google Scholar] [CrossRef]
- Weiergräber, M.; Papazoglou, A.; Broich, K.; Müller, R. Sampling rate, signal bandwidth and related pitfalls in EEG analysis. J. Neurosci. Methods 2016, 268, 53–55. [Google Scholar] [CrossRef]
- Zhu, Q.; Du, B.; Turkbey, B.; Choyke, P.L.; Yan, P. Deeply-supervised CNN for prostate segmentation. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 178–184. [Google Scholar]
- Mahmud, S.; Hossain, M.S.; Chowdhury, M.E.; Reaz, M.B.I. MLMRS-Net: Electroencephalography (EEG) motion artifacts removal using a multi-layer multi-resolution spatially pooled 1D signal reconstruction network. Neural Comput. Appl. 2023, 35, 8371–8388. [Google Scholar] [CrossRef]
- Xu, Z.-Q.J.; Zhang, Y.; Luo, T.; Xiao, Y.; Ma, Z. Frequency principle: Fourier analysis sheds light on deep neural networks. arXiv 2019, arXiv:1901.06523. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions, and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions, or products referred to in the content. |




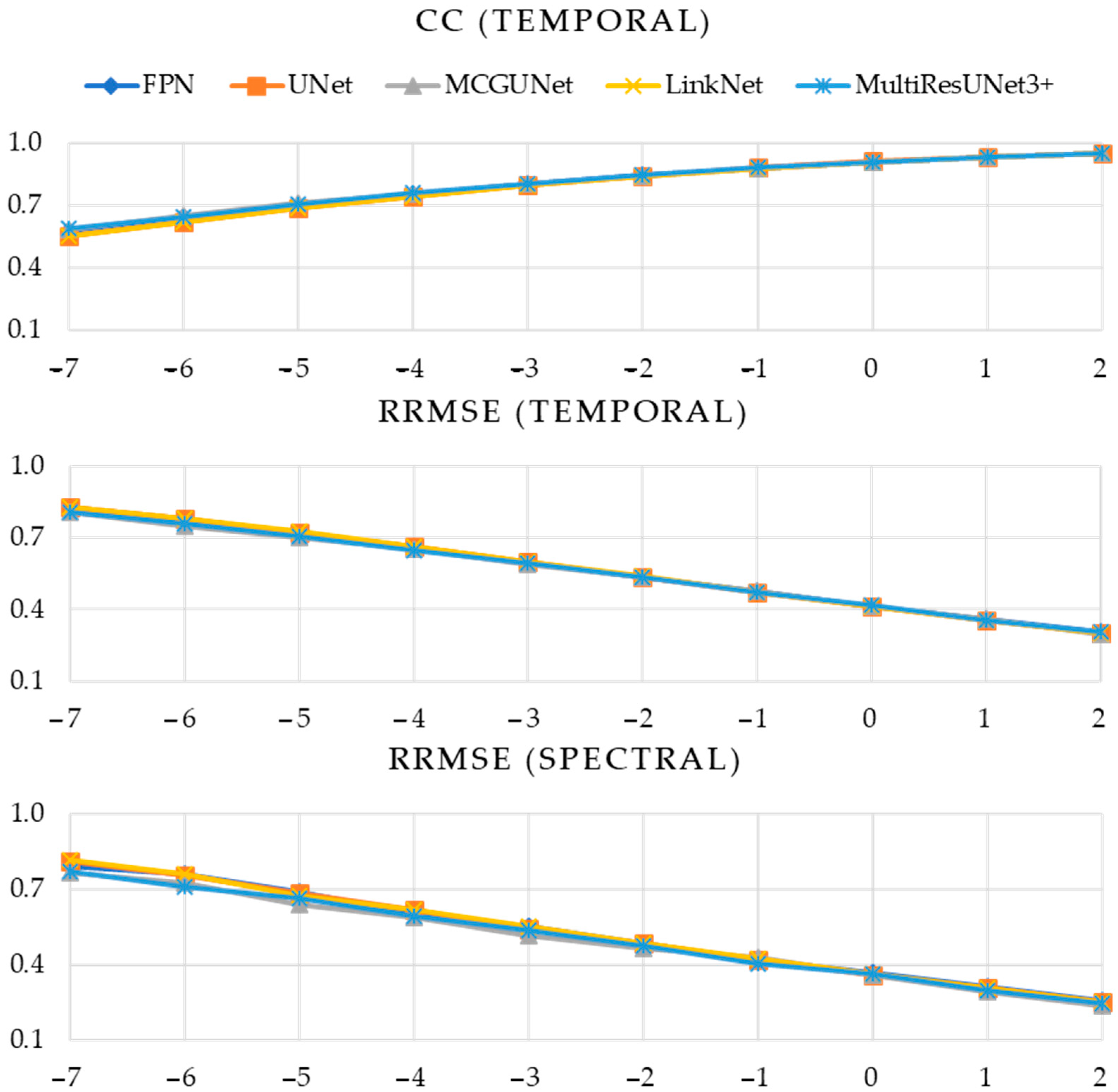
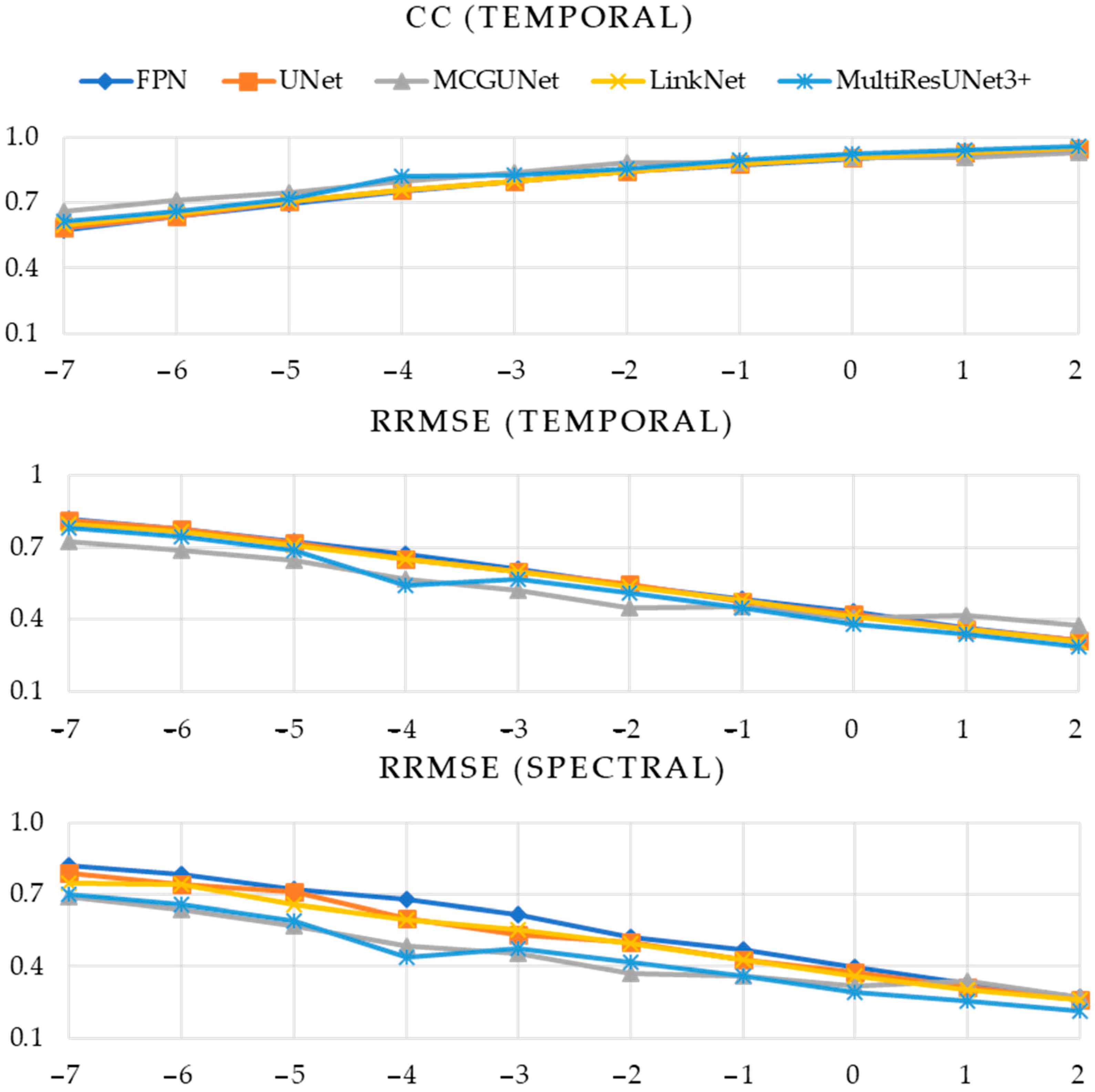


| Performance Metric | SNR (dB) | Model | ||||
|---|---|---|---|---|---|---|
| FPN | UNet | MCGUNet | LinkNet | MultiResUNet3+ (Proposed) | ||
| CC (Temporal) | −7 | 0.8074 | 0.8200 | 0.7913 | 0.8269 | 0.8636 |
| −6 | 0.8320 | 0.8507 | 0.8308 | 0.8566 | 0.8865 | |
| −5 | 0.8522 | 0.8646 | 0.8459 | 0.8579 | 0.9032 | |
| −4 | 0.8695 | 0.8912 | 0.8506 | 0.8793 | 0.9152 | |
| −3 | 0.8819 | 0.8986 | 0.8597 | 0.8946 | 0.9329 | |
| −2 | 0.9004 | 0.9299 | 0.8617 | 0.9204 | 0.9347 | |
| −1 | 0.9136 | 0.9389 | 0.8710 | 0.9261 | 0.9437 | |
| 0 | 0.9286 | 0.9420 | 0.8783 | 0.9388 | 0.9534 | |
| 1 | 0.9322 | 0.9442 | 0.8844 | 0.9494 | 0.9633 | |
| 2 | 0.9493 | 0.9554 | 0.8948 | 0.9537 | 0.9644 | |
| RRMSE (Temporal) | −7 | 0.5903 | 0.5693 | 0.5733 | 0.5554 | 0.4694 |
| −6 | 0.5567 | 0.5146 | 0.5378 | 0.5098 | 0.4279 | |
| −5 | 0.5184 | 0.4970 | 0.4982 | 0.5146 | 0.3954 | |
| −4 | 0.4939 | 0.4377 | 0.4942 | 0.4793 | 0.3728 | |
| −3 | 0.4739 | 0.4341 | 0.4768 | 0.4416 | 0.3193 | |
| −2 | 0.4357 | 0.3386 | 0.4785 | 0.3735 | 0.3232 | |
| −1 | 0.3949 | 0.3208 | 0.4698 | 0.3662 | 0.3021 | |
| 0 | 0.3552 | 0.3134 | 0.4630 | 0.3256 | 0.2674 | |
| 1 | 0.3501 | 0.3073 | 0.4584 | 0.2840 | 0.2413 | |
| 2 | 0.2907 | 0.2666 | 0.4197 | 0.2744 | 0.2338 | |
| RRMSE (Spectral) | −7 | 0.6219 | 0.5854 | 0.5066 | 0.5677 | 0.4419 |
| −6 | 0.5827 | 0.5278 | 0.4807 | 0.5328 | 0.4234 | |
| −5 | 0.5601 | 0.5280 | 0.4372 | 0.5514 | 0.3948 | |
| −4 | 0.5471 | 0.4492 | 0.4048 | 0.5331 | 0.3827 | |
| −3 | 0.5164 | 0.4754 | 0.4022 | 0.4687 | 0.3219 | |
| −2 | 0.4902 | 0.3605 | 0.3992 | 0.3996 | 0.3382 | |
| −1 | 0.4354 | 0.3498 | 0.3849 | 0.4131 | 0.3224 | |
| 0 | 0.3834 | 0.3471 | 0.3615 | 0.3621 | 0.2878 | |
| 1 | 0.3897 | 0.3384 | 0.3584 | 0.3134 | 0.2707 | |
| 2 | 0.3168 | 0.2992 | 0.3207 | 0.3080 | 0.2668 | |
| Performance Metric | SNR (dB) | Model | ||||
|---|---|---|---|---|---|---|
| FPN | UNet | MCGUNet | LinkNet | MultiResUNet3+ (Proposed) | ||
| CC (Temporal) | −7 | 0.5779 | 0.5548 | 0.5862 | 0.5552 | 0.5897 |
| −6 | 0.6425 | 0.6198 | 0.6533 | 0.6224 | 0.6463 | |
| −5 | 0.7013 | 0.6879 | 0.7095 | 0.6864 | 0.7056 | |
| −4 | 0.7545 | 0.7447 | 0.7561 | 0.7448 | 0.7589 | |
| −3 | 0.8015 | 0.7992 | 0.8035 | 0.7973 | 0.8039 | |
| −2 | 0.8438 | 0.8418 | 0.8410 | 0.8417 | 0.8447 | |
| −1 | 0.8785 | 0.8803 | 0.8793 | 0.8793 | 0.8826 | |
| 0 | 0.91 | 0.9113 | 0.9088 | 0.9106 | 0.9092 | |
| 1 | 0.9336 | 0.9345 | 0.9336 | 0.9343 | 0.9343 | |
| 2 | 0.9517 | 0.9529 | 0.9519 | 0.9526 | 0.9536 | |
| RRMSE (Temporal) | −7 | 0.8136 | 0.8266 | 0.8048 | 0.8263 | 0.8049 |
| −6 | 0.7672 | 0.7813 | 0.7486 | 0.7792 | 0.7597 | |
| −5 | 0.7119 | 0.7215 | 0.6994 | 0.7249 | 0.7087 | |
| −4 | 0.6544 | 0.6654 | 0.6536 | 0.6643 | 0.6483 | |
| −3 | 0.5963 | 0.6003 | 0.5884 | 0.6008 | 0.5924 | |
| −2 | 0.5345 | 0.5378 | 0.5355 | 0.5387 | 0.5333 | |
| −1 | 0.4775 | 0.4738 | 0.4746 | 0.4741 | 0.4695 | |
| 0 | 0.4130 | 0.4102 | 0.4151 | 0.4115 | 0.4158 | |
| 1 | 0.3570 | 0.3548 | 0.3571 | 0.3566 | 0.3565 | |
| 2 | 0.3055 | 0.3029 | 0.2968 | 0.3034 | 0.3058 | |
| RRMSE (Spectral) | −7 | 0.7920 | 0.8127 | 0.7670 | 0.8157 | 0.7686 |
| −6 | 0.7622 | 0.7540 | 0.7255 | 0.7581 | 0.7087 | |
| −5 | 0.6905 | 0.6857 | 0.6389 | 0.6716 | 0.6643 | |
| −4 | 0.5997 | 0.6180 | 0.5870 | 0.6162 | 0.5926 | |
| −3 | 0.5512 | 0.5404 | 0.5167 | 0.5508 | 0.5344 | |
| −2 | 0.4843 | 0.4836 | 0.4664 | 0.4825 | 0.4770 | |
| −1 | 0.4206 | 0.4208 | 0.4283 | 0.4246 | 0.4042 | |
| 0 | 0.3685 | 0.3595 | 0.3552 | 0.3617 | 0.3615 | |
| 1 | 0.3115 | 0.3054 | 0.2908 | 0.3064 | 0.2971 | |
| 2 | 0.2544 | 0.2527 | 0.2361 | 0.2520 | 0.2479 | |
| Performance Metric | SNR (dB) | Model | ||||
|---|---|---|---|---|---|---|
| FPN | UNet | MCGUNet | LinkNet | MultiResUNet3+ (Proposed) | ||
| CC (Temporal) | −7 | 0.5771 | 0.5856 | 0.6630 | 0.5987 | 0.6152 |
| −6 | 0.6370 | 0.6355 | 0.7113 | 0.6512 | 0.6582 | |
| −5 | 0.6932 | 0.7039 | 0.7449 | 0.7052 | 0.7188 | |
| −4 | 0.7507 | 0.7565 | 0.8009 | 0.7576 | 0.8191 | |
| −3 | 0.7982 | 0.8003 | 0.8388 | 0.8010 | 0.8245 | |
| −2 | 0.8423 | 0.8428 | 0.8819 | 0.8431 | 0.8580 | |
| −1 | 0.8757 | 0.8803 | 0.8832 | 0.8780 | 0.8934 | |
| 0 | 0.9025 | 0.9084 | 0.9094 | 0.9098 | 0.9228 | |
| 1 | 0.9308 | 0.9325 | 0.9100 | 0.9332 | 0.9411 | |
| 2 | 0.9496 | 0.9504 | 0.9277 | 0.9506 | 0.9579 | |
| RRMSE (Temporal) | −7 | 0.8198 | 0.8122 | 0.7235 | 0.7989 | 0.7830 |
| −6 | 0.7758 | 0.7755 | 0.6873 | 0.7638 | 0.7446 | |
| −5 | 0.7247 | 0.7189 | 0.6479 | 0.7088 | 0.6883 | |
| −4 | 0.6706 | 0.6524 | 0.5688 | 0.6532 | 0.5440 | |
| −3 | 0.6108 | 0.6017 | 0.5222 | 0.5994 | 0.5675 | |
| −2 | 0.5438 | 0.5458 | 0.4476 | 0.5370 | 0.5108 | |
| −1 | 0.4871 | 0.4736 | 0.4526 | 0.4821 | 0.4480 | |
| 0 | 0.4338 | 0.4207 | 0.4054 | 0.4143 | 0.3821 | |
| 1 | 0.3664 | 0.3603 | 0.4183 | 0.3610 | 0.3375 | |
| 2 | 0.3159 | 0.3118 | 0.3744 | 0.3107 | 0.2867 | |
| RRMSE (Spectral) | −7 | 0.8202 | 0.7903 | 0.6894 | 0.7447 | 0.7017 |
| −6 | 0.7842 | 0.7429 | 0.6364 | 0.7399 | 0.6587 | |
| −5 | 0.7222 | 0.7088 | 0.5690 | 0.6578 | 0.5879 | |
| −4 | 0.6812 | 0.5999 | 0.4865 | 0.5969 | 0.4401 | |
| −3 | 0.6136 | 0.5341 | 0.4545 | 0.5559 | 0.4768 | |
| −2 | 0.5216 | 0.5027 | 0.3698 | 0.4972 | 0.4188 | |
| −1 | 0.4701 | 0.4287 | 0.3625 | 0.4262 | 0.3577 | |
| 0 | 0.3945 | 0.3763 | 0.3196 | 0.3576 | 0.2934 | |
| 1 | 0.3289 | 0.3134 | 0.3374 | 0.3048 | 0.2542 | |
| 2 | 0.2716 | 0.2635 | 0.2722 | 0.2622 | 0.2142 | |
| Model | (%) | (%) | STD | STD |
|---|---|---|---|---|
| FPN | 88.26 | 81.31 | 0.23141 ± 0.07250 | 0.25518 ± 0.08122 |
| UNet | 94.59 | 91.59 | 0.11342 ± 0.03825 | 0.12123 ± 0.04411 |
| MCGUNet | 73.28 | 70.39 | 0.43087 ± 0.08775 | 0.43669 ± 0.13015 |
| LinkNet | 94.40 | 91.30 | 0.12072 ± 0.04134 | 0.13229 ± 0.04826 |
| MultiResUNet3+ (Proposed) | 94.82 | 92.84 | 0.13190 ± 0.05364 | 0.13660 ± 0.05587 |
| Model/Method | Delta | Theta | Alpha | Beta | Gamma |
|---|---|---|---|---|---|
| FPN | 0.4147 | 0.5429 | 0.1278 | 0.0797 | 0.0208 |
| UNet | 0.4338 | 0.5297 | 0.1230 | 0.0761 | 0.0200 |
| MCGUNet | 0.3997 | 0.6057 | 0.1289 | 0.0543 | 0.0101 |
| LinkNet | 0.4320 | 0.5318 | 0.1234 | 0.0762 | 0.0199 |
| MultiResUNet3+ (Proposed) | 0.4337 | 0.5295 | 0.1233 | 0.0760 | 0.0197 |
| EOG-contaminated EEG | 0.8301 | 0.1639 | 0.0368 | 0.0244 | 0.0069 |
| Ground Truth EEG | 0.4459 | 0.5184 | 0.1206 | 0.0749 | 0.0195 |
| Model | (in %) | (in %) | STD | STD |
|---|---|---|---|---|
| FPN | 85.06 | 75.96 | 0.31727 ± 0.11152 | 0.26395 ± 0.11695 |
| UNet | 89.59 | 80.61 | 0.22394 ± 0.07785 | 0.19231 ± 0.08107 |
| MCGUNet | 87.19 | 79.37 | 0.29214 ± 0.10520 | 0.23798 ± 0.10421 |
| LinkNet | 88.94 | 82.60 | 0.25091 ± 0.10112 | 0.19961 ± 0.10910 |
| MultiResUNet3+ (Proposed) | 89.33 | 83.21 | 0.23769 ± 0.08841 | 0.18931 ± 0.08931 |
| Model/Method | Delta | Theta | Alpha | Beta | Gamma |
|---|---|---|---|---|---|
| FPN | 0.4500 | 0.5534 | 0.1115 | 0.0566 | 0.0125 |
| UNet | 0.4452 | 0.5452 | 0.1150 | 0.0612 | 0.0147 |
| MCGUNet | 0.4393 | 0.5436 | 0.1193 | 0.0648 | 0.0155 |
| LinkNet | 0.4480 | 0.5303 | 0.1195 | 0.0656 | 0.0162 |
| MultiResUNet3+ (Proposed) | 0.4453 | 0.5344 | 0.1178 | 0.0658 | 0.0165 |
| EMG contaminated EEG | 0.1333 | 0.1046 | 0.0622 | 0.2079 | 0.5514 |
| Ground Truth EEG | 0.4421 | 0.5163 | 0.1230 | 0.0756 | 0.0197 |
| Model | (in %) | (in %) | STD | STD |
|---|---|---|---|---|
| FPN | 84.19 | 77.97 | 0.34448 ± 0.13849 | 0.27145 ± 0.15104 |
| UNet | 89.63 | 83.63 | 0.22991 ± 0.09619 | 0.18805 ± 0.10819 |
| MCGUNet | 87.03 | 80.31 | 0.29993 ± 0.10971 | 0.25156 ± 0.11219 |
| LinkNet | 89.77 | 83.39 | 0.22439 ± 0.09180 | 0.18340 ± 0.10208 |
| MultiResUNet3+ (Proposed) | 89.16 | 82.71 | 0.24891 ± 0.09445 | 0.20085 ± 0.09989 |
| Model/Method | Delta | Theta | Alpha | Beta | Gamma |
|---|---|---|---|---|---|
| FPN | 0.4543 | 0.5332 | 0.1185 | 0.0647 | 0.0153 |
| UNet | 0.4537 | 0.5304 | 0.1178 | 0.0650 | 0.0158 |
| MCGUNet | 0.4543 | 0.5443 | 0.1141 | 0.0595 | 0.0143 |
| LinkNet | 0.4537 | 0.5288 | 0.1175 | 0.0659 | 0.0163 |
| MultiResUNet3+ (Proposed) | 0.4532 | 0.5416 | 0.1131 | 0.0608 | 0.0151 |
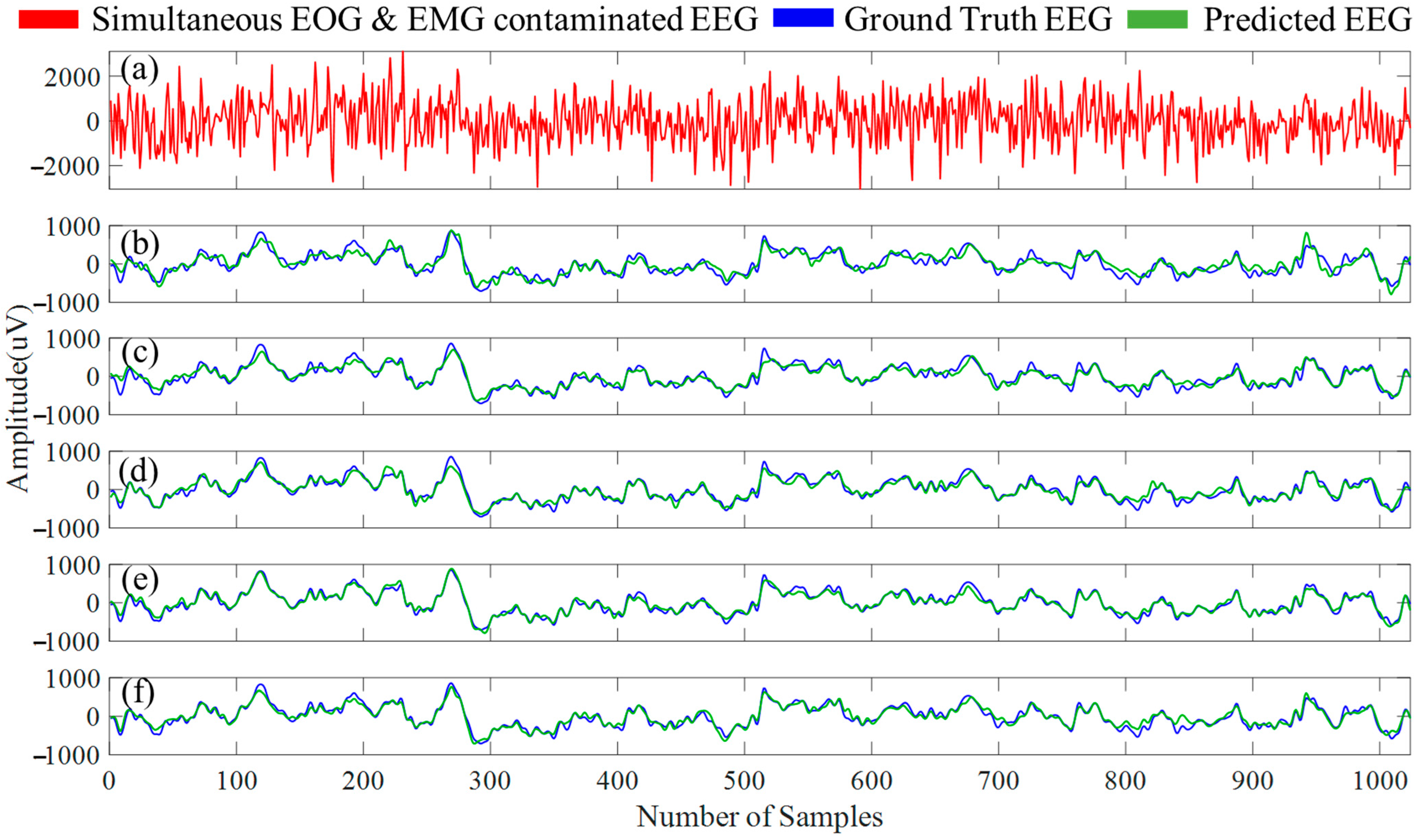
| Simultaneous EOG-EMG contaminated EEG | 0.1355 | 0.1046 | 0.0614 | 0.0196 | 0.5503 |
| Ground Truth EEG | 0.4458 | 0.5180 | 0.1208 | 0.0749 | 0.0196 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.S.; Mahmud, S.; Khandakar, A.; Al-Emadi, N.; Chowdhury, F.A.; Mahbub, Z.B.; Reaz, M.B.I.; Chowdhury, M.E.H. MultiResUNet3+: A Full-Scale Connected Multi-Residual UNet Model to Denoise Electrooculogram and Electromyogram Artifacts from Corrupted Electroencephalogram Signals. Bioengineering 2023, 10, 579. https://doi.org/10.3390/bioengineering10050579
Hossain MS, Mahmud S, Khandakar A, Al-Emadi N, Chowdhury FA, Mahbub ZB, Reaz MBI, Chowdhury MEH. MultiResUNet3+: A Full-Scale Connected Multi-Residual UNet Model to Denoise Electrooculogram and Electromyogram Artifacts from Corrupted Electroencephalogram Signals. Bioengineering. 2023; 10(5):579. https://doi.org/10.3390/bioengineering10050579
Chicago/Turabian StyleHossain, Md Shafayet, Sakib Mahmud, Amith Khandakar, Nasser Al-Emadi, Farhana Ahmed Chowdhury, Zaid Bin Mahbub, Mamun Bin Ibne Reaz, and Muhammad E. H. Chowdhury. 2023. "MultiResUNet3+: A Full-Scale Connected Multi-Residual UNet Model to Denoise Electrooculogram and Electromyogram Artifacts from Corrupted Electroencephalogram Signals" Bioengineering 10, no. 5: 579. https://doi.org/10.3390/bioengineering10050579
APA StyleHossain, M. S., Mahmud, S., Khandakar, A., Al-Emadi, N., Chowdhury, F. A., Mahbub, Z. B., Reaz, M. B. I., & Chowdhury, M. E. H. (2023). MultiResUNet3+: A Full-Scale Connected Multi-Residual UNet Model to Denoise Electrooculogram and Electromyogram Artifacts from Corrupted Electroencephalogram Signals. Bioengineering, 10(5), 579. https://doi.org/10.3390/bioengineering10050579








