Model-Driven Analysis of ECG Using Reinforcement Learning
Abstract
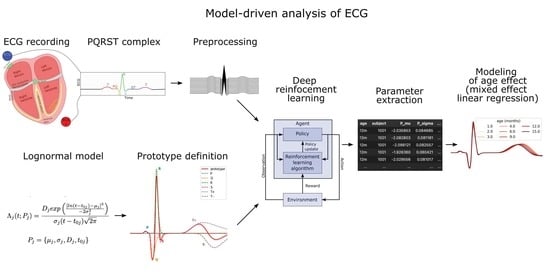
:1. Introduction
2. The Generation of ECG
2.1. The Cardiac Rhythm and Its Modulation
2.2. PQRST Waves
3. Materials and Methods
3.1. Lognormal Modeling
3.2. ECG Sample
3.3. Preprocessing
3.4. The PQRST Lognormal Prototype
3.5. Reinforcement Learning for Parameter Extraction
- Action space: Our model has 24 parameters. We consider these as latent variables. We defined the parameter space as a bounded box in , using the upper bound and the lower bound previously defined. Furthermore, we consider the middle of this bounded box as a reference point, i.e., . At the start of the fitting process, the estimated solution is set equal to , where the index in indicates the step number, with 0 standing for the initial estimate. The action space is a box . At each step of the fitting process, the action taken by the agent is used to update the estimated solution following the rule . However, we note that even within this relatively narrow box, the sigma–lognormal parameters can take values such that the order of the PQRST lognormal components is changed (i.e., the Q component may move after the R component). Since such an inversion is contrary to the intent of the model, we further constrain this ordering. To this end, we first define the order of lognormal components by the timing of their peak. For a lognormal defined by parameters (as defined in (2)), we can show this peak to happen at time . Thus, we constrain the impact of the action on so that it is canceled whenever it results in (i.e., the action is such that it may cause the timing of the peaks of two consecutive components to become inverted), with j and referring to two consecutive lognormal components in the set of components. Alternatively, such restrictions could have been introduced within the reward function, e.g., by adding a penalty term that reduces the reward when these constraints are violated. However, constraining the problem that way would not preclude the algorithm from reaching solutions that violate these constraints. Since these solutions are biologically irrelevant, we preferred to limit the actions to categorically prevent them. We further limit the action so that the resulting parameters remain within the box defined by and .
- Observation space: The observation space for this model is a dictionary containing values for the estimated parameters and the fitting errors. The fitting error space is a box of dimension 250. The PQRST signals are normalized to 500 points equally spaced between −1 and +1 (see the Preprocessing Section), but we observe only half of this interval, between −0.3 and 0.7. ECG signals in the remaining portion of the normalized time interval are mostly flat and contain little information. We set lower and upper bounds for that box at 1.5 times the minimum and maximum values observed for each of these points across all recorded PQRST time series. The observed values for the fitting error are taken as the difference between the PQRST time series being analyzed and the signal synthesized from . The observation space for the estimated parameters is the 24-dimensional box bounded by and , and the observed values are . We further normalized the observation space, as is generally recommended when using a heterogeneous observation space. We confirmed that the normalization of the observation space resulted in a significant improvement in performance for our application.
- Reward: In reinforcement learning, the reward is the objective function to maximize and depends on the action performed. Thus, reinforcement learning algorithms aim at finding the action that maximizes the reward associated with any given state. For our application, we use as reward the difference in fitting SNR (as defined in (3)) before and after the action was taken.
- Training: The optimization of a PQRST time series terminates when the algorithm reaches its maximal number of steps (1000) or when the agent fails to find a solution (i.e., a set of parameter values) improving over its best SNR for 100 consecutive steps. Every time the optimization of a PQRST time series terminated, another time series was picked at random, and a new optimization was started. We trained our model for 3,000,000 steps, at which point performances were stable, and no additional training seemed likely to provide any advantage.
- Hyperparameter tuning: We attempted to improve the learning and convergence of the PPO algorithm by tuning the hyperparameters using the Optuna-based [20] stable-baselines3-zoo package. The first attempt with 500 trials of 100,000 iterations failed to improve upon the default hyperparameterization provided with stable-baselines3’s implementation of PPO. We tried a second round with 1000 trials of 3,000,000 iterations with similar results. Consequently, we used the default hyperparameterization for PPO that comes with stable-baselines3.
- Deep reinforcement learning and network architecture: The PPO algorithm is implemented using deep learning and the architecture illustrated in Figure 5.
3.6. Parameter Denormalization
3.7. Software
4. Results
4.1. Parameter Extraction
4.2. Use Case: Analysis of the Impact of Age
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANS | autonomic nervous system |
| AV | atrioventricular |
| ECG | electrocardiogram |
| ODEs | ordinary differential equations |
| PPO | proximal policy optimization |
| RR | inter-beat interval |
| SA | sinoatrial node |
| SNR | signal-to-noise ratio |
References
- Murphy, S.L.; Xu, J.; Kochanek, K.D. Deaths: Final data for 2010. Natl. Vital Stat. Rep. 2013, 61, 117. [Google Scholar]
- Ahmad, F.B. Provisional Mortality Data—United States, 2021. MMWR Morb. Mortal. Wkly. Rep. 2022, 71, 597. [Google Scholar] [CrossRef]
- Becker, D.E. Fundamentals of Electrocardiography Interpretation. Anesth. Prog. 2006, 53, 53–64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lake, D.E.; Fairchild, K.D.; Moorman, J.R. Complex signals bioinformatics: Evaluation of heart rate characteristics monitoring as a novel risk marker for neonatal sepsis. J. Clin. Monit. Comput. 2014, 28, 329–339. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fairchild, K.D.; Aschner, J.L. HeRO monitoring to reduce mortality in NICU patients. Res. Rep. Neonatol. 2012, 2, 65–76. [Google Scholar] [CrossRef] [Green Version]
- Quiroz-Juárez, M.A.; Jiménez-Ramírez, O.; Vázquez-Medina, R.; Breña-Medina, V.; Aragón, J.L.; Barrio, R.A. Generation of ECG signals from a reaction-diffusion model spatially discretized. Sci. Rep. 2019, 9, 19000. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cardarilli, G.C.; Di Nunzio, L.; Fazzolari, R.; Re, M.; Silvestri, F. Improvement of the Cardiac Oscillator Based Model for the Simulation of Bundle Branch Blocks. Appl. Sci. 2019, 9, 3653. [Google Scholar] [CrossRef] [Green Version]
- Manju, B.R.; Akshaya, B. Simulation of Pathological ECG Signal Using Transform Method. Procedia Comput. Sci. 2020, 171, 2121–2127. [Google Scholar] [CrossRef]
- Kubicek, J.; Penhaker, M.; Kahankova, R. Design of a synthetic ECG signal based on the Fourier series. In Proceedings of the 2014 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Delhi, India, 24–27 September 2014; pp. 1881–1885. [Google Scholar] [CrossRef]
- Awal, M.A.; Mostafa, S.S.; Ahmad, M.; Alahe, M.A.; Rashid, M.A.; Kouzani, A.Z.; Mahmud, M.A.P. Design and Optimization of ECG Modeling for Generating Different Cardiac Dysrhythmias. Sensors 2021, 21, 1638. [Google Scholar] [CrossRef] [PubMed]
- Plamondon, R.; Marcelli, A.; Ferrer-Ballester, M.A. (Eds.) The Lognormality Principle and Its Applications in e-Security, e-Learning and e-Health; Number 88 in Series in Machine Perception and Artificial Intelligence; World Scientific Publishing Co. Pte. Ltd.: Singapore; Hackensack, NJ, USA, 2021. [Google Scholar]
- van Gent, P.; Farah, H.; van Nes, N.; van Arem, B. HeartPy: A novel heart rate algorithm for the analysis of noisy signals. Transp. Res. Part F Traffic Psychol. Behav. 2019, 66, 368–378. [Google Scholar] [CrossRef] [Green Version]
- O’Reilly, C.; Plamondon, R. A Globally Optimal Estimator for the Delta-Lognormal Modeling of Fast Reaching Movements. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 1428–1442. [Google Scholar] [CrossRef] [PubMed]
- O’Reilly, C.; Plamondon, R. Prototype-Based Methodology for the Statistical Analysis of Local Features in Stereotypical Handwriting Tasks. In Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 1864–1867. [Google Scholar] [CrossRef]
- O’Reilly, C.; Plamondon, R. Development of a Sigma–Lognormal representation for on-line signatures. Pattern Recognit. 2009, 42, 3324–3337. [Google Scholar] [CrossRef]
- Djioua, M.; Plamondon, R. A New Algorithm and System for the Characterization of Handwriting Strokes with Delta-Lognormal Parameters. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2060–2072. [Google Scholar] [CrossRef]
- Ghavamzadeh, M.; Mannor, S.; Pineau, J.; Tamar, A. Bayesian Reinforcement Learning: A Survey. Found. Trends Mach. Learn. 2015, 8, 359–483. [Google Scholar] [CrossRef] [Green Version]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Bellman, R. Dynamic Programming, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar] [CrossRef]
- Plamondon, R.; Feng, C.; Woch, A. A kinematic theory of rapid human movement. Part IV: A formal mathematical proof and new insights. Biol. Cybern. 2003, 89, 126–138. [Google Scholar] [CrossRef] [PubMed]
- Plamondon, R. A kinematic theory of rapid human movements: Part III. Kinetic outcomes. Biol. Cybern. 1998, 78, 133–145. [Google Scholar] [CrossRef] [PubMed]
- Plamondon, R. A kinematic theory of rapid human movements. Part II. Movement time and control. Biol. Cybern. 1995, 72, 309–320. [Google Scholar] [CrossRef] [PubMed]
- Plamondon, R. A kinematic theory of rapid human movements. Part I. Movement representation and generation. Biol. Cybern. 1995, 72, 295–307. [Google Scholar] [CrossRef]
- Plamondon, R.; O’Reilly, C.; Rémi, C.; Duval, T. The lognormal handwriter: Learning, performing, and declining. Front. Psychol. 2013, 4, 945. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friston, K.J.; Harrison, L.; Penny, W. Dynamic causal modelling. Neuroimage 2003, 19, 1273–1302. [Google Scholar] [CrossRef] [PubMed]
- Xiao, H.B.; Gibson, D.G. Absent septal q wave: A marker of the effects of abnormal activation pattern on left ventricular diastolic function. Heart 1994, 72, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Taylor, E.C.; Livingston, L.A.; Callan, M.J.; Ashwin, C.; Shah, P. Autonomic dysfunction in autism: The roles of anxiety, depression, and stress. Autism 2021, 25, 744–752. [Google Scholar] [CrossRef] [PubMed]








| P | −2.4 | −1.6 | 0.08 | 0.12 | −0.288 | −0.192 | 0 | 3.6 |
| Q | −3.6 | −2.4 | 0.32 | 0.48 | −0.096 | −0.064 | −60 | 0 |
| R | −3.6 | −2.4 | 0.2 | 0.3 | −0.054 | −0.036 | 0 | 96 |
| S | −4.2 | −2.8 | 0.32 | 0.48 | 0.012 | 0.018 | −12 | 0 |
| −1.2 | −0.8 | 0.32 | 0.48 | 0.12 | 0.18 | 0 | 204 | |
| −1.2 | −0.8 | 0.184 | 0.276 | 0.176 | 0.264 | −144 | 0 |
| D | ||||
|---|---|---|---|---|
| P | −2.0 | 0.1 | −0.24 | 3 |
| Q | −3.0 | 0.4 | −0.08 | −50 |
| R | −3.0 | 0.25 | −0.045 | 80 |
| S | −3.5 | 0.4 | 0.015 | −10 |
| −1.0 | 0.4 | 0.15 | 150 | |
| −1.0 | 0.23 | 0.22 | −120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
O’Reilly, C.; Oruganti, S.D.R.; Tilwani, D.; Bradshaw, J. Model-Driven Analysis of ECG Using Reinforcement Learning. Bioengineering 2023, 10, 696. https://doi.org/10.3390/bioengineering10060696
O’Reilly C, Oruganti SDR, Tilwani D, Bradshaw J. Model-Driven Analysis of ECG Using Reinforcement Learning. Bioengineering. 2023; 10(6):696. https://doi.org/10.3390/bioengineering10060696
Chicago/Turabian StyleO’Reilly, Christian, Sai Durga Rithvik Oruganti, Deepa Tilwani, and Jessica Bradshaw. 2023. "Model-Driven Analysis of ECG Using Reinforcement Learning" Bioengineering 10, no. 6: 696. https://doi.org/10.3390/bioengineering10060696
APA StyleO’Reilly, C., Oruganti, S. D. R., Tilwani, D., & Bradshaw, J. (2023). Model-Driven Analysis of ECG Using Reinforcement Learning. Bioengineering, 10(6), 696. https://doi.org/10.3390/bioengineering10060696