An EMG-to-Force Processing Approach to Estimating Knee Muscle Forces during Adult, Self-Selected Speed Gait
Abstract
:1. Introduction
2. Subjects
3. Methods
3.1. Kinematics Plus Kinetics (KIN)
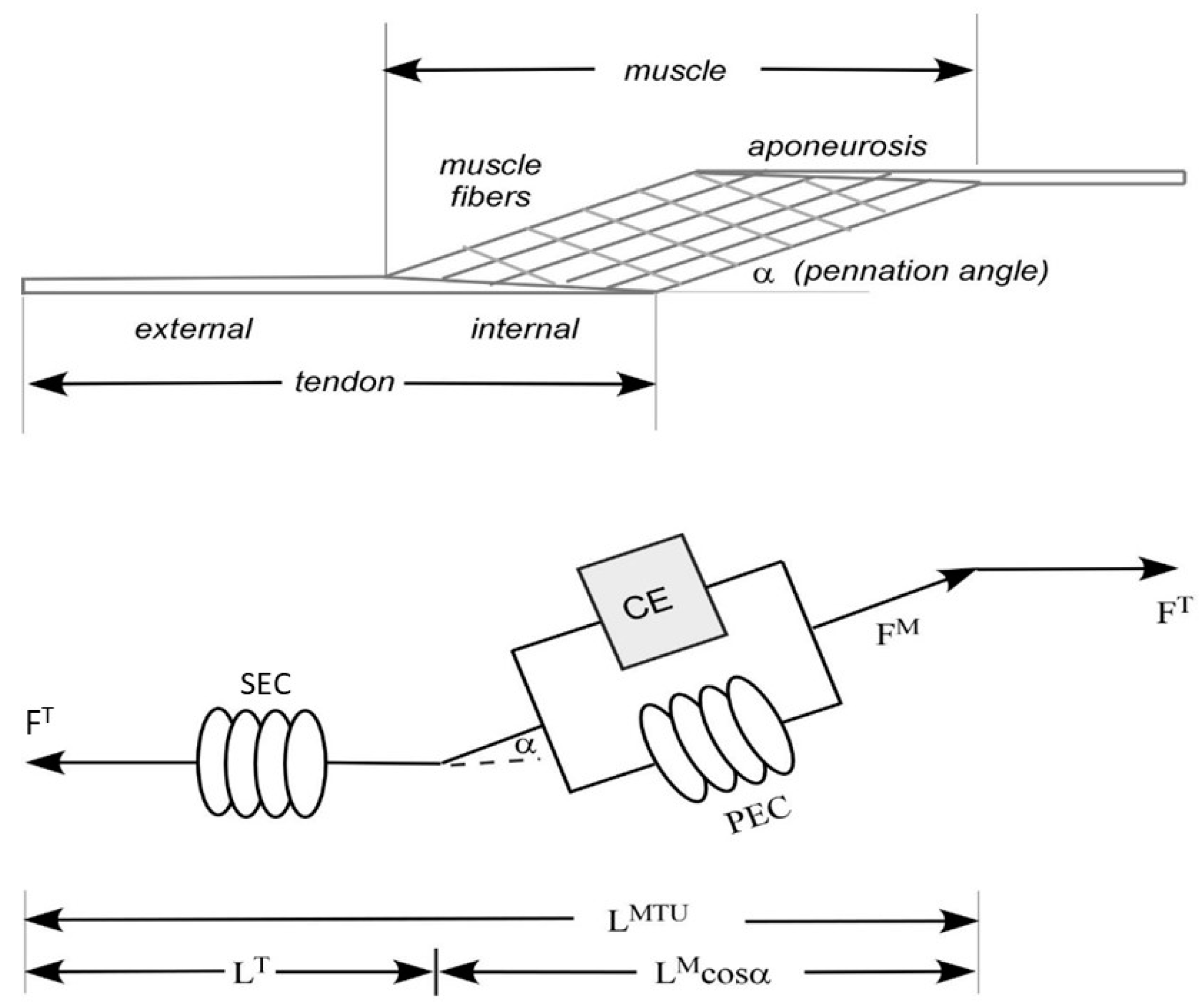
3.2. EMG-to-Force Processing—Force Processor
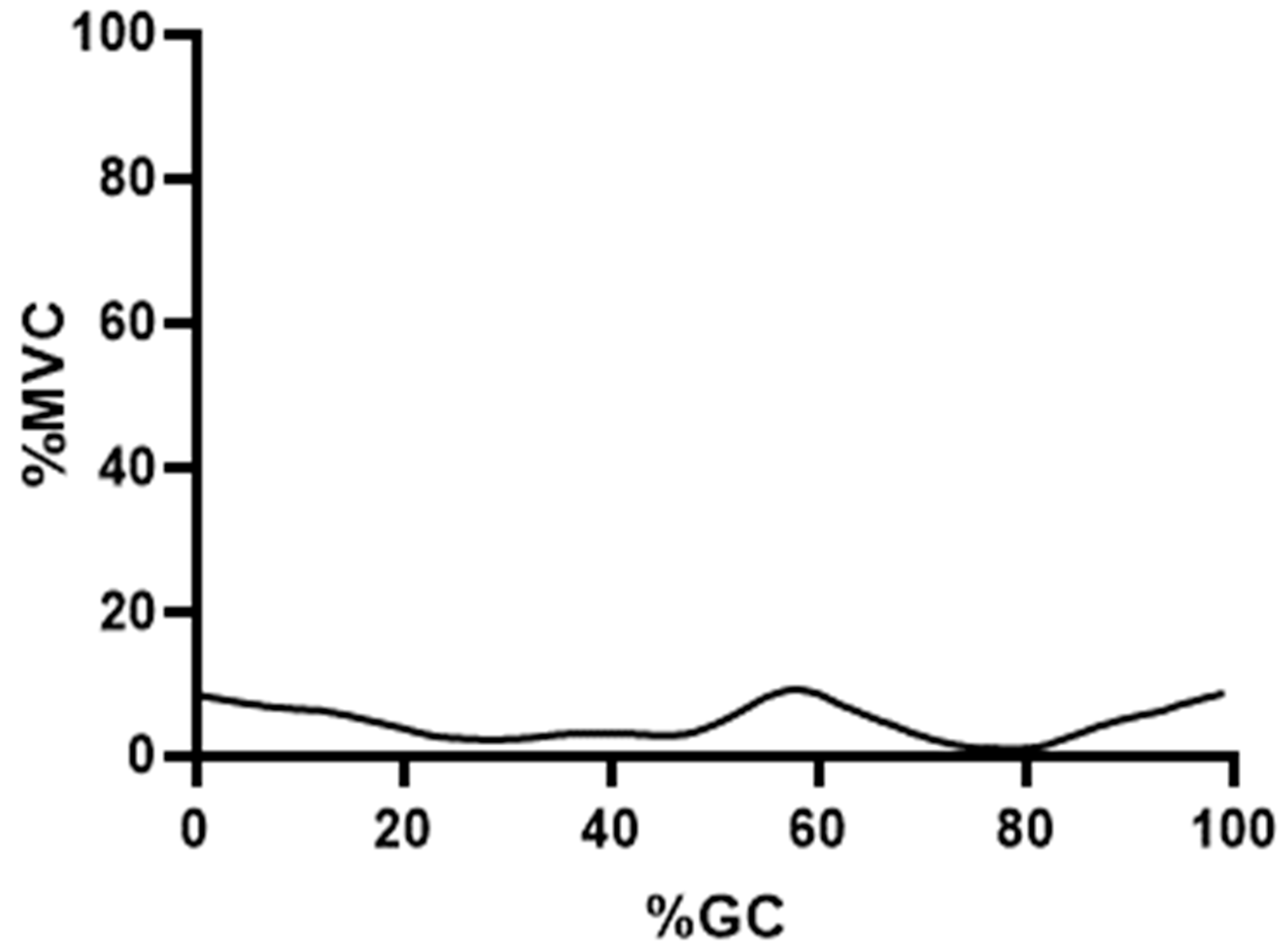
3.3. METHODS: EMG-to-Force Processing—Dynamic Electromyography (EMG)
3.4. Statistics
3.4.1. Gait Duration
3.4.2. Assessment of Model (Analysis)
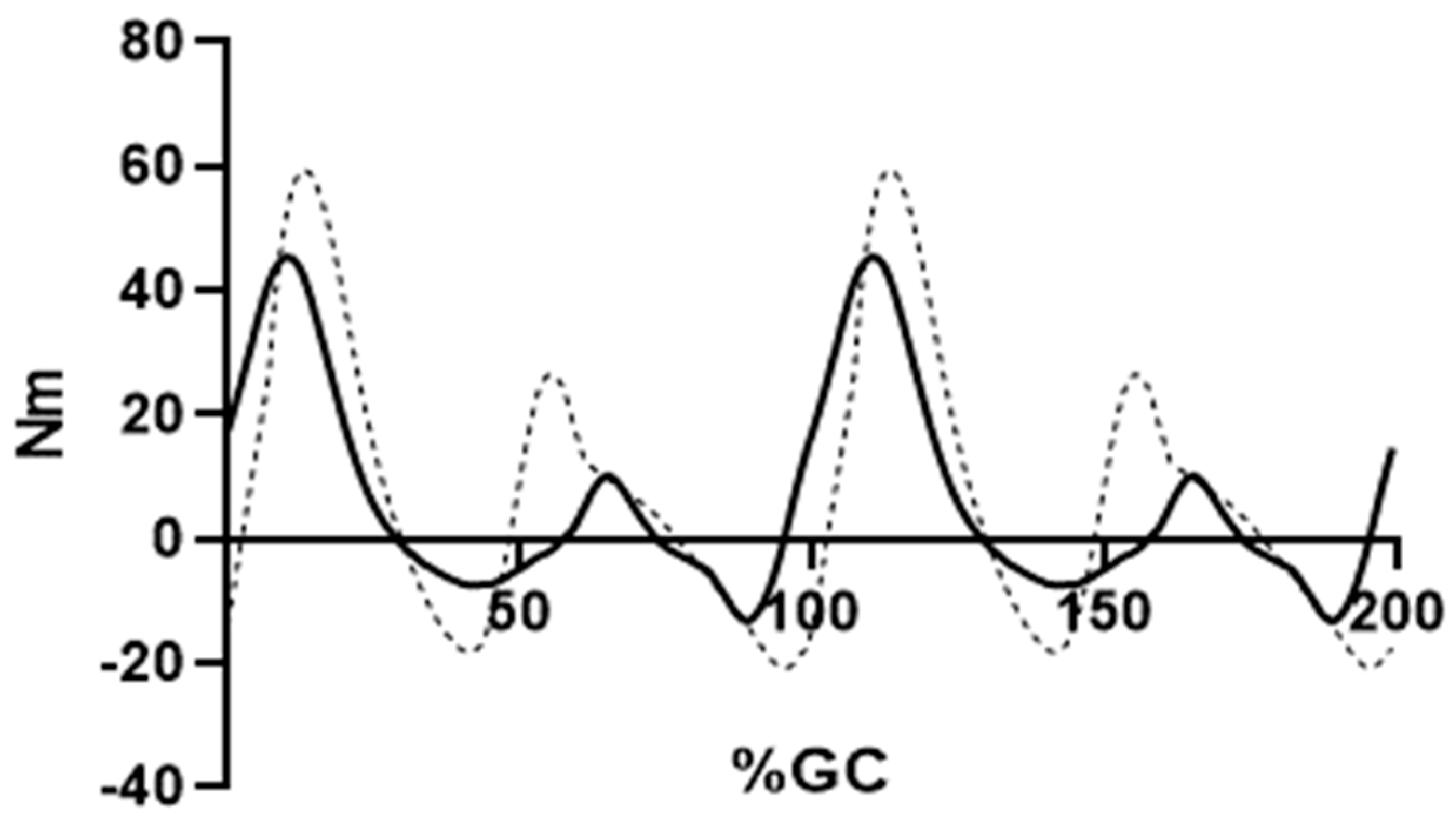
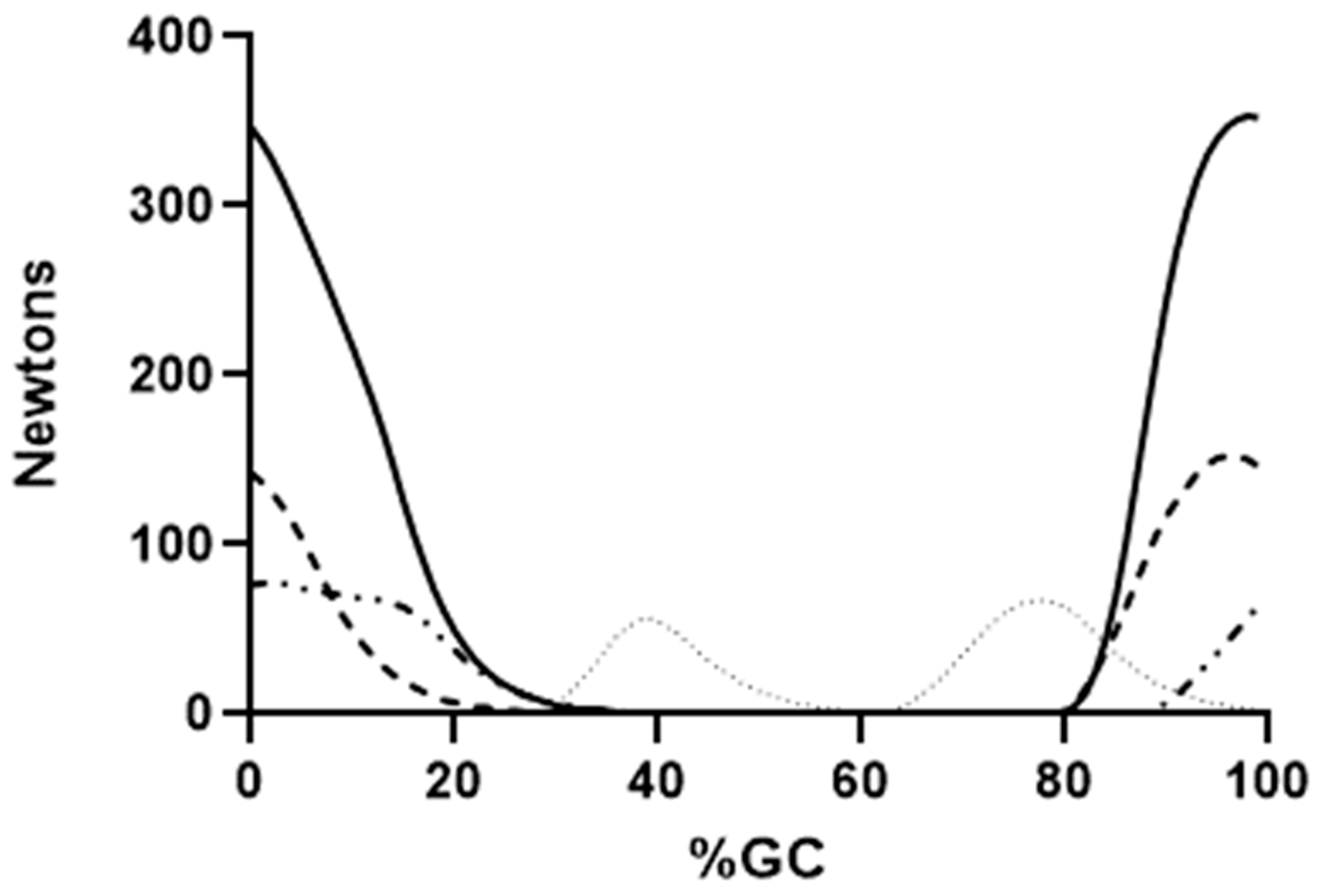
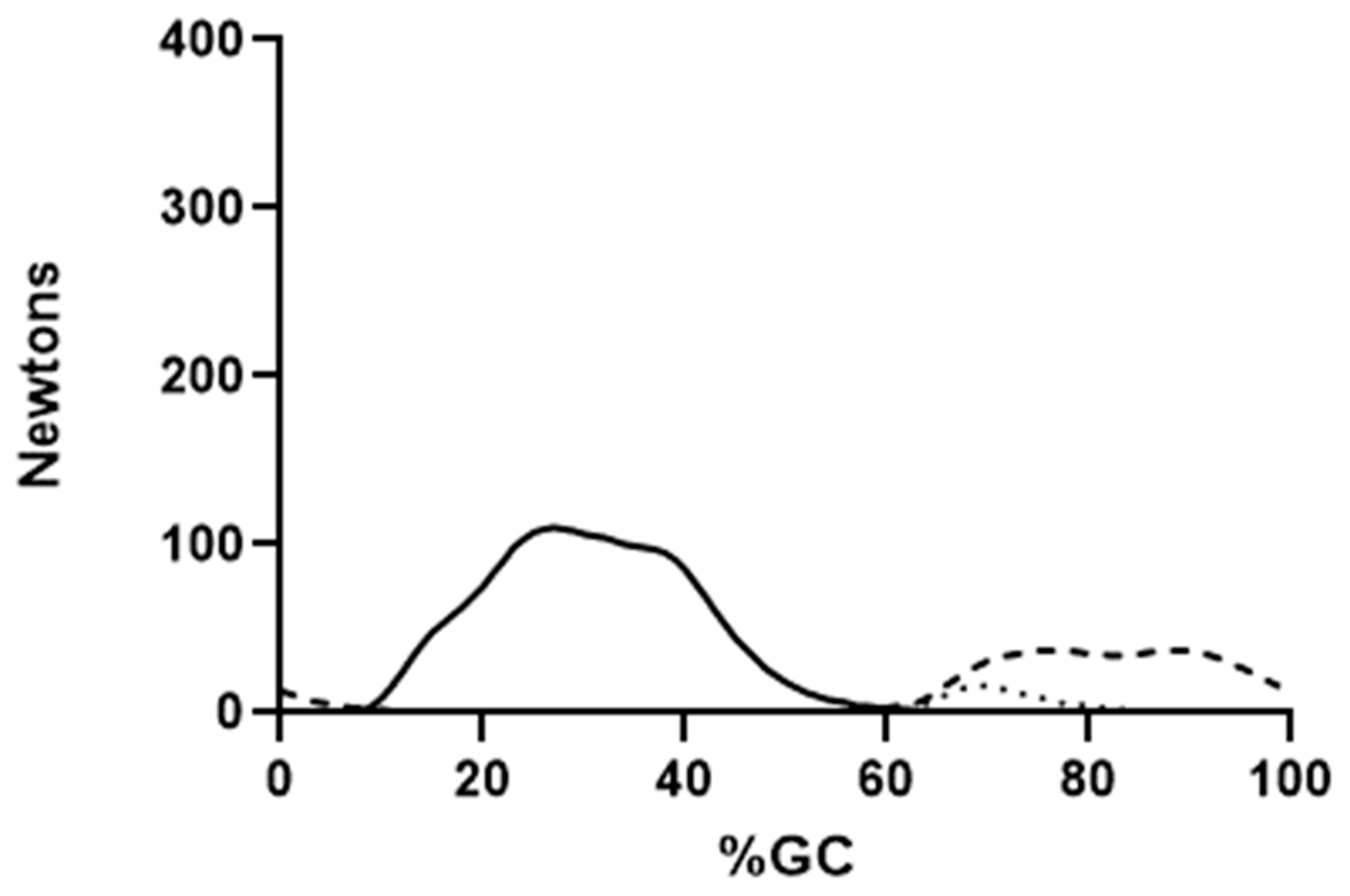
4. Results
5. Discussion
5.1. Closeness of Fit
5.2. Force Production by Individual Muscles
5.3. EMG and Muscle Force Variability in Selected Muscles
5.4. Potential “Error” Sources
5.5. Contribution of Non-Muscle Tissues to the Net Joint Moment
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADD MAG | Adductor magnus |
| BFLH | Long head of the biceps femoris |
| BFSH | Short head of the biceps femoris |
| EFP | EMG-to-force processing |
| EMD | Electromechanical delay |
| EMG | Electromyogram |
| FMTU | Muscle–tendon unit force |
| GC | Gait cycle |
| GMED | Gluteus medius |
| GMIN | Gluteus minimus |
| GRAC | Gracilis |
| GRF | Ground reaction force |
| Hz | Hertz |
| Kg | Kilograms |
| KIN | Combination of kinetics plus kinematics |
| LE | Linear envelope |
| LGAST | Lateral gastrocnemius |
| LMTU | Muscle–tendon unit length |
| M | Moment |
| MGAST | Medial gastrocnemius |
| MMT | Maximum muscle test |
| MTU | Muscle–tendon unit |
| MVC | Maximum voluntary contraction |
| POP | Popliteus |
| RF | Rectus femoris |
| SART | Sartorius |
| SMEMB | Semimembranosis |
| STEND | Semitendinosis |
| TFL | Tensor fascia lata |
| VI | Vastus intermedius |
| VL | Vastus lateralis |
| VMO | Vastus medialis oblique |
| %GC | Percent gait cycle |
References
- Olney, S.; Winter, D. Predictions of knee and ankle moments of force in walking from EMG and kinematic data. J. Biomech. 1985, 18, 9–20. [Google Scholar] [CrossRef] [PubMed]
- Bogey, R.; Barnes, L. Estimates of individual muscle power production in normal walking. J. Neuroeng. Rehabil. 2017, 14, 92. [Google Scholar] [CrossRef]
- Seirig, A.; Arkivar, R.J. A mathematical model for evaluation of forces in lower extremities of the musculo-skeletal system. J. Biomech. 1973, 6, 313–326. [Google Scholar]
- Chao, E.-S.; Rim, K. Application of optimization principles in determining the applied moments in human leg joints during gait. J. Biomech. 1973, 6, 497–510. [Google Scholar] [CrossRef] [PubMed]
- Pedotti, A.; Krishnan, V.; Stark, L. Optimization of muscle-force sequencing in human locomotion. Math. Biosci. 1978, 38, 57–76. [Google Scholar] [CrossRef]
- Hatze, H. The complete optimization of a human motion. Math. Biosci. 1976, 28, 99–135. [Google Scholar] [CrossRef]
- Amarantini, D.; Martin, L. A method to combine numerical optimization and EMG data for the estimation of joint moments under dynamic conditions. J. Biomech. 2004, 37, 1393–1404. [Google Scholar] [CrossRef]
- Anderson, F.; Pandy, M. Dynamic optimization of human walking. J. Biomech. Eng. 2001, 123, 381–390. [Google Scholar] [CrossRef] [PubMed]
- Hardt, D. Determining muscle forces in the leg during normal human walking—An application and evaluation of optimization methods. Trans. Am. Soc. Mech. Eng. 1978, 100, 72–78. [Google Scholar] [CrossRef]
- Hof, A.; Van den Berg, J. EMG to force processing I: An electrical analogue of the Hill muscle model. J. Biomech. 1981, 14, 747–758. [Google Scholar] [CrossRef]
- Hof, A.; Van den Berg, J. EMG to force processing II: Estimation of parameters of the Hill muscle model for the human triceps surae by means of a calfergometer. J. Biomech. 1981, 14, 759–770. [Google Scholar] [CrossRef] [PubMed]
- Hof, A.; Van den Berg, J. EMG to force processing III: Estimation of model parameters for the human triceps surae muscle and assessment of the accuracy by means of a torque plate. J. Biomech. 1981, 14, 771–785. [Google Scholar] [CrossRef] [PubMed]
- Hof, A.; Van den Berg, J. EMG to force processing IV: Eccentric-concentric contractions on a spring-flywheel set up. J. Biomech. 1981, 14, 787–792. [Google Scholar] [CrossRef] [PubMed]
- Bogey, R.; Perry, J.; Gitter, A. An EMG-to-force processing approach for determining ankle muscle forces during normal human gait. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 302–310. [Google Scholar] [CrossRef]
- Bogey, R.; Barnes, L. An EMG-to-force processing approach for estimating in vivo hip forces in normal adult walking. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 1172–1179. [Google Scholar] [CrossRef]
- Hof, A. EMG and muscle force: An introduction. Hum. Mov. Sci. 1984, 3, 119–153. [Google Scholar] [CrossRef]
- Komi, P.; Salonen, M.; Jarvinen, M. In vivo measurements of Achilles tendon forces in man. Med. Sci. Sports Exerc. 1984, 16, 165–166. [Google Scholar] [CrossRef]
- Komi, P.; Salonen, M.; Jarvinen, M.; Kokko, O. In vivo registration of Achilles tendon forces in man. I. Methological development. Int. J. Sports Med. 1987, 8, 3–8. [Google Scholar] [CrossRef]
- Zajac, F.; Neptune, R.; Kautz, S. Biomechanics and muscle coordination of human walking, Part I: Introduction to concepts, power transfer, dynamics, and stimulations. Gait Posture 2002, 16, 215–232. [Google Scholar] [CrossRef]
- Murray, M.P. Gait as a total pattern of movement. Am. J. Phys. Med. 1967, 46, 290–326. [Google Scholar]
- Perry, J. The technics and concepts of gait analysis. Bull. Prosthet. Res. 1981, 18, 279–281. [Google Scholar]
- Rab, G. Flexible marker set for human gait analysis. J. Electromyogr. Kinesiol. 1991, 1, 139–145. [Google Scholar] [CrossRef]
- Arsenault, A.; Winter, D.; Marteniuk, R. Is there a ‘normal’ profile of EMG activity in gait? Med. Biol. Eng. Comput. 1986, 24, 337–343. [Google Scholar] [CrossRef] [PubMed]
- Gitter, A.; Czerniecki, J.; DeGroot, D. Biomechanical analysis of the influence of prosthetic feet on below-knee amputee walking. Am. J. Phys. Med. Rehabil. 1991, 70, 142–148. [Google Scholar] [CrossRef]
- Dempster, W. Space Requirements of the Seated Operator. Geometrical, Kinematic, and Mechanical Aspects of the Body with Special Reference to the Limbs; WADC Technical Report 55–159; Aero Medical Laboratory; Wright Air Development Center, Air Research and Development Command, Wright-Patterson Air Force Base: Dayton, OH, USA, 1955; pp. 1–253. [Google Scholar]
- Delp, S.; Loan, J.; Hoy, M.; Zajak, F.; Topp, E.; Rosen, J. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans. Biomed. Eng. 1990, 37, 757–767. [Google Scholar] [CrossRef] [PubMed]
- Fox, M.; Reinbolt, J.; Ounpuu, S.; Delp, S. Mechanisms of improved knee function after rectus femoris transfer surgery. J. Biomech. 2009, 42, 614–619. [Google Scholar] [CrossRef] [PubMed]
- Hill, A. The heat of shortening and the dynamic constants in muscle. Proc. R. Soc. (Biol.) 1938, B-126, 136–195. [Google Scholar]
- Hoy, M.; Zajac, F.; Gordon, M. A musculoskeletal model of the human lower extremity: The effect of muscle, tendon, and moment arm on the moment-angle relationship of musculotendon actuators at the hip, knee, and ankle. J. Biomech. 1990, 23, 157–169. [Google Scholar] [CrossRef]
- Cavagna, G. Storage and utilization of eleastic energy in skeletal muscle. Exerc. Sports Sci. Rev. 1977, 5, 89–129. [Google Scholar] [CrossRef]
- Cavagna, G.; Kaneko, M. Mechanical work and efficiency in level walking and running. J. Physiol. 1977, 268, 467–481. [Google Scholar] [CrossRef]
- Basmajian, J.V.; Stedio, G.A. A new bipolar indwelling electrode for electromyography. J. Appl. Physiol. 1962, 17, 849–858. [Google Scholar] [CrossRef]
- Park, T.; Harris, G. Guided intramuscular fine wire electrode placement: A new technique. Am. J. Phys. Med. Rehabil. 1996, 75, 232–234. [Google Scholar] [CrossRef]
- Hoffer, M.; Perry, J. Pathodynamics of gait alterations in cerebral palsy and the significance of kinetic electromyography in evaluating foot and ankle problems. Foot Ankle 1983, 4, 128–134. [Google Scholar] [CrossRef] [PubMed]
- Perry, J.; Ireland, M.; Gronley, J.; Hoffer, M. Predictive value of manual muscle testing and gait analysis in normal ankles by electromyography. Foot Ankle 1986, 6, 254–259. [Google Scholar] [CrossRef]
- Hislop, H.; Montgomery, J. Daniels and Worthingham’s Muscle Testing: Techniques of Manual Examination; WB Saunders Company: New York, NY, USA, 2007. [Google Scholar]
- Bogey, R.; Barnes, L.; Perry, J. Computer algorithms to characterize individual subject EMG profiles during gait. Arch. Phys. Med. Rehabil. 1992, 73, 835–841. [Google Scholar]
- Milner-Brown, H.; Stein, R. The relation between the surface electromyogram and muscular force. J. Physiol. 1975, 246, 549–569. [Google Scholar] [CrossRef]
- Metral, S.; Cassar, G. Relationship between force and integrated EMG activity during voluntary isometric anisotonic contraction. Eur. J. Appl. Physiol. 1981, 46, 185–198. [Google Scholar] [CrossRef] [PubMed]
- Zajac, F. Muscle and tendon: Properties, models, scaling, and application to biomechanics and motor control. CRC Crit. Rev. Biomed. Eng. 1989, 17, 359–411. [Google Scholar]
- Crosby, P. Use of surface electromyography as a measure of dynamic force in human limb muscles. Med. Biol. Eng. Comput. 1978, 16, 519–524. [Google Scholar] [CrossRef]
- Milner-Brown, H.; Stein, R.; Yemm, R. The contractile properties of human motor units during voluntary isometric contractions. J. Physiol. 1973, 228, 285–306. [Google Scholar] [CrossRef]
- Anderson, F.; Goldberg, S.; Pandy, M.; Delp, S. Contributions of muscle forces and toe-off kinematics to peak knee flexion during the swing phase of normal gait: An induced position analysis. J. Biomech. 2004, 37, 731–737. [Google Scholar] [CrossRef] [PubMed]
- Kerrigan, D.; Todd, M.; Croce, U.D. Gender differences in joint biomechanics during walking. Am. J. Phys. Med. Rehabil. 1998, 77, 2–7. [Google Scholar] [CrossRef]
- Piazza, S.; Delp, S. The influence of muscles on knee flexion during the swing phase of gait. J. Biomech. 1996, 29, 723–733. [Google Scholar] [CrossRef]
- Perry, J. Gait Analysis: Normal and Pathological Function; McGraw-Hill, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Neptune, R.; Zajac, F.; Kautz, S. Muscle force redistributes segmental power for body progression during walking. Gait Posture 2004, 19, 194–205. [Google Scholar] [CrossRef]
- Takizawa, M.; Suzuki, D.; Fujimiya, M.; Uchiyama, E. Why the adductor magnus is large: The function based on muscle morphology in cadavers. Scand. J. Med. Sci. Sports 2014, 24, 197–203. [Google Scholar] [CrossRef] [PubMed]
- Semciw, A.; Pizzari, T.; Murley, G.; Green, R. Gluteus medius: An intramuscular investigation of anterior, middle and posterior segments during gait. J. Electromyogr. Kinesiol. 2013, 23, 858–864. [Google Scholar] [CrossRef] [PubMed]
- Thiranagama, R. Nerve supply of the human vastus lateralis muscle. J. Anat. 1990, 170, 193–198. [Google Scholar] [PubMed]
- Gottschalk, F.; Kourosh, S.; Leveau, B. The functional anatomy of tensor fasciae latae and gluteus medius and minimus. J. Anat. 1989, 166, 179–189. [Google Scholar] [PubMed]
- Bogey, R.; Gitter, A.; Barnes, L. Determination of ankle muscle power in normal gait using an EMG-to-force processing approach. J. Electromyogr. Kinesiol. 2010, 20, 46–54. [Google Scholar] [CrossRef]
- Kirk, R. Experimental Design: Procedures for the Behavioral Sciences; Wadsworth Publishing Company: Belmont, CA, USA, 1968; p. 577. [Google Scholar]
- Frigo, C.; Pavan, E.; Brunner, R. A dynamic model of quadriceps and hamstrings function. Gait Posture 2010, 31, 100–103. [Google Scholar] [CrossRef]
- Jonsson, B.; Steen, B. Function of the gracilis muscle. an electromyographic study. Acta Morphol. Neerl. Scand. 1966, 6, 325–341. [Google Scholar]
- Markolf, K.; Gorek, J.; Kabo, M.; Shapiro, M. Direct measurement of resultant forces in the anterior cruciate ligament. J. Bone Jt. Surg. 1990, 72-A, 557–567. [Google Scholar] [CrossRef]
- Correa, T.; Baker, R.; Graham, H.; Pandy, M. Accuracy of generic musculoskeletal models in predicting the functional roles of muscles in human gait. J. Biomech. 2011, 44, 20962105. [Google Scholar] [CrossRef] [PubMed]
- Yagi, M.; Tateuchi, H.; Kuriu, M.; Ichihashi, N. The function of the poplitues muscle: An in vivo ultrasound wave elastography study. Human Movement. Sci. 2021, 76, 1. [Google Scholar] [CrossRef]
- Amonoo-Kuofi, H. Morphology of muscle spindles in the human popliteus muscle. Evidence of a possible monitoring role of the popliteus muscle in the locked knee joint? Acta Anat. 1989, 134, 48–53. [Google Scholar] [CrossRef]
- Davis, M.; Newsam, C.; Perry, J. Electromyographic analysis of the popliteus muscle in level and downhill walking. Clin. Orthop. Relat. Res. 1995, 310, 211–217. [Google Scholar]
- Wood, A.; Boren, M.; Dodgen, T.; Wagner, R.; Patterson, R. Muscular architecture of the popliteus muscle and the basic science implications. Knee 2020, 27, 308–314. [Google Scholar] [CrossRef] [PubMed]
- Arnold, A.; Schwartz, M.; Thelen, D.; Delp, S. Contributions of muscles to terminal-swing knee motions vary with walking speed. J. Biomech. 2007, 40, 3660–3671. [Google Scholar] [CrossRef]
- Wickiewicz, T.; Roy, R.; Powell, P.; Edgerton, V. Muscle architecture of the human lower limb. Clin. Orthop. Relat. Res. 1983, 179, 275–283. [Google Scholar] [CrossRef]
- Gordon, A.; Huxley, A.; Julian, F. The variation in isometric tension with sarcomere length in vertebrate muscle fibres. J. Physiol. 1966, 184, 170–192. [Google Scholar] [CrossRef]
- Friedrich, J.; Brand, R. Muscle fiber architecture in the human lower limb. J. Biomech. 1990, 23, 91–95. [Google Scholar] [CrossRef] [PubMed]
- Yoon, Y.; Mansour, J. The passive elastic moment at the hip. J. Biomech. 1982, 15, 905–910. [Google Scholar] [CrossRef]
- Mena, D.; Mansour, J.; Simon, S. Analysis and synthesis of human swing leg motion during gait and its clinical implications. J. Biomech. 1981, 14, 823–832. [Google Scholar] [CrossRef] [PubMed]
- Mansour, J.; Audu, M. The passive elastic moment at the knee and its influence on human gait. J. Biomech. 1986, 19, 369–373. [Google Scholar] [CrossRef] [PubMed]
- Whittington, B.; Silder, A.; Heiderscheit, B.; Thelen, D. The contribution of passive-elastic mechanisms to lower extremity joint kinetics during human walking. Gait Posture 2008, 27, 628–634. [Google Scholar] [CrossRef] [PubMed]
- Silder, A.; Whittington, B.; Heidershcelt, B.; Thalen, D. Identification of passive elestic joint moment-angle relationships in the lower extremity. J. Biomech. 2007, 40, 2628–2635. [Google Scholar] [CrossRef]
- Jamari, J.; Ammarullah, M.I.; Santoso, G.; Sugiharto, S.; Supriyono, T.; Permana, M.S.; Winarni, T.I.; van der Heide, E. Adopted walking condition for computaitonal simulation approach on bearing of hip joint prostheis: Review over the past 30 years. Heliyon 2022, 8, e12050. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogey, R. An EMG-to-Force Processing Approach to Estimating Knee Muscle Forces during Adult, Self-Selected Speed Gait. Bioengineering 2023, 10, 980. https://doi.org/10.3390/bioengineering10080980
Bogey R. An EMG-to-Force Processing Approach to Estimating Knee Muscle Forces during Adult, Self-Selected Speed Gait. Bioengineering. 2023; 10(8):980. https://doi.org/10.3390/bioengineering10080980
Chicago/Turabian StyleBogey, Ross. 2023. "An EMG-to-Force Processing Approach to Estimating Knee Muscle Forces during Adult, Self-Selected Speed Gait" Bioengineering 10, no. 8: 980. https://doi.org/10.3390/bioengineering10080980
APA StyleBogey, R. (2023). An EMG-to-Force Processing Approach to Estimating Knee Muscle Forces during Adult, Self-Selected Speed Gait. Bioengineering, 10(8), 980. https://doi.org/10.3390/bioengineering10080980





