Selective Auditory Attention Detection Using Combined Transformer and Convolutional Graph Neural Networks
Abstract
1. Introduction
- Presenting of a hybrid end-to-end transformer and convolutional graph neural network for selective auditory attention detection;
- Developing a transformer-based module to process sequences of EEG data responsible for temporal information of auditory attention; and
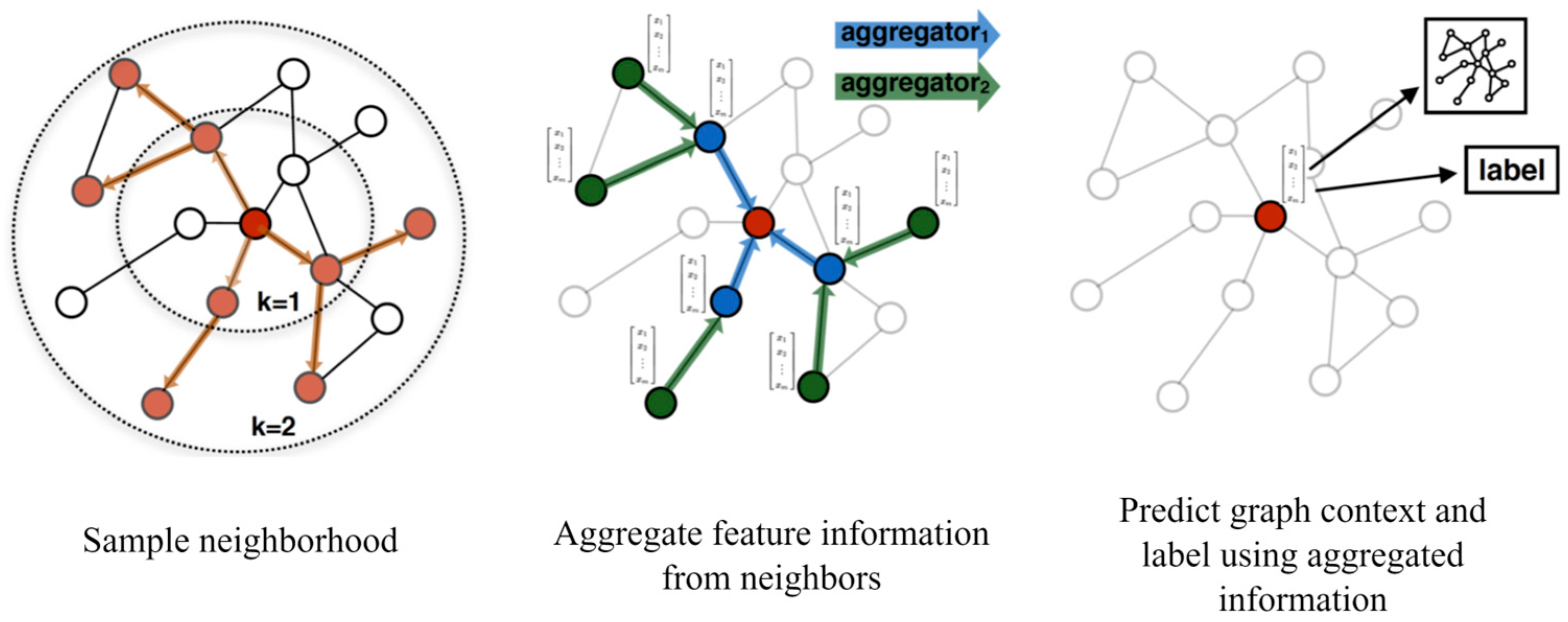
- Incorporation of spatial module, including GraphSAGE, GCN, and graph attention layers to find important EEG electrodes for further processing, and consequently reduce the computational load of the attention detection.
2. Materials and Methods
2.1. Data Description
2.2. Theoretical Background
2.3. Related Works
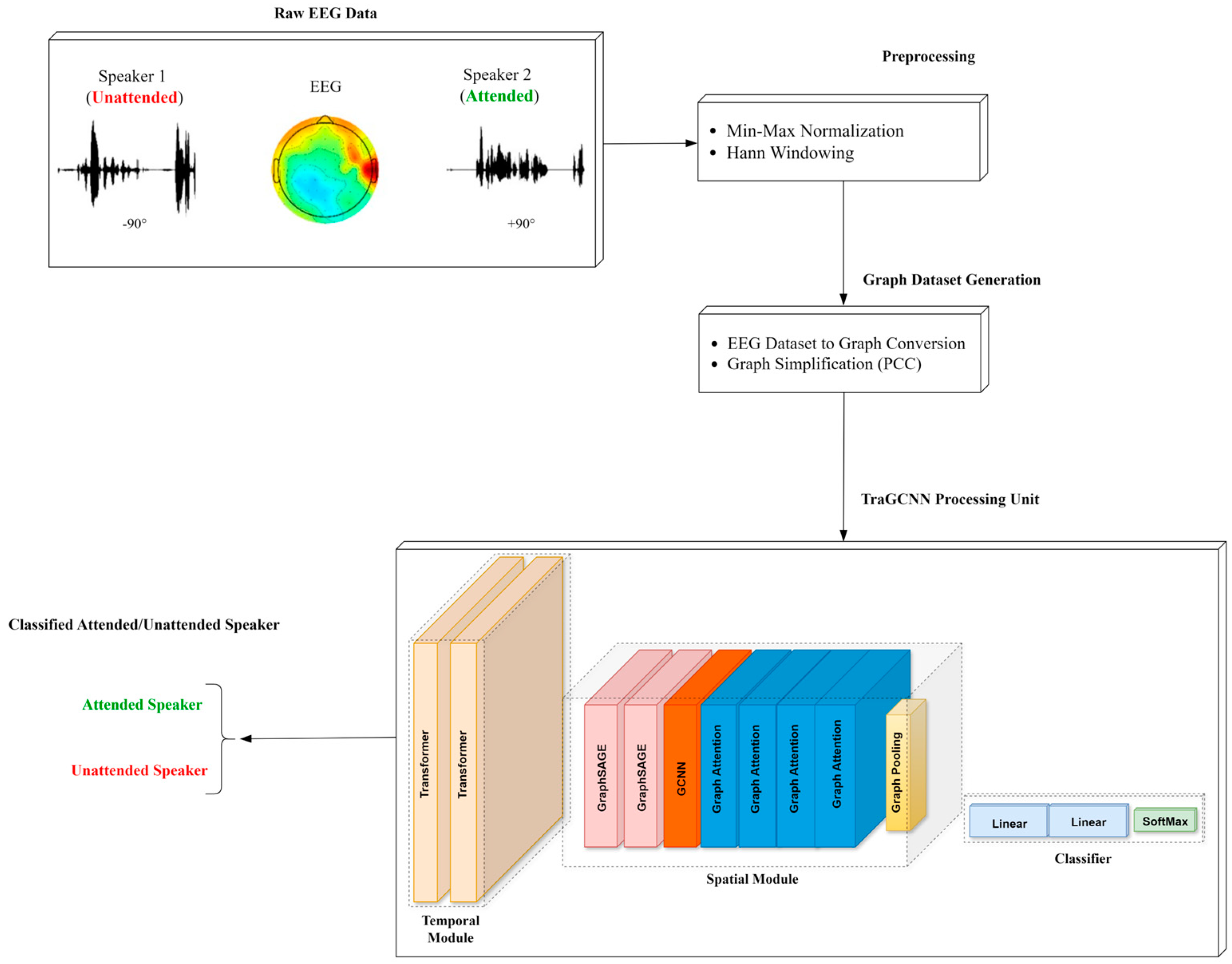
2.4. Proposed Selective Auditory Attention Detection Model
2.4.1. Graph Dataset Generation
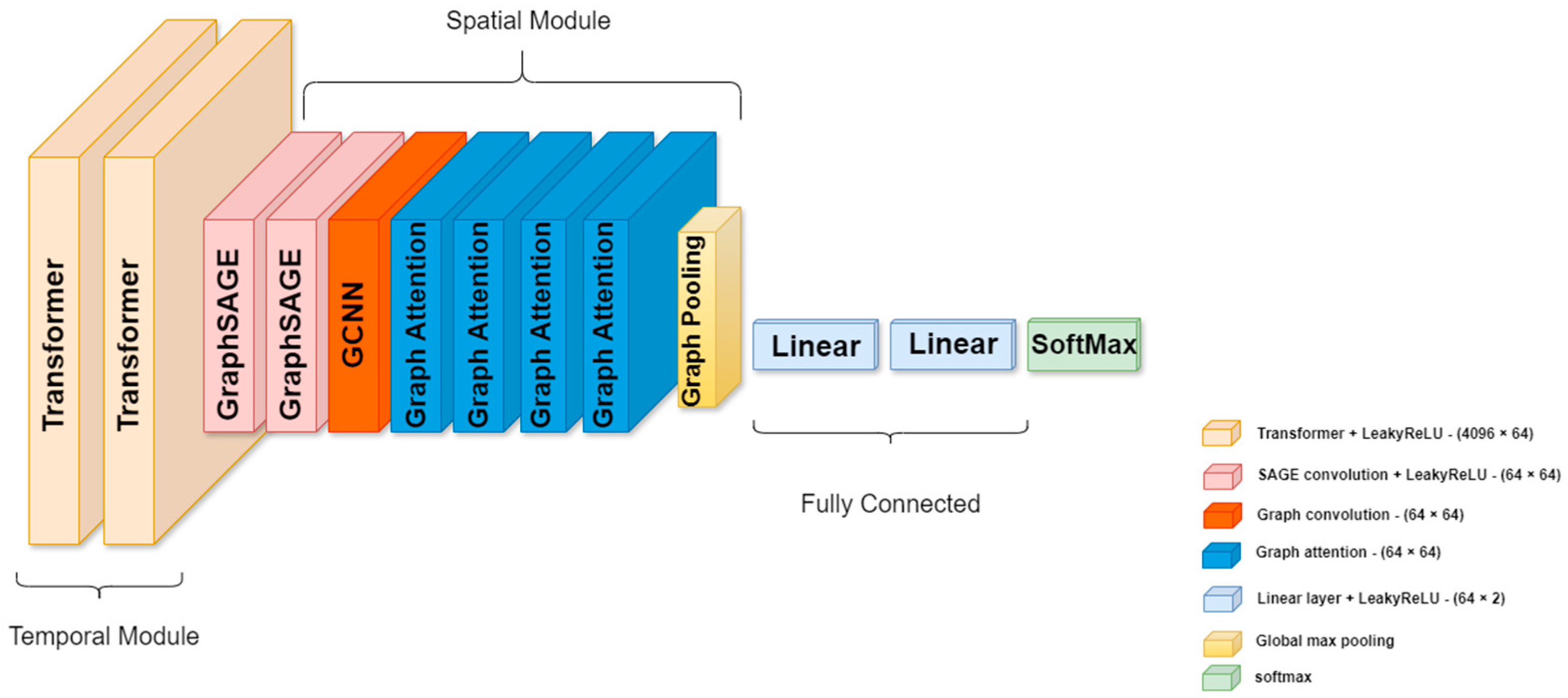
2.4.2. TraGCNN Processing Unit
3. Results
3.1. Experimental Setup
3.2. Performance Measures
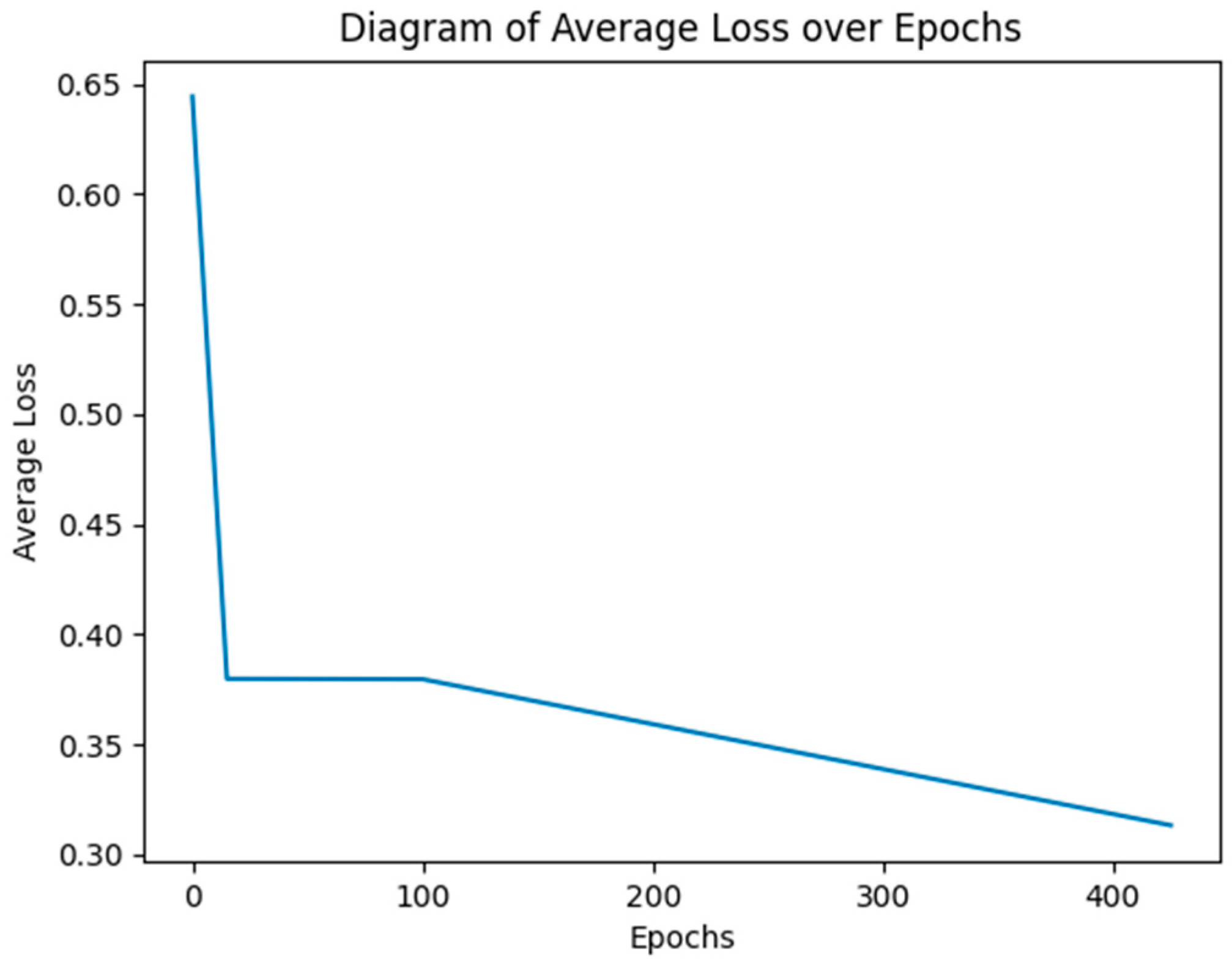
3.3. Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lindsay, G.W. Attention in psychology, neuroscience, and machine learning. Front. Comput. Neurosci. 2020, 14, 516985. [Google Scholar] [CrossRef]
- de Santana Correia, A.; Colombini, E.L. Attention, please! A survey of neural attention models in deep learning. Artif. Intell. Rev. 2022, 55, 6037–6124. [Google Scholar] [CrossRef]
- Cherry, E.C. Some experiments on the recognition of speech, with one and with two ears. J. Acoust. Soc. Am. 1953, 25, 975–979. [Google Scholar] [CrossRef]
- Alickovic, E.; Lunner, T.; Gustafsson, F.; Ljung, L. A tutorial on auditory attention identification methods. Front. Neurosci. 2019, 13, 153. [Google Scholar] [CrossRef]
- Fritz, J.B.; Elhilali, M.; David, S.V.; Shamma, S.A. Auditory attention—Focusing the searchlight on sound. Curr. Opin. Neurobiol. 2007, 17, 437–455. [Google Scholar] [CrossRef]
- Nguyen, Q.; Choi, J. Selection of the closest sound source for robot auditory attention in multi-source scenarios. J. Intell. Robot. Syst. 2016, 83, 239–251. [Google Scholar] [CrossRef]
- Scheich, H.; Baumgart, F.; Gaschler-Markefski, B.; Tegeler, C.; Tempelmann, C.; Heinze, H.J.; Schindler, F.; Stiller, D. Functional magnetic resonance imaging of a human auditory cortex area involved in foreground–background decomposition. Eur. J. Neurosci. 1998, 10, 803–809. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Z.; Gu, J.; Yao, D.; Li, J. Enhancing spatial auditory attention decoding with neuroscience-inspired prototype training. arXiv 2024, arXiv:2407.06498. [Google Scholar]
- Geravanchizadeh, M.; Zakeri, S. Ear-EEG-based binaural speech enhancement (ee-BSE) using auditory attention detection and audiometric characteristics of hearing-impaired subjects. J. Neural Eng. 2021, 18, 0460d0466. [Google Scholar] [CrossRef]
- Das, N.; Bertrand, A.; Francart, T. EEG-based auditory attention detection: Boundary conditions for background noise and speaker positions. J. Neural Eng. 2018, 15, 066017. [Google Scholar] [CrossRef] [PubMed]
- Han, C.; O’Sullivan, J.; Luo, Y.; Herrero, J.; Mehta, A.D.; Mesgarani, N. Speaker-independent auditory attention decoding without access to clean speech sources. Sci. Adv. 2019, 5, eaav6134. [Google Scholar] [CrossRef]
- O'sullivan, J.A.; Power, A.J.; Mesgarani, N.; Rajaram, S.; Foxe, J.J.; Shinn-Cunningham, B.G.; Slaney, M.; Shamma, S.A.; Lalor, E.C. Attentional selection in a cocktail party environment can be decoded from single-trial EEG. Cereb. Cortex 2015, 25, 1697–1706. [Google Scholar] [CrossRef] [PubMed]
- Wong, D.D.; Fuglsang, S.A.; Hjortkjær, J.; Ceolini, E.; Slaney, M.; De Cheveigne, A. A comparison of regularization methods in forward and backward models for auditory attention decoding. Front. Neurosci. 2018, 12, 531. [Google Scholar] [CrossRef] [PubMed]
- Ciccarelli, G.; Nolan, M.; Perricone, J.; Calamia, P.T.; Haro, S.; O’sullivan, J.; Mesgarani, N.; Quatieri, T.F.; Smalt, C.J. Comparison of two-talker attention decoding from EEG with nonlinear neural networks and linear methods. Sci. Rep. 2019, 9, 11538. [Google Scholar] [CrossRef] [PubMed]
- Teoh, E.S.; Lalor, E.C. EEG decoding of the target speaker in a cocktail party scenario: Considerations regarding dynamic switching of talker location. J. Neural Eng. 2019, 16, 036017. [Google Scholar] [CrossRef] [PubMed]
- Geravanchizadeh, M.; Gavgani, S.B. Selective auditory attention detection based on effective connectivity by single-trial EEG. J. Neural Eng. 2020, 17, 026021. [Google Scholar] [CrossRef] [PubMed]
- Cai, S.; Zhang, R.; Zhang, M.; Wu, J.; Li, H. EEG-based Auditory Attention Detection with Spiking Graph Convolutional Network. IEEE Trans. Cogn. Dev. Syst. 2024, 16, 1698–1706. [Google Scholar] [CrossRef]
- Roushan, H.; Bakhshalipour Gavgani, S.; Geravanchizadeh, M. Auditory attention detection in cocktail-party: A microstate study. bioRxiv 2023. [Google Scholar] [CrossRef]
- Crosse, M.J.; Di Liberto, G.M.; Bednar, A.; Lalor, E.C. The multivariate temporal response function (mTRF) toolbox: A MATLAB toolbox for relating neural signals to continuous stimuli. Front. Hum. Neurosci. 2016, 10, 604. [Google Scholar] [CrossRef]
- Mesgarani, N.; Chang, E.F. Selective cortical representation of attended speaker in multi-talker speech perception. Nature 2012, 485, 233–236. [Google Scholar] [CrossRef]
- Geravanchizadeh, M.; Roushan, H. Dynamic selective auditory attention detection using RNN and reinforcement learning. Sci. Rep. 2021, 11, 15497. [Google Scholar] [CrossRef] [PubMed]
- Kuruvila, I.; Muncke, J.; Fischer, E.; Hoppe, U. Extracting the auditory attention in a dual-speaker scenario from EEG using a joint CNN-LSTM model. Front. Physiol. 2021, 12, 700655. [Google Scholar] [CrossRef] [PubMed]
- Cai, S.; Sun, P.; Schultz, T.; Li, H. Low-latency auditory spatial attention detection based on spectro-spatial features from EEG. In Proceedings of the 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Mexico, 1–5 November 2021; pp. 5812–5815. [Google Scholar]
- Xu, X.; Wang, B.; Yan, Y.; Wu, X.; Chen, J. A DenseNet-based method for decoding auditory spatial attention with EEG. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 1946–1950. [Google Scholar]
- Fuglsang, S.A.; Märcher-Rørsted, J.; Dau, T.; Hjortkjær, J. Effects of sensorineural hearing loss on cortical synchronization to competing speech during selective attention. J. Neurosci. 2020, 40, 2562–2572. [Google Scholar] [CrossRef]
- Zhang, X.-M.; Liang, L.; Liu, L.; Tang, M.-J. Graph neural networks and their current applications in bioinformatics. Front. Genet. 2021, 12, 690049. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Tang, J. Deep Learning on Graphs; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. Adv. Neural Inf. Process. Syst. 2013, 26. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, F.; Zhang, L.; Ji, T.; Fu, K.; Zhao, L.; Chen, F.; Wu, L.; Aggarwal, C.; Lu, C.-T. Bridging the gap between spatial and spectral domains: A survey on graph neural networks. arXiv 2020, arXiv:2002.11867. [Google Scholar]
- Georgousis, S.; Kenning, M.P.; Xie, X. Graph deep learning: State of the art and challenges. IEEE Access 2021, 9, 22106–22140. [Google Scholar] [CrossRef]
- Mikolov, T. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Zhou, Y.; Zheng, H.; Huang, X.; Hao, S.; Li, D.; Zhao, J. Graph neural networks: Taxonomy, advances, and trends. ACM Trans. Intell. Syst. Technol. (TIST) 2022, 13, 1–54. [Google Scholar] [CrossRef]
- Micheli, A. Neural network for graphs: A contextual constructive approach. IEEE Trans. Neural Netw. 2009, 20, 498–511. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Kenton, J.D.M.-W.C.; Toutanova, L.K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Annual Conference of the North American Chapter of the Association for Computational Linguistics, Minneapolis, MN, USA, 3–5 June 2019; p. 2. [Google Scholar]
- Shehzad, A.; Xia, F.; Abid, S.; Peng, C.; Yu, S.; Zhang, D.; Verspoor, K. Graph transformers: A survey. arXiv 2024, arXiv:2407.09777. [Google Scholar]
- Zhang, Z.; Zhong, S.-h.; Liu, Y. TorchEEGEMO: A deep learning toolbox towards EEG-based emotion recognition. Expert Syst. Appl. 2024, 249, 123550. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation coefficients: Appropriate use and interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.-C.; Tsai, H.; Bhojanapalli, S.; Chung, H.W.; Chang, Y.-W.; Ferng, C.-S. A simple and effective positional encoding for transformers. arXiv 2021, arXiv:2104.08698. [Google Scholar]
- Shaw, P.; Uszkoreit, J.; Vaswani, A. Self-attention with relative position representations. arXiv 2018, arXiv:1803.02155. [Google Scholar]
- Shi, Y.; Huang, Z.; Feng, S.; Zhong, H.; Wang, W.; Sun, Y. Masked label prediction: Unified message passing model for semi-supervised classification. arXiv 2020, arXiv:2009.03509. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Fey, M.; Lenssen, J.E. Fast graph representation learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar]
- Xu, D.; Ruan, C.; Korpeoglu, E.; Kumar, S.; Achan, K. Inductive Representation Learning on Temporal Graphs. arXiv 2020, arXiv:2002.07962. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. arXiv 2018, arXiv:1710.10903. [Google Scholar]
- Casanova, P.; Lio, A.R.P.; Bengio, Y. Graph attention networks. ICLR. Petar Velickovic Guillem Cucurull Arantxa Casanova Adriana Romero Pietro Liò Yoshua Bengio 2018, 1050, 10–48550. [Google Scholar]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical evaluation of rectified activations in convolutional network. arXiv 2015, arXiv:1505.00853. [Google Scholar]
- Raschka, S. Model evaluation, model selection, and algorithm selection in machine learning. arXiv 2018, arXiv:1811.12808. [Google Scholar]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv 2020, arXiv:2010.16061. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in Pytorch. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]

| Parameter | Value |
|---|---|
| Learning rate | 0.001 |
| Activation function | LeakyReLU [49] |
| Optimizer | Adam [53] |
| Loss | Cross entropy |
| Batch size | 64 |
| Nr. Of Epochs | 15 for each fold |
| Dropout rate | 0.2 [54] |
| Method | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| SAADconnectivity (our previous model) | 68.33% | 0.46 | 1.00 | 0.63 |
| EEGWaveNet-K1 [8] | 68.73% | - | - | - |
| EEGWaveNet-K10 [8] | 69.97% | - | - | - |
| TraGCNN-SAAD (proposed) | 80.12% | 0.79 | 0.87 | 0.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geravanchizadeh, M.; Shaygan Asl, A.; Danishvar, S. Selective Auditory Attention Detection Using Combined Transformer and Convolutional Graph Neural Networks. Bioengineering 2024, 11, 1216. https://doi.org/10.3390/bioengineering11121216
Geravanchizadeh M, Shaygan Asl A, Danishvar S. Selective Auditory Attention Detection Using Combined Transformer and Convolutional Graph Neural Networks. Bioengineering. 2024; 11(12):1216. https://doi.org/10.3390/bioengineering11121216
Chicago/Turabian StyleGeravanchizadeh, Masoud, Amir Shaygan Asl, and Sebelan Danishvar. 2024. "Selective Auditory Attention Detection Using Combined Transformer and Convolutional Graph Neural Networks" Bioengineering 11, no. 12: 1216. https://doi.org/10.3390/bioengineering11121216
APA StyleGeravanchizadeh, M., Shaygan Asl, A., & Danishvar, S. (2024). Selective Auditory Attention Detection Using Combined Transformer and Convolutional Graph Neural Networks. Bioengineering, 11(12), 1216. https://doi.org/10.3390/bioengineering11121216








