Development of a Microfluidic Viscometer for Non-Newtonian Blood Analog Fluid Analysis
Abstract
:1. Introduction
2. Materials and Methods
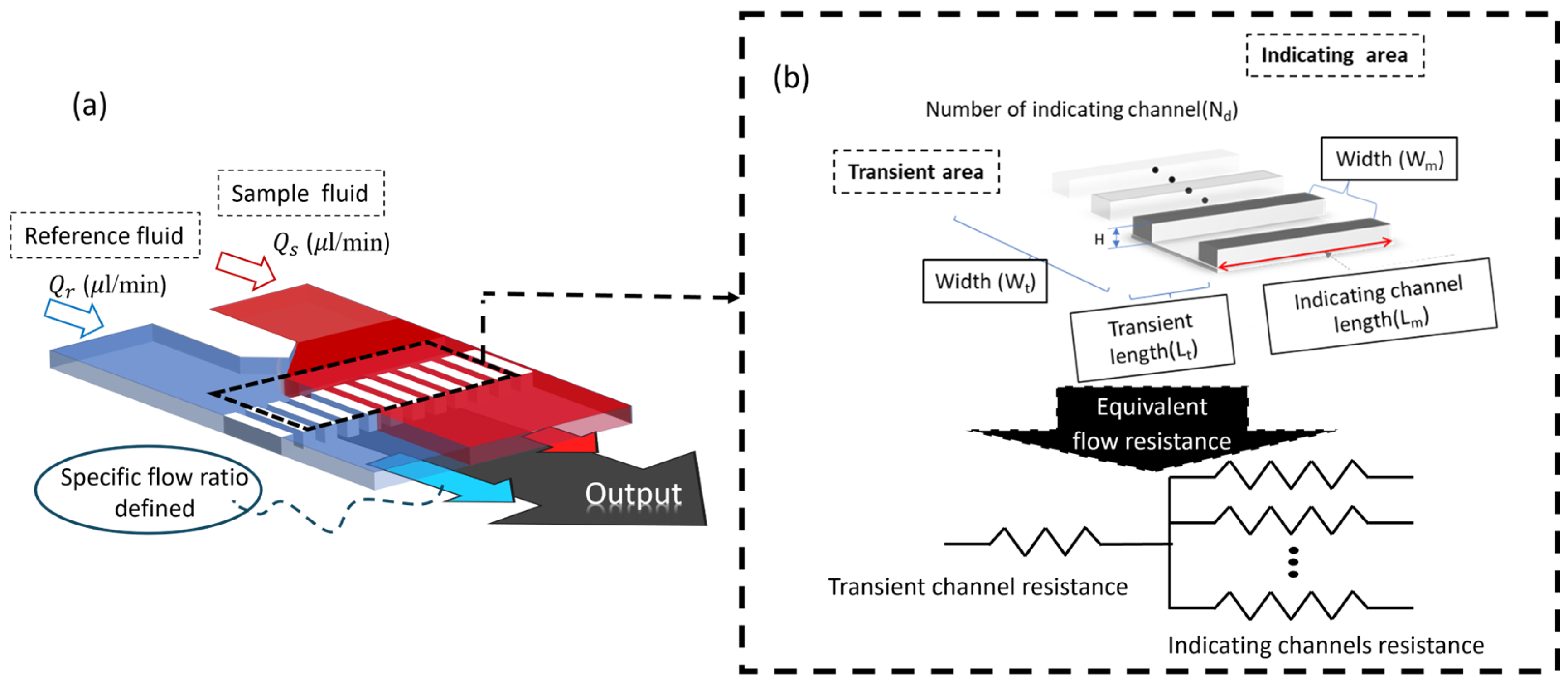
2.1. Parallel Laminar Flow Microchip System
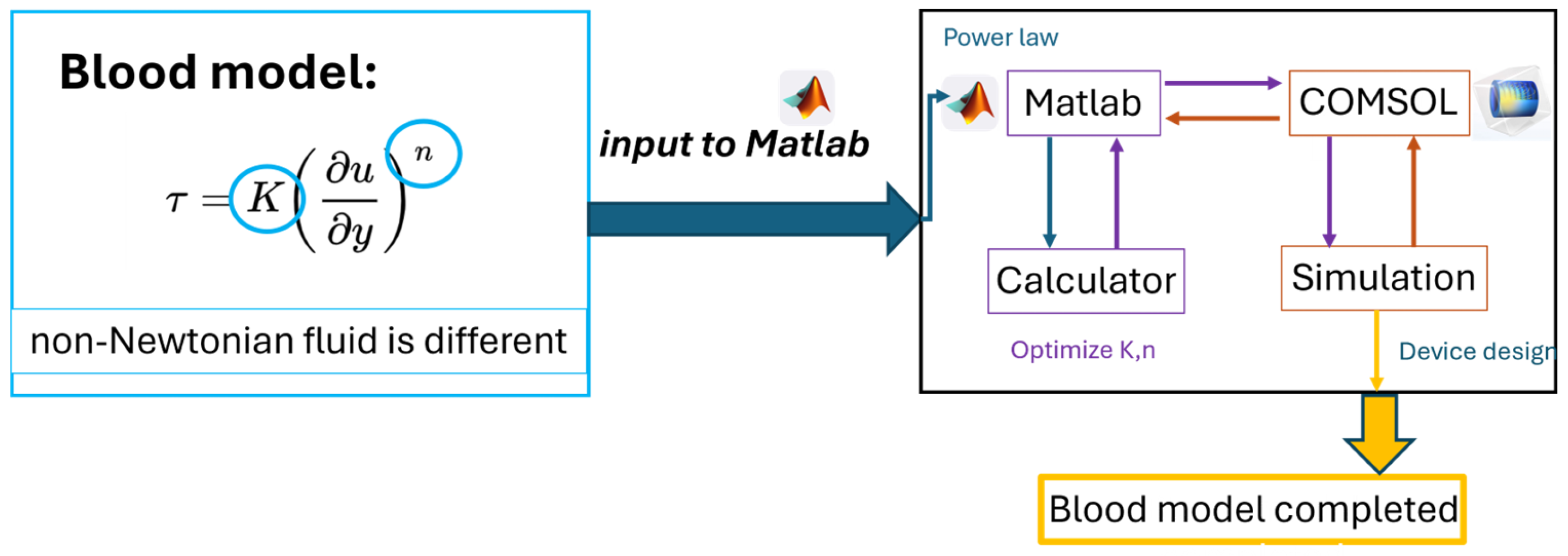
2.2. Sources of Newtonian and Non-Newtonian Flow Samples in the Experiments
2.3. Chip Design and Fabrication
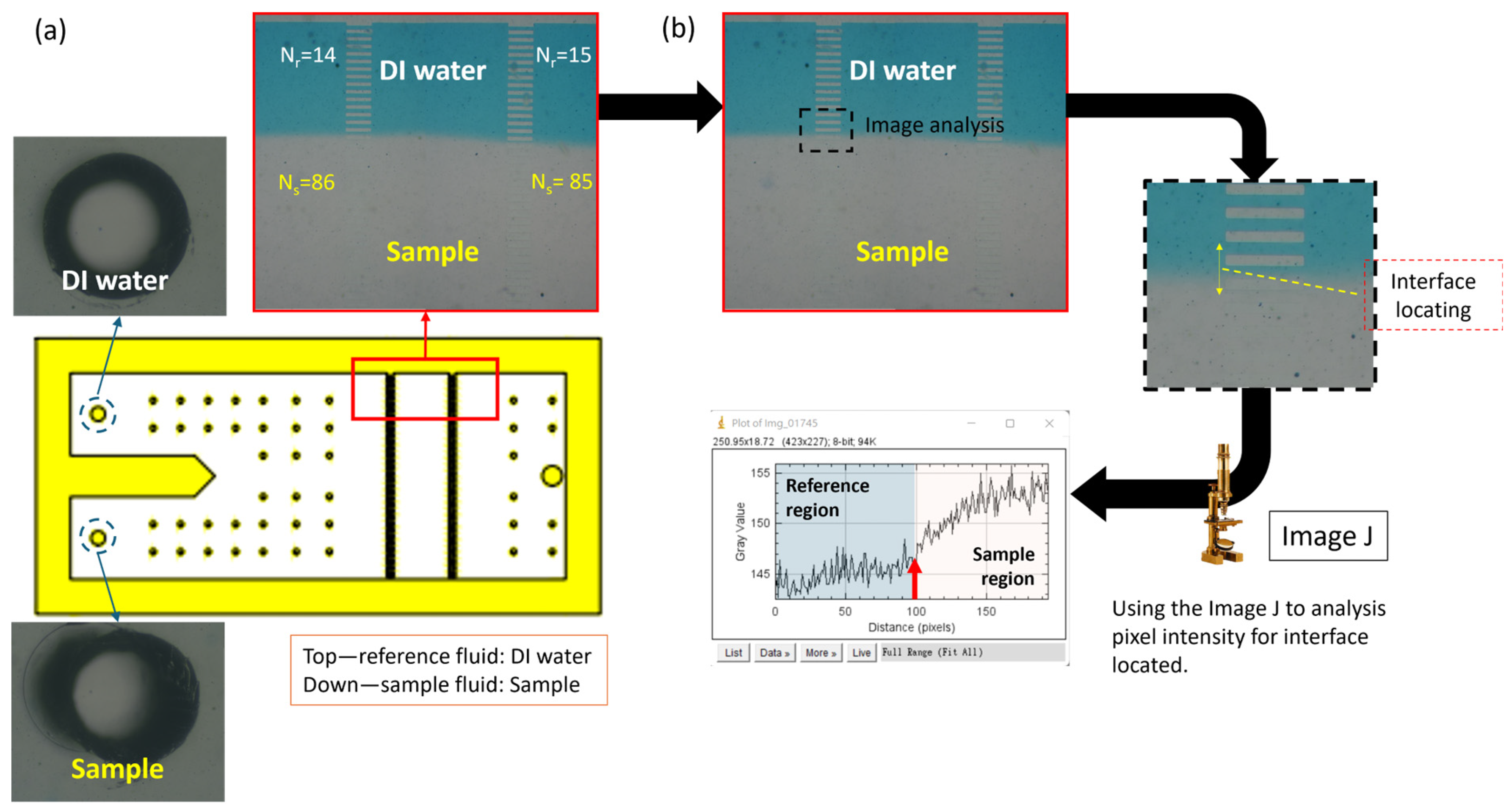
2.4. Principle of Viscosity Measurement
2.5. Microarray Design
3. Results and Discussion
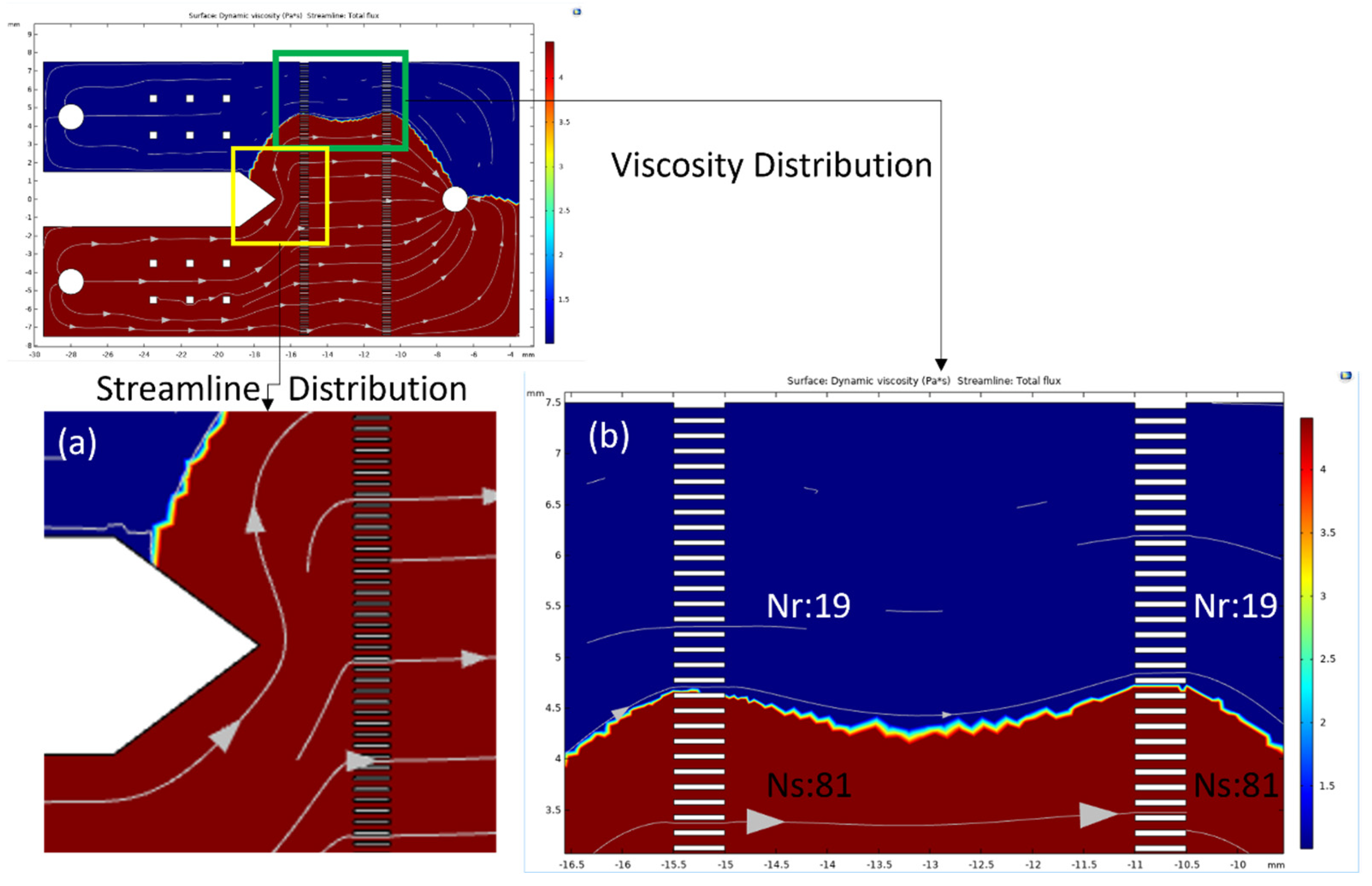
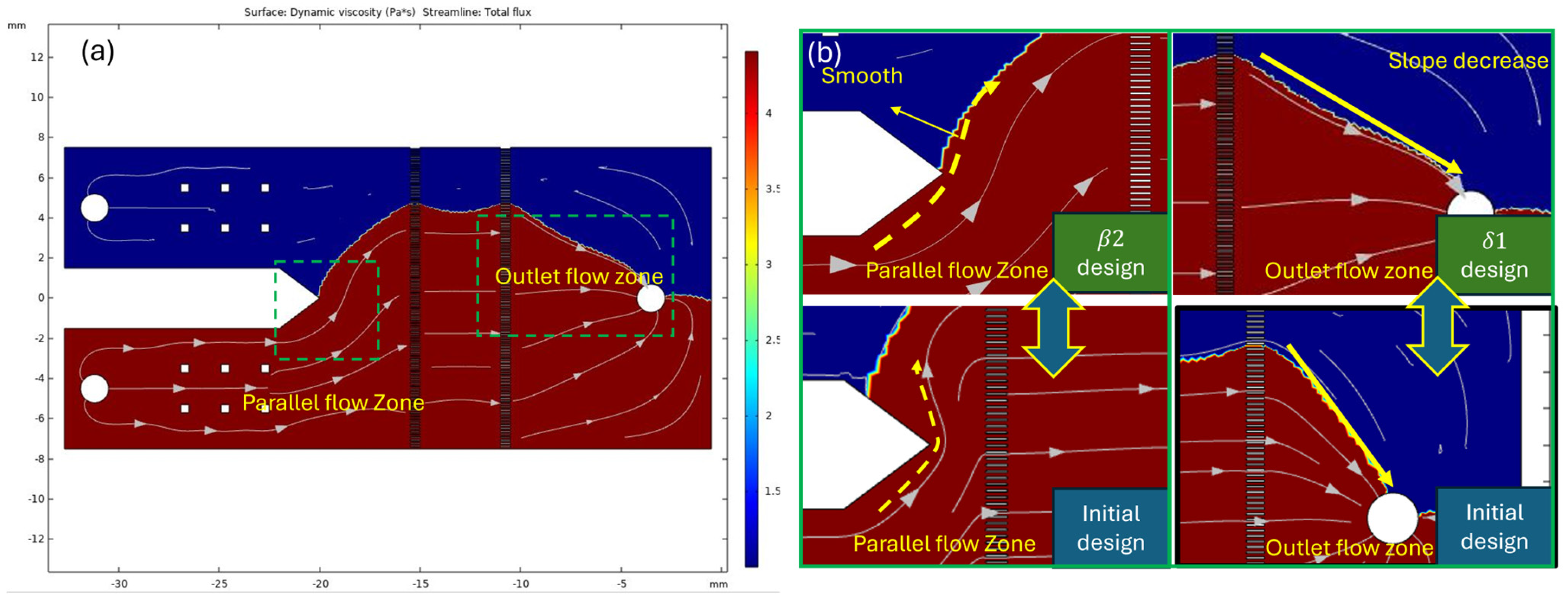
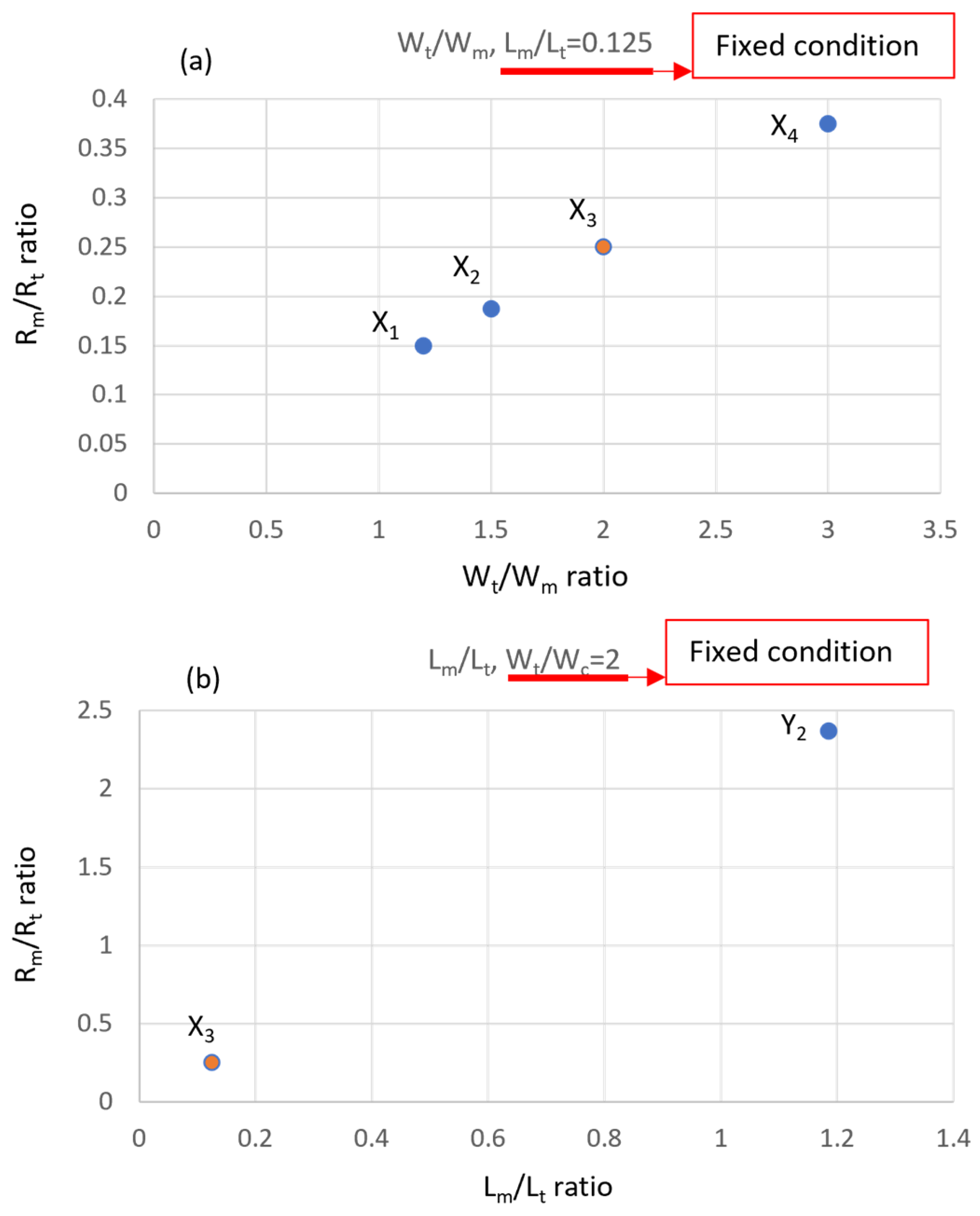
3.1. Physical Numerical Simulating Results
3.2. Implementation of Measurement Zone Design of Microarray Chip
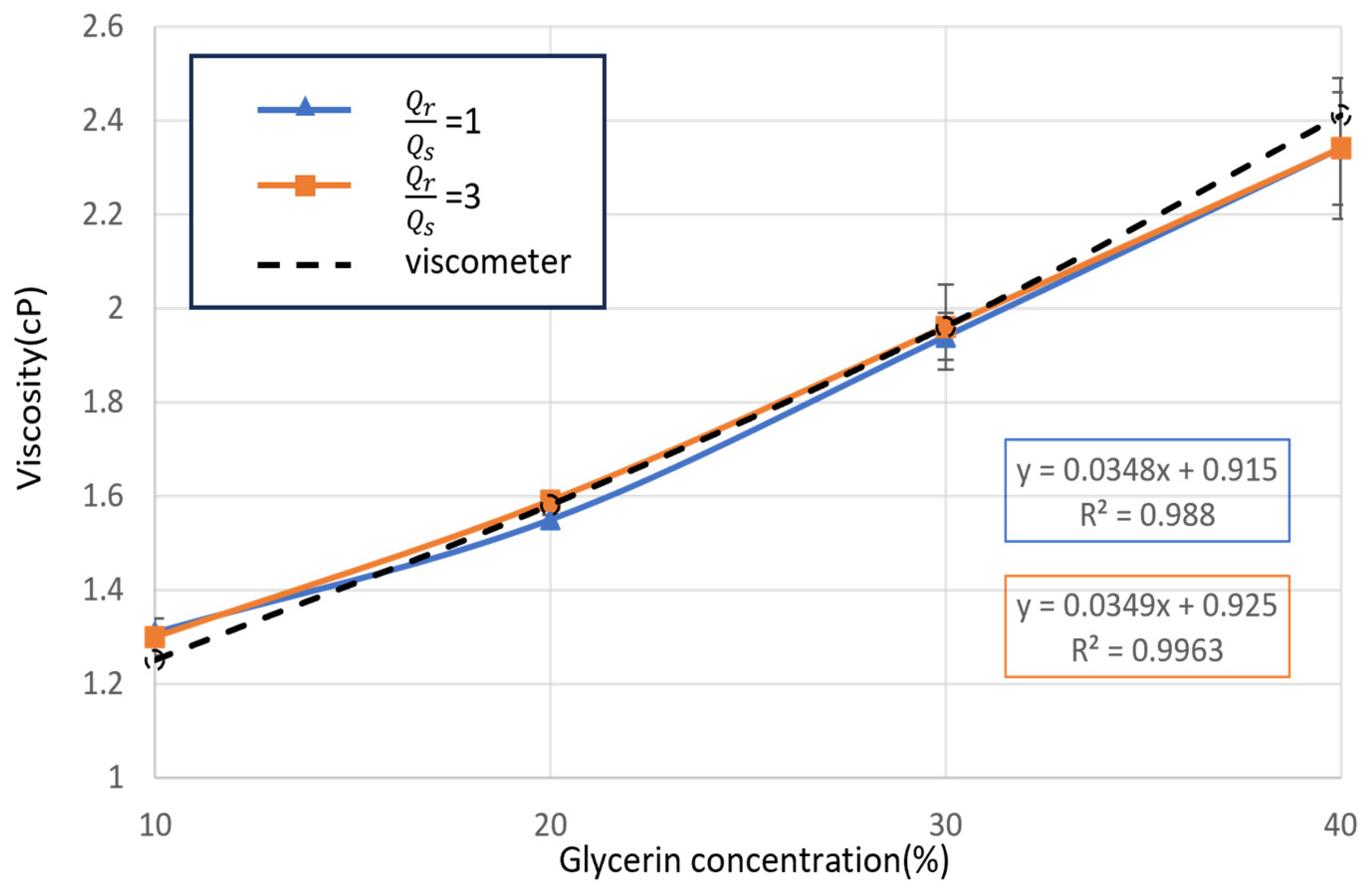
3.3. Implementation of Newtonian Sample Viscosity Measurement
3.4. Implementation of Non-Newtonian Sample Viscosity Measurement
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Letham, B.; Rudin, C.; McCormick, T.H.; Madigan, D. Interpretable classifiers using rules and bayesian analysis: Building a better stroke prediction model. Ann. Appl. Stat. 2015, 9, 1350–1371. [Google Scholar] [CrossRef]
- Boehme, A.K.; Esenwa, C.; Elkind, M.S. Stroke risk factors, genetics, and prevention. Circ. Res. 2017, 120, 472–495. [Google Scholar] [CrossRef] [PubMed]
- Arboix, A. Cardiovascular risk factors for acute stroke: Risk profiles in the different subtypes of ischemic stroke. World J. Clin. Cases: WJCC 2015, 3, 418. [Google Scholar] [CrossRef] [PubMed]
- Avan, A.; Digaleh, H.; Di Napoli, M.; Stranges, S.; Behrouz, R.; Shojaeianbabaei, G.; Amiri, A.; Tabrizi, R.; Mokhber, N.; Spence, J.D. Socioeconomic status and stroke incidence, prevalence, mortality, and worldwide burden: An ecological analysis from the Global Burden of Disease Study 2017. BMC Med. 2019, 17, 191. [Google Scholar] [CrossRef] [PubMed]
- Feigin, V.L.; Norrving, B.; Mensah, G.A. Global burden of stroke. Circ. Res. 2017, 120, 439–448. [Google Scholar] [CrossRef] [PubMed]
- Katan, M.; Luft, A. Global burden of stroke. In Seminars in Neurology; Thieme Medical Publishers: Leipzig, Germany, 2018; pp. 208–211. [Google Scholar]
- Song, S.H.; Kim, J.H.; Lee, J.H.; Yun, Y.-M.; Choi, D.-H.; Kim, H.Y. Elevated blood viscosity is associated with cerebral small vessel disease in patients with acute ischemic stroke. BMC Neurol. 2017, 17, 20. [Google Scholar] [CrossRef]
- Fisher, M.; Meiselman, H.J. Hemorheological factors in cerebral ischemia. Stroke 1991, 22, 1164–1169. [Google Scholar] [CrossRef]
- Tikhomirova, I.A.; Oslyakova, A.O.; Mikhailova, S.G. Microcirculation and blood rheology in patients with cerebrovascular disorders. Clin. Hemorheol. Microcirc. 2011, 49, 295–305. [Google Scholar] [CrossRef]
- Furukawa, K.; Abumiya, T.; Sakai, K.; Hirano, M.; Osanai, T.; Shichinohe, H.; Nakayama, N.; Kazumata, K.; Hida, K.; Houkin, K. Increased blood viscosity in ischemic stroke patients with small artery occlusion measured by an electromagnetic spinning sphere viscometer. J. Stroke Cerebrovasc. Dis. 2016, 25, 2762–2769. [Google Scholar] [CrossRef] [PubMed]
- Gyawali, P.; Lillicrap, T.P.; Esperon, C.G.; Bhattarai, A.; Bivard, A.; Spratt, N. Whole Blood Viscosity and Cerebral Blood Flow in Acute Ischemic Stroke. In Seminars in Thrombosis and Hemostasis; Thieme Medical Publishers: New York, NY, USA, 2023. [Google Scholar]
- Gyawali, P.; Lillicrap, T.P.; Tomari, S.; Bivard, A.; Holliday, E.; Parsons, M.; Levi, C.; Garcia-Esperon, C.; Spratt, N. Whole blood viscosity is associated with baseline cerebral perfusion in acute ischemic stroke. Neurol. Sci. 2022, 43, 2375–2381. [Google Scholar] [CrossRef] [PubMed]
- Grotemeyer, K.C.; Kaiser, R.; Grotemeyer, K.-H.; Husstedt, I.W. Association of elevated plasma viscosity with small vessel occlusion in ischemic cerebral disease. Thromb. Res. 2014, 133, 96–100. [Google Scholar] [CrossRef] [PubMed]
- Han, J.E.; Kim, T.; Park, J.H.; Baik, J.S.; Kim, J.Y.; Park, J.H.; Han, S.W.; Yu, H.-J. Middle cerebral artery pulsatility is highly associated with systemic blood viscosity in acute ischemic stroke within 24 hours of symptom onset. J. Neurosonol. Neuroimaging 2019, 11, 126–131. [Google Scholar] [CrossRef]
- Kim, T.; Oh, J.; Han, J.E.; Park, J.H.; Baik, J.S.; Kim, J.Y.; Park, J.H.; Han, S.W.; Kim, E.-G. The relationship between changes in systemic blood viscosity and transcranial Doppler pulsatility in lacunar stroke. J. Neurosonol. Neuroimaging 2020, 12, 67–72. [Google Scholar] [CrossRef]
- Baeckström, P.; Folkow, B.; Kendrick, E.; Löfving, B.; ÖBerg, B. Effects of vasoconstriction on blood viscosity in vivo. Acta Physiol. Scand. 1971, 81, 376–384. [Google Scholar] [CrossRef] [PubMed]
- Cadroy, Y.; Horbett, T.; Hanson, S. Discrimination between platelet-mediated and coagulation-mediated mechanisms in a model of complex thrombus formation in vivo. J. Lab. Clin. Med. 1989, 113, 436–448. [Google Scholar]
- Somer, T.; Meiselman, H.J. Disorders of blood viscosity. Ann. Med. 1993, 25, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Tamariz, L.J.; Young, J.H.; Pankow, J.S.; Yeh, H.-C.; Schmidt, M.I.; Astor, B.; Brancati, F.L. Blood viscosity and hematocrit as risk factors for type 2 diabetes mellitus: The atherosclerosis risk in communities (ARIC) study. Am. J. Epidemiol. 2008, 168, 1153–1160. [Google Scholar] [CrossRef]
- Sakariassen, K.S.; Orning, L.; Turitto, V.T. The impact of blood shear rate on arterial thrombus formation. Future Sci. OA 2015, 1, FSO30. [Google Scholar] [CrossRef]
- Sakariassen, K.S.; Houdijk, W.P.; Sixma, J.J.; Aarts, P.A.; de Groot, P.G. A perfusion chamber developed to investigate platelet interaction in flowing blood with human vessel wall cells, their extracellular matrix, and purified components. J. Lab. Clin. Med. 1983, 102, 522–535. [Google Scholar] [PubMed]
- Barstad, R.M.; Roald, H.E.; Cui, Y.; Turitto, V.T.; Sakariassen, K.S. A perfusion chamber developed to investigate thrombus formation and shear profiles in flowing native human blood at the apex of well-defined stenoses. Arterioscler. Thromb. J. Vasc. Biol. 1994, 14, 1984–1991. [Google Scholar] [CrossRef] [PubMed]
- Rosenson, R.S.; Mccormick, A.; Uretz, E.F. Distribution of blood viscosity values and biochemical correlates in healthy adults. Clin. Chem. 1996, 42, 1189–1195. [Google Scholar] [CrossRef]
- Lee, A.J.; Mowbray, P.I.; Lowe, G.D.; Rumley, A.; Fowkes, F.G.R.; Allan, P.L. Blood viscosity and elevated carotid intima-media thickness in men and women: The Edinburgh Artery Study. Circulation 1998, 97, 1467–1473. [Google Scholar] [CrossRef] [PubMed]
- Lowe, G.; Lee, A.; Rumley, A.; Price, J.; Fowkes, F. Blood viscosity and risk of cardiovascular events: The Edinburgh Artery Study. Br. J. Haematol. 1997, 96, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Cho, Y.I.; Lee, D.-H.; Park, C.-M.; Moon, H.-W.; Hur, M.; Kim, J.Q.; Yun, Y.-M. Analytical performance evaluation of the scanning capillary tube viscometer for measurement of whole blood viscosity. Clin. Biochem. 2013, 46, 139–142. [Google Scholar] [CrossRef]
- Gupta, S.; Wang, W.S.; Vanapalli, S.A. Microfluidic viscometers for shear rheology of complex fluids and biofluids. Biomicrofluidics 2016, 10, 043402. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.J.; Lee, S.-J. In vitro and ex vivo measurement of the biophysical properties of blood using microfluidic platforms and animal models. Analyst 2018, 143, 2723–2749. [Google Scholar] [CrossRef]
- Zilberman-Rudenko, J.; White, R.M.; Zilberman, D.A.; Lakshmanan, H.H.; Rigg, R.A.; Shatzel, J.J.; Maddala, J.; McCarty, O.J. Design and utility of a point-of-care microfluidic platform to assess hematocrit and blood coagulation. Cell. Mol. Bioeng. 2018, 11, 519–529. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.I.; Abaci, H.E.; Shuler, M.L. Microfluidic blood–brain barrier model provides in vivo-like barrier properties for drug permeability screening. Biotechnol. Bioeng. 2017, 114, 184–194. [Google Scholar] [CrossRef] [PubMed]
- Vanapalli, S.; Van den Ende, D.; Duits, M.; Mugele, F. Scaling of interface displacement in a microfluidic comparator. Appl. Phys. Lett. 2007, 90, 114109. [Google Scholar] [CrossRef]
- Solomon, D.E.; Vanapalli, S.A. Multiplexed microfluidic viscometer for high-throughput complex fluid rheology. Microfluid. Nanofluidics 2014, 16, 677–690. [Google Scholar] [CrossRef]
- Kim, B.J.; Lee, S.Y.; Jee, S.; Atajanov, A.; Yang, S. Micro-viscometer for measuring shear-varying blood viscosity over a wide-ranging shear rate. Sensors 2017, 17, 1442. [Google Scholar] [CrossRef] [PubMed]
- Perktold, K.; Peter, R.O.; Resch, M.; Langs, G. Pulsatile non-Newtonian blood flow in three-dimensional carotid bifurcation models: A numerical study of flow phenomena under different bifurcation angles. J. Biomed. Eng. 1991, 13, 507–515. [Google Scholar] [CrossRef] [PubMed]
- Brookshier, K.; Tarbell, J. Evaluation of a transparent blood analog fluid: Aqueous xanthan gum/glycerin. Biorheology 1993, 30, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Hardeman, M.; Goedhart, P.; Shin, S. Methods in hemorheology. In Handbook of Hemorheology and Hemodynamics; IOS Press: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Kang, Y.J.; Yang, S. Integrated microfluidic viscometer equipped with fluid temperature controller for measurement of viscosity in complex fluids. Microfluid. Nanofluidics 2013, 14, 657–668. [Google Scholar] [CrossRef]
- Wells, R.E.; Merrill, E.W. Influence of flow properties of blood upon viscosity-hematocrit relationships. J. Clin. Investig. 1962, 41, 1591–1598. [Google Scholar] [CrossRef] [PubMed]
- Poole, R.; Ridley, B. Development-length requirements for fully developed laminar pipe flow of inelastic non-Newtonian liquids. J. Fluids Eng. 2007, 129, 1281–1287. [Google Scholar] [CrossRef]
- Lee, W. General principles of carotid Doppler ultrasonography. Ultrasonography 2014, 33, 11. [Google Scholar] [CrossRef] [PubMed]
- Meng, W.; Yu, F.; Chen, H.; Zhang, J.; Zhang, E.; Dian, K.; Shi, Y. Concentration polarization of high-density lipoprotein and its relation with shear stress in an in vitro model. BioMed Res. Int. 2009, 2009, 695838. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.I.; Kensey, K.R. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: Steady flows. Biorheology 1991, 28, 241–262. [Google Scholar] [CrossRef]
- Kee, D.-D.; Kim, Y.-D.; Nguyen, Q.D. Measuring rheological properties using a slotted plate device. Korea-Aust. Rheol. J. 2007, 19, 75–80. [Google Scholar]
- SEKONIC. Bench Type Viscometers VM Series. Available online: https://www.sekonic.co.jp/english/product/viscometer/vm/vm_series.html (accessed on 1 October 2024).
- Chen, P.; Jiang, Q.; Horikawa, S.; Li, S. Magnetoelastic-sensor integrated microfluidic chip for the measurement of blood plasma viscosity. J. Electrochem. Soc. 2017, 164, B247. [Google Scholar] [CrossRef]
- Mustafa, A.; Eser, A.; Aksu, A.C.; Kiraz, A.; Tanyeri, M.; Erten, A.; Yalcin, O. A micropillar-based microfluidic viscometer for Newtonian and non-Newtonian fluids. Anal. Chim. Acta 2020, 1135, 107–115. [Google Scholar] [CrossRef] [PubMed]
- Khnouf, R.; Karasneh, D.; Abdulhay, E.; Abdelhay, A.; Sheng, W.; Fan, Z.H. Microfluidics-based device for the measurement of blood viscosity and its modeling based on shear rate, temperature, and heparin concentration. Biomed. Microdevices 2019, 21, 80. [Google Scholar] [CrossRef] [PubMed]
- Mark, D.; Haeberle, S.; Roth, G.; Von Stetten, F.; Zengerle, R. Microfluidic lab-on-a-chip platforms: Requirements, characteristics and applications. Microfluid. Based Microsyst. Fundam. Appl. 2010, 305–376. [Google Scholar]
- Kovarik, M.L.; Ornoff, D.M.; Melvin, A.T.; Dobes, N.C.; Wang, Y.; Dickinson, A.J.; Gach, P.C.; Shah, P.K.; Allbritton, N.L. Micro total analysis systems: Fundamental advances and applications in the laboratory, clinic, and field. Anal. Chem. 2013, 85, 451–472. [Google Scholar] [CrossRef]
- Yang, S.-M.; Lv, S.; Zhang, W.; Cui, Y. Microfluidic point-of-care (POC) devices in early diagnosis: A review of opportunities and challenges. Sensors 2022, 22, 1620. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.-K.; Cho, Y.I.; Duey, M.; Rosenson, R.S. Cardiovascular risks of anemia correction with erythrocyte stimulating agents: Should blood viscosity be monitored for risk assessment? Cardiovasc. Drugs Ther. 2010, 24, 151–160. [Google Scholar] [CrossRef]
- Babu, N.; Singh, M. Influence of hyperglycemia on aggregation, deformability and shape parameters of erythrocytes. Clin. Hemorheol. Microcirc. 2004, 31, 273–280. [Google Scholar] [PubMed]






| Viscosity (cP) | Density (kg/m3) | |
|---|---|---|
| Glycerin | 5.21 | 1270 |
| Artificial blood dry | 4.9 | 1100 |
| Function Design | Setting Condition | ||
|---|---|---|---|
| Inlet flow zone | Flow model | Laminar flow | |
| Parallel flow zone | Inlet velocity | 10 (μL/min) | |
| Measurement zone | Outlet pressure | 0 (Pa) | |
| Outlet flow zone | Mesh size | 10–1000 (μm) | |
| Mesh number | 272,857 (unit) | ||
| A | Inlet of reference fluid | ||
| B | Inlet of simulation blood | ||
| C | Outlet of pipe geometry | ||
| a | Width of inlet flow zone | ||
| b | length of parallel flow zone | ||
| c | Length of outlet flow zone | ||
| Design Regions | a | b | c |
|---|---|---|---|
| Initial | 6 | 1.29 | 3.5 |
| 6 | 3 | 3.5 | |
| 6 | 4.5 | 3.5 | |
| 6 | 1.29 | 7 | |
| 6 | 4.5 | 7 |
| Structure/ Condition | Advantage | Sample Limitation | Accuracy (%) | Functional Range (cP) | Resolution (cP) | Shear Rate (s−1) | Reference |
|---|---|---|---|---|---|---|---|
| Rheometer | High precision, high accuracy | Non-Newtonian fluid, 25 mL sample | - | 1–107 | 0.1 | 10−3 | [43] |
| Vibration viscometer | Simple operation | 20 mL sample | 95% | 0.4–1000 | 0.2 | - | [44] |
| Magnetoelastic/Sensor | Quick, low-cost measurement | Newtonian fluid, 100 μL sample | - | 1–10 | 0.001 | - | [45] |
| Pressure sensor | The sensitivity was better than 0.5 cP | Non-Newtonian fluid | 81.5% | 2– 100 | 0.5 | 20–345.1 | [46] |
| Microfluidic/coflowing | Simultaneously measured the multiple samples | 1.5 mL | 92% | 1–10,000 | 1 | 1–6000 | [32] |
| Microfluidic/coflowing | Less than 10 μL sample requirement | 10 μL | 95% | 1–10 | 0.1 | 20,000–40,000 | [47] |
| Microfluidic/coflowing | Low shear rate, High accuracy | 1 mL, Waste: 120 μL | 95% | 1–10 | 0.01 | 10–100 | Our model |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.-N.; Yao, D.-J. Development of a Microfluidic Viscometer for Non-Newtonian Blood Analog Fluid Analysis. Bioengineering 2024, 11, 1298. https://doi.org/10.3390/bioengineering11121298
Chang Y-N, Yao D-J. Development of a Microfluidic Viscometer for Non-Newtonian Blood Analog Fluid Analysis. Bioengineering. 2024; 11(12):1298. https://doi.org/10.3390/bioengineering11121298
Chicago/Turabian StyleChang, Yii-Nuoh, and Da-Jeng Yao. 2024. "Development of a Microfluidic Viscometer for Non-Newtonian Blood Analog Fluid Analysis" Bioengineering 11, no. 12: 1298. https://doi.org/10.3390/bioengineering11121298
APA StyleChang, Y.-N., & Yao, D.-J. (2024). Development of a Microfluidic Viscometer for Non-Newtonian Blood Analog Fluid Analysis. Bioengineering, 11(12), 1298. https://doi.org/10.3390/bioengineering11121298








