Enzyme-Mediated Exponential Glucose Release: A Model-Based Strategy for Continuous Defined Fed-Batch in Small-Scale Cultivations
Abstract
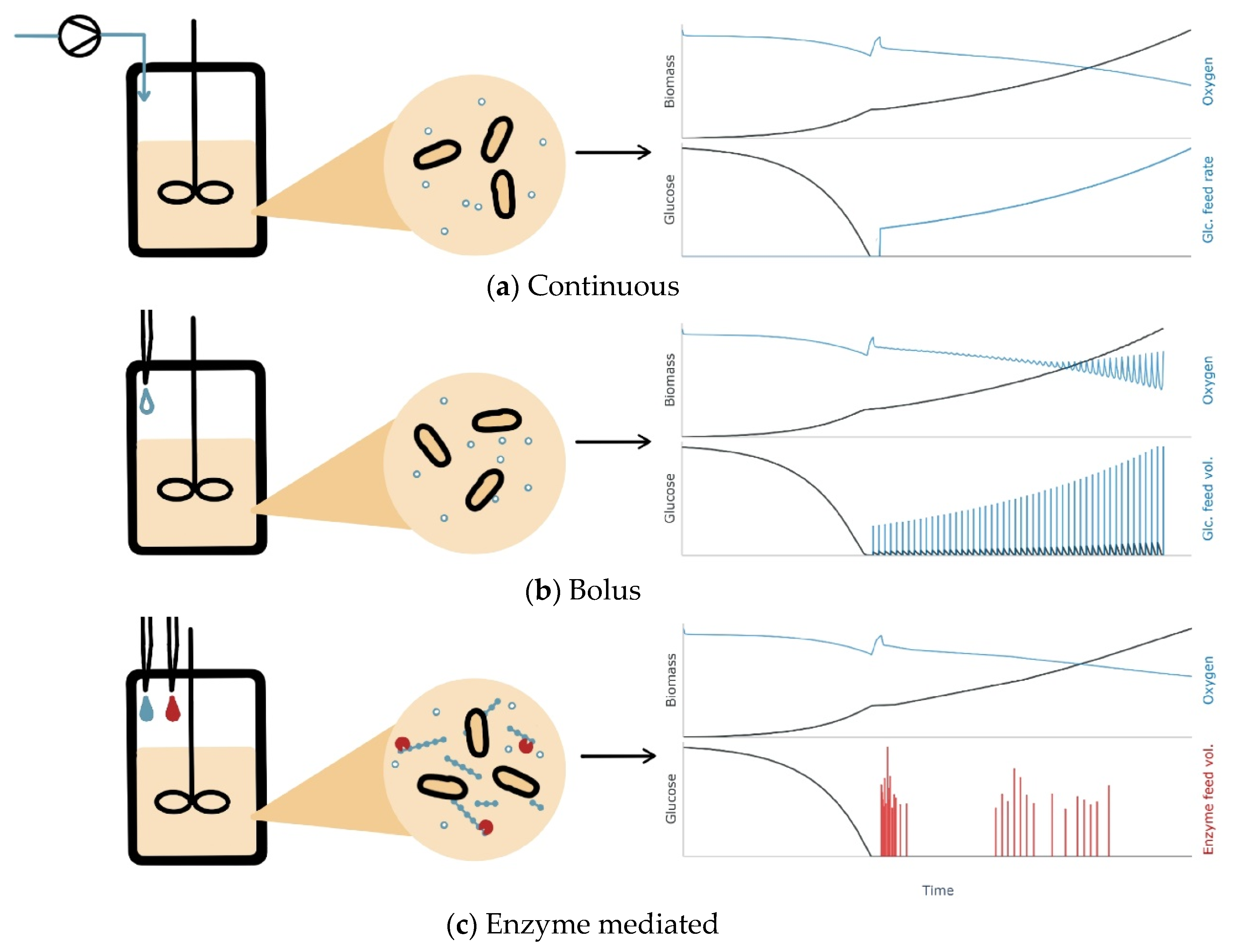
1. Introduction
2. Materials and Methods
2.1. General Experimental Set-Up
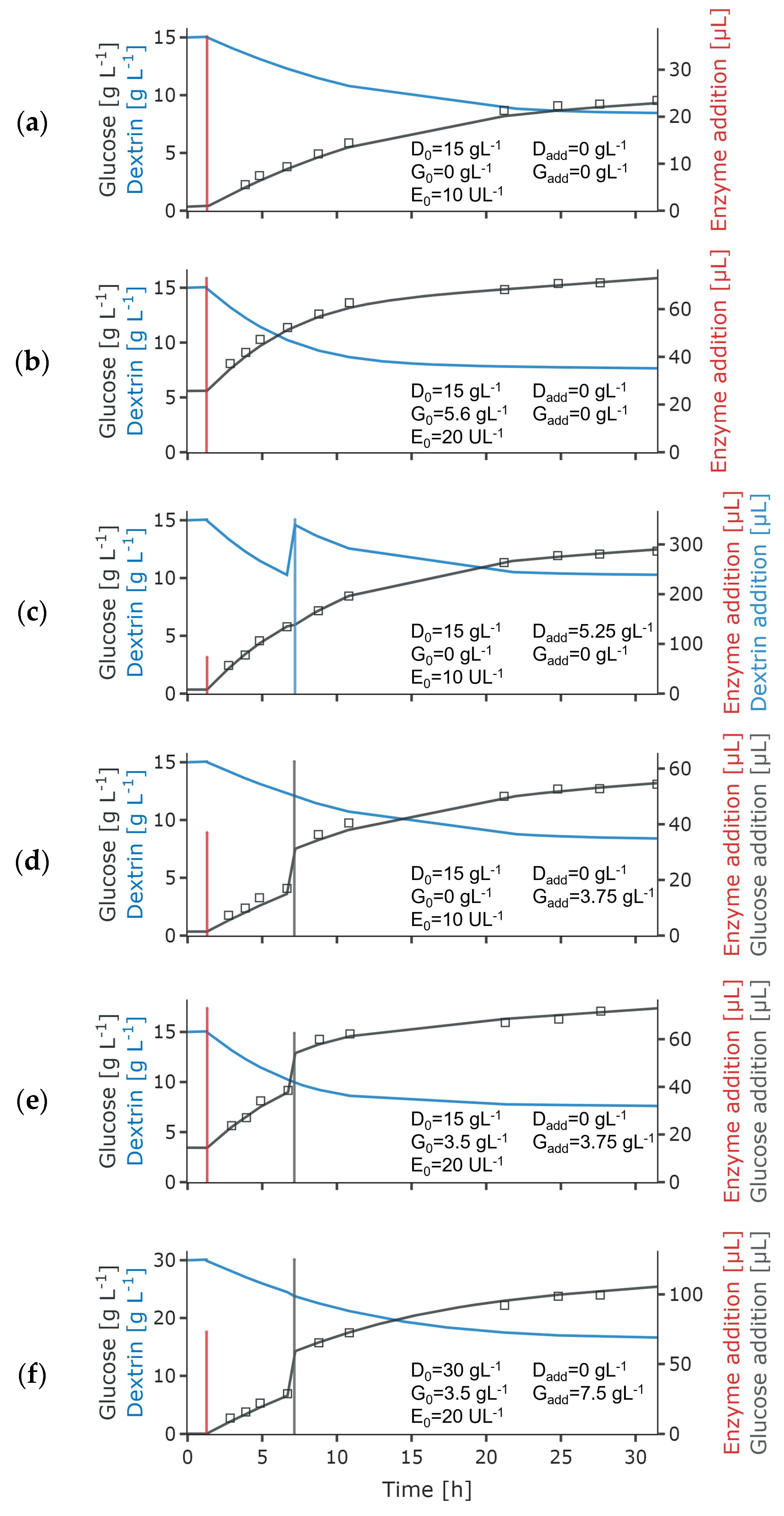
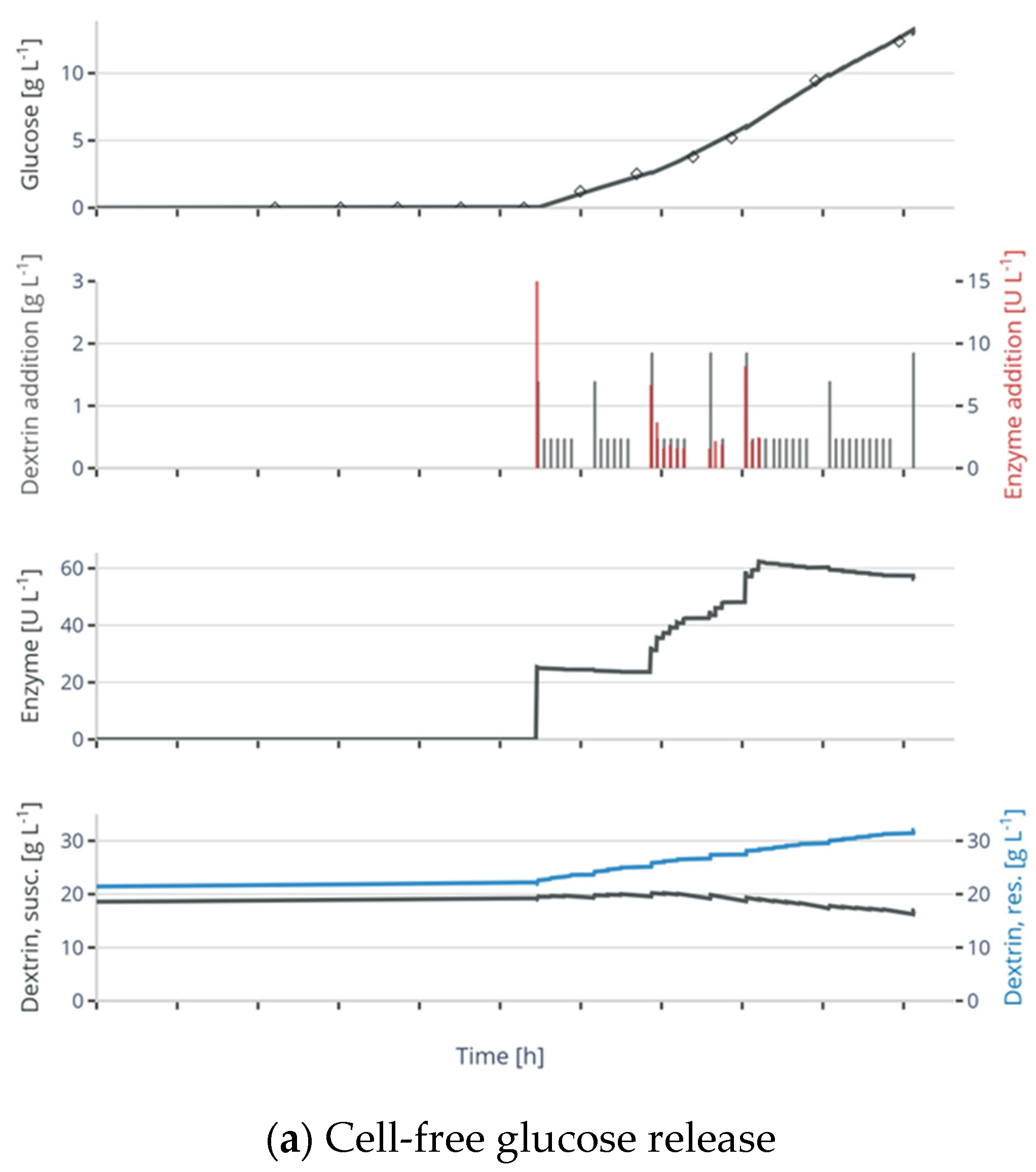
2.2. Cell-Free Experiments for Selection of the Glucose Release Model
2.3. Enzymatic Fed-Batch Experiments
2.4. Modeling and Simulation
3. Results
3.1. Selection and Parameter Fitting of the Glucose Release Model
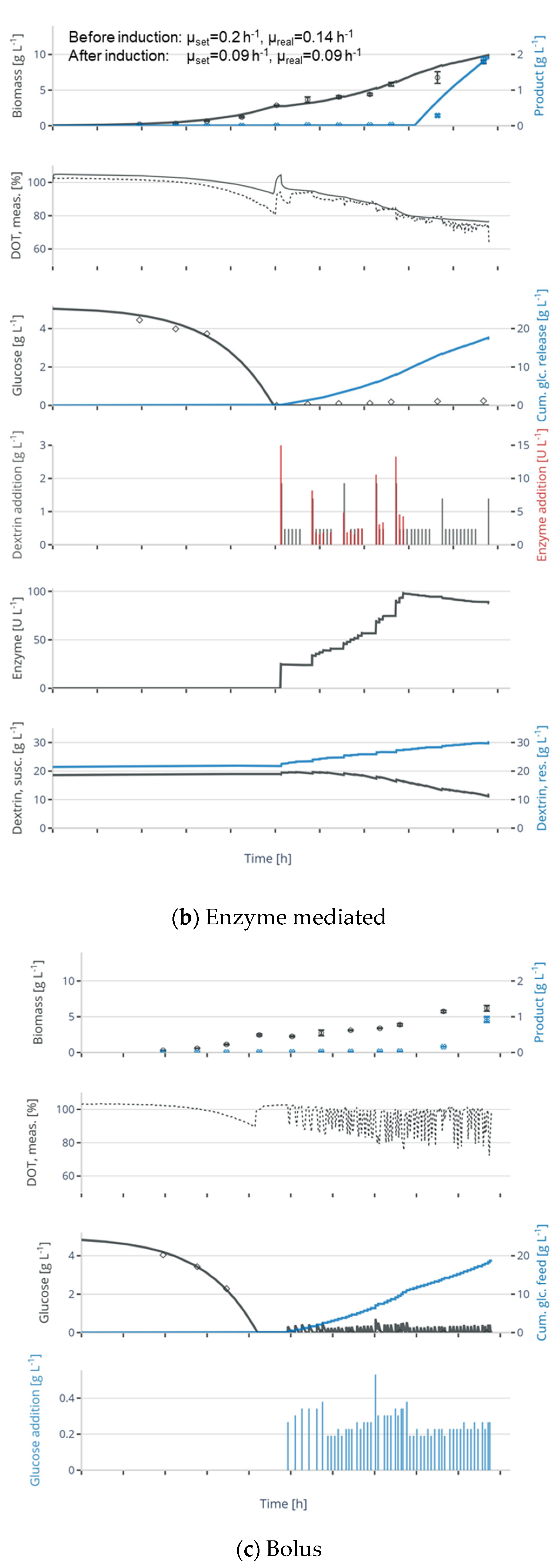
3.2. Application of Enzyme-Mediated Glucose Release in Microbial Fed-Batch Cultivations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lara, A.R.; Galindo, E.; Ramirez, O.T.; Palomares, L.A. Living with Heterogeneities in Bioreactors. Mol. Biotechnol. 2006, 34, 355–381. [Google Scholar] [CrossRef] [PubMed]
- Enfors, S.O.; Jahic, M.; Rozkov, A.; Xu, B.; Hecker, M.; Jürgen, B.; Krüger, E.; Schweder, T.; Hamer, G.; O’Beirne, D.; et al. Physiological Responses to Mixing in Large Scale Bioreactors. J. Biotechnol. 2001, 85, 175–185. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Jahic, M.; Enfors, S.-O. Modeling of Overflow Metabolism in Batch and Fed-Batch Cultures of Escherichia Coli. Biotechnol. Progress 1999, 15, 81–90. [Google Scholar] [CrossRef] [PubMed]
- Teworte, S.; Malcı, K.; Walls, L.E.; Halim, M.; Rios-Solis, L. Recent Advances in Fed-Batch Microscale Bioreactor Design. Biotechnol. Adv. 2022, 55, 107888. [Google Scholar] [CrossRef] [PubMed]
- Neubauer, P.; Junne, S. Scale-down Simulators for Metabolic Analysis of Large-Scale Bioprocesses. Curr. Opin. Biotechnol. 2010, 21, 114–121. [Google Scholar] [CrossRef] [PubMed]
- Anane, E.; García, Á.C.; Haby, B.; Hans, S.; Krausch, N.; Krewinkel, M.; Hauptmann, P.; Neubauer, P.; Cruz Bournazou, M.N. A Model-Based Framework for Parallel Scale-down Fed-Batch Cultivations in Mini-Bioreactors for Accelerated Phenotyping. Biotechnol. Bioeng. 2019, 116, 2906–2918. [Google Scholar] [CrossRef]
- Gebhardt, G.; Hortsch, R.; Kaufmann, K.; Schragenhofstrasse, J.; Ag, D.; Weuster-botz, D. A New Microfluidic Concept for Parallel Operated Milliliter-Scale Stirred Tank Bioreactors. Biotechnol. Prog. 2011, 27, 684–690. [Google Scholar] [CrossRef]
- Funke, M.; Buchenauer, A.; Schnakenberg, U.; Mokwa, W.; Diederichs, S.; Mertens, A.; Müller, C.; Kensy, F.; Büchs, J. Microfluidic Biolector-Microfluidic Bioprocess Control in Microtiter Plates. Biotechnol. Bioeng. 2010, 107, 497–505. [Google Scholar] [CrossRef]
- Jeude, M.; Dittrich, B.; Niederschulte, H.; Anderlei, T.; Knocke, C.; Klee, D.; Büchs, J. Fed-Batch Mode in Shake Flasks by Slow-Release Technique. Biotechnol. Bioeng. 2006, 95, 433–445. [Google Scholar] [CrossRef]
- Scheidle, M.; Jeude, M.; Dittrich, B.; Denter, S.; Kensy, F.; Suckow, M.; Klee, D.; Büchs, J. High-Throughput Screening of Hansenula Polymorpha Clones in the Batch Compared with the Controlled-Release Fed-Batch Mode on a Small Scale. FEMS Yeast Res. 2010, 10, 83–92. [Google Scholar] [CrossRef][Green Version]
- Bähr, C.; Leuchtle, B.; Lehmann, C.; Becker, J.; Jeude, M.; Peinemann, F.; Arbter, R.; Büchs, J. Dialysis Shake Flask for Effective Screening in Fed-Batch Mode. Biochem. Eng. J. 2012, 69, 182–195. [Google Scholar] [CrossRef]
- Habicher, T.; Rauls, E.K.A.; Egidi, F.; Keil, T.; Klein, T.; Daub, A.; Büchs, J. Establishing a Fed-Batch Process for Protease Expression with Bacillus Licheniformis in Polymer-Based Controlled-Release Microtiter Plates. Biotechnol. J. 2020, 15, 1900088. [Google Scholar] [CrossRef] [PubMed]
- Panula-Perälä, J.; Šiurkus, J.; Vasala, A.; Wilmanowski, R.; Casteleijn, M.G.; Neubauer, P. Enzyme Controlled Glucose Auto-Delivery for High Cell Density Cultivations in Microplates and Shake Flasks. Microb. Cell Factories 2008, 7, 31. [Google Scholar] [CrossRef] [PubMed]
- Krause, M.; Ukkonen, K.; Haataja, T.; Ruottinen, M.; Glumoff, T.; Neubauer, A.; Neubauer, P.; Vasala, A. A Novel Fed-Batch Based Cultivation Method Provides High Cell-Density and Improves Yield of Soluble Recombinant Proteins in Shaken Cultures. Microb. Cell Factories 2010, 9, 11. [Google Scholar] [CrossRef] [PubMed]
- Zarschler, K.; Witecy, S.; Kapplusch, F.; Foerster, C.; Stephan, H. High-Yield Production of Functional Soluble Single-Domain Antibodies in the Cytoplasm of Escherichia coli. Microb. Cell Factories 2013, 12, 97. [Google Scholar] [CrossRef] [PubMed]
- Šiurkus, J.; Panula-Perälä, J.; Horn, U.; Kraft, M.; Rimšeliene, R.; Neubauer, P. Novel Approach of High Cell Density Recombinant Bioprocess Development: Optimisation and Scale-up from Microlitre to Pilot Scales while Maintaining the Fed-Batch Cultivation Mode of E. coli Cultures. Microb. Cell Factories 2010, 9, 35. [Google Scholar] [CrossRef] [PubMed]
- Cruz Bournazou, M.N.; Barz, T.; Nickel, D.B.; Lopez, D.C.; Glauche, F.; Knepper, A.; Neubauer, P. Online Optimal Experimental Re-Design in Robotic Parallel Fed-Batch Cultivation Facilities. Biotechnol. Bioeng. 2017, 114, 610–619. [Google Scholar] [CrossRef]
- Jansen, R.; Tenhaef, N.; Moch, M.; Wiechert, W.; Noack, S.; Oldiges, M. FeedER: A Feedback-Regulated Enzyme-Based Slow-Release System for Fed-Batch Cultivation in Microtiter Plates. Bioprocess Biosyst. Eng. 2019, 42, 1843–1852. [Google Scholar] [CrossRef]
- Appl, C.; Baganz, F.; Hass, V.C. Development of a Digital Twin for Enzymatic Hydrolysis Processes. Processes 2021, 9, 1734. [Google Scholar] [CrossRef]
- Hiromi, K.; Takahashi, K.; Hamauzu, Z.I.; Ono, S. Kinetic Studies on Gluc-Amylase: III. The Influence of Ph on the Rates of Hydrolysis of Maltose and Panose. J. Biochem. 1966, 59, 469–475. [Google Scholar] [CrossRef]
- Sauer, J.; Sigurskjold, B.W.; Christensen, U.; Frandsen, T.P.; Mirgorodskaya, E.; Harrison, M.; Roepstorff, P.; Svensson, B. Glucoamylase: Structure/Function Relationships, and Protein Engineering. Biochim. Biophys. Acta (BBA)—Protein Struct. Mol. Enzymol. 2000, 1543, 275–293. [Google Scholar] [CrossRef]
- James, J.A.; Lee, B.H. Glucoamylases: Microbial Sources, Industrial Applications and Molecular Biology—A Review. J. Food Biochem. 1997, 21, 1–52. [Google Scholar] [CrossRef]
- Marc, A.; Engasser, J.M.; Moll, M.; Flayeux, R. A Kinetic Model of Starch Hydrolysis by α- and β-Amylase during Mashing. Biotechnol. Bioeng. 1983, 25, 481–496. [Google Scholar] [CrossRef] [PubMed]
- Ono, S.; Hiromi, K.; Zinbo, M. Kinetic Studies of Gluc-Amylase. I. The Influence of Chain Length of Linear Substrates on the Rate Parameters. J. Biochem. 1964, 55, 315–320. [Google Scholar] [CrossRef][Green Version]
- Miranda, M.; Murado, M.A.; Sanroman, A.; Lema, J.M. Mass Transfer Control of Enzymatic Hydrolysis of Polysaccharides by Glucoamylase. Enzym. Microb. Technol. 1991, 13, 142–147. [Google Scholar] [CrossRef]
- Sanromán, A.; Murado, M.A.; Lema, J.M. The Influence of Substrate Structure on the Kinetics of the Hydrolysis of Starch by Glucoamylase. Appl. Biochem. Biotechnol. 1996, 59, 329–336. [Google Scholar] [CrossRef]
- Hiromi, K.; Hamauzu, Z.-I.; Takahashi, K.; Ono, S. Kinetic Studies on Gluc-Amylase. II. Competition between Two Types of Substrate Having α-1,4 and α-1,6 Glucosidic Linkage. J. Biochem. 1966, 59, 411–418. [Google Scholar] [CrossRef]
- Hiromi, K.; Ohnishi, M.; Tanaka, A. Subsite Structure and Ligand Binding Mechanism of Glucoamylase. Mol. Cell. Biochem. 1983, 51, 79–95. [Google Scholar] [CrossRef]
- Polakovič, M.; Bryjak, J. Modelling of the Kinetics of Thermal Inactivation of Glucoamylase from Aspergillus niger. J. Mol. Catal. B Enzym. 2002, 20, 443–450. [Google Scholar] [CrossRef]
- Wojciechowski, P.M.; Koziol, A.; Noworyta, A. Iteration Model of Starch Hydrolysis by Amylolytic Enzymes. Biotechnol. Bioeng. 2001, 75, 530–539. [Google Scholar] [CrossRef]
- Bryjak, J.; Murlikiewicz, K.; Zbiciński, I.; Stawczyk, J. Application of Artificial Neural Networks to Modelling of Starch Hydrolysis by Glucoamylase. Bioprocess Eng. 2000, 23, 351–357. [Google Scholar] [CrossRef]
- Polakovič, M.; Bryjak, J. Modelling of Potato Starch Saccharification by an Aspergillus niger Glucoamylase. Biochem. Eng. J. 2004, 18, 57–63. [Google Scholar] [CrossRef]
- Kemmer, A.; Fischer, N.; Wilms, T.; Cai, L.; Groß, S.; King, R.; Neubauer, P.; Cruz Bournazou, M.N. Nonlinear State Estimation as Tool for Online Monitoring and Adaptive Feed in High Throughput Cultivations. Biotechnol. Bioeng. 2023, 120, 3261–3275. [Google Scholar] [CrossRef] [PubMed]
- Kemmer, A.; Cai, L.; Cruz Bournazou, M.N.; Neubauer, P. High-Throughput Expression of Inclusion Bodies on an Automated Platform. In Inclusion Bodies—Methods and Protocols; Methods in Molecular Biology; Springer Protocols; Humana: New York, NY, USA, 2023. [Google Scholar]
- Huber, M.C.; Schreiber, A.; Wild, W.; Benz, K.; Schiller, S.M. Introducing a Combinatorial DNA-Toolbox Platform Constituting Defined Protein-Based Biohybrid-Materials. Biomaterials 2014, 35, 8767–8779. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, A.; Stühn, L.G.; Huber, M.C.; Geissinger, S.E.; Rao, A.; Schiller, S.M. Self-Assembly Toolbox of Tailored Supramolecular Architectures Based on an Amphiphilic Protein Library. Small 2019, 15, 1900163. [Google Scholar] [CrossRef]
- Andersson, J.; Åkesson, J.; Diehl, M. CasADi: A Symbolic Package for Automatic Differentiation and Optimal Control. In Recent Advances in Algorithmic Differentiation; Lecture Notes in Computational Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2012; Volume 87, pp. 297–307. [Google Scholar]
- Newville, M.; Stensitzki, T.; Allen, D.B.; Ingargiola, A. LMFIT: Non-Linear Least-Square Minimization and Curve-Fitting for Python; Astrophysics Source Code Library: College Park, MD, USA, 2014. [Google Scholar] [CrossRef]
- Biscani, F.; Izzo, D. A Parallel Global Multiobjective Framework for Optimization: Pagmo. J. Open Source Softw. 2020, 5, 2338. [Google Scholar] [CrossRef]
- Wang, J.P.; Zeng, A.W.; Liu, Z.; Yuan, X.G. Kinetics of Glucoamylase Hydrolysis of Corn Starch. J. Chem. Technol. Biotechnol. 2006, 81, 727–729. [Google Scholar] [CrossRef]
- Meagher, M.M.; Nikolov, Z.L.; Reilly, P.J. Subsite Mapping of Aspergillus niger Glucoamylases I and II with Malto- and Isomaltooligosaccharides. Biotechnol. Bioeng. 1989, 34, 681–688. [Google Scholar] [CrossRef]
- Fujii, M.; Kawamura, Y. Synergistic Action of α-Amylase and Glucoamylase on Hydrolysis of Starch. Biotechnol. Bioeng. 1985, 27, 260–265. [Google Scholar] [CrossRef]
- Zanin, G.M.; Moraes, F.F.D. Modeling Cassava Starch Saccharification with Amyloglucosidase. Appl. Biochem. Biotechnol. 1996, 57, 617–625. [Google Scholar] [CrossRef]
- Dalmia, B.K.; Nikolov, Z.L. Characterization of Glucoamylase Adsorption to Raw Starch. Enzym. Microb. Technol. 1991, 13, 982–990. [Google Scholar] [CrossRef]
- Vandersall, A.S.; Cameron, R.G.; Nairn, C.J.; Yelenosky, G.; Wodzinski, R.J. Identification, Characterization, and Partial Purification of Glucoamylase from Aspergillus niger (Syn A. ficuum) NRRL 3135. Prep. Biochem. 1995, 25, 29–55. [Google Scholar] [CrossRef] [PubMed]
- Anane, E.; López Cárdenas, D.C.; Neubauer, P.; Cruz Bournazou, M.N. Modelling Overflow Metabolism in Escherichia coli by Acetate Cycling. Biochem. Eng. J. 2017, 125, 23–30. [Google Scholar] [CrossRef]
- Maa, Y.-F.; Hsu, C.C. Protein Denaturation by Combined Effect of Shear and Air-Liquid Interface. Biotechnol. Bioeng. 1997, 54, 503–512. [Google Scholar] [CrossRef]
- Guzmán-Maldonado, H.; Paredes-López, O.; Biliaderis, D.C.G. Amylolytic Enzymes and Products Derived from Starch: A Review. Crit. Rev. Food Sci. Nutr. 1995, 35, 373–403. [Google Scholar] [CrossRef]
- Franceschini, G.; Macchietto, S. Model-Based Design of Experiments for Parameter Precision: State of the Art. Chem. Eng. Sci. 2008, 63, 4846–4872. [Google Scholar] [CrossRef]
- López Cárdenas, D.C.; Barz, T.; Peñuela, M.; Villegas, A.; Ochoa, S.; Wozny, G. Model-Based Identifiable Parameter Determination Applied to a Simultaneous Saccharification and Fermentation Process Model for Bio-Ethanol Production. Biotechnol. Prog. 2013, 29, 1064–1082. [Google Scholar] [CrossRef]
- Anane, E.; López Cárdenas, D.C.; Barz, T.; Sin, G.; Gernaey, K.V.; Neubauer, P.; Cruz Bournazou, M.N. Output Uncertainty of Dynamic Growth Models: Effect of Uncertain Parameter Estimates on Model Reliability. Biochem. Eng. J. 2019, 150, 107247. [Google Scholar] [CrossRef]

| Parameter | Description | Unit | Values |
|---|---|---|---|
| Initial dextrin concentration | g L−1 | 15, 30 | |
| Initial glucose concentration | g L−1 | 0, 3.75, 7.5, 15 | |
| Initial enzyme concentration | U L−1 | 10, 20 | |
| Dextrin addition | g L−1 | 0, 5.25, 10.5 | |
| Glucose addition | g L−1 | 0, 3.75, 7.5 |
| Condition | Feed Method | μset [h−1] before ind | after ind | [g L−1] | [g L−1] | Additions | Cells |
|---|---|---|---|---|---|---|
| Data set 2 | ||||||
| 1—control pulse | Bolus feed | 0.18 | 0.09 | 5 | 2 | Glucose | Yes |
| 2—control pulse | Bolus feed | 0.21 | 0.11 | 5 | 2 | Glucose | Yes |
| 3—enzymatic feed | Enzymatic release | 0.18 | 0.09 | 5 | 40 | Dextrin, enzyme | Yes |
| 4—enzymatic feed | Enzymatic release | 0.21 | 0.11 | 5 | 40 | Dextrin, enzyme | Yes |
| 5—enzymatic feed | Enzymatic release (two additions) | 0.18 | 0.09 | 5 | 40 | Dextrin, enzyme | Yes |
| 6—enzymatic feed | Enzymatic release (two additions) | 0.21 | 0.11 | 5 | 40 | Dextrin, enzyme | Yes |
| 7—control cell-free | Enzymatic release | 0.18 | 0.09 | 0 | 40 | Dextrin, enzyme | No |
| 8—control cell-free | Enzymatic release | 0.21 | 0.11 | 0 | 40 | Dextrin, enzyme | No |
| Data set 3 | ||||||
| 9—enzymatic feed | Enzymatic release | 0.14 | 0.07 | 5 | 40 | Dextrin, enzyme | Yes |
| 10—enzymatic feed | Enzymatic release | 0.21 | 0.11 | 5 | 40 | Dextrin, enzyme | Yes |
| 11—enzymatic feed | Enzymatic release (two additions) | 0.25 | 0.12 | 5 | 80 | Dextrin, enzyme | Yes |
| 12—control cell-free | Enzymatic release | 0.14 | 0.07 | 0 | 40 | Dextrin, enzyme | No |
| 13—control cell-free | Enzymatic release | 0.21 | 0.11 | 0 | 40 | Dextrin, enzyme | No |
| Description | Residual Sum of Squared Errors |
|---|---|
| Simple MM | 4.54 |
| Simple MM with product inhibition | 3.17 |
| Simple MM with substrate inhibition | 4.51 |
| Simple MM with product and substrate inhibition | 4.51 |
| MM considering two substrates | 1.25 |
| MM considering two substrates with product inhibition | 1.18 |
| MM considering two substrates with product and substrate inhibition | 1.14 |
| Parameter | Unit | Value | Standard Deviation |
|---|---|---|---|
| g L−1 | 0.001 | (fixed) | |
| g (U h)−1 | 0.134 | 0.00435 (3.25%) | |
| g (U h)−1 | 0.00212 | 0.000459 (21.68%) | |
| g g−1 | 0.464 | 0.0107 (2.31%) |
| Before Induction | After Induction | ||
|---|---|---|---|
| µset [h−1] | µreal [h−1] | µset [h−1] | µreal [h−1] |
| 0.088 | 0.093 ± 0.013 | 0.034 | 0.066 ± 0.005 |
| 0.124 | 0.142 ± 0.012 | 0.052 | 0.063 ± 0.021 |
| 0.197 | 0.167 ± 0.026 | 0.088 | 0.051 ± 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kemmer, A.; Cai, L.; Born, S.; Cruz Bournazou, M.N.; Neubauer, P. Enzyme-Mediated Exponential Glucose Release: A Model-Based Strategy for Continuous Defined Fed-Batch in Small-Scale Cultivations. Bioengineering 2024, 11, 107. https://doi.org/10.3390/bioengineering11020107
Kemmer A, Cai L, Born S, Cruz Bournazou MN, Neubauer P. Enzyme-Mediated Exponential Glucose Release: A Model-Based Strategy for Continuous Defined Fed-Batch in Small-Scale Cultivations. Bioengineering. 2024; 11(2):107. https://doi.org/10.3390/bioengineering11020107
Chicago/Turabian StyleKemmer, Annina, Linda Cai, Stefan Born, M. Nicolas Cruz Bournazou, and Peter Neubauer. 2024. "Enzyme-Mediated Exponential Glucose Release: A Model-Based Strategy for Continuous Defined Fed-Batch in Small-Scale Cultivations" Bioengineering 11, no. 2: 107. https://doi.org/10.3390/bioengineering11020107
APA StyleKemmer, A., Cai, L., Born, S., Cruz Bournazou, M. N., & Neubauer, P. (2024). Enzyme-Mediated Exponential Glucose Release: A Model-Based Strategy for Continuous Defined Fed-Batch in Small-Scale Cultivations. Bioengineering, 11(2), 107. https://doi.org/10.3390/bioengineering11020107









