Computational Rhinology: Unraveling Discrepancies between In Silico and In Vivo Nasal Airflow Assessments for Enhanced Clinical Decision Support
Abstract
1. Introduction
- Unresolved transitional or turbulent effects.
- Unresolved spatial phenomena such as vortices and eddies.
- Transient effects like hysteresis, developing boundary layers, and meandering.
2. Part I—Computational Rhinology
2.1. Rhinology
2.2. The Relationship between Obstructive Sleep Apnea and Nasal Airway Obstruction
2.3. Clinical Evaluation of Nasal Patency
2.3.1. Nasal Flow Resistance
2.3.2. Rhinomanometry
2.3.3. Mathematical Illustration of the Principles of Rhinomanometry and Inherent Hysteresis Using Bernoulli’s Equation
- Steady, laminar pressure–flow curves are straight lines passing through the origin.
- The slope of the pressure–flow curve decreases with increasing flow resistance. That is, laminar pressure–flow curves are steeper than turbulent ones due to the higher friction factor in turbulent flow. Distinct change in slope in in vivo RMM pressure–flow curves may thus be an indication of transition to turbulence.
- The unsteady flow resistance term causes a hysteresis effect, such that the pressure–flow curve becomes a closed loop not passing through the origin.
- The relative hysteresis width is determined by the hydraulic diameter and the period of the respiratory cycle.
2.4. Computational Fluid Dynamics in Rhinology
2.4.1. Virtual Surgery
2.4.2. The Creation and Utilization of a CFD Model
- Acquisition and preparation of an adequately accurate digital model of the flow geometry (airway).
- Spatial discretization of the geometry model to obtain a computational mesh on which the governing equations of the CFD model can be numerically solved.
- Setting up the flow physics, e.g., which physical phenomena to include, boundary conditions, fluid and solid material properties, etc.
- Determination of solution strategy, e.g., steady state or transient formulation, which numerical scheme to use, turbulence models, convergence criteria, etc.
- Running the simulation until convergence.
- Evaluation of the accuracy of the simulation. In case of unsatisfactory results, return to an earlier point, implement necessary improvements and modifications to the model, and repeat the process.
2.4.3. Acquisition and Preparation of the Digital Airway Geometry Model
2.4.4. Computational Meshes
2.4.5. Flow Physics
2.4.6. Correlations between CFD and Clinical Measures of Nasal Patency
2.5. A Review of Sources of Errors and Uncertainties Affecting Comparison of In Vivo and In Silico Rhinomanometry
2.5.1. Physiological Factors Affecting the Temporal Variability of the Nasal Cavity Geometry
Nasal Cycle
Nasal Cavity Compliance
2.5.2. Sources of Uncertainties and Errors in the Acquisition of Digital Nasal Cavity Geometry Models
- CT and MRI data have relatively low spatial resolution compared to the small-scale features of the nasal cavity. This may cause inaccurate description of the small features of the nasal cavity. Cone beam CT has been proposed as an alternative due to better resolution at lower radiation dosage [141].
- Low temporal resolution of CT and MRI data requires the patient to hold still while data are acquired to avoid blurred images. Effects of heartbeat, breathing, and swallowing may affect image quality adversely. This suggests that CT is preferred over MRI due to better temporal resolution.
- Good communication with the radiologist is required to ensure that the entirety of the nasal cavity is included in the data.
- For comparison of pre- and postoperative airways, the patient’s posture and positioning in the CT/MRI scanner during postoperative examination should be identical to the preoperative situation. For instance, the apparent shape and volume of the pharyngeal tract may be affected by the relative tongue, jaw, head, and neck positions.
- The nasal cycle can be observed in medical imaging data. Medical imaging should thus be performed in the decongested state similar to decongested RMM, preferably in rapid succession after the clinical RMM procedure.
- The radiodensity threshold used to determine the interface between air and tissue can have a severe effect on the cross-sectional area, hence the nasal resistance. A low/high threshold will result in a narrower/more voluminous airway geometry, respectively, potentially affecting flow variables [100].
- Automatic segmentation methods may overlook important details or include secondary air spaces such as the paranasal sinuses, Eustachian tubes, or nasolacrimal ducts. It is recommended to confer with medical expertise such as radiology experts or surgeons to assess the resulting geometry model.
2.5.3. Sources of Uncertainties and Errors in In Vivo Rhinomanometry (Clinical)
- Air leakage along the edge of the face mask or contralateral nostril closure.
- Open mouth and oral breathing.
- Malfunction of the RMM equipment or post processing software.
- The nasal cycle may affect the unilateral nasal resistance.
- Posture has been shown to influence the nasal cycle [33]. Therefore, positioning of the patient may affect the RMM measurements.
- Compliance of the nasal walls can cause the nasal cavity to expand due to over-pressure during exhalation and contract due to under-pressure during inhalation or due to Venturi effect. This dynamic behavior may affect the nasal resistance and result in asymmetry and hysteresis in RMM pressure–flow curves. In situations where hysteresis is prominent, the inspiratory and expiratory segments of the pressure–flow curves may yield markedly distinct measurements of nasal resistance.
- Excessive temporal NAO due to inflammatory reactions or other causes may cause exaggerated nasal resistance that may affect RMM measurements and sometimes even prevent the patient from generating the required volumetric flowrate to conclude the RMM examination.
2.5.4. Sources of Uncertainties and Errors in In Silico Rhinomanometry (CFD)
- Poor computational mesh quality [94].
- Inadequate spatial or temporal refinement.
- Poorly selected solver settings and numerical schemes [148].
- Incorrect definition of flow physics, including, e.g., boundary conditions, material properties, and approximations.
- Inaccurate or incorrect solution due to poor convergence and/or failure to conserve mass, momentum, or energy.
Flow Physics
- (A)
- Modelling of temporal phenomena in respiratory flow
- (B)
- Modelling of turbulent, transitional, and laminar flow
- (C)
- Other aspects
- Temperature and humidity may affect the material properties of air. Some authors have suggested that these effects should be taken into account [76]. Other authors have dismissed these effects [151]. In the relevant temperature range, the mass density and viscosity of air varies by less than ten percent, and the effect of humidity is of the same order. For most situations, it is thus expected that this is of minor importance.
- Due to the small effect of pressure on air material properties within the relevant pressure range, and low flow velocities, it is safe to assume atmospheric ambient pressure and constant air material properties.
Geometry
- How much of the surrounding volume outside the nose and in the oropharyngeal tract should be included? This consideration will affect to what extent the boundary conditions will affect the simulated flow fields. This question is closely intertwined with the discussion about boundary conditions, below.
- How much of the paranasal sinuses should be included? CFD simulation of the flow in the maxillary sinus was performed by Zang et al. [170]. Their conclusion was that the airflow inside the maxillary sinus was much lower (<5%) than the airflow in the nasal cavity. Due to the narrow passage connecting the paranasal sinuses with the nasal cavity, it is expected that negligible gas exchange takes place between the two [171]. This was supported by simulation results presented by Bradshaw et al. [159]. Kaneda et al. [126] reported that the inclusion of the paranasal sinuses did not improve the disagreement between computed and measured nasal resistances.
- What is the role of the oral cavity? Paz et al. [172] investigated the distribution between nasal and oral breathing under steady and unsteady flow. Chen et al. [173] concluded that the inclusion of the oral cavity in CFD simulations of steady and unsteady nasal cavity flow had very little impact. Open mouth and oral breathing may, however, affect the RMM pressure–flow curve.
- Should minor geometrical features such as nasal hair or the mucosal lining be considered?
- ⚬
- Hahn et al. [151] found that the inclusion of nasal hair increased turbulent intensity in the external nares during inspiratory flow but had little effect on downstream velocity profiles. Stoddard et al. [174] found that a reduction in nasal hair density had a positive impact on both subjective and objective measures of nasal obstruction, however.
- ⚬
- Lee et al. [175] illustrated how the mucous layer may affect local flow velocities in the nasal cavity.
Required Spatial and Temporal Numerical Resolution
- (A)
- Spatial Resolution
- (B)
- Temporal Resolution
Boundary Conditions
- The walls are typically treated as smooth non-slip boundaries. Nevertheless, the presence of the mucosal lining introduces the possibility that surface roughness and slip conditions might need consideration. While the nasal wall temperature is commonly assumed to fall within the range of normal body core temperature, this assumption may require more careful consideration if the inhaled air is significantly colder.
- The nostrils serve as inlets to the nasal cavity during inhalation and outlets during exhalation. However, it is reasonable to suspect that truncating the computational domain at the nostrils may compromise the accurate description of airflow entering or exiting the nasal cavity. An alternative approach is to extend the computational domain to encompass the external airspace around the nose to achieve a more realistic airflow distribution at the nostrils. A study by Taylor et al. [180] suggested that the qualitative description of the inflow conditions at the nares may not be critical when computing general flow patterns and overall measures, but for detailed regional flow patterns, carefully chosen inflow conditions may be necessary.
- Modeling the entire airway, including the lungs and alveoli, is impractical in nasal airflow studies. Therefore, the airway is typically truncated somewhere in the laryngopharyngeal tract. The location of this truncation has traditionally been based on available computational resources and the specific phenomena of interest. Although the location of truncation may be less critical during inhalation, more attention may be warranted during exhalation. Wu et al. [181] demonstrated, in a physical experiment, that the flow in the pharynx is laminar during normal breathing, but Bradshaw et al. [159] highlighted the importance of including a realistic pharyngeal tract to achieve accurate flow conditions in the nasopharynx during exhalation. The pharyngeal tract is a complex, soft-tissue-enclosed flow channel susceptible to head and neck movements, swallowing, tongue movement, and compliance with over-/under-pressure due to breathing. The exhalatory flow pattern entering the nasopharynx is likely to be affected by this. The level of realism required in the pharyngeal tract to attain acceptable inflow to the nasopharynx is still unresolved.
2.6. Summary of Part I
- Rhinology, a specialized branch of otorhinolaryngology, is dedicated to advancing diagnostics and treatment methods for nasal and sinonasal disorders, including conditions like nasal airway obstruction (NAO).
- The discord between objective and subjective clinical assessments of NAO severity has created an opening for mathematical modeling tools, such as computational fluid dynamics (CFD), to enhance our understanding of nasal function.
- Computational rhinology, a subfield of biomechanics, employs numerical simulations, like CFD, to gain deeper insights into nasal and sinus function and pathology.
- Computational rhinology is poised to exert a substantial influence on clinical medicine by offering objective, simulation-based decision support for tailoring patient-specific treatment options within the realm of otorhinolaryngology. Furthermore, it may facilitate research and development of novel or improved treatment methods, as well as comparisons between patient-specific and cohort studies.
- While substantial progress has been made over the past three decades toward the clinical application of CFD, there is a lack of robust evidence supporting its applicability and value, and it is yet to attain widespread acceptance as a viable clinical decision support tool.
- Despite significant collaborative efforts from experts in both rhinology and CFD over several decades, CFD is not able to reproduce results from objective clinical measurements, such as rhinomanometry (RMM). In particular, in silico RMM consistently underpredicts nasal resistance compared to in vivo RMM.
- A comprehensive overview of sources of error and uncertainty affecting the comparison of in vivo and in silico RMM has been presented. The observed discrepancies may be the result of a combination of multiple independent factors, rather than a single, isolated cause. Major sources of uncertainty include the following:
- ⚬
- Comparability of nasal cavity geometry during RMM and medical imaging examinations.
- ⚬
- The impact of nasal compliance.
- ⚬
- CFD modelling strategies (e.g., turbulence modelling, unsteady/steady flow).
- Regardless of RMM’s capability to predict a patient’s subjective sensation of nasal patency, it serves as one of few opportunities for validating in silico nasal airflow models. Consequently, RMM plays an indispensable role in the field of computational rhinology.
- The lacking agreement between in vivo and in silico RMM results is a fundamental problem that must be addressed for CFD to gain recognition as a reliable, objective clinical decision support tool.
3. Part II—Overview of Published Literature on In Vitro and In Silico Nasal Airflow Studies
3.1. In Vitro Studies in Physical Nasal Replicas
3.2. In Silico Cohort Studies
3.3. Modelling Approaches in In Silico Studies
| Volumetric Flowrate | ||||
|---|---|---|---|---|
| Steady | Transient | |||
| Experiments in physical replicas (in vitro) | [42,83,117,151,173,203,204,205,214,215,216,219,220,221] | [42,127,129,130,149,151,157,197,200,201,202,203,204,206,222,223,224] | ||
| Navier–Stokes-based models (in silico) | Laminar | [5,50,57,58,59,61,62,63,65,68,83,86,88,90,100,101,106,116,117,123,126,129,131,148,152,158,172,175,176,180,192,199,205,207,208,209,211,219,225,226,227,228,229,230,231,232,233,234,235,236] The present study | [126,129,153,158,172] | |
| RANS | [3,4,42,83,170,204,210,220,226,230,237,238,239] The present study | [224] | ||
| [83,117,121,122,173,204,205,207,226,229,237,240,241,242] | [173,197] | |||
| SST | [83,101,124,148,172,175,199,204,205,212,213,220,243,244,245] The present study | [118,160,172,194,223] | ||
| Spalart–Allmaras | [204,226,246] | |||
| Reynolds stress model | [83] | |||
| LES and RANS-LES hybrid models | [83,148,204,206,217,237,247] | [159,248,249,250] The present study | ||
| DNS | [83] | |||
| Lattice–Boltzmann-based methods (in silico) | [42,125,195,251,252,253] | [127] | ||
3.4. Summary of Part II
- An increasing number of scientific publications are being published in the cross-disciplinary field of computational rhinology. As of 2018, the publication rate was approximately 80 papers per year after several years of near-exponential increase.
- The rapid increase in the publication rate is mainly attributed to the advancements made in automatic segmentation of medical imaging data, streamlining the process of 3D geometry generation, and automatic, unstructured meshing of complex geometries.
- There is no consensus regarding the choice of turbulence model in nasal airflow simulations. Laminar flow modelling appears to be the most popular approach, by far, followed by RANS models. Few publications have reported from LES or DNS modelling.
- Most studies have investigated steady, inspiratory flow. Relatively few publications have reported from expiratory or transient/respiratory flow.
4. Part III—In Silico RMM Simulation Results
4.1. Methods
4.1.1. Clinical Data
4.1.2. Geometry Retrieval
4.1.3. In Silico Rhinomanometry (CFD Modelling)
| Turbulence Model | Turbulence Model Options Activated | Computational Mesh | Volumetric Flowrate | Solver Settings | Discretization |
|---|---|---|---|---|---|
| Laminar | Coarse | Steady |
|
| |
| realizable |
| ||||
| SST |
|
| |||
| LES | WALE | Fine | Transient | SIMPLE pressure-velocity coupling |
|
Turbulence Modelling
Boundary and Initial Conditions
Spatial and Temporal Resolution
4.2. Results
4.2.1. In Silico RMM-Results
4.2.2. Spatial and Temporal Resolution
4.2.3. Flow Velocity Fields
4.2.4. Stress Fields
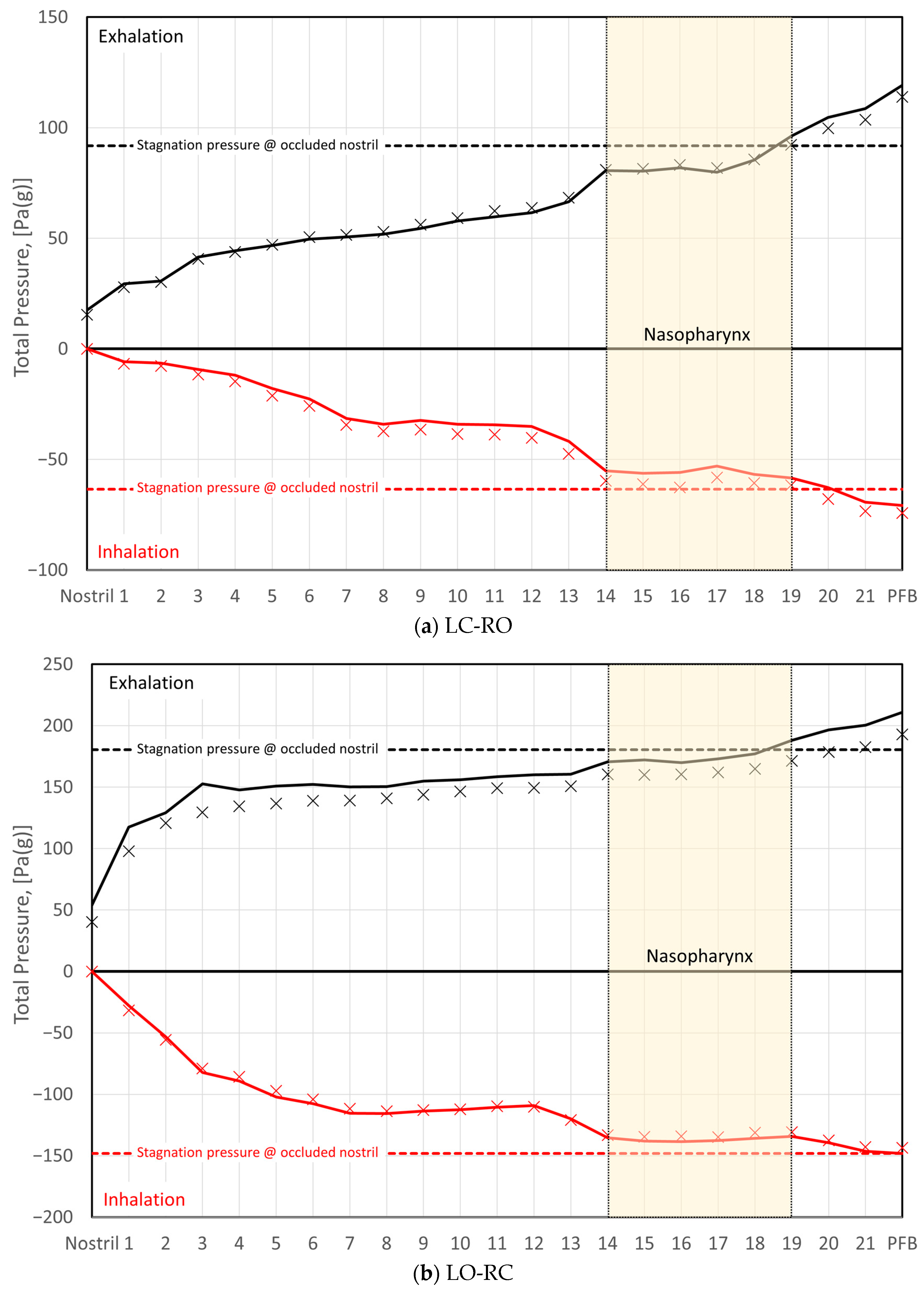
- Comparison of the total pressure development along the length of the nasal cavity indicates varying pressure losses and local flow resistance in different parts of the nose, depending on the flow direction. This suggests that the total unilateral nasal resistance, derived from the integral of the local resistances along the nasal cavity passage, may exhibit dependence on the flow direction.
- During inhalation, the stagnation pressure at the occluded nostril corresponds well to the static pressure in the nasopharynx for both sides of the nose. Conversely, during exhalation, a closer correspondence is observed between the stagnation pressure at the occluded nostril and the total pressure in the nasopharynx.

4.3. Discussion
4.3.1. Turbulence Modelling
4.3.2. Spatial and Temporal Resolution
4.3.3. Transient Effects
4.3.4. Geometry
- During in vivo RMM, nasal cavity decongestion was achieved through the application of xylometazoline. This is expected to maximize nasal cavity volume, through a reduction in turbinate swelling, and minimize nasal resistance. However, the CT image acquisition, the basis for the digital patient-specific geometry model, took place in the natural, non-decongested state. As a result, it was subject to the nasal cycle and various factors affecting spontaneous turbinate and nasal mucosa swelling. For instance, in the natural non-decongested state, postural effect on the nasal resistance and nasal cycle may be anticipated [33,133,134]. The nasal resistance is expected to be higher in the supine position, in which CT images were obtained, than in the sitting position, in which the in vivo RMM data were obtained.The lack of decongestion and the postural effect are both expected to increase the nasal resistance. Hence, the correction of these sources of error would presumably reduce the nasal resistance predicted by the in silico RMM, further increasing the disagreement with the in vivo RMM data.
- It has been proposed that nasal compliance may affect RMM curves (see Part I, Section 2.5.1), and that rigid CFD geometries will fail to reproduce in vivo RMM curves due to this. However, for the current patient, it is observed that the patient-specific in vivo RMM curves are almost symmetrical with respect to in/exhalation (see Figure 12a). At the same time, particularly on the left side, the in vivo RMM pressure–flow curve plateaus, suggesting a significant increase in nasal resistance beyond a critical flowrate. To explain these observations by nasal compliance, a collapsible constriction is required, where the Venturi effect dominates over the static pressure in such a way that the collapse is independent of the flow direction. Without such a constriction, asymmetrical collapse would be expected due to the under-/over-pressures in the nasal cavity during the inspiratory and expiratory phases, respectively. For instance, the phenomenon of nasal gateway collapse exemplifies this, where the collapse occurs exclusively during inhalation [265,266].
4.3.5. Final Remarks and Observations Regarding the Analysis of Rhinomanometry
Pressure Measurements
The Use of Bernoulli’s Equation
4.4. Summary and Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Time derivative operator, | |
| Gradient operator, | |
| Channel cross-sectional area, | |
| Specific heat capacity, | |
| Courant–Friedrich–Lewy number, dimensionless | |
| Channel hydraulic diameter, | |
| Relative wall roughness, dimensionless | |
| Turbulent dissipation rate, | |
| Frequency, | |
| Darcy friction factor, dimensionless | |
| Kolmogorov length scale, | |
| Thermal conductivity, | |
| Turbulent kinetic energy, | |
| Taylor length scale, | |
| Channel length, | |
| Dynamic viscosity, | |
| Kinematic viscosity, | |
| Turbulent kinematic viscosity, | |
| Angular frequency, | |
| Specific turbulent dissipation rate, | |
| Channel perimeter, | |
| Pressure, | |
| Pressure difference, | |
| Volumetric flowrate, | |
| Mass density, | |
| Flow resistance, | |
| Reynolds number, dimensionless | |
| Time step size, | |
| Period of the breathing cycle, | |
| Kolmogorov time scale, | |
| Subgrid-scale stress tensor, | |
| Wall shear stress, | |
| Temperature, | |
| Flow velocity vector, | |
| Flow velocity, | |
| Shear velocity, | |
| Grid size, | |
| Distance to the wall, | |
| Womersley number, dimensionless | |
| In silico | In a digital computer model, e.g., CFD |
| In vitro | In a physical replica |
| In vivo | In a living patient |
| AR | Acoustic rhinometry |
| AAR | Active anterior rhinomanometry |
| AHI | Apnea–hypopnea Index |
| CFD | Computational fluid dynamics |
| CT | Computed tomography |
| DNS | Direct numerical simulation |
| LB | Lattice–Boltzmann |
| LES | Large eddy simulation |
| MRI | Magnetic resonance imaging |
| NAO | Nasal airway obstruction |
| NR | Nasal resistance |
| NS | Navier–Stokes |
| NOSE | Nasal obstruction symptom evaluation |
| OSA | Obstructive sleep apnea |
| PNIF | Peak nasal inspiratory flow |
| RANS | Reynolds-averaged Navier–Stokes |
| RMM | Rhinomanometry |
| VAS | Visual analogue scale |
References
- Broschek, B.; Sonora, C.M.G. Experimental Study of Fluid-Structure Interaction in a Simplified Geometry of the Human Upper Airways. Master’s Thesis, NTNU, Trondheim, Norway, 2015. Available online: https://bibsys-almaprimo.hosted.exlibrisgroup.com/permalink/f/13q4kuj/BRAGE11250/2385338 (accessed on 1 January 2024).
- Jordal, M.R. Patient Specific Numerical Simulation of Flow in the Human Upper Airways. Master’s Thesis, NTNU, Trondheim, Norway, 2016. Available online: https://bibsys-almaprimo.hosted.exlibrisgroup.com/permalink/f/13q4kuj/BRAGE11250/2405975 (accessed on 1 January 2024).
- Aasgrav, E. CFD Simulations of Turbulent Flow in the Human Upper Airways. In Proceedings of the 12th International Conference on CFD in Oil & Gas, Metallurgical and Process Industries, Trondheim, Norway, 30 May 2017. [Google Scholar]
- Aasgrav, E. Investigation of CFD Simulations of Flow in the Upper Airways. Master’s Thesis, NTNU, Trondheim, Norway, 2017. Available online: https://bibsys-almaprimo.hosted.exlibrisgroup.com/permalink/f/13q4kuj/BRAGE11250/2454893 (accessed on 1 January 2024).
- Jordal, M.R.; Johnsen, S.G.; Dahl, S.K.; Müller, B. Patient Specific Numerical Simulation of Flow in the Human Upper Airways for Assessing the Effect of Nasal Surgery. In Proceedings of the 12th International Conference on CFD in Oil & Gas, Metallurgical and Process Industries, Trondheim, Norway, 30 May 2017; p. 10. [Google Scholar]
- Liu, H.; Moxness, M.H.S.; Prot, V.E.; Skallerud, B.H. Palatal Implant Surgery Effectiveness in Treatment of Obstructive Sleep Apnea: A Numerical Method with 3D Patient-Specific Geometries. J. Biomech. 2018, 66, 86–94. [Google Scholar] [CrossRef] [PubMed]
- Moxness, M.H.S. The Influence of the Nasal Airway in Obstructive Sleep Apnea. Ph.D. Thesis, NTNU, Trondheim, Norway, 2018. [Google Scholar]
- Moxness, M.H.S.; Wülker, F.; Helge Skallerud, B.; Nordgård, S. Simulation of the Upper Airways in Patients with Obstructive Sleep Apnea and Nasal Obstruction: A Novel Finite Element Method: Novel FE Method for OSA and Nasal Obstruction. Laryngoscope Investig. Otolaryngol. 2018, 3, 82–93. [Google Scholar] [CrossRef] [PubMed]
- Khalili, M.E.; Larsson, M.; Müller, B. High-Order Ghost-Point Immersed Boundary Method for Viscous Compressible Flows Based on Summation-by-Parts Operators. Int. J. Numer. Methods Fluids 2019, 89, 256–282. [Google Scholar] [CrossRef]
- Akbar, B. Mathematical Modelling and Simulation of Flow in Collapsible Tubes. Master’s Thesis, NTNU, Trondheim, Norway, 2022. Available online: https://bibsys-almaprimo.hosted.exlibrisgroup.com/permalink/f/13q4kuj/BRAGE11250/3023112 (accessed on 1 January 2024).
- Ayyalasomayajula, V.; Moxness, M.; Skallerud, B. Potential of Computational Models in Personalized Treatment of Obstructive Sleep Apnea: A Patient-Specific Partial 3D Finite Element Study. Biomech. Model. Mechanobiol. 2023. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zhao, G.; Li, Y.; Zang, H.; Wang, T.; Wang, D.; Han, D. Apnea–Hypopnea Index Decreased Significantly after Nasal Surgery for Obstructive Sleep Apnea: A Meta-Analysis. Medicine 2017, 96, e6008. [Google Scholar] [CrossRef] [PubMed]
- Schoustra, E.; Van Maanen, P.; Den Haan, C.; Ravesloot, M.J.L.; De Vries, N. The Role of Isolated Nasal Surgery in Obstructive Sleep Apnea Therapy—A Systematic Review. Brain Sci. 2022, 12, 1446. [Google Scholar] [CrossRef]
- Johnsen, S.G. In Silico Rhinomanometry—A High Fidelity LES CFD Simulation Study [Data Set]; Norstore, Sigma2: Trondheim, Norway, 2023. [Google Scholar] [CrossRef]
- Zwicker, D.; Ostilla-Mónico, R.; Lieberman, D.E.; Brenner, M.P. Physical and Geometric Constraints Shape the Labyrinth-like Nasal Cavity. Proc. Natl. Acad. Sci. USA 2018, 115, 2936–2941. [Google Scholar] [CrossRef] [PubMed]
- Cingi, C.; Bayar Muluk, N. (Eds.) All Around the Nose: Basic Science, Diseases and Surgical Management; Springer International Publishing: Cham, Switzerland, 2020; ISBN 978-3-030-21216-2. [Google Scholar]
- Singh, S.; Awasthi, N.; Gupta, T. Mouth Breathing-Its Consequences, Diagnosis & Treatment. Acta Sci. Dent. Sci. 2020, 4, 32–41. [Google Scholar] [CrossRef]
- Zhao, K.; Dalton, P. The Way the Wind Blows: Implications of Modeling Nasal Airflow. Curr. Allergy Asthma Rep. 2007, 7, 117–125. [Google Scholar] [CrossRef]
- Leite, S.H.P.; Jain, R.; Douglas, R.G. The Clinical Implications of Computerised Fluid Dynamic Modelling in Rhinology. Rhinol. J. 2018, 57, 2–9. [Google Scholar] [CrossRef]
- Wong, E.; Inthavong, K.; Singh, N. Comment on the European Position Paper on Diagnostic Tools in Rhinology—Computational Fluid Dynamics. Rhinol. J. 2019, 57, 477–478. [Google Scholar] [CrossRef] [PubMed]
- Spicuzza, L.; Caruso, D.; Di Maria, G. Obstructive Sleep Apnoea Syndrome and Its Management. Ther. Adv. Chronic Dis. 2015, 6, 273–285. [Google Scholar] [CrossRef] [PubMed]
- Trosman, I.; Trosman, S.J. Cognitive and Behavioral Consequences of Sleep Disordered Breathing in Children. Med. Sci. 2017, 5, 30. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, A.; Gupta, S.S.; Sabharwal, N.; Meghrajani, V.; Sharma, S.; Kamholz, S.; Kupfer, Y. A Comprehensive Review of Obstructive Sleep Apnea. Sleep Sci. Sao Paulo Braz. 2021, 14, 142–154. [Google Scholar]
- Reutrakul, S.; Mokhlesi, B. Obstructive Sleep Apnea and Diabetes. Chest 2017, 152, 1070–1086. [Google Scholar] [CrossRef] [PubMed]
- Yeghiazarians, Y.; Jneid, H.; Tietjens, J.R.; Redline, S.; Brown, D.L.; El-Sherif, N.; Mehra, R.; Bozkurt, B.; Ndumele, C.E.; Somers, V.K.; et al. Obstructive Sleep Apnea and Cardiovascular Disease: A Scientific Statement from the American Heart Association. Circulation 2021, 144, e56–e67. [Google Scholar] [CrossRef] [PubMed]
- Castaneda, A.; Jauregui-Maldonado, E.; Ratnani, I.; Varon, J.; Surani, S. Correlation between Metabolic Syndrome and Sleep Apnea. World J. Diabetes 2018, 9, 66–71. [Google Scholar] [CrossRef]
- Bonsignore, M.R.; Randerath, W.; Riha, R.; Smyth, D.; Gratziou, C.; Goncalves, M.; McNicholas, W.T. New Rules on Driver Licensing for Patients with Obstructive Sleep Apnoea: EU Directive 2014/85/EU. Eur. Respir. J. 2016, 47, 39–41. [Google Scholar] [CrossRef]
- Sawada, D.; Tomooka, K.; Tanigawa, T. Changes in Attitudes of Life Insurance Companies Towards Patients with Sleep Apnea Syndrome Undergoing Continuous Positive Airway Pressure in Japan. Juntendo Med. J. 2022, 68, 606–612. [Google Scholar] [CrossRef]
- Young, T.; Finn, L.; Kim, H. Nasal Obstruction as a Risk Factor for Sleep-Disordered Breathing. J. Allergy Clin. Immunol. 1997, 99, S757–S762. [Google Scholar] [CrossRef] [PubMed]
- Li, H.-Y.; Wang, P.-C.; Hsu, C.-Y.; Cheng, M.; Liou, C.-C.; Chen, N.-H. Nasal Resistance in Patients with Obstructive Sleep Apnea. ORL 2005, 67, 70–74. [Google Scholar] [CrossRef]
- Tagaya, M.; Nakata, S.; Yasuma, F.; Noda, A.; Morinaga, M.; Yagi, H.; Sugiura, M.; Teranishi, M.; Nakashima, T. Pathogenetic Role of Increased Nasal Resistance in Obese Patients with Obstructive Sleep Apnea Syndrome. Am. J. Rhinol. Allergy 2010, 24, 51–54. [Google Scholar] [CrossRef]
- Blomster, H.; Kemppainen, T.; Numminen, J.; Ruoppi, P.; Sahlman, J.; Peltonen, M.; Seppa, J.; Tuomilehto, H. Impaired Nasal Breathing May Prevent the Beneficial Effect of Weight Loss in the Treatment of OSA. Rhinol. J. 2011, 49, 587–592. [Google Scholar] [CrossRef]
- Hueto, J.; Santaolalla, F.; Sanchez-del-Rey, A.; Martinez-Ibargüen, A. Usefulness of Rhinomanometry in the Identification and Treatment of Patients with Obstructive Sleep Apnoea: An Algorithm for Predicting the Relationship between Nasal Resistance and Continuous Positive Airway Pressure. a Retrospective Study. Clin. Otolaryngol. 2016, 41, 750–757. [Google Scholar] [CrossRef]
- Hoven, K.M.; Aarstad, H.-J.; Steinsvag, S.K. Associations between Nasal Characteristics and Sleep Polygraphic Data in Patients Suspected Obstructive Sleep Apnea. Rhinol. Online 2020, 3, 79–86. [Google Scholar] [CrossRef]
- Hoel, H.C.; Kvinnesland, K.; Berg, S. Impact of Nasal Resistance on the Distribution of Apneas and Hypopneas in Obstructive Sleep Apnea. Sleep Med. 2020, 71, 83–88. [Google Scholar] [CrossRef] [PubMed]
- Hoel, H.C.; Kvinnesland, K.; Berg, S. Outcome of Nasal Measurements in Patients with OSA—Mounting Evidence of a Nasal Endotype. Sleep Med. 2023, 103, 131–137. [Google Scholar] [CrossRef] [PubMed]
- Scott, W.C.; Kent, D.T. Nasal Obstruction and Sleep-Disordered Breathing. In Management of Obstructive Sleep Apnea; Kim, K.B., Movahed, R., Malhotra, R.K., Stanley, J.J., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 243–257. ISBN 978-3-030-54145-3. [Google Scholar] [CrossRef]
- Chambers, K.J.; Horstkotte, K.A.; Shanley, K.; Lindsay, R.W. Evaluation of Improvement in Nasal Obstruction Following Nasal Valve Correction in Patients With a History of Failed Septoplasty. JAMA Facial Plast. Surg. 2015, 17, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Nakata, S.; Noda, A.; Yagi, H.; Yanagi, E.; Mimura, T.; Okada, T.; Misawa, H.; Nakashima, T. Nasal Resistance for Determinant Factor of Nasal Surgery in CPAP Failure Patients with Obstructive Sleep Apnea Syndrome. Rhinology 2005, 43, 296–299. [Google Scholar] [PubMed]
- Moxness, M.H.S.; Nordgård, S. An Observational Cohort Study of the Effects of Septoplasty with or without Inferior Turbinate Reduction in Patients with Obstructive Sleep Apnea. BMC Ear Nose Throat Disord. 2014, 14, 11. [Google Scholar] [CrossRef] [PubMed]
- Pang, K.P.; Montevecchi, F.; Vicini, C.; Carrasco-Llatas, M.; Baptista, P.M.; Olszewska, E.; Braverman, I.; Kishore, S.; Chandra, S.; Yang, H.C.; et al. Does Nasal Surgery Improve Multilevel Surgical Outcome in Obstructive Sleep Apnea: A Multicenter Study on 735 Patients. Laryngoscope Investig. Otolaryngol. 2020, 5, 1233–1239. [Google Scholar] [CrossRef]
- Berger, M.; Pillei, M.; Mehrle, A.; Recheis, W.; Kral, F.; Kraxner, M.; Bardosi, Z.; Freysinger, W. Nasal Cavity Airflow: Comparing Laser Doppler Anemometry and Computational Fluid Dynamic Simulations. Respir. Physiol. Neurobiol. 2021, 283, 103533. [Google Scholar] [CrossRef]
- Malm, L. Measurement of Nasal Patency. Allergy 1997, 52, 19–23. [Google Scholar] [CrossRef]
- Ottaviano, G.; Fokkens, W.J. Measurements of Nasal Airflow and Patency: A Critical Review with Emphasis on the Use of Peak Nasal Inspiratory Flow in Daily Practice. Allergy 2016, 71, 162–174. [Google Scholar] [CrossRef]
- Eccles, R. Measurement of the Nasal Airway. In Scott-Brown’s Otorhinolaryngology and Head and Neck Surgery; CRC Press: Boca Raton, FL, USA, 2018; Volume 1, p. 1402. ISBN 978-0-203-73103-1. [Google Scholar]
- Rimmer, J.; Hellings, P.; Lund, V.J.; Alobid, I.; Beale, T.; Dassi, C.; Douglas, R.; Hopkins, C.; Klimek, L.; Landis, B.; et al. European Position Paper on Diagnostic Tools in Rhinology. Rhinol. J. 2019, 57, 1–41. [Google Scholar] [CrossRef]
- Rhee, J.S.; Sullivan, C.D.; Frank, D.O.; Kimbell, J.S.; Garcia, G.J.M. A Systematic Review of Patient-Reported Nasal Obstruction Scores: Defining Normative and Symptomatic Ranges in Surgical Patients. JAMA Facial Plast. Surg. 2014, 16, 219–225. [Google Scholar] [CrossRef] [PubMed]
- André, R.F.; Vuyk, H.D.; Ahmed, A.; Graamans, K.; Nolst Trenité, G.J. Correlation between Subjective and Objective Evaluation of the Nasal Airway. A Systematic Review of the Highest Level of Evidence: Subjective and Objective Evaluation of Nasal Patency. Clin. Otolaryngol. 2009, 34, 518–525. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Blacker, K.; Luo, Y.; Bryant, B.; Jiang, J. Perceiving Nasal Patency through Mucosal Cooling Rather than Air Temperature or Nasal Resistance. PLoS ONE 2011, 6, e24618. [Google Scholar] [CrossRef] [PubMed]
- Casey, K.P.; Borojeni, A.A.T.; Koenig, L.J.; Rhee, J.S.; Garcia, G.J.M. Correlation between Subjective Nasal Patency and Intranasal Airflow Distribution. Otolaryngol. Neck Surg. 2017, 156, 741–750. [Google Scholar] [CrossRef] [PubMed]
- Mozzanica, F.; Gera, R.; Bulgheroni, C.; Ambrogi, F.; Schindler, A.; Ottaviani, F. Correlation between Objective and Subjective Assessment of Nasal Patency. Iran. J. Otorhinolaryngol. 2016, 28, 313–319. [Google Scholar] [PubMed]
- Hellgren, J.; Lundberg, M.; Rubek, N.; von Buchwald, C.; Steinsvåg, S.; Mäkitie, A. Unmet Challenges in Septoplasty–Nordic Studies from a Uniform Healthcare and Geographical Area. Front. Surg. 2022, 9, 1061440. [Google Scholar] [CrossRef] [PubMed]
- Quine, S.M.; Eccles, R. Nasal Resistance from the Laboratory to the Clinic. Curr. Opin. Otolaryngol. Head Neck Surg. 1999, 7, 20–25. [Google Scholar] [CrossRef]
- Eccles, R.; Jones, A.S. The Effect of Menthol in Nasal Resistance to Air Flow. J. Laryngol. Otol. 1983, 97, 705–709. [Google Scholar] [CrossRef] [PubMed]
- Eccles, R.; Jawad, M.S.; Morris, S. The Effects of Oral Administration of (—)-Menthol on Nasal Resistance to Airflow and Nasal Sensation of Airflow in Subjects Suffering from Nasal Congestion Associated with the Common Cold. J. Pharm. Pharmacol. 1990, 42, 652–654. [Google Scholar] [CrossRef] [PubMed]
- Gill, A.S.; Said, M.; Tollefson, T.T.; Steele, T.O. Update on Empty Nose Syndrome: Disease Mechanisms, Diagnostic Tools, and Treatment Strategies. Curr. Opin. Otolaryngol. Head Neck Surg. 2019, 27, 237–242. [Google Scholar] [CrossRef] [PubMed]
- Malik, J.; Otto, B.A.; Zhao, K. Computational Fluid Dynamics (CFD) Modeling as an Objective Analytical Tool for Nasal/Upper Airway Breathing. Curr. Otorhinolaryngol. Rep. 2022, 10, 116–120. [Google Scholar] [CrossRef]
- Di, M.-Y.; Jiang, Z.; Gao, Z.-Q.; Li, Z.; An, Y.-R.; Lv, W. Numerical Simulation of Airflow Fields in Two Typical Nasal Structures of Empty Nose Syndrome: A Computational Fluid Dynamics Study. PLoS ONE 2013, 8, e84243. [Google Scholar] [CrossRef]
- Li, C.; Farag, A.A.; Leach, J.; Deshpande, B.; Jacobowitz, A.; Kim, K.; Otto, B.A.; Zhao, K. Computational Fluid Dynamics and Trigeminal Sensory Examinations of Empty Nose Syndrome Patients: Computational and Trigeminal Studies of ENS. Laryngoscope 2017, 127, E176–E184. [Google Scholar] [CrossRef]
- Li, C.; Farag, A.A.; Maza, G.; McGhee, S.; Ciccone, M.A.; Deshpande, B.; Pribitkin, E.A.; Otto, B.A.; Zhao, K. Investigation of the Abnormal Nasal Aerodynamics and Trigeminal Functions among Empty Nose Syndrome Patients: Abnormal Nasal Aerodynamics in ENS Patients. Int. Forum Allergy Rhinol. 2018, 8, 444–452. [Google Scholar] [CrossRef]
- Kimbell, J.S.; Frank, D.O.; Laud, P.; Garcia, G.J.M.; Rhee, J.S. Changes in Nasal Airflow and Heat Transfer Correlate with Symptom Improvement after Surgery for Nasal Obstruction. J. Biomech. 2013, 46, 2634–2643. [Google Scholar] [CrossRef]
- Sullivan, C.D.; Garcia, G.J.M.; Frank-Ito, D.O.; Kimbell, J.S.; Rhee, J.S. Perception of Better Nasal Patency Correlates with Increased Mucosal Cooling after Surgery for Nasal Obstruction. Otolaryngol. Neck Surg. 2014, 150, 139–147. [Google Scholar] [CrossRef]
- Zhao, K.; Jiang, J.; Blacker, K.; Lyman, B.; Dalton, P.; Cowart, B.J.; Pribitkin, E.A. Regional Peak Mucosal Cooling Predicts the Perception of Nasal Patency. Laryngoscope 2014, 124, 589–595. [Google Scholar] [CrossRef] [PubMed]
- Bailey, R.S.; Casey, K.P.; Pawar, S.S.; Garcia, G.J.M. Correlation of Nasal Mucosal Temperature With Subjective Nasal Patency in Healthy Individuals. JAMA Facial Plast. Surg. 2017, 19, 46–52. [Google Scholar] [CrossRef]
- Gaberino, C.; Rhee, J.S.; Garcia, G.J.M. Estimates of Nasal Airflow at the Nasal Cycle Mid-Point Improve the Correlation between Objective and Subjective Measures of Nasal Patency. Respir. Physiol. Neurobiol. 2017, 238, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Radulesco, T.; Meister, L.; Bouchet, G.; Varoquaux, A.; Giordano, J.; Mancini, J.; Dessi, P.; Perrier, P.; Michel, J. Correlations between Computational Fluid Dynamics and Clinical Evaluation of Nasal Airway Obstruction Due to Septal Deviation: An Observational Study. Clin. Otolaryngol. 2019, 44, 603–611. [Google Scholar] [CrossRef]
- Borojeni, A.A.T.; Garcia, G.J.M.; Moghaddam, M.G.; Frank-Ito, D.O.; Kimbell, J.S.; Laud, P.W.; Koenig, L.J.; Rhee, J.S. Normative Ranges of Nasal Airflow Variables in Healthy Adults. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 87–98. [Google Scholar] [CrossRef] [PubMed]
- Tjahjono, R.; Salati, H.; Inthavong, K.; Singh, N. Correlation of Nasal Mucosal Temperature and Nasal Patency—A Computational Fluid Dynamics Study. Laryngoscope 2023, 133, 1328–1335. [Google Scholar] [CrossRef]
- Frank, D.O.; Kimbell, J.S.; Cannon, D.; Pawar, S.S.; Rhee, J.S. Deviated Nasal Septum Hinders Intranasal Sprays: A Computer Simulation Study. Rhinol. J. 2012, 50, 311–318. [Google Scholar] [CrossRef]
- Al_Omari, A.K.; Saied, H.F.I.; Avrunin, O.G. Analysis of Changes of the Hydraulic Diameter and Determination of the Air Flow Modes in the Nasal Cavity. In Image Processing and Communications Challenges 3; Advances in Intelligent and Soft, Computing; Choraś, R.S., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 102, pp. 303–310. ISBN 978-3-642-23153-7. [Google Scholar]
- Pirozzoli, S. On Turbulent Friction in Straight Ducts with Complex Cross-Section: The Wall Law and the Hydraulic Diameter. J. Fluid Mech. 2018, 846, R1. [Google Scholar] [CrossRef]
- O’Neill, G.; Tolley, N.S. The Complexities of Nasal Airflow: Theory and Practice. J. Appl. Physiol. 2019, 127, 1215–1223. [Google Scholar] [CrossRef]
- Benim, A.C.; Maddala, S.B. Numerical Investigation of Friction Laws for Laminar and Turbulent Flow in Undulated Channels. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 1837–1856. [Google Scholar] [CrossRef]
- Hasegawa, M.; Kern, E.B. Variations in Nasal Resistance in Man: A Rhinomanometric Study of the Nasal Cycle in 50 Human Subjects. Rhinology 1978, 16, 19–29. [Google Scholar] [PubMed]
- Flanagan, P.; Eccles, R. Spontaneous Changes of Unilateral Nasal Airflow in Man. A Re-Examination of the ‘Nasal Cycle’. Acta Otolaryngol. (Stockh.) 1997, 117, 590–595. [Google Scholar] [CrossRef]
- Bozdemir, K.; Korkmaz, H.; Franzese, C.B. The Evaluation of the Nose, Nasal Cavity and Airway. In All Around the Nose; Cingi, C., Bayar Muluk, N., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 85–91. ISBN 978-3-030-21216-2. [Google Scholar] [CrossRef]
- Vogt, K.; Jalowayski, A.A.; Althaus, W.; Cao, C.; Han, D.; Hasse, W.; Hoffrichter, H.; Mösges, R.; Pallanch, J.; Shah-Hosseini, K.; et al. 4-Phase-Rhinomanometry (4PR)—Basics and Practice 2010. Rhinol. Suppl. 2010, 21, 1–50. [Google Scholar] [PubMed]
- Mlynski, G.; Löw, J. Die Rhinoresistometrie—Eine Weiterentwicklung der Rhinomanometrie. Laryngo-Rhino-Otol. 1993, 72, 608–610. [Google Scholar] [CrossRef] [PubMed]
- Naito, K.; Iwata, S.; Cole, P.; Fraschetti, J.; Humphrey, D. An International Comparison of Rhinomanometry between Canada and Japan. Rhinology 1991, 29, 287–294. [Google Scholar]
- Moore, M.; Eccles, R. Objective Evidence for the Efficacy of Surgical Management of the Deviated Septum as a Treatment for Chronic Nasal Obstruction: A Systematic Review: Objective Evidence for the Efficacy of Surgical Management of the Deviated Septum: A Systematic Review. Clin. Otolaryngol. 2011, 36, 106–113. [Google Scholar] [CrossRef]
- Blevins, R.D. Applied Fluid Dynamics Handbook; Van Nostrand Reinhold Co.: New York, NY, USA, 1984; ISBN 978-0442212964. [Google Scholar]
- Haaland, S.E. Simple and Explicit Formulas for the Friction Factor in Turbulent Pipe Flow. J. Fluids Eng. 1983, 105, 89–90. [Google Scholar] [CrossRef]
- Li, C.; Jiang, J.; Dong, H.; Zhao, K. Computational Modeling and Validation of Human Nasal Airflow under Various Breathing Conditions. J. Biomech. 2017, 64, 59–68. [Google Scholar] [CrossRef]
- Fletcher, D.F. Use of CFD to Stimulate Flow in the Nose and Airway: Best Practices, Quality and Future Perspectives. In Proceedings of the SCONA 2023 Conference, Brisbane, Australia, 8 March 2023. [Google Scholar]
- Inthavong, K. Current State of the Art, Controversies, and the Future of Nose and Airway Simulations. In Proceedings of the SCONA 2023 Conference, Brisbane, Australia, 8 March 2023. [Google Scholar]
- Burgos, M.A.; Sanmiguel-Rojas, E.; Singh, N.; Esteban-Ortega, F. DigBody®: A New 3D Modeling Tool for Nasal Virtual Surgery. Comput. Biol. Med. 2018, 98, 118–125. [Google Scholar] [CrossRef] [PubMed]
- Quammen, C.W.; Taylor, R.M.; Krajcevski, P.; Mitran, S.; Enquobahrie, A.; Superfine, R.; Davis, B.; Davis, S.; Zdanski, C. The Virtual Pediatric Airways Workbench. Stud. Health Technol. Inform. 2016, 220, 295–300. [Google Scholar] [PubMed]
- Sanmiguel-Rojas, E.; Burgos, M.A.; Esteban-Ortega, F. Nasal Surgery Handled by CFD Tools. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3126. [Google Scholar] [CrossRef] [PubMed]
- Vanhille, D.L.; Garcia, G.J.M.; Asan, O.; Borojeni, A.A.T.; Frank-Ito, D.O.; Kimbell, J.S.; Pawar, S.S.; Rhee, J.S. Virtual Surgery for the Nasal Airway: A Preliminary Report on Decision Support and Technology Acceptance. JAMA Facial Plast. Surg. 2018, 20, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Moghaddam, M.G.; Garcia, G.J.M.; Frank-Ito, D.O.; Kimbell, J.S.; Rhee, J.S. Virtual Septoplasty: A Method to Predict Surgical Outcomes for Patients with Nasal Airway Obstruction. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 725–735. [Google Scholar] [CrossRef] [PubMed]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Series in Computational Methods in Mechanics and Thermal Sciences; Hemisphere Publishing Corporation/Taylor & Francis: New York, NY, USA, 1980; ISBN 0-89116-522-3. [Google Scholar]
- Anderson, J.D. Computational Fluid Dynamics: The Basics with Applications; McGraw-Hill Series in Mechanical Engineering; McGraw-Hill: New York, NY, USA, 1995; ISBN 978-0-07-001685-9. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson Education Ltd.: Harlow, UK, 2007; ISBN 978-0-13-127498-3. [Google Scholar]
- Rodriguez, S. Applied Computational Fluid Dynamics and Turbulence Modeling: Practical Tools, Tips and Techniques; Springer International Publishing: Cham, Switzerland, 2019; ISBN 978-3-030-28690-3. [Google Scholar]
- Roychowdhury, D.G. Best Practice Guidelines in CFD. In Computational Fluid Dynamics for Incompressible Flow; CRC Press: Boca Raton, FL, USA, 2020; pp. 323–334. ISBN 978-0-367-80917-1. [Google Scholar]
- Cercos-Pita, J.L. Computational Reconstruction of the Human Nasal Airway. In Clinical and Biomedical Engineering in the Human Nose; Inthavong, K., Singh, N., Wong, E., Tu, J., Eds.; Biological and Medical Physics, Biomedical Engineering; Springer: Singapore, 2021; pp. 63–84. ISBN 9789811567155. [Google Scholar]
- DenOtter, T.D.; Schubert, J. Hounsfield Unit. In StatPearls [Internet]; StatPearls Publishing: Treasure Island, FL, USA, 2023. Available online: https://www.ncbi.nlm.nih.gov/books/NBK547721/ (accessed on 1 January 2024).
- Dance, D.R. (Ed.) Diagnostic Radiology Physics: A Handbook for Teachers and Students; Non-serial Publications; International Atomic Energy Agency: Vienna, Austria, 2014; ISBN 978-92-0-131010-1. [Google Scholar]
- Ayodele, O.J.; Oluwatosin, A.E.; Taiwo, O.C.; Dare, A.A. Computational Fluid Dynamics Modeling in Respiratory Airways Obstruction: Current Applications and Prospects. Int. J. Biomed. Sci. Eng. 2021, 9, 16–26. [Google Scholar] [CrossRef]
- Cherobin, G.B.; Voegels, R.L.; Gebrim, E.M.M.S.; Garcia, G.J.M. Sensitivity of Nasal Airflow Variables Computed via Computational Fluid Dynamics to the Computed Tomography Segmentation Threshold. PLoS ONE 2018, 13, e0207178. [Google Scholar] [CrossRef]
- Quadrio, M.; Pipolo, C.; Corti, S.; Messina, F.; Pesci, C.; Saibene, A.M.; Zampini, S.; Felisati, G. Effects of CT Resolution and Radiodensity Threshold on the CFD Evaluation of Nasal Airflow. Med. Biol. Eng. Comput. 2016, 54, 411–419. [Google Scholar] [CrossRef]
- Lintermann, A. Computational Meshing for CFD Simulations. In Clinical and Biomedical Engineering in the Human Nose; Inthavong, K., Singh, N., Wong, E., Tu, J., Eds.; Biological and Medical Physics, Biomedical Engineering; Springer: Singapore, 2021; pp. 85–115. ISBN 9789811567155. [Google Scholar]
- Bass, K.; Boc, S.; Hindle, M.; Dodson, K.; Longest, W. High-Efficiency Nose-to-Lung Aerosol Delivery in an Infant: Development of a Validated Computational Fluid Dynamics Method. J. Aerosol Med. Pulm. Drug Deliv. 2019, 32, 132–148. [Google Scholar] [CrossRef]
- Thomas, M.L.; Longest, P.W. Evaluation of the Polyhedral Mesh Style for Predicting Aerosol Deposition in Representative Models of the Conducting Airways. J. Aerosol Sci. 2022, 159, 105851. [Google Scholar] [CrossRef]
- Inthavong, K.; Das, P.; Singh, N.; Sznitman, J. In Silico Approaches to Respiratory Nasal Flows: A Review. J. Biomech. 2019, 97, 109434. [Google Scholar] [CrossRef] [PubMed]
- Inthavong, K.; Chetty, A.; Shang, Y.; Tu, J. Examining Mesh Independence for Flow Dynamics in the Human Nasal Cavity. Comput. Biol. Med. 2018, 102, 40–50. [Google Scholar] [CrossRef]
- Ashraf, W.; Jacobson, N.; Popplewell, N.; Moussavi, Z. Fluid–Structure Interaction Modelling of the Upper Airway with and without Obstructive Sleep Apnea: A Review. Med. Biol. Eng. Comput. 2022, 60, 1827–1849. [Google Scholar] [CrossRef]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; Nachdruck des Originals von 1972; The MIT Press: Cambridge, MA, USA, 1972; ISBN 978-0-262-53630-1. [Google Scholar]
- Pope, S.B. Turbulent Flows, 1st ed.; Cambridge University Press: Cambridge, UK, 2000; ISBN 978-0-521-59125-6. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 3rd ed.; 2 print; DCW Industries: La Cañada, CA, USA, 2010; ISBN 978-1-928729-08-2. [Google Scholar]
- Menter, F.R. Best Practice: Scale-Resolving Simulations in Ansys CFD; ANSYS Rep.; ANSYS, Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Menter, F.R.; Lechner, R.; Matyushenko, A. Best Practice: RANS Turbulence Modeling in Ansys CFD; ANSYS Rep.; ANSYS, Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- ANSYS. ANSYS Fluent Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Rumsey, C.; Smith, B.; Huang, G. NASA Turbulence Modeling Resource; NASA, Langley Research Center: Hampton, VA, USA, 2023. Available online: https://turbmodels.larc.nasa.gov (accessed on 11 November 2023).
- Frank-Ito, D.O.; Garcia, G. Clinical Implications of Nasal Airflow Simulations. In Clinical and Biomedical Engineering in the Human Nose; Biological and Medical Physics, Biomedical Engineering; Inthavong, K., Singh, N., Wong, E., Tu, J., Eds.; Springer: Singapore, 2021; pp. 157–192. ISBN 9789811567155. [Google Scholar]
- Kimbell, J.S.; Garcia, G.J.M.; Frank, D.O.; Cannon, D.E.; Pawar, S.S.; Rhee, J.S. Computed Nasal Resistance Compared with Patient-Reported Symptoms in Surgically Treated Nasal Airway Passages: A Preliminary Report. Am. J. Rhinol. Allergy 2012, 26, 94–98. [Google Scholar] [CrossRef]
- Cherobin, G.B.; Voegels, R.L.; Pinna, F.R.; Gebrim, E.M.M.S.; Bailey, R.S.; Garcia, G.J.M. Rhinomanometry Versus Computational Fluid Dynamics: Correlated, but Different Techniques. Am. J. Rhinol. Allergy 2021, 35, 245–255. [Google Scholar] [CrossRef] [PubMed]
- Zachow, S.; Muigg, P.; Hildebrandt, T.; Doleisch, H.; Hege, H.-C. Visual Exploration of Nasal Airflow. IEEE Trans. Vis. Comput. Graph. 2009, 15, 1407–1414. [Google Scholar] [CrossRef]
- Hildebrandt, T. Das Konzept der Rhinorespiratorischen Homöostase—Ein Neuer Theoretischer Ansatz für die Diskussion Physiologischer und Physikalischer Zusammenhänge bei der Nasenatmung. Ph.D. Thesis, Albert-Ludwigs-Universität, Freiburg im Breisgau, Germany, 2011. Available online: https://freidok.uni-freiburg.de/data/8177 (accessed on 1 January 2024).
- Hildebrandt, T.; (Charité–Universitätsmedizin Berlin, Berlin, Germany). Personal communication, 2020.
- Schmidt, N.; Behrbohm, H.; Goubergrits, L.; Hildebrandt, T.; Brüning, J. Comparison of Rhinomanometric and Computational Fluid Dynamic Assessment of Nasal Resistance with Respect to Measurement Accuracy. Int. J. Comput. Assist. Radiol. Surg. 2022, 17, 1519–1529. [Google Scholar] [CrossRef]
- Dong, J.; Sun, Q.; Shang, Y.; Zhang, Y.; Tian, L.; Tu, J. Numerical Comparison of Inspiratory Airflow Patterns in Human Nasal Cavities with Distinct Age Differences. Int. J. Numer. Methods Biomed. Eng. 2022, 38, e3565. [Google Scholar] [CrossRef] [PubMed]
- Hemtiwakorn, K.; Mahasitthiwat, V.; Tungjitkusolmun, S.; Hamamoto, K.; Pintavirooj, C. Patient-Specific Aided Surgery Approach of Deviated Nasal Septum Using Computational Fluid Dynamics. IEEJ Trans. Electr. Electron. Eng. 2015, 10, 274–286. [Google Scholar] [CrossRef]
- Osman, J.; Großmann, F.; Brosien, K.; Kertzscher, U.; Goubergrits, L.; Hildebrandt, T. Assessment of Nasal Resistance Using Computational Fluid Dynamics. Curr. Dir. Biomed. Eng. 2016, 2, 617–621. [Google Scholar] [CrossRef]
- Berger, M.; Giotakis, A.I.; Pillei, M.; Mehrle, A.; Kraxner, M.; Kral, F.; Recheis, W.; Riechelmann, H.; Freysinger, W. Agreement between Rhinomanometry and Computed Tomography-Based Computational Fluid Dynamics. Int. J. Comput. Assist. Radiol. Surg. 2021, 16, 629–638. [Google Scholar] [CrossRef]
- Kaneda, S.; Goto, F.; Okami, K.; Mitsutani, R.; Takakura, Y. Numerical Simulation of Nasal Resistance Using Three-Dimensional Models of the Nasal Cavity and Paranasal Sinus. Tokai J. Exp. Clin. Med. 2023, 48, 56–61. [Google Scholar]
- Hebbink, R.H.J.; Wessels, B.J.; Hagmeijer, R.; Jain, K. Computational Analysis of Human Upper Airway Aerodynamics. Med. Biol. Eng. Comput. 2023, 61, 541–553. [Google Scholar] [CrossRef]
- Guide: Guide for the Verification and Validation of Computational Fluid Dynamics Simulations (AIAA G-077-1998(2002)). In Guide: Guide for the Verification and Validation of Computational Fluid Dynamics Simulations (AIAA G-077-1998(2002)); Computational Fluid Dynamics Committee, Ed.; American Institute of Aeronautics and Astronautics, Inc.: Washington, DC, USA, 1998; ISBN 978-1-56347-285-5. [Google Scholar] [CrossRef]
- Pawade, A.R. Computational Modeling of Airflow in a Human Nasal Cavity. Master’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2021. [Google Scholar]
- Reid, A.W.N.; Chen, D.H.; Wen, H.; Li, H.; Wang, Z.; Hu, Y.; Zhang, F.; Bele, E.; Tan, P.J.; East, C. The Virtual Nose: Assessment of Static Nasal Airway Obstruction Using Computational Simulations and 3D-Printed Models. Facial Plast. Surg. Aesthetic Med. 2022, 24, 20–26. [Google Scholar] [CrossRef]
- Patel, R.G.; Garcia, G.J.M.; Frank-Ito, D.O.; Kimbell, J.S.; Rhee, J.S. Simulating the Nasal Cycle with Computational Fluid Dynamics. Otolaryngol. Neck Surg. 2015, 152, 353–360. [Google Scholar] [CrossRef] [PubMed]
- Susaman, N.; Cingi, C.; Mullol, J. Is the Nasal Cycle Real? How Important Is It? In Challenges in Rhinology; Cingi, C., Bayar Muluk, N., Scadding, G.K., Mladina, R., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 1–8. ISBN 978-3-030-50898-2. [Google Scholar]
- Hasegawa, M. Nasal Cycle and Postural Variations in Nasal Resistance. Ann. Otol. Rhinol. Laryngol. 1982, 91, 112–114. [Google Scholar] [CrossRef] [PubMed]
- Haight, J.S.; Cole, P. Unilateral Nasal Resistance and Asymmetrical Body Pressure. J. Otolaryngol. Suppl. 1986, 16, 1–31. [Google Scholar]
- Fodil, R.; Brugel-Ribere, L.; Croce, C.; Sbirlea-Apiou, G.; Larger, C.; Papon, J.-F.; Delclaux, C.; Coste, A.; Isabey, D.; Louis, B. Inspiratory Flow in the Nose: A Model Coupling Flow and Vasoerectile Tissue Distensibility. J. Appl. Physiol. 2005, 98, 288–295. [Google Scholar] [CrossRef]
- Bailie, N.; Hanna, B.; Watterson, J.; Gallagher, G. An Overview of Numerical Modelling of Nasal Airflow. Rhinology 2006, 44, 53–57. [Google Scholar]
- Akmenkalne, L.; Prill, M.; Vogt, K. Nasal Valve Elastography: Quantitative Determination of the Mobility of the Nasal Valve. Rhinol. Online 2019, 2, 81–86. [Google Scholar] [CrossRef]
- Vogt, K.; Zhang, L. Airway Assessment by Four-Phase Rhinomanometry in Septal Surgery. Curr. Opin. Otolaryngol. Head Neck Surg. 2012, 20, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Vogt, K.; Wernecke, K.-D.; Behrbohm, H.; Gubisch, W.; Argale, M. Four-Phase Rhinomanometry: A Multicentric Retrospective Analysis of 36,563 Clinical Measurements. Eur. Arch. Otorhinolaryngol. 2016, 273, 1185–1198. [Google Scholar] [CrossRef] [PubMed]
- Groß, T.F.; Peters, F. A Fluid Mechanical Interpretation of Hysteresis in Rhinomanometry. ISRN Otolaryngol. 2011, 2011, 126520. [Google Scholar] [CrossRef] [PubMed]
- Bui, N.L.; Ong, S.H.; Foong, K.W.C. Automatic Segmentation of the Nasal Cavity and Paranasal Sinuses from Cone-Beam CT Images. Int. J. Comput. Assist. Radiol. Surg. 2015, 10, 1269–1277. [Google Scholar] [CrossRef] [PubMed]
- Aanderaa, L.Ø. Experimental Investigation of Rhinomanometry. Master’s Thesis, NTNU, Trondheim, Norway, 2021. [Google Scholar]
- Silkoff, P.E.; Chakravorty, S.; Chapnik, J.; Cole, P.; Zamel, N. Reproducibility of Acoustic Rhinometry and Rhinomanometry in Normal Subjects. Am. J. Rhinol. 1999, 13, 131–136. [Google Scholar] [CrossRef] [PubMed]
- Carney, A.S.; Bateman, N.D.; Jones, N.S. Reliable and Reproducible Anterior Active Rhinomanometry for the Assessment of Unilateral Nasal Resistance. Clin. Otolaryngol. Allied Sci. 2000, 25, 499–503. [Google Scholar] [CrossRef] [PubMed]
- Thulesius, H.L.; Cervin, A.; Jessen, M. Can We Always Trust Rhinomanometry? Rhinol. J. 2011, 49, 46–52. [Google Scholar] [CrossRef] [PubMed]
- ERCOFTAC. Best Practice Guidelines, Industrial Computational Fluid Dynamics of Single-Phase Flows; ERCOFTAC: London, UK, 2000; ISBN 978-0-9955779-2-3. [Google Scholar]
- Andersson, B.; Andersson, R.; Håkansson, L.; Mortensen, M.; Sudiyo, R.; Van Wachem, B. Best Practice Guidelines. In Computational Fluid Dynamics for Engineers; Cambridge University Press: Cambridge, UK, 2011; pp. 174–180. ISBN 978-1-107-01895-2. [Google Scholar]
- Schillaci, A.; Quadrio, M. Importance of the Numerical Schemes in the CFD of the Human Nose. J. Biomech. 2022, 138, 111100. [Google Scholar] [CrossRef]
- Proetz, A.W. Air Currents in the Upper Respiratory Tract and Their Clinical Importance. Ann. Otol. Rhinol. Laryngol. 1951, 60, 439–467. [Google Scholar] [CrossRef]
- Sullivan, K.J.; Chang, H.K. Steady and Oscillatory Transnasal Pressure-Flow Relationships in Healthy Adults. J. Appl. Physiol. 1991, 71, 983–992. [Google Scholar] [CrossRef]
- Hahn, I.; Scherer, P.W.; Mozell, M.M. Velocity Profiles Measured for Airflow through a Large-Scale Model of the Human Nasal Cavity. J. Appl. Physiol. 1993, 75, 2273–2287. [Google Scholar] [CrossRef]
- Keyhani, K.; Scherer, P.W.; Mozell, M.M. Numerical Simulation of Airflow in the Human Nasal Cavity. J. Biomech. Eng. 1995, 117, 429–441. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Kleinstreuer, C.; Zhang, Z. Laminar Airflow and Nanoparticle or Vapor Deposition in a Human Nasal Cavity Model. J. Biomech. Eng. 2006, 128, 697–706. [Google Scholar] [CrossRef] [PubMed]
- Hörschler, I.; Schröder, W.; Meinke, M. On the Assumption of Steadiness of Nasal Cavity Flow. J. Biomech. 2010, 43, 1081–1085. [Google Scholar] [CrossRef] [PubMed]
- Womersley, J.R. Method for the Calculation of Velocity, Rate of Flow and Viscous Drag in Arteries When the Pressure Gradient Is Known. J. Physiol. 1955, 127, 553–563. [Google Scholar] [CrossRef] [PubMed]
- Loudon, C.; Tordesillas, A. The Use of the Dimensionless Womersley Number to Characterize the Unsteady Nature of Internal Flow. J. Theor. Biol. 1998, 191, 63–78. [Google Scholar] [CrossRef]
- Doorly, D.J.; Taylor, D.J.; Schroter, R.C. Mechanics of Airflow in the Human Nasal Airways. Respir. Physiol. Neurobiol. 2008, 163, 100–110. [Google Scholar] [CrossRef]
- Bosykh, L.Y.; Ganimedov, V.L.; Muchnaya, M.I.; Sadovskii, A.S. Influence of the Respiratory Cycle Structure on the Flow Field in Human Nasal Cavity at a Fixed Level of Breath Depth. AIP Conf. Proc. 2016, 1770, 030085. [Google Scholar]
- Bradshaw, K.; Warfield-McAlpine, P.; Vahaji, S.; Emmerling, J.; Salati, H.; Sacks, R.; Fletcher, D.F.; Singh, N.; Inthavong, K. New Insights into the Breathing Physiology from Transient Respiratory Nasal Simulation. Phys. Fluids 2022, 34, 115103. [Google Scholar] [CrossRef]
- Tretiakow, D.; Tesch, K.; Markiet, K.; Przewoźny, T.; Kusiak, A.; Cichońska, D.; Skorek, A. Numerical Analysis of the Ostiomeatal Complex Aeration Using the CFD Method. Sci. Rep. 2023, 13, 3980. [Google Scholar] [CrossRef]
- Koeppen, B.M.; Stanton, B.A. (Eds.) Berne & Levy Physiology, 7th ed.; Elsevier: Philadelphia, PA, USA, 2018; ISBN 978-0-323-39394-2. [Google Scholar]
- He, S.; Seddighi, M. Transition of Transient Channel Flow after a Change in Reynolds Number. J. Fluid Mech. 2015, 764, 395–427. [Google Scholar] [CrossRef]
- Guerrero, B.; Lambert, M.F.; Chin, R.C. Transient Dynamics of Accelerating Turbulent Pipe Flow. J. Fluid Mech. 2021, 917, A43. [Google Scholar] [CrossRef]
- Guerrero, B.; Lambert, M.F.; Chin, R.C. Transient Behaviour of Decelerating Turbulent Pipe Flows. J. Fluid Mech. 2023, 962, A44. [Google Scholar] [CrossRef]
- Yellin, E.L. Laminar-Turbulent Transition Process in Pulsatile Flow. Circ. Res. 1966, 19, 791–804. [Google Scholar] [CrossRef] [PubMed]
- Gündoğdu, M.Y.; Çarpinlioğlu, M.Ö. Present State of Art on Pulsatile Flow Theory. Part 1. Laminar and Transitional Flow Regimes. JSME Int. J. Ser. B 1999, 42, 384–397. [Google Scholar] [CrossRef]
- Gündoğdu, M.Y.; Çarpinlioğlu, M.Ö. Present State of Art on Pulsatile Flow Theory. Part 2. Turbulent Flow Regime. JSME Int. J. Ser. B 1999, 42, 398–410. [Google Scholar] [CrossRef]
- Xu, D.; Warnecke, S.; Song, B.; Ma, X.; Hof, B. Transition to Turbulence in Pulsating Pipe Flow. J. Fluid Mech. 2017, 831, 418–432. [Google Scholar] [CrossRef]
- Sayadi, T.; Moin, P. Large Eddy Simulation of Controlled Transition to Turbulence. Phys. Fluids 2012, 24, 114103. [Google Scholar] [CrossRef]
- Zang, H.; Liu, Y.; Han, D.; Zhang, L.; Wang, T.; Sun, X.; Li, L. Airflow and Temperature Distribution inside the Maxillary Sinus: A Computational Fluid Dynamics Simulation. Acta Otolaryngol. (Stockh.) 2012, 132, 637–644. [Google Scholar] [CrossRef]
- Kim, S.K.; Na, Y.; Kim, J.-I.; Chung, S.-K. Patient Specific CFD Models of Nasal Airflow: Overview of Methods and Challenges. J. Biomech. 2013, 46, 299–306. [Google Scholar] [CrossRef]
- Paz, C.; Suarez, E.; Concheiro, M.; Porteiro, J. CFD Transient Simulation of a Breathing Cycle in an Oral-Nasal Extrathoracic Model. J. Appl. Fluid Mech. 2017, 10, 777–784. [Google Scholar] [CrossRef]
- Chen, S.; Wang, J.; Liu, D.; Lei, L.; Wu, W.; Liu, Z.; Lee, C. Open Oral Cavity Has Little Effects on Upper Airway Aerodynamics in Children with Obstructive Sleep Apnea Syndrome: A Computational Fluid Dynamics Study Based on Patient-Specific Models. J. Biomech. 2021, 121, 110383. [Google Scholar] [CrossRef] [PubMed]
- Stoddard, D.G.; Pallanch, J.F.; Hamilton, G.S. The Effect of Vibrissae on Subjective and Objective Measures of Nasal Obstruction. Am. J. Rhinol. Allergy 2015, 29, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.F.; Arifin Ahmad, K.; Ismail, R.; Abdul Hamid, S. Numerical Study of Mucous Layer Effects on Nasal Airflow. Biomed. Eng. Appl. Basis Commun. 2012, 24, 327–332. [Google Scholar] [CrossRef]
- Frank-Ito, D.O.; Wofford, M.; Schroeter, J.D.; Kimbell, J.S. Influence of Mesh Density on Airflow and Particle Deposition in Sinonasal Airway Modeling. J. Aerosol Med. Pulm. Drug Deliv. 2016, 29, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK; New York, NY, USA, 1972; ISBN 978-0-12-438050-9. [Google Scholar]
- Courant, R.; Friedrichs, K.; Lewy, H. Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 1928, 100, 32–74. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. On the Partial Difference Equations of Mathematical Physics. IBM J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Taylor, D.J.; Doorly, D.J.; Schroter, R.C. Inflow Boundary Profile Prescription for Numerical Simulation of Nasal Airflow. J. R. Soc. Interface 2010, 7, 515–527. [Google Scholar] [CrossRef]
- Wu, H.; Wang, M.; Wang, J.; An, Y.; Wang, H.; Huang, Y. Direct Visualizations of Air Flow in the Human Upper Airway Using In-Vitro Models. Sci. China Life Sci. 2019, 62, 235–243. [Google Scholar] [CrossRef] [PubMed]
- Han, J.K.; Stringer, S.P.; Rosenfeld, R.M.; Archer, S.M.; Baker, D.P.; Brown, S.M.; Edelstein, D.R.; Gray, S.T.; Lian, T.S.; Ross, E.J.; et al. Clinical Consensus Statement: Septoplasty with or without Inferior Turbinate Reduction. Otolaryngol. Neck Surg. 2015, 153, 708–720. [Google Scholar] [CrossRef]
- Puccia, R.; Pawar, S.S. Key Points on Functional Rhinoplasty Patient Evaluation. Curr. Otorhinolaryngol. Rep. 2022, 10, 127–133. [Google Scholar] [CrossRef]
- Urban, M.J.; Friedman, J.J.; Husain, I.; LoSavio, P.S. Overview of Recent Advances in Surgical Treatments for OSA. Curr. Sleep Med. Rep. 2020, 6, 199–207. [Google Scholar] [CrossRef]
- Vicory, J.; Garcia, G.J.M.; Rhee, J.S.; Enquobahrie, A. Toward Automatic Atlas-Based Surgical Planning for Septoplasty. Int. J. Comput. Assist. Radiol. Surg. 2022, 17, 403–411. [Google Scholar] [CrossRef] [PubMed]
- Lintermann, A. Application of Computational Fluid Dynamics Methods to Understand Nasal Cavity Flows. In All Around the Nose; Cingi, C., Bayar Muluk, N., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 75–84. ISBN 978-3-030-21216-2. [Google Scholar]
- Tu, J.; Inthavong, K.; Ahmadi, G. Computational Fluid and Particle Dynamics in the Human Respiratory System; Biological and Medical Physics, Biomedical Engineering; Springer: Dordrecht, The Netherlands; New York, NY, USA, 2012; ISBN 978-94-007-4487-5. [Google Scholar] [CrossRef]
- Inthavong, K.; Singh, N.; Wong, E.; Tu, J. (Eds.) Clinical and Biomedical Engineering in the Human Nose: A Computational Fluid Dynamics Approach; Biological and Medical Physics, Biomedical Engineering; Springer: Singapore, 2021; ISBN 9789811567155. [Google Scholar]
- Leong, S.C. A Review of the Implications of Computational Fluid Dynamic Studies on Nasal Airflow and Physiology. Rhinol. J. 2010, 48, 139–145. [Google Scholar] [CrossRef]
- Radulesco, T.; Meister, L.; Bouchet, G.; Giordano, J.; Dessi, P.; Perrier, P.; Michel, J. Functional Relevance of Computational Fluid Dynamics in the Field of Nasal Obstruction: A Literature Review. Clin. Otolaryngol. 2019, 44, 801–809. [Google Scholar] [CrossRef]
- Faizal, W.M.; Ghazali, N.N.N.; Khor, C.Y.; Badruddin, I.A.; Zainon, M.Z.; Yazid, A.A.; Ibrahim, N.B.; Razi, R.M. Computational Fluid Dynamics Modelling of Human Upper Airway: A Review. Comput. Methods Programs Biomed. 2020, 196, 105627. [Google Scholar] [CrossRef]
- Burgos, M.A.; Sanmiguel-Rojas, E.; del Pino, C.; Sevilla-García, M.A.; Esteban-Ortega, F. New CFD Tools to Evaluate Nasal Airflow. Eur. Arch. Otorhinolaryngol. 2017, 274, 3121–3128. [Google Scholar] [CrossRef]
- Pugachev, A.; Arnold, M.; Burgmann, S.; Janoske, U.; Bicsák, Á.; Abel, D.; Linssen, J.; Bonitz, L. Application of Patient-specific Simulation Workflow for Obstructive Sleep Apnea Diagnosis and Treatment with a Mandibular Advancement Device. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3350. [Google Scholar] [CrossRef] [PubMed]
- Tretiakow, D.; Tesch, K.; Meyer-Szary, J.; Markiet, K.; Skorek, A. Three-Dimensional Modeling and Automatic Analysis of the Human Nasal Cavity and Paranasal Sinuses Using the Computational Fluid Dynamics Method. Eur. Arch. Otorhinolaryngol. 2021, 278, 1443–1453. [Google Scholar] [CrossRef]
- Waldmann, M.; Grosch, A.; Witzler, C.; Lehner, M.; Benda, O.; Koch, W.; Vogt, K.; Kohn, C.; Schröder, W.; Göbbert, J.H.; et al. An Effective Simulation- and Measurement-Based Workflow for Enhanced Diagnostics in Rhinology. Med. Biol. Eng. Comput. 2022, 60, 365–391. [Google Scholar] [CrossRef] [PubMed]
- Quadrio, M.; Pipolo, C.; Corti, S.; Lenzi, R.; Messina, F.; Pesci, C.; Felisati, G. Review of Computational Fluid Dynamics in the Assessment of Nasal Air Flow and Analysis of Its Limitations. Eur. Arch. Otorhinolaryngol. 2014, 271, 2349–2354. [Google Scholar] [CrossRef]
- Le, T.B.; Moghaddam, M.G.; Woodson, B.T.; Garcia, G.J.M. Airflow Limitation in a Collapsible Model of the Human Pharynx: Physical Mechanisms Studied with Fluid-structure Interaction Simulations and Experiments. Physiol. Rep. 2019, 7, e14099. [Google Scholar] [CrossRef] [PubMed]
- Xi, J.; Wang, J.; Si, X.A.; Dong, H. Direct Numerical Simulations and Flow-Pressure Acoustic Analyses of Flapping-Uvula-Induced Flow Evolutions within Normal and Constricted Pharynx. Theor. Comput. Fluid Dyn. 2023, 37, 131–149. [Google Scholar] [CrossRef]
- Larimi, M.M.; Babamiri, A.; Biglarian, M.; Ramiar, A.; Tabe, R.; Inthavong, K.; Farnoud, A. Numerical and Experimental Analysis of Drug Inhalation in Realistic Human Upper Airway Model. Pharmaceuticals 2023, 16, 406. [Google Scholar] [CrossRef]
- Stuiver, M. Biophysics of the Sense of Smell. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 1958. [Google Scholar]
- Masing, H. Investigations about the Course of Flow in the Nose Model. Arch Klin Exp Ohr Nas Kehlkopf 1967, 189, 371–381. [Google Scholar] [CrossRef]
- Hornung, D.E.; Leopold, D.A.; Youngentob, S.L.; Sheehe, P.R.; Gagne, G.M.; Thomas, F.D.; Mozell, M.M. Airflow Patterns in a Human Nasal Model. Arch. Otolaryngol. Head Neck Surg. 1987, 113, 169–172. [Google Scholar] [CrossRef]
- Kelly, J.T.; Prasad, A.K.; Wexler, A.S. Detailed Flow Patterns in the Nasal Cavity. J. Appl. Physiol. 2000, 89, 323–337. [Google Scholar] [CrossRef]
- Mylavarapu, G.; Murugappan, S.; Mihaescu, M.; Kalra, M.; Khosla, S.; Gutmark, E. Validation of Computational Fluid Dynamics Methodology Used for Human Upper Airway Flow Simulations. J. Biomech. 2009, 42, 1553–1559. [Google Scholar] [CrossRef] [PubMed]
- Ormiskangas, J.; Valtonen, O.; Kivekäs, I.; Dean, M.; Poe, D.; Järnstedt, J.; Lekkala, J.; Harju, T.; Saarenrinne, P.; Rautiainen, M. Assessment of PIV Performance in Validating CFD Models from Nasal Cavity CBCT Scans. Respir. Physiol. Neurobiol. 2020, 282, 103508. [Google Scholar] [CrossRef]
- Van Strien, J.; Shrestha, K.; Gabriel, S.; Lappas, P.; Fletcher, D.F.; Singh, N.; Inthavong, K. Pressure Distribution and Flow Dynamics in a Nasal Airway Using a Scale Resolving Simulation. Phys. Fluids 2021, 33, 011907. [Google Scholar] [CrossRef]
- Zhao, K.; Jiang, J. What Is Normal Nasal Airflow? A Computational Study of 22 Healthy Adults: Normal Human Nasal Airflow. Int. Forum Allergy Rhinol. 2014, 4, 435–446. [Google Scholar] [CrossRef]
- Ramprasad, V.H.; Frank-Ito, D.O. A Computational Analysis of Nasal Vestibule Morphologic Variabilities on Nasal Function. J. Biomech. 2016, 49, 450–457. [Google Scholar] [CrossRef]
- Sanmiguel-Rojas, E.; Burgos, M.A.; del Pino, C.; Sevilla-García, M.A.; Esteban-Ortega, F. Robust Nondimensional Estimators to Assess the Nasal Airflow in Health and Disease: Mathematical Estimators to Assess Nasal Airflow. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2906. [Google Scholar] [CrossRef]
- Li, L.; Han, D.; Zang, H.; London, N.R. Aerodynamics Analysis of the Impact of Nasal Surgery on Patients with Obstructive Sleep Apnea and Nasal Obstruction. ORL 2022, 84, 62–69. [Google Scholar] [CrossRef]
- Ormiskangas, J.; Valtonen, O.; Harju, T.; Rautiainen, M.; Kivekäs, I. Computational Fluid Dynamics Calculations in Inferior Turbinate Surgery: A Cohort Study. Eur. Arch. Otorhinolaryngol. 2023, 280, 4923–4931. [Google Scholar] [CrossRef]
- Sagandykova, N.S.; Fakhradiyev, I.R.; Sajjala, S.R.; Taukeleva, S.A.; Shemetova, D.E.; Saliev, T.M.; Tanabayeva, S.B.; Zhao, Y. Patient-Specific CFD Simulation of Aerodynamics for Nasal Pathology: A Combined Computational and Experimental Study. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2021, 9, 470–479. [Google Scholar] [CrossRef]
- Corda, J.V.; Shenoy, B.S.; Lewis, L.; Khader, S.M.A.; Ahmad, K.A.; Zuber, M. Nasal Airflow Patterns in a Patient with Septal Deviation and Comparison with a Healthy Nasal Cavity Using Computational Fluid Dynamics. Front. Mech. Eng. 2022, 8, 1009640. [Google Scholar] [CrossRef]
- Swift, D.L.; Proctor, D.F. Access of Air to the Respiratory Tract. In Respiratory Defense Mechanisms, Part I; Brain, J.D., Proctor, D.F., Reid, L.M., Eds.; Marcel Dekker: New York, NY, USA, 1977; pp. 63–95. [Google Scholar]
- Schreck, S.; Sullivan, K.J.; Ho, C.M.; Chang, H.K. Correlations between Flow Resistance and Geometry in a Model of the Human Nose. J. Appl. Physiol. 1993, 75, 1767–1775. [Google Scholar] [CrossRef] [PubMed]
- Simmen, D.; Scherrer, J.L.; Moe, K.; Heinz, B. A Dynamic and Direct Visualization Model for the Study of Nasal Airflow. Arch. Otolaryngol. Neck Surg. 1999, 125, 1015. [Google Scholar] [CrossRef] [PubMed]
- Xi, J.; Kim, J.; Si, X.A. Effects of Nostril Orientation on Airflow Dynamics, Heat Exchange, and Particle Depositions in Human Noses. Eur. J. Mech. BFluids 2016, 55, 215–228. [Google Scholar] [CrossRef]
- Bates, A.J. Fundamentals of Fluid Dynamics. In Clinical and Biomedical Engineering in the Human Nose; Biological and Medical Physics, Biomedical Engineering; Inthavong, K., Singh, N., Wong, E., Tu, J., Eds.; Springer: Singapore, 2021; pp. 117–156. ISBN 9789811567155. [Google Scholar]
- Segal, R.A.; Kepler, G.M.; Kimbell, J.S. Effects of Differences in Nasal Anatomy on Airflow Distribution: A Comparison of Four Individuals at Rest. Ann. Biomed. Eng. 2008, 36, 1870–1882. [Google Scholar] [CrossRef] [PubMed]
- Phuong, N.L.; Ito, K. Investigation of Flow Pattern in Upper Human Airway Including Oral and Nasal Inhalation by PIV and CFD. Build. Environ. 2015, 94, 504–515. [Google Scholar] [CrossRef]
- Cozzi, F.; Felisati, G.; Quadrio, M. Velocity Measurements in Nasal Cavities by Means of Stereoscopic PIV—Preliminary Tests. J. Phys. Conf. Ser. 2017, 882, 012010. [Google Scholar] [CrossRef]
- Chung, S.-K.; Son, Y.R.; Shin, S.J.; Kim, S.-K. Nasal Airflow during Respiratory Cycle. Am. J. Rhinol. 2006, 20, 379–384. [Google Scholar] [CrossRef]
- Van Hove, S.C.; Storey, J.; Adams, C.; Dey, K.; Geoghegan, P.H.; Kabaliuk, N.; Oldfield, S.D.; Spence, C.J.T.; Jermy, M.C.; Suresh, V.; et al. An Experimental and Numerical Investigation of CO2 Distribution in the Upper Airways During Nasal High Flow Therapy. Ann. Biomed. Eng. 2016, 44, 3007–3019. [Google Scholar] [CrossRef]
- Kleven, M.; Singh, N.P.; Messina, J.C.; Djupesland, P.G.; Inthavong, K. Development of Computational Fluid Dynamics Methodology for Characterization of Exhalation Delivery System Performance in a Nasal Airway with Draf-III Surgery. J. Aerosol Sci. 2023, 169, 106121. [Google Scholar] [CrossRef]
- Subramaniam, R.P.; Richardson, R.B.; Morgan, K.T.; Kimbell, J.S.; Guilmette, R.A. Computational Fluid Dynamics Simulations of Inspiratory Airflow in the Human Nose and Nasopharynx. Inhal. Toxicol. 1998, 10, 473–502. [Google Scholar] [CrossRef]
- Zhao, K.; Dalton, P.; Yang, G.C.; Scherer, P.W. Numerical Modeling of Turbulent and Laminar Airflow and Odorant Transport during Sniffing in the Human and Rat Nose. Chem. Senses 2006, 31, 107–118. [Google Scholar] [CrossRef]
- Rhee, J.S. Role of Virtual Surgery in Preoperative Planning: Assessing the Individual Components of Functional Nasal Airway Surgery. Arch. Facial Plast. Surg. 2012, 14, 354–359. [Google Scholar] [CrossRef]
- Hildebrandt, T.; Goubergrits, L.; Heppt, W.; Bessler, S.; Zachow, S. Evaluation of the Intranasal Flow Field through Computational Fluid Dynamics. Facial Plast. Surg. 2013, 29, 093–098. [Google Scholar] [CrossRef][Green Version]
- Zhu, J.H.; Lee, H.P.; Lim, K.M.; Lee, S.J.; Teo Li San, L.; Wang, D.Y. Inspirational Airflow Patterns in Deviated Noses: A Numerical Study. Comput. Methods Biomech. Biomed. Engin. 2013, 16, 1298–1306. [Google Scholar] [CrossRef]
- Cheng, G.C.; Koomullil, R.P.; Ito, Y.; Shih, A.M.; Sittitavornwong, S.; Waite, P.D. Assessment of Surgical Effects on Patients with Obstructive Sleep Apnea Syndrome Using Computational Fluid Dynamics Simulations. Math. Comput. Simul. 2014, 106, 44–59. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Garcia, G.J.M.; Hariri, B.M.; Patel, R.G.; Rhee, J.S. The Relationship between Nasal Resistance to Airflow and the Airspace Minimal Cross-Sectional Area. J. Biomech. 2016, 49, 1670–1678. [Google Scholar] [CrossRef] [PubMed]
- Inthavong, K.; Ma, J.; Shang, Y.; Dong, J.; Chetty, A.S.R.; Tu, J.; Frank-Ito, D. Geometry and Airflow Dynamics Analysis in the Nasal Cavity during Inhalation. Clin. Biomech. 2019, 66, 97–106. [Google Scholar] [CrossRef]
- Brüning, J.; Hildebrandt, T.; Heppt, W.; Schmidt, N.; Lamecker, H.; Szengel, A.; Amiridze, N.; Ramm, H.; Bindernagel, M.; Zachow, S.; et al. Characterization of the Airflow within an Average Geometry of the Healthy Human Nasal Cavity. Sci. Rep. 2020, 10, 3755. [Google Scholar] [CrossRef]
- Ormiskangas, J.; Valtonen, O.; Harju, T.; Rautiainen, M.; Kivekäs, I. Computational Fluid Dynamics Assessed Changes of Nasal Airflow after Inferior Turbinate Surgery. Respir. Physiol. Neurobiol. 2022, 302, 103917. [Google Scholar] [CrossRef]
- Siu, J.; Inthavong, K.; Dong, J.; Shang, Y.; Douglas, R.G. Nasal Air Conditioning Following Total Inferior Turbinectomy Compared to Inferior Turbinoplasty—A Computational Fluid Dynamics Study. Clin. Biomech. 2021, 81, 105237. [Google Scholar] [CrossRef]
- Corda, J.V.; Shenoy, B.S.; Ahmad, K.A.; Lewis, L.; Khader, S.M.A.; Zuber, M. Nasal Airflow Comparison in Neonates, Infant and Adult Nasal Cavities Using Computational Fluid Dynamics. Comput. Methods Programs Biomed. 2022, 214, 106538. [Google Scholar] [CrossRef]
- Mihaescu, M.; Murugappan, S.; Kalra, M.; Khosla, S.; Gutmark, E. Large Eddy Simulation and Reynolds-Averaged Navier–Stokes Modeling of Flow in a Realistic Pharyngeal Airway Model: An Investigation of Obstructive Sleep Apnea. J. Biomech. 2008, 41, 2279–2288. [Google Scholar] [CrossRef]
- Mihaescu, M.; Murugappan, S.; Gutmark, E.; Donnelly, L.F.; Kalra, M. Computational Modeling of Upper Airway Before and After Adenotonsillectomy for Obstructive Sleep Apnea. Laryngoscope 2008, 118, 360–362. [Google Scholar] [CrossRef]
- Ito, Y.; Cheng, G.C.; Shih, A.M.; Koomullil, R.P.; Soni, B.K.; Sittitavornwong, S.; Waite, P.D. Patient-Specific Geometry Modeling and Mesh Generation for Simulating Obstructive Sleep Apnea Syndrome Cases by Maxillomandibular Advancement. Math. Comput. Simul. 2011, 81, 1876–1891. [Google Scholar] [CrossRef][Green Version]
- De Backer, J.W.; Vanderveken, O.M.; Vos, W.G.; Devolder, A.; Verhulst, S.L.; Verbraecken, J.A.; Parizel, P.M.; Braem, M.J.; Van de Heyning, P.H.; De Backer, W.A. Functional Imaging Using Computational Fluid Dynamics to Predict Treatment Success of Mandibular Advancement Devices in Sleep-Disordered Breathing. J. Biomech. 2007, 40, 3708–3714. [Google Scholar] [CrossRef]
- Chen, X.B.; Lee, H.P.; Hin Chong, V.F.; Wang, D.Y. Assessment of Septal Deviation Effects on Nasal Air Flow: A Computational Fluid Dynamics Model. Laryngoscope 2009, 119, 1730–1736. [Google Scholar] [CrossRef]
- Gökcan, M.K.; Wanyonyi, S.N.; Kurtuluş, D.F. Computational Fluid Dynamics: Analysis of a Real Nasal Airway. In Challenges in Rhinology; Cingi, C., Bayar Muluk, N., Scadding, G.K., Mladina, R., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 501–517. ISBN 978-3-030-50898-2. [Google Scholar]
- Mylavarapu, G.; Mihaescu, M.; Fuchs, L.; Papatziamos, G.; Gutmark, E. Planning Human Upper Airway Surgery Using Computational Fluid Dynamics. J. Biomech. 2013, 46, 1979–1986. [Google Scholar] [CrossRef]
- Karbowski, K.; Kopiczak, B.; Chrzan, R.; Gawlik, J.; Szaleniec, J. Accuracy of Virtual Rhinomanometry. Pol. J. Med. Phys. Eng. 2023, 29, 59–72. [Google Scholar] [CrossRef]
- Faizal, W.M.; Khor, C.Y.; Yaakob, M.N.C.; Ghazali, N.N.N.; Zainon, M.Z.; Ibrahim, N.B.; Razi, R.M. Turbulent Kinetic Energy of Flow during Inhale and Exhale to Characterize the Severity of Obstructive Sleep Apnea Patient. Comput. Model. Eng. Sci. 2023, 136, 43–61. [Google Scholar] [CrossRef]
- Wakayama, T.; Suzuki, M.; Tanuma, T. Effect of Nasal Obstruction on Continuous Positive Airway Pressure Treatment: Computational Fluid Dynamics Analyses. PLoS ONE 2016, 11, e0150951. [Google Scholar] [CrossRef]
- Ghahramani, E.; Abouali, O.; Emdad, H.; Ahmadi, G. Numerical Investigation of Turbulent Airflow and Microparticle Deposition in a Realistic Model of Human Upper Airway Using LES. Comput. Fluids 2017, 157, 43–54. [Google Scholar] [CrossRef]
- Lu, M.Z.; Liu, Y.; Ye, J.Y.; Luo, H.Y. Large Eddy Simulation of Flow in Realistic Human Upper Airways with Obstructive Sleep. Procedia Comput. Sci. 2014, 29, 557–564. [Google Scholar] [CrossRef][Green Version]
- Calmet, H.; Gambaruto, A.M.; Bates, A.J.; Vázquez, M.; Houzeaux, G.; Doorly, D.J. Large-Scale CFD Simulations of the Transitional and Turbulent Regime for the Large Human Airways during Rapid Inhalation. Comput. Biol. Med. 2016, 69, 166–180. [Google Scholar] [CrossRef] [PubMed]
- Calmet, H.; Inthavong, K.; Owen, H.; Dosimont, D.; Lehmkuhl, O.; Houzeaux, G.; Vázquez, M. Computational Modelling of Nasal Respiratory Flow. Comput. Methods Biomech. Biomed. Engin. 2021, 24, 440–458. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Elghobashi, S. On Locating the Obstruction in the Upper Airway via Numerical Simulation. Respir. Physiol. Neurobiol. 2014, 193, 1–10. [Google Scholar] [CrossRef]
- Lintermann, A.; Meinke, M.; Schröder, W. Fluid Mechanics Based Classification of the Respiratory Efficiency of Several Nasal Cavities. Comput. Biol. Med. 2013, 43, 1833–1852. [Google Scholar] [CrossRef]
- Aljawad, H.; Rüttgers, M.; Lintermann, A.; Schröder, W.; Lee, K.C. Effects of the Nasal Cavity Complexity on the Pharyngeal Airway Fluid Mechanics: A Computational Study. J. Digit. Imaging 2021, 34, 1120–1133. [Google Scholar] [CrossRef]
- Otopront. Available online: https://www.otopront.de (accessed on 1 January 2024).
- Yushkevich, P.A.; Piven, J.; Hazlett, H.C.; Smith, R.G.; Ho, S.; Gee, J.C.; Gerig, G. User-Guided 3D Active Contour Segmentation of Anatomical Structures: Significantly Improved Efficiency and Reliability. NeuroImage 2006, 31, 1116–1128. [Google Scholar] [CrossRef]
- ANSYS. Available online: https://www.ansys.com (accessed on 1 January 2024).
- ANSYS. ANSYS Fluent User’s Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A New K-ϵ Eddy Viscosity Model for High Reynolds Number Turbulent Flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Weickert, M.; Teike, G.; Schmidt, O.; Sommerfeld, M. Investigation of the LES WALE Turbulence Model within the Lattice Boltzmann Framework. Comput. Math. Appl. 2010, 59, 2200–2214. [Google Scholar] [CrossRef]
- Patton, K.T.; Thibodeau, G.A. Anatomy & Physiology, 8th ed.; Mosby/Elsevier: St. Louis, MO, USA, 2013; ISBN 978-0-323-08357-7. [Google Scholar]
- Yeung, P.K.; Sreenivasan, K.R.; Pope, S.B. Effects of Finite Spatial and Temporal Resolution in Direct Numerical Simulations of Incompressible Isotropic Turbulence. Phys. Rev. Fluids 2018, 3, 064603. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds Numbers. Proc. R. Soc. Lond. 1991, 434, 9–13. [Google Scholar] [CrossRef]
- Rubinstein, R.; Clark, T.T. “Equilibrium” and “Non-Equilibrium” Turbulence. Theor. Appl. Mech. Lett. 2017, 7, 301–305. [Google Scholar] [CrossRef]
- De Bonilla, J.S.-D.; McCaffrey, T.V.; Kern, E.B. The Nasal Valve: A Rhinomanometric Evaluation of Maximum Nasal Inspiratory Flow and Pressure Curves. Ann. Otol. Rhinol. Laryngol. 1986, 95, 229–232. [Google Scholar] [CrossRef] [PubMed]
- Schumacher, M.J. Nasal Dyspnea: The Place of Rhinomanometry in Its Objective Assessment. Am. J. Rhinol. 2004, 18, 41–46. [Google Scholar] [CrossRef] [PubMed]
- Haghnegahdar, A.; Bharadwaj, R.; Feng, Y. Exploring the Role of Nasal Hair in Inhaled Airflow and Coarse Dust Particle Dynamics in a Nasal Cavity: A CFD-DEM Study. Powder Technol. 2023, 427, 118710. [Google Scholar] [CrossRef]
- OSASMOD. PI: Müller, B. Grant Title: Modeling of Obstructive Sleep Apnea by Fluid-Structure Interaction in the Upper Airways. Grant Number: 231741. Funding Body: The Research Council of Norway. Start-End Dates: 2014–2018. 2014. Available online: https://prosjektbanken.forskningsradet.no/project/FORISS/231741 (accessed on 1 January 2024).
- VIRTUOSA. PI: Skallerud, B.H. Grant Title: Virtual Surgery in the Upper Airways—New Solutions to Obstructive Sleep Apnea Treatment. Grant Number: 303218. Funding Body: The Research Council of Norway. Start-End Dates: 2020–2024. 2020. Available online: https://prosjektbanken.forskningsradet.no/project/FORISS/303218 (accessed on 1 January 2024).
- SINTEF. Available online: http://www.sintef.no (accessed on 1 January 2024).
- Sigma2—The National Infrastructure for High Performance Computing and Data Storage in Norway. Available online: https://www.sigma2.no (accessed on 1 January 2024).
- Norwegian Research Infrastructure Services (NRIS). NIRD Research Data Archive. Available online: https://archive.sigma2.no/ (accessed on 1 January 2024).
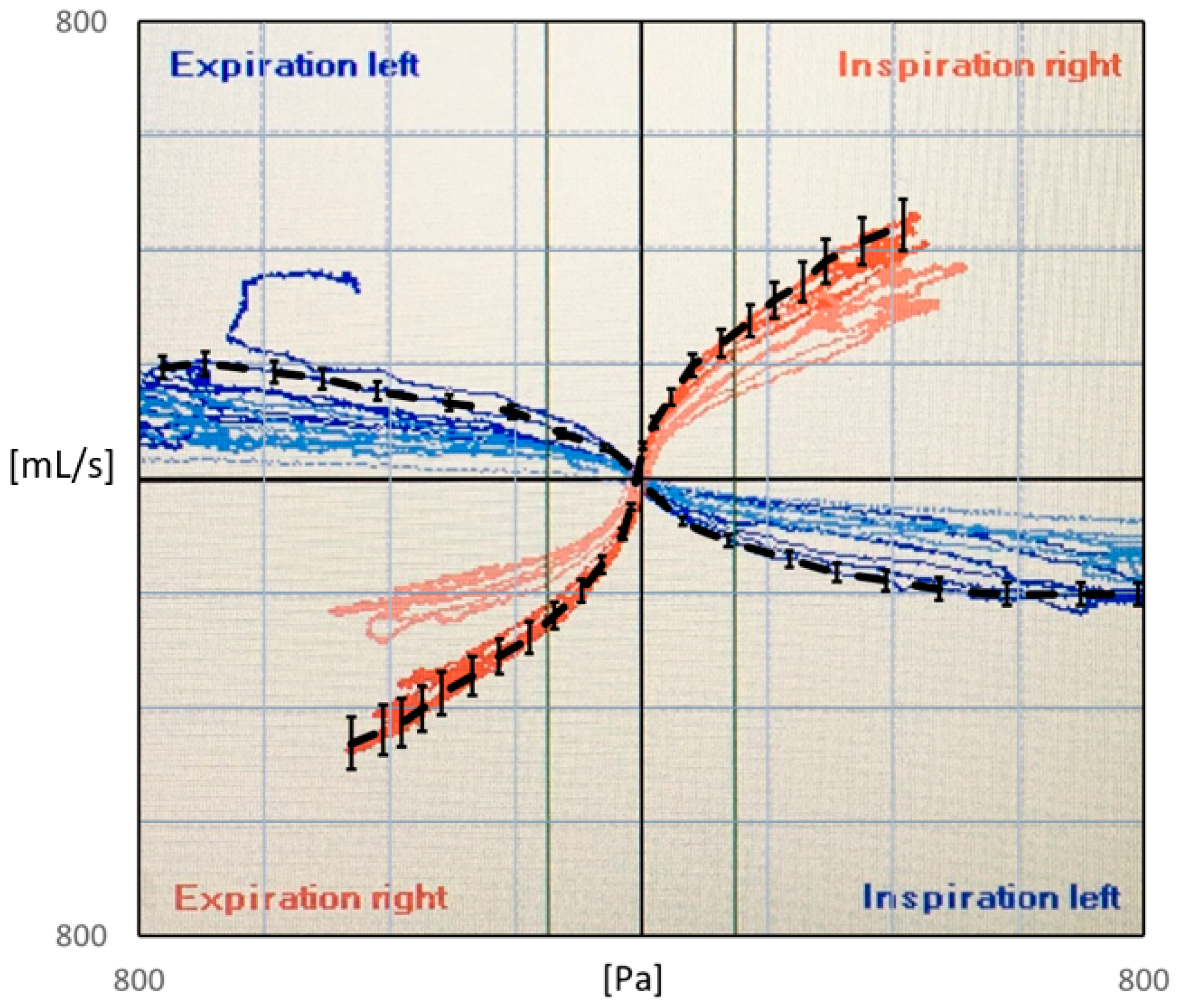
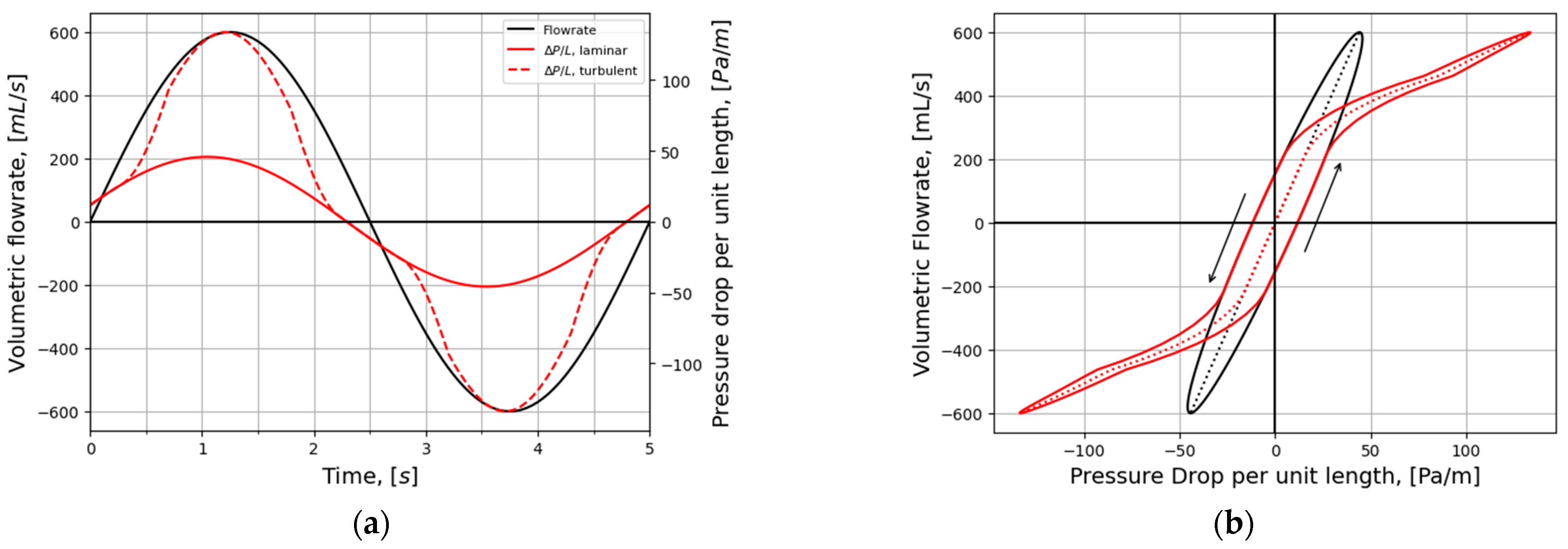
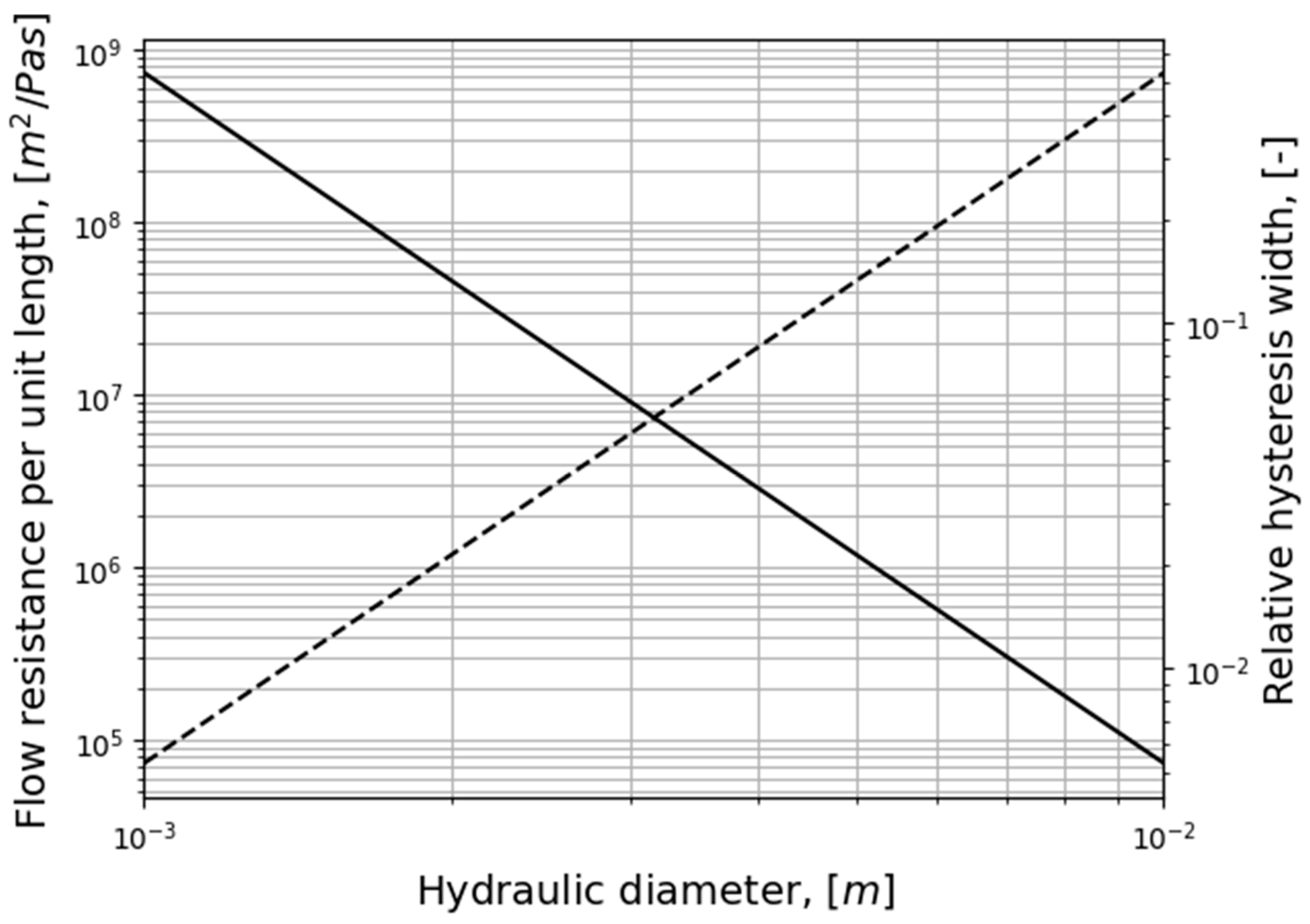
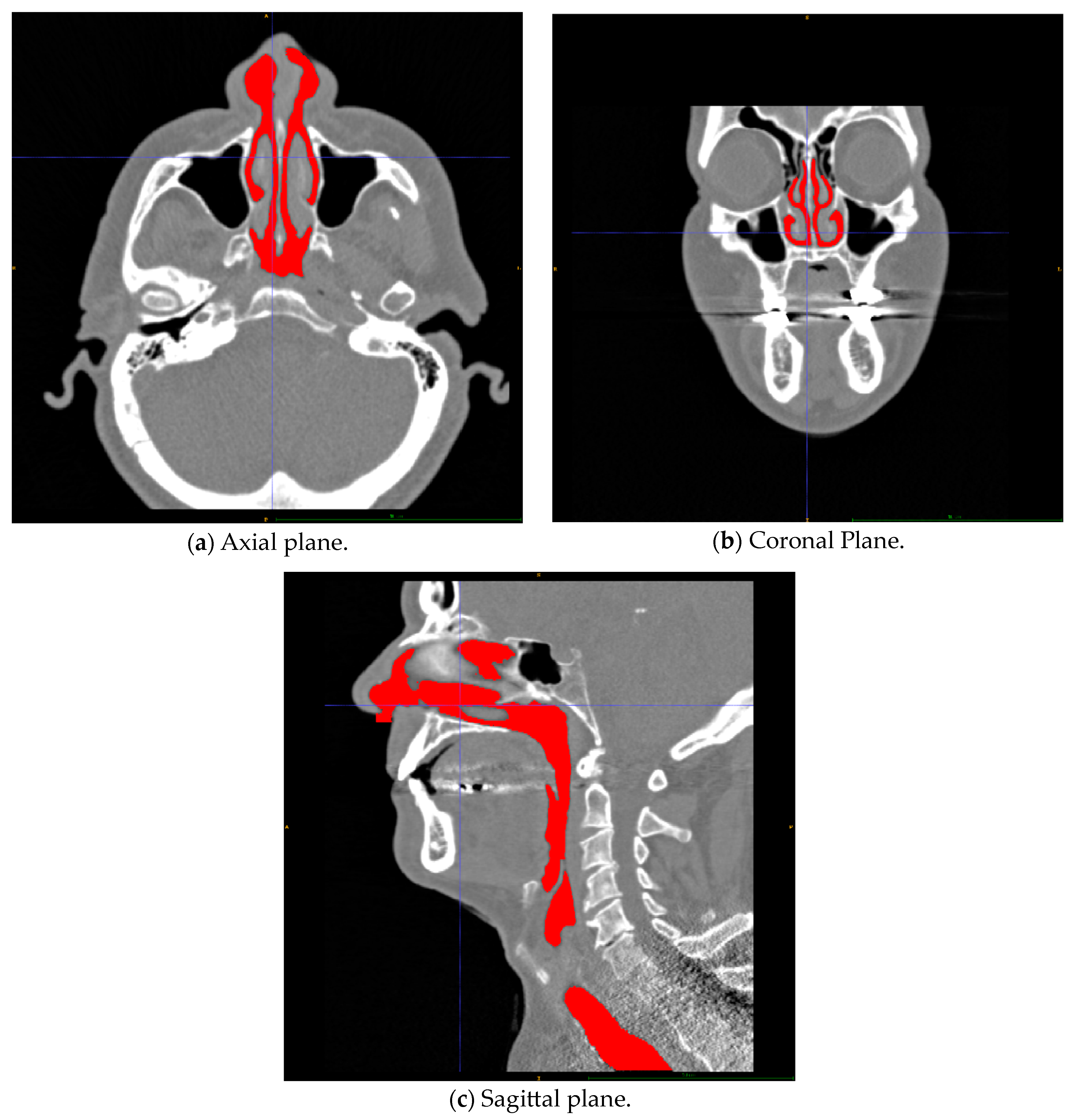
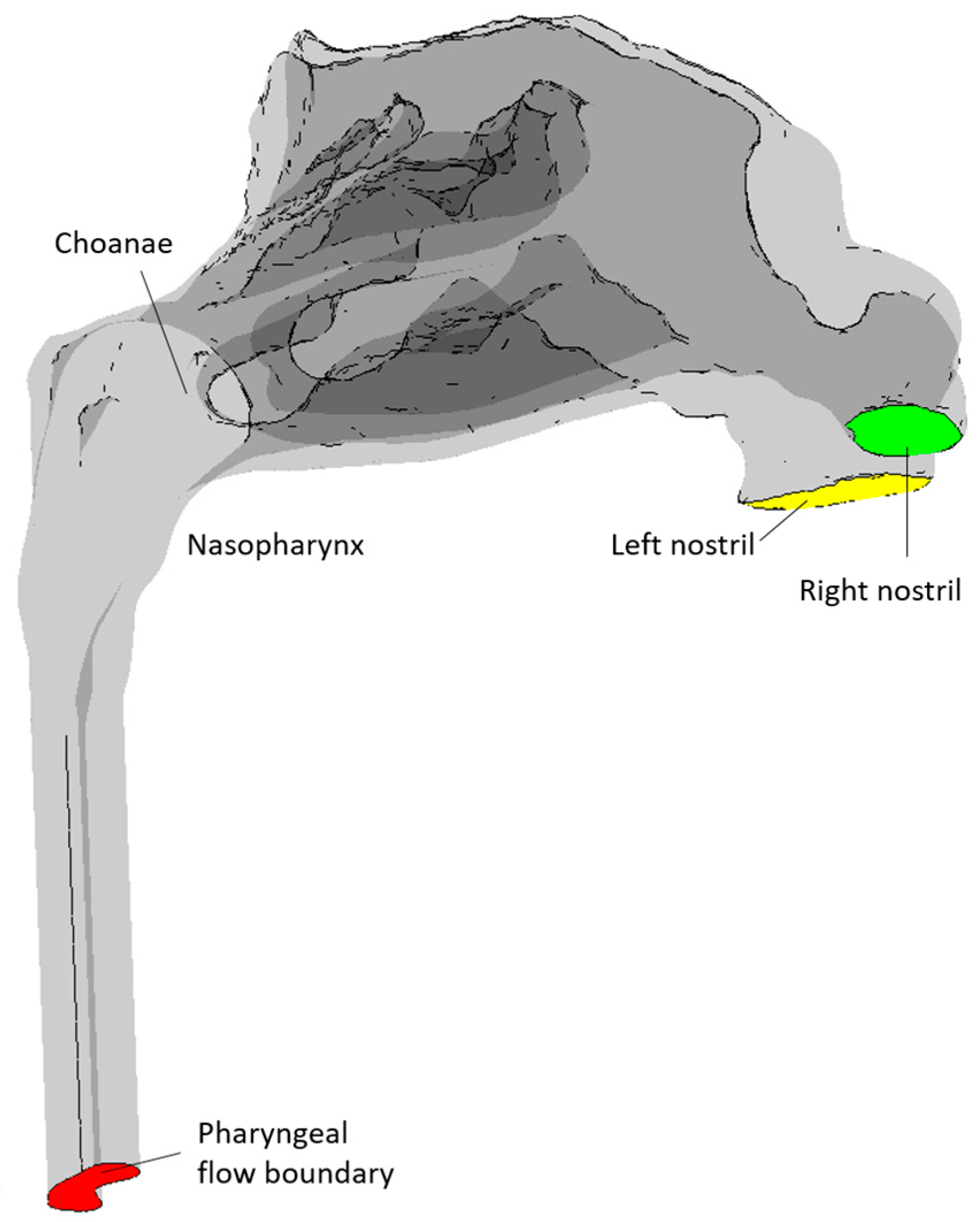
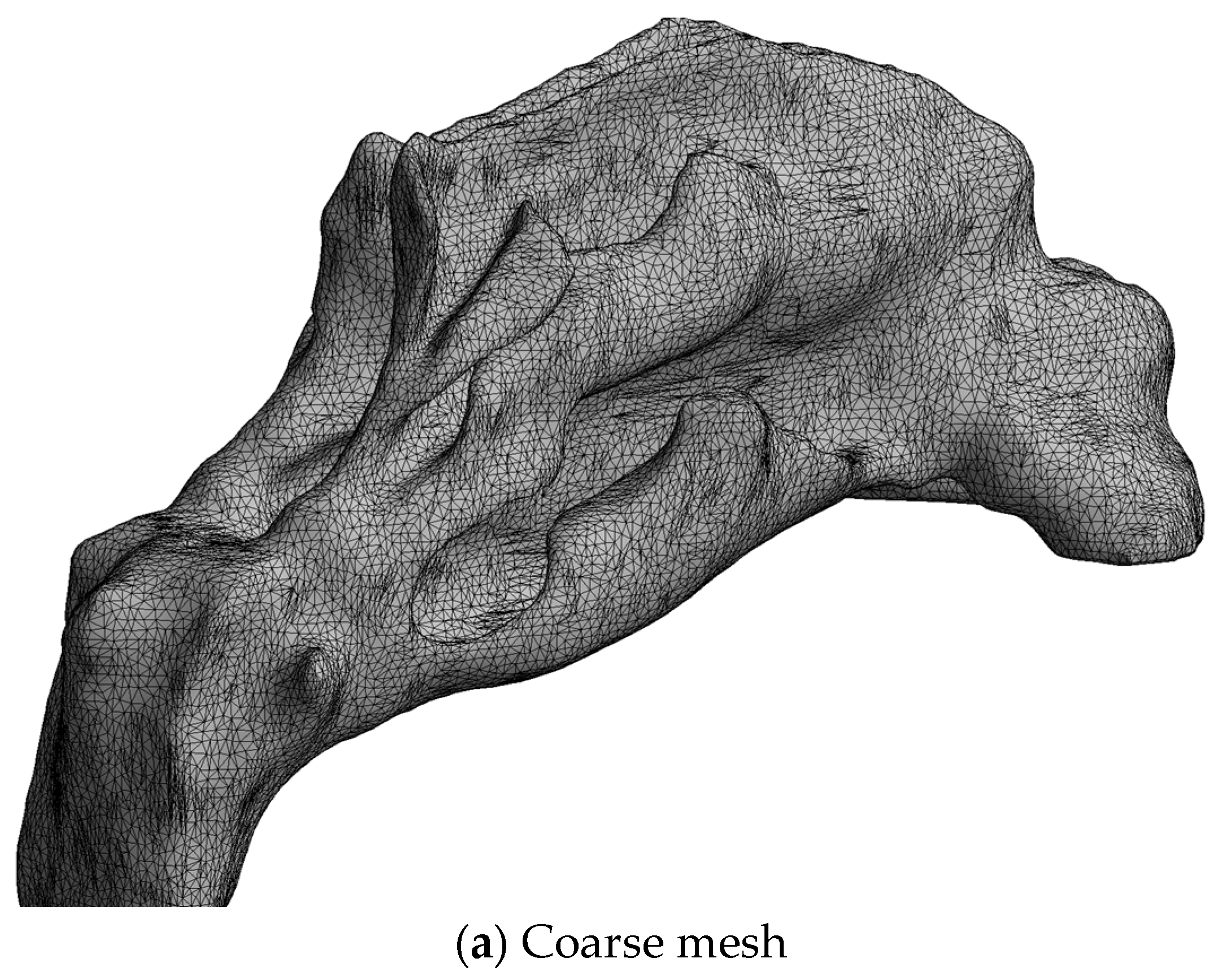


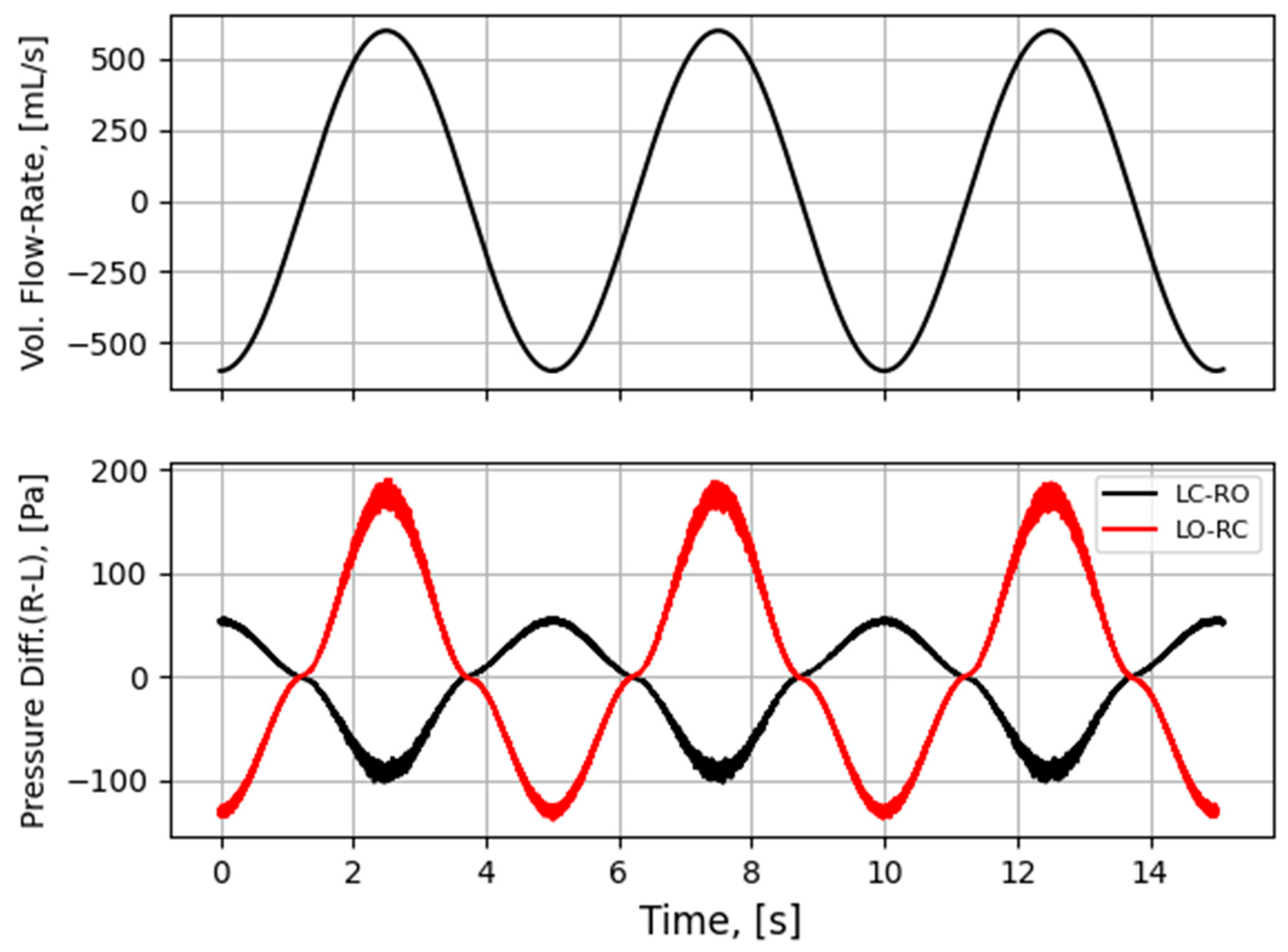




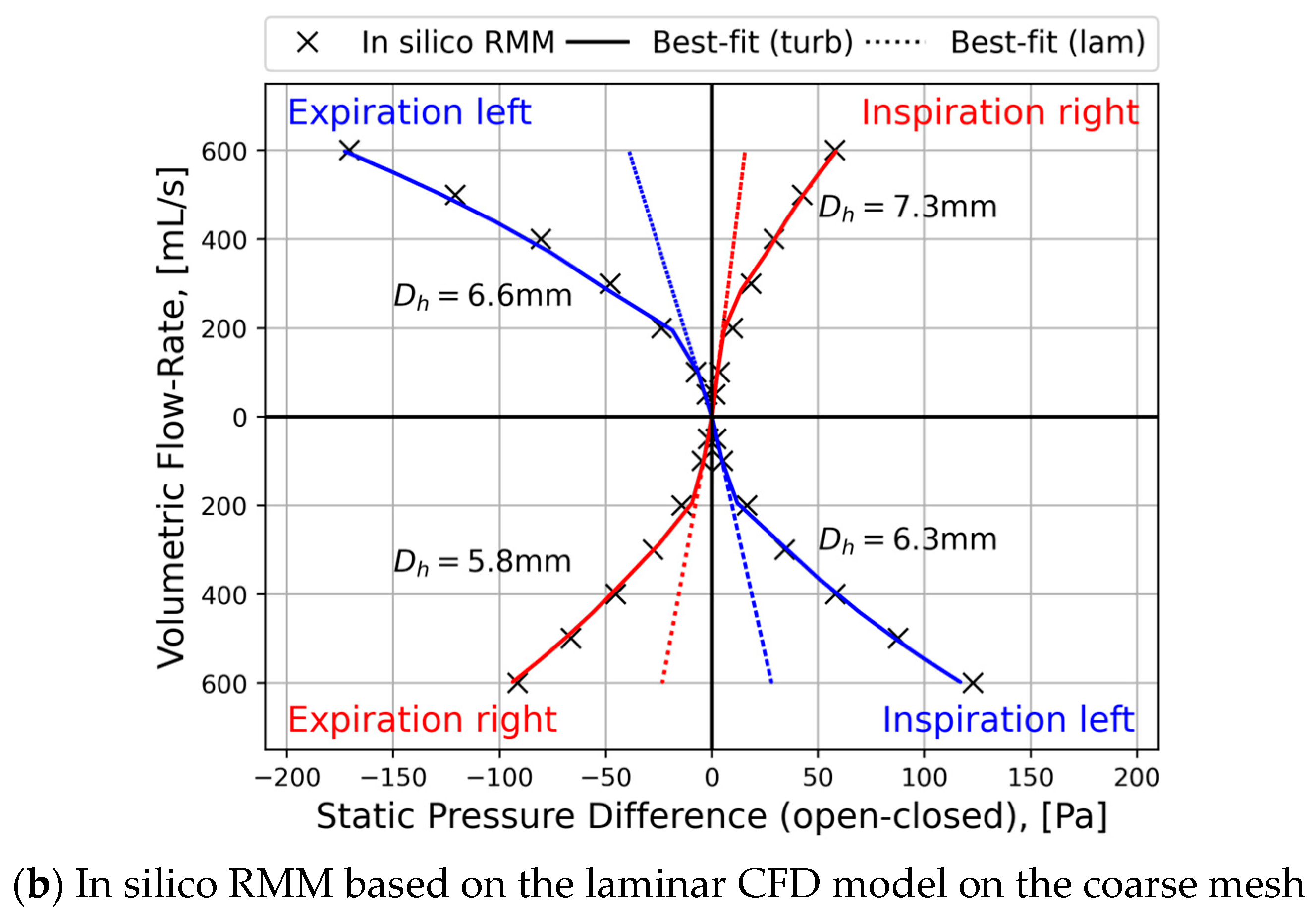



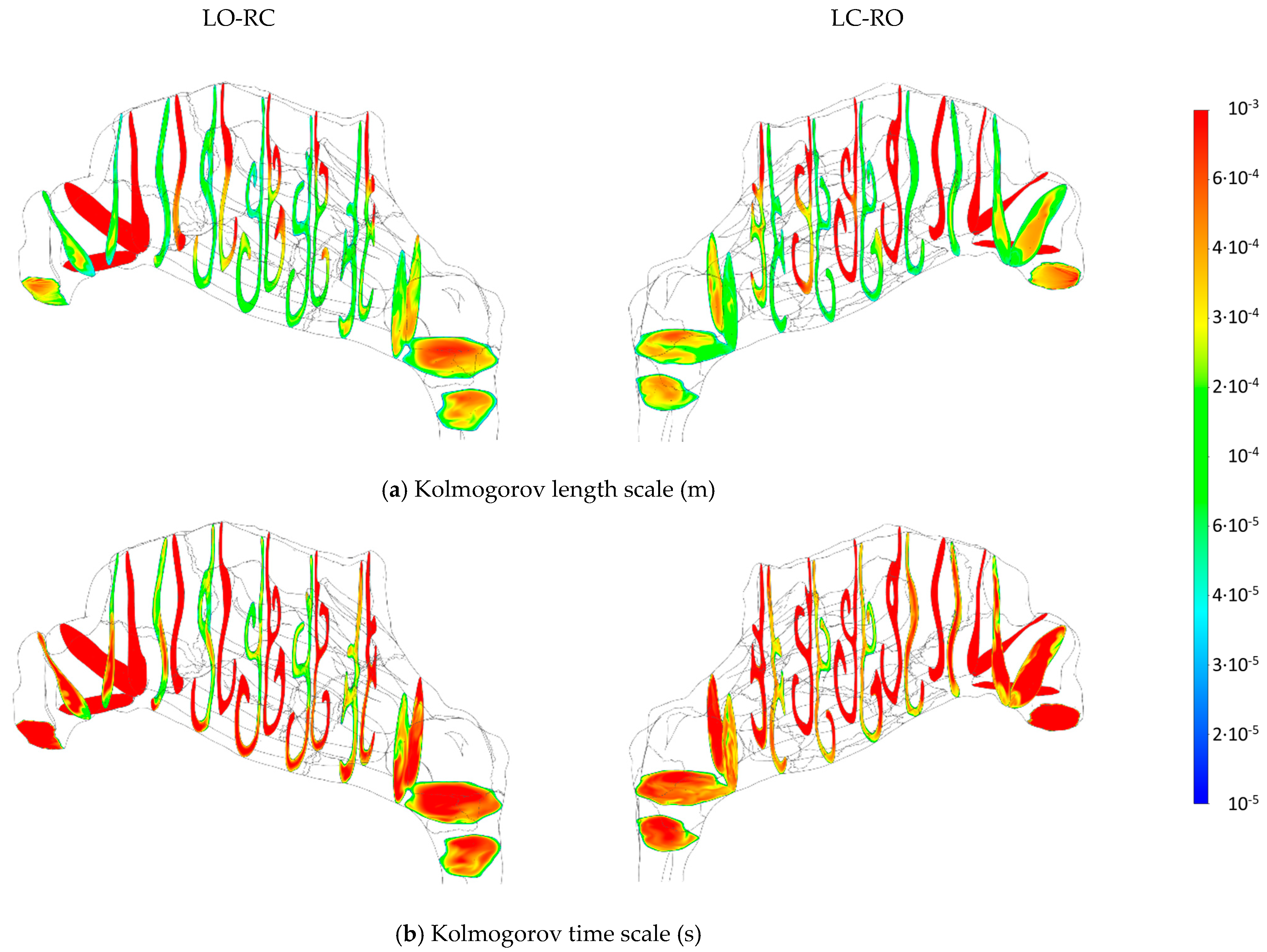
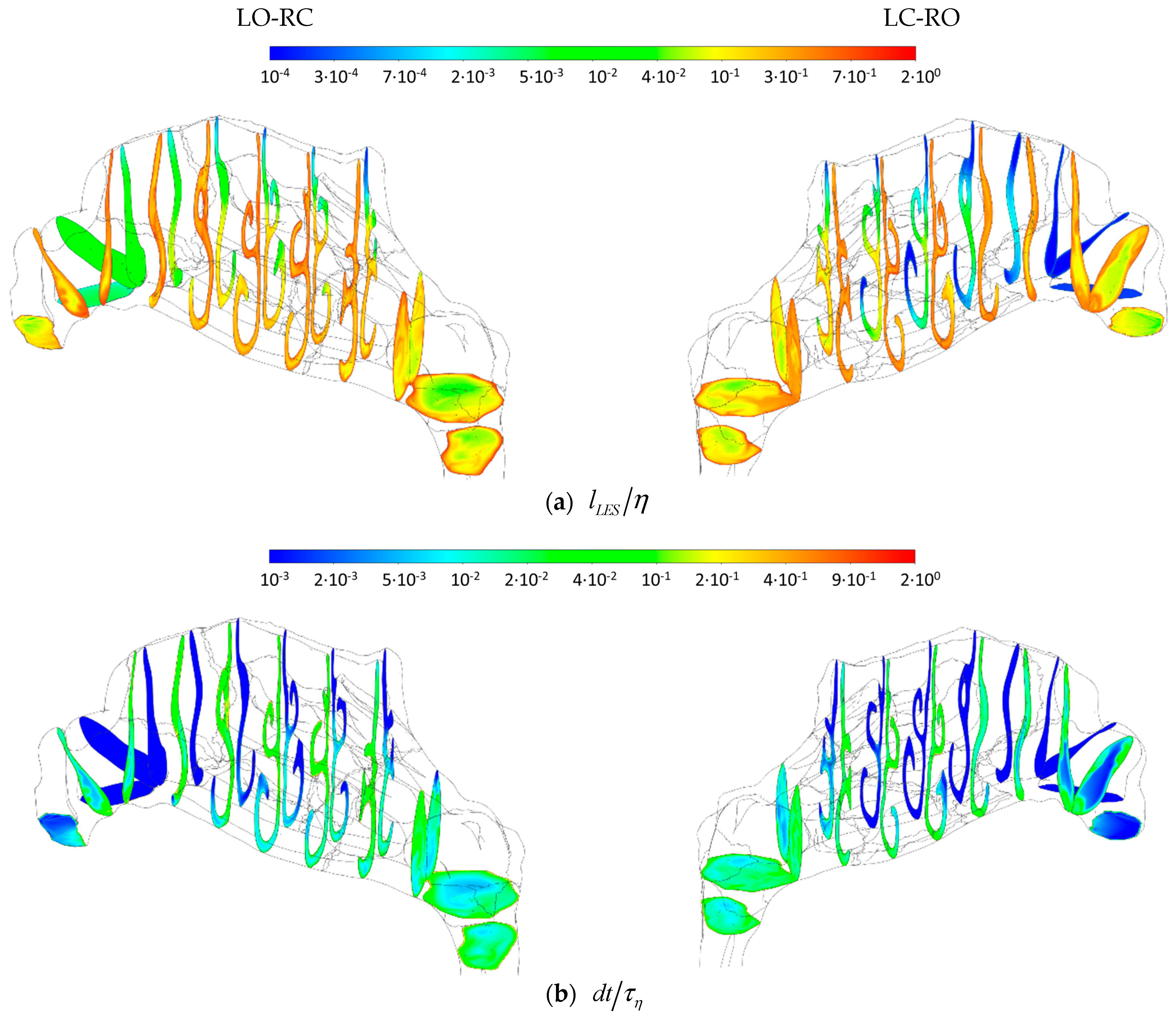

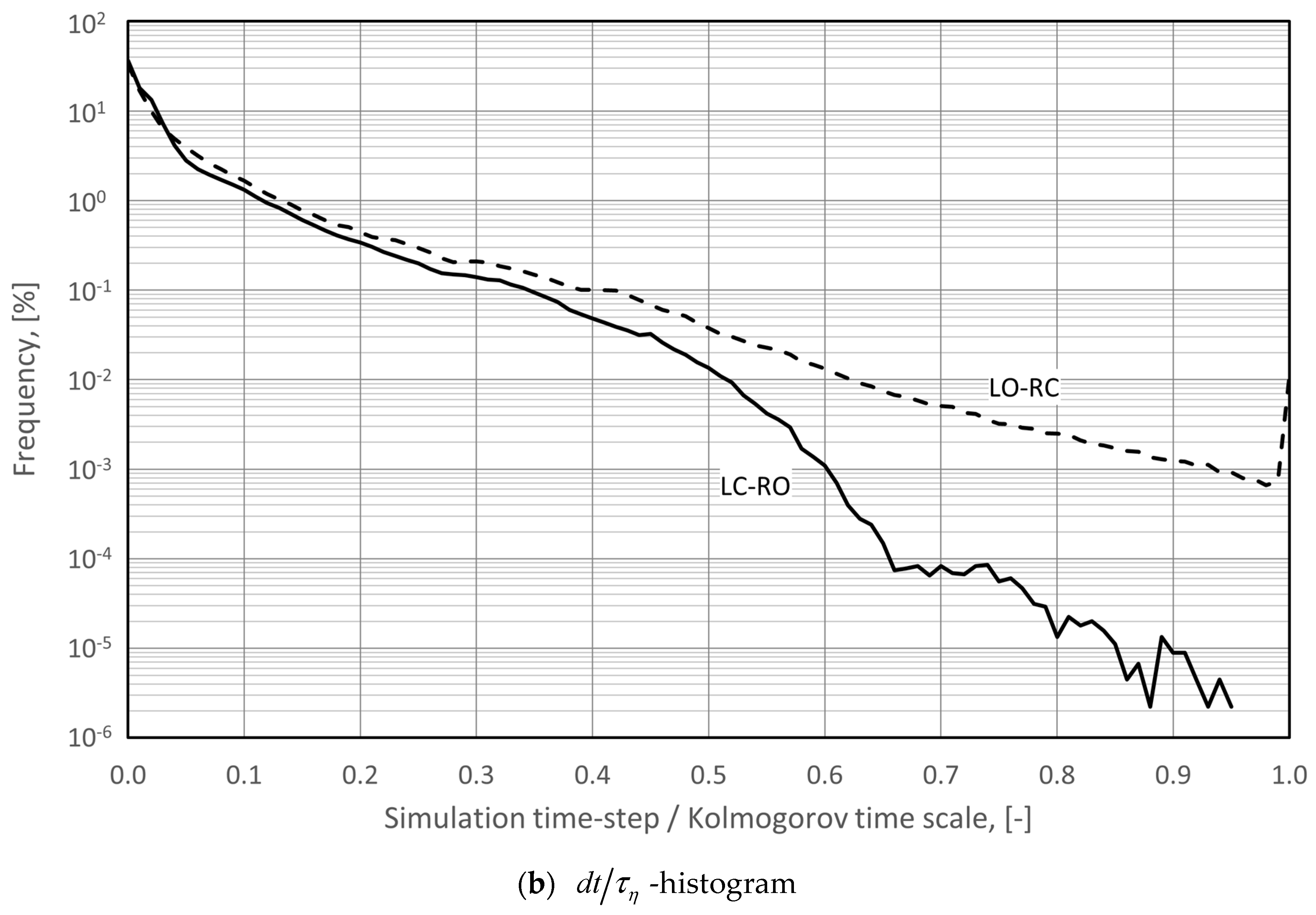
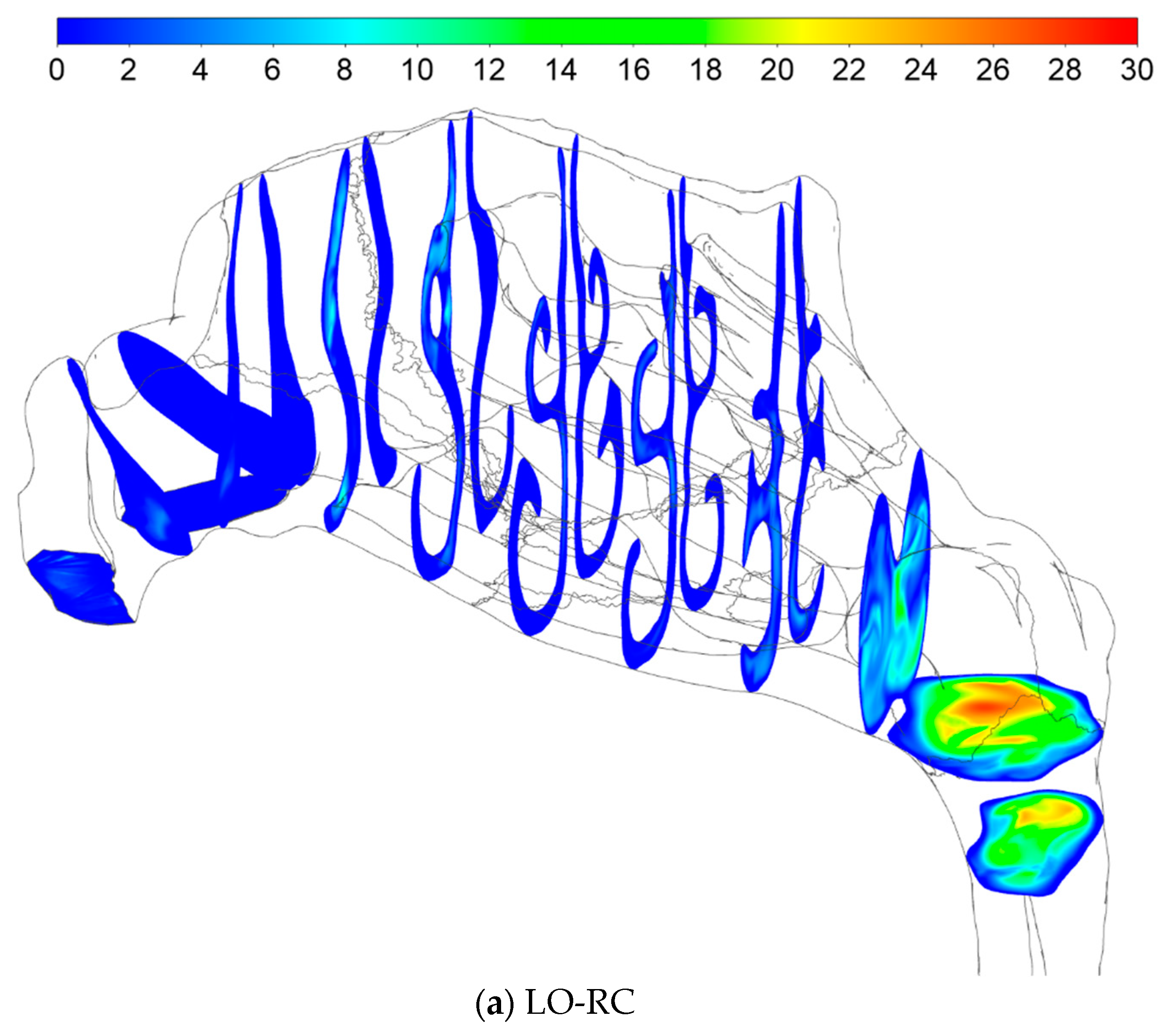
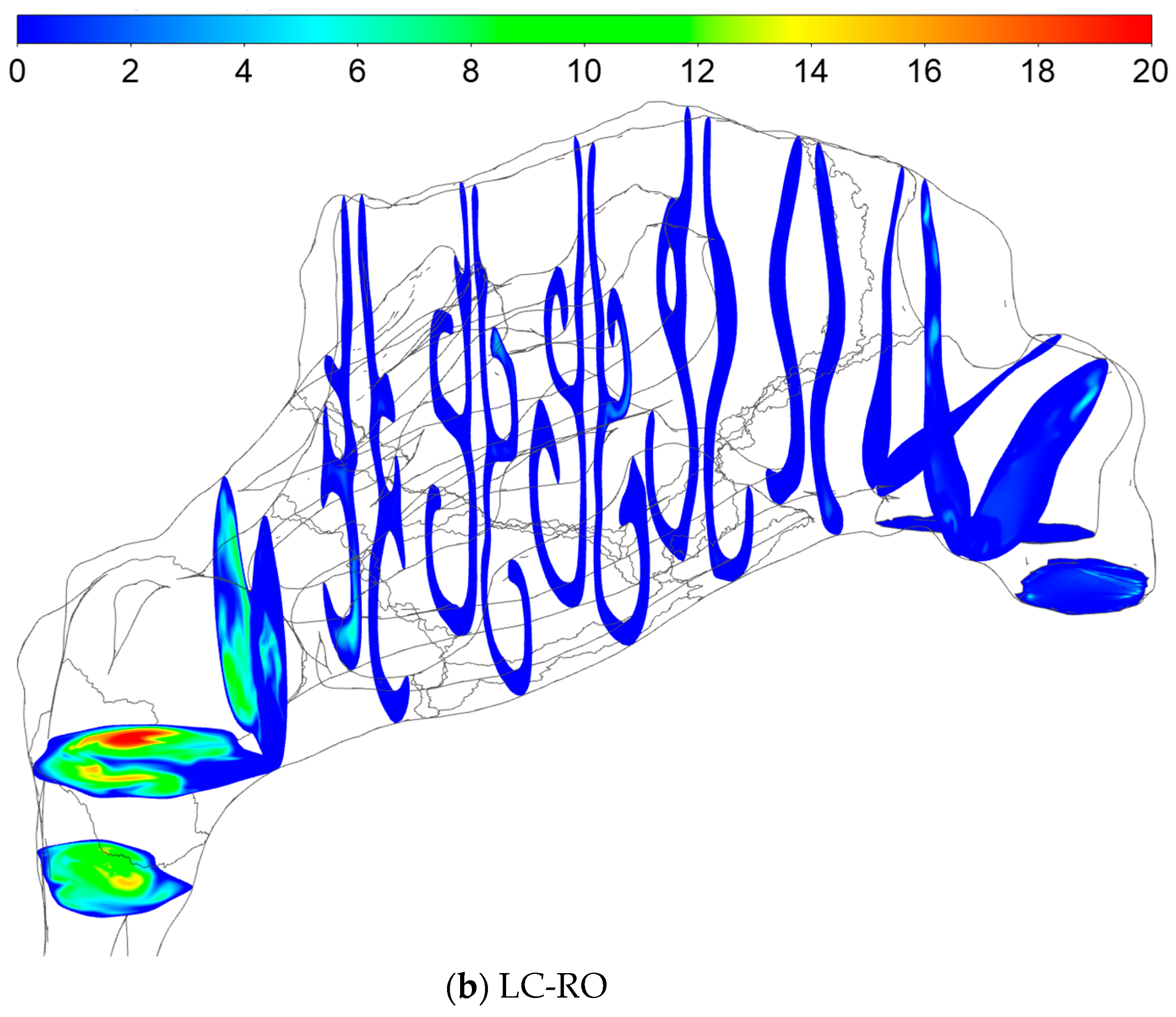
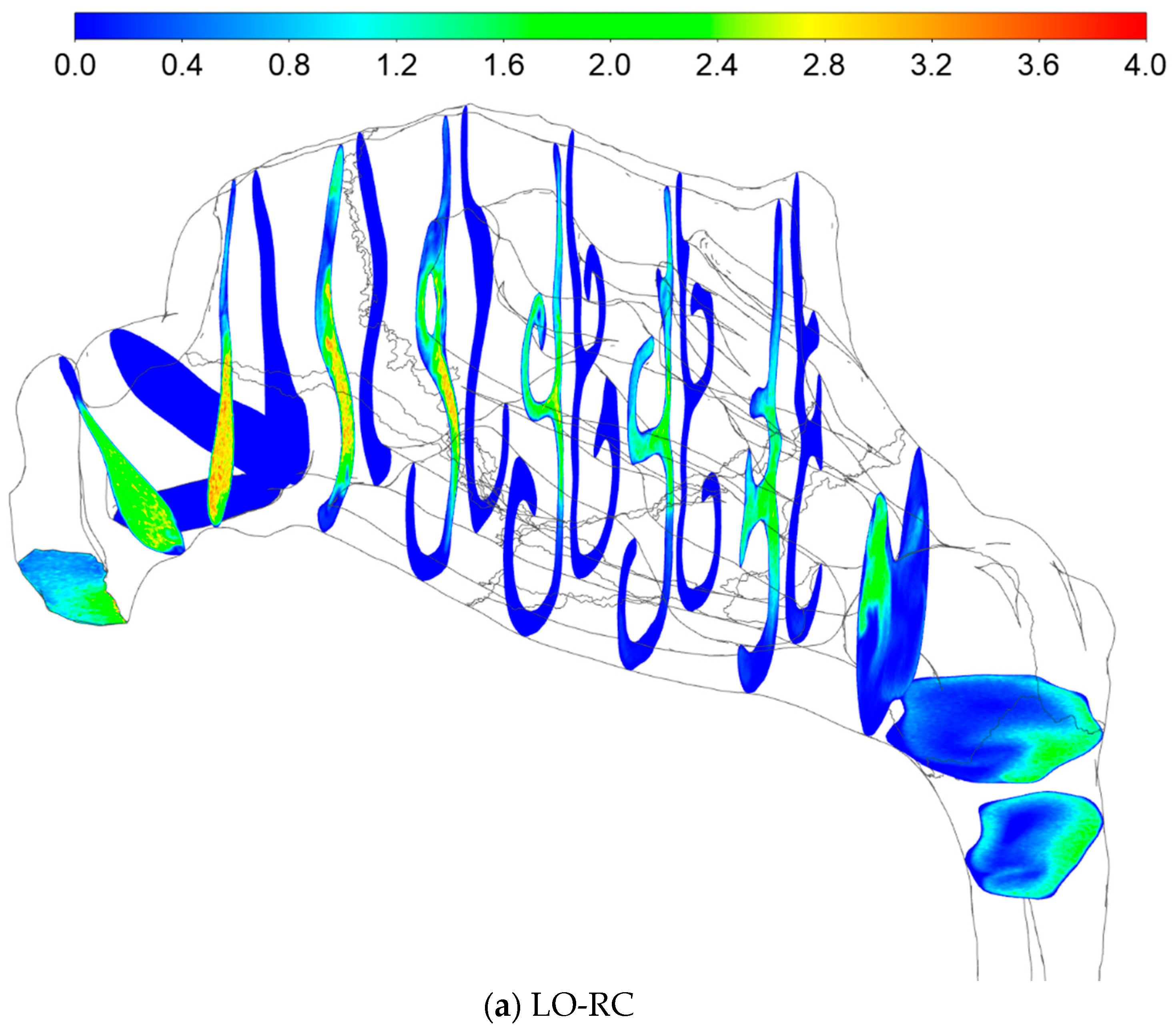

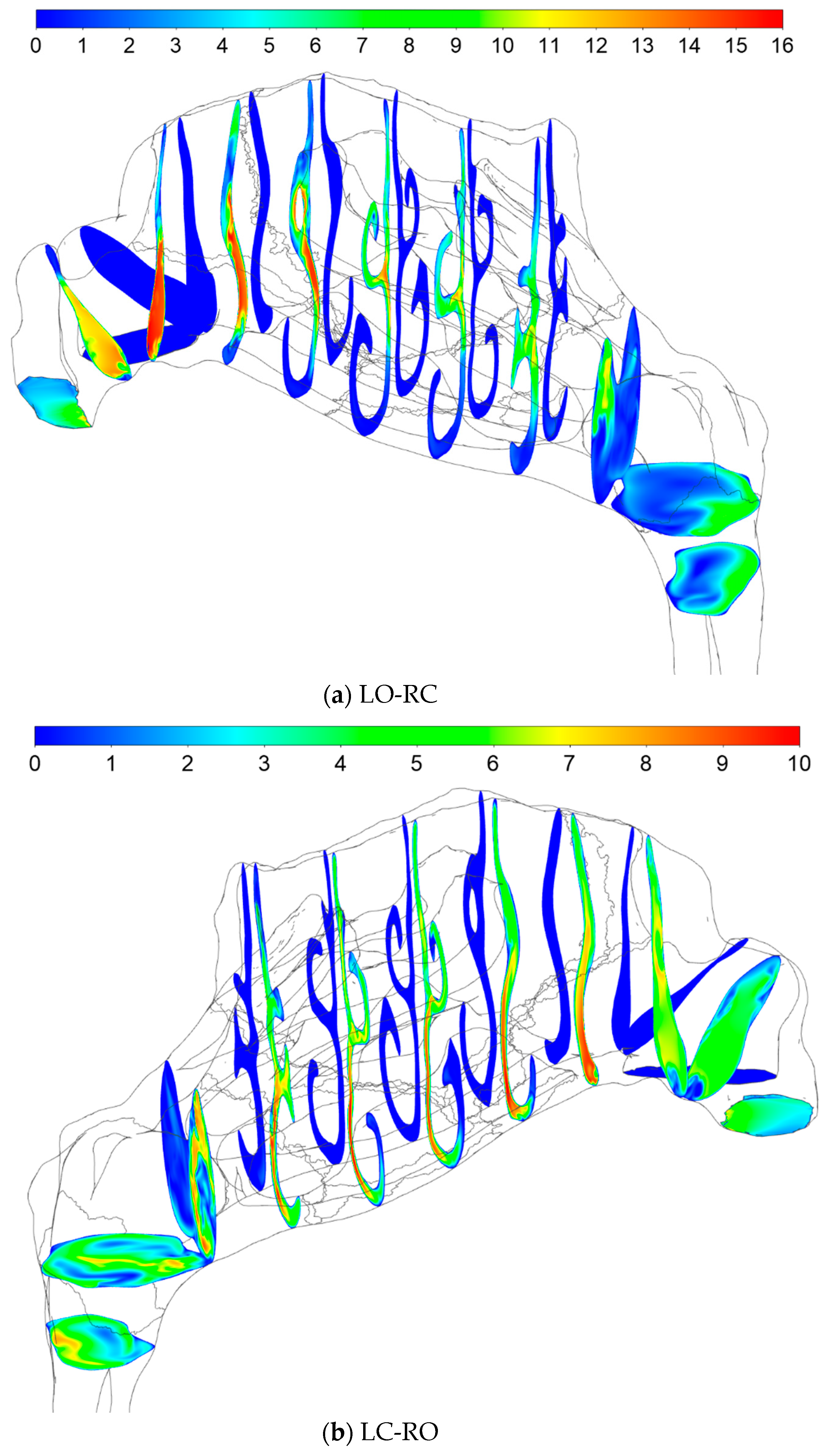




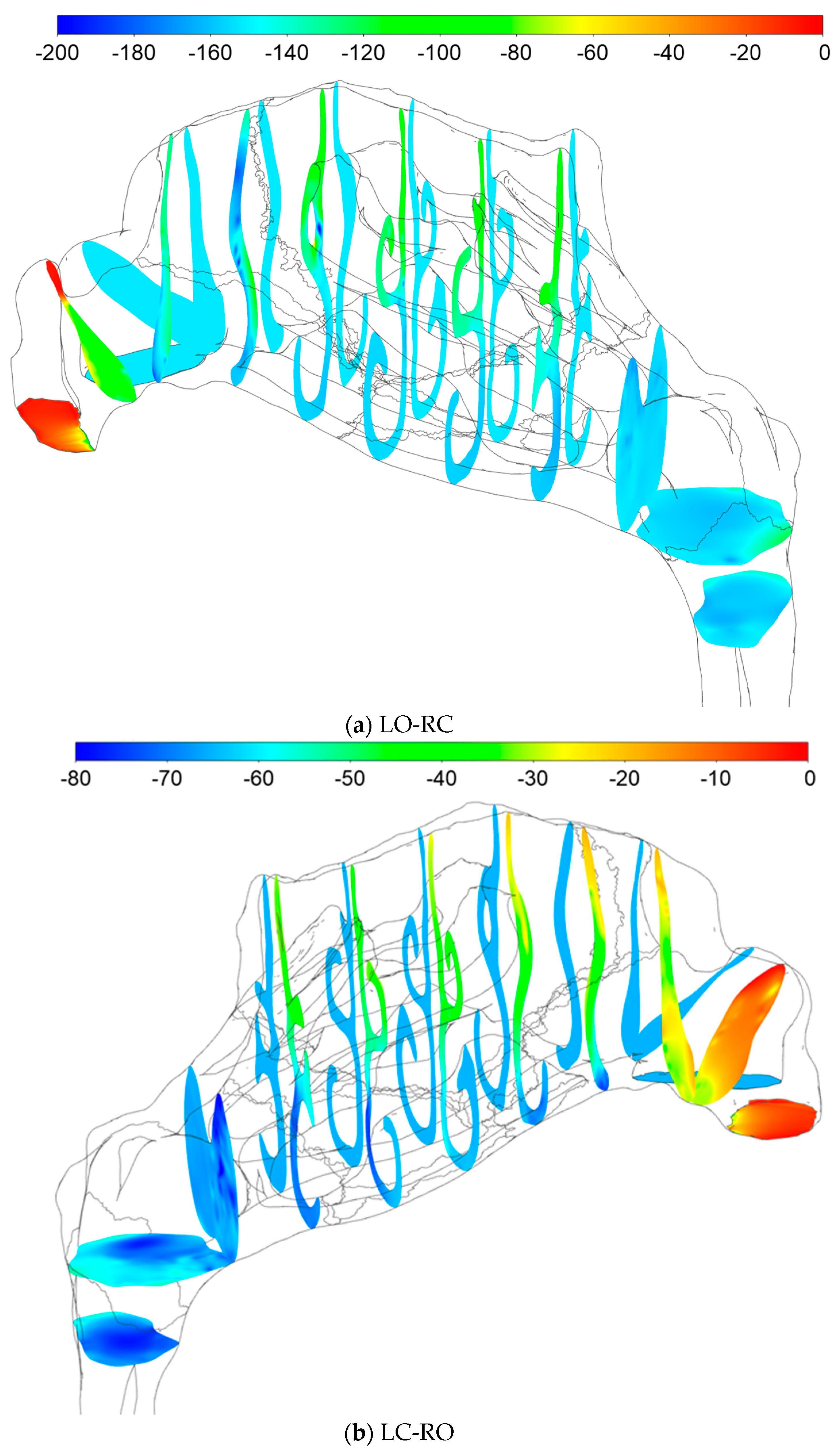
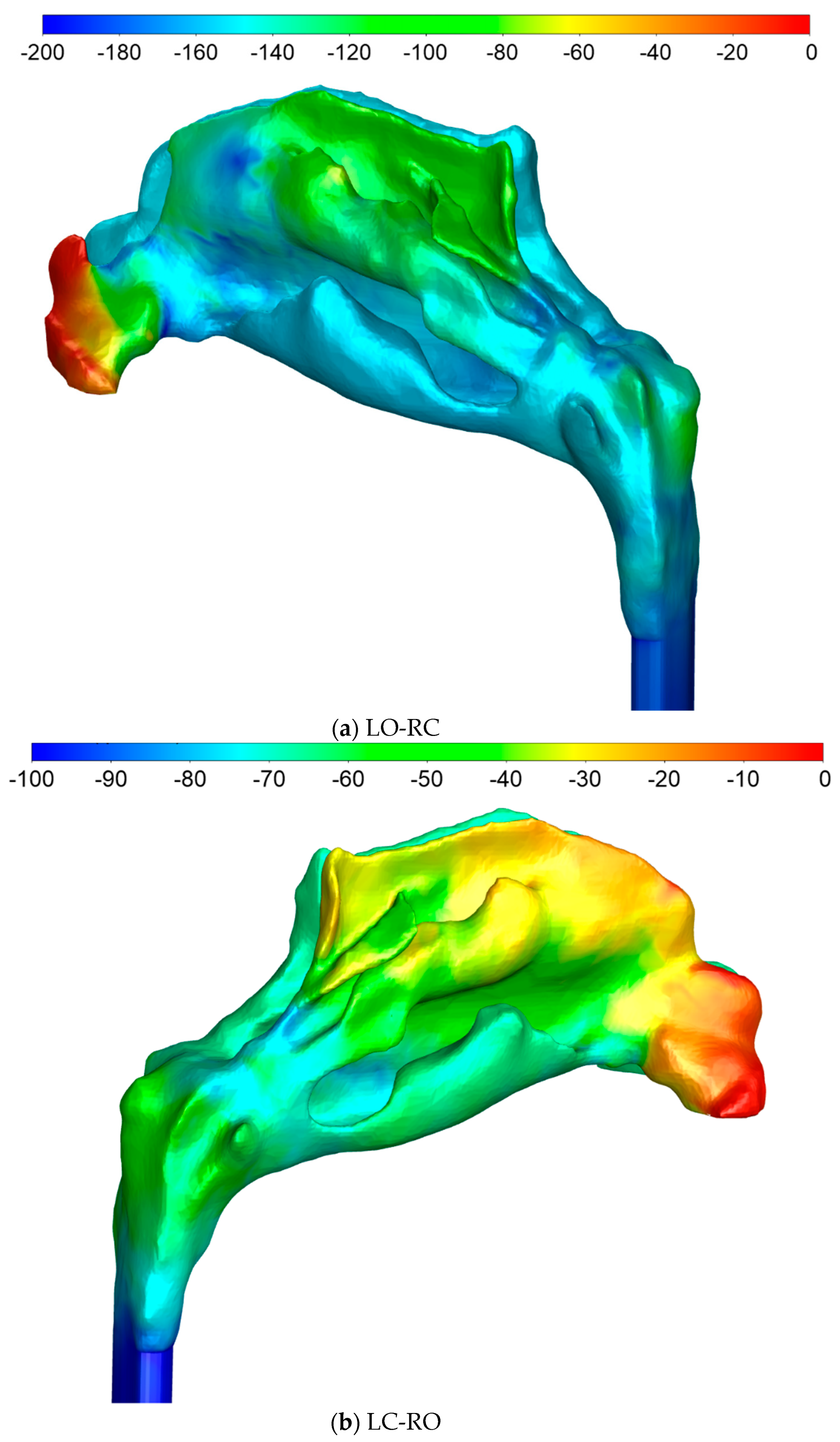
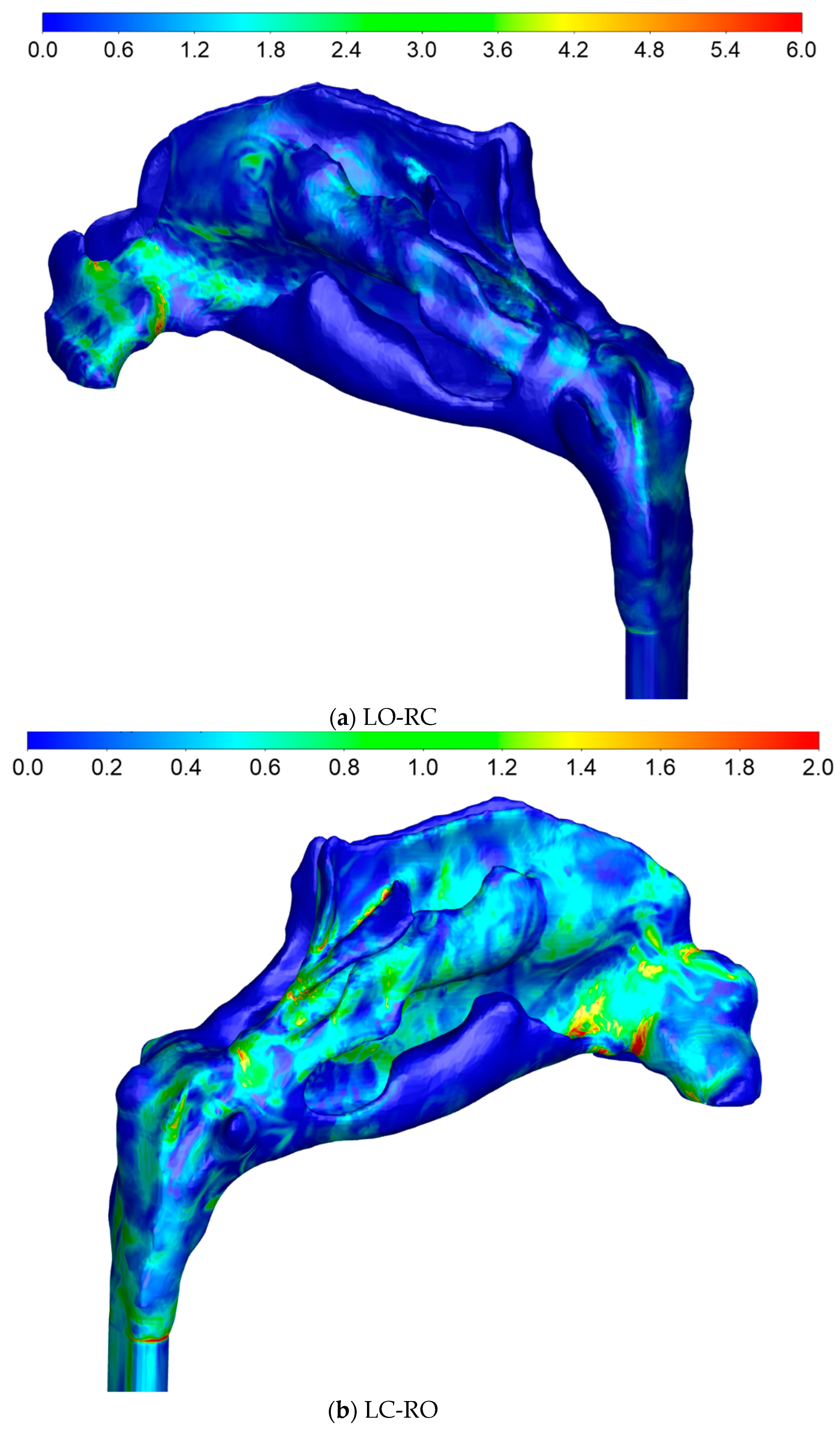
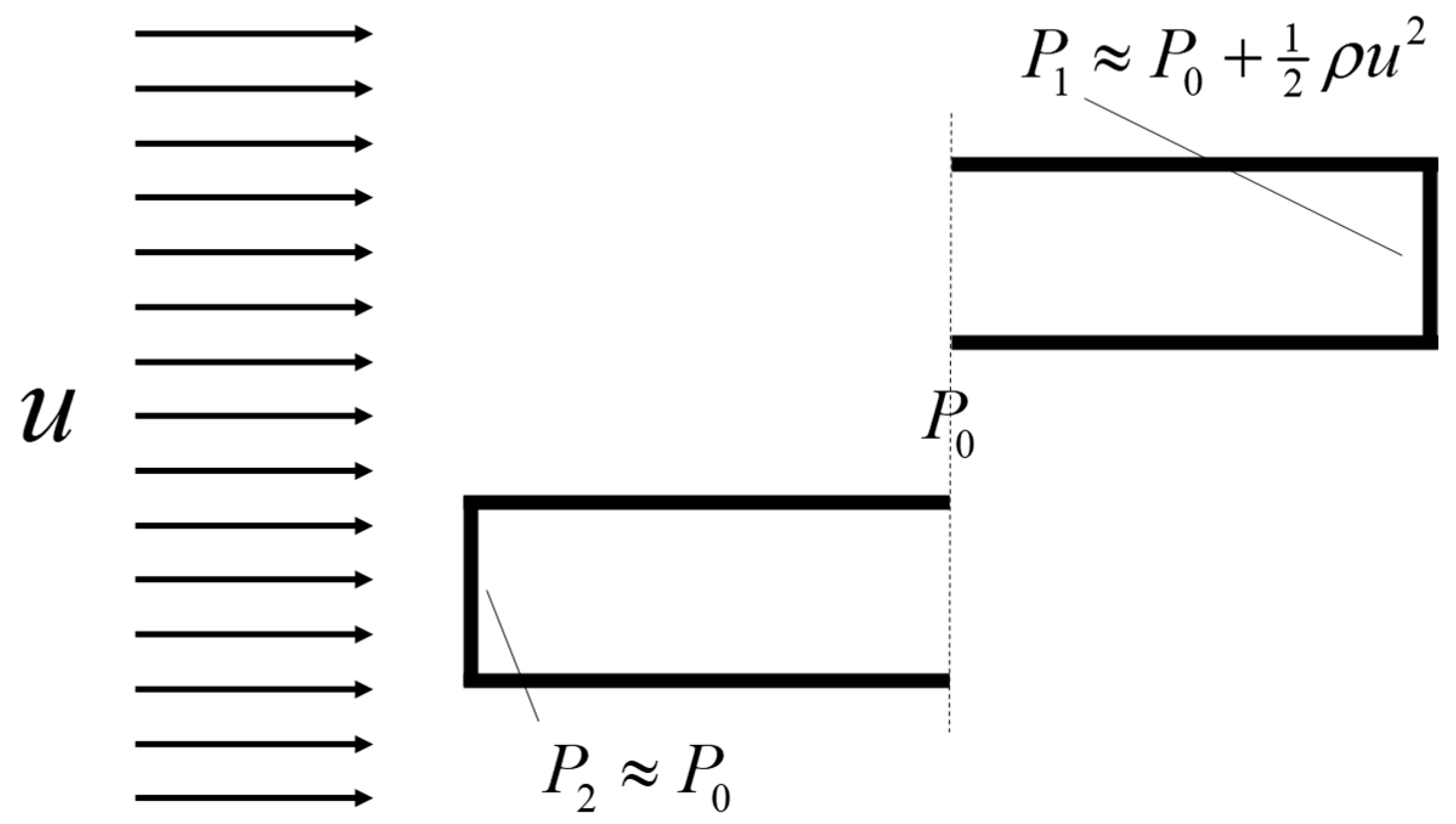
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johnsen, S.G. Computational Rhinology: Unraveling Discrepancies between In Silico and In Vivo Nasal Airflow Assessments for Enhanced Clinical Decision Support. Bioengineering 2024, 11, 239. https://doi.org/10.3390/bioengineering11030239
Johnsen SG. Computational Rhinology: Unraveling Discrepancies between In Silico and In Vivo Nasal Airflow Assessments for Enhanced Clinical Decision Support. Bioengineering. 2024; 11(3):239. https://doi.org/10.3390/bioengineering11030239
Chicago/Turabian StyleJohnsen, Sverre Gullikstad. 2024. "Computational Rhinology: Unraveling Discrepancies between In Silico and In Vivo Nasal Airflow Assessments for Enhanced Clinical Decision Support" Bioengineering 11, no. 3: 239. https://doi.org/10.3390/bioengineering11030239
APA StyleJohnsen, S. G. (2024). Computational Rhinology: Unraveling Discrepancies between In Silico and In Vivo Nasal Airflow Assessments for Enhanced Clinical Decision Support. Bioengineering, 11(3), 239. https://doi.org/10.3390/bioengineering11030239





